Chemical reaction optimization (CRO) algorithm (Part II): Assembling and results

Contents

1. Introduction
2. Implementation of the algorithm
3. Test results

1. Introduction

In the second part of our article, we continue our dive into the fascinating world of chemical reaction optimization (CRO). Based on the concept of "molecules" and "elementary reactions", we familiarized ourselves with the underlying algorithm principles and considered how these concepts are applied to solve complex optimization problems. We also learned about the key points of energy conservation within CRO and the algorithm functions, such as decomposition, synthesis, intramolecular and intermolecular inefficient collisions, which play a major role in exploring the search space and finding optimal solutions.

Now that we have covered the basic concepts and principles of operation of the chemical operators of the chemical reaction optimization algorithm, it is now time to move on to the general assembly of the algorithm and its practical application. Here we will focus on the results of the algorithm on various test functions to analyze its efficiency and potential in solving real-world problems. We will examine its performance, convergence, and ability to find global optima, which will allow us to evaluate its applicability, and also compare the results of the CRO algorithm with other optimization methods, identifying its advantages and disadvantages.

2. Algorithm implementation

Let's continue writing the algorithm code using the template that is already familiar to you for all algorithms, which includes standard Init, Moving and Revision functions. Since we have already declared the structure and implemented the main operators of chemical reactions, let's move on to writing the algorithm class to tie all the components together.

We will need a pseudocode to implement the algorithm assembly:

If the revision flag is reset - initialization:
    For each molecule i from 0 to popSize:
        For each coordinate c from 0 to coords
            Generate a random value for the structure of a molecule from rangeMin to rangeMax
            Limit the value of a structure to a given range
    Save the structure to the Array a
Exit
Kinetic energy calculation:
    minKE = maximum value of type double
For each molecule i from 0 to popSize:
        If fitness of the molecule is less than minKE:
            minKE = fitness of the molecule
    For each molecule i from 0 to popSize:
        Calculate the kinetic energy of a molecule KE as scaling fitness from the range from minKE to fB (best global solution) to the range from 0.0 to 1.0
molCNT = 0
Not stopped yet:
    If the random number is less than moleColl:
        Select two random molecules M1 and M2
        If KE of both molecules is greater than or equal to β:
            Perform synthesis of molecules M1 and M2
        Otherwise:
            Perform intermolecular ineffective collision between M1 and M2
    Otherwise:
        Select a random molecule M
        If NumHit of the molecule exceeds α:
            Perform decomposition of the molecule M
        Otherwise:
            Perform a collision of the molecule M
Copy molecular structures from Mfilial to a
Calculate fitness for individuals of the population a
Copy molecular structures from a to Mfilial
Initialization: ind = -1
For each molecule i from 0 to popSize:
    If fitness of the molecule exceeds fB:
        fB = fitness of the molecule
        ind = i
If ind is not equal to -1:
    Copy the structure of the molecule to cB
Molecule update:
    If there is no revision:
        For each molecule i from 0 to popSize:
            Update fitness of the molecule in Mparent
        Set revision to true
Exit
For each molecule i from 0 to popSize:
    Update fitness of the molecule in Mfilial
    Depending on the type of molecule (synthesis, intermolecular ineffective collision, decomposition, collision):
        Perform the appropriate post-operation

Now that we have the pseudocode and chemical operators described in the first part of the article, we can start building the implementation of the CRO algorithm in code.

Declare the C_AO_CRO class, which is an inheritor of the C_AO base class and is an implementation of the Chemical Reaction Optimisation (CRO) algorithm.

1. Public fields:

• popSize - population size.
• moleColl, alpha, beta, molecPerturb - algorithm parameters.
• params - array for storing algorithm parameters.
• Mparent[], Mfilial[] - objects of the S_CRO_Agent structure, representing molecules.

2. The options available are:

• C_AO_CRO() - class constructor that initializes the class fields.
• SetParams() - method for setting algorithm parameters.
• Init() - method for initializing the algorithm. The method accepts minimum and maximum search ranges, search step and number of epochs.
• Moving() and Revision() - methods that implement the basic operations of the algorithm.

3. Private fields and methods:

• Synthesis(), InterMolInefColl(), Decomposition(), InefCollision() - methods that implement different types of reactions.
• PostSynthesis(), PostInterMolInefColl(), PostDecomposition(), PostInefCollision() - methods that perform actions after corresponding reactions.
• N() - method for modifying a component (coordinate) of a molecule's structure.

This class is a complete implementation of the Chemical Reaction Optimisation (CRO) algorithm and contains all the data and methods required for it.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_CRO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_CRO () { }
  C_AO_CRO ()
  {
    ao_name = "CRO";
    ao_desc = "Chemical Reaction Optimisation";
    ao_link = "https://www.mql5.com/en/articles/15041";

    popSize      = 50;   //population size

    moleColl     = 0.9;
    alpha        = 200;
    beta         = 0.01;
    molecPerturb = 0.5;

    ArrayResize (params, 5);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "moleColl";     params [1].val = moleColl;
    params [2].name = "alpha";        params [2].val = alpha;
    params [3].name = "beta";         params [3].val = beta;
    params [4].name = "molecPerturb"; params [4].val = molecPerturb;

  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;

    moleColl     = params      [1].val;
    alpha        = (int)params [2].val;
    beta         = params      [3].val;
    molecPerturb = params      [4].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  S_CRO_Agent Mparent [];
  S_CRO_Agent Mfilial [];


  //----------------------------------------------------------------------------
  double moleColl;
  int    alpha;
  double beta;
  double molecPerturb;

  private: //-------------------------------------------------------------------
  bool Synthesis            (int index1, int index2, int &molCNT);
  bool InterMolInefColl     (int index1, int index2, int &molCNT);
  bool Decomposition        (int index,  int &molCNT);
  bool InefCollision        (int index,  int &molCNT);

  void PostSynthesis        (S_CRO_Agent &mol);
  void PostInterMolInefColl (S_CRO_Agent &mol);
  void PostDecomposition    (S_CRO_Agent &mol);
  void PostInefCollision    (S_CRO_Agent &mol);

  void N                    (double &coord, int coordPos);
};
//——————————————————————————————————————————————————————————————————————————————

The Init method of the C_AO_CRO class is used to initialize class variables based on the passed parameters. Here is what happens in this method:

1. The method calls the StandardInit function, which takes the minimum and maximum search ranges as well as the search step. If StandardInit returns false, the Init method also returns false and completes its work.

2. The method then resizes the Mparent and Mfilial arrays to popSize, which represents the population size.

3. Next, for each element in the Mparent and Mfilial arrays, the Init method is called with the coords parameter. This method initializes the fields of each agent in the population.

4. At the end, the method returns true indicating that initialization has completed successfully.

This method performs the initial setup of the Chemical Reaction Optimization (CRO) algorithm with given parameters and prepares it to perform optimization.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_CRO::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (Mparent, popSize);
  ArrayResize (Mfilial, popSize);

  for (int i = 0; i < popSize; i++)
  {
    Mparent [i].Init (coords);
    Mfilial [i].Init (coords);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

The Moving method of the C_AO_CRO class is used to call chemical operators that perform changes in the structures of molecules, thereby moving molecules during the optimization. The method does the following:

1. If revision is equal to false, then for each molecule in the Mparent population, structures are initialized with random values in a given range from rangeMin to rangeMax. These values are then copied into the array a.

2. If revision is not equal to false, the minimum value of the function f among all molecules in the Mparent population is calculated. The KE value is then calculated for each molecule based on the scaling of its function value f, minimum value f by the population of parent molecules and the best global solution fB in the range from 0.0 to 1.0.

3. Next, until one of the chemical operators returns false (this means that the daughter population has run out of room for daughter molecules), the following happens:

• If the random number is less than moleColl, then two random molecules M1 and M2 are selected. If KE of both molecules are greater than or equal to beta, then the synthesis is performed (i.e., the synthesis is performed for molecules not lower than the relative fitness value specified in the parameters; it was for these purposes that the fitness values of the molecules were previously scaled to the range from 0.0 to 1.0). Otherwise, an intermolecular ineffective collision occurs.

• If the random number is greater than or equal to moleColl, then one random molecule M is selected. If the molecule's NumHit exceeds alpha (if the molecule has undergone more collisions than specified in the algorithm parameters, then the molecule "breaks up"), the decomposition is performed. Otherwise, a collision occurs.

4. At the end of the method, the structures of all molecules in Mfilial are copied to the a population array.

This method is responsible for updating the molecular structures in the Chemical Reaction Optimization (CRO) algorithm according to the current state of the system and the given parameters. The method implements the basic operations of the CRO algorithm, such as synthesis, intermolecular inefficient collision, decomposition and collision.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CRO::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Mparent [i].structure [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Random structure in the range from rangeMin to rangeMax
        Mparent [i].structure [c] = u.SeInDiSp  (Mparent [i].structure [c], rangeMin [c], rangeMax [c], rangeStep [c]);

        a [i].c [c] = Mparent [i].structure [c];
      }
    }

    return;
  }

  //----------------------------------------------------------------------------
  double minKE = DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (Mparent [i].f < minKE) minKE = Mparent [i].f;
  }
  for (int i = 0; i < popSize; i++)
  {
    Mparent [i].KE = u.Scale (Mparent [i].f, minKE, fB, 0.0, 1.0);
  }

  //----------------------------------------------------------------------------
  int molCNT = 0;

  while (!IsStopped ())
  {
    if (u.RNDprobab () < moleColl)
    {
      // Select two random molecules M1 and M2
      int index1 = u.RNDminusOne (popSize);
      int index2 = u.RNDminusOne (popSize);

      // If KE ≤ β:
      if (Mparent [index1].KE >= beta && Mparent [index2].KE >= beta)
      {
        // Perform Synthesis
        if (!Synthesis (index1, index2, molCNT)) break;
      }
      else
      {
        // Perform Intermolecular Inefficient Collision
        if (!InterMolInefColl (index1, index2, molCNT)) break;
      }
    }
    else
    {
      // Select a random molecule M
      int index = u.RNDminusOne (popSize);

      // If NumHit > α:
      if (Mparent [index].NumHit > alpha)
      {
        // Perform Decomposition
        if (!Decomposition (index, molCNT)) break;
      }
      else
      {
        // Perform Collision
        if (!InefCollision (index, molCNT)) break;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    ArrayCopy (a [i].c, Mfilial [i].structure);
  }
}
//——————————————————————————————————————————————————————————————————————————————

The Revision method of the C_AO_CRO class is used to update the best global solution and update the states of molecules in the parent population by performing chemical post-operators. Actions performed by this method:

1. Updating the global solution. In the for loop, the method iterates through all molecules. If the value of the function f of the current molecule exceeds the current best fB value, fB is updated and the array of coordinates of the current molecule is copied to the array cB.

2. If revision is equal to false, then for each molecule in the Mparent population, the f value is set equal to the f value from the a array. Then revision is set to true and the method exits. At this stage, it is important to obtain the fitness values of the parent molecules so that in subsequent epochs, chemical operators that depend on the kinetic energy (the fitness function value normalized to the range from 0.0 to 1.0).

3. If revision is not false, then for each molecule in the Mfilial population the f is set equal to f from the a array. Then, depending on the molecule rType reaction type (reaction the molecule participated in), the appropriate PostSynthesis, PostInterMolInefColl, PostDecomposition, PostInefCollision method is called.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_CRO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        Mparent [i].f = a [i].f;
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      Mfilial [i].f = a [i].f;
    }

    switch (Mfilial [i].rType)
    {
      case synthesis:
        PostSynthesis        (Mfilial [i]);
        break;
      case interMolecularInefColl:
        PostInterMolInefColl (Mfilial [i]);
        break;
      case decomposition:
        PostDecomposition    (Mfilial [i]);
        break;
      case inefCollision:
        PostInefCollision    (Mfilial [i]);
        break;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Test results

The CRO algorithm was tested on the Hilly, Forest and Megacity functions. In each case, ten function runs were performed for each landscape type (5, 25 and 500 functions) and optimization results were obtained.

CRO|Chemical Reaction Optimisation|50.0|0.9|200.0|0.01|0.5|
=============================
5 Hilly's; Func runs: 10000; result: 0.9462894520167225
25 Hilly's; Func runs: 10000; result: 0.6611186250435438
500 Hilly's; Func runs: 10000; result: 0.2985263035668822
=============================
5 Forest's; Func runs: 10000; result: 0.8790568514481787
25 Forest's; Func runs: 10000; result: 0.584216839762206
500 Forest's; Func runs: 10000; result: 0.2114595696419046
=============================
5 Megacity's; Func runs: 10000; result: 0.7584615384615384
25 Megacity's; Func runs: 10000; result: 0.4264615384615384
500 Megacity's; Func runs: 10000; result: 0.12686153846153955
=============================
All score: 4.89245 (54.36%)

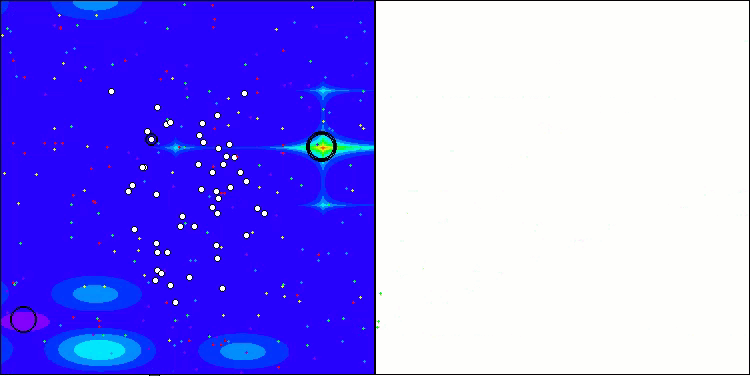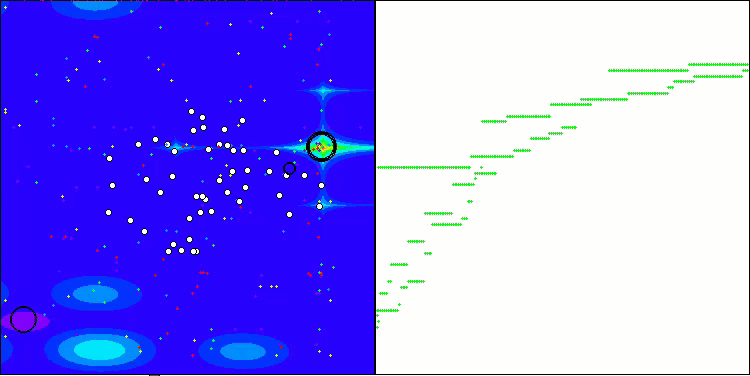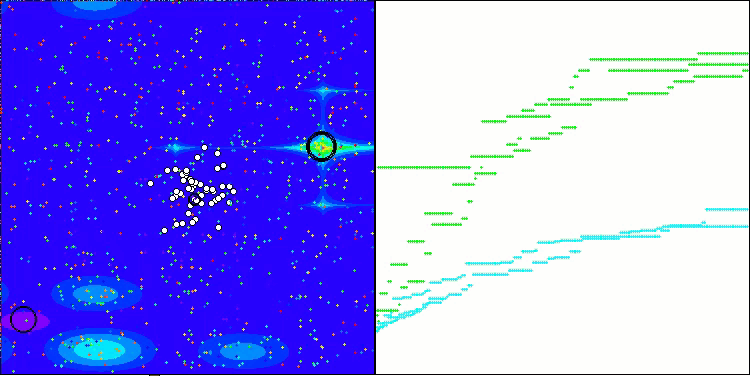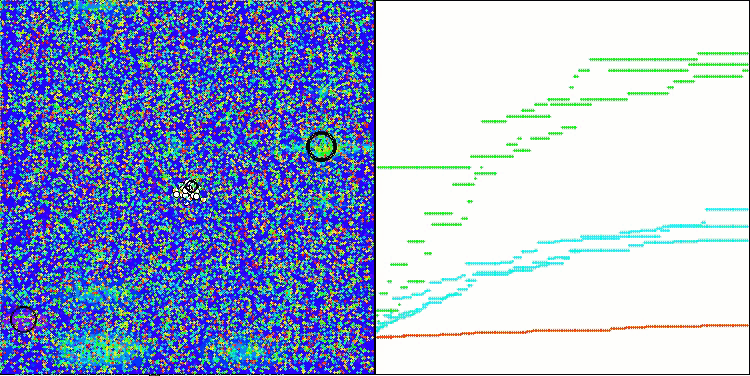
Visualization of the test bench operation with the CRO algorithm demonstrates interesting algorithm features. While CRO can get stuck at times, as evidenced by the long flat sections of the convergence graph, it still shows decent overall results.

One of the noticeable aspects of CRO work is the movement of "molecules" in the search area. At first glance, this movement appears chaotic and resembles Brownian motion. However, despite the external randomness, the "molecules" manage to find a zone of global optimum. This demonstrates the complex and sophisticated nature of the CRO algorithm, which uses principles of chemical reactions to solve optimization problems.

Overall, the CRO algorithm is a powerful optimization tool that can handle a variety of tasks, despite some difficulties. Its unique properties and ability to find global optima make it a valuable tool in the field of optimization.

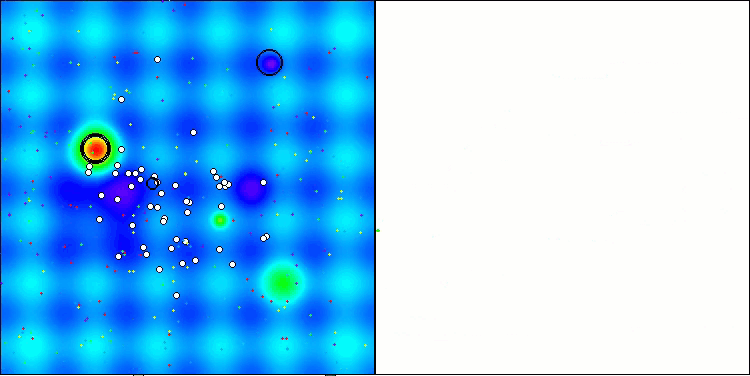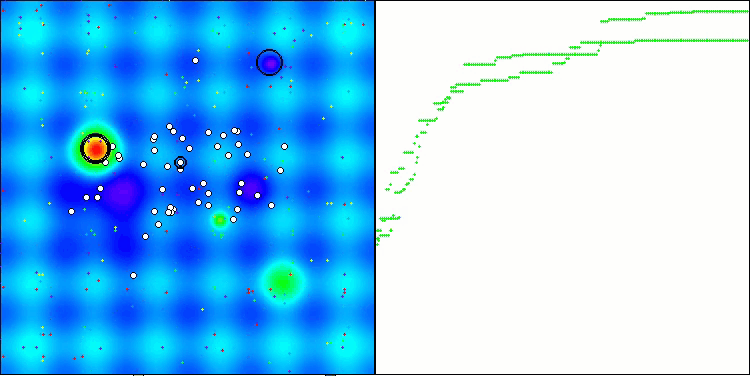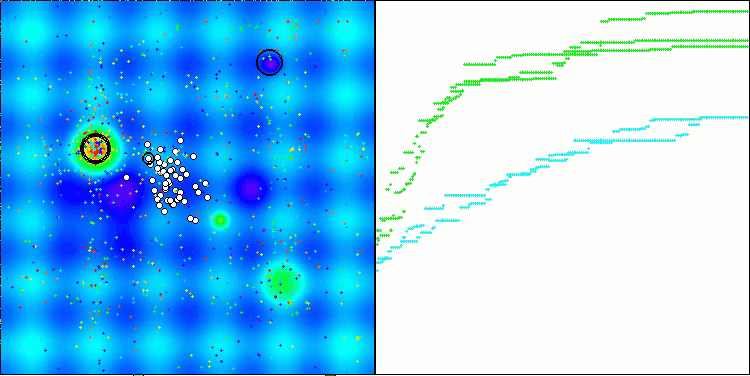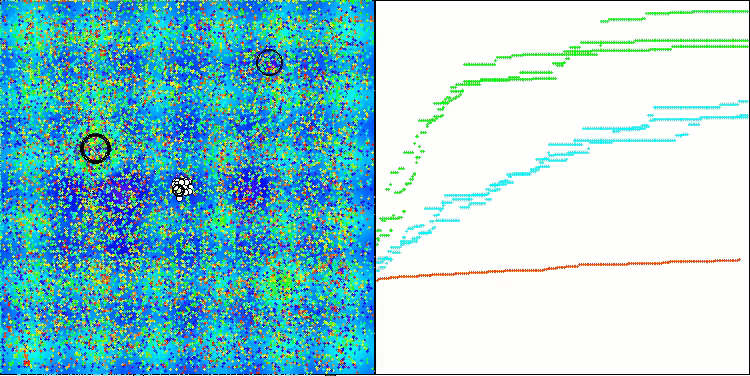
  CRO on the Hilly test function

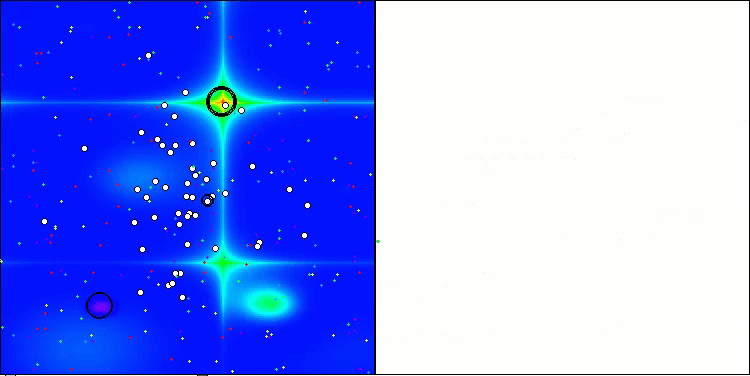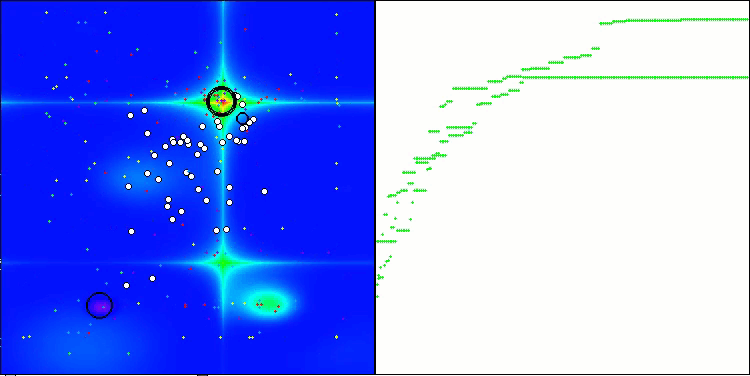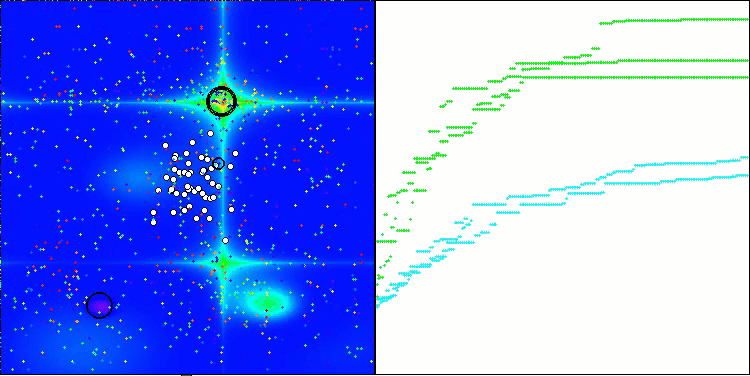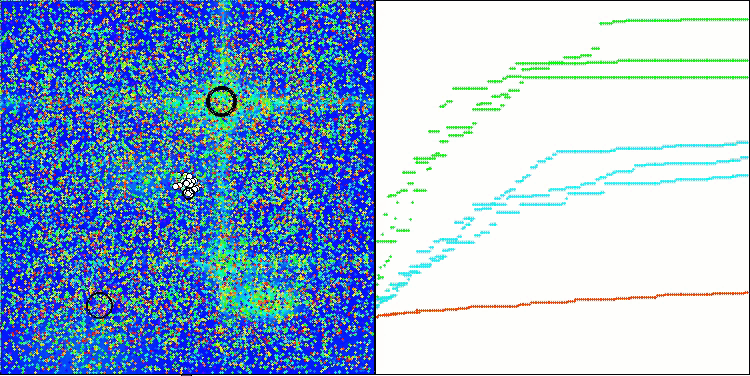
  CRO on the Forest test function

  CRO on the Megacity test function.

#	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0.99989	0.99518	0.42835	2.42341	0.96153	0.96181	0.32027	2.24360	0.91385	0.95908	0.24220	2.11512	6.782	75.36
2	CLA	code lock algorithm	0.95345	0.87107	0.37590	2.20042	0.98942	0.91709	0.31642	2.22294	0.79692	0.69385	0.19303	1.68380	6.107	67.86
3	(P+O)ES	(P+O) evolution strategies	0.92256	0.88101	0.40021	2.20379	0.97750	0.87490	0.31945	2.17185	0.67385	0.62985	0.18634	1.49003	5.866	65.17
4	CTA	comet tail algorithm	0.95346	0.86319	0.27770	2.09435	0.99794	0.85740	0.33949	2.19484	0.88769	0.56431	0.10512	1.55712	5.846	64.96
5	SDSm	stochastic diffusion search M	0.93066	0.85445	0.39476	2.17988	0.99983	0.89244	0.19619	2.08846	0.72333	0.61100	0.10670	1.44103	5.709	63.44
6	ESG	evolution of social groups	0.99906	0.79654	0.35056	2.14616	1.00000	0.82863	0.13102	1.95965	0.82333	0.55300	0.04725	1.42358	5.529	61.44
7	SIA	simulated isotropic annealing	0.95784	0.84264	0.41465	2.21513	0.98239	0.79586	0.20507	1.98332	0.68667	0.49300	0.09053	1.27020	5.469	60.76
8	ACS	artificial cooperative search	0.75547	0.74744	0.30407	1.80698	1.00000	0.88861	0.22413	2.11274	0.69077	0.48185	0.13322	1.30583	5.226	58.06
9	TSEA	turtle shell evolution algorithm	0.96798	0.64480	0.29672	1.90949	0.99449	0.61981	0.22708	1.84139	0.69077	0.42646	0.13598	1.25322	5.004	55.60
10	DE	differential evolution	0.95044	0.61674	0.30308	1.87026	0.95317	0.78896	0.16652	1.90865	0.78667	0.36033	0.02953	1.17653	4.955	55.06
11	CRO	chemical reaction optimization	0.94629	0.66112	0.29853	1.90593	0.87906	0.58422	0.21146	1.67473	0.75846	0.42646	0.12686	1.31178	4.892	54.36
12	BSA	bird swarm algorithm	0.89306	0.64900	0.26250	1.80455	0.92420	0.71121	0.24939	1.88479	0.69385	0.32615	0.10012	1.12012	4.809	53.44
13	HS	harmony search	0.86509	0.68782	0.32527	1.87818	0.99999	0.68002	0.09590	1.77592	0.62000	0.42267	0.05458	1.09725	4.751	52.79
14	SSG	saplings sowing and growing	0.77839	0.64925	0.39543	1.82308	0.85973	0.62467	0.17429	1.65869	0.64667	0.44133	0.10598	1.19398	4.676	51.95
15	(PO)ES	(PO) evolution strategies	0.79025	0.62647	0.42935	1.84606	0.87616	0.60943	0.19591	1.68151	0.59000	0.37933	0.11322	1.08255	4.610	51.22
16	BSO	brain storm optimization	0.93736	0.57616	0.29688	1.81041	0.93131	0.55866	0.23537	1.72534	0.55231	0.29077	0.11914	0.96222	4.498	49.98
17	WOAm	wale optimization algorithm M	0.84521	0.56298	0.26263	1.67081	0.93100	0.52278	0.16365	1.61743	0.66308	0.41138	0.11357	1.18803	4.476	49.74
18	ACOm	ant colony optimization M	0.88190	0.66127	0.30377	1.84693	0.85873	0.58680	0.15051	1.59604	0.59667	0.37333	0.02472	0.99472	4.438	49.31
19	BFO-GA	bacterial foraging optimization - ga	0.89150	0.55111	0.31529	1.75790	0.96982	0.39612	0.06305	1.42899	0.72667	0.27500	0.03525	1.03692	4.224	46.93
20	MEC	mind evolutionary computation	0.69533	0.53376	0.32661	1.55569	0.72464	0.33036	0.07198	1.12698	0.52500	0.22000	0.04198	0.78698	3.470	38.55
21	IWO	invasive weed optimization	0.72679	0.52256	0.33123	1.58058	0.70756	0.33955	0.07484	1.12196	0.42333	0.23067	0.04617	0.70017	3.403	37.81
22	Micro-AIS	micro artificial immune system	0.79547	0.51922	0.30861	1.62330	0.72956	0.36879	0.09398	1.19233	0.37667	0.15867	0.02802	0.56335	3.379	37.54
23	COAm	cuckoo optimization algorithm M	0.75820	0.48652	0.31369	1.55841	0.74054	0.28051	0.05599	1.07704	0.50500	0.17467	0.03380	0.71347	3.349	37.21
24	SDOm	spiral dynamics optimization M	0.74601	0.44623	0.29687	1.48912	0.70204	0.34678	0.10944	1.15826	0.42833	0.16767	0.03663	0.63263	3.280	36.44
25	NMm	Nelder-Mead method M	0.73807	0.50598	0.31342	1.55747	0.63674	0.28302	0.08221	1.00197	0.44667	0.18667	0.04028	0.67362	3.233	35.92
26	FAm	firefly algorithm M	0.58634	0.47228	0.32276	1.38138	0.68467	0.37439	0.10908	1.16814	0.28667	0.16467	0.04722	0.49855	3.048	33.87
27	GSA	gravitational search algorithm	0.64757	0.49197	0.30062	1.44016	0.53962	0.36353	0.09945	1.00260	0.32667	0.12200	0.01917	0.46783	2.911	32.34
28	BFO	bacterial foraging optimization	0.61171	0.43270	0.31318	1.35759	0.54410	0.21511	0.05676	0.81597	0.42167	0.13800	0.03195	0.59162	2.765	30.72
29	ABC	artificial bee colony	0.63377	0.42402	0.30892	1.36671	0.55103	0.21874	0.05623	0.82600	0.34000	0.14200	0.03102	0.51302	2.706	30.06
30	BA	bat algorithm	0.59761	0.45911	0.35242	1.40915	0.40321	0.19313	0.07175	0.66810	0.21000	0.10100	0.03517	0.34617	2.423	26.93
31	SA	simulated annealing	0.55787	0.42177	0.31549	1.29513	0.34998	0.15259	0.05023	0.55280	0.31167	0.10033	0.02883	0.44083	2.289	25.43
32	IWDm	intelligent water drops M	0.54501	0.37897	0.30124	1.22522	0.46104	0.14704	0.04369	0.65177	0.25833	0.09700	0.02308	0.37842	2.255	25.06
33	PSO	particle swarm optimisation	0.59726	0.36923	0.29928	1.26577	0.37237	0.16324	0.07010	0.60572	0.25667	0.08000	0.02157	0.35823	2.230	24.77
34	Boids	boids algorithm	0.43340	0.30581	0.25425	0.99346	0.35718	0.20160	0.15708	0.71586	0.27846	0.14277	0.09834	0.51957	2.229	24.77
35	MA	monkey algorithm	0.59107	0.42681	0.31816	1.33604	0.31138	0.14069	0.06612	0.51819	0.22833	0.08567	0.02790	0.34190	2.196	24.40
36	SFL	shuffled frog-leaping	0.53925	0.35816	0.29809	1.19551	0.37141	0.11427	0.04051	0.52618	0.27167	0.08667	0.02402	0.38235	2.104	23.38
37	FSS	fish school search	0.55669	0.39992	0.31172	1.26833	0.31009	0.11889	0.04569	0.47467	0.21167	0.07633	0.02488	0.31288	2.056	22.84
38	RND	random	0.52033	0.36068	0.30133	1.18234	0.31335	0.11787	0.04354	0.47476	0.25333	0.07933	0.02382	0.35648	2.014	22.37
39	GWO	grey wolf optimizer	0.59169	0.36561	0.29595	1.25326	0.24499	0.09047	0.03612	0.37158	0.27667	0.08567	0.02170	0.38403	2.009	22.32
40	CSS	charged system search	0.44252	0.35454	0.35201	1.14907	0.24140	0.11345	0.06814	0.42299	0.18333	0.06300	0.02322	0.26955	1.842	20.46
41	EM	electroMagnetism-like algorithm	0.46250	0.34594	0.32285	1.13129	0.21245	0.09783	0.10057	0.41085	0.15667	0.06033	0.02712	0.24412	1.786	19.85

Summary

Based on the provided table and results, the following conclusions can be made about the performance of the CRO algorithm:

1. CRO shows excellent results on the Hilly test function. With 5 parameters the result was about 0.95, with 25 parameters - about 0.66, and with 500 parameters - about 0.30. This indicates that CRO is effective on smooth functions, especially with fewer parameters.

2. On the Forest test function, CRO also shows good results. With 5 parameters the result was about 0.88, with 25 parameters - about 0.58, and with 500 parameters - about 0.21. This suggests that CRO is also effective on functions with "sharp" extremes, but has some difficulty finding point optima.

3. On the Megacity test function, CRO continues to demonstrate good performance. With 5 parameters the result was about 0.76, with 25 parameters - about 0.43, and with 500 parameters - about 0.13. This indicates that CRO is effective on this discrete function, its results are uniformly "green" compared to other algorithms, even those higher in the table.

Based on the provided table, the CRO algorithm shows strong results compared to other algorithms. In particular, on the Hilly, Forest and Megacity functions, CRO demonstrates competitiveness, especially with fewer parameters.

The CRO algorithm took 11 th place in the ranking table. Based on the color gradation in the table below (where dark green indicates better results), it can be said that CRO generally shows good and stable performance (stable and uniform coloring). On the Hilly function with 1000 parameters the results look somewhat weaker.

The CRO algorithm has proven to be a promising optimization approach. It uses two agent populations (in my implementation) that interact with each other to provide diversity and avoid getting stuck in local optima. One of the distinctive features of the algorithm is the use of special operators similar to chemical reactions, decomposition, synthesis and others.

In general, the CRO algorithm is a promising optimization method distinguished by its originality and ability to achieve high results in various optimization problems.

The choice of optimization algorithm should be based on the specific task and performance requirements, and our ranking table will help with this. By reworking the original version of the CRO algorithm to inherit from the C_AO class I have adopted for population algorithms, this interesting algorithm can be applied to optimization problems in general.

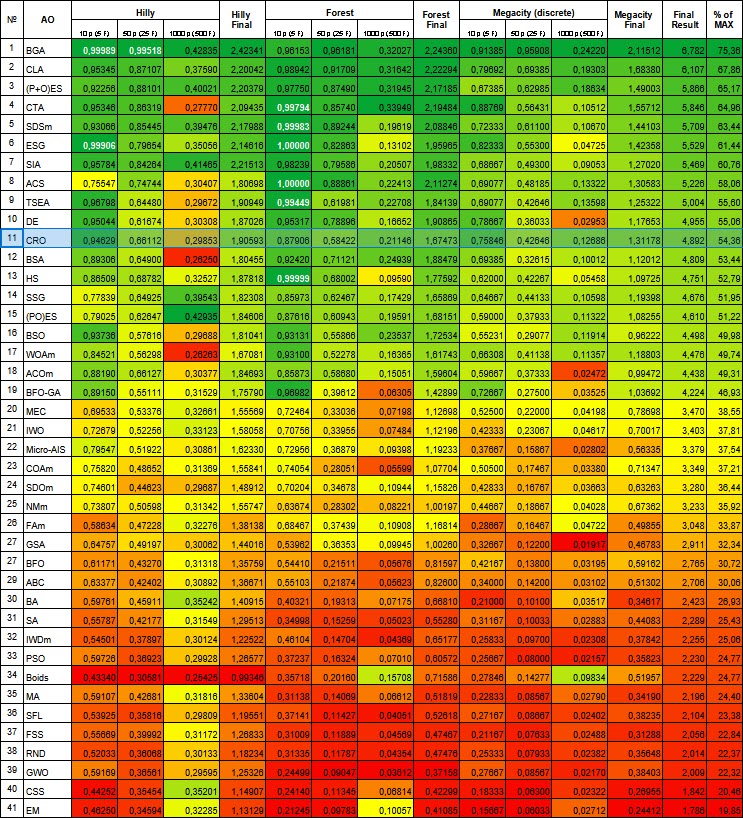
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white

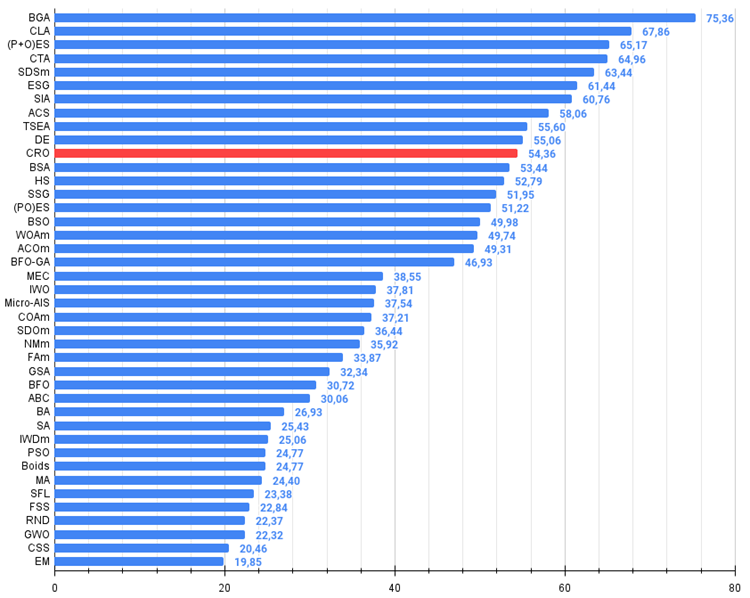
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)

CRO general pros and cons:

Advantages:

1. Good convergence on various types of functions.
2. Very fast despite its complex architecture.
3. Good scalability.
   

Disadvantages:

1. Sometimes gets stuck in local extremes.
   

The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/ru/code/49355