
Artificial Cooperative Search (ACS) algorithm
Contents
1. Introduction
2. Algorithm implementation
3.Test results
1. Introduction
Nature is an inexhaustible source of inspiration for scientists and engineers seeking to create innovative solutions. One of such remarkable phenomena is mutualism - a mutually beneficial biological interaction between different species. Living organisms participating in mutualistic relationships strive to obtain mutual benefits from this interaction, aimed at the development and diversity of the population. To understand this, I will give several examples of mutualistic (symbiotic) relationships between living organisms, in which they receive mutual benefits:
1. Flowering plants and pollinators:
- Plants produce nectar and other rewards to attract pollinators such as insects, birds, and bats.
- Pollinators, in turn, transfer pollen from one flower to another, which promotes plant reproduction.
2. Fungi and plant roots (mycorrhiza):
- Fungi penetrate the roots of plants and receive organic compounds (products of photosynthesis) from them.
- Fungi, in turn, expand the absorption surface of the roots, increasing the availability of water and minerals for plants.
3. Termites and symbiotic bacteria:
- Termites contain symbiotic bacteria in their guts that help them digest cellulose, the main component of wood.
- The bacteria get nutrients from the termites, and the termites get the ability to digest the fiber.
These examples demonstrate how living organisms interact to gain mutual benefit and increase their chances of survival.
The ACS algorithm also draws inspiration from the migratory behavior of eusocial superorganisms that share a common environment. Below are some examples of such migratory behavior of eusocial superorganisms:
1. Ant colonies:
- During a colony migration, ants carry larvae, pupae and other important elements of the nest along with them.
2. Bee families:
- When swarming, bee colonies may temporarily migrate from their hive to start a new colony elsewhere.
- During the migration of a swarm, bees carry queens, larvae and the necessary honey supplies to establish a new nest.
A common feature of these examples is that eusocial superorganisms, such as ants, termites, bees and wasps, are capable of collectively moving their colonies in response to environmental changes or resource depletion. This migratory ability allows them to adapt to changing conditions and ensures the survival of the entire superorganism. The mutualistic and cooperative biological interaction of two eusocial superorganisms living in the same environment served as the inspiration for the ACS algorithm. In this algorithm, the concept of habitat corresponds to the concept of search space related to the corresponding optimization problem.
Conceptually, the ACS algorithm views random solutions to the corresponding problem as artificial superorganisms migrating to more productive feeding areas. The two main superorganisms, referred to as α and β, contain artificial sub-superorganisms equal to the size of the population. The population size corresponds to the number of individuals in these sub-superorganisms. In the process of co-evolution, α and β superorganisms interact as predators and prey, using two dynamic populations to efficiently explore the search space and find the global optimum for numerical optimization problems.
The ACS algorithm was proposed by Pinar Civicioglu in 2013. It starts by using two base populations containing candidate solutions within the confidence region. The algorithm then creates two new populations, predators and prey, by mapping values from the initial α and β populations using random steps and a binary matrix. In addition, the fifth population is calculated based on the values in the predator and prey populations. The process involves updating the initial populations for a specified number of iterations, with the best solution being taken from these two populations.
The migration and evolution of two artificial superorganisms that interact biologically with each other to reach the global extremum of the objective function, and the process similar to the cooperative behavior in nature, are the key to the high performance of ACS in numerical optimization problems. This unique approach to biologically motivated interactions between populations allows the ACS algorithm to achieve impressive convergence speed and high solution accuracy. Due to its ability to quickly and accurately find optimal solutions, ACS has proven itself to be a powerful tool for solving a wide range of numerical optimization problems.
In this article, I will describe in detail the concept behind the ACS algorithm and demonstrate its remarkable capabilities. Readers will gain a deep understanding of how biological inspiration can be successfully implemented in advanced optimization algorithms capable of solving complex problems with high efficiency.
2. Algorithm implementation
The Artificial Cooperative Search (ACS) algorithm works as follows:
1. Initialization. The "popSize" population size, "N" number of variables, lower "XLow" and upper "XHi" variable borders, as well as the "Probab" probability of biological interaction are set. The initial "A" and "B" population positions are then generated and their "YA" and "YB" fitness values are calculated.
2. Loop by iterations. The following steps are performed at each iteration:
- Selection. It is determined which set of agents from A or B populations will be used as a "predator" in the current iteration.
- Shuffling the "prey". The agent positions in the selected set are shuffled.
- Mutation. Agent positions are updated using a randomly generated R scaling factor. "Predators" mutate using information about the "prey" decision vectors.
- Filling the M binary matrix. The M binary matrix is created to determine which variables will be updated in the current iteration.
- Updating agent positions. Agent positions are updated taking into account the values in the M matrix. If the value in M is 1, then the corresponding agent variable is updated.
- Border control. If the agent's updated position is outside the specified boundaries, it is adjusted.
- Selection update. At this stage, the best solutions are saved for the next algorithm iteration.
- Global best solution update. If a better solution is found, it is saved.
3. Return the result. At the end of the algorithm, the global best solution and its fitness value are returned.
The algorithm features some unique operators such as the "prey" shuffle operator and the mutation operator, which involve the use of the M binary matrix.
The M matrix is a two-dimensional array with "popSize" rows (the number of candidates in the population) and "N" columns (the number of variables in each candidate). Each element of the matrix can be either 0 or 1. The M matrix is used to determine which candidates will be selected for further renewal in the population. The values 0 and 1 in the matrix indicate whether the corresponding candidate will be selected for update based on the random Rand values and the Probab interaction probability.
The M matrix helps to regulate the selection of candidates for renewal in the population. Thus, the M matrix plays a key role in the population evolution and the search for the optimal solution in ACS.
Let's take a detailed look at each step of the ACS algorithm in pseudocode:
1. Initialization:
- The following parameters are set:
- popSize - population size
- N - number of variables
- MaxIter - maximum number of iterations
- XLow - lower boundary for variables
- XHi - upper boundary for variables
- Probab - probability of biological interaction
- Rand - function that returns uniformly distributed numbers in the range (0, 1)
- GlobMax is initialized by the negative DBL_MAX
2. Main loop:
- For each element of the population (I = 1 to popSize):
- For each variable (J = 1 to N):
- Initial values A(I,J) and B(I,J) in the range [XLow(J), XHi(J)] are calculated
- Initial values of the target function YA(I) = Fx(A(I,:)) and YB(I) = Fx(B(I,:)) are calculated
- The main loop by (Iter = 1 to MaxIter) iterations starts
3. Selection:
- We randomly choose if A or B is to be used as a Predator:
- If Rand < 0.5, Predator= A, Ypred = YA, Key = 1
- Otherwise, Predator = B, Ypred = YB, Key = 2
- We randomly choose if A or B is to be used as a Prey:
- If Rand < 0.5, Prey = A
- Otherwise, Prey = B
- Prey is randomly shuffled
- The R parameter is calculated:
- If Rand < 0.5, R = 4 * Rand * (Rand - Rand)
- Otherwise, R = 1/exp(4 * Rand)
- The M binary matrix of popSize x N filled with ones is created
- Some elements of the M matrix are randomly set to 0 with the Probab probability
- If Rand < Probab, some elements of the M matrix are randomly set to 0 or 1
- For each row of the M matrix, if the sum of the elements is N, then one element is randomly selected and set to 0
4. Mutation:
- The new value X = Predator + R * (Prey - Predator) is calculated
- For each element of the population (I = 1 to popSize) and each variable (J = 1 to N):
- If the corresponding element of the M matrix exceeds 0, then X(I,J) = Predator(I,J)
- If X(I,J) is outside the range [XLow(J), XHi(J)], then X(I,J) is set to a random value in that range
5. Selection update:
- For each element of the population (I = 1 to popSize):
- If Fx(X(I,:)) < Ypred(i), then Predator(I,:) = X(I,:) and Ypred(I) = Fx(X(I,:))
- If Key = 1, then A = Predator and YA = Ypred, otherwise B = Predator and YB = Ypred
- Ybest = min(Ypred)
- Ibest = Predator row index corresponding to Ybest
- If Ybest > GlobMax, then GlobMax = Ybest and GlobMax = Predator(Ibest,:)
6. Return the result:
- Return GlobMax and GlobMaxX vector
Let's move on to the description of the ACS algorithm implementation. We will use the simplest structure "S_D " to describe the population (of which there are five in the algorithm):
- c [] is an array for storing coordinates (optimized parameters of the task)
- Init (int coords) - method changes the size of the c array to the size specified in coords (number of coordinates) using the ArrayResize function
In general, this structure is used to create an object that contains an array of real numbers. The Init method is used to resize the array.
//—————————————————————————————————————————————————————————————————————————————— struct S_D { void Init (int coords) { ArrayResize (c, coords); } double c []; }; //——————————————————————————————————————————————————————————————————————————————
To describe the M matrix, create the S_C structure, which is different from the structure of the S_D field type:
- c[] - array storing the "0" and "1" matrix symbols
- Init (int coords) - method changes the c array size to the size specified in coords using the ArrayResize function
//—————————————————————————————————————————————————————————————————————————————— struct S_C { void Init (int coords) { ArrayResize (c, coords); } char c []; }; //——————————————————————————————————————————————————————————————————————————————
The algorithm will be described as the C_AO_ACS class derived from the C_AO base class and will contain the following fields:
- ~C_AO_ACS () { } - class destructor called when the class object is deleted. In this case, the destructor is empty.
- C_AO_ACS () - class constructor that initializes the class data members, resizes the params array and assigns default values to the algorithm parameters.
- SetParams () - method sets the popSize values and bioProbab based on the values in the params array.
- Init () - method takes several arguments and returns a Boolean value.
- Moving () and Revision () are methods that contain the main logic of the algorithm.
- bioProbab - data member that stores the probability of a biological interaction.
- S_D A [], S_D B [], S_D Predator [], S_D Prey [], S_C M [], double YA [], double YB [], double Ypred [], int Key, int phase - class data private members.
- ArrayShuffle () - private method, which shuffles array elements.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ACS () { } C_AO_ACS () { ao_name = "ACS"; ao_desc = "Artificial Cooperative Search"; ao_link = "https://www.mql5.com/ru/articles/15004"; popSize = 1; //population size bioProbab = 0.9; //biological interaction probability ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "bioProbab"; params [1].val = bioProbab; } void SetParams () { popSize = (int)params [0].val; bioProbab = params [1].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double bioProbab; //biological interaction probability private: //------------------------------------------------------------------- S_D A []; S_D B []; S_D Predator []; S_D Prey []; S_C M []; double YA []; double YB []; double Ypred []; int Key; int phase; void ArrayShuffle (double &arr []); }; //——————————————————————————————————————————————————————————————————————————————
Next, present the Init method of the C_AO_ACS class. The method initializes the class object:
- Init () - method declaration. It takes four arguments: minimum search range "rangeMinP", maximum search range "rangeMaxP", "rangeStepP" search step and the number of epochs "epochsP", which is 0 by default.
- if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - call the StandardInit function, which performs standard initialization of the base class. If StandardInit returns false, the Init method terminates immediately and returns false.
- In the loop for (int i = 0; i < popSize; i++), each element of the A, B, Predator, Prey and M arrays is initialized using the Init method.
- ArrayResize (YA, popSize) and similar rows change the size of the YA, YB and Ypred arrays to popSize.
- ArrayInitialize (YA, -DBL_MAX) and similar rows initialize all elements of the YA, YB and Ypred arrays using the -DBL_MAX value.
- In the nested for loop, each c element of each object in the A and B arrays is initialized using a random value in the given range.
- phase = 0 sets 'phase' to 0.
The original algorithm does not have a division of logic into phases. I had to add phases to implement the algorithm in the style I have adopted for all population algorithms. This was necessary because the ACS uses a pre-calculation of the agent fitness for А and B populations. A phase division was added to perform these operations sequentially in the methods.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ACS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (A, popSize); ArrayResize (B, popSize); ArrayResize (Predator, popSize); ArrayResize (Prey, popSize); ArrayResize (M, popSize); for (int i = 0; i < popSize; i++) { A [i].Init (coords); B [i].Init (coords); Predator [i].Init (coords); Prey [i].Init (coords); M [i].Init (coords); } ArrayResize (YA, popSize); ArrayResize (YB, popSize); ArrayResize (Ypred, popSize); ArrayInitialize (YA, -DBL_MAX); ArrayInitialize (YB, -DBL_MAX); ArrayInitialize (Ypred, -DBL_MAX); // Initialization for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab(); } } phase = 0; return true; } //——————————————————————————————————————————————————————————————————————————————
The Moving method of the C_AO_ACS class implements the basic logic of moving individuals in the algorithm. This method performs several operations including array copying, selection, permutation, mutation, and crossover.
- if (phase == 0) - individuals from the A population are copied at this phase.
- if (phase == 1) - at this phase we return the fitness of individuals of the А population and copy individuals from the B population.
- if (phase == 2) - at this phase we return the fitness of individuals of the B population and the entire further algorithm logic is executed afterwards.
- Selection - the block performs selection. Depending on a random number, the A or B arrays are copied to the Predator array, while the corresponding values are copied into the Ypred array.
- Permutation of Prey - permutation of the Prey array elements is performed here.
- R - a variable is declared, which is then initialized to one of two possible values depending on the random number.
- Fill binary matrix M with 1s - the M binary matrix is filled with ones here.
- Additional operations with matrix M - the block performs additional operations with the M matrix, including changing some of its elements to 0 or 1, depending on the random number and the bioProbab probability of biological interaction.
- Mutation - the block performs a mutation, in which the a array elements are changed based on the Predator and Prey array elements, as well as the R value.
- Crossover - the block performs a crossover operation, in which some a array elements are replaced with the Predator array elements.
- Boundary control - the block performs boundary control, in which the a array elements outside the specified range of optimized parameters are replaced with random values within the range.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Moving () { //---------------------------------------------------------------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 1) { for (int i = 0; i < popSize; i++) YA [i] = a [i].f; for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c); phase++; return; } //---------------------------------------------------------------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) YB [i] = a [i].f; phase++; } //---------------------------------------------------------------------------- // Selection if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, A [i].c); } ArrayCopy (Ypred, YA); Key = 1; } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Predator [i].c, B [i].c); } ArrayCopy (Ypred, YB); Key = 2; } if (u.RNDprobab () < 0.5) { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, A [i].c); } } else { for (int i = 0; i < popSize; i++) { ArrayCopy (Prey [i].c, B [i].c); } } // Permutation of Prey for (int i = 0; i < popSize; i++) { ArrayShuffle (Prey [i].c); } double R; if (u.RNDprobab () < 0.5) { R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0); } else R = 1 / MathExp (4 * MathRand () / 32767.0); // Fill binary matrix M with 1s for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = 1; } } // Additional operations with matrix M for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { if (u.RNDprobab () < bioProbab) { M [i].c [j] = 1; } else { M [i].c [j] = 0; } } } for (int i = 0; i < popSize; i++) { int sum = 0; for (int c = 0; c < coords; c++) sum += M [i].c [c]; if (sum == coords) { int j = MathRand () % coords; M [i].c [j] = 0; } } // Mutation for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]); // Crossover if (M [i].c [j] > 0) { a [i].c [j] = Predator [i].c [j]; } // Boundary control if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j]) { a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab (); } } } for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Revision method of the C_AO_ACS class. The method performs a number of operations: sorting and reverse copying of arrays, as well as updating the best value of the global solution.
- if (phase < 3) return - the basic logic of the method is not executed until all three phases of preparing populations for further interaction are completed.
- Selection update - the block updates selection of individuals. For each a array individual, we check whether its f fitness value exceeds the appropriate value in the Ypred array.
- if (Key == 1) and else - in these blocks, depending on the Key value, Predator array elements are copied from the A or B array, while the corresponding Ypred values are copied from the YA or YB array.
- ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY) - the Ypred array containing the fitness values is sorted and then reversed so that the values are in descending order.
- Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred) - here Ybest is a maximum value in Ypred, while Ibest is an index of this maximum value.
- if (Ybest > fB) - if Ybest exceeds the current fB, then fB is updated, while the appropriate a and cB array elements are copied from the Predator array.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::Revision () { if (phase < 3) return; // Selection update for (int i = 0; i < popSize; i++) { double d = a [i].f; if (d > Ypred [i]) { ArrayCopy (Predator [i].c, a [i].c); Ypred [i] = d; } } if (Key == 1) { for (int i = 0; i < popSize; i++) { ArrayCopy (A [i].c, Predator [i].c); } ArrayCopy (YA, Ypred); } else { for (int i = 0; i < popSize; i++) { ArrayCopy (B [i].c, Predator [i].c); } ArrayCopy (YB, Ypred); } ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY); double Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred); if (Ybest > fB) { fB = Ybest; ArrayCopy (a [Ibest].c, Predator [Ibest].c); ArrayCopy (cB, Predator [Ibest].c); } } //——————————————————————————————————————————————————————————————————————————————
The ArrayShuffle method of the C_AO_ACS class performs random shuffling of the elements in the array.
- for (int i = n - 1; i > 0; i--) - the loop iterates through the arr array in reverse order, starting from the last element.
- j = MathRand () % (i + 1) - here j is a random number from 0 to i.
- tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp - these rows perform the swap of arr[i] and arr[j] elements.
As a result, the arr array elements are shuffled randomly.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACS::ArrayShuffle (double &arr []) { int n = ArraySize (arr); for (int i = n - 1; i > 0; i--) { int j = MathRand () % (i + 1); double tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp; } } //——————————————————————————————————————————————————————————————————————————————
3. Test results
The originality of the algorithm is confirmed by the conducted tests. This algorithm is unique in its ability to achieve excellent results when the population is reduced. As the number of iterations increases, the algorithm can have 100% convergence on individual test functions, which distinguishes it from other algorithms, for which any increase in the number of fitness function runs still does not give the opportunity to converge. This feature is characterized by the fact that it has resistance to getting stuck in local "traps".
Let's see how the algorithm results change depending on the population size. I typically use an average of 50 individuals in a population. However, while testing, this algorithm starts to show decent results at lower population sizes.
In case of 10 individuals in the population and the number of fitness function launches remaining at 10,000, the algorithm achieves the result of 49.97%.
ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8213829114300768
25 Hilly's; Func runs: 10000; result: 0.5418951009344799
500 Hilly's; Func runs: 10000; result: 0.2811381329747021
=============================
5 Forest's; Func runs: 10000; result: 0.9750514085798038
25 Forest's; Func runs: 10000; result: 0.5078176955906151
500 Forest's; Func runs: 10000; result: 0.20112458337102135
=============================
5 Megacity's; Func runs: 10000; result: 0.736923076923077
25 Megacity's; Func runs: 10000; result: 0.31446153846153846
500 Megacity's; Func runs: 10000; result: 0.11721538461538572
=============================
All score: 4.49701 (49.97%)
In case of 3 individuals in the population and the number of fitness function launches remaining at 10,000, the algorithm achieves the result of 55.23%.
ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8275253778390631
25 Hilly's; Func runs: 10000; result: 0.6349216357701294
500 Hilly's; Func runs: 10000; result: 0.29382093872076825
=============================
5 Forest's; Func runs: 10000; result: 0.9998874875962974
25 Forest's; Func runs: 10000; result: 0.6985911632646721
500 Forest's; Func runs: 10000; result: 0.2132502183011688
=============================
5 Megacity's; Func runs: 10000; result: 0.7507692307692307
25 Megacity's; Func runs: 10000; result: 0.4270769230769231
500 Megacity's; Func runs: 10000; result: 0.1252615384615397
=============================
All score: 4.97110 (55.23%)
In case of 1 individual in the population and the number of fitness function launches remaining at 10,000, the algorithm achieves the result of 58.06%.
ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7554725186591347
25 Hilly's; Func runs: 10000; result: 0.7474431551529281
500 Hilly's; Func runs: 10000; result: 0.3040669213089683
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999993218
25 Forest's; Func runs: 10000; result: 0.888607840003743
500 Forest's; Func runs: 10000; result: 0.2241289484506152
=============================
5 Megacity's; Func runs: 10000; result: 0.6907692307692308
25 Megacity's; Func runs: 10000; result: 0.4818461538461539
500 Megacity's; Func runs: 10000; result: 0.1332153846153859
=============================
All score: 5.22555 (58.06%)
You may ask how interaction occurs in a population with only one individual. As you might remember, the algorithm uses five populations, and interaction occurs between individuals in these populations. Despite the very small number of individuals, the algorithm preserves diversity in populations and does not have a "bottleneck" effect.
In the visualization, we can see the absence of any clustering effect and the fact that the agents seemingly behave chaotically. Agents enter areas of the search space even where there are no promising directions. This feature is clearly visible in the Forest and Megacity features, which have large, flat areas with little variation in terrain.
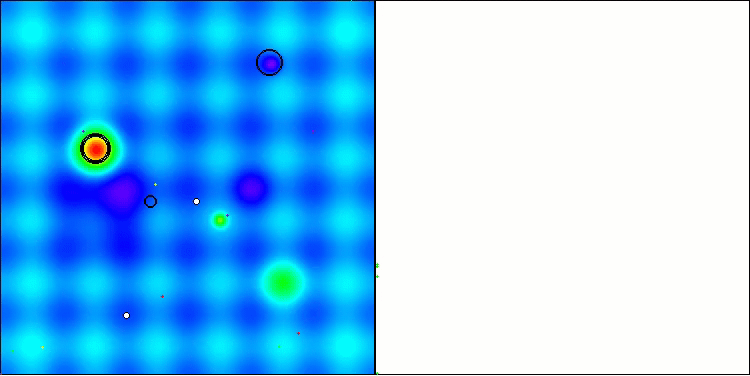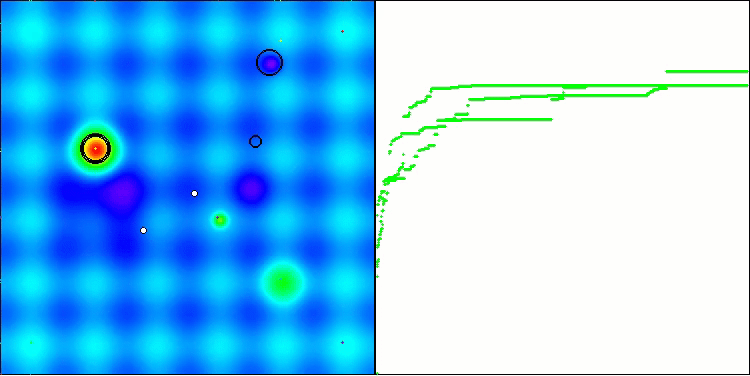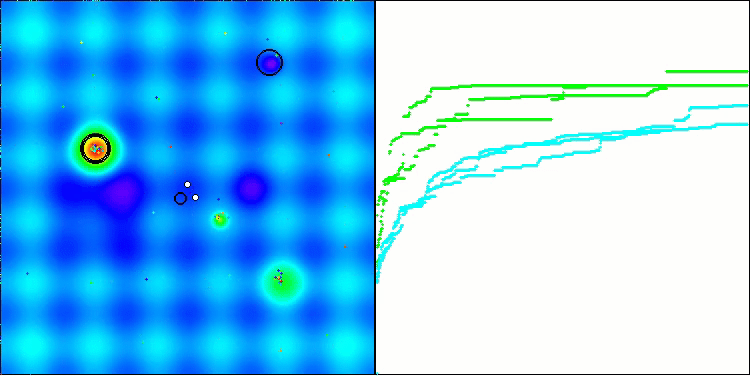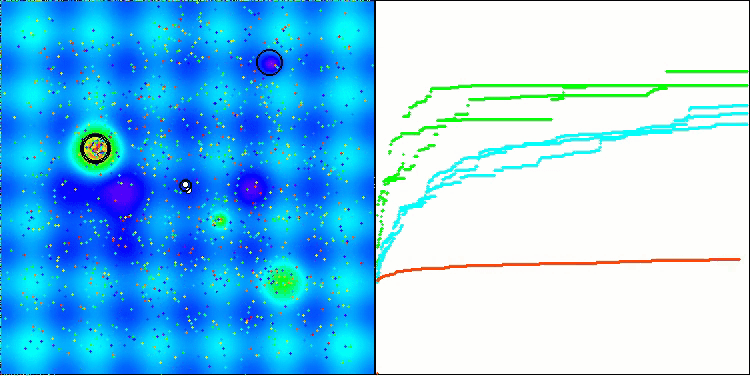
ACS on the Hilly test function
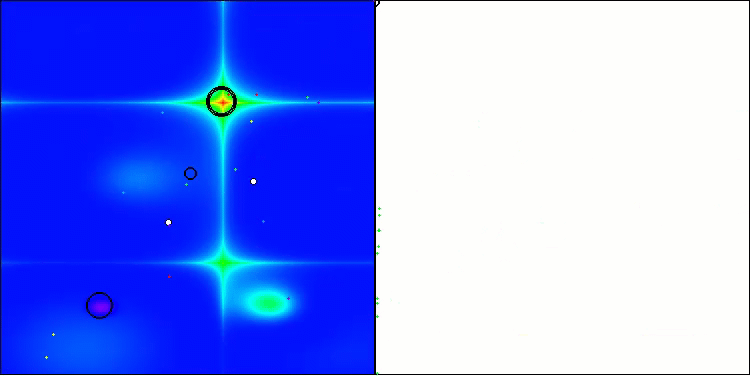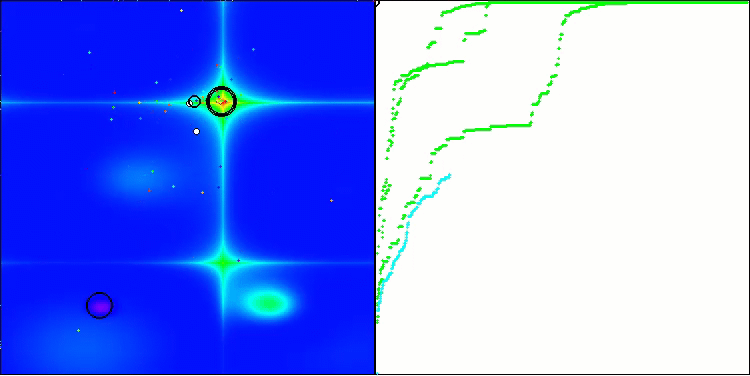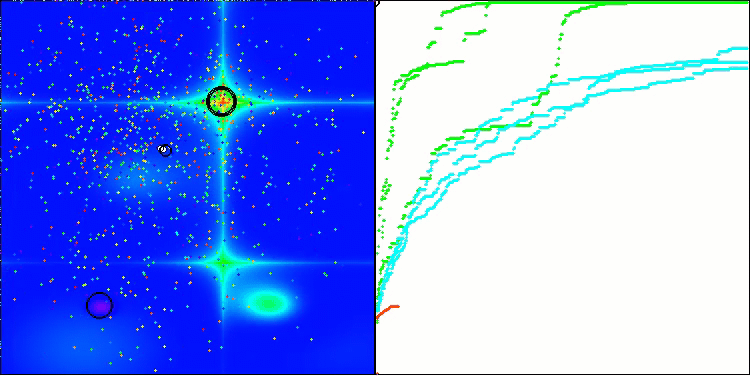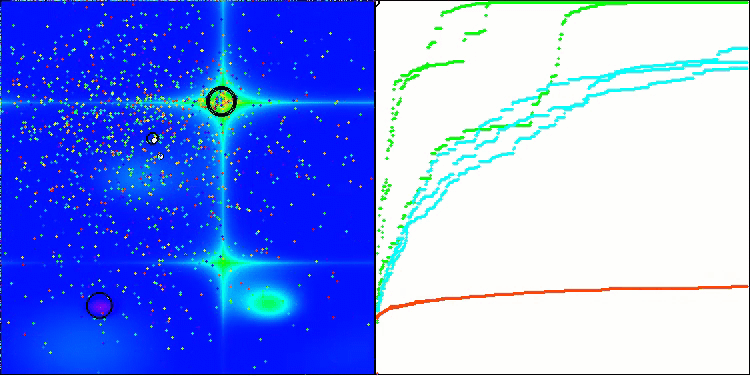
ACS on the Forest test function
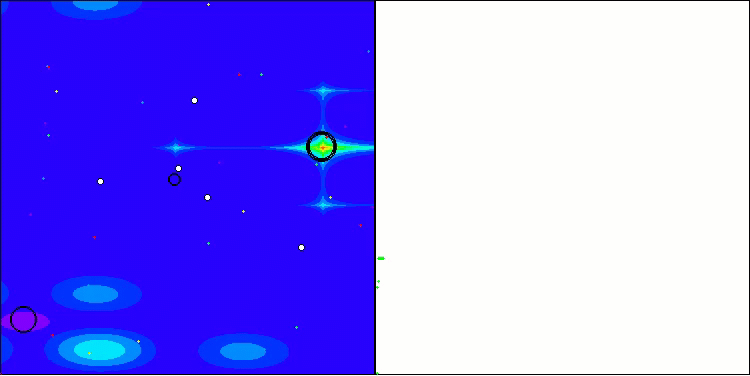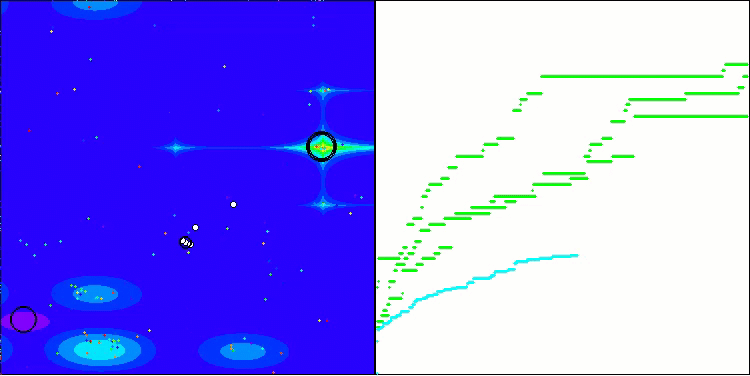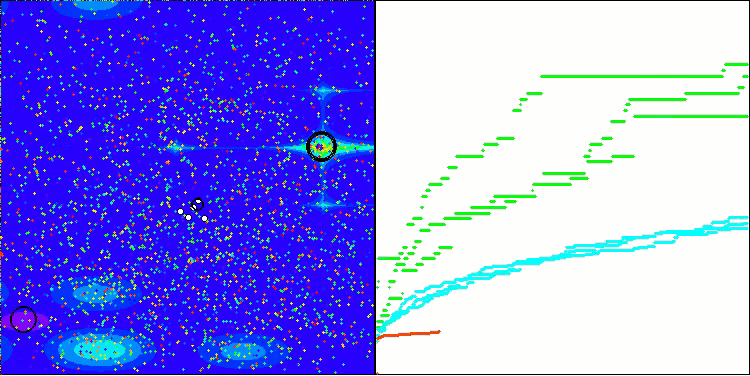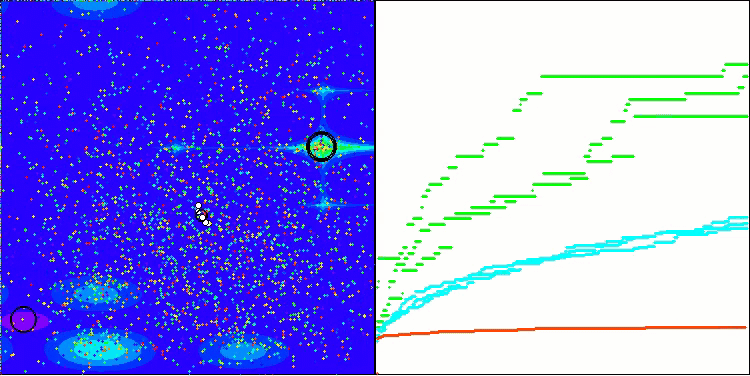
ACS on the Megacity test function
Based on the test results, the algorithm took 8 th place. ACS particularly excelled in the Forest and Megacity functions.
# | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0.99989 | 0.99518 | 0.42835 | 2.42341 | 0.96153 | 0.96181 | 0.32027 | 2.24360 | 0.91385 | 0.95908 | 0.24220 | 2.11512 | 6.782 | 75.36 |
| 2 | CLA | code lock algorithm | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 4 | CTA | comet tail algorithm | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 5 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 6 | ESG | evolution of social groups | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 7 | SIA | simulated isotropic annealing | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 8 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 9 | TSEA | turtle shell evolution algorithm | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 10 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 11 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 12 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 13 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 14 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 15 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 16 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 17 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 18 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 19 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 20 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 21 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 22 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 23 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 24 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 25 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 26 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 27 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 28 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 29 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
| 30 | SA | simulated annealing | 0.55787 | 0.42177 | 0.31549 | 1.29513 | 0.34998 | 0.15259 | 0.05023 | 0.55280 | 0.31167 | 0.10033 | 0.02883 | 0.44083 | 2.289 | 25.43 |
| 31 | IWDm | intelligent water drops M | 0.54501 | 0.37897 | 0.30124 | 1.22522 | 0.46104 | 0.14704 | 0.04369 | 0.65177 | 0.25833 | 0.09700 | 0.02308 | 0.37842 | 2.255 | 25.06 |
| 32 | PSO | particle swarm optimisation | 0.59726 | 0.36923 | 0.29928 | 1.26577 | 0.37237 | 0.16324 | 0.07010 | 0.60572 | 0.25667 | 0.08000 | 0.02157 | 0.35823 | 2.230 | 24.77 |
| 33 | Boids | boids algorithm | 0.43340 | 0.30581 | 0.25425 | 0.99346 | 0.35718 | 0.20160 | 0.15708 | 0.71586 | 0.27846 | 0.14277 | 0.09834 | 0.51957 | 2.229 | 24.77 |
| 34 | MA | monkey algorithm | 0.59107 | 0.42681 | 0.31816 | 1.33604 | 0.31138 | 0.14069 | 0.06612 | 0.51819 | 0.22833 | 0.08567 | 0.02790 | 0.34190 | 2.196 | 24.40 |
| 35 | SFL | shuffled frog-leaping | 0.53925 | 0.35816 | 0.29809 | 1.19551 | 0.37141 | 0.11427 | 0.04051 | 0.52618 | 0.27167 | 0.08667 | 0.02402 | 0.38235 | 2.104 | 23.38 |
| 36 | FSS | fish school search | 0.55669 | 0.39992 | 0.31172 | 1.26833 | 0.31009 | 0.11889 | 0.04569 | 0.47467 | 0.21167 | 0.07633 | 0.02488 | 0.31288 | 2.056 | 22.84 |
| 37 | RND | random | 0.52033 | 0.36068 | 0.30133 | 1.18234 | 0.31335 | 0.11787 | 0.04354 | 0.47476 | 0.25333 | 0.07933 | 0.02382 | 0.35648 | 2.014 | 22.37 |
| 38 | GWO | grey wolf optimizer | 0.59169 | 0.36561 | 0.29595 | 1.25326 | 0.24499 | 0.09047 | 0.03612 | 0.37158 | 0.27667 | 0.08567 | 0.02170 | 0.38403 | 2.009 | 22.32 |
| 39 | CSS | charged system search | 0.44252 | 0.35454 | 0.35201 | 1.14907 | 0.24140 | 0.11345 | 0.06814 | 0.42299 | 0.18333 | 0.06300 | 0.02322 | 0.26955 | 1.842 | 20.46 |
| 40 | EM | electroMagnetism-like algorithm | 0.46250 | 0.34594 | 0.32285 | 1.13129 | 0.21245 | 0.09783 | 0.10057 | 0.41085 | 0.15667 | 0.06033 | 0.02712 | 0.24412 | 1.786 | 19.85 |
Summary
The artificial cooperative search (ACS) algorithm has proven to be an interesting approach to optimization, which is manifested in the use of several populations of agents interacting with each other, providing diversity and resistance to getting stuck in local optima, in the use of special operators, such as shuffling of the "prey" and mutation using a binary matrix. The latter gave the algorithm originality and the ability to achieve high results with a very small population size (down to 1 individual in each of the five populations). Original approach and the ability to work with small populations (which emphasizes the resistance to colony degeneration) make ACS a truly promising optimization algorithm. 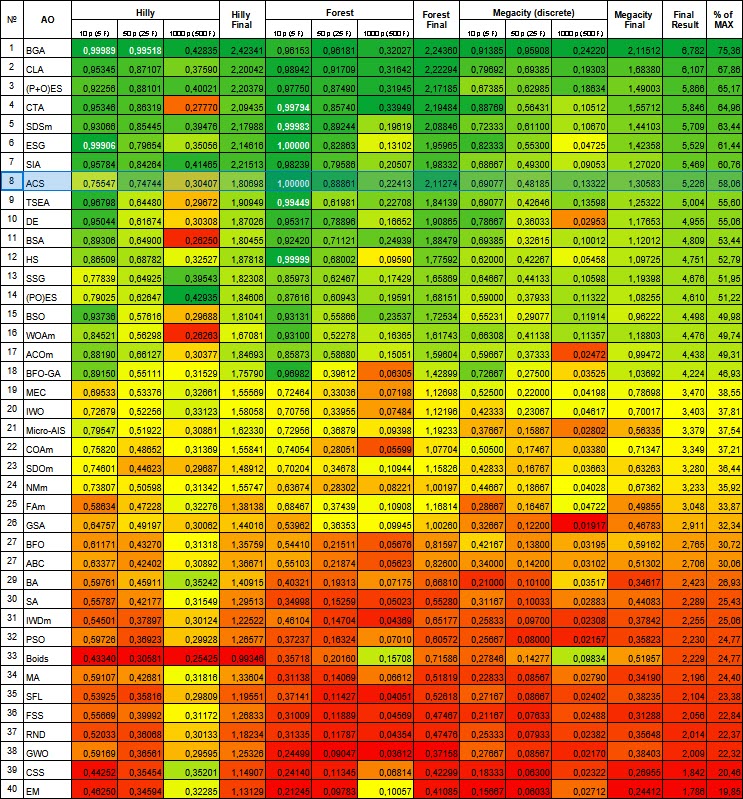
Figure 1. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white
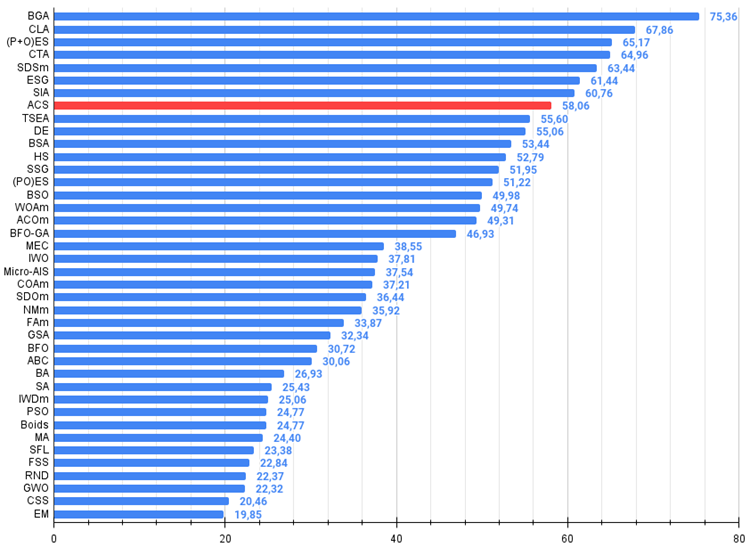
Figure 2. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,
where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)
ACS pros and cons:
Advantages:
- Small number of external parameters (only one).
- Good convergence on various types of functions.
Disadvantages:
- Scatter of results on low-dimensional functions.
The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.
Translated from Russian by MetaQuotes Ltd.
Original article: https://www.mql5.com/ru/articles/15004
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 News Trading Made Easy (Part 4): Performance Enhancement
News Trading Made Easy (Part 4): Performance Enhancement
 Neural Networks Made Easy (Part 90): Frequency Interpolation of Time Series (FITS)
Neural Networks Made Easy (Part 90): Frequency Interpolation of Time Series (FITS)
 Trading with the MQL5 Economic Calendar (Part 1): Mastering the Functions of the MQL5 Economic Calendar
Trading with the MQL5 Economic Calendar (Part 1): Mastering the Functions of the MQL5 Economic Calendar
 Connexus Helper (Part 5): HTTP Methods and Status Codes
Connexus Helper (Part 5): HTTP Methods and Status Codes
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use