Population optimization algorithms: Ant Colony Optimization (ACO)

The great secret of any behavior is social behavior...

F. Bartlett

Contents

1. Introduction
2. Algorithm principles
3. Modified version
4. Test results

1. Introduction

Belgian researcher Marco Dorigo has created a mathematical model that scientifically describes the process of collective intelligence in an ant colony. He published it in his doctoral dissertation in 1992 and implemented it as an algorithm.

Ant colony optimization (ACO) is a population-based stochastic search method for solving a wide range of combinatorial optimization problems. ACO is based on the concept of stigmergy. In 1959, Pierre-Paul Grasset invented the theory of stigmergy to explain the nest-building behavior of termites. Stigmergy consists of two Greek words: stigma - sign and ergon - action.

The canonical definition is an indirect type of interaction between members of a population extended in time through interaction with the environment. In other words, one of the agents leaves a trail or somehow modifies the locale so that another agent receives some information when entering its area. In case of ants, stigmergy is pheromones. An example of stigmergy is the communication of ants in the process of foraging: ants communicate indirectly with each other, leaving pheromone trails on the ground and thereby influencing the decision-making processes of other ants. This simple form of communication between individual ants gives rise to the complex behavior and capabilities of the colony as a whole.

Ants are social insects, they live in colonies. The behavior of ants is controlled by the purpose of searching for food. While searching, they roam their colonies. The ant repeatedly jumps from one place to another in search of food, and as it moves, it deposits an organic compound called a pheromone on the ground. Thus, ants communicate with each other using pheromone traces.

When an ant finds food, it carries as much as it can carry. When returning, it deposits pheromones along the way, depending on the quantity and quality of food. As a result, other ants can follow this route. The higher the pheromone level, the higher the probability of choosing this particular path, and the more ants pass a particular path, the more pheromone will be left on this route.

Let's see the following example. Suppose there are two ways to get food from the colony. First, there is no pheromone on the ground. So, the probability of choosing these two paths is equal (50%). Let's assume that two ants choose two different paths to the food. The distances of these two paths are different. The ant taking the shorter route will get to the food before the other one. When it finds the food, it takes some of it and returns to the colony. As it traces its way back, it deposits a pheromone on the ground. The ant taking a shorter path will reach the colony earlier.

When the third ant wants to go out in search of food, it will take a path that has a shorter distance depending on the level of pheromone on the ground. Because the shorter path has more pheromones than the longer one, the third ant will follow the path that has more pheromones. By the time the ant, following the longer path, returned to the colony, more ants had already passed the path with higher levels of pheromones. Then, when another ant tries to get to its destination (food) from the colony, it will find that each path has the same pheromone level. So it randomly chooses one of them. By repeating this process over and over again, after a while, the shorter path will gain more pheromones than the others and the probability of ants taking this path will be higher.

The ACO algorithm is a kind of swarm intelligence algorithm. By modeling the foraging process of an ant colony, the shortest path in various environments is established using the ant colony's internal data transfer mechanism. The higher the concentration of the pheromone remaining on the path, the higher the likelihood that the ant will choose this path. At the same time, the concentration of the pheromone diminishes over time. Therefore, due to the behavior of the ant colony, the ants are constantly learning and optimizing through a feedback mechanism to determine the shortest foraging path. The ACO algorithm is widely used in path planning.

2. Algorithm principles

In ACO, a set of software agents called artificial ants look for good solutions to a given optimization problem. To apply ACO, the optimization problem is transformed into the problem of finding the best path on a weighted graph. Artificial ants (hereinafter referred to as ants) gradually build solutions moving along the graph. The process of constructing a solution is stochastic and depends on the pheromone model - a set of parameters associated with graph components (nodes or edges) whose values are changed by ants during execution.

Let's consider the algorithm for the traveling salesman problem. We have a set of locations (cities) and distances between them. The problem is to find a closed path of minimum length that visits each city only once. A graph defined by associating a set of cities with a set of graph vertices is called a construction graph. Since it is possible to move from any given city to any other city, the construction graph is fully connected, and the number of vertices is equal to the number of cities. We set edge lengths between vertices proportional to the distances between cities represented by those vertices, and associate pheromone values and heuristic values with graph edges. The pheromone values change at runtime and represent the cumulative experience of the ant colony, while heuristic values are problem dependent values.

Ants construct solutions in the following way. Each ant starts from a randomly selected city (construction graph vertex). Then, at each construction step, it moves along the edges of the graph. Each ant stores the memory of its path, and, on subsequent steps, chooses among the edges that do not lead to the already visited vertices. The ant has built a solution as soon as it has visited all the vertices of the graph. At each construction step, the ant probabilistically chooses an edge to follow from among those that lead to yet unvisited vertices. The probabilistic rule is based on pheromone values and heuristic information: the higher the pheromone and heuristic value associated with an edge, the higher the probability that the ant will choose that particular edge. Once all the ants have completed their journey, the pheromones at the edges are updated. Each of the pheromone values is initially reduced by a certain percentage. This procedure is repeated until the termination criterion is satisfied.

Pheromone-based communication is one of the most effective communication methods widespread in nature. The pheromone is used by social insects such as bees, ants and termites for communication between agents. Because of their feasibility, artificial pheromones have been adopted in multi-robot and swarm robot systems.

How can we understand that our ants have really found the shortest route? There is a great test case for this: dots arranged in a circle. For them, the shortest path will always be the same - a circle.  

The first ACO algorithm was called the ant system and was aimed at solving the traveling salesman problem, the goal of which is to find the shortest way back and forth to connect a number of cities. The general algorithm is relatively simple and is based on a set of ants, each of which makes one of the possible rounds of cities. At each stage, the ant chooses a path from one city to another according to some rules:

1. It should visit each city exactly once;
2. A distant city is less likely to be selected (visibility);
3. The more intense the pheromone trail laid on the border between two cities, the more likely that this border will be chosen;
4. Having completed its path, the ant deposits more pheromones on all the edges it has passed if the path is short;
5. After each iteration, the pheromone trails evaporate.

Fig. 1. An example of possible paths at five nodal points

3. Modified version

Several of the most popular variants of ACO algorithms are known. Let's consider them:

Ant system (AS).
The ant system is the first ACO algorithm.

Ant colony system (ACS).
In the ant colony system algorithm, the original ant system has been modified in three aspects:
1. Edge selection is biased towards exploitation (i.e., in favor of the probability of choosing the shortest edges with more pheromones);
2. When building a solution, the ants change the level of pheromones on the edges they choose by applying a local pheromone update rule;
3. At the end of each iteration, only the best ant can update the tracks by applying the modified global pheromone update rule.

Elite ant system.
In this algorithm, the global best solution deposits the pheromone on its trail after each iteration (even if the trail has not been revisited) along with all other ants. The goal of the elite strategy is to direct the search of all ants to construct a solution containing links of the current best route.

Max-min ant system (MMAS).
This algorithm controls the maximum and minimum number of pheromones on each trail. Only the best global tour or the best repeat tour can add pheromones to their trail. To avoid stagnation of the search algorithm, the range of possible amounts of pheromones on each trace is limited by the interval [τ max, τ min]. All edges are initialized with τ max to speed up the exploration of the solution. The traces are reinitialized to τ max when approaching stagnation.

Ant system based on ranks (Asrank).
All solutions are ranked according to their length. Only a fixed number of the best ants in this iteration can update their challenges. The amount of pheromone deposited is weighed for each solution, so that solutions with shorter paths deposit more pheromone than solutions with longer paths.

Parallel ant colony optimization (PACO).
Ant colony system (ACS) with communication strategies.
Artificial ants are divided into several groups. Seven communication methods are proposed to update pheromone levels between groups in the ACS that work on the traveling salesman problem.

Continuous orthogonal ant colony (COAC).
The COAC pheromone deposition mechanism allows ants to seek solutions collaboratively and efficiently. By using the orthogonal design method, ants in the allowable area can quickly and efficiently explore their chosen areas with enhanced global search capabilities and accuracy. The orthogonal design method and the adaptive radius tuning method can also be extended to other optimization algorithms to provide broader advantages in solving practical problems.

Recursive optimization of an ant colony.
This is a recursive form of an ant colony that divides the entire search area into several subdomains and solves the problem in these subdomains. The results of all subdomains are compared, and the few best ones move to the next level. The subdomains corresponding to the selected results are further subdivided and the process is repeated until the desired accuracy is obtained. This method has been tested on incorrect geophysical inversion problems proving its efficiency.

The ant colony algorithms considered above were originally developed for solving optimization problems on graphs. The problem is integrated into such algorithms, and the problem conditions are given as algorithm parameters - the coordinates of the graph nodes. Therefore, the algorithms based on the ACO principles are highly specialized. Such algorithms are not applicable for our tasks since we do not use fixed coordinates. We may have any coordinates, including the similar ones. To solve a wide range of optimization problems in the field of trading financial instruments, including training neural networks, we need to develop a new universal algorithm, so that it can pass our special tests, i.e. it should be a brand new ACO.

Let's think over the basic concept of the algorithm. Just like in the canonical version, we will have an ant colony. We cannot mark the traveled paths with pheromones, they can go anywhere in a multidimensional space, memorize and save routes. With a continuous step, it does not seem appropriate, because the probability of going along the same route tends to zero. In addition, there is no need to memorize nodes at all, since there is no problem of sequential passage without repetitions - it is necessary to take the problem out of the algorithm. So, what should we do? At this stage, it is completely unclear, which direction to take in the development of the concept.

Well, then once again we note the main points that distinguish our new algorithm from the canonical one:

1. There are no fixed points in space.

2. There is no need to go through the path in a certain order.

3. Since there are no paths, there is nothing to mark with pheromones.

Then, let's find out what we have keeping in mind the idea of an ant colony. We can mark with pheromones the very points where the ants walked, not the path they traveled. Let's set the value of the fitness function as the number of pheromones at the ant's location at the current iteration. Then the ants will have to move towards the coordinates where the most pheromones are. But we can run into a problem when all the ants simply run to one point - the one that has the most pheromones. This is not necessarily the best solution to the problem considering that the points are the variables of the optimized function. We remember that in classical ACO the length of the path to the node also matters. The shorter the chosen path, the better. So we have to calculate the distance from the current location to where the ant should go. The next place is where the other ants are, i.e. we accept the concept that ants move towards each other with a certain amount of randomness.

What kind of randomness can we add to the movement?

• First, add the random factor when choosing the next position PheromoneEffect_P.
• Second, add a random factor taking into account the distance to the next position PathLengthEffect_P (the smaller the distance, the better the choice).

So, we have two criteria for choosing the next position - the amount of pheromones in each specific position where the ants are located and the distance between all these points in pairs. However, even if we do this using only these two selection criteria, then the ants will move in space along the edges of an imaginary figure, the nodes of which are their own location. So, there will be no progress in finding a better place.

In this case, add the radius of influence of the pheromone PheromoneRadius_P (ratio of the distance between points), within which the ants can feel it. Then the ants will be able to slip past the point it moved to. This will give an additional degree of freedom to the ants when moving in multidimensional space.

In order for the ants to explore new areas, they need to be allowed to deviate from the direction vector along any of the coordinates. Let's introduce the PathDeviation_P ratio, which will give the deviation from the increment at a specific coordinate. Since we have a multidimensional space, following the displacement vector, some coordinates can have a positive increment, while others can have a negative one, and the increments can have different modulo values. This ratio will make it possible to take all this into account and will give some degree of freedom to the ants in the search for food (the extremum of the function).

So what is the displacement vector and how do we measure the distance the ant has to travel? To answer these questions, use the equation for calculating the distance between two points in three-dimensional space:

A visual representation of the displacement vector can be obtained by looking at Figure 2.

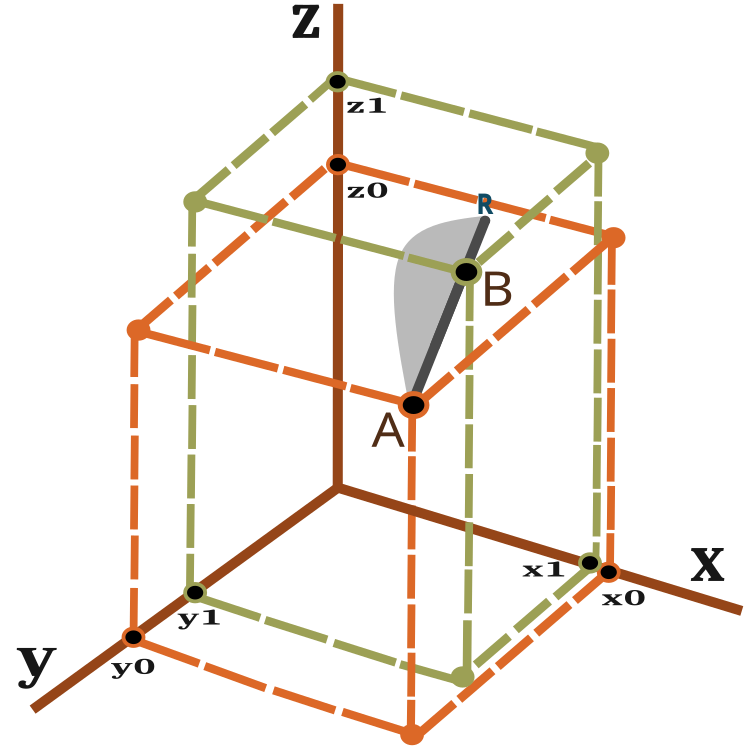
Fig 2. Ant moving vector

For n-dimensional spaces, the calculation is similar.

An ant in one iteration (epoch) moves from point A to point B with possible slippage to point R. The distance to point R from point B depends on the PheromoneRadius_P ratio and can be calculated as BR = AB x PheromoneRadius_P.

The probability of a new location on the AR line is shown in Figure 2 as a gray area schematically (not to scale). Thus, the new location of the ant is more likely to tend to the point B. The principle of probability shift has been discussed in the previous article.

The algorithm includes the following steps at each iteration:

1) Random arrangement of ants in space.
2) Determining the value of the amount of pheromone (fitness function) for ants.
3) Calculation of the distance from one ant to another.
4) The choice of the preferred point where the ant will move.
5) Calculation of the probability of a point on the AR vector.
6) Calculation of the coordinates of the point obtained on the AR vector.
7) Repeat from step 2 until the stop condition is met.

Let's proceed to the description of the algorithm code. First of all, let's write a structure containing a description of the ant, where:

• c [] - ant coordinates, 
• cLast [] - previous coordinates,
• cB [] - best coordinates for all iterations,
• f - current pheromone value,
• fB - maximum pheromone value reached in all iterations.

In the constructor of the ant structure, we initialize the value of f and fB with the minimum possible value that can be represented by the 'double' type.

//——————————————————————————————————————————————————————————————————————————————
struct S_Ants
{
    double cLast  []; //last coordinates
    double c      []; //coordinates
    double cB     []; //best coordinates

    double f;     //pheromone of the current coordinates
    double fB;    //pheromone of the best coordinates

    S_Ants ()
    {
      f  = -DBL_MAX;
      fB = -DBL_MAX;
    }
};
//——————————————————————————————————————————————————————————————————————————————

We need a structure whose array will allow us to store pairwise distances between all ants.

struct S_Paths
{
    double a [];
};

I will write our modified ACO algorithm as a class, in which there are still only three public methods that are sufficient and necessary within the framework of the developed concept of constructing optimization algorithms, considered in previous articles - InitAnts (), Preparation () and Dwelling (). There are also GenerateRNDants () and AntsMovement () private methods, as well as other private methods that have already become standard for our algorithms. The ants [] structure array is a colony of ants.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACO
{
  public:
  //----------------------------------------------------------------------------
  S_Ants ants      []; //ants
  double rangeMax  []; //maximum search range
  double rangeMin  []; //manimum search range
  double rangeStep []; //step search
  double cB        []; //best coordinates
  double fB;           //pheromone of the best coordinates

  void InitAnts (const int    coordinatesP,       //number of opt. parameters
                 const int    antHillSizeP,
                 double       pheromoneEffectP,
                 double       pathLengthEffectP,
                 double       pheromoneRadiusP,
                 double       pathDeviationP);

  void Preparation ();
  void Dwelling ();

  private:
  //----------------------------------------------------------------------------
  S_Paths paths [];
  int coordinates;        //number of coordinates
  int antHillSize;        //ant hill size

  double goals     [];

  double pheromoneEffect;
  double pathLengthEffect;
  double pheromoneRadius;
  double pathDeviation;
  bool   dwelling;

  void   GenerateRNDants ();
  void   AntsMovement    ();

  double SeInDiSp             (double in, double inMin, double inMax, double step);
  double RNDfromCI            (double min, double max);
  double Scale                (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

In the initialization method, assign initial values to variables and the array size.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::InitAnts (const int    coordinatesP,       //number of opt. parameters
                         const int    antHillSizeP,
                         double       pheromoneEffectP,
                         double       pathLengthEffectP,
                         double       pheromoneRadiusP,
                         double       pathDeviationP)
{
  fB = -DBL_MAX;

  coordinates      = coordinatesP;
  antHillSize      = antHillSizeP;
  pheromoneEffect  = pheromoneEffectP;
  pathLengthEffect = pathLengthEffectP;
  pheromoneRadius  = pheromoneRadiusP;
  pathDeviation    = pathDeviationP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);

  dwelling = false;

  ArrayResize (ants,  antHillSize);
  ArrayResize (paths, antHillSize);

  for (int i = 0; i < antHillSize; i++)
  {
    ArrayResize (ants  [i].c,      coordinates);
    ArrayResize (ants  [i].cLast,  coordinates);
    ArrayResize (ants  [i].cB,     coordinates);
    ArrayResize (paths [i].a,      antHillSize);
  }

  ArrayResize (cB,    coordinates);
  ArrayResize (goals, antHillSize);
}
//——————————————————————————————————————————————————————————————————————————————

The Preparation () method is called first at each iteration.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Preparation ()
{
  if (!dwelling)
  {
    fB = -DBL_MAX;
    GenerateRNDants ();
    dwelling = true;
  }
  else AntsMovement ();
}
//——————————————————————————————————————————————————————————————————————————————

The GenerateRNDants () method is responsible for creating a random ant colony. Ant coordinates are randomly assigned within the given limits.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::GenerateRNDants ()
{
  for (int s = 0; s < antHillSize; s++)
  {
    for (int k = 0; k < coordinates; k++)
    {
      ants [s].c     [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      ants [s].c     [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
      ants [s].cLast [k] = ants [s].c [k];
      ants [s].cB    [k] = ants [s].c [k];
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Remember the current coordinates of the ants in the Dwelling () method and update the maximum pheromone values obtained at the time of the current iteration.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::Dwelling ()
{
  for (int i = 0; i < antHillSize; i++)
  {
    ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY);

    //remember the best coordinates for the ant
    if (ants [i].f > ants [i].fB)
    {
      ants [i].fB = ants [i].f;
      ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }

    //remember the best coordinates for the anthill
    if (ants [i].f > fB)
    {
      fB = ants [i].f;
      ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

The main method of the AntsMovement () algorithm. It performs the following actions: calculating the distance from one ant to another, calculating the choice of a preferred point where the ant will move, calculating the probability of a point on the AR vector. Calculation of the coordinates of the point obtained on the AR vector.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACO::AntsMovement ()
{
  double rndPh;
  double rndPt;
  double summCoordinates = 0.0;
  double scores [];
  ArrayResize (scores, antHillSize);

  double maxPh = -DBL_MAX;
  double minPh =  DBL_MAX;
  double maxPt = -DBL_MAX;
  double minPt =  DBL_MAX;
  double goal;
  double goalBest = -DBL_MAX;
  int    goalInd  = 0;

  //measure the distance between all the ants-----------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    for (int k = 0; k < antHillSize; k++)
    {
      if (i == k)
      {
        paths [i].a [k] = DBL_MAX;
        continue;
      }
         
      for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0);

      paths [i].a [k] = pow (summCoordinates, 0.5);

      if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k];
      if (minPt > paths [i].a [k]) minPt = paths [i].a [k];
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < antHillSize; i++)
  {
    maxPh = -DBL_MAX;
    minPh =  DBL_MAX;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        if (maxPh < ants [k].f) maxPh = ants [k].f;
        if (minPh > ants [k].f) minPh = ants [k].f;
      }
    }

    goalBest = -DBL_MAX;
    goalInd  = 0;

    for (int k = 0; k < antHillSize; k++)
    {
      if (i != k)
      {
        rndPh = RNDfromCI (0.0, pheromoneEffect);
        rndPt = RNDfromCI (0.0, pathLengthEffect);

        goal = Scale (ants  [k].f,     minPh, maxPh, 0.0, 1.0, false) * rndPh *
               Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true)  * rndPt;

        if (goalBest < goal)
        {
          goalBest = goal;
          goalInd  = k;
        }
      }
    }
    
    double wayToGoal      = paths [i].a [goalInd];
    double radiusNearGoal = wayToGoal * pheromoneRadius;
    double endWay         = wayToGoal + radiusNearGoal;

    double x = RNDfromCI (-1.0, 1.0);
    double y = x * x;
    
    if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay,    false);
    else         y = Scale (y, 0.0, 1.0, 0.0,       wayToGoal, true);

    for (int j = 0; j < coordinates; j++)
    {
      double incrementFactor = y / wayToGoal;
      double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j];
      
      ants [i].c [j] =  ants [i].cLast [j] + (coordDistance * incrementFactor);
      double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation;
      ants [i].c [j] += w;
      
      ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

It is worth paying attention to the function of scaling a number from one numerical range to another. I have already considered it in previous articles. This time I will expand its functionality. The revers input is used to change the scaling direction as shown in the figure below.

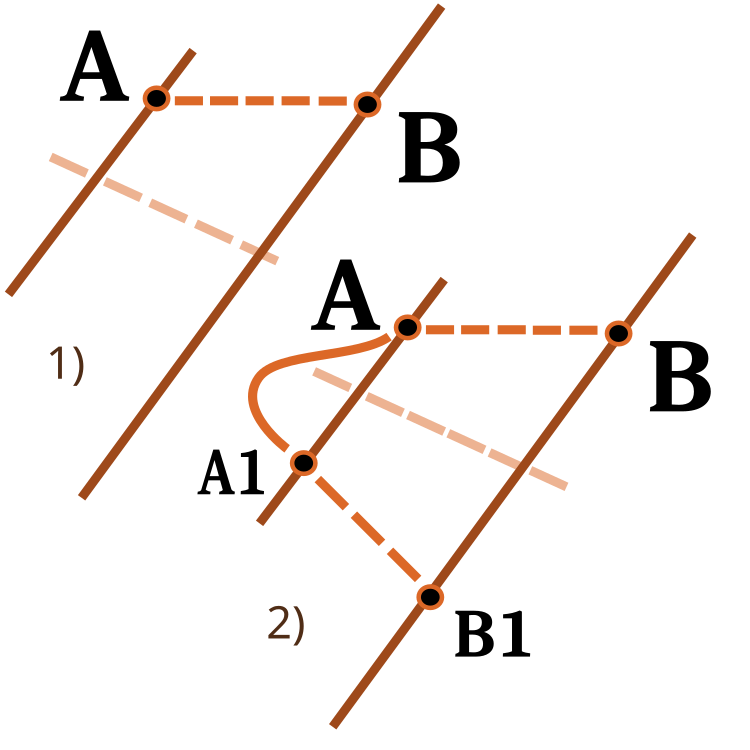
Fig. 3. Scaling a number from one numeric range to another.

1) Direct scaling; 2) Reverse scaling

//——————————————————————————————————————————————————————————————————————————————
double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers)
{
  if (OutMIN == OutMAX) return (OutMIN);
  if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0));
  else
  {
    if (In < InMIN) return revers ? OutMAX : OutMIN;
    if (In > InMAX) return revers ? OutMIN : OutMAX;

    double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN);

    if (!revers) return res;
    else         return OutMAX - res;
  }
}
//——————————————————————————————————————————————————————————————————————————————

4. Test results

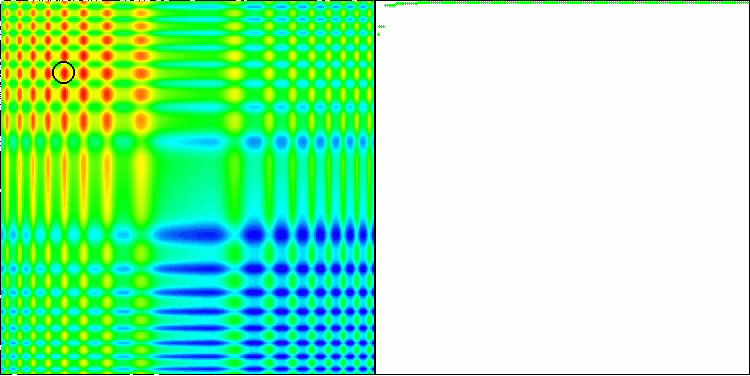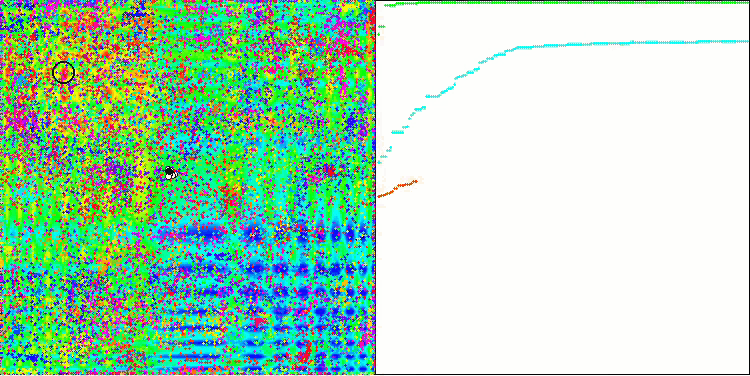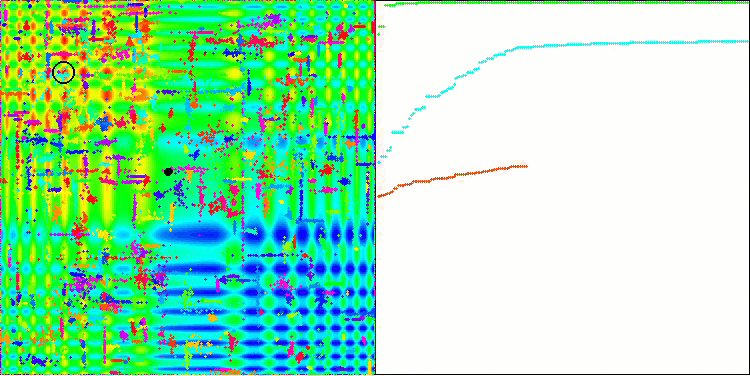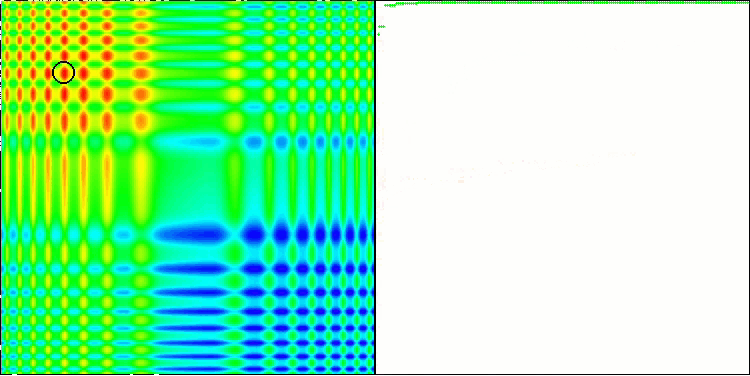
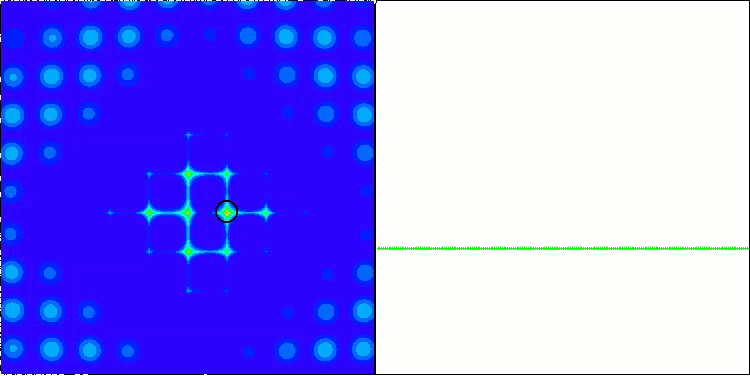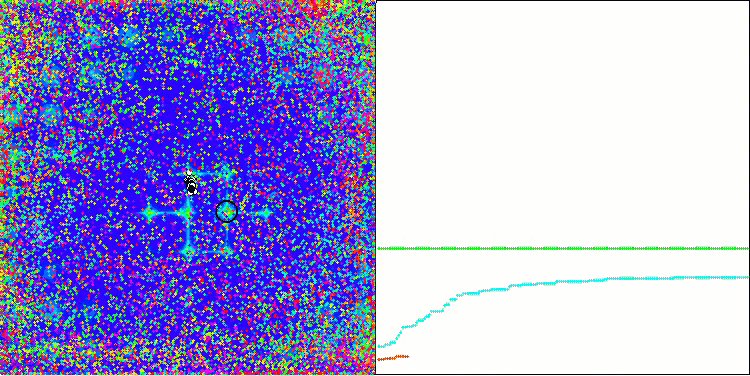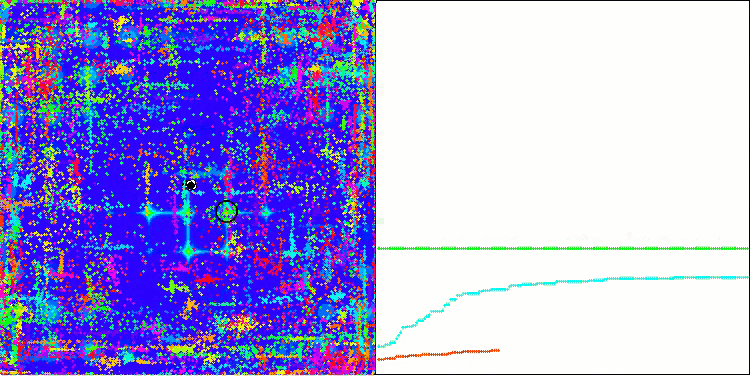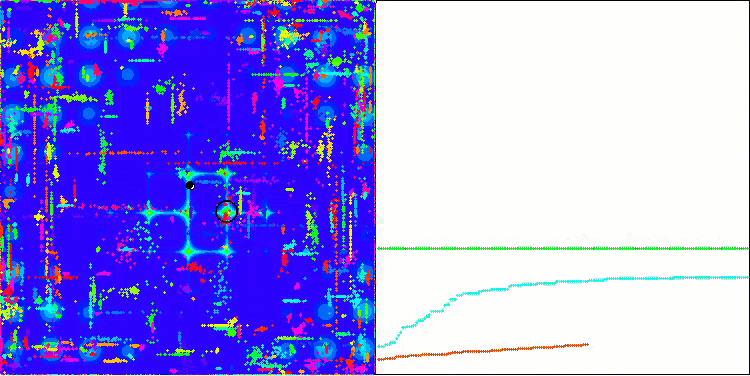
ACO on the Skin test function

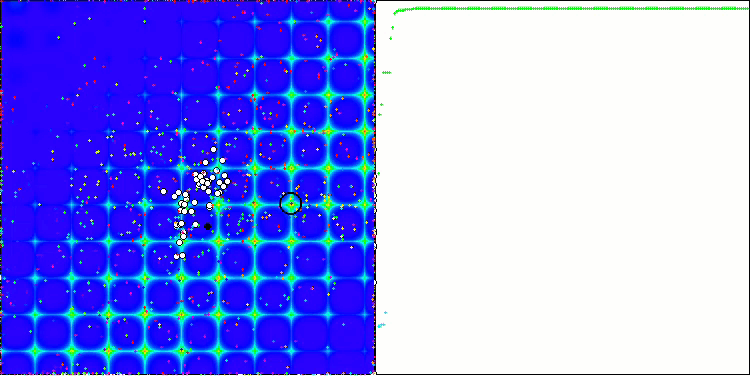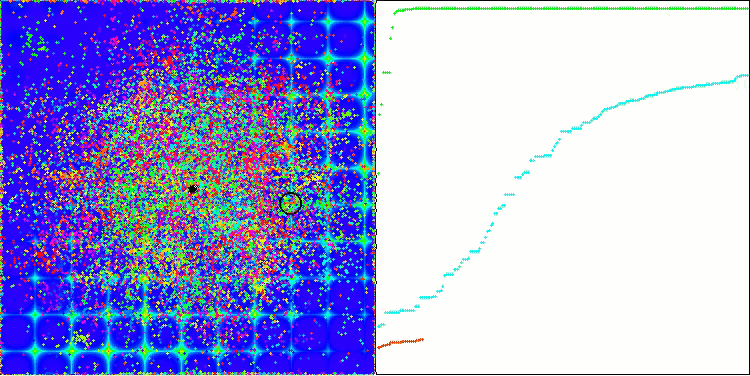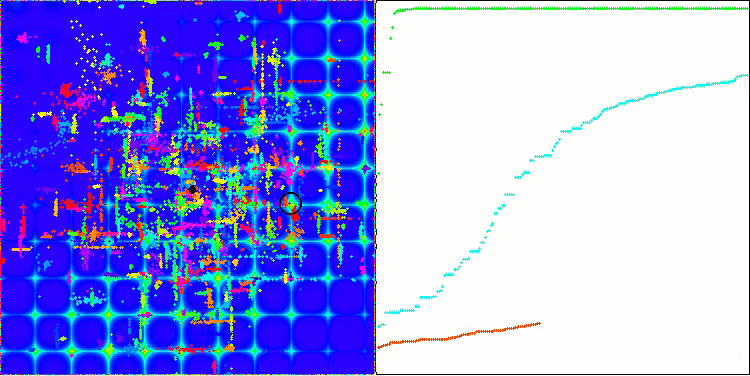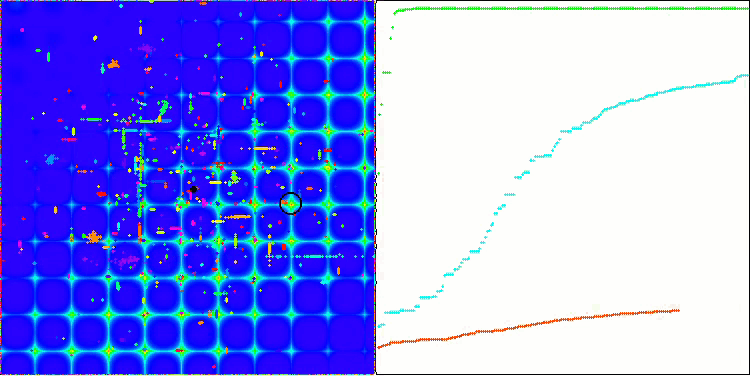
ACO on the Forest test function

ACO on the Megacity test function

So, it is time for conclusions. On the one hand, the conventional Ant Colony algorithm is not applicable to optimization problems for trading financial instruments. However, in an attempt to avoid the limitations of the conventional version, we have witnessed the emergence of a completely new concept of the Ant Colony algorithm allowing for further ACO development. Such an algorithm can already be applied to a wide range of problems, including the traveling salesman problem.

In addition, we now have a new leader of the rating table. Let's consider the results in more detail. First, pay attention to the results of the test stand:

2022.10.27 16:46:28.678    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085
2022.10.27 16:46:50.599    Test_AO_ACO (EURUSD,M1)    Score1: 0.99502; Score2: 0.99599
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023
2022.10.27 16:47:12.424    Test_AO_ACO (EURUSD,M1)    Score1: 0.69826; Score2: 0.86403
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    Score1: 0.50498; Score2: 0.58800
2022.10.27 16:48:04.200    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518
2022.10.27 16:48:25.999    Test_AO_ACO (EURUSD,M1)    Score1: 0.99087; Score2: 0.99302
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266
2022.10.27 16:48:47.897    Test_AO_ACO (EURUSD,M1)    Score1: 0.22374; Score2: 0.65571
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    Score1: 0.08408; Score2: 0.17442
2022.10.27 16:49:41.855    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8
2022.10.27 16:50:03.740    Test_AO_ACO (EURUSD,M1)    Score1: 0.78667; Score2: 0.78667
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004
2022.10.27 16:50:26.002    Test_AO_ACO (EURUSD,M1)    Score1: 0.11667; Score2: 0.26133
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    Score1: 0.04224; Score2: 0.08208

2022.10.27 16:49:41.075    Test_AO_ACO (EURUSD,M1)    =============================
2022.10.27 16:51:21.075    Test_AO_ACO (EURUSD,M1)    All score for C_AO_ACO: 0.5468768583006471

The algorithm performed well on the smooth Skin function, demonstrating excellent convergence and good scaling capabilities, being especially well ahead in the 20 and 500 function tests. On the smooth Forest function with sharp breaks, the separation is even more noticeable. The algorithm continues the search even when it hits local extrema. On the discrete Megacity function, the algorithm yielded to the random RND algorithm only on the problem with 500 functions.

AO	Runs	Skin			Forest			Megacity (discrete)			Final result
		2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)	2 params (1 F)	40 params (20 F)	1000 params (500 F)
ACOm	1000	0.99502	0.69826	0.50498	0.99087	0.22374	0.08408	0.78667	0.11667	0.04224	0.54688
	10,000	0.99599	0.86403	0.58800	0.99302	0.65571	0.17442	0.78667	0.26133	0.08208
RND	1000	0.98744	0.61852	0.49408	0.89582	0.19645	0.14042	0.77333	0.19000	0.14283	0.51254
	10,000	0.99977	0.69448	0.50188	0.98181	0.24433	0.14042	0.88000	0.20133	0.14283
PSO	1000	0.98436	0.72243	0.65483	0.71122	0.15603	0.08727	0.53333	0.08000	0.04085	0.47695
	10,000	0.99836	0.72329	0.65483	0.97615	0.19640	0.09219	0.82667	0.10600	0.04085
PSOm	1000	0.96678	0.64727	0.57654	0.80616	0.13388	0.06800	0.53333	0.08067	0.04211	0.45144
	10,000	0.99505	0.64986	0.57654	0.90401	0.18194	0.07104	0.74667	0.10400	0.04211

Conclusions

The algorithm has a lot of settings, so it is possible to get even better results. Ability to customize for specific types of tasks. The first parameter PheromoneEffect_P directly affects the rate of convergence. This is especially good for smooth monotonic functions, for example, a parabola. The convergence will be 100%, but this will simultaneously contribute to getting stuck in local extrema on discrete functions if it is set large.

The second parameter PathLengthEffect_P shows the degree of laziness of the ants. In case of a high parameter value, closer targets will be selected for moving. It is necessary to balance this parameter with the first one in order to obtain the best result. This parameter is designed to provide a counterweight to the desire of the ant to go to the point where there is more food, instead sometimes choosing the nearest targets for a more detailed examination of small areas, which can be very useful as in the example of the Forest function, where the best point may turn out to be very close.

The most important achievement is that we have managed to get rid of the main problem of the canonical ACO: the ability to solve only discrete combinatorial problems. Now the Ant Colony algorithm can be used to train neural networks.

Visually, the test stand is very interesting to observe due to a certain clustering, the ants are concentrated in the measurements of a multidimensional function in a certain way highlighting the characteristic groups of local extrema. Perhaps, this effect can be used to solve specific problems, but this will require additional research.

The algorithm has an interesting property: when solving a problem with two variables, the probability of getting stuck in a local extremum is somewhat higher than when optimizing 40 variables. The algorithm continues to search for solutions involving multiple variables. I assume that this is the effect of using a vector as a means of linking all the coordinates of the search space. For example, if an ant moved to a new better place, then all the coordinates changed spatially for the better, rather than some of the coordinates changing separately.

The created algorithm is new and unexplored in detail, so I will be grateful if someone shares the algorithm settings, in which the test stand will show a final value greater than 0.6 so that I can update the results of the table. This request applies to previously considered algorithms.

Pros:
1. The algorithm is quite fast.
2. Versatility. The algorithm can be used in a variety of optimization problems.
3. The ability to not focus only on local extrema.
4. Fairly good convergence for both smooth and discrete functions.
5. Scalable.

Cons:
1. Perhaps, more iterations are required for convergence than the same PSO for smooth functions, but this is partially offset by the ability to continue the search even where PSO has already stopped.
2. Strong influence of the algorithm parameters on the result.