Neuronale Netze im Handel: Modelle mit Wavelet-Transformation und Multitasking-Aufmerksamkeit

Einführung

Die Vorhersage von Vermögensrenditen ist ein weithin untersuchtes Thema im Finanzwesen. Die Herausforderung der Renditeprognose ergibt sich aus mehreren Faktoren. Erstens ist es aufgrund der Vielzahl von Variablen, die die Renditen von Vermögenswerten beeinflussen, und des geringen Verhältnisses von Signal zu Rauschen in großen, spärlichen Matrizen schwierig, mit herkömmlichen ökonometrischen Modellen aussagekräftige Informationen zu gewinnen. Zweitens sind die funktionalen Beziehungen zwischen den prädiktiven Merkmalen und den Renditen von Vermögenswerten nach wie vor unklar, sodass es schwierig ist, die nichtlinearen Strukturen zwischen ihnen zu erfassen.

In den letzten Jahren hat sich Deep Learning zu einem unverzichtbaren Instrument für quantitatives Investieren entwickelt, insbesondere bei der Verfeinerung von Multifaktor-Strategien, die die Grundlage für das Verständnis der Preisentwicklung von Finanzanlagen bilden. Durch die Automatisierung des Merkmalslernens und die Erfassung nichtlinearer Beziehungen in Finanzmarktdaten decken Deep-Learning-Algorithmen komplexe Muster auf und verbessern so die Vorhersagegenauigkeit. Die weltweite Forschungsgemeinschaft erkennt das Potenzial von tiefen neuronalen Netzen wie rekurrenten neuronalen Netzen (RNNs) und faltbaren neuronalen Netzen (CNNs) für die Preisvorhersage von Aktien und Futures. Während RNNs und CNNs weit verbreitet sind, sind tiefere neuronale Architekturen, die sequenzielle Markt- und Signalinformationen extrahieren und konstruieren, noch nicht ausreichend erforscht. Dies eröffnet Möglichkeiten für weitere Fortschritte bei der Anwendung von Deep Learning auf Aktienmärkte.

Heute stellen wir das System Multitask-Stockformer vor, das in dem Artikel „Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks“. Trotz der Ähnlichkeit des Namens mit dem zuvor besprochenen Systems StockFormer sind diese beiden Modelle nicht miteinander verwandt – bis auf ihr gemeinsames Ziel: die Erstellung zeines profitablen Aktienportfolios für den Handel auf den Finanzmärkten.

Der Multitask-Stockformer baut ein Multitasking-Aktienprognosemodell auf, das auf Wavelet-Transformation und Selbstaufmerksamkeitsmechanismen basiert.

Der Algorithmus von Multitask-Stockformer

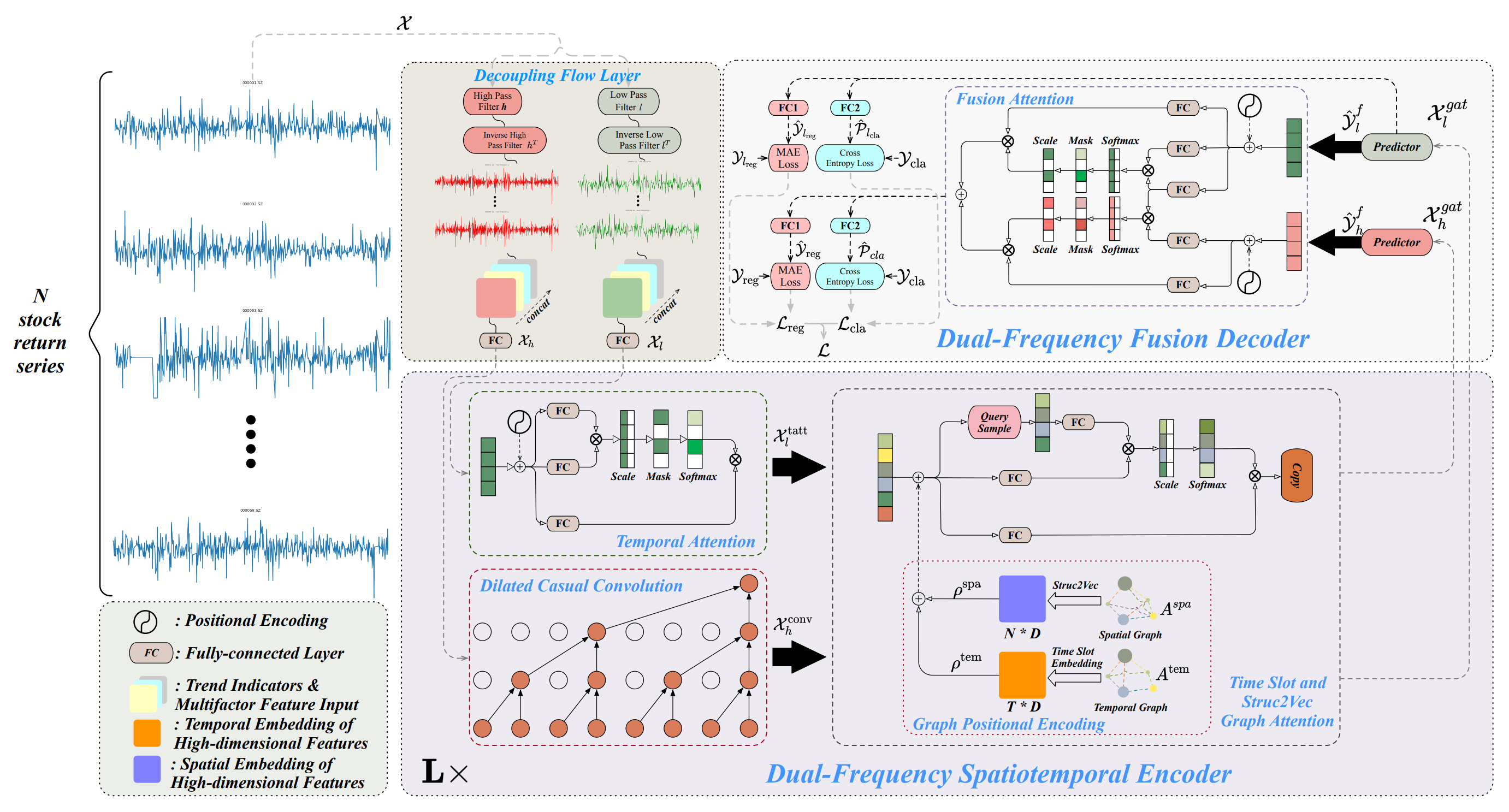
Die Architektur des Systems Multitask-Stockformer ist in drei Module unterteilt: ein Flow-Separationsmodul, einen raum-zeitlichen Zweifrequenz-Encoder und einen Zweifrequenz-Decoder. Die analysierten historischen Bestandsdaten 𝒳 ∈ RT1×N×362 werden im Stromtrennungsmodul verarbeitet. In diesem Stadium wird der Renditetensor der Vermögenswerte mit Hilfe einer diskreten Wavelet-Transformation in hoch- und niederfrequente Komponenten zerlegt, während Trendmerkmale und Preis-Volumen-Verhältnisse unverändert bleiben. Diese Komponenten werden dann mit den unveränderten Teilen des Signals entlang der letzten Dimension verkettet.

Die Niederfrequenzkomponente steht für langfristige Trends, während die Hochfrequenzkomponente kurzfristige Schwankungen und starke Ereignisse erfasst. Diese werden bezeichnet als 𝒳l bzw. 𝒳h ∈ RT1×N×362. Anschließend werden sowohl 𝒳h und 𝒳l linear durch eine vollständig verbundene Schicht in die Dimension RT1×N×D. Dabei bezeichnet T1 die Tiefe der analysierten historischen Daten.

Der Zweifrequenz-Raum-Zeit-Kodierer wurde entwickelt, um diese unterschiedlichen Zeitreihenmuster darzustellen: Niederfrequente Merkmale werden in ein zeitliches Aufmerksamkeitsmodul (bezeichnet als tatt) eingespeist, während hochfrequente Merkmale durch eine erweiterte kausale Faltungsschicht (bezeichnet als conv) verarbeitet werden. Diese Komponenten werden dann in Graphen-Aufmerksamkeitsnetzwerke (bezeichnet als gat) eingegeben. Durch die Interaktion mit den Informationen der Graphen kann das Modell komplexe Beziehungen und Abhängigkeiten zwischen Vermögenswerten und Zeit erfassen. In diesem Modul werden der räumliche Graph Aspa und der zeitliche Graph Atem durch vollständig verbundene Schichten und Tensor-Translationsoperationen in mehrdimensionale Einbettungen transformiert, die mit ρspa, ρtem ∈ RT1×N×D, die dann mit 𝒳 kombiniert werdenl,tatt, 𝒳h,conv durch Addition und Graph-Attention-Operationen kombiniert werden, um 𝒳l,gat, 𝒳h,gat ∈ RT1×N×D. Der Zweifrequenz-Raum-Zeit-Kodierer besteht aus L Schichten, die darauf abzielen, multiskalige Raum-Zeit-Muster von nieder- und hochfrequenten Wellen effizient darzustellen. Im Zweifrequenzdecoder schließlich erzeugen die Prädiktoren 𝒴l,f, 𝒴h,f ∈ RT2×N×D, die mit Hilfe von Fusion Attention Interactions aggregiert werden, um eine latente Repräsentation von zweiskaligen zeitlichen Mustern zu erhalten. Getrennte, vollständig verknüpfte Schichten (eine Regressionsschicht, FC1, und eine Klassifizierungsschicht, FC2) erzeugen Multitasking-Ausgaben, einschließlich Prognosen für Aktienrenditen (die Regressionsausgabe, bezeichnet mit reg) und Wahrscheinlichkeiten für Aktientrendvorhersagen (die Klassifizierungsausgabe, bezeichnet mit cla).

Zusätzlich werden Regressionswerte und Trendvorhersagewahrscheinlichkeiten für die niederfrequente Komponente abgeleitet, wodurch der Lernprozess des niederfrequenten Signals verbessert wird.

Eine vom Autor zur Verfügung gestellte Visualisierung des Systems Multitask-Stockformer ist unten abgebildet.

Die Implementation in MQL5

Dies ist nur eine kurze Beschreibung des Systems Multitask-Stockformer. Der Rahmen ist ziemlich komplex. Ich glaube, dass es effektiver ist, sich während der Umsetzung mit den einzelnen Algorithmen vertraut zu machen. Wir werden mit der Arbeit am Modul zur Trennung der Rohdaten beginnen.

Modul für die Signalaufspaltung

Um das analysierte Signal in niederfrequente und hochfrequente Komponenten aufzuteilen, schlagen die Autoren des Systems die diskrete Wavelet-Transformation vor. Im Gegensatz zur Fourier-Zerlegung ist die Wavelet-Transformation in der Lage, nicht nur den Frequenzinhalt, sondern auch die Struktur des Signals zu erfassen. Dies macht es für die Finanzmarktanalyse vorteilhafter, bei der nicht nur die Häufigkeit, sondern auch die Reihenfolge der Signale wichtig ist.

Zuvor haben wir bereits die diskrete Wavelet-Transformation bei der Erstellung des FEDformer verwendet, aber nur die niederfrequente Komponente extrahiert. Jetzt brauchen wir auch noch die Hochfrequenzkomponente. Dennoch können wir bestehende Entwicklungen wiederverwenden.

Die diskrete Wavelet-Transformation ist im Wesentlichen eine Faltungsoperation, bei der ein bestimmtes Wavelet als Filter verwendet wird. Dies ermöglicht es uns, Faltungsschichtalgorithmen als Basisfunktionalität zu verwenden. Es ist zu beachten, dass wir bei der Transformation statische Wavelets verwenden, deren Parameter sich während des Trainings nicht ändern. Daher müssen wir den Optimierungsmechanismus für die Parameter unseres Objekts deaktivieren.

Vor diesem Hintergrund erstellen wir ein neues Objekt zur Extraktion von hoch- und niederfrequenten Signalkomponenten unter Verwendung der diskreten Wavelet-Transformation CNeuronLegendreWaveletsHL.

class CNeuronLegendreWaveletsHL :  public CNeuronConvOCL
  {
protected:
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL)   { return true; }

public:
                     CNeuronLegendreWaveletsHL(void) {};
                    ~CNeuronLegendreWaveletsHL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                          uint window, uint step, uint units_count, 
                          uint filters, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch) override;
   //---
   virtual int       Type(void)   const   {  return defNeuronLegendreWaveletsHL;   }
   //---
   virtual uint      GetFilters(void)  const {return (iWindowOut / 2); }
   virtual uint      GetVariables(void)  const {return (iVariables); }
   virtual uint      GetUnits(void)  const {return (Neurons() / (iVariables * iWindowOut)); }
  };

Wie bereits erwähnt, ist die diskrete Wavelet-Transformation eine Faltung mit einem Wavelet-Filter. Auf diese Weise können wir die Funktionalität der übergeordneten Faltungsschichtklasse bei der Erstellung des Algorithmus vollständig nutzen. Es genügt, die Initialisierungsmethode außer Kraft zu setzen und die zufälligen Filterparameter durch die Wavelet-Daten zu ersetzen.

Die verwendeten Wavelet-Filter sind jedoch statisch. Daher überschreiben wir die Parameteroptimierungsmethode updateInputWeights mit einer No-op-Implementierung.

Die Initialisierung des neuen Objekts wird in der Methode Init durchgeführt. Wie üblich erhält diese Methode von dem externen Programm eine Reihe von Konstanten, die die Architektur des zu erstellenden Objekts eindeutig identifizieren. Dazu gehören:

• window – die Größe des Analysefensters;
• step – die Schrittweite des Analysefensters;
• units_count – die Anzahl der Faltungsoperationen pro einzelner Sequenz;
• filter – die Anzahl der verwendeten Filter;
• variables – die Anzahl der einzelnen Sequenzen in der analysierten multimodalen Zeitreihe. 

bool CNeuronLegendreWaveletsHL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                     uint window, uint step, uint units_count, 
                                     uint filters, uint variables, 
                                     ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, window, step, 2 * filters, 
                                  units_count, variables, optimization_type, batch))
      return false;

Innerhalb des Methodenkörpers übergeben wir die erhaltenen Parameter sofort an die gleichnamige Methode der Elternklasse. Beachten Sie jedoch, dass wir beim Aufruf der übergeordneten Methode die Anzahl der Filter verdoppeln. Dies ist darauf zurückzuführen, dass Filter für die Extraktion sowohl der nieder- als auch der hochfrequenten Komponenten erstellt werden müssen.

Nach erfolgreicher Beendigung der übergeordneten Methode wird der Puffer für die Faltungsparameter mit Nullen gefüllt und im Puffer ein konstanter Abstand zwischen den Elementen der Nieder- und Hochfrequenzfilter definiert.

   WeightsConv.BufferInit(WeightsConv.Total(), 0);
   const uint shift_hight = (iWindow + 1) * filters;

Wir organisieren dann ein System von verschachtelten Schleifen, um die erforderliche Anzahl von Filtern zu erzeugen. Hier verwenden wir eine rekursive Generierung von Legendre-Wavelets und füllen die Filtermatrix sequentiell mit Wavelets höherer Ordnung.

   for(uint i = 0; i < iWindow; i++)
     {
      uint shift = i;
      float k = float(2.0 * i - 1.0) / iWindow;
      for(uint f = 1; f <= filters; f++)
        {
         float value = 0;
         switch(f)
           {
            case 1:
               value = k;
               break;
            case 2:
               value = (3 * k * k - 1) / 2;
               break;
            default:
               value = ((2 * f - 1) * k * WeightsConv.At(shift - (iWindow + 1)) - 
                       (f - 1) * WeightsConv.At(shift - 2 * (iWindow + 1))) / f;
               break;
           }

Für jedes Element des Analysefensters erstellen wir eine innere Schleife, um Filterelemente zu erzeugen. In dieser Schleife erzeugen wir zunächst das Element des entsprechenden Niederfrequenzfilters.

Anschließend erstellen wir eine weitere verschachtelte Schleife, in der wir das erzeugte Element in die Filter für alle unabhängigen Variablen der multimodalen Sequenz übertragen. Gleichzeitig fügen wir das Hochfrequenz-Filterelement hinzu, das auf dem entsprechenden Niederfrequenz-Filterelement basiert.

         for(uint v = 0; v < iVariables; v++)
           {
            uint shift_var = 2 * shift_hight * v;
            if(!WeightsConv.Update(shift + shift_var, value))
               return false;
            if(!WeightsConv.Update(shift + shift_var + shift_hight, 
                                    MathPow(-1.0f, float(i))*value))
               return false;
           }

Dann passen wir den Versatz zum nächsten Filterelement an und fahren mit der nächsten Iteration des Schleifensystems fort.

         shift += iWindow + 1;
        }
     }

Der Rest dieser Initialisierungsmethode unterscheidet sich von denen, die wir zuvor untersucht haben. Bislang haben wir bei der Objektinitialisierung keine Fragmente von OpenCL-Code verwendet. Diese Methode ist eine Ausnahme. Hier normalisieren wir die erhaltenen Wavelet-Filter.

   if(!!OpenCL)
     {
      if(!WeightsConv.BufferWrite())
         return false;
      uint global_work_size[] = {iWindowOut * iVariables};
      uint global_work_offset[] = {0};
      OpenCL.SetArgumentBuffer(def_k_NormilizeWeights, def_k_norm_buffer, WeightsConv.GetIndex());
      OpenCL.SetArgument(def_k_NormilizeWeights, def_k_norm_dimension, (int)iWindow + 1);
      if(!OpenCL.Execute(def_k_NormilizeWeights, 1, global_work_offset, global_work_size))
        {
         string error;
         CLGetInfoString(OpenCL.GetContext(), CL_ERROR_DESCRIPTION, error);
         printf("Error of execution kernel %s Normalize: %s", __FUNCSIG__, error);
         return false;
        }
     }
//---
   return true;
  }

Nach erfolgreicher Normalisierung der Parameter schließt die Methode ihre Ausführung ab und gibt ein boolesches Ergebnis an das aufrufende Programm zurück.

Der vollständige Code für das vorgestellte Objekt und alle seine Methoden sind im Anhang verfügbar.

Es ist erwähnenswert, dass die Funktionsweise des Moduls für die Signalzerlegung über die diskrete Wavelet-Transformation hinausgeht, auch wenn dies seine Kernkomponente bleibt. Wir planen, das Objekt in unseren Modellen zu verwenden, wobei die Eingabe ein zweidimensionaler Tensor einer multimodalen Zeitreihe mit den Dimensionen {Bar, Indicator-Value} ist. Damit die diskrete Wavelet-Transformation richtig funktioniert, müssen die Eingangsdaten transponiert werden. Dies kann extern erfolgen, bevor die Daten in das Objekt eingegeben werden. Aber unser Ziel ist es, Objekte zu bauen, die so nutzerfreundlich wie möglich sind. Daher erstellen wir ein Flow Decomposition Module-Objekt mit leicht erweiterter Funktionsweise, CNeuronDecouplingFlow, das das zuvor erstellte diskrete Wavelet-Transformationsobjekt als übergeordnete Klasse verwendet.

class CNeuronDecouplingFlow   :  public   CNeuronLegendreWaveletsHL
  {
protected:
   CNeuronTransposeOCL  cTranspose;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronDecouplingFlow(void) {};
                    ~CNeuronDecouplingFlow(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint units_count,
                          uint filters, uint variables,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronDecouplingFlow;   }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Innerhalb des neuen Objekts fügen wir eine Schicht zur Vorverlagerung von Daten hinzu und definieren den externen Parameter units_count in der Init-Methode neu, um sie nutzerfreundlicher zu gestalten. Dabei steht units_count für die Länge der analysierten Sequenz (die Anzahl der Balken), während variables für die Anzahl der analysierten Indikatoren steht.

Betrachten wir nun die Umsetzung dieses Ansatzes in der Init-Methode. Im Hauptteil der Methode wird zunächst die Anzahl der Faltungsoperationen für eine einzelne Sequenz auf der Grundlage der ursprünglichen Sequenzlänge, der Größe des Faltungsfensters und des Schrittes neu berechnet. Anschließend rufen wir die Init-Methode der übergeordneten Klasse mit diesen angepassten Parametern auf.

bool CNeuronDecouplingFlow::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint units_count,
                                 uint filters, uint variables,
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   uint units_out = (units_count - window + step) / step;
   if(!CNeuronLegendreWaveletsHL::Init(numOutputs, myIndex, open_cl, window, step, units_out, 
                                                filters, variables, optimization_type, batch))
      return false;

Nach erfolgreicher Ausführung der übergeordneten Methode initialisieren wir die Datenumsetzungsschicht.

   if(!cTranspose.Init(0, 0, OpenCL, units_count, variables, optimization, iBatch))
      return false;
//---
   return true;
  }

Die Methode endet mit der Rückgabe eines logischen Ergebnisses an das aufrufende Programm.

Die Algorithmen für den Vorwärts- und den Rückwärtsdurchlauf einfach zu handhaben. Beim Vorwärtsdurchlauf beispielsweise werden die Eingabedaten zunächst transponiert, und der resultierende Tensor wird an die entsprechende übergeordnete Klassenmethode übergeben.

bool CNeuronDecouplingFlow::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;
   if(!CNeuronLegendreWaveletsHL::feedForward(cTranspose.AsObject()))
      return false;
//---
   return true;
  }

Daher werden wir sie hier nicht im Detail untersuchen. Der vollständige Code für dieses Objekt und alle seine Methoden ist im Anhang enthalten.

Was die Ausgabe des Moduls zur Signalzerlegung betrifft: Der konstruierte Operationsablauf erlaubt es der neuronalen Schicht nicht, zwei separate Tensoren zurückzugeben. Daher werden die Ergebnisse der Nieder- und Hochfrequenzfilter als ein einziger Tensor ausgegeben. Folglich ähnelt die Ausgabe einem vierdimensionalen Tensor {Variables, Units,[Low, High], Filters}. Die Trennung in verschiedene Datenströme ist für den Zweifrequenz-Raum-Zeit-Kodierer vorgesehen.

Nach dem Erstellen des Moduls zur Zerlegung der Ausgangsdaten implementieren wir den Zweifrequenz-Raum-Zeit-Kodierer, der aus drei Hauptkomponenten besteht: temporale Aufmerksamkeit, erweiterte kausale Faltung (dilated causal convolution) und ein temporaler Slot mit Graph-Attention-Netzwerken (Struc2Vec).

Die Autoren des Systems Multitask-Stockformer organisieren zwei unabhängige Streams für nieder- und hochfrequente Komponenten. Diese Streams unterscheiden sich architektonisch, sodass sich das Modell getrennt auf Trends und saisonale Komponenten konzentrieren kann.

Niederfrequente Komponenten werden in den räumlich-zeitlichen Aufmerksamkeitsblock eingespeist, um langfristige, niederfrequente Trends und globale Sequenzbeziehungen zu erfassen.

Hochfrequente Komponenten werden von einer erweiterten kausalen Faltungsschicht verarbeitet, die sich auf lokale Muster, hochfrequente Fluktuationen und plötzliche Ereignisse konzentriert.

Es wird erwartet, dass dieser Dual-Stream-Modellierungsansatz die Vorhersagegenauigkeit komplexer Finanzabläufe verbessert.

Für den räumlich-zeitlichen Aufmerksamkeitsblock können wir bestehende transformatorbasierte Encoderobjekte nutzen. Der Algorithmus der erweiterte kausalen Faltung erfordert jedoch eine individuelle Implementierung.

Erweiterte kausale Faltungsschicht

Der Rahmen schlägt eine erweiterte kausale Faltung vor, eine 1D-Faltung, die Eingabewerte in einem bestimmten Schritt überspringt. Formal gilt für eine Folge x ∈ RT und Filter f ∈ RJ ist die erweiterte kausale Faltung im Zeitschritt t definiert als:

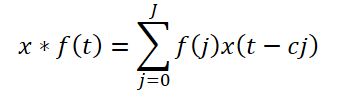
Dabei ist c der Erweiterungsfaktor. Die erweiterte kausale Faltung der Hochfrequenzkomponente wird wie folgt ausgedrückt:

In der ursprünglichen Implementierung gibt es einen weiteren Hyperparameter – den Erweiterungsfaktor. Er ist konstant. Jedoch ist der Abstand zwischen den abhängigen Elementen über die gesamte Sequenz hinweg fest. Außerdem wird dieser Faktor im ursprünglichen Algorithmus einheitlich auf verschiedene Sequenzen angewendet.

In unserer Implementierung haben wir diese Architektur leicht verändert. Anstelle von festen Sprüngen führen wir den Algorithmus Segment, Shuffle, Stitch (S3) ein, gefolgt von einer Standard-Faltungsschicht.

S3 ermöglicht es dem Modell, adaptive Permutationen von Eingabesegmenten zu erlernen, wodurch das Netz Abhängigkeiten innerhalb hochfrequenter Komponenten entdecken kann. Durch das Stapeln mehrerer S3-Blöcke wird die Fähigkeit des Modells, komplexe Hochfrequenz-Interaktionen zu erfassen, weiter verbessert.

Wir implementieren diesen Ansatz in dem Objekt CNeuronDilatedCasualConv. Der Algorithmus ist linear. Daher verwenden wir die Klasse CNeuronRMAT als übergeordnetes Objekt, das die Basisfunktionalität und die Schnittstellen für die Implementierung des linearen Algorithmus bereitstellt. Die Struktur des neuen Objekts wird im Folgenden dargestellt.

class CNeuronDilatedCasualConv   :  public CNeuronRMAT
  {
public:
                     CNeuronDilatedCasualConv(void) {};
                    ~CNeuronDilatedCasualConv(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint dimension,
                          uint units_count, uint variables, uint layers,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDilatedCasualConv; }
  };

Wie aus der Struktur des neuen Objekts ersichtlich ist, können wir uns durch die Wahl der „richtigen“ Elternklasse darauf beschränken, die Objektarchitektur in der Init-Methode festzulegen. Alle anderen Funktionen sind bereits in den Methoden der Elternklasse implementiert, von der wir sie erfolgreich ableiten.

In der Init-Methode erhalten wir vom externen Programm eine Reihe von Konstanten, die die Architektur des zu erstellenden Objekts eindeutig definieren:

• window – die Größe des Analysefensters;
• step – die Schrittweite des Analysefensters;
• dimension – Dimension eines einzelnen Sequenzelement-Vektors;
• units_count – Anzahl der Elemente in der Sequenz;
• Variablen – Anzahl der analysierten Elemente in der multimodalen Sequenz;
• layers – Anzahl der Faltungsschichten.

Es ist wichtig zu beachten, wie diese Variablen verwendet werden. Erinnern wir uns zunächst an die Dimensionen des Tensors der analysierten Eingabedaten. Wie bereits erwähnt, gibt das Modul zur Signalzerlegung einen vierdimensionalen Tensor {Variables, Units, [Low, High], Filters} aus. Nach der Trennung der Hoch- und Tieffrequenzkomponenten entlang der dritten Dimension bleibt nur ein einziger Wert übrig, wodurch der Tensor effektiv dreidimensional wird {Variables, Units, Filters}.

Im OpenCL-Kontext arbeiten wir mit eindimensionalen Datenpuffern. Die Aufteilung des Puffers in Dimensionen ist konzeptionell, folgt aber der entsprechenden Reihenfolge der Werte.

Die Kenntnis der Tensordimensionen ermöglicht es uns, sie mit den vom externen Programm erhaltenen Parametern abzugleichen. Offensichtlich entspricht variables der ersten Dimension (Variables), units_count gibt die Sequenzlänge entlang der zweiten Dimension (Units) an, und dimension definiert die letzte Dimension (Filters). Zusammen bestimmen diese Parameter die rohen Tensordimensionen der Eingabedaten.

Zusätzlich werden die Größe des Analysefensters (window) und dessen Schritt (step) in Einheiten der zweiten Dimension (Units) angegeben. Ist z. B. window = 2, verarbeitet die Faltung 2 * Dimensionselemente aus dem Eingabepuffer.

Mit diesem Verständnis können wir zum Algorithmus der Initialisierungsmethode des Objekts zurückkehren.

bool CNeuronDilatedCasualConv::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                    uint window, uint step, uint dimension, uint units_count,
                                    uint variables, uint layers,
                                    ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 1, optimization_type, batch))
      return false;

Wie üblich wird innerhalb des Methodenkörpers zunächst die gleichnamige Methode der Elternklasse aufgerufen, in der die notwendigen Kontrollen und die Initialisierung der geerbten Objekte organisiert werden. An dieser Stelle ergeben sich zwei Probleme. Erstens unterscheidet sich die Struktur der Objekte in der übergeordneten Klasse CNeuronRMAT erheblich von dem, was wir brauchen. Daher rufen wir die Methode nicht von der direkten Elternklasse aus auf, sondern von der Basisschicht, die vollständig verbunden ist. Wie Sie sich vielleicht erinnern, dient sie als Grundlage für die Erstellung aller neuronalen Schichten in unserer Bibliothek.

Es gibt jedoch noch ein zweites Problem: Während der Faltung ändert sich die Größe des Ergebnistensors. Derzeit liegen uns noch nicht die endgültigen Abmessungen vor, um die Größen der Basisschnittstellen festzulegen. Daher initialisieren wir die Basisschnittstellen mit einem einzigen nominalen Ausgangselement.

Als Nächstes löschen wir das dynamische Array, in dem Zeiger auf interne Objekte gespeichert sind, und bereiten Hilfsvariablen vor.

   cLayers.Clear();
   cLayers.SetOpenCL(OpenCL);
   uint units = units_count;
   CNeuronConvOCL *conv = NULL;
   CNeuronS3 *s3 = NULL;

Nach Abschluss der vorbereitenden Arbeiten gehen wir zur direkten Konstruktion unserer Objektarchitektur über. Zu diesem Zweck organisieren wir eine Schleife mit einer Anzahl von Iterationen, die der Anzahl der internen Schichten entspricht.

   for(uint i = 0; i < layers; i++)
     {
      s3 = new CNeuronS3();
      if(!s3 ||
         !s3.Init(0, i*2, OpenCL, dimension, dimension*units*variables, optimization, iBatch) ||
         !cLayers.Add(s3))
        {
         if(!!s3)
            delete s3;
         return false;
        }
      s3.SetActivationFunction(None);

Innerhalb der Schleife wird zunächst das Objekt S3 initialisiert. Es ist jedoch zu beachten, dass dieses Objekt nur mit einem eindimensionalen Tensor arbeitet. Um eine „Lücke“ im Repräsentationsvektor der Sequenzelemente zu vermeiden, muss die Segmentgröße daher ein Vielfaches der Dimensionalität dieses Vektors sein. In diesem Fall setzen wir sie gleich. Gleichzeitig wird die Sequenzlänge als volle Tensorgröße angegeben, wobei alle analysierten Variablen berücksichtigt werden.

Nach erfolgreicher Initialisierung des Objekts fügen wir seinen Zeiger zu unserem dynamischen Array hinzu, das Zeiger auf interne Objekte speichert, und deaktivieren die Aktivierungsfunktion.

Als Nächstes folgt die Initialisierung der Faltungsschicht. Bevor wir mit der Initialisierung des neuen Objekts beginnen, berechnen wir die Anzahl der Faltungsoperationen für die zu erstellende Schicht und speichern diesen Wert in einer lokalen Variablen. Der Wert dieser spezifischen Variable wurde im vorherigen Schritt bei der Festlegung der analysierten Sequenzdimensionen verwendet. Folglich wird in der nächsten Schleifeniteration ein S3-Objekt mit der aktualisierten Größe erstellt.

      conv = new CNeuronConvOCL();
      units = MathMax((units - window + step) / step, 1);
      if(!conv ||
         !conv.Init(0, i * 2 + 1, OpenCL, window * dimension, step * dimension, dimension,
                                                   units, variables, optimization, iBatch) ||
         !cLayers.Add(conv))
        {
         if(!!conv)
            delete conv;
         return false;
        }
      conv.SetActivationFunction(GELU);
     }

Anders als das S3-Objekt kann die von uns verwendete Faltungsschicht mit univariaten Sequenzen arbeiten. Auf diese Weise kann nicht nur jede einzelne Zeitreihe gefaltet werden, sondern es können auch verschiedene Filter auf univariate Sequenzen angewendet werden, sodass deren Analyse völlig unabhängig ist.

Am Ausgang der Faltungsschicht verwenden wir die Aktivierungsfunktion GELU anstelle von ReLU, die von den Autoren des Systems vorgeschlagen wurde.

Wir fügen einen Zeiger auf das initialisierte Objekt zu unserem dynamischen Array hinzu und fahren mit der nächsten Schleifeniteration fort, um die nächste Ebene zu erstellen.

Nachdem wir alle internen Schichten unseres Objekts erfolgreich initialisiert haben, rufen wir erneut die Initialisierungsmethode der Basisschicht auf, um korrekte externe Schnittstellenpuffer zu erstellen, wobei wir die Größe der letzten internen Schicht in unserem Block angeben.

  if(!CNeuronBaseOCL::Init(numOutputs, myIndex, OpenCL, conv.Neurons(), optimization_type, batch))
      return false;

Schließlich ersetzen wir die Zeiger auf die Puffer der externen Schnittstelle durch die entsprechenden Puffer der letzten internen Schicht.

   if(!SetGradient(conv.getGradient(), true) ||
      !SetOutput(conv.getOutput(), true))
      return false;
   SetActivationFunction((ENUM_ACTIVATION)conv.Activation());
//---
   return true;
  }

Wir kopieren den Zeiger der Aktivierungsfunktion, geben das logische Ergebnis der Operationen an das aufrufende Programm zurück und schließen die Ausführung der Methode ab.

Wie Sie vielleicht bemerkt haben, haben wir in dieser Blockarchitektur interne Objekte verwendet, die mit Tensoren unterschiedlicher Dimensionalität arbeiten. Zunächst ordnet die S3-Schicht die Elemente im gesamten Datenpuffer ohne Rücksicht auf univariate Sequenzen neu an. In diesem Fall ist das „Mischen“ von Elementen zwischen univariaten Sequenzen durchaus möglich. Einerseits beschränken wir die Umordnung von Elementen nicht auf die Grenzen univariater Sequenzen. Andererseits wird die Umordnungsreihenfolge auf der Grundlage des Trainingsdatensatzes gelernt. Wenn das Modell Abhängigkeiten zwischen Elementen verschiedener Unit-Sequenzen identifiziert, kann dies die Leistung des Modells möglicherweise verbessern. Es wird sehr interessant sein, das Lernergebnis zu beobachten.

Der Umfang der Artikel nähert sich seiner Grenze, aber unsere Arbeit ist noch nicht zu Ende. Wir werden dies im nächsten Artikel unserer Serie fortsetzen.

Schlussfolgerung

In dieser Arbeit haben wir das System Multitask-Stockformer untersucht, ein innovatives Aktienauswahlmodell, das Wavelet-Transformation mit Multitask-Self-Attention-Modulen kombiniert. Die Verwendung von Wavelet-Transformationen ermöglicht die Identifizierung von Zeit- und Frequenzmerkmalen der Marktdaten, während Self-Attention-Mechanismen eine präzise Modellierung komplexer Wechselwirkungen zwischen den analysierten Faktoren gewährleisten.

Im praktischen Teil haben wir unsere eigene Interpretation der einzelnen Blöcke des vorgeschlagenen Systems mit MQL5 umgesetzt. In der nächsten Arbeit werden wir die Implementierung des besprochenen Rahmens vervollständigen und auch die Effektivität der implementierten Ansätze an realen historischen Daten bewerten.

Referenzen

• Stockformer: A Price-Volume Factor Stock Selection Model Based on Wavelet Transform and Multi-Task Self-Attention Networks
• Andere Artikel dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	Expert Advisor für die Probenahme
2	ResearchRealORL.mq5	Expert Advisor	Expert Advisor für die Probenahme mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Expert Advisor für Modelltests
5	Trajectory.mqh	Klassenbibliothek	Struktur der Beschreibung des Systemzustands und der Modellarchitektur
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Code Base	OpenCL-Programmcode-Bibliothek