MetaTrader 5 / Beispiele
English Русский 日本語
preview
Algorithmen zur Optimierung mit Populationen: Der Boids-Algorithmus

Algorithmen zur Optimierung mit Populationen: Der Boids-Algorithmus

MetaTrader 5 — Beispiele | 20 August 2024, 10:04
10 0
Andrey Dik
Andrey Dik

Inhalt

1. Einführung
2. Beschreibung des Algorithmus
3. Testergebnisse


1. Einführung

Wenn wir das Herdenverhalten von Tieren in der Natur beobachten, bewundern wir unwillkürlich ihr gut koordiniertes und effektives Zusammenspiel. Wie von einer unsichtbaren Kraft gesteuert, ordnen sie sich synchron als ein einziger Organismus neu an, überwinden Hindernisse und finden den optimalen Weg. Diese faszinierende Harmonie der Bewegungen, die auf einfachen Regeln der Interaktion beruht, hat die Entwicklung zahlreicher metaheuristischer Optimierungsalgorithmen inspiriert.

Bei der Untersuchung der komplexen Zugrouten von Vogelschwärmen haben Wissenschaftler entdeckt, dass sie ähnlichen Prinzipien folgen wie Algorithmen der Schwarmintelligenz. So bilden Fischschwärme, ähnlich wie lebende Zellen, pulsierende Strukturen, die an Optimierungsmethoden auf der Grundlage von zellulären Automaten erinnern. Das Herdenverhalten von Hufsäugetieren, ihre koordinierten Reaktionen auf Gefahren und der synchrone Flug einer Gruppe von Staren zeigen die unglaubliche Fähigkeit von Tieren, gemeinsame Aktionen zu koordinieren.

Diese faszinierenden Beispiele aus der Natur haben leistungsstarke Optimierungswerkzeuge inspiriert, mit denen sich komplexe Probleme lösen lassen, von der Planung logistischer Routen bis hin zum Entwurf effizienter Kontrollsysteme.

Boids Algorithmus (kurz für „bird“ und „oid“ - analog) ist ein 1986 von Craig Reynolds entwickelter Computeralgorithmus, der das Verhalten von Tierschwärmen, insbesondere von Vögeln, modelliert. Dieser Algorithmus wurde entwickelt, um das natürliche Verhalten von Schwärmen zu imitieren, in denen sich jedes Individuum nach einfachen Regeln bewegt, was schließlich zur Entstehung eines kollektiven Verhaltens führt. Sie beruht auf den folgenden drei Regeln:

1. Separation. Jedes Objekt (oder „Boid“) versucht, die Möglichkeit eines Zusammenstoßes mit benachbarten Objekten zu minimieren.
2. Ausrichtung. Jedes Objekt strebt danach, dass seine Bewegungsrichtung der durchschnittlichen Bewegungsrichtung der umliegenden Objekte entspricht.
3. Kohäsion. Jedes Objekt ist bestrebt, seine Position nahe der durchschnittlichen Position der benachbarten Objekte zu halten.

Diese drei einfachen Regeln ermöglichen es uns, das komplexe Verhalten eines Vogelschwarms oder eines Insektenschwarms zu modellieren. Der Boids-Algorithmus wird in der Computergrafik häufig verwendet, um Animationen eines Vogelschwarms, eines Insektenschwarms oder eines Fischschwarms zu erstellen.

Der ursprüngliche Boids-Algorithmus hatte mehrere Ziele und Anwendungen:

1. Erstellen realistischer Animationen. Der Boids-Algorithmus ermöglicht die Erstellung realistischer Animationen von Tierschwärmen, was für die Entwicklung der Computergrafik und -animation von großer Bedeutung war.
2. Modellierung von Verhaltensweisen. Boids ermöglicht die Simulation von komplexem kollektivem Verhalten auf der Grundlage einfacher Regeln für jedes Individuum. Dies findet Anwendung in verschiedenen Bereichen wie der Tierverhaltensforschung, der Robotik, dem Verkehrsmanagement und anderen.

Boids Algorithmus hat die Entwicklung anderer Algorithmen inspiriert, wie die Partikelschwarmoptimierung (PSO) und Algorithmen zur Modellierung des Verhaltens von Menschenmengen.

Der Boids-Algorithmus ist nach wie vor ein beliebtes Instrument zur Modellierung kollektiven Verhaltens und ist weiterhin Gegenstand von Forschung und Entwicklung in verschiedenen Bereichen von Wissenschaft und Technik.

In der Animation unten sehen wir das Verhalten dieser Boids, die sich zu kompakten Gruppen zusammenschließen, auseinanderfliegen und auch ihre Geschwindigkeit gegenüber ihren Nachbarn synchronisieren können. Bei der Aufzeichnung der Animation wurden die Einstellungen des Algorithmus im laufenden Betrieb geändert, sodass die Auswirkungen der entsprechenden Einstellungen auf das Verhalten der Boids beobachtet werden konnten.

Boids

Visualisierung des Boids-Algorithmus

Konfiguration

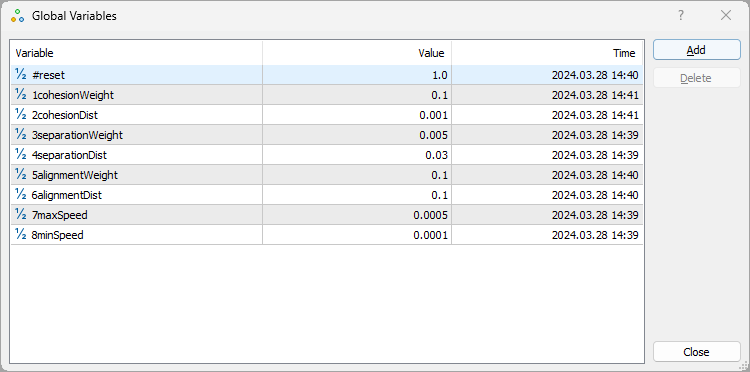
Das Fenster für die Einstellungen des Boids-Algorithmus, das durch Drücken der Taste F3 aufgerufen wird. Mit dem Parameter #reset können wir den Algorithmus neu starten, indem wir den Wert „1“ eingeben.


2. Der Algorithmus

Der von Craig Reynolds entwickelte Boids-Algorithmus wurde ursprünglich für die Modellierung des Schwarmverhaltens von Tieren, wie z. B. Vogelschwärmen, Insektenschwärmen und anderen, entwickelt. Aufgrund seiner Flexibilität und Anpassungsfähigkeit findet dieser Algorithmus jedoch in verschiedenen Bereichen Anwendung, einschließlich Optimierung und Suche. Im Zusammenhang mit Optimierung und Suche kann der Boids-Algorithmus verwendet werden, um Probleme im Zusammenhang mit dem koordinierten Verhalten einer Gruppe von Agenten zu lösen. So lässt sich beispielsweise das Verhalten eines Schwarms modellieren, der ein unbekanntes Gebiet erkundet.

Es sei jedoch darauf hingewiesen, dass der Boids-Algorithmus selbst kein Suchalgorithmus im herkömmlichen Sinne ist. Er ist nicht darauf ausgelegt, eine optimale Lösung in einem gegebenen Raum möglicher Lösungen zu finden, wie dies beispielsweise bei Gradientenabstiegsalgorithmen oder genetischen Algorithmen der Fall ist. Stattdessen modelliert der Boids-Algorithmus das Verhalten einer Gruppe von Agenten auf der Grundlage einer Reihe von einfachen Regeln, die es ihm ermöglichen, komplexes und koordiniertes Verhalten auf Gruppenebene zu modellieren.

Der Boids-Algorithmus kann für die verteilte Suche nach dem Extremum einer Funktion angepasst werden. In diesem Zusammenhang stellt jedes „Boid“ einen Suchagenten dar, der sich durch den Raum der möglichen Lösungen bewegt. Anstatt einfach anderen „Boids“ zu folgen, kann jeder Agent den Wert der Funktion an seiner aktuellen Position nutzen, um seine Bewegung anzupassen oder die Fitness anderer Boids in der Population zu berücksichtigen.

Craig Reynolds Arbeit am Boids-Algorithmus, der das Verhalten von Schwärmen simuliert, inspirierte das Konzept der Schwarmintelligenz. Schwarmintelligenz beschreibt das kollektive Verhalten eines dezentralisierten, selbstorganisierenden Systems und beinhaltet den PSO-Algorithmus.

Schwarmintelligenzsysteme bestehen in der Regel aus mehreren Agenten (Boids), die lokal miteinander und mit der Umwelt interagieren. Verhaltensideen stammen in der Regel aus der Natur, insbesondere aus biologischen Systemen. Jedes Boid folgt sehr einfachen Regeln. Obwohl es kein zentrales Verhaltenskontrollsystem gibt, das jedem von ihnen sagt, was er zu tun hat, führen lokale und eher zufällige Interaktionen zu einem intelligenten Gruppenverhalten, das sich der Kontrolle der einzelnen Boids entzieht.

Der Boids-Algorithmus verfügt über eine ganze Reihe von externen Parametern, und jeder von ihnen beeinflusst die Art der Bewegung der Boids erheblich. Schauen wir uns diese Parameter an:

  1. cohesionWeight - Das Kohäsionsgewicht bestimmt die Anziehungskraft der Herdenmitglieder zueinander.
  2. cohesionDist - Die Kohäsionsdistanz bestimmt den Abstand zwischen den Mitgliedern einer Herde, bei dem sie beginnen, sich zueinander hingezogen zu fühlen.
  3. separationWeight - Das Separationsgewicht bestimmt, wie stark sich die Mitglieder der Herde gegenseitig abstoßen.
  4. separationDist - Der Separationsabstand bestimmt den Abstand zwischen den Herdenmitgliedern, bei dem sie beginnen, sich gegenseitig abzustoßen.
  5. alignmentWeight - Das Ausrichtungsgewicht bestimmt, wie stark sich die Mitglieder der Herde an der Bewegungsrichtung der anderen ausrichten.
  6. alignmentDist - Die Ausrichtungsdistanz bestimmt den Abstand zwischen den Herdenmitgliedern, bei dem sie beginnen, sich in Richtung der gegenseitigen Bewegung auszurichten.
  7. minSpeed - Mindestgeschwindigkeit, um ein Anhalten der Boids zu verhindern.
  8. maxSpeed - maximale Geschwindigkeit der Boids.

Es ist wichtig, eine Reihe von Experimenten durchzuführen, um diese Parameter so anzupassen, dass das gewünschte Herdenverhalten erreicht wird. Sie können mit den vorgeschlagenen Werten beginnen und sie schrittweise anpassen, um zu sehen, wie sie das Verhalten der Herde beeinflussen. Bitte beachten Sie, dass es keine „richtigen“ oder „besten“ Parameterwerte für den Boids-Algorithmus im absoluten Sinne gibt. Es hängt alles von der jeweiligen Aufgabe und dem Szenario ab.

Gehen wir nun dazu über, den Code für den Boids-Algorithmus zu schreiben. Um jeden Agenten zu beschreiben, definieren wir die Struktur S_Boids_Agent. Schauen wir uns an, was hier vor sich geht:


1. Die Struktur enthält folgende Felder:

  • x[] - Array zum Speichern der aktuellen Koordinaten des Agenten.
  • dx[] - Array der aktuellen Agentengeschwindigkeiten.
  • m - Masse des Erregers.

2. Init - S_Boids_Agent Strukturmethode zur Initialisierung der Strukturfelder. Sie nimmt das ganzzahlige Argument „coords“, das zur Größenänderung der Arrays „x“ und „dx“ mit der Funktion ArrayResize verwendet wird.

Dieser Code stellt die grundlegende Datenstruktur für Agenten im Boids-Algorithmus dar und initialisiert ihre Felder, wenn ein neuer Agent erstellt wird. Dies ermöglicht es jedem Agenten, seine eigenen Koordinaten und Geschwindigkeiten zu haben, was ein Schlüsselaspekt des Boids-Algorithmus ist. Das Feld „m“ wurde auf meine Initiative hin hinzugefügt, um die Oberfläche der Fitnessfunktion beim Bewegen von Boids zu berücksichtigen, wobei die Masse den Fitnesswert darstellt. 

//——————————————————————————————————————————————————————————————————————————————
struct S_Boids_Agent
{
    double x  [];
    double dx [];
    double m;

    void Init (int coords)
    {
      ArrayResize (x,  coords);
      ArrayResize (dx, coords);
    }
};
//——————————————————————————————————————————————————————————————————————————————

Definieren wir die Klasse C_AO_Boids des Boids-Algorithmus, die ein Erbe der Basisklasse der C_AO-Populationsalgorithmen ist und die folgenden Felder und Methoden enthält:

1. Öffentliche Felder:

  • ao_name - Name des Optimierungsalgorithmus.
  • ao_desc - Beschreibung des Optimierungsalgorithmus.
  • popSize - Größe der Population.
  • params - Array der Algorithmusparameter.
  • cohesionWeight - Gewicht der Kohäsion.
  • cohesionDist - Kohäsionsabstand.
  • separationWeight - Gewicht der Separation.
  • separationDist - Separationsabstand.
  • alignmentWeight - Gewicht der Ausrichtung.
  • alignmentDist - Ausrichtungsabstand.
  • maxSpeed - maximale Geschwindigkeit.
  • minSpeed - minimale Geschwindigkeit.
  • agent - Vektor der Agenten.

2. Die verfügbaren Optionen sind:

  • C_AO_Boids - Klassenkonstruktor, der die Klassenfelder initialisiert.
  • SetParams - Methode zur Einstellung der Algorithmusparameter.
  • Init - Methode zur Initialisierung des Algorithmus. Die Methode akzeptiert minimale und maximale Suchbereiche, Suchschritte und die Anzahl der Epochen.
  • Moving - Methode für die Bewegung der Agenten.
  • Revision - Methode zur Revision der Agenten.

3. Private Felder:

  • distanceMax - maximal möglicher euklidischer Abstand im Suchraum.
  • speedMax - maximale Geschwindigkeit.
//——————————————————————————————————————————————————————————————————————————————
class C_AO_Boids : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_Boids () { }
  C_AO_Boids ()
  {
    ao_name = "Boids";
    ao_desc = "Boids Algorithm";
    ao_link = "https://www.mql5.com/en/articles/14576";

    popSize          = 50;   //population size

    cohesionWeight   = 0.6;
    cohesionDist     = 0.001;

    separationWeight = 0.005;
    separationDist   = 0.03;

    alignmentWeight  = 0.1;
    alignmentDist    = 0.1;

    maxSpeed         = 0.001;
    minSpeed         = 0.0001;

    ArrayResize (params, 9);

    params [0].name = "popSize";          params [0].val = popSize;

    params [1].name = "cohesionWeight";   params [1].val = cohesionWeight;
    params [2].name = "cohesionDist";     params [2].val = cohesionDist;


    params [3].name = "separationWeight"; params [3].val = separationWeight;
    params [4].name = "separationDist";   params [4].val = separationDist;

    params [5].name = "alignmentWeight";  params [5].val = alignmentWeight;
    params [6].name = "alignmentDist";    params [6].val = alignmentDist;

    params [7].name = "maxSpeed";         params [7].val = maxSpeed;
    params [8].name = "minSpeed";         params [8].val = minSpeed;
  }

  void SetParams ()
  {
    popSize          = (int)params [0].val;

    cohesionWeight   = params [1].val;
    cohesionDist     = params [2].val;

    separationWeight = params [3].val;
    separationDist   = params [4].val;

    alignmentWeight  = params [5].val;
    alignmentDist    = params [6].val;

    maxSpeed         = params [7].val;
    minSpeed         = params [8].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();
  void Injection (const int popPos, const int coordPos, const double value);

  //----------------------------------------------------------------------------
  double cohesionWeight;   //cohesion weight
  double cohesionDist;     //cohesion distance

  double separationWeight; //separation weight
  double separationDist;   //separation distance

  double alignmentWeight;  //alignment weight
  double alignmentDist;    //alignment distance

  double minSpeed;         //minimum velocity
  double maxSpeed;         //maximum velocity

  S_Boids_Agent agent [];

  private: //-------------------------------------------------------------------
  double distanceMax;
  double speedMax [];

  void   CalculateMass    ();
  void   Cohesion         (S_Boids_Agent &boid, int pos);
  void   Separation       (S_Boids_Agent &boid, int pos);
  void   Alignment        (S_Boids_Agent &boid, int pos);
  void   LimitSpeed       (S_Boids_Agent &boid);
  void   KeepWithinBounds (S_Boids_Agent &boid);
  double Distance         (S_Boids_Agent &boid1, S_Boids_Agent &boid2);
};
//——————————————————————————————————————————————————————————————————————————————

Die Init-Methode der Klasse C_AO_Boids dient der Initialisierung von Klassenvariablen auf der Grundlage der übergebenen Parameter. Diese Methode führt eine Standardinitialisierung mit der Methode StandardInit durch, die den minimalen und maximalen Suchbereich sowie den Suchschritt übernimmt.

Wenn die Standardinitialisierung erfolgreich ist, ändert die Methode die Größe des „Agenten“ auf die Größe „popSize“. Die Methode Init wird mit dem Parameter „coords“ für jedes Element in „agent“ aufgerufen.

Die Methode berechnet dann die maximale Entfernung und die maximale Geschwindigkeit, die im Boids-Algorithmus verwendet werden, um die Bewegung der Agenten zu bestimmen.

Die Methode setzt dann globale Variablen für verschiedene Parameter des Boids-Algorithmus, wie Kohäsionsgewicht, Kohäsionsabstand, Separationsgewicht, Separationsabstand, Ausrichtungsgewicht, Ausrichtungsabstand, Höchstgeschwindigkeit und Mindestgeschwindigkeit.

Die Methode gibt „true“ zurück, wenn die Initialisierung erfolgreich war, andernfalls „false“.

Diese Methode führt die anfängliche Einrichtung des Boids-Optimierungsalgorithmus mit gegebenen Parametern durch und bereitet ihn auf die Durchführung der Optimierung vor.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_Boids::Init (const double &rangeMinP  [], //minimum search range
                       const double &rangeMaxP  [], //maximum search range
                       const double &rangeStepP [], //step search
                       const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (agent, popSize);
  for (int i = 0; i < popSize; i++) agent [i].Init (coords);

  distanceMax = 0;
  ArrayResize (speedMax, coords);

  for (int c = 0; c < coords; c++)
  {
    speedMax [c] = rangeMax [c] - rangeMin [c];
    distanceMax += pow (speedMax [c], 2);
  }

  distanceMax = sqrt (distanceMax);

  GlobalVariableSet ("#reset", 1.0);

  GlobalVariableSet ("1cohesionWeight",   params [1].val);
  GlobalVariableSet ("2cohesionDist",     params [2].val);

  GlobalVariableSet ("3separationWeight", params [3].val);
  GlobalVariableSet ("4separationDist",   params [4].val);

  GlobalVariableSet ("5alignmentWeight",  params [5].val);
  GlobalVariableSet ("6alignmentDist",    params [6].val);

  GlobalVariableSet ("7maxSpeed",         params [7].val);
  GlobalVariableSet ("8minSpeed",         params [8].val);


  return true;
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Moving der Klasse C_AO_Boids wird verwendet, um Agenten während der Optimierung zu bewegen. Die Methode geht folgendermaßen vor:

  1. Der Wert der globalen Variable „reset“ wird überprüft. Ist sie 1,0, wird das Flag „revision“ auf „false“ gesetzt. Der Wert der globalen Variable „reset“ wird auf 0,0 gesetzt, und die Methode wird beendet.
  2. Die Werte der Algorithmusparameter werden aus globalen Variablen extrahiert.
  3. Wenn das Flag „revision“ „false“ ist, werden die Koordinaten und Geschwindigkeiten der Agenten mit Zufallswerten in den angegebenen Bereichen initialisiert. Das Flag „revision“ wird dann auf „true“ gesetzt und die Methode wird beendet.
  4. Wenn das Flag „revision“ nicht „false“ ist, werden die folgenden Aktionen für jeden Bearbeiter durchgeführt:
    • Die Methoden CalculateMass, Cohesion, Separation, Alignment, LimitSpeed und KeepWithinBounds werden zur Aktualisierung der Agentengeschwindigkeiten aufgerufen.
    • Die Koordinaten des Agenten werden auf der Grundlage seiner Geschwindigkeiten aktualisiert.
    • Die Koordinaten des Agenten werden in das entsprechende Element des Arrays „a“ kopiert.
/——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Moving ()
{
  double reset = GlobalVariableGet ("#reset");
  if (reset == 1.0)
  {
    revision = false;
    GlobalVariableSet ("#reset", 0.0);
  }

  cohesionWeight   = GlobalVariableGet ("1cohesionWeight");
  cohesionDist     = GlobalVariableGet ("2cohesionDist");

  separationWeight = GlobalVariableGet ("3separationWeight");
  separationDist   = GlobalVariableGet ("4separationDist");

  alignmentWeight  = GlobalVariableGet ("5alignmentWeight");
  alignmentDist    = GlobalVariableGet ("6alignmentDist");

  maxSpeed         = GlobalVariableGet ("7maxSpeed");
  minSpeed         = GlobalVariableGet ("8minSpeed");

  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        agent [i].x [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        agent [i].dx [c] = (rangeMax [c] - rangeMin [c]) * u.RNDfromCI (-1.0, 1.0) * 0.001;

        a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    CalculateMass    ();
    Cohesion         (agent [i], i);
    Separation       (agent [i], i);
    Alignment        (agent [i], i);
    LimitSpeed       (agent [i]);
    KeepWithinBounds (agent [i]);

    for (int c = 0; c < coords; c++)
    {
      agent [i].x [c] += agent [i].dx [c];
      a [i].c [c] = u.SeInDiSp  (agent [i].x [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode CalculateMass der Klasse C_AO_Boids wird zur Berechnung der „Masse“ jedes Agenten im Boids-Algorithmus verwendet. Bei dieser Methode geschieht Folgendes:

  1. Die Variablen „maxMass“ und „minMass“ werden initialisiert, um die maximalen und minimalen Werte der Fitnessfunktion aller Agenten zu speichern.
  2. Für jeden Agenten in der Population wird geprüft, ob seine Fitnessfunktion „a[i].f“ größer als der aktuelle Maximalwert „maxMass“ und kleiner als der aktuelle Minimalwert „minMass“ ist. Wenn die Bedingungen erfüllt sind, werden die entsprechenden Höchst- und Mindestwerte aktualisiert.
  3. Nachdem alle Agenten getestet wurden, wird die „Masse“ jedes Agenten als skalierter Wert seiner Fitnessfunktion im Verhältnis zu den Mindest- und Höchstwerten berechnet.

Diese Methode ermöglicht die Berechnung der „Masse“ jedes Agenten im Boids-Algorithmus, die in der ursprünglichen Logik des Algorithmus nicht vorhanden ist. Sie ermöglicht es uns, die „Oberfläche“ des Geländes zu berücksichtigen, auf dem sich die Boids bewegen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::CalculateMass ()
{
  double maxMass = -DBL_MAX;
  double minMass =  DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > maxMass) maxMass = a [i].f;
    if (a [i].f < minMass) minMass = a [i].f;
  }

  for (int i = 0; i < popSize; i++)
  {
    agent [i].m = u.Scale (a [i].f, minMass, maxMass, 0.0, 1.0);
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Cohesion-Methode der Klasse C_AO_Boids wird verwendet, um das „Kohäsions“-Verhalten im Boids-Algorithmus zu implementieren. Dieses Verhalten führt dazu, dass sich die Agenten auf das „Zentrum der Masse“ ihrer Nachbarn zubewegen. Die Methode erfüllt die folgenden Aufgaben:

  1. Das Array „centerX“ wird initialisiert, um die Koordinaten des Massenschwerpunkts zu speichern, während die Variable „numNeighbors“ die Anzahl der Nachbarn zählt.
  2. Für jeden Agenten in der Population wird geprüft, ob er nicht selbst ein Nachbar ist (da der Agent sich selbst nicht als Nachbar betrachten sollte) und ob er sich innerhalb einer bestimmten Entfernung befindet (definiert als „distanceMax * cohesionDist“). Wenn beide Bedingungen erfüllt sind, werden die Koordinaten des Agenten zu „centerX“ hinzugefügt und „numNeighbors“ wird um 1 erhöht.
  3. Wurde mindestens ein Nachbar gefunden, werden die „centerX“-Koordinaten durch die Anzahl der Nachbarn geteilt, um die Koordinaten des Massenschwerpunkts der Nachbarn zu erhalten. Die Geschwindigkeit des Agenten „boid.dx“ wird dann unter Berücksichtigung des Kohäsionsgewichts „cohesionWeight“ in Richtung des Massenschwerpunkts angepasst.

Diese Methode implementiert das „Kohäsions“-Verhalten im Boids-Algorithmus, das den Agenten hilft, sich gemeinsam als Gruppe zu bewegen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Cohesion (S_Boids_Agent &boid, int pos)
{
  double centerX [];
  ArrayResize     (centerX, coords);
  ArrayInitialize (centerX, 0.0);

  int    numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * cohesionDist)
      {
        for (int c = 0; c < coords; c++)
        {
          centerX [c] += agent [i].x [c];
        }

        numNeighbors++;
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    centerX [c] /= numNeighbors;
    boid.dx [c] += (centerX [c] - boid.x [c]) * cohesionWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Separation der Klasse C_AO_Boids wird verwendet, um das „Separationsverhalten“ im Boids-Algorithmus zu implementieren. Dieses Verhalten veranlasst die Agenten, sich in die entgegengesetzte Richtung von Nachbarn zu bewegen, die zu nahe sind, um Kollisionen zu vermeiden. Bei dieser Methode geschieht Folgendes:

  1. Das Array „moveX“ wird initialisiert, um Änderungen in den Koordinaten des Agenten zu speichern.
  2. Für jeden Agenten in der Population wird geprüft, ob er nicht selbst ein Nachbar ist (da der Agent sich selbst nicht als Nachbar betrachten sollte) und ob er sich innerhalb einer bestimmten Entfernung befindet (definiert als „distanceMax * separationDist“). Wenn beide Bedingungen erfüllt sind, wird die Differenz zwischen den Koordinaten des aktuellen Agenten und seines Nachbarn zu „moveX“ addiert.
  3. Nachdem alle Nachbarn überprüft worden sind, wird die Geschwindigkeit des Agenten „boid.dx“ unter Berücksichtigung des Separationsgewichts „separationWeight“ in die entgegengesetzte Richtung zu „moveX“ angepasst.

Diese Methode implementiert das „Separationsverhalten“ des Boids-Algorithmus, das den Agenten hilft, Zusammenstöße zu vermeiden.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Separation (S_Boids_Agent &boid, int pos)
{
  double moveX [];
  ArrayResize     (moveX, coords);
  ArrayInitialize (moveX, 0.0);

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * separationDist)
      {
        for (int c = 0; c < coords; c++)
        {
          moveX [c] += boid.x [c] - agent [i].x [c];
        }
      }
    }
  }

  for (int c = 0; c < coords; c++)
  {
    boid.dx [c] += moveX [c] * separationWeight;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode „Alignment“ der Klasse C_AO_Boids wird verwendet, um das „Alignment“-Verhalten im Boids-Algorithmus zu implementieren. Dieses Verhalten veranlasst die Agenten, sich in dieselbe Richtung wie ihre Nachbarn zu bewegen. Mit dieser Methode:

  1. Das Array „avgDX“ wird initialisiert, um die Durchschnittsgeschwindigkeit der Nachbarn zu speichern, und die Variable „numNeighbors“ wird initialisiert, um die Anzahl der Nachbarn zu zählen.
  2. Für jeden Agenten in der Population wird geprüft, ob er nicht selbst ein Nachbar ist (da der Agent sich selbst nicht als Nachbar betrachten sollte) und ob er sich innerhalb einer bestimmten Entfernung befindet (definiert als „distanceMax * alignmentDist“). Wenn beide Bedingungen erfüllt sind, wird die Geschwindigkeit des Nachbarn zu „avgDX“ addiert und „numNeighbors“ um 1 erhöht.
  3. Wurde mindestens ein Nachbar gefunden, werden die „avgDX“-Geschwindigkeiten durch die Anzahl der Nachbarn geteilt, um die Durchschnittsgeschwindigkeit zu erhalten. Die Geschwindigkeit des Agenten „boid.dx“ wird dann unter Berücksichtigung der Ausrichtungsgewichtung „alignmentWeight“ an die Durchschnittsgeschwindigkeit angepasst.

Diese Methode implementiert das „Ausrichtungsverhalten“ des Boids-Algorithmus, das den Agenten hilft, sich gemeinsam in dieselbe Richtung zu bewegen.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Alignment (S_Boids_Agent &boid, int pos)
{
  double avgDX [];
  ArrayResize     (avgDX, coords);
  ArrayInitialize (avgDX, 0.0);

  int numNeighbors = 0;

  for (int i = 0; i < popSize; i++)
  {
    if (pos != i)
    {
      if (Distance (boid, agent [i]) < distanceMax * alignmentDist)
      {
        for (int c = 0; c < coords; c++)
        {
          avgDX [c] += agent [i].dx [c];
        }

        numNeighbors++;
      }
    }
  }

    for (int c = 0; c < coords; c++)
    {
      avgDX   [c] /= numNeighbors;
      boid.dx [c] += (avgDX [c] - boid.dx [c]) * alignmentWeight;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode LimitSpeed der Klasse C_AO_Boids wird verwendet, um die Geschwindigkeit der Agenten im Boids-Algorithmus zu begrenzen. Dieses Verhalten verhindert, dass die Agenten ihre Geschwindigkeit unendlich erhöhen, was für echte Tiere unnatürlich ist. Die Methode geht folgendermaßen vor:

  1. Die Variable „speed“ wird initialisiert, um die aktuelle Geschwindigkeit des Agenten zu speichern, und die Variable „d“ wird initialisiert, um Daten vorübergehend zu speichern.
  2. Die aktuelle Geschwindigkeit des Agenten wird auf der Grundlage seiner Geschwindigkeiten für jede Koordinate berechnet.
  3. Die folgenden Aktionen werden für jede Agentenkoordinate durchgeführt:
    • „d“ wird berechnet als die Differenz zwischen dem maximalen und dem minimalen Reichweitenwert, multipliziert mit dem Mindestgeschwindigkeitsfaktor. 
    • Die Geschwindigkeit des Agenten „boid.dx“ wird entsprechend der maximal möglichen Geschwindigkeit „speedMax“ und dem maximalen Geschwindigkeitsfaktor „maxSpeed“ angepasst.
    • Wenn der absolute Wert der Agentengeschwindigkeit kleiner als „d“ ist, wird die Agentengeschwindigkeit gleich „d“ gesetzt (wobei das Vorzeichen erhalten bleibt).

Diese Methode implementiert das Verhalten eines „Geschwindigkeitslimits“ Verhalten im Boids-Algorithmus, das dazu beiträgt, die Bewegungsgeschwindigkeit der Agenten zu kontrollieren und zu verhindern, dass die Boids stehen bleiben.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::LimitSpeed (S_Boids_Agent &boid)
{
  double speed = 0;

  for (int c = 0; c < coords; c++)
  {
    speed += boid.dx [c] * boid.dx [c];
  }

  speed = sqrt (speed);

  double d = 0;

  for (int c = 0; c < coords; c++)
  {
    d = (rangeMax [c] - rangeMin [c]) * minSpeed;

    boid.dx [c] = (boid.dx [c] / speed) * speedMax [c] * maxSpeed;

    if (fabs (boid.dx [c]) < d)
    {
      if (boid.dx [c] < 0.0) boid.dx [c] = -d;
      else                   boid.dx [c] =  d;
    }

  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode KeepWithinBounds der Klasse C_AO_Boids wird verwendet, um die Bewegung von Agenten innerhalb der angegebenen Grenzen im Boids-Algorithmus zu beschränken. Dieses Verhalten verhindert, dass die Agenten die festgelegten Grenzen überschreiten.

  1. Für jede Agentenkoordinate wird geprüft, ob sie außerhalb der festgelegten Grenzen liegt (definiert als „rangeMin“ und „rangeMax“).
  2. Ist die Koordinate des Agenten kleiner als „rangeMin“, wird sie auf „rangeMax“ gesetzt und der Agent auf die gegenüberliegende Seite der Begrenzung verschoben.
  3. Ist die Koordinate des Agenten größer als „rangeMax“, wird sie auf „rangeMin“ gesetzt und der Agent auf die gegenüberliegende Seite der Begrenzung verschoben.

Diese Methode bietet eine „Grenzbeschränkung“ im Boids-Algorithmus, die den Agenten hilft, innerhalb der vorgegebenen Grenzen zu bleiben.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::KeepWithinBounds (S_Boids_Agent &boid)
{
  for (int c = 0; c < coords; c++)
  {
    double margin     = 0; //(rangeMax [c] - rangeMin [c])* 0.00001;
    double turnFactor = (rangeMax [c] - rangeMin [c]) * 0.0001;

    /*
    if (boid.x [c] < rangeMin [c] + margin)
    {
      boid.dx [c] += turnFactor;
    }
    if (boid.x [c] > rangeMax [c] - margin)
    {
      boid.dx [c] -= turnFactor;
    }
    */
    if (boid.x [c] < rangeMin [c]) 
    {
      //boid.x [c] = rangeMax [c];
      boid.dx [c] *= -1;
      
    }
    if (boid.x [c] > rangeMax [c])
    {
      //boid.x [c] = rangeMin [c];
      boid.dx [c] *= -1;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Die Methode Distance der Klasse C_AO_Boids wird verwendet, um den euklidischen Abstand zwischen zwei Agenten im Boids-Algorithmus zu berechnen.

  1. Die Variable „dist“ wird initialisiert, um den Abstand zu speichern.
  2. Für jede Agentenkoordinate wird das Quadrat der Differenz zwischen ihren Koordinaten berechnet und dann zu „dist“ addiert.
  3. Am Ende gibt die Methode die Quadratwurzel von „dist“ zurück, was dem euklidischen Abstand zwischen den Agenten entspricht.

Diese Methode ermöglicht die Berechnung des Abstands zwischen den Agenten im Boids-Algorithmus, der zur Bestimmung ihrer Interaktion untereinander verwendet wird.

//——————————————————————————————————————————————————————————————————————————————
double C_AO_Boids::Distance (S_Boids_Agent &boid1, S_Boids_Agent &boid2)
{
  double dist = 0;

  for (int c = 0; c < coords; c++)
  {
    dist += pow (boid1.x [c] - boid1.x [c], 2);
  }

  return sqrt (dist);
}
//——————————————————————————————————————————————————————————————————————————————

Die Revisionsmethode der Klasse C_AO_Boids wird zur Aktualisierung der besten Lösung im Boids-Algorithmus verwendet.

  1. Die Variable „ind“ wird mit dem Wert -1 initialisiert. Diese Variable wird verwendet, um den Index des Agenten mit der besten Lösung zu speichern.
  2. Für jeden Agenten in der Population wird geprüft, ob seine Fitnessfunktion „a[i].f“ kleiner ist als die aktuell beste Lösung „fB“. Wenn ja, wird „ind“ auf den Index des Agenten gesetzt.
  3. Wenn ein Agent mit einer besseren Lösung gefunden wurde („ind“ ist ungleich -1), dann werden die beste Lösung „fB“ und die besten Koordinaten „cB“ mit den Werten dieses Agenten aktualisiert.

Diese Methode liefert eine Aktualisierung der besten Lösung im Boids-Algorithmus, was dem Algorithmus hilft, sich auf die vielversprechendsten Bereiche des Lösungsraums zu konzentrieren.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_Boids::Revision ()
{
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) ind = i;
  }

  if (ind != -1)
  {
    fB = a [ind].f;
    ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————


3. Testergebnisse

Ich möchte auf die Ergebnisse des Boids-Algorithmus für verschiedene Funktionsmengen näher eingehen. Die Gesamtpunktzahl der Boids für alle Testfunktionen betrug 2,22889, was 24,77 % der maximal möglichen Punktzahl entspricht. Dieses Ergebnis deutet auf eine geringe Effizienz des Algorithmus hin. Daraus können wir schließen, dass der Boids-Algorithmus wenig Potenzial für die Lösung von Optimierungsproblemen für verschiedene Funktionen hat.

Boids|50.0|0.05|0.002|0.01|0.01|0.0001|0.01|0.001|0.0001|
=============================
5 Hilly's; Func runs: 100000; result: 0.43339505349362384
25 Hilly's; Func runs: 100000; result: 0.3058074706767012
500 Hilly's; Func runs: 100000; result: 0.2542539219446322
=============================
5 Forest's; Func runs: 100000; result: 0.35717696198531945
25 Forest's; Func runs: 100000; result: 0.20160005990319796
500 Forest's; Func runs: 100000; result: 0.15708435238635948
=============================
5 Megacity's; Func runs: 100000; result: 0.2784615384615384
25 Megacity's; Func runs: 100000; result: 0.14276923076923081
500 Megacity's; Func runs: 100000; result: 0.09833846153846236
=============================
All score: 2.22889 (24.77%)

Der Boids-Algorithmus belegte in der Bewertungstabelle den 28. Platz, neben seinem „Bruder“ in Schwarmintelligenzsystemen, dem PSO-Algorithmus.

# AO Beschreibung Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
1 BGA binärer genetischer Algorithmus 0.99992 0.99484 0.50483 2.49959 1.00000 0.99975 0.32054 2.32029 0.90667 0.96400 0.23035 2.10102 6.921 76.90
2 (P+O)ES (P+O) Entwicklungsstrategien 0.99934 0.91895 0.56297 2.48127 1.00000 0.93522 0.39179 2.32701 0.83167 0.64433 0.21155 1.68755 6.496 72.18
3 SDSm stochastische Diffusionssuche M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
4 ESG Entwicklung der sozialen Gruppen 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
5 SIA Simuliertes isotropes Abkühlen 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
6 DE differentielle Evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
7 BSA Vogelschwarm-Algorithmus 0.90857 0.73661 0.25767 1.90285 0.90437 0.81619 0.16401 1.88457 0.61692 0.54154 0.10951 1.26797 5.055 56.17
8 HS Harmoniesuche 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
9 SSG Setzen, Säen und Wachsen 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
10 (PO)ES (PO) Entwicklungsstrategien 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
11 WOAm Wal-Optimierungsalgorithmus M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
12 ACOm Ameisen-Kolonie-Optimierung M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
13 BFO-GA Optimierung der bakteriellen Futtersuche - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
14 MEC Evolutionäre Berechnung des Geistes 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
15 IWO Optimierung mit invasiven Unkräutern 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
16 Micro-AIS Künstliches Mikro-Immunsystem 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
17 COAm Kuckuck-Optimierungsalgorithmus M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
18 SDOm Optimierung der Spiraldynamik M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
19 NMm Nelder-Mead-Verfahren M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
20 FAm Firefly-Algorithmus M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
21 GSA Algorithmus für die Schwerkraftsuche 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
22 BFO Optimierung der bakteriellen Futtersuche 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
23 ABC Künstliches Bienenvolk (Artificial Bee Colony, ABC) 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
24 BA Fledermaus-Algorithmus 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
25 SA simuliertes Abkühlen 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
26 IWDm intelligente Wassertropfen M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
27 PSO Partikelschwarmoptimierung 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
28 Gebote Boids-Algorithmus 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
29 MA Affen-Algorithmus 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
30 SFL schlurfender Froschsprung 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
31 FSS Fischschulsuche 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
32 RND zufällig 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
33 GWO Grauer-Wolf-Optimierung 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
34 CSS Suche geladener Systeme 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
35 EM elektromagnetismusähnlicher Algorithmus 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


Zusammenfassung

Trotz der schwachen Ergebnisse bei den Testfunktionen ist es erwähnenswert, dass die Ergebnisse bei den Funktionen Forest und Megacity mit 1000 Variablen recht anständig sind und den Ergebnissen der Algorithmen in der oberen Hälfte der Tabelle entsprechen. Dies könnte darauf hinweisen, dass der Boids-Algorithmus bei einer größeren Anzahl von Variablen effizienter ist. Insgesamt zeigen diese Ergebnisse, dass es schwierig wäre, vom Boids-Algorithmus mehr Potenzial zu erwarten.

Tabelle

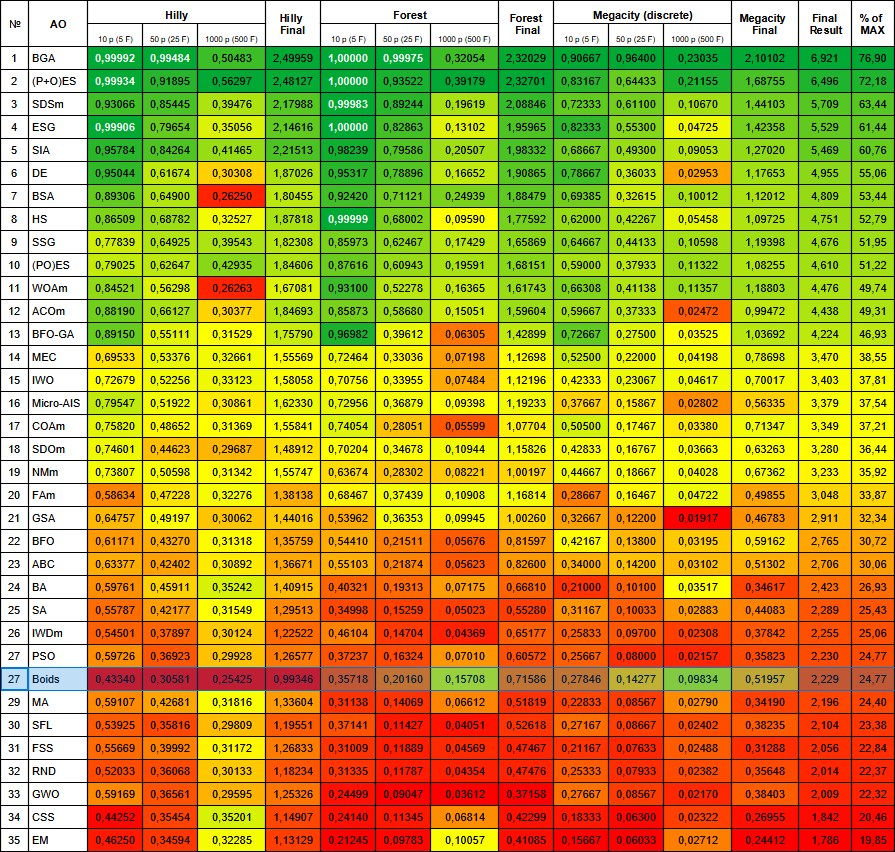
Abbildung 1. Die farblichen Abstufungen der Algorithmen nach relevanten Tests Ergebnisse größer oder gleich 0,99 sind weiß hervorgehoben

Histogramm

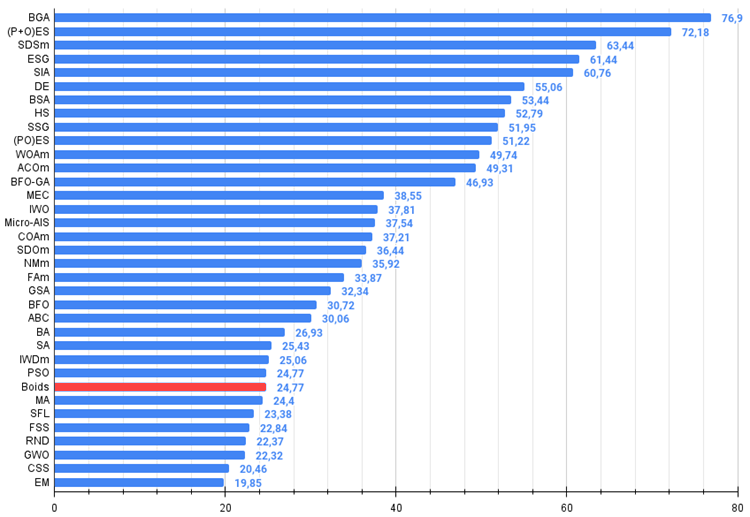
Bild 2. Das Histogramm der Algorithmus-Testergebnisse (auf einer Skala von 0 bis 100, größer ist besser,

wobei 100 das maximal mögliche theoretische Ergebnis ist; das Archiv enthält ein Skript zur Berechnung der Bewertungstabelle)

Boids Vor- und Nachteile:

Vorteile:

  1. Realistische Simulation des Herdenverhaltens.

Nachteile

  1. Geringe Konvergenz.
  2. Hohe rechnerische Komplexität.
  3. Geringe Skalierbarkeit bei glatten Funktionen wie Hilly (Probleme mit hochdimensionalen Aufgaben).

Der Artikel wird von einem Archiv mit den aktuellen Code-Versionen begleitet. Der Autor des Artikels übernimmt keine Verantwortung für die absolute Richtigkeit der Beschreibung der kanonischen Algorithmen. An vielen von ihnen wurden Änderungen vorgenommen, um die Suchmöglichkeiten zu verbessern. Die in den Artikeln dargelegten Schlussfolgerungen und Urteile beruhen auf den Ergebnissen der Versuche.

Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/14576

Beigefügte Dateien |
ZIP herunterladen
Boids.zip (28.61 KB)
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.

Andere Artikel von diesem Autor

Zur Diskussion im Händlerforum
Die Übertragung der Trading-Signale in einem universalen Expert Advisor. Die Übertragung der Trading-Signale in einem universalen Expert Advisor.
In diesem Artikel wurden die verschiedenen Möglichkeiten beschrieben, um die Trading-Signale von einem Signalmodul des universalen EAs zum Steuermodul der Positionen und Orders zu übertragen. Es wurden die seriellen und parallelen Interfaces betrachtet.
Aufbau des Kerzenmodells Trend-Constraint (Teil 5): Nachrichtensystem (Teil III) Aufbau des Kerzenmodells Trend-Constraint (Teil 5): Nachrichtensystem (Teil III)
Dieser Teil der Artikelserie ist der Integration von WhatsApp mit MetaTrader 5 für Benachrichtigungen gewidmet. Zum besseren Verständnis haben wir ein Flussdiagramm beigefügt und werden die Bedeutung von Sicherheitsmaßnahmen bei der Integration erörtern. Der Hauptzweck von Indikatoren besteht darin, die Analyse durch Automatisierung zu vereinfachen, und sie sollten Benachrichtigungsmethoden enthalten, um Nutzer zu alarmieren, wenn bestimmte Bedingungen erfüllt sind. Erfahren Sie mehr in diesem Artikel.
Eine alternative Log-datei mit der Verwendung der HTML und CSS Eine alternative Log-datei mit der Verwendung der HTML und CSS
In diesem Artikel werden wir eine sehr einfache, aber leistungsfähige Bibliothek zur Erstellung der HTML-Dateien schreiben, dabei lernen wir auch, wie man eine ihre Darstellung einstellen kann (nach seinem Geschmack) und sehen wir, wie man es leicht in seinem Expert Advisor oder Skript hinzufügen oder verwenden kann.
Entwicklung eines Roboters in Python und MQL5 (Teil 1): Vorverarbeitung der Daten Entwicklung eines Roboters in Python und MQL5 (Teil 1): Vorverarbeitung der Daten
Entwicklung eines auf maschinellem Lernen basierenden Handelsroboters: Ein detaillierter Leitfaden. Der erste Artikel in dieser Reihe befasst sich mit der Erfassung und Aufbereitung von Daten und Merkmalen. Das Projekt wird unter Verwendung der Programmiersprache Python und der Bibliotheken sowie der Plattform MetaTrader 5 umgesetzt.