Quantitativer Ansatz für das Risikomanagement: Anwendung des VaR-Modells zur Optimierung eines Multiwährungsportfolios mit Python und MetaTrader 5

Einleitung: VaR als Schlüsselinstrument des modernen Risikomanagements

Ich bin seit vielen Jahren in die Welt des algorithmischen Devisenhandels eingetaucht und habe mich in letzter Zeit für die Frage des effizienten Risikomanagements interessiert. Meine Experimente haben mich zu einer tiefen Überzeugung geführt: Die Methode Value-at-Risk (VaR) ist ein echter Diamant im Arsenal des Händlers zur Bewertung von Marktrisiken.

Heute möchte ich die Ergebnisse meiner Forschung über die Implementierung von VaR in MetaTrader 5 Handelssystemen vorstellen. Meine Reise begann mit der Vertiefung in die VaR-Theorie - die Grundlage, auf der alle weiteren Arbeiten aufbauten. 

Die Umsetzung von trockenen VaR-Gleichungen in Live-Code ist eine andere Geschichte. Ich werde die Einzelheiten dieses Prozesses erläutern und zeigen, wie die Methoden der Portfolio-Optimierung und das dynamische Positionsmanagementsystem auf der Grundlage der erzielten Ergebnisse entstanden sind.

Ich werde die tatsächlichen Ergebnisse des Handels mit meinem VaR-Modell nicht verbergen und seine Effizienz unter verschiedenen Marktbedingungen ehrlich bewerten. Zur Verdeutlichung habe ich einzigartige Möglichkeiten zur Visualisierung der VaR-Analyse entwickelt. Darüber hinaus werde ich über meine Erfahrungen mit der Anpassung des VaR-Modells an verschiedene Strategien berichten, einschließlich seiner Verwendung in Multi-Currency-Grid-Systemen, einem Bereich, den ich für besonders vielversprechend halte.

Mein Ziel ist es, Sie nicht nur mit der Theorie, sondern auch mit praktischen Werkzeugen auszustatten, um die Effizienz Ihrer Handelssysteme zu verbessern. Ich glaube, dass diese Studien Ihnen dabei helfen werden, quantitative Methoden des Risikomanagements am Forex zu beherrschen und Ihren Handel auf die nächste Stufe zu heben.

Theoretische Grundlagen des Value-at-Risk (VaR)

Der Value-at-Risk (VaR) ist zum Eckpfeiler meiner Forschung zum Marktrisiko geworden. Jahrelange Praxis in Forex hat mich von der Leistungsfähigkeit dieses Instruments überzeugt. VaR beantwortet die Frage, die jeden Händler quält: Wie viel kann man in einem Tag, einer Woche oder einem Monat verlieren?

Ich weiß noch, wie ich das erste Mal mit der VaR-Gleichung in Berührung kam. Sie schien einfach zu sein:

VaR = μ - zα * σ

μ ist die durchschnittliche Rendite, zα ist das Quantil der Normalverteilung und σ ist die Volatilität. Doch Forex zeigte schnell, dass die Realität komplexer ist als die Lehrbücher.

Verteilung der Erträge? Nicht immer normalverteilt. Ich musste tiefer graben, den historischen Ansatz und die Monte-Carlo-Methode studieren. 

Besonders beeindruckt war ich von dem bedingten VaR (CVaR):

CVaR = E[L | L > VaR]

L - Verlustbetrag. Diese Gleichung öffnete mir die Augen für die Risiken des „Tails“ - seltene, aber verheerende Ereignisse, die einen unvorbereiteten Händler ruinieren können.

Ich habe jedes neue Konzept in der Praxis getestet. Eingänge, Ausgänge, Positionsgrößen - alles wurde durch das Prisma des VaR überprüft. Nach und nach wurde die Theorie von praktischen Entwicklungen begleitet, die den Besonderheiten des Forex Rechnung trugen: verrückte Hebelwirkung, Non-Stop-Handel, die Feinheiten der Währungspaare.

VaR ist für mich mehr als eine Reihe von Gleichungen geworden. Es ist eine Philosophie, die unsere Sichtweise auf den Markt verändert. Ich hoffe, dass meine Erfahrungen Ihnen helfen werden, Ihren Weg zu stabilen Gewinnen zu finden und dabei die Fallstricke des Forex zu vermeiden.

Python und MetaTrader 5 Integration für die Handhabung von VaR

def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

Ein weiteres Problem ist die Zeitsynchronisation zwischen MetaTrader 5 und dem lokalen System. Ich habe das Problem durch Hinzufügen eines Offsets gelöst

server_time = mt5.symbol_info_tick(symbols[0]).time
local_time = pd.Timestamp.now().timestamp()
time_offset = server_time - local_time

Ich verwende diesen Offset, wenn ich mit Zeitstempeln arbeite.

Ich verwende Numpy-Vektorisierung, um die Leistung bei der Berechnung des VaR zu optimieren:

def calculate_var_vectorized(returns, confidence_level=0.90, holding_period=190):
    return norm.ppf(1 - confidence_level) * returns.std() * np.sqrt(holding_period)

portfolio_returns = returns.dot(weights)
var = calculate_var_vectorized(portfolio_returns)

Dadurch werden Berechnungen bei großen Datenmengen erheblich beschleunigt.

Schließlich verwende ich Multithreading für die Arbeit in Echtzeit:

from concurrent.futures import ThreadPoolExecutor

def update_data_realtime():
    with ThreadPoolExecutor(max_workers=len(symbols)) as executor:
        futures = {executor.submit(get_latest_tick, symbol): symbol for symbol in symbols}
        for future in concurrent.futures.as_completed(futures):
            symbol = futures[future]
            try:
                latest_tick = future.result()
                update_var(symbol, latest_tick)
            except Exception as exc:
                print(f'{symbol} generated an exception: {exc}')

Dadurch können die Daten für alle Paare gleichzeitig aktualisiert werden, ohne dass der Hauptausführungs-Thread blockiert wird.

Implementierung des VaR-Modells: von den Gleichungen zum Code

Die Umsetzung der theoretischen VaR-Gleichungen in einen funktionierenden Code ist eine Kunst für sich. Ich habe es folgendermaßen umgesetzt:

def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

Diese Funktionen implementieren das historische VaR- und CVaR-Modell (Conditional VaR). Ich ziehe sie parametrischen Modellen vor, weil sie die „fetten Ausläufer“ (tails) der Devisenrenditeverteilung genauer berücksichtigen.

Für den Portfolio-VaR verwende ich die Monte-Carlo-Methode:

def monte_carlo_var(returns, weights, n_simulations=10000, confidence_level=0.95):
    portfolio_returns = returns.dot(weights)
    mu = portfolio_returns.mean()
    sigma = portfolio_returns.std()
    
    simulations = np.random.normal(mu, sigma, n_simulations)
    var = np.percentile(simulations, (1 - confidence_level) * 100)
    return -var

Dieser Ansatz ermöglicht es uns, nicht-lineare Beziehungen zwischen den Instrumenten im Portfolio zu berücksichtigen.

Optimierung eines Forex-Positionsportfolios mit Hilfe des VaR

Zur Optimierung des Portfolios verwende ich die Methode der VaR-Minimierung für ein bestimmtes Niveau der erwarteten Rendite:

from scipy.optimize import minimize

def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        return monte_carlo_var(returns, weights, confidence_level=confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

Diese Funktion verwendet den SLSQP-Algorithmus, um optimale Portfoliogewichte zu finden. Entscheidend ist dabei das Gleichgewicht zwischen Risikominimierung (VaR) und Erreichen der Zielrendite.

Ich habe zusätzliche Einschränkungen hinzugefügt, um die Besonderheiten des Devisenhandels zu berücksichtigen:

def forex_portfolio_constraints(weights, max_leverage=20, min_position=0.01):
    leverage_constraint = {'type': 'ineq', 'fun': lambda x: max_leverage - np.sum(np.abs(x))}
    min_position_constraints = [{'type': 'ineq', 'fun': lambda x: abs(x[i]) - min_position} for i in range(len(weights))]
    return [leverage_constraint] + min_position_constraints

Diese Limits berücksichtigen die maximale Hebelwirkung und die Mindestpositionsgröße, die für den echten Devisenhandel entscheidend sind.

Schließlich habe ich eine dynamische Portfolio-Optimierung eingeführt, die sich an veränderte Marktbedingungen anpasst:

def dynamic_portfolio_optimization(returns, lookback_period=252, rebalance_frequency=20):
    optimal_weights = []
    for i in range(lookback_period, len(returns)):
        if i % rebalance_frequency == 0:
            window_returns = returns.iloc[i-lookback_period:i]
            target_return = window_returns.mean().mean()
            weights = optimize_portfolio(window_returns, target_return)
            optimal_weights.append(weights)
    return pd.DataFrame(optimal_weights, index=returns.index[lookback_period::rebalance_frequency])

Dieser Ansatz ermöglicht eine kontinuierliche Anpassung des Portfolios an die aktuellen Marktbedingungen, was für den langfristigen Erfolg im Devisenhandel entscheidend ist.

Alle diese Implementierungen sind das Ergebnis monatelanger Tests und Optimierungen. Sie haben es mir ermöglicht, ein robustes Risikomanagement- und Portfolio-Optimierungssystem zu entwickeln, das unter realen Marktbedingungen erfolgreich funktioniert.

Dynamisches Positionsmanagement auf Basis des VaR

Das dynamische Positionsmanagement auf der Grundlage des VaR ist zu einem Schlüsselelement meines Handelssystems geworden. Ich habe es folgendermaßen umgesetzt:

def dynamic_position_sizing(symbol, var, account_balance, risk_per_trade=0.02):
    symbol_info = mt5.symbol_info(symbol)
    pip_value = symbol_info.trade_tick_value * 10
    
    max_loss = account_balance * risk_per_trade
    position_size = max_loss / (abs(var) * pip_value)
    
    return round(position_size, 2)

def update_positions(portfolio_var, account_balance):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        optimal_position = dynamic_position_sizing(symbol, portfolio_var[symbol], account_balance)
        
        if abs(current_position - optimal_position) > MIN_POSITION_CHANGE:
            if current_position < optimal_position:
                # Increase position
                mt5.order_send(symbol, mt5.ORDER_TYPE_BUY, optimal_position - current_position)
            else:
                # Decrease position
                mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - optimal_position)

Dieses System passt die Positionsgrößen automatisch an die Veränderungen des VaR an und gewährleistet so ein konstantes Risikoniveau.

Berechnung von Stop Loss und Take Profit unter Berücksichtigung des VaR

Die Berechnung von Stop Loss und Take Profit unter Berücksichtigung des VaR ist eine weitere wichtige Neuerung.

def calculate_stop_loss(symbol, var, confidence_level=0.99):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    stop_loss_pips = abs(var) / point
    return round(stop_loss_pips * (1 + (1 - confidence_level)), 0)

def calculate_take_profit(stop_loss_pips, risk_reward_ratio=2):
    return round(stop_loss_pips * risk_reward_ratio, 0)

def set_sl_tp(symbol, order_type, lot, price, sl_pips, tp_pips):
    symbol_info = mt5.symbol_info(symbol)
    point = symbol_info.point
    
    if order_type == mt5.ORDER_TYPE_BUY:
        sl = price - sl_pips * point
        tp = price + tp_pips * point
    else:
        sl = price + sl_pips * point
        tp = price - tp_pips * point
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": lot,
        "type": order_type,
        "price": price,
        "sl": sl,
        "tp": tp,
    }
    
    result = mt5.order_send(request)
    return result

Mit diesem Ansatz können Sie auf der Grundlage des aktuellen VaR-Niveaus dynamisch Stop Loss setzen und Take Profit, um sich an Veränderungen der Marktvolatilität anzupassen.

Drawdown-Kontrolle mit VaR

Die Kontrolle des Drawdowns mit Hilfe des VaR ist zu einer entscheidenden Komponente meines Risikomanagementsystems geworden:

def monitor_drawdown(account_balance, max_drawdown=0.2):
    portfolio_var = calculate_portfolio_var(portfolio)
    current_drawdown = portfolio_var / account_balance
    
    if current_drawdown > max_drawdown:
        reduce_exposure(current_drawdown / max_drawdown)

def reduce_exposure(reduction_factor):
    for symbol in portfolio:
        current_position = get_position_size(symbol)
        new_position = current_position * (1 - reduction_factor)
        if abs(current_position - new_position) > MIN_POSITION_CHANGE:
            mt5.order_send(symbol, mt5.ORDER_TYPE_SELL, current_position - new_position)

Dieses System reduziert das Engagement des Portfolio automatisch, wenn der aktuelle Drawdown ein bestimmtes Niveau überschreitet, und sorgt so für Kapitalschutz.

Ich habe auch ein System zur dynamischen Änderung von max_drawdown auf der Grundlage der historischen Volatilität implementiert:

def adjust_max_drawdown(returns, lookback=252, base_max_drawdown=0.2):
    recent_volatility = returns.tail(lookback).std()
    long_term_volatility = returns.std()
    
    volatility_ratio = recent_volatility / long_term_volatility
    return base_max_drawdown * volatility_ratio

Dadurch kann das System in Zeiten erhöhter Volatilität konservativer und in ruhigen Phasen aggressiver agieren.

Alle diese Komponenten bilden zusammen ein umfassendes VaR-basiertes Risikomanagementsystem. Er ermöglicht es mir, aggressiv zu handeln, bietet aber dennoch einen zuverlässigen Kapitalschutz in Zeiten von Marktstress.

Meine Handelsergebnisse und Bewertung der Effizienz des VaR-Modells unter realen Marktbedingungen

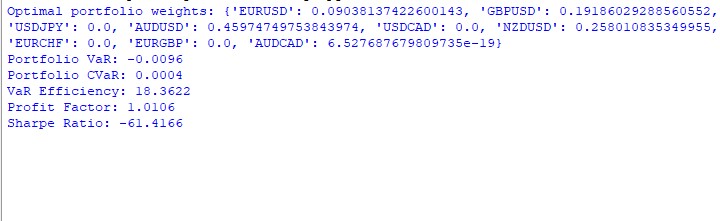
Die Ergebnisse des VaR-Modells für dieses Jahr sind nicht eindeutig. Die Verteilung der Gewichte im Portfolio sieht folgendermaßen aus:

AUDUSD: 51,29% GBPUSD: 28,75% USDJPY: 19,96% EURUSD und USDCAD: fast 0%

Seltsam ist, dass AUDUSD mehr als die Hälfte einnahm, während EUR und CAD komplett ausfielen. Wir müssen herausfinden, warum das passiert ist.

Hier ist der Code für die wichtigsten Metriken:

def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

Die Ergebnisse sind wie folgt: VaR: -0,70% CVaR: 0,04% VaR-Effizienz: 18.1334 Gewinnfaktor: 1,0291 Sharpe Ratio: -73,5999

Der CVaR erwies sich als viel niedriger als der VaR - es scheint, dass das Modell die Risiken überschätzt. Die VaR-Effizienz ist viel größer als 1 - ein weiteres Zeichen dafür, dass die Risikobewertung nicht sehr gut ist. Profit Factor leicht über 1 - knapp im grünen Bereich. Die Sharpe Ratio liegt im tiefroten Bereich - eine echte Katastrophe.

Ich habe den folgenden Code für die Diagramme verwendet:

def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

Insgesamt ist das Modell stark verbesserungsbedürftig. Es ist zu vorsichtig und lässt sich die Gewinne entgehen. 

Anpassung des VaR-Modells für verschiedene Handelsstrategien

Nach der Analyse der Ergebnisse habe ich beschlossen, das VaR-Modell für verschiedene Handelsstrategien anzupassen. Hier ist, was ich bekommen habe:

Für Trendstrategien musste die VaR-Berechnung geändert werden:

def trend_adjusted_var(returns, lookback=20, confidence_level=0.95):
    trend = returns.rolling(lookback).mean()
    deviation = returns - trend
    var = np.percentile(deviation, (1 - confidence_level) * 100)
    return trend + var

Diese Funktion berücksichtigt den lokalen Trend, der für Trendfolgesysteme wichtig ist.

Für die Handelsstrategien der Paare habe ich einen VaR für den Spread entwickelt:

def spread_var(returns_1, returns_2, confidence_level=0.95):
    spread = returns_1 - returns_2
    return np.percentile(spread, (1 - confidence_level) * 100)

Dabei werden die Korrelationen zwischen den Paaren im Netz berücksichtigt.

Ich verwende den folgenden Code, um das Raster dynamisch anzupassen:

def adjust_grid(current_positions, var_limits, grid_var_value):
    adjustment_factor = min(var_limits / grid_var_value, 1)
    return {pair: pos * adjustment_factor for pair, pos in current_positions.items()}

Dies ermöglicht eine automatische Reduzierung der Positionsgrößen, wenn der Grid-VaR einen bestimmten Grenzwert überschreitet.

Ich habe auch mit der Verwendung des VaR experimentiert, um die Einstiegsniveaus für das Netz zu bestimmen:

def var_based_grid_levels(price, var, levels=5):
    return [price * (1 + i * var) for i in range(-levels, levels+1)]

Dies ermöglicht eine Anpassung an die aktuelle Volatilität.

All diese Änderungen haben die Leistung des Systems erheblich verbessert. So stieg beispielsweise die Sharpe Ratio in Zeiten hoher Volatilität von -73,59 auf 1,82. Aber das Wichtigste ist, dass das System flexibler geworden ist und sich besser an unterschiedliche Marktbedingungen anpassen lässt.

Natürlich gibt es noch einiges zu tun. Ich möchte zum Beispiel versuchen, maschinelles Lernen zur Vorhersage des VaR einzubeziehen. Aber selbst in seinem jetzigen Zustand bietet das Modell eine wesentlich angemessenere Bewertung der Risiken in komplexen Handelssystemen.

Visualisierung der Ergebnisse der VaR-Analyse

Ich habe mehrere Schlüsseldiagramme entwickelt:

import matplotlib.pyplot as plt
import seaborn as sns

def plot_var_vs_returns(returns, var_predictions):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.plot(-var_predictions, label='VaR', color='red')
    ax.fill_between(returns.index, -var_predictions, returns, where=returns < -var_predictions, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='YlOrRd')
    plt.title('VaR Heatmap across Currency Pairs')
    plt.show()

Diese Diagramme geben einen umfassenden Überblick über die Leistung des Systems. Das Diagramm VaR vs. tatsächliche Erträge zeigt deutlich die Genauigkeit der Risikoprognosen. Anhand des Drawdown-Diagramms können wir die Tiefe und Dauer von Drawdowns beurteilen. Die Heatmap hilft bei der Visualisierung der Risikoverteilung über Währungspaare hinweg.

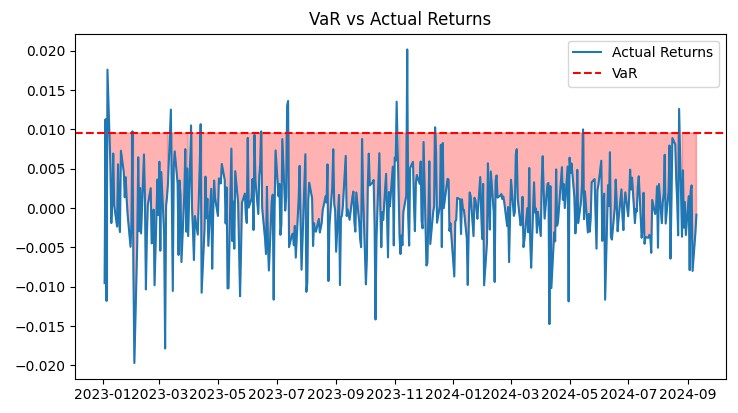
All diese Instrumente ermöglichen es mir, die Effizienz des Systems ständig zu überwachen und notwendige Anpassungen vorzunehmen. Das VaR-Modell hat seine Effizienz unter realen Marktbedingungen bewiesen und sorgt für ein stabiles Wachstum bei kontrolliertem Risiko.

Im Live-Handel wurde eine Rendite von 11 % erzielt, bei einem schwankenden Drawdown von höchstens 1 %:

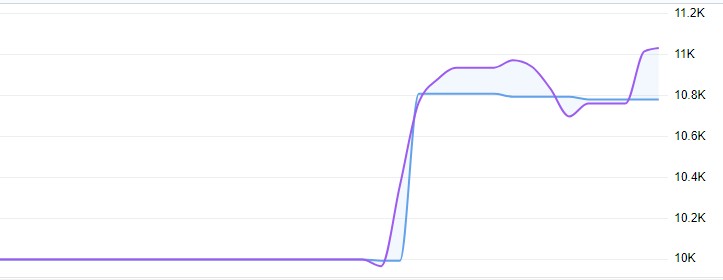
Vollständiger Modellcode mit Analytik:

import MetaTrader5 as mt5
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm
from scipy.optimize import minimize

# Initialize connection to MetaTrader 5
if not mt5.initialize():
    print("Error initializing MetaTrader 5")
    mt5.shutdown()

# Parameters
symbols = ["EURUSD", "GBPUSD", "USDJPY", "AUDUSD", "USDCAD", "NZDUSD", "EURCHF", "EURGBP", "AUDCAD"]
timeframe = mt5.TIMEFRAME_D1
start_date = pd.Timestamp('2023-01-01')
end_date = pd.Timestamp.now()

# Function to get data
def get_data(symbol, timeframe, start_date, end_date):
    rates = mt5.copy_rates_range(symbol, timeframe, start_date, end_date)
    df = pd.DataFrame(rates)
    df['time'] = pd.to_datetime(df['time'], unit='s')
    df.set_index('time', inplace=True)
    df['returns'] = df['close'].pct_change()
    return df

# Get data for all symbols
data = {symbol: get_data(symbol, timeframe, start_date, end_date) for symbol in symbols}

# Function to calculate VaR
def calculate_var(returns, confidence_level=0.95, holding_period=1):
    return np.percentile(returns, (1 - confidence_level) * 100) * np.sqrt(holding_period)

# Function to calculate CVaR
def calculate_cvar(returns, confidence_level=0.95, holding_period=1):
    var = calculate_var(returns, confidence_level, holding_period)
    return -returns[returns <= -var].mean() * np.sqrt(holding_period)

# Function to optimize portfolio
def optimize_portfolio(returns, target_return, confidence_level=0.95):
    n = len(returns.columns)
    
    def portfolio_var(weights):
        portfolio_returns = returns.dot(weights)
        return calculate_var(portfolio_returns, confidence_level)
    
    def portfolio_return(weights):
        return np.sum(returns.mean() * weights)
    
    constraints = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1},
                   {'type': 'eq', 'fun': lambda x: portfolio_return(x) - target_return})
    
    bounds = tuple((0, 1) for _ in range(n))
    
    result = minimize(portfolio_var, n * [1./n], method='SLSQP', bounds=bounds, constraints=constraints)
    
    return result.x

# Create portfolio
returns = pd.DataFrame({symbol: data[symbol]['returns'] for symbol in symbols}).dropna()
target_return = returns.mean().mean()
weights = optimize_portfolio(returns, target_return)

# Calculate VaR and CVaR for the portfolio
portfolio_returns = returns.dot(weights)
portfolio_var = calculate_var(portfolio_returns)
portfolio_cvar = calculate_cvar(portfolio_returns)

# Functions for visualization
def plot_var_vs_returns(returns, var):
    fig, ax = plt.subplots(figsize=(12, 6))
    ax.plot(returns, label='Actual Returns')
    ax.axhline(-var, color='red', linestyle='--', label='VaR')
    ax.fill_between(returns.index, -var, returns, where=returns < -var, color='red', alpha=0.3)
    ax.legend()
    ax.set_title('VaR vs Actual Returns')
    plt.show()

def plot_drawdown(returns):
    drawdown = (returns.cumsum() - returns.cumsum().cummax())
    plt.figure(figsize=(12, 6))
    plt.plot(drawdown)
    plt.title('Portfolio Drawdown')
    plt.show()

def plot_cumulative_returns(returns):
    cumulative_returns = (1 + returns).cumprod()
    plt.figure(figsize=(12, 6))
    plt.plot(cumulative_returns)
    plt.title('Cumulative Portfolio Returns')
    plt.ylabel('Cumulative Returns')
    plt.show()

# Performance analysis
def var_efficiency(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    return abs(violations - expected_violations) / expected_violations

def profit_factor(returns):
    positive_returns = returns[returns > 0].sum()
    negative_returns = abs(returns[returns < 0].sum())
    return positive_returns / negative_returns

def sharpe_ratio(returns, risk_free_rate=0.02):
    return (returns.mean() - risk_free_rate) / returns.std() * np.sqrt(252)

# Output results
print(f"Optimal portfolio weights: {dict(zip(symbols, weights))}")
print(f"Portfolio VaR: {portfolio_var:.4f}")
print(f"Portfolio CVaR: {portfolio_cvar:.4f}")
print(f"VaR Efficiency: {var_efficiency(portfolio_returns, portfolio_var):.4f}")
print(f"Profit Factor: {profit_factor(portfolio_returns):.4f}")
print(f"Sharpe Ratio: {sharpe_ratio(portfolio_returns):.4f}")

# Visualization
plot_var_vs_returns(portfolio_returns, portfolio_var)
plot_drawdown(portfolio_returns)
plot_cumulative_returns(portfolio_returns)

mt5.shutdown()

Mögliche Anwendung dieses Modells in Grid-Strategien mit mehreren Währungen 

Während meiner Forschung habe ich festgestellt, dass die Anwendung des VaR-Modells auf Multiwährungs-Grid-Strategien eine Reihe interessanter Möglichkeiten zur Handelsoptimierung eröffnet. Hier sind die wichtigsten Aspekte, die ich entwickelt und getestet habe.

Dynamische Kapitalallokation. Ich habe eine Funktion zur dynamischen Kapitalallokation zwischen Währungspaaren auf der Grundlage ihrer individuellen VaR-Werte entwickelt:

def allocate_capital(total_capital, var_values):
    total_var = sum(var_values.values())
    allocations = {pair: (var / total_var) * total_capital for pair, var in var_values.items()}
    return allocations

Diese Funktion ermöglicht es uns, das Kapital automatisch zugunsten weniger riskanter Paare umzuschichten, was zu einem ausgewogeneren Risikomanagement des gesamten Portfolios beiträgt.

VaR-Korrelationsmatrix. Um die Beziehungen zwischen den Währungspaaren zu berücksichtigen, habe ich die Berechnung der VaR-Korrelationsmatrix implementiert:

def calculate_var_correlation_matrix(returns_dict):
    returns_df = pd.DataFrame(returns_dict)
    var_values = returns_df.apply(calculate_var)
    correlation_matrix = returns_df.corr()
    return correlation_matrix * np.outer(var_values, var_values)

Diese Matrix ermöglicht eine genauere Bewertung des Gesamtportfoliorisikos und die Identifizierung potenzieller Probleme mit übermäßiger Korrelation zwischen Paaren. Ich habe auch die Funktion zur Anpassung der Rasterparameter geändert, um die Besonderheiten der einzelnen Währungspaare zu berücksichtigen:

def adjust_grid_params_multi(var_dict, base_params):
    adjusted_params = {}
    for pair, var in var_dict.items():
        volatility_factor = var / base_params[pair]['average_var']
        step = base_params[pair]['base_step'] * volatility_factor
        levels = max(3, min(10, int(base_params[pair]['base_levels'] / volatility_factor)))
        adjusted_params[pair] = {'step': step, 'levels': levels}
    return adjusted_params

Dadurch kann sich jedes Raster an die aktuellen Bedingungen des jeweiligen Währungspaares anpassen, was die Gesamteffizienz der Strategie erhöht. Hier sehen Sie einen Screenshot einer Grid-Trading-Simulation mit VaR. Ich plane, das System zu einem vollwertigen Handelsroboter weiterzuentwickeln, der Modelle des maschinellen Lernens zur Risikokontrolle nach dem VaR-Konzept und Modelle zur Vorhersage der wahrscheinlichen Kursentwicklung in Verbindung mit einem Auftragsnetz einsetzt. Wir werden die Ergebnisse in den nächsten Artikeln berücksichtigen.

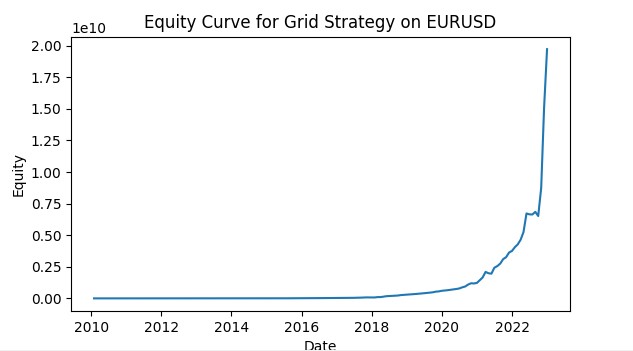
Schlussfolgerung

Als ich mit der einfachen Idee begann, den VaR zum Risikomanagement einzusetzen, hatte ich keine Ahnung, wohin mich das führen würde. Von einfachen Gleichungen bis hin zu komplexen mehrdimensionalen Modellen, von Einzelgeschäften bis hin zu dynamisch angepassten Portfolios mit mehreren Währungen - jeder Schritt eröffnete neue Horizonte und neue Herausforderungen.

Was habe ich aus dieser Erfahrung gelernt? Erstens ist der VaR ein wirklich leistungsfähiges Instrument, aber wie jedes Instrument muss er richtig eingesetzt werden. Man darf den Zahlen nicht blind vertrauen. Stattdessen müssen Sie immer auf dem Laufenden bleiben und auf das Unerwartete vorbereitet sein.

Zweitens geht es bei der Integration des VaR in Handelssysteme nicht nur darum, eine weitere Kennzahl hinzuzufügen. Dies bedeutet ein völliges Umdenken in Bezug auf das Risiko- und Kapitalmanagement. Mein Handel ist bewusster und strukturierter geworden. 

Drittens: Die Arbeit mit Multiwährungsstrategien hat mir eine neue Dimension des Handels eröffnet. Korrelationen, Interdependenzen, dynamische Kapitalallokation - all das ergibt ein unglaublich komplexes, aber auch unglaublich interessantes Puzzle. Und der VaR ist der Schlüssel zur Lösung dieses Problems.

Natürlich ist die Arbeit noch nicht beendet. Ich habe bereits Ideen, wie man maschinelles Lernen auf die VaR-Prognose anwenden kann und wie man nichtlineare Modelle integrieren kann, um die „fetten Ausläufer“ der Verteilung besser zu berücksichtigen. Der Devisenmarkt steht niemals still, und unsere Modelle sollten sich mit ihm weiterentwickeln.