Neuronale Netze im Handel: Hierarchisches Lernen der Merkmale von Punktwolken

Einführung

Eine geometrische Punktmenge stellt eine Sammlung von Punkten im euklidischen Raum dar. Als Menge müssen diese Daten gegenüber Permutationen ihrer Elemente unveränderlich bleiben. Außerdem definiert die Abstandsmetrik lokale Nachbarschaften, die unterschiedliche Eigenschaften aufweisen können. So können beispielsweise die Punktdichte und andere Attribute in verschiedenen Regionen unterschiedlich sein.

Im vorigen Artikel haben wir uns mit dem PointNet Methode untersucht, deren Kernidee darin besteht, für jeden Punkt eine räumliche Kodierung zu erlernen und anschließend alle individuellen Repräsentationen zu einer globalen Signatur der Punktwolke zusammenzufassen. PointNet erfasst jedoch nicht die lokale Struktur. Die Nutzung lokaler Strukturen hat sich jedoch als entscheidend für den Erfolg von Faltungsarchitekturen erwiesen. Faltungsmodelle verarbeiten Eingabedaten, die auf regelmäßigen Gittern angeordnet sind, und können schrittweise Objekte in immer größeren Maßstäben entlang einer Hierarchie mit mehreren Auflösungen erfassen. Auf niedrigeren Ebenen haben die Neuronen kleinere aufnahmebereite Felder, während sie auf höheren Ebenen größere Regionen umfassen. Die Fähigkeit, lokale Muster über diese Hierarchie hinweg zu abstrahieren, verbessert die Generalisierung.

Ein ähnlicher Ansatz wurde bei dem Modell PointNet++ angewandt, das in dem Artikel „PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space“ vorgestellt wurde. Die Kernidee von PointNet++ besteht darin, die Punktmenge auf der Grundlage einer Abstandsmetrik im zugrunde liegenden Raum in sich überschneidende lokale Regionen zu unterteilen. Ähnlich wie bei Faltungsnetzen extrahiert PointNet++ lokale Merkmale und erfasst feinkörnige geometrische Strukturen aus kleinen Regionen. Diese lokalen Strukturen werden dann zu größeren Elementen gruppiert und verarbeitet, um Darstellungen auf höherer Ebene abzuleiten. Dieser Vorgang wird iterativ wiederholt, bis die Merkmale für die gesamte Punktmenge vorliegen.

Bei der Entwicklung von PointNet++ stellten sich die Autoren zwei zentralen Herausforderungen: die Partitionierung der Punktmenge und die Abstraktion von Punktmengen oder lokalen Merkmalen durch lokalisiertes Merkmalslernen. Diese Herausforderungen sind voneinander abhängig, da die Partitionierung der Punktmenge die Beibehaltung gemeinsamer Strukturen über die Segmente hinweg erfordert, um ein gemeinsames Gewichtslernen für lokale Merkmale zu ermöglichen, ähnlich wie bei Faltungsmodellen. Die Autoren wählten PointNet als lokale Lerneinheit, da es sich um eine effiziente Architektur für die Verarbeitung ungeordneter Punktmengen und die Extraktion semantischer Merkmale handelt. Außerdem ist diese Architektur robust gegenüber Rauschen in den Eingangsdaten. Als grundlegender Baustein abstrahiert PointNet Mengen von lokalen Punkten oder Objekten zu übergeordneten Darstellungen. In diesem Rahmen wendet PointNet++ PointNet rekursiv auf verschachtelte Unterteilungen der Eingabedaten an.

Eine weitere Herausforderung ist die Methode zur Erstellung überlappender Partitionen der Punktwolke. Jede Region wird als eine Form von einer Nachbarschaft im euklidischen Raum definiert, die durch Parameter wie die Lage des Schwerpunkts und den Maßstab charakterisiert wird. Um eine gleichmäßige Abdeckung des gesamten Satzes zu gewährleisten, werden die Mittelpunkte aus den ursprünglichen Punkten mit Hilfe eines Algorithmus zur Auswahl des weitesten Punktes ausgewählt. Im Vergleich zu volumetrischen Faltungsmodellen, die den Raum mit festen Schritten abtasten, hängen die lokalen aufnahmebereiten Felder in PointNet++ sowohl von den Eingabedaten als auch von der Abstandsmetrik ab. Dies erhöht ihre Effizienz.

1. Der Algorithmus PointNet++

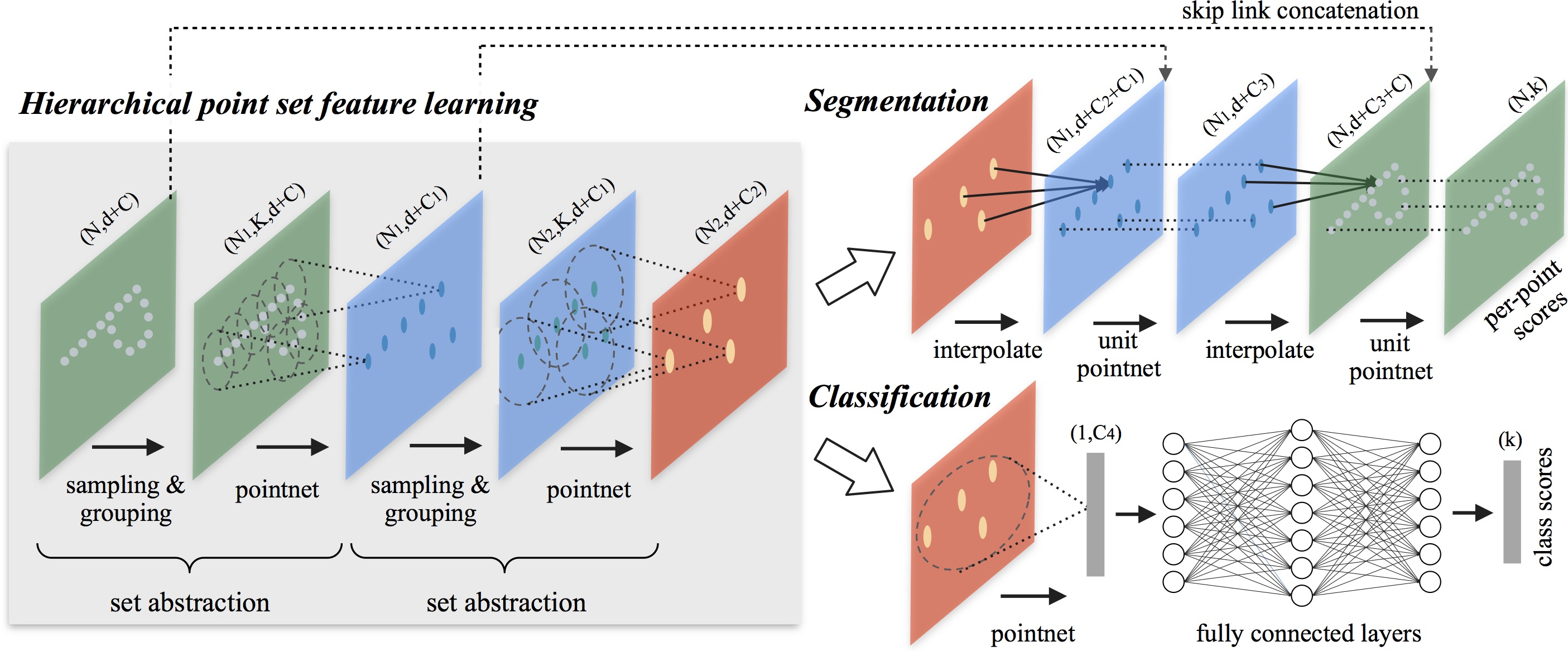
Die Architektur von PointNet verwendet eine einzige MaxPooling-Operation, um die gesamte Punktmenge zu aggregieren. Im Gegensatz dazu führen die Autoren von PointNet++ eine hierarchische Architektur ein, die lokale Regionen schrittweise über mehrere Hierarchieebenen abstrahiert.

Die vorgeschlagene hierarchische Struktur besteht aus mehreren vordefinierten Abstraktionsebenen. Auf jeder Ebene wird die Punktwolke verarbeitet und abstrahiert, um einen neuen Datensatz mit weniger Elementen zu erstellen. Jede Abstraktionsebene umfasst drei Schlüsselebenen: Sampling-Schicht, Gruppierungsschicht und PointNet-Schicht. Die Sampling-Schicht wählt eine Teilmenge von Punkten aus der ursprünglichen Punktwolke aus und definiert die Zentren lokaler Regionen. Die Gruppierungsschicht bildet dann lokale Punktmengen, indem sie „benachbarte“ Punkte um jeden Schwerpunkt identifiziert. Schließlich wendet die PointNet-Schicht ein Mini-PointNet an, um lokale Muster in Merkmalsvektoren zu kodieren.

Die Abstraktionsebene nimmt eine Eingabematrix der Größe N×(d+C), wobei N die Anzahl der Punkte, d die Dimensionalität der Koordinaten und C die Dimensionalität der Merkmale ist. Es gibt eine Matrix der Größe N′×(d+C′), wobei N′ die Anzahl der Punkte in der Teilstichprobe und C′ die Dimensionalität des neuen Merkmalsvektors ist, der den lokalen Kontext einschließt.

Die Autoren von PointNet++ schlagen ein iteratives „Farthest Point Sampling“ (FPS) vor, um eine Teilmenge von Schwerpunktpunkten auszuwählen. Im Vergleich zu Zufallsstichproben bietet diese Methode eine bessere Abdeckung der gesamten Punktwolke bei gleichbleibender Anzahl von Zentroiden. Im Gegensatz zu Faltungsnetzen, die den Vektorraum unabhängig von der Datenverteilung abtasten, erzeugt diese Abtaststrategie aufnahmebereite Felder, die von Natur aus datenabhängig sind.

Die Gruppierungsschicht übernimmt als Eingabe eine Punktwolke der Größe N×(d+C) und einen Reihe von Schwerpunktkoordinaten der Größe N′×d. Die Ausgabe besteht aus gruppierten Punktmengen der Größe N′×K×(d+C), wobei jede Gruppe einer lokalen Region entspricht und K die Anzahl der Punkte in der Nachbarschaft des Schwerpunkts ist.

Beachten Sie, dass K von Gruppe zu Gruppe variiert, aber die nachfolgende PointNet-Schicht kann eine flexible Anzahl von Punkten in einen Merkmalsvektor fester Länge umwandeln, der die lokale Region repräsentiert.

In Faltungsneuronalen Netzen (CNNs) besteht die lokale Nachbarschaft eines Pixels aus benachbarten Pixeln innerhalb eines bestimmten Manhattan-Abstands (Kernelgröße). In einer Punktwolke, in der Punkte im metrischen Raum existieren, werden Nachbarschaftsbeziehungen durch die Abstandsmetrik bestimmt.

Während des Gruppierungsprozesses identifiziert das Modell alle Punkte, die innerhalb eines vordefinierten Radius um den Abfragepunkt liegen (wobei K als Hyperparameter gedeckelt wird).

In der PointNet-Schicht besteht die Eingabe aus N′ lokalen Regionen mit einer Datengröße von N′×K×(d+C). Jede lokale Region wird schließlich in ihren Schwerpunkt und ein entsprechendes lokales Merkmal abstrahiert, das ihre Umgebung kodiert. Die resultierende Tensorgröße ist N′×(d+C).

Die Koordinaten der Punkte innerhalb jeder lokalen Region werden zunächst in ein lokales Koordinatensystem relativ zu ihrem Schwerpunkt transformiert:

für i = 1, 2,…, K ad j = 1, 2,…, d, wobei die Koordinaten des Schwerpunkts darstellt.

Die Autoren von PointNet++ verwenden PointNet als grundlegenden Baustein für das Lernen lokaler Muster. Durch die Verwendung relativer Koordinaten zusammen mit individuellen Punktmerkmalen erfasst das Modell effektiv die Beziehungen zwischen Punkten innerhalb einer lokalen Region.

Häufig weisen Punktwolken eine ungleichmäßige Punktdichte in verschiedenen Regionen auf. Diese Heterogenität stellt ein großes Problem beim Lernen von Punktmengenmerkmalen dar. Merkmale, die in dichten Teilstichprobe erlernt wurden, lassen sich möglicherweise nicht gut auf dünne Teilstichproben übertragen. Folglich können Modelle, die auf spärlichen Punktwolken trainiert wurden, feinkörnige lokale Strukturen nicht erkennen.

Idealerweise sollte die Verarbeitung von Punktwolken so präzise wie möglich sein, um die feinsten Details in dicht abgetasteten Regionen zu erfassen. Eine solche detaillierte Analyse ist jedoch in Gebieten mit geringer Punktdichte ineffizient, da lokale Muster aufgrund unzureichender Daten verzerrt werden können. In diesen Fällen muss eine breitere Nachbarschaft betrachtet werden, um größere Strukturen zu erkennen. Um dieses Problem zu lösen, schlagen die Autoren von PointNet++ dichteadaptive Schichten für PointNet vor, die so konzipiert sind, dass sie Merkmale aus mehreren Maßstäben zusammenfassen und dabei Schwankungen der Punktdichte berücksichtigen.

Jede Abstraktionsebene in PointNet++ extrahiert mehrere Skalen lokaler Muster und kombiniert sie auf intelligente Weise auf der Grundlage der lokalen Punktdichte. In der Originalarbeit werden zwei Arten von dichteadaptiven Schichten vorgestellt.

Ein einfacher, aber effektiver Ansatz zur Erfassung von Mustern mit mehreren Maßstäben besteht in der Anwendung mehrerer Gruppierungsebenen mit unterschiedlichen Maßstäben und der Zuweisung entsprechender PointNet-Module zur Extraktion von Merkmalen in jedem Maßstab. Die daraus resultierenden Darstellungen mit mehreren Skalen werden dann zu einem einheitlichen Merkmal kombiniert.

Das Netz erlernt eine optimale Strategie für die Zusammenführung von Merkmalen mit mehreren Skalen. Dies wird durch das zufällige Fallenlassen von Eingabepunkten mit einer jeder Instanz zugewiesenen Wahrscheinlichkeit erreicht.

Der oben beschriebene Ansatz erfordert erhebliche Rechenressourcen, da er für jeden Schwerpunktpunkt lokale PointNet-Operationen innerhalb großer Nachbarschaften anwendet. Um diesen Rechenaufwand zu verringern und gleichzeitig die Fähigkeit zur adaptiven Informationsverdichtung zu erhalten, schlagen die Autoren eine alternative Methode zur Merkmalsfusion vor, die auf der Verkettung zweier Merkmalsvektoren basiert. Ein Vektor wird durch die Aggregation von Merkmalen aus jeder Teilregion auf der niedrigeren Ebene Li-1 unter Verwendung der gegebenen Abstraktionsebene abgeleitet. Der zweite Vektor wird durch direkte Verarbeitung aller Originalpunkte innerhalb einer lokalen Region mit einem einzigen PointNet-Modul gewonnen.

Wenn die Dichte der lokalen Region gering ist, kann der erste Vektor weniger zuverlässig sein als der zweite, da die für die Merkmalsberechnung verwendete Teilregion noch weniger Punkte enthält und stärker von der spärlichen Probenahme betroffen ist. In diesem Fall sollte der zweite Vektor ein höheres Gewicht haben. Umgekehrt liefert der erste Vektor bei hoher Punktdichte feinere Details, da er lokale Strukturen mit höherer Auflösung auf niedrigeren Ebenen rekursiv untersuchen kann.

Diese Methode ist rechnerisch effizienter, da sie die Berechnung von Merkmalen für großräumige Nachbarschaften auf den untersten Ebenen vermeidet.

In der Abstraktionsschicht wird die ursprüngliche Punktmenge einer Unterabtastung unterzogen. Bei Segmentierungsaufgaben wie der semantischen Punktbeschriftung ist es jedoch wünschenswert, Merkmale pro Punkt für alle ursprünglichen Punkte zu erhalten. Eine mögliche Lösung besteht darin, alle Punkte als Zentroide über alle Abstraktionsebenen hinweg abzutasten, was jedoch die Rechenkosten erheblich erhöht. Eine andere Möglichkeit besteht darin, Objekte von den unterabgetasteten Punkten auf die ursprünglichen Punkte zu übertragen.

Die Visualisierung der PointNet++-Methode durch den Autor wird im Folgenden dargestellt.

2. Implementation in MQL5

Nachdem wir die theoretischen Aspekte der Methode PointNet++ erläutert haben, kommen wir nun zum praktischen Teil unseres Artikels, in dem wir unsere Interpretation der vorgeschlagenen Ansätze mit MQL5 umsetzen. Es ist erwähnenswert, dass sich unsere Implementierung in einigen Punkten von der oben beschriebenen Originalversion unterscheidet. Aber das Wichtigste zuerst.

Wir werden unsere Arbeit in zwei Hauptabschnitte unterteilen. Zunächst wird ein lokale Schicht für die Teilstichprobe erstellt, der die zuvor besprochenen Schichten für die Teilstichproben und Gruppierungen integriert. Dann werden wir eine High-Level-Klasse entwickeln, die die einzelnen Komponenten zu einem vollständigen Algorithmus von PointNet++ zusammenfügt.

2.1 Erweiterung des OpenCL-Programms

Der Algorithmus für lokale Teilstichproben wird in der Klasse CNeuronPointNet2Local implementiert. Bevor wir jedoch mit der Arbeit an dieser Klasse beginnen, müssen wir zunächst die Funktionsweise von unserm OpenCL erweitern.

Zunächst erstellen wir den Kernel CalcDistance, der die Abstände zwischen den Punkten in der analysierten Punktwolke berechnet.

Es ist wichtig zu beachten, dass die Entfernungen in einem mehrdimensionalen Merkmalsraum berechnet werden, in dem jeder Punkt durch einen Merkmalsvektor dargestellt wird. Die Ausgabe des Kernels ist eine N×N-Matrix mit Nullwerten auf der Diagonalen.

Die Kernel-Parameter enthalten Zeiger auf zwei Datenpuffer (einen für die Eingabedaten und einen für die Speicherung der Ergebnisse) und eine Konstante, die die Dimension des Vektors der Punktmerkmale angibt.

__kernel void CalcDistance(__global const float *data,
                           __global float *distance,
                           const int dimension
                          )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

Im Kernel identifizieren wir den Thread innerhalb des Aufgabenbereichs.

Unsere erwartete Ausgabe ist eine quadratische Matrix. Daher definieren wir einen zweidimensionalen Aufgabenraum mit der entsprechenden Größe. Dadurch wird sichergestellt, dass jeder einzelne Thread ein einzelnes Element der resultierenden Matrix berechnet.

An dieser Stelle führen wir die erste Abweichung vom ursprünglichen Algorithmus von PointNet++ ein. Wir werden keine Zentren für lokale Regionen iterativ bestimmen. Bei unserer Implementierung wird jetzt jeder Punkt in der Wolke als Schwerpunkt behandelt. Um die Anpassungsfähigkeit der Regionsgrößen zu realisieren, normalisieren wir die Abstände zu jedem Punkt in der Wolke. Die Normalisierung von Abständen erfordert einen Datenaustausch zwischen einzelnen Threads. Um dies zu erleichtern, organisieren wir lokale Arbeitsgruppen entlang der Zeilen der Ergebnismatrix.

Für einen effizienten Datenaustausch innerhalb einer Arbeitsgruppe erstellen wir ein lokales Array.

   __local float Temp[LOCAL_ARRAY_SIZE];
   int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

Dann bestimmen wir die Offset-Konstanten zu den benötigten Elementen in den Datenpuffern.

   const int shift_main = main * dimension;
   const int shift_slave = slave * dimension;
   const int shift_dist = main * total + slave;

Danach erstellen wir eine Schleife zur Berechnung des Abstands zwischen zwei Objekten in einem mehrdimensionalen Raum.

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
      for(int d = 0; d < dimension; d++)
         dist += pow(data[shift_main + d] - data[shift_slave + d], 2.0f);
     }

Bitte beachten Sie, dass die Berechnungen nur für Nicht-Diagonal-Elemente durchgeführt werden. Das liegt daran, dass der Abstand von einem Punkt zu sich selbst gleich „0“ ist. So verschwenden wir keine Ressourcen für unnötige Berechnungen.

Der nächste Schritt besteht darin, den maximalen Abstand innerhalb der Arbeitsgruppe zu bestimmen. Zunächst sammeln wir die Maximalwerte der einzelnen Blöcke in einem lokalen Array.

//--- Look Max
   for(int i = 0; i < total; i += ls)
     {
      if(!isinf(dist) && !isnan(dist))
        {
         if(i <= slave && (i + ls) > slave)
            Temp[slave - i] = max((i == 0 ? 0 : Temp[slave - i]), dist);
        }
      else
         if(i == 0)
            Temp[slave] = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Dann suchen wir den höchsten Wert in der Matrix.

   int count = ls;
   do
     {
      count = (count + 1) / 2;
      if(slave < count && (slave + count) < ls)
        {
         if(Temp[slave] < Temp[slave + count])
            Temp[slave] = Temp[slave + count];
         Temp[slave + count] = 0;
        }
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Nachdem wir den Maximalwert für den untersuchten Punkt gefunden haben, teilen wir die oben berechneten Entfernungen durch diesen Wert. Infolgedessen werden alle Abstände zwischen den Punkten im Bereich [0, 1] normalisiert.

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];
   if(isinf(dist) || isnan(dist))
      dist = 1;
//--- result
   distance[shift_dist] = dist;
  }

Wir speichern den berechneten Wert im entsprechenden Element des globalen Ergebnispuffers.

Natürlich ist uns bewusst, dass der maximale Abstand zwischen zwei Punkten in der Analyse wahrscheinlich variieren wird. Durch die Normalisierung der Werte innerhalb verschiedener Skalen geht dieser Unterschied verloren. Aber genau das ermöglicht die Anpassung der aufnahmebereiten Felder.

Befindet sich der untersuchte Punkt in einer dichten Region der Wolke, liegt der am weitesten entfernte Punkt in der Regel an einer der Grenzen der Wolke. Befindet sich der untersuchte Punkt dagegen am Rand der Wolke, liegt der am weitesten entfernte Punkt am gegenüberliegenden Rand. Im zweiten Fall wird der Abstand zwischen den Punkten größer sein. Folglich wird das aufnahmebereite Feld im zweiten Fall größer sein.

Wir gehen auch davon aus, dass die Punktdichte innerhalb der Wolke höher ist als an ihren Rändern. Angesichts dessen ist die Vergrößerung der aufnahmebereiten Felder an der Peripherie der Wolke ein gerechtfertigter Ansatz, um eine sinnvolle Merkmalsextraktion zu gewährleisten.

Die Autoren von PointNet++ schlagen vor, lokale Punktverschiebungen relativ zu ihren Zentroiden zu berechnen und dann Mini-PointNet auf diese lokalen Teilmengen anzuwenden. Trotz ihrer scheinbaren Einfachheit stellt diese Methode jedoch ein erhebliches Umsetzungsproblem dar.

Wie bereits erwähnt, variiert die Anzahl der Elemente in jeder lokalen Region und ist im Voraus nicht bekannt. Dies wirft ein Problem bezüglich der Pufferzuweisung auf. Eine mögliche Lösung besteht darin, eine Höchstzahl von Punkten pro Empfangsfeld festzulegen und einen Puffer mit Überkapazität zuzuweisen. Dies würde jedoch zu einem höheren Speicherverbrauch und einer höheren Rechenkomplexität führen. Infolgedessen wird das Training schwieriger und die Modellleistung sinkt.

Stattdessen haben wir einen einfacheren und universelleren Ansatz gewählt. Wir haben die Berechnung lokaler Verschiebungen eliminiert. Zum Trainieren von Punktmerkmalen verwenden wir eine einzige Gewichtungsmatrix für alle Elemente, ähnlich wie beim einfachen PointNet. MaxPooling kann jedoch in aufnahmebereiten Feldern implementiert werden. Zu diesem Zweck erstellen wir einen neuen Kernel FeedForwardLocalMax, der drei Pufferzeiger als Parameter benötigt: Matrix der Punktmerkmale, normalisierte Distanzmatrix und Ergebnispuffer. Zusätzlich führen wir eine Konstante für den Radius des aufnahmebereiten Feldes ein.

__kernel void FeedForwardLocalMax(__global const float *matrix_i,
                                  __global const float *distance,
                                  __global float *matrix_o,
                                  const float radius
                                 )
  {
   const size_t i = get_global_id(0);
   const size_t total = get_global_size(0);
   const size_t d = get_global_id(1);
   const size_t dimension = get_global_size(1);

Wir planen die Ausführung des Kernels in einem zweidimensionalen Aufgabenraum. In der ersten Dimension geben wir die Anzahl der Elemente in der Punktwolke an, in der zweiten die Dimension der Merkmale eines Elements. Im Hauptteil des Kernels identifizieren wir sofort den aktuellen Thread in beiden Dimensionen des Aufgabenraums. In diesem Fall arbeitet jeder Thread unabhängig, sodass wir keine Arbeitsgruppen bilden und keine Daten zwischen den Threads austauschen müssen.

Als Nächstes definieren wir Offset-Konstanten in Datenpuffern.

   const int shift_dist = i * total;
   const int shift_out = i * dimension + d;

Dann erstellen wir eine Schleife, um den Höchstwert zu ermitteln.

   float result = -3.402823466e+38;
   for(int k = 0; k < total; k++)
     {
      if(distance[shift_dist + k] > radius)
         continue;
      int shift = k * dimension + d;
      result = max(result, matrix_i[shift]);
     }
   matrix_o[shift_out] = result;
  }

Achten Sie darauf, dass wir vor der Überprüfung des Wertes des nächsten Elements zunächst prüfen, ob er in das Empfangsfeld des entsprechenden Punktes in der Wolke fällt.

Sobald die Schleifeniterationen abgeschlossen sind, speichern wir den berechneten Wert im Ergebnispuffer.

In ähnlicher Weise implementieren wir den Kernel CalcInputGradientLocalMax für den Rückwärtsdurchgang, der den Fehlergradienten auf die entsprechenden Elemente verteilt. Die Kernels der Vorwärts- und Rückwärtsdurchgänge haben viele Gemeinsamkeiten. Ich möchte Sie ermutigen, sie unabhängig zu überprüfen. Den vollständigen Kernel-Code finden Sie im Anhang. Nun geht es an die Umsetzung des Hauptprogramms.

2.2 Klasse der lokalen Unterprobenahme

Nachdem wir die Vorarbeiten auf der OpenCL-Seite abgeschlossen haben, wenden wir uns nun der Entwicklung der Klasse für lokalen Teilstichproben zu. Bei der Implementierung der OpenCL-Kernel haben wir bereits die grundlegenden Prinzipien des Algorithmusentwurfs angesprochen. Wenn wir jedoch mit der Implementierung der Klasse CNeuronPointNet2Local fortfahren, werden wir diese Prinzipien genauer untersuchen und ihre praktische Umsetzung in Code prüfen. Die Struktur der neuen Klasse ist unten dargestellt.

class CNeuronPointNet2Local   :  public CNeuronConvOCL
  {
protected:
   float                fRadius;
   uint                 iUnits;
   //---
   CBufferFloat         cDistance;
   CNeuronConvOCL       cFeatureNet[3];
   CNeuronBatchNormOCL  cFeatureNetNorm[3];
   CNeuronBaseOCL       cLocalMaxPool;
   CNeuronConvOCL       cFinalMLP;
   //---
   virtual bool         CalcDistance(CNeuronBaseOCL *NeuronOCL);
   virtual bool         LocalMaxPool(void);
   virtual bool         LocalMaxPoolGrad(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronPointNet2Local(void) {};
                    ~CNeuronPointNet2Local(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint window_out, float radius,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2LocalOCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

In der oben dargestellten Struktur können wir mehrere interne neuronale Schichtobjekte und zwei Variablen beobachten, deren Zweck wir bei der Implementierung der Klassenmethoden erkunden werden.

Wir sehen auch eine vertraute Reihe von überschreibbaren Methoden. Zusätzlich gibt es drei Methoden, die den zuvor implementierten Kerneln entsprechen:

• CalcDistance(CNeuronBaseOCL *NeuronOCL);
• LocalMaxPool(void);
• LocalMaxPoolGrad(void).

Wie Sie vielleicht schon erraten haben, stellen diese Methoden die Ausführung der Kernel in die Warteschlange. Da wir diesen Algorithmus bereits eingehend untersucht haben, werden wir ihn in diesem Artikel nicht weiter vertiefen.

Es ist auch erwähnenswert, dass diese Klasse von der Faltungsschichtklasse CNeuronConvOCL abgeleitet wird. Dies ist in unserer Arbeit unüblich und liegt vor allem an der unabhängigen Verarbeitung von Merkmalen in lokalen Gruppen.

Alle internen Objekte der Klasse werden statisch deklariert, was es uns ermöglicht, den Klassenkonstruktor und -destruktor leer zu lassen. Die Initialisierung einer neuen Objektinstanz wird in der Methode Init durchgeführt.

bool CNeuronPointNet2Local::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, 
                                 uint window, uint units_count, uint window_out, float radius, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronConvOCL::Init(numOutputs, myIndex, open_cl, 128, 128, window_out, 
                                        units_count, 1, optimization_type, batch))
      return false;

In den Methodenparametern erhalten wir die wichtigsten Konstanten, die die Architektur des Objekts definieren. Diese Parameter ähneln denen, die in einer Faltungsschicht verwendet werden. Es gibt einen zusätzlichen Parameter: Radius, der den Radius des aufnahmebereiten Feldes eines Elements definiert.

Im Hauptteil der Methode rufen wir sofort die entsprechende Methode der übergeordneten Klasse auf, in der die notwendige Datenvalidierung und Initialisierung der geerbten Objekte bereits implementiert ist. Es ist wichtig zu beachten, dass die Werte, die an die Methode der Elternklasse übergeben werden, sich leicht von denen unterscheiden, die vom externen Programm empfangen werden. Diese Diskrepanz ergibt sich aus der spezifischen Verwendung von Objekten der Elternklasse, ein Thema, auf das wir bei der Implementierung der Methode feedForward zurückkommen werden.

Nach erfolgreicher Ausführung der Methode der Elternklasse speichern wir einige der erhaltenen Konstanten, während andere bereits während der Operationen der Elternklasse gespeichert wurden.

   fRadius = MathMax(0.1f, radius);
   iUnits = units_count;

Als Nächstes gehen wir zur Initialisierung der internen Objekte über. Zunächst wird ein Puffer für die Erfassung der Abstände zwischen den Objekten in der analysierten Punktwolke angelegt. Wie bereits erwähnt, handelt es sich um eine quadratische Matrix.

   cDistance.BufferFree();
   if(!cDistance.BufferInit(iUnits * iUnits, 0) ||
      !cDistance.BufferCreate(OpenCL))
      return false;

Zur Extraktion von Punktmerkmalen erstellen wir einen Block aus 3 Faltungsschichten und 3 Batch-Normalisierungsschichten, ähnlich dem Merkmalsextraktionsblock des PointNet-Algorithmus. Wir erstellen keinen Projektionsblock für die Quelldaten, da wir davon ausgehen, dass dieser in der Top-Level-Klasse vorhanden ist.

   if(!cFeatureNet[0].Init(0, 0, OpenCL, window, window, 64, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[0].Init(0, 1, OpenCL, 64 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[0].SetActivationFunction(LReLU);
   if(!cFeatureNet[1].Init(0, 2, OpenCL, 64, 64, 128, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[1].Init(0, 3, OpenCL, 128 * iUnits, iBatch, optimization))
      return false;
   cFeatureNetNorm[1].SetActivationFunction(LReLU);
   if(!cFeatureNet[2].Init(0, 4, OpenCL, 128, 128, 256, iUnits, 1, optimization, iBatch))
      return false;
   if(!cFeatureNetNorm[2].Init(0, 5, OpenCL, 256 * iUnits, iBatch, optimization))
      cFeatureNetNorm[2].SetActivationFunction(None);

Als Nächstes erstellen wir eine Ebene für die Aufzeichnung der lokalen Ergebnisse von MaxPooling.

   if(!cLocalMaxPool.Init(0, 6, OpenCL, cFeatureNetNorm[2].Neurons(), optimization, iBatch))
      return false;

Wir fügen eine Schicht des resultierenden MLP hinzu.

   if(!cFinalMLP.Init(0, 7, OpenCL, 256, 256, 128, iUnits, 1, optimization, iBatch))
      return false;
   cFinalMLP.SetActivationFunction(LReLU);

Wir planen, vererbte Funktionalität als zweite Schicht zu verwenden.

Bitte beachten Sie, dass wir im Gegensatz zum einfachen PointNet am Ausgang Faltungsschichten verwenden. Dies ist auf die unabhängige Verarbeitung lokaler Bereichsdeskriptoren zurückzuführen.

Am Ende der Operationen der Initialisierungsmethode weisen wir ausdrücklich darauf hin, dass es keine Aktivierungsfunktion für unsere Klasse gibt, und geben das boolesche Ergebnis der Operationen an das aufrufende Programm zurück.

   SetActivationFunction(None);
   return true;
  }

Nachdem die Initialisierung des neuen Objekts abgeschlossen ist, werden in der Methode feedForward die Vorwärtsdurchgangs-Algorithmen konstruiert. In den Parametern dieser Methode erhalten wir einen Zeiger auf das Quelldatenobjekt.

bool CNeuronPointNet2Local::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!CalcDistance(NeuronOCL))
      return false;

Wie bereits erwähnt, haben wir in dieser Klasse nicht vor, Daten in einen kanonischen Raum zu projizieren. Es wird davon ausgegangen, dass dieser Vorgang erforderlichenfalls auf der obersten Ebene durchgeführt wird. Daher berechnen wir sofort den Abstand zwischen den Elementen der ursprünglichen Daten.

Als Nächstes erstellen wir eine Schleife zur Berechnung der Merkmale der analysierten Elemente.

   CNeuronBaseOCL *temp = NeuronOCL;
   uint total = cFeatureNet.Size();
   for(uint i = 0; i < total; i++)
     {
      if(!cFeatureNet[i].FeedForward(temp))
         return false;
      if(!cFeatureNetNorm[i].FeedForward(cFeatureNet[i].AsObject()))
         return false;
      temp = cFeatureNetNorm[i].AsObject();
     }

Führen Sie MaxPooling-Operationen für lokale Bereiche von Punkten durch.

   if(!LocalMaxPool())
      return false;

Am Ende der Methodenoperationen wenden wir einen unabhängigen, zweischichtigen MLP auf die Deskriptoren aller lokalen Regionen an.

   if(!cFinalMLP.FeedForward(cLocalMaxPool.AsObject()))
      return false;
   if(!CNeuronConvOCL::feedForward(cFinalMLP.AsObject()))
      return false;
//---
   return true;
  }

Als erste Schicht des MLPverwenden wir die interne Schicht cFinalMLP. Die Operationen der zweiten Ebene werden unter Verwendung der von der übergeordneten Klasse geerbten Funktionalität durchgeführt.

Vergessen Sie nicht, die Arbeitsabläufe in jeder Phase zu überwachen. Nach erfolgreichem Abschluss aller Operationen geben wir ein logisches Ergebnis an das aufrufende Programm zurück.

Die Algorithmen der Rückwärtsdurchgänge sind in den Methoden calcInputGradients und pdateInputWeights implementiert. Die Methode calcInputGradients verteilt den Fehlergradienten auf alle Elemente entsprechend ihrem Einfluss auf das Endergebnis. Der Algorithmus folgt der gleichen Logik wie die der Methode feedForward, führt die Operationen jedoch in umgekehrter Richtung aus. Die Methode updateInputWeights aktualisiert die trainierbaren Parameter des Modells. Hier rufen wir einfach die entsprechenden Methoden der internen Objekte auf, die die trainierbaren Parameter enthalten. Beide Methoden sind recht einfach. Ich möchte Sie dazu ermutigen, ihre Implementierungen selbst zu erkunden. Den vollständigen Quellcode für diese Klasse und alle ihre Methoden finden Sie im Anhang.

2.3 Zusammenstellung des Algorithmus für PointNet++

Wir haben den größten Teil der Arbeit abgeschlossen. Wir nähern uns nun der letzten Phase unserer Umsetzung. In diesem Schritt werden wir die einzelnen Komponenten zu einem einheitlichen Algorithmus von PointNet++ kombinieren. Diese Integration findet innerhalb der Klasse CNeuronPointNet2OCL statt, deren Struktur im Folgenden skizziert wird.

class CNeuronPointNet2OCL   :  public CNeuronPointNetOCL
  {
protected:
   CNeuronPointNetOCL   *cTNetG;
   CNeuronBaseOCL       *cTurnedG;
   //---
   CNeuronPointNet2Local caLocalPointNet[2];
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override ;
   //---
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
public:
                     CNeuronPointNet2OCL(void) {};
                    ~CNeuronPointNet2OCL(void) ;
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count, uint output, bool use_tnets,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronPointNet2OCL; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Seltsamerweise deklariert diese Klasse nur zwei statische Objekte für die lokale Datendiskretisierung und zwei dynamische Objekte, die nur initialisiert werden, wenn eine Datenprojektion in den kanonischen Raum erforderlich ist. Diese Einfachheit wird durch die Vererbung von der PointNet-Klasse erreicht, in der die meisten Funktionen bereits implementiert sind.

Wie bereits erwähnt, werden dynamische Objekte nur bei Bedarf initialisiert. Deshalb lassen wir den Konstruktor leer, aber im Destruktor prüfen wir, ob die Zeiger auf dynamische Objekte gültig sind und löschen sie gegebenenfalls.

CNeuronPointNet2OCL::~CNeuronPointNet2OCL(void)
  {
   if(!!cTNetG)
      delete cTNetG;
   if(!!cTurnedG)
      delete cTurnedG;
  }

Die Initialisierung des Klassenobjekts wird wie üblich in der Methode Init durchgeführt. In den Methodenparametern erhalten wir die wichtigsten Konstanten, die die Klassenarchitekturen definieren. Wir haben sie vollständig von der übergeordneten Klasse übernommen.

bool CNeuronPointNet2OCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,

                               uint window, uint units_count, uint output, bool use_tnets, 
                               ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronPointNetOCL::Init(numOutputs, myIndex, open_cl, 64, units_count, 
                                output, use_tnets, optimization_type, batch))
      return false;

In der Methode rufen wir sofort eine ähnliche Methode der übergeordneten Klasse auf. Danach prüfen wir, ob wir Projektionsobjekte der Originaldaten in den kanonischen Raum erstellen müssen.

//--- Init T-Nets
   if(use_tnets)
     {
      if(!cTNetG)
        {
         cTNetG = new CNeuronPointNetOCL();
         if(!cTNetG)
            return false;
        }
      if(!cTNetG.Init(0, 0, OpenCL, window, units_count, window * window, false, optimization, iBatch))
         return false;

Falls erforderlich, erstellen wir zunächst die erforderlichen Objekte und initialisieren sie dann.

      if(!cTurnedG)
        {
         cTurnedG = new CNeuronBaseOCL();
         if(!cTurned1)
            return false;
        }
      if(!cTurnedG.Init(0, 1, OpenCL, window * units_count, optimization, iBatch))
         return false;
     }

Wenn der Nutzer nicht angegeben hat, dass Projektionsobjekte erstellt werden müssen, wird geprüft, ob es aktuelle Zeiger auf die Objekte gibt. Wenn es solche Zeiger gibt, entfernen wir überflüssige Objekte.

   else
     {
      if(!!cTNetG)
         delete cTNetG;
      if(!!cTurnedG)
         delete cTurnedG;
     }

Wir initialisieren dann 2 lokale Datensampling-Objekte mit unterschiedlichen aufnahmebereiten Fensterradien. Ende der Methode.

   if(!caLocalPointNet[0].Init(0, 0, OpenCL, window, units_count, 64, 0.2f, optimization, iBatch))
      return false;
   if(!caLocalPointNet[1].Init(0, 0, OpenCL, 64, units_count, 64, 0.4f, optimization, iBatch))
      return false;
//---
   return true;
  }

Man beachte, dass wir mit einem kleinen, aufnahmebereiten Fenster beginnen und es dann vergrößern. Wir vergrößern jedoch nicht das aufnahmebereite Fenster bis zur vollständigen Abdeckung, da dies durch die von der Klasse des einfachen PointNet geerbte Funktionsweise durchgeführt wird.

Nachdem die Arbeit mit der Methode zur Initialisierung des Klassenobjekts abgeschlossen ist, gehen wir zur Konstruktion des Vorwärtsdurchgangs-Algorithmus innerhalb von feedForward über.

bool CNeuronPointNet2OCL::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
//--- LocalNet
   if(!cTNetG)
     {
      if(!caLocalPointNet[0].FeedForward(NeuronOCL))
         return false;
     }

In den Methodenparametern erhalten wir einen Zeiger auf das Quelldatenobjekt. Im Hauptteil der Methode wird zunächst geprüft, ob eine Projektion in den kanonischen Raum erforderlich ist. Die Vorgehensweise ist hier ähnlich wie in der Klasse für das einfache PointNet. Wenn keine Datenprojektion erforderlich ist, wird der empfangene Zeiger sofort an die Methode feedForward der ersten lokalen Diskretisierungsschicht übergeben.

Andernfalls wird zunächst die Projektionsmatrix für die Daten erstellt.

   else
     {
      if(!cTurnedG)
         return false;
      if(!cTNetG.FeedForward(NeuronOCL))
         return false;

Danach führen wir die Projektion der Originaldaten durch, indem wir sie mit der Projektionsmatrix multiplizieren.

      int window = (int)MathSqrt(cTNetG.Neurons());
      if(IsStopped() ||
         !MatMul(NeuronOCL.getOutput(), cTNetG.getOutput(), cTurnedG.getOutput(), 
                                    NeuronOCL.Neurons() / window, window, window))
         return false;

Erst dann geben wir die erhaltenen Werte an die Methode feedForward der Daten-Diskreditierungsschicht weiter.

      if(!caLocalPointNet[0].FeedForward(cTurnedG.AsObject()))
         return false;
     }

Als Nächstes führen wir eine Diskreditierung mit einer größeren Größe des aufnahmebereiten Fensters durch.

   if(!caLocalPointNet[1].FeedForward(caLocalPointNet[0].AsObject()))
      return false;

In der letzten Stufe werden die angereicherten Daten an die Methode feedForward der übergeordneten Klasse übergeben, wo der Deskriptor der analysierten Punktwolke als Ganzes bestimmt wird.

   if(!CNeuronPointNetOCL::feedForward(caLocalPointNet[1].AsObject()))
      return false;
//---
   return true;
  }

Wie Sie sehen, ist es uns dank der komplexen Vererbungsstruktur gelungen, eine übersichtliche feedForward-Methode für unsere neue Klasse zu konstruieren. Die Methoden der Rückwärtsdurchgänge folgen ähnlichen Implementierungen, die Sie in den beigefügten Dateien selbst erkunden können. Der vollständige Code für alle in diesem Artikel verwendeten Programme ist im Anhang enthalten. Dazu gehören vollständige Trainingsskripte für die Modelle und ihre Interaktion mit der Umgebung. Es ist erwähnenswert, dass diese Skripte unverändert aus dem vorherigen Artikel übernommen wurden. Außerdem haben wir die Modellarchitektur weitgehend beibehalten. Die einzige Änderung im Encoder des Umgebungszustands bestand darin, dass der Typ einer einzelnen Schicht geändert wurde, während alle anderen Parameter unverändert blieben.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronPointNet2OCL;
   descr.window = BarDescr;                        // Variables
   descr.count = HistoryBars;                      // Units
   descr.window_out = LatentCount;                 // Output Dimension
   descr.step = int(true);                         // Use input and feature transformation
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!encoder.Add(descr))
     {
      delete descr;
      return false;
     }

Umso interessanter ist es, die Ergebnisse der neuen Trainings der Politik des Akteurs zu bewerten.

3. Tests

Damit haben wir unsere Implementierung der von den Autoren von PointNet++ vorgeschlagenen Ansätze abgeschlossen. Nun ist es an der Zeit, die Wirksamkeit unserer Umsetzung anhand echter historischer Daten zu bewerten. Wie zuvor werden wir die Modelle auf historischen EURUSD-Daten für das gesamte Jahr 2023 trainieren. Wir verwenden einen H1-Zeitrahmen. Alle Indikatorparameter werden auf ihre Standardwerte gesetzt. Das trainierte Modell wird mit dem MetaTrader 5 Strategie-Tester getestet.

Wie bereits erwähnt, unterscheidet sich unser neues Modell von dem bisherigen nur durch eine einzige Schicht. Außerdem ist diese neue Schicht lediglich eine verbesserte Version unserer früheren Arbeit. Daher ist es besonders interessant, die Leistung beider Modelle zu vergleichen. Um einen fairen Vergleich zu gewährleisten, trainieren wir beide Modelle mit genau demselben Datensatz, der im vorherigen Experiment verwendet wurde.

Ich betone immer wieder, dass die regelmäßige Aktualisierung des Trainingsdatensatzes für eine optimale Modellleistung entscheidend ist. Die Abstimmung des Datensatzes auf die aktuelle Politik des Akteurs gewährleistet eine genauere Bewertung seiner Maßnahmen, was zu einer Verbesserung der Politik führt. In diesem Fall konnte ich jedoch der Gelegenheit nicht widerstehen, zwei ähnliche Ansätze zu vergleichen und die Wirksamkeit einer hierarchischen Methode zu bewerten. In unserem vorangegangenen Artikel haben wir erfolgreich eine Akteurspolitik trainiert, die in der Lage war, Gewinne zu erzielen. Wir gehen davon aus, dass das neue Modell mindestens genauso gut abschneiden wird.

Nach dem Training lernte unser neues Modell erfolgreich eine gewinnbringende Strategie und erzielte sowohl in den Trainings- als auch in den Testdatensätzen positive Ergebnisse. Die Testergebnisse für das neue Modell werden im Folgenden vorgestellt.

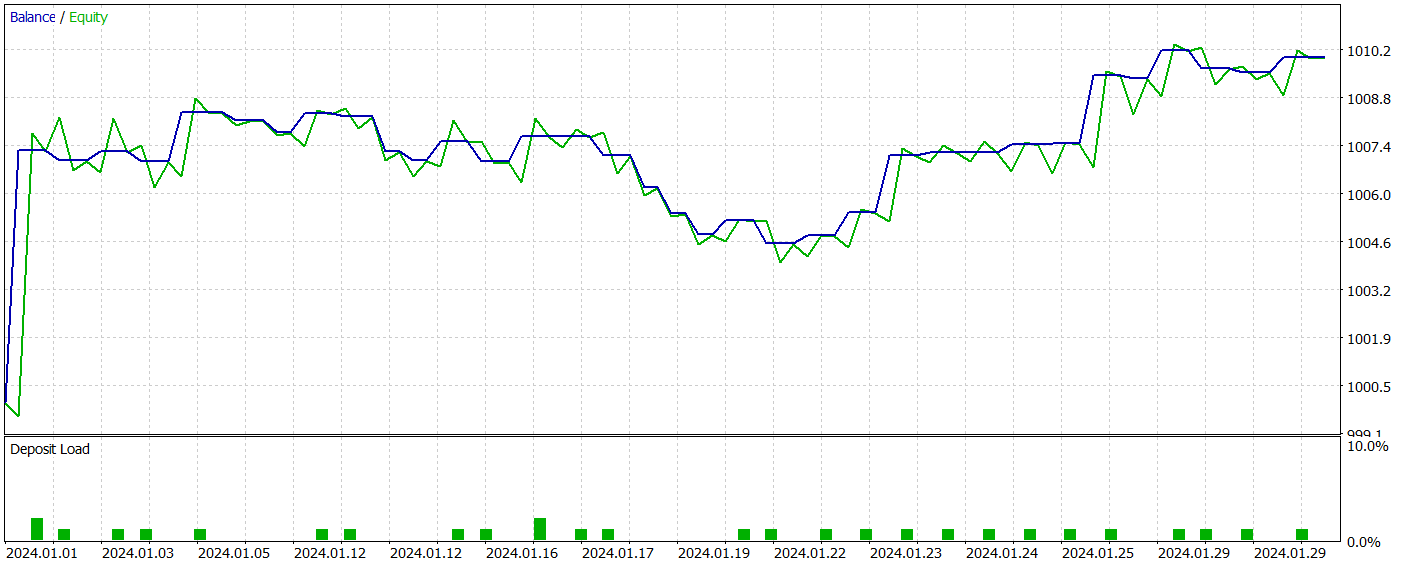
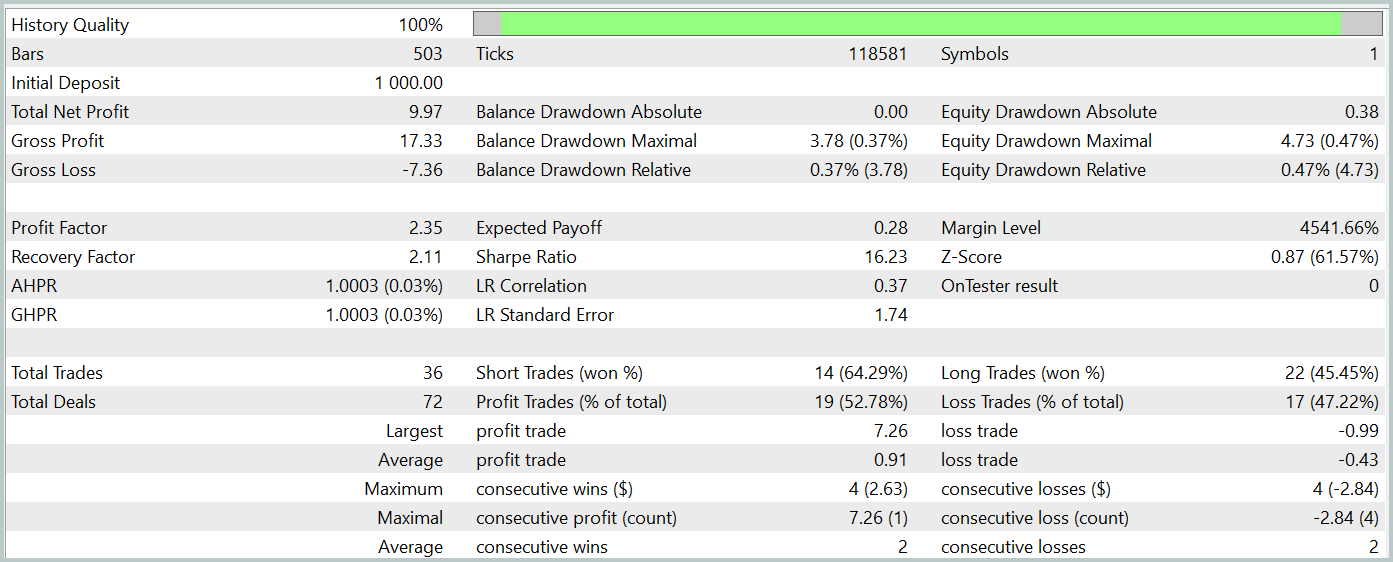
Ich muss zugeben, dass der Vergleich der Ergebnisse der beiden Modelle eine ziemliche Herausforderung darstellt. Während des Testzeitraums erzielten beide Modelle nahezu den gleichen Gewinn. Die Drawdown-Abweichungen sowohl beim Saldo als auch beim Kapital bleiben innerhalb einer vernachlässigbaren Fehlermarge. Das neue Modell führte jedoch weniger Handelsgeschäfte aus, was zu einem leichten Anstieg des Gewinnfaktors führte.

Allerdings lässt die geringe Anzahl der von beiden Modellen ausgeführten Handelsgeschäfte keine endgültigen Rückschlüsse auf ihre langfristige Leistung zu.

Schlussfolgerung

Die Möglichkeit PointNet++ bietet eine effiziente Möglichkeit, sowohl lokale als auch globale Muster in komplexen Finanzdaten zu analysieren und dabei ihre multidimensionale Struktur zu berücksichtigen. Der verbesserte Ansatz zur Verarbeitung von Punktwolken verbessert die Vorhersagegenauigkeit und die Stabilität von Handelsstrategien, was zu einer fundierteren und erfolgreicheren Entscheidungsfindung auf dynamischen Märkten führen kann.

Im praktischen Teil dieses Artikels haben wir unsere eigene Vision des PointNet++ Ansatzes umgesetzt. Bei den Tests hat das Modell seine Fähigkeit unter Beweis gestellt, auf dem Testdatensatz Gewinne zu erzielen. Es ist jedoch wichtig, darauf hinzuweisen, dass die vorgestellten Programme nur zu Demonstrationszwecken dienen und ausschließlich zur Veranschaulichung der Arbeitsweise gedacht sind.

Referenzen

• PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space
• Weitere Artikel aus dieser Serie

Programme, die im diesem Artikel verwendet werden

#	Name	Typ	Beschreibung
1	Research.mq5	Expert Advisor	EA zum Sammeln von Beispielen
2	ResearchRealORL.mq5	Expert Advisor	EA zum Sammeln von Beispielen mit der Real-ORL-Methode
3	Study.mq5	Expert Advisor	Modelltraining EA
4	Test.mq5	Expert Advisor	Modelltraining EA
5	Trajectory.mqh	Klassenbibliothek	Struktur der Systemzustandsbeschreibung
6	NeuroNet.mqh	Klassenbibliothek	Eine Bibliothek von Klassen zur Erstellung eines neuronalen Netzes
7	NeuroNet.cl	Bibliothek	OpenCL-Programmcode-Bibliothek