MetaTrader 5 / 示例
English Русский Español Deutsch 日本語 Português 한국어 Français Italiano Türkçe
preview
种群优化算法：萤火虫算法（FA）

种群优化算法：萤火虫算法（FA）

MetaTrader 5 — 示例 | 4 五月 2023, 09:02
1 363 0
Andrey Dik
Andrey Dik

内容

1. 概述
2. 算法描述
3. 测试结果


1. 概述

自然界一直是许多元启发式算法的灵感来源。 它设法在没有提示的情况下，基于个体经验找到问题的解决方案。 自然选择和适者生存是创建早期元启发式算法的主要动机。 在自然界中，动物以多种方式相互交流。 萤火虫则是利用眨眼的能力进行交流。 大约有 2000 种萤火虫，都拥有自己特殊的闪烁图案。 它们通常会产生具有特定图案的短闪烁。 光亮及其强度成为称为生物发光的生化过程的成果。 据信，这种闪烁的主要功能是求偶和吸引潜在的受害者。 一些热带萤火虫可以同步它们的闪烁，从而展示了生物自组织的一个例子。 光亮的强度作为与其光源距离的函数，遵循平方反比定律，因此来自萤火虫的闪烁光线会导致它周围的萤火虫在闪烁的视线范围内做出反应。

受萤火虫行为启发的种群优化算法有两种变体：萤火虫算法，和萤火虫群优化（GSO）算法。 萤火虫（firefly）和发光甲虫（glowworms）的主要区别在于后者是无翅的。 在本文中，我们将研究前一种类的优化算法。

2. 算法说明

萤火虫算法（F-算法）由 X-Sh. Yang 于 2007 年在英国剑桥大学提出，并立即引起了优化研究人员的注意。 萤火虫算法是群体智能算法家族的一部分，最近在解决优化问题方面取得了令人印象深刻的成果。 特别是，萤火虫算法在求解连续和离散优化问题的能力。

萤火虫算法基于真实萤火虫的闪烁特性，有三条规则。 规则如下：

  1. 所有萤火虫都会朝着更有吸引力和更明亮的对应物移动。
  2. 萤火虫的吸引力程度与其亮度成正比，由于空气吸收光线的事实，随着与另一只萤火虫的距离增加，亮度会降低。 故此，在任何两只闪烁的萤火虫之间，不太亮的萤火虫会向较亮的萤火虫移动。 如果没有更亮或更具吸引力的对应物，则萤火虫将随机移动。
  3. 萤火虫的亮度或光线强度由问题的目标函数的值决定。


最初，在算法开始时，所有萤火虫都随机分散在整个搜索空间当中。 然后，该算法根据两个阶段判定最佳分区：

  1. 光线强度的变化 — 萤火虫在其当前位置的亮度反映在其适应性值中，朝着有吸引力的萤火虫移动。
  2. 萤火虫通过观察邻近萤火虫的光线强度来改变其位置。


现在，我们可以更详尽地深入了解萤火虫优化的复杂性。 该算法本质上如图例 1 所示。

Fas

图例 1. 搜索空间中的萤火虫。 能见度随着距离的增加而降低

搜索原理背后的主要思路是随着萤火虫之间距离的增加，能见度呈非线性降低。 如果没有这种非线性关系，每只萤火虫都会确定性地向更明亮的光源移动。 然而，正如我们在图例 1 中看到的，萤火虫不会选择其最亮的近邻，因为由于环境对光线的吸收，它发出的光线很难被注意到。 取而代之，它选择了一个不太明亮的对应物（尽管是其环境中最亮的）。 此特征解释了算法划分为较小群落的良好能力。 由于远距离光吸收的非线性函数，这现象会很自然地发生。 在下面的图例 2 中，我们可以看到具有不同 gamma 介质吸收系数值的算法的可见性与距离的函数，这是算法参数之一。


可见度

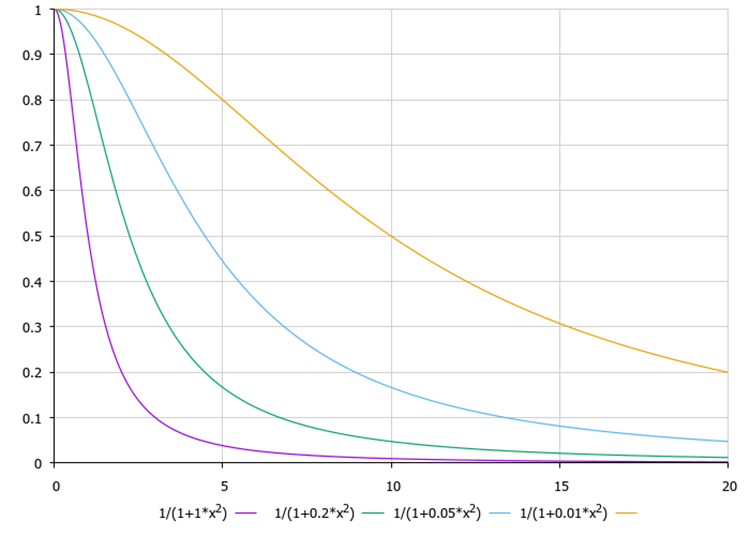
图例 2. 介质透明度与距离f(x) 的函数，其中 gamma 透明度系数分别等于 1.0、0.2、0.05、0.01。

当 gamma 趋于无穷大时，环境变得不透明；当 gamma 为零时，环境是完全透明的；每只萤火虫在搜索空间中的任何距离都能看到对方。 如果 gamma = 0.0 会发生什么？ 所有的萤火虫都会飞到最明亮的相对位置，汇聚到某个非最佳点。 如此，算法不会收敛停留在某个局部极值。 如果环境完全不透明，会发生什么情况？ 萤火虫不会看到比自己更有吸引力的同类。 根据算法作者提出的概念，看不到比自己更好的同类，那么萤火虫就会随机移动。 该算法将退化为随机搜索。 在我们的算法分类评级表格中，随机搜索算法排在最后。  

我们来深入分析算法，并考虑描述萤火虫运动的方程。 能见度与距离的函数是计算所谓吸引力指数的基础：

attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

其中:
attractiveness - 吸引力，不言自明
gamma - 环境不透明度系数
distance - 萤火虫之间的欧氏距离
fireflies [k].f - 第 k 只萤火虫的光线强度

该方程清楚地表明，吸引力函数直接取决于问题的维度和距离值的限制，因此该算法的作者建议为特定的优化问题选择透明度系数。 我认为，在事先不知算法将如何表现的情况下就这样做，既不方便又耗时；因此我认为有必要对 0 到 20 范围内的距离值进行规范化。 为达此目的，应用我们在其它算法中反复使用的 Scale() 函数。 在计算吸引力之前，“distance” 的转换如下所示：

distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);

其中:

maxDist — 在一对萤火虫之间的最大欧几里得距离

在这种情况下，萤火虫的吸引力将不取决于问题的维度，也无需为特定的优化问题选择 gamma 系数。 吸引力函数判定每只萤火虫将做出什么样的配偶选择。 这个选择是有严格判定的。 萤火虫相互吸引力的影响决定了 beta 系数（算法的第二个参数）。 如果在每次迭代中萤火虫已经提前确定了相应的选择，如何确保算法的搜索能力？ 为此，引入了随机向量分量，和第三个算法参数（alpha）。 萤火虫的复杂行为关系如下所示：

fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];

其中:
fireflies [i].c [c] - 第 i 个萤火虫的第 c 个坐标
beta - 萤火虫吸引力影响系数
alpha - 当萤火虫移动时影响随机分量的系数，给出与移动目标的偏差
r - 范围 [-1.0;1.0] 内的随机数
v[c] - 向量分量，通过第 c 个坐标表征搜索范围极点之间的距离
Хj - 萤火虫对中的对应坐标，其将有运动
Xi - 计算运动的萤火虫的对应坐标

现在是时候讲述算法代码了。 它相对简单。 我们来研究细节。

萤火虫将用一个简单的结构来描述 S_Firefly，该结构具有两个组成部分，即 c[] - 坐标，f - 萤火虫的亮度（适应度函数）。 鉴于对于每只萤火虫，在相应的迭代中只有单一个体，它移动后会形成新的配对，因此在计算下一次移动时，我们不会冒覆盖坐标的风险。 为此目的，我将引入下面研究的特殊结构。
//——————————————————————————————————————————————————————————————————————————————
struct S_Firefly
{
  double c  []; //coordinates
  double f;     //the value of the fitness function
};
//——————————————————————————————————————————————————————————————————————————————

S_Attractiveness 结构的用意是存储成对的吸引力值和相应萤火虫的数量。 每只萤火虫不会朝向最吸引人的萤火虫的坐标移动，而是朝向其伙伴已经移动的坐标。 这与作者描述的算法版本存在一些差异，但这就是它能更好地工作的方式。

//——————————————————————————————————————————————————————————————————————————————
struct S_Attractiveness
{
  double a; //attractiveness
  int    i; //index of the most attractive firefly
};
//——————————————————————————————————————————————————————————————————————————————

萤火虫算法由 C_AO_FA 类进行定义。 这里有三个公开方法，其中一个是用于初始初始化的 Init()，两个需要在每次迭代时调用的公开方法 — Flight() 和 Luminosity()，私密帮助方法，和存储参数常量的成员。

//——————————————————————————————————————————————————————————————————————————————
class C_AO_FA
{
  //----------------------------------------------------------------------------
  public: S_Firefly fireflies []; //fireflies
  public: double    rangeMax  []; //maximum search range
  public: double    rangeMin  []; //minimum search range
  public: double    rangeStep []; //step search
  public: double    cB        []; //best coordinates
  public: double    fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,  //number of opt. parameters
                     const int    sizeP,    //swarm size
                     const double alphaP,   //alpha, randomness in motion
                     const double betaP,    //beta, effect of attractiveness
                     const double gammaP);  //gamma, transparency of the environment

  public: void Flight ();
  public: void Luminosity ();

  //----------------------------------------------------------------------------
  private: S_Attractiveness att [];
  private: int    swarmSize;
  private: int    params;
  private: double maxDist;
  private: double v [];

  private: double alpha;      //randomness in motion
  private: double beta;       //effect of attractiveness
  private: double gamma;      //transparency of the environment
  private: bool   luminosity;

  private: double SeInDiSp  (double In, double inMin, double inMax, double step);
  private: double RNDfromCI (double min, double max);
  protected: double Scale   (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Init() 公开方法用于初始化，应在每次优化开始之前调用。 其参数是算法的补充参数。 该方法将为数组分配内存，并重置全局和每个单独萤火虫的光线亮度值。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Init (const int    paramsP, //number of opt. parameters
                    const int    sizeP,   //swarm size
                    const double alphaP,  //alpha, randomness in motion
                    const double betaP,   //beta, effect of attractiveness
                    const double gammaP)  //gamma, transparency of the environment
{
  fB = -DBL_MAX;

  params    = paramsP;
  swarmSize = sizeP;
  alpha     = alphaP;
  beta      = betaP;
  gamma     = gammaP;

  ArrayResize (rangeMax,  params);
  ArrayResize (rangeMin,  params);
  ArrayResize (rangeStep, params);
  ArrayResize (v,         params);
  ArrayResize (att,       swarmSize);

  luminosity = false;

  ArrayResize (fireflies, swarmSize);

  for (int i = 0; i < swarmSize; i++)
  {
    ArrayResize (fireflies [i].c,  params);
    fireflies [i].f = -DBL_MAX;
  }

  ArrayResize (cB, params);
}
//——————————————————————————————————————————————————————————————————————————————

来研究每次迭代时调用的第一个公开方法 — Flight()。 算法的主要逻辑集中在该方法当中，因此有必要详尽地研究它。 'luminosity' 变量当作一个标志，允许我们判定算法是处于第一次迭代，还是在后续迭代中运行。 如果标志尚未设置，则需要按照均匀分布将萤火虫随机分布到坐标空间之中。 在执行此操作的同时，我们为每个坐标设置位移向量，并立即计算萤火虫之间可以达到的最大可能欧氏距离（如前所述，这对于规范化萤火虫之间的距离是必要的，以避免环境透明度系数对问题维度的依赖性）。 完成这些操作后，启用 “luminosity” 标志。

if (!luminosity)
{
  fB = -DBL_MAX;

  //--------------------------------------------------------------------------
  double summCoordinates = 0.0;
  for (int c = 0; c < params; c++)
  {
    v [c] = rangeMax [c] - rangeMin [c];
    summCoordinates += pow (v [c], 2.0);
  }
  maxDist = pow (summCoordinates, 0.5);

  //--------------------------------------------------------------------------
  for (int s = 0; s < swarmSize; s++)
  {
    for (int k = 0; k < params; k++)
    {
      fireflies [s].c  [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      fireflies [s].c  [k] = SeInDiSp (fireflies [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
  }

  luminosity = true;
}

从第二次及苏随后的迭代中，在第一次迭代中随机发送出去的萤火虫开始发光（适应度函数开始针对它们进行计算）之后，可以计算出每只萤火虫的吸引力程度。 为此，我们需要针对所有可能的萤火虫配对，计算它们之间的欧几里得距离。 为此，只需将坐标差的平方相加，然后取它们总和的平方根。 计算出的距离会应用到吸引力计算方程。 这就是我们为何每只萤火虫仅取可能的配对。 判定所有萤火虫的最大亮度。 这是判定最亮萤火虫所需的做法，因为不可能找到一对萤火虫，且独自在空间中徘徊。 好吧，也许，在下一次迭代中会更幸运。

//measure the distance between all------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  att [i].a = -DBL_MAX;

  for (int k = 0; k < swarmSize; k++)
  {
    if (i == k) continue;

    summCoordinates = 0.0;
    for (int c = 0; c < params; c++) summCoordinates += pow (fireflies [i].c [c] - fireflies [k].c [c], 2.0);

    distance = pow (summCoordinates, 0.5);
    distance = Scale (distance, 0.0, maxDist, 0.0, 20.0, false);
    attractiveness = fireflies [k].f / (1.0 + gamma * distance * distance);

    if (attractiveness > att [i].a)
    {
      att [i].a = attractiveness;
      att [i].i = k;
    }

    if (fireflies [i].f > maxF) maxF = fireflies [i].f;
  }
}

Flight() 方法的这一部分代码负责萤火虫的飞行。 对于那些不幸的萤火虫，其亮度大于所有其它萤火虫，计算方式略有不同。 我们添加了一个移动向量到其当前位置，即 alpha 系数乘以随机数 [-1.0;1.0]。 理论上，在算法中，这一行动是对最佳解的附加研究，期望它能更好，但是，正如我们稍后将看到的，这种技术将被证明无甚大用。 在此阶段，我们研究算法的经典版本。

对于所有其它萤火虫，若已经找到配对萤火虫，计算运动时将包括朝向相应配对的萤火虫移动（通过添加的随机分量，我之前提到过）。

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      fireflies [i].c [c] = fireflies [i].c [c] + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); 
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r  = RNDfromCI (-1.0, 1.0);
      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];
      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

在每次迭代时调用的简单公开方法。 在此处，我们将更新最佳解。 

//——————————————————————————————————————————————————————————————————————————————
void C_AO_FA::Luminosity ()
{
  for (int i = 0; i < swarmSize; i++)
  {
    if (fireflies [i].f > fB)
    {
      fB = fireflies [i].f;
      ArrayCopy (cB, fireflies [i].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

我们进入测试环节。 我们来看一下算法在测试函数上的结果：

2022.12.16 13:39:00.102    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.901742065217812
2022.12.16 13:39:05.930    Test_AO_FA (EURUSD,M1)    Score: 0.99603
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    20 Skin's; Func runs 10000 result: 3.2208359936020665
2022.12.16 13:39:13.579    Test_AO_FA (EURUSD,M1)    Score: 0.59468
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    500 Skin's; Func runs 10000 result: 0.98491319842575
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    Score: 0.06082
2022.12.16 13:39:53.607    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.578196881663454
2022.12.16 13:39:59.313    Test_AO_FA (EURUSD,M1)    Score: 0.89271
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.3101994341994826
2022.12.16 13:40:07.274    Test_AO_FA (EURUSD,M1)    Score: 0.17546
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.06829102669136165
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    Score: 0.03863
2022.12.16 13:40:49.159    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 8.2
2022.12.16 13:40:54.895    Test_AO_FA (EURUSD,M1)    Score: 0.68333
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.5900000000000003
2022.12.16 13:41:02.777    Test_AO_FA (EURUSD,M1)    Score: 0.13250
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.2892
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    Score: 0.02410
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    =============================
2022.12.16 13:41:43.901    Test_AO_FA (EURUSD,M1)    All score for C_AO_FA: 0.39980648892951776

委婉地说，结果并不令人印象深刻。 该算法在个别测试中仅略好于 PSO、FSS、GWO。 然而，在总评级指标中，它位于倒数第二的位置，其后只剩下随机搜索算法。 考虑到所有这些，出现了修订测试中估测指标计算的想法。 在下面的文章中，我将切换到更方便的评级计算方案，而在当前文章中，我将添加最终结果的直方图。 它能清晰地展示各种算法之间的性能比率。

经典的萤火虫算法很容易实现。 然而，研究表明，它收敛缓慢，很容易堕入多模态问题的局部极值陷阱。 此外，它缺少依赖当前迭代系数的参数化。 因此，该研究的目标之一是修订标准萤火虫算法，从而提高其性能。

该算法的思路非常原始，如果一切都保持原样而不尝试改进其特性，那就太可惜了。 因此，我尝试通过用 Levy 飞行替换随机分量来修改算法。 Levy 飞行无法提高每种算法的搜索能力。 在研究过杜鹃搜索算法后，我尝试利用这种方法改进其它算法，但这并没有带来预期的结果。 显然，这应该是在某种程度上与补充它的算法中的内部搜索策略保持一致。 在这种特殊情况下，Levy 飞行的应用产生了惊人的效果 —算法的能力明显提升。 我们将在文章有关测试结果的章节讨论这一点。

此处是修改过的代码部分。 首先，在经典版本中，具有最佳亮度的萤火虫从其当前位置沿随机方向移动。 然后，我们最好的萤火虫从全局最佳位置移动，试图改善的不是它当前的位置，而是整个解。 将具有相同 alpha 系数的 Levy 飞行分布（具有重尾分布）的随机数添加到最佳解的坐标之中。 这确实令通过细化邻近区域来改善全局解的坐标成为可能。

如您所见，其余萤火虫的行为现在遵循相同的经典规则，尽管针对 Levy 飞行的随机分量进行了调整。 这就是对算法所做的全部修改。 

//flight--------------------------------------------------------------------
for (int i = 0; i < swarmSize; i++)
{
  if (fireflies [i].f >= maxF)
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      fireflies [i].c [c] = cB [c] + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
  else
  {
    for (int c = 0; c < params; c++)
    {
      r1 = RNDfromCI (0.0, 1.0);
      r1 = r1 > 0.5 ? 1.0 : -1.0;
      r2 = RNDfromCI (1.0, 20.0);

      Xi = fireflies [i].c [c];
      Xj = fireflies [att [i].i].c [c];

      fireflies [i].c [c] = Xj + beta * (Xi - Xj) + alpha * r1 * pow (r2, -2.0) * v [c];
      fireflies [i].c [c] = SeInDiSp (fireflies [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

图例 3. Levy 飞行函数图表 函数方程中的指数如何影响算法的行为？ 根据我的研究，随着度数的增加，长（重尾）跳跃的次数相对于短跳跃次数减少，而算法在最佳解附近细化坐标的能力有所提高。 由于跳远很少的事实，卡顿在局部极值的可能性增加。 这种效应在研究离散函数时会更加明显，而在平滑函数上则不那么明显。 与之对比，随着指数的减小，长跳跃次数增加，算法的搜索能力提高，但收敛精度变差，因此我们需要在准确性和搜索之间采取中间立场。 此外，根据优化问题的不同，它可能会有所不同。


Levi

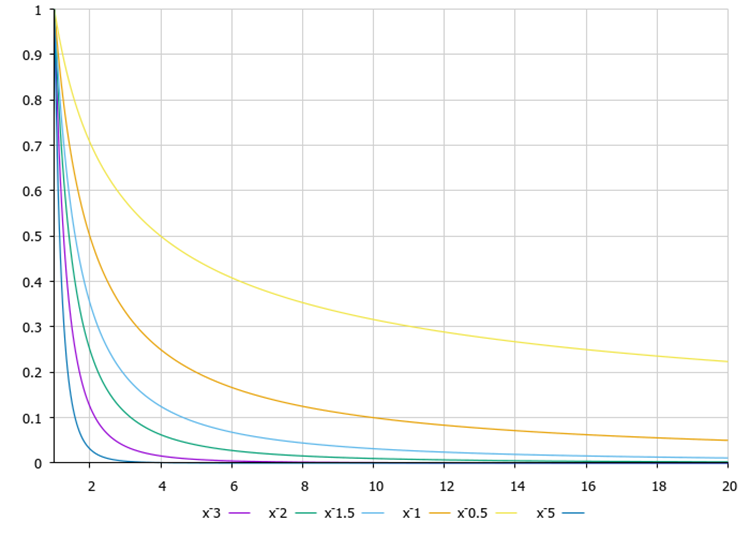
图例 3. Levy 飞行函数，度数 0.5...3.0 


故此，我们进入讨论测试台上修改后的算法版本的结果。 下面您可以看到与经典版本相比，原始版本的性能提高了多少。

2022.12.16 13:07:15.925    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    1 Skin's; Func runs 10000 result: 4.854437214435259
2022.12.16 13:07:21.544    Test_AO_FAm (EURUSD,M1)    Score: 0.98473
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    20 Skin's; Func runs 10000 result: 4.588539001298423
2022.12.16 13:07:29.518    Test_AO_FAm (EURUSD,M1)    Score: 0.92124
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    500 Skin's; Func runs 10000 result: 1.981278990090829
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    Score: 0.29872
2022.12.16 13:08:12.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    1 Forest's; Func runs 10000 result: 1.7665409595127233
2022.12.16 13:08:18.336    Test_AO_FAm (EURUSD,M1)    Score: 0.99924
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    20 Forest's; Func runs 10000 result: 0.6261364994589462
2022.12.16 13:08:26.432    Test_AO_FAm (EURUSD,M1)    Score: 0.35417
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.14269062630878
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    Score: 0.08071
2022.12.16 13:09:10.587    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    1 Megacity's; Func runs 10000 result: 10.0
2022.12.16 13:09:16.393    Test_AO_FAm (EURUSD,M1)    Score: 0.83333
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    20 Megacity's; Func runs 10000 result: 1.7899999999999998
2022.12.16 13:09:24.373    Test_AO_FAm (EURUSD,M1)    Score: 0.14917
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5076
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    Score: 0.04230
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    =============================
2022.12.16 13:10:09.298    Test_AO_FAm (EURUSD,M1)    All score for C_AO_FAm: 0.5181804234713119

如您所见，修改后的算法不仅展现出更好的结果，而且在评级表中处于领先地位。 我们仔细查看在下一节中的结果。 下面是测试台上算法修改版本的动画。

Skin

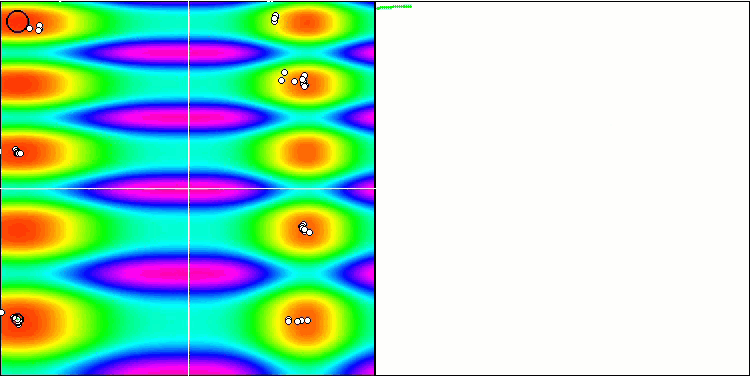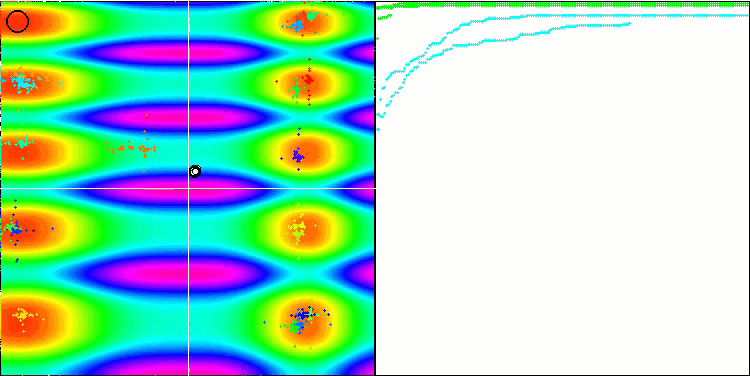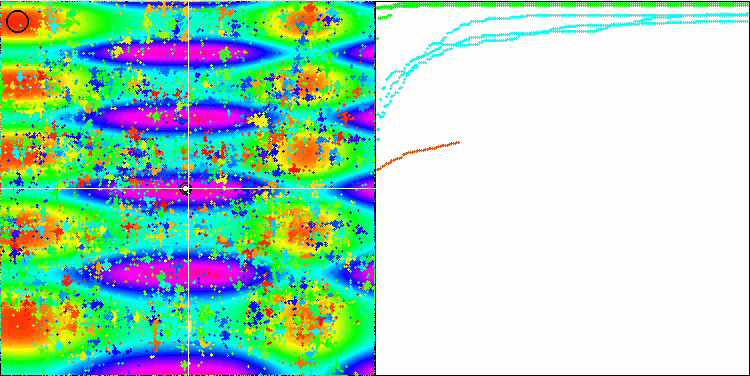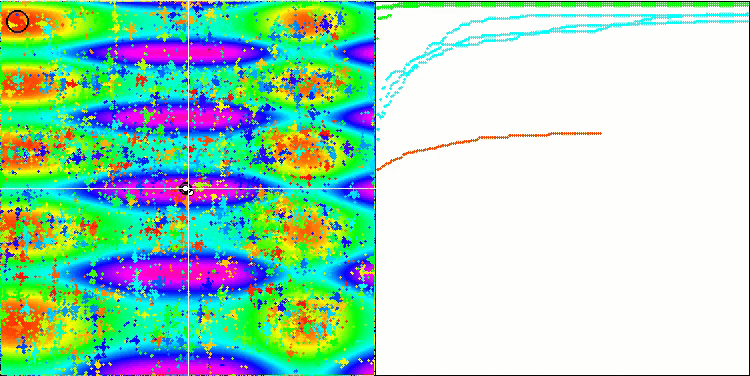
  基于 Skin 测试函数的 FAm。

Forest

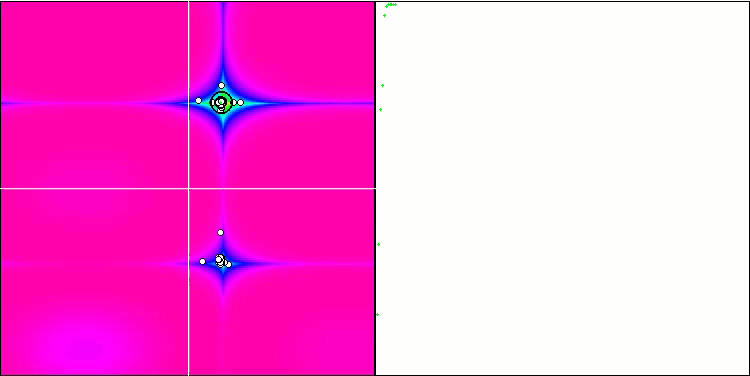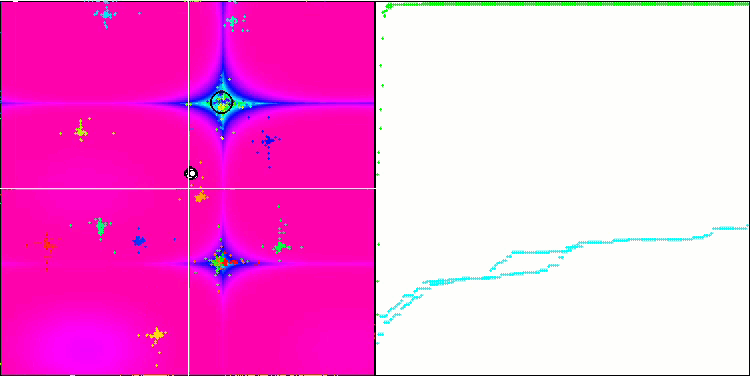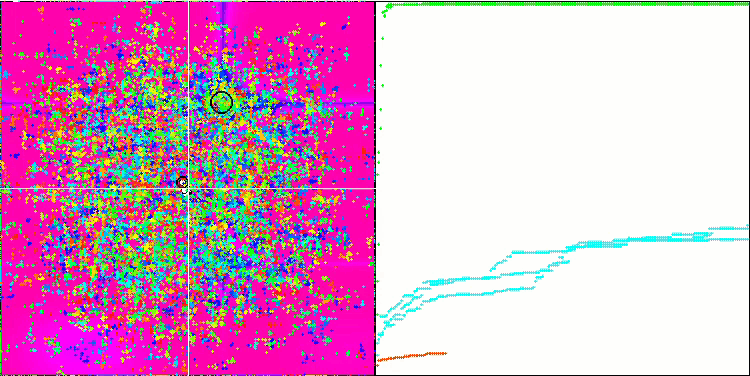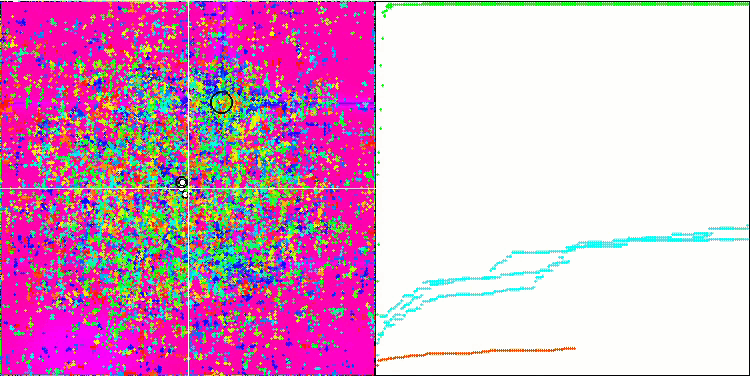
  Forest 测试函数上的 FAm。

Megacity

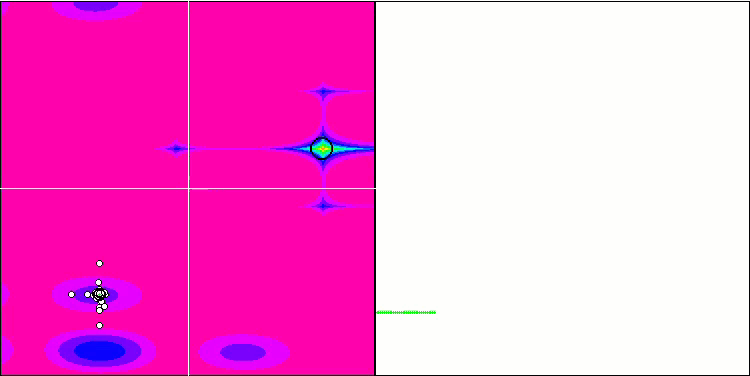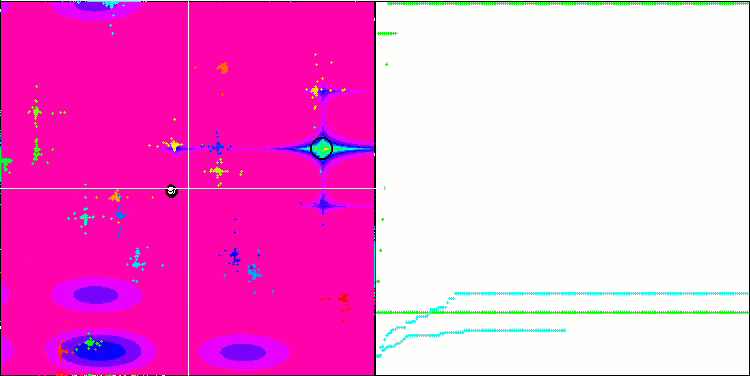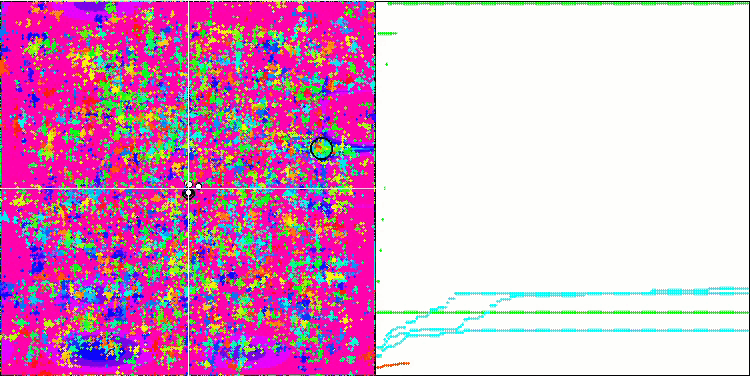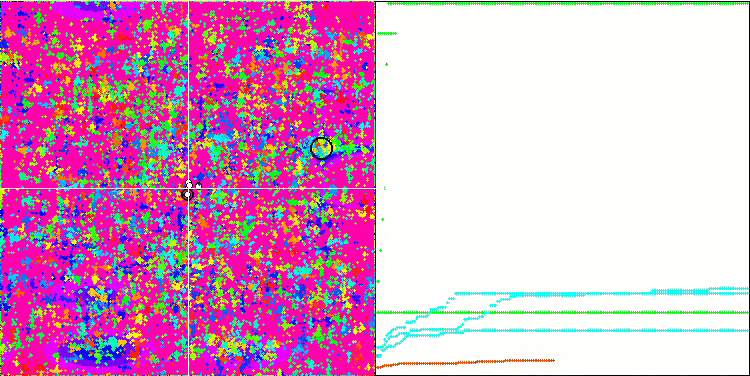
  Megacity 测试函数上的 FAm。


3. 测试结果

改进的萤火虫算法（FAm）在所有测试环节都表现出色。 通常，结果取决于算法的设置。 在某些设置的情况下，使用两个变量在所有三个函数上实现了 100% 收敛。 该算法的高可扩展性在具有 40 个和 1000 个参数的测试中处于领先地位。 beta 和 gamma 参数具有很强的影响，令获得高收敛性和抗卡在局部极值的能力成为可能。 结果变化很广，这通常可以归因于算法的缺点。 在其它条件相同的情况下，该算法是之前研究过的算法中最强的。 可以推荐将其用于非常广泛的任务，包括机器学习和人工智能任务，尤其是在训练神经网络时。

下面是最终的评级表，其中修改后的萤火虫算法处于领先。 不幸的是，经典算法尽管具有独创性，但未能取得良好的结果。 调谐参数的选择也没有带来成功。

算法

说明

Skin

Skin 最终

Forest

Forest 最终

Megacity (离散)

Megacity 最终

最终结果

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

2 参数 (1 F)

40 参数 (20 F)

1000 参数 (500 F)

FAm

萤火虫算法 M

0.98473

0.92124

0.29872

0.73490

0.99924

0.35417

0.08071

0.47804

0.83333

0.14917

0.04230

0.34160

0.51817889

COAm

杜鹃优化算法 M

1.00000

0.85911

0.14316

0.66742

0.99283

0.28787

0.04551

0.44207

1.00000

0.24917

0.03537

0.42818

0.51255778

ACOm

蚁群优化 M

0.98229

0.79108

0.12602

0.63313

1.00000

0.62077

0.11521

0.57866

0.38333

0.44000

0.02377

0.28237

0.49805222

ABCm

人工蜂群 M

1.00000

0.63922

0.08076

0.57333

0.99908

0.20112

0.03785

0.41268

1.00000

0.16333

0.02823

0.39719

0.46106556

ABC

人工蜂群

0.99339

0.73381

0.11118

0.61279

0.99934

0.21437

0.04215

0.41862

0.85000

0.16833

0.03130

0.34988

0.46043000

GWO

灰狼优化器

0.99900

0.48033

0.18924

0.55619

0.83844

0.08755

0.02555

0.31718

1.00000

0.10000

0.02187

0.37396

0.41577556

FSS

鱼群搜索

0.99391

0.5692

0.11341

0.55884

0.85172

0.12143

0.03223

0.33513

0.91667

0.08583

0.02583

0.34278

0.41224778

PSO

粒子群优化

0.99627

0.38080

0.05089

0.47599

0.93772

0.14540

0.04856

0.37723

1.00000

0.09333

0.02233

0.37189

0.40836667

FA

萤火虫算法

0.99603

0.59468

0.06082

0.55051

0.89271

0.17546

0.03863

0.36893

0.68333

0.13250

0.02410

0.27998

0.39980649

RND

随机

0.99932

0.44276

0.06827

0.50345

0.83126

0.11524

0.03048

0.32566

0.83333

0.09000

0.02403

0.31579

0.38163222


从本文开始，我将发布一个直方图，在该直方图上，测试时最好的算法将有 100 个条件点，而最差的算法只有 1 个点。 我认为，就直观感知而言，这是最方便的展示方法，因为我们可以清楚地看到评级表算法的最终结果的规模。 现在我们可以看到随机算法落后于领先者的程度。

评级

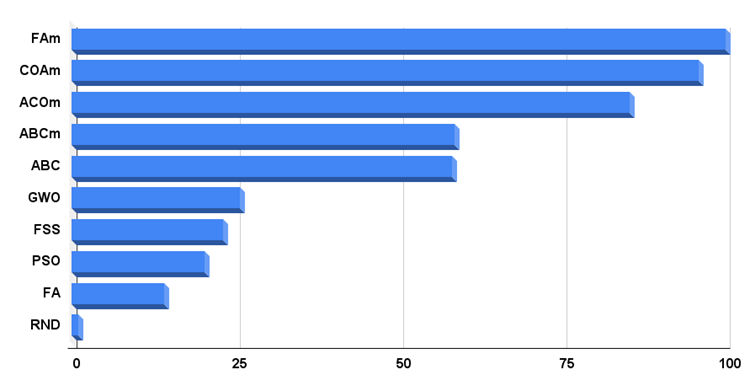
图例 4. 测试算法最终结果的直方图


您可能还记得，元启发式算法是解决优化问题的近似方法，它们在其搜索引擎中使用具有合理假设的随机性属性，并尝试通过检查和使用解空间，通过随机生成的一组有效解的迭代来提高可用解的质量。 虽然这些算法不能保证结果是最佳的，但它们是经测试给出的合理且可接受的解。 此外，它们的优势在于问题的行为不会对它们产生很大影响，这就是它们在许多任务中有用的原因。 许多可用算法的存在令我们可以根据其行为选择相应的算法来解决问题。

自从进化算法出现以来，对启发式算法进行了大量研究。 新算法的实现一直是领先的研究领域之一。 目前，有 40 多种元启发式算法。 它们中的大多数是通过模拟自然场景而创建的。

优缺点是指萤火虫算法（FAm）的修改版本。

优点:
  • 实现简单。 易于修改。
  • 高可扩展性。
  • 高收敛性（可能因算法设置而异）。
  • 能够将搜索空间的区域聚类到围绕局部极值的单独组中。

缺点:
  • 设置对优化结果的影响很大。
  • 在某些设置下，算法很容易卡顿在局部极值。

每篇文章都提供一个存档，其中包含所有以前文章的算法代码的当前更新版本。 每篇新文章都是作者积累的个人经验，结论和判断是基于为此目的开发的特殊测试台上进行的实验。



本文由MetaQuotes Ltd译自俄文
原文地址： https://www.mql5.com/ru/articles/11873

附加的文件 |
下载ZIP
8_The_world_of_AO_vFA2.zip (77.04 KB)
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。

该作者的其他文章

前往讨论
DoEasy. 控件（第三十一部分）：滚动条控件内内容的滚动 DoEasy. 控件（第三十一部分）：滚动条控件内内容的滚动
在本文中，我将实现通过按钮滚动水平滚动条容器内容的功能。
数据科学与机器学习（第 10 部分）：岭回归 数据科学与机器学习（第 10 部分）：岭回归
岭回归是一种简单的技术，可降低模型复杂度，并防止简单线性回归可能导致的过度拟合。
构建自动运行的 EA（第 09 部分）：自动化（I） 构建自动运行的 EA（第 09 部分）：自动化（I）
尽管创建自动 EA 并非一项非常困难的任务，但在缺乏必要知识的情况下可能会犯许多错误。 在本文中，我们将研究如何构建初级自动化，其中包括创建一个触发器来激活盈亏平衡和尾随停止价位。
DoEasy. 控件（第三十部分）：动画态滚动条控件 DoEasy. 控件（第三十部分）：动画态滚动条控件
在本文中，我将继续开发滚动条（ScrollBar）控件，并开始实现鼠标交互功能。 此外，我将扩展鼠标状态标志和事件的列表。