
种群优化算法:细菌觅食优化(BFO)
内容
1. 概述
细菌觅食优化(BFO)算法是一种引人入胜的优化技术,可在极其复杂或不可能的数值函数里找到最大化/最小化问题得近似解。 该算法被广泛认为应对分布式优化和控制的全局优化算法。 BFO 的灵感来自大肠杆菌的社会觅食行为。 BFO 已经引起了研究人员的注意,因为它已表现出在多个应用领域中解决实际优化问题方面的有效性。 大肠杆菌觅食策略背后的生物学,是以原始方式模拟,并作为一种简单的优化算法。
细菌,如大肠杆菌或沙门氏菌,是地球上最成功的生物之一。 这些灵动的细菌具有称为鞭毛的半刚性附属物,它们通过扭曲运动推动自己。 当所有的鞭毛逆时针旋转时,会产生螺旋桨效应,推动细菌或多或少地沿直线方向移动。 在这种情况下,细菌执行称为游泳的运动。 所有鞭毛都顺同一方向旋转。
鞭毛帮助大肠杆菌翻滚或游泳,这是细菌在觅食期间执行的两项主要操作。 当它们顺时针旋转鞭毛时,每个鞭毛都会反向推动细胞。 当鞭毛向不同方向旋转时,细菌就会翻滚。 细菌在有利的环境中移动时翻滚较少,而在有害的环境中,它经常翻滚,从而感知营养梯度。 鞭毛的逆时针运动有助于细菌以非常高的速度游泳。
在上述算法中,细菌的行为是由一种称为细菌趋化性的机制决定的,该机制是这些微生物对环境中化学刺激的运动反应。 这种机制允许细菌向引诱剂(最常见的营养物质)移动,并远离驱虫剂(对细菌有潜在危害的物质)。 检测引诱剂和驱虫剂的受体位于细菌的两极。
由于细菌体积小,它无法捕捉两极之间有用和有害物质浓度的差异。 细菌通过测量运动过程中浓度的变化来判定这些物质的梯度。 这种运动的速度可以达到每秒几十个细菌长度。 例如,大肠杆菌通常以每秒 10-20 倍其体长的速度移动。
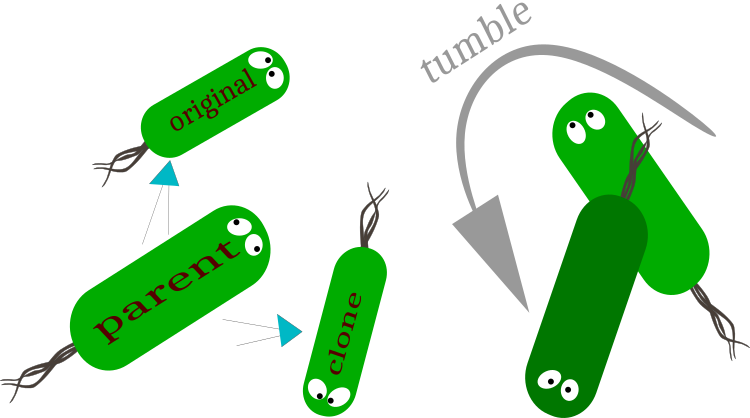
图例 1. 复制:分为原始(保持运动向量)和克隆(运动向量变化)细菌。
翻滚 - 细菌运动向量的变化
如果细菌选择的运动方向对应于引诱剂浓度的增加(驱虫剂浓度的降低),则至下一次翻滚之前的时间增加。 由于细菌体形小,其运动受到布朗运动的强烈影响。 结果就是,细菌只平均朝着有益物质的方向移动,远离有害物质。
所研究的细菌运动机制并不是唯一的。 有些细菌有一个鞭毛。 在这种情况下,细菌运动的变体提供了不同的旋转和停止模式。 然而,在所有情况下,如果细菌朝正确的方向移动,那么这种运动的持续时间就会增加。 因此,一般来说,细菌趋化性可以定义为游泳和翻滚的复杂组合,它允许细菌停留在营养物质浓度高的地方,躲避不可接受的有害物质浓度。
在搜索引擎优化问题的背景下,细菌趋化性也可以解释为一种机制,用于优化细菌对已知食物资源的利用,并寻找新的、潜在的、更有价值的区域。足够丰度的细菌种群可以形成复杂的时空结构 — 在细菌种群中形成的结构影响。 这种影响可能是由趋化性和许多其它原因引起的。
对于一些细菌,这种结构的形成可以通过其代谢产物的调节特性来解释。 基于磁性(对磁场的敏感性)、生物对流、负地质趋向性(微生物对重力方向的优先运动)、和其它现象,类似的效果是可能的。 常规下,细菌在友好的环境中能传播更远的距离。 当它们获得足够的食物时,它们的长度会更长,并在适当的温度下从中间断裂,变成自己的精确复制品。
这种现象激发了帕西诺(Passino)将繁衍事件引入BFO。 由于环境的突然变化或攻击,趋化过程可能会被破坏,那么细菌群落可以移动到其它地方。 这代表了真实细菌种群中的消除和扩散事件,当该区域中的所有细菌死亡、或一组细菌扩散到环境的新部分时。 此外,所研究的趋化性和繁衍过程通常不足以找到多极值目标函数的全局最大值,因为这些过程不允许细菌离开它们发现的该函数的局部最大值。 消除和扩散过程旨在克服这一缺点。 根据自然选择(适者生存),适应性差的细菌将会消亡,适应性较高的细菌会自我繁衍。
2. 算法说明
BFO 的规范版本包括以下主要步骤:
- 初始化细菌群落。
- 趋化性。
- 聚集。
- 繁衍。
- 流动和分群。
1. 初始化细菌群落。
细菌可以在一些半固体营养物质中形成复杂、稳定的时空模式,如果最初一同安置在中心,它们就可以在环境中生存。 甚至,在某些条件下,它们会分泌细胞间引诱信号,以便它们相互聚集和保护。
2. 趋化性。
细菌寻找食物的运动特征可以通过两种方式判定,即一同游动和翻滚被称为趋化性。 据说细菌如果朝正确的方向移动,就会“游动”,如果它向环境恶化的方向移动,就会“翻滚”。
3. 聚集。
细菌为了到达食物最丰富的地方,希望在搜索期间最佳细菌于某个时间点尝试吸引其它细菌,如此它们就能更快地在所需位置聚合在一起。 为此,根据每个细菌从适者菌落到此搜索持续时间的相对距离,在原始成本函数中添加一个惩罚函数。 最后,当所有细菌融合到决策点时,这个惩罚函数变为零。 聚集的效果是细菌成群聚拢,并以同心模式移动,细菌密度高。
4. 繁衍。
最初的一组细菌经过几个趋化阶段,达到繁衍阶段。 此刻,最好的一组细菌分为两组。 更健康的一半被另一半细菌所取代,寻找食物能力较低的则消亡。 这令细菌的数量在进化过程中保持不变。
5. 消除和扩散。
在进化过程中,可能会发生突然的不可预见的事件,该事件可以极大地改变进化过程的顺畅,并导致许多细菌的消除和/或它们扩散到新的环境中。 具有讽刺意味的是,这种未知事件并不会破坏一组细菌的正常趋化性生长,反而可能会令较新的一组细菌更接近食物的位置。 从广义上讲,消除和扩散是种群长距离行为的一部分。 当应用于优化时,这有助于减少此类并行搜索算法中常见的停滞。
我实现的 BFO 与规范版本略有不同。 在研究代码的特定部分时,除了需要这些更改的理由外,我还将详细介绍差异。 一般来讲,实现中的修改不能被认为是重要的,因此我不会将 “m”(修改版本)标记分配给算法名称。 我只想提示,已实现的修改改善了结果。
接下来,研究我实现的算法和代码。
算法步骤:
1. 细菌菌落初始化。
2. 测量细菌健康(适应度)。
3. 繁衍?
3.1. 是的。 执行繁衍。
3.2. 不。 第四步。
4. 老化 (达到生命极限)?
4.1. 是的。 执行翻滚(更改移动矢量)。
4.2. 不。 第五步。
5. 移至正确方向?
5.1. 是的。 按相同矢量继续移动。
5.2. 不。 执行翻滚 (改变运动矢量)。
6. 测量细菌健康(适应度)。
7. 从地三步继续,直到满足停止条件。
该算法的逻辑方案如图例 1 所示。
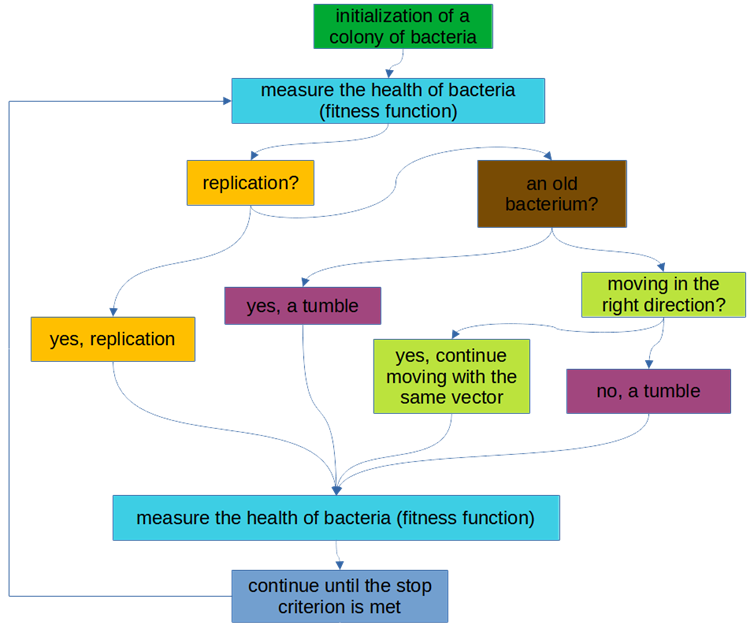
图例 2. BFO 算法逻辑框图
我们看一下代码。
描述细菌的最佳方式是包含坐标和运动矢量数组的结构。 细菌当前和以前的健康值和生命计数器。 从本质上讲,生命计数器对于限制一个方向的顺序运动量是必要的,这与原始版本不同,在原始版本中,达到寿命极限时,细菌将消亡,并在搜索空间的随机位置创建一个新的细菌。 然而,由于我们在之前的文章中已经触及了这个主题,因此在随机位置创建新代理者没有实际意义,只会降低搜索功能。 在这种情况下,最好在最佳解的位置创建新代理者,或者继续从当前位置移动,但更改方向矢量。 第二个选项表现出更好的结果。
规范版本使用常量运动矢量。 由于有大量的活物,这将导致细菌在搜索空间中沿直线移动。 如果这条线不能穿过任何更好的极值,那么这种直线运动的过程将无限发生,但在这里计数器起着强制翻滚的作用,这令细菌在其整个生命周期中避免直线运动。 在不具有梯度的区域函数上,它最终仍然会导致一个可以开始改善其适应性的地方。
//—————————————————————————————————————————————————————————————————————————————— struct S_Bacteria { double c []; //coordinates double v []; //vector double f; //current health double fLast; //previous health double lifeCNT; //life counter }; //——————————————————————————————————————————————————————————————————————————————
我们将 BFO 算法类声明为 C_AO_BFO。 该类包含细菌菌落的声明、搜索空间的边界、最佳解的值和最佳解的坐标数组。 此外,声明算法参数的常量值。
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BFO { //---------------------------------------------------------------------------- public: S_Bacteria b []; //bacteria public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: void Init (const int paramsP, //number of opt. parameters const int populationSizeP, //population size const double lambdaP, //lambda const double reproductionP, //probability of reproduction const int lifeCounterP); //life counter public: void Swimming (); public: void Evaluation (); //---------------------------------------------------------------------------- private: double NewVector (int paramInd); private: S_Bacteria bT []; //bacteria private: double v []; private: int ind []; private: double val []; private: int populationSize; //population size private: int parameters; //number of optimized parameters private: double lambda; //lambda private: double reproduction; //probability of reproduction private: int lifeCounter; //life counter private: bool evaluation; private: void Sorting (); private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
公开的 Init() 方法初始化常量变量、分配数组大小、和重置标志、以及最佳解的值。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BFO::Init (const int paramsP, //number of opt. parameters const int populationSizeP, //population size const double lambdaP, //lambda const double reproductionP, //probability of reproduction const int lifeCounterP) //life counter { fB = -DBL_MAX; evaluation = false; parameters = paramsP; populationSize = populationSizeP; lambda = lambdaP; reproduction = reproductionP; lifeCounter = lifeCounterP; ArrayResize (rangeMax, parameters); ArrayResize (rangeMin, parameters); ArrayResize (rangeStep, parameters); ArrayResize (v, parameters); ArrayResize (ind, populationSize); ArrayResize (val, populationSize); ArrayResize (b, populationSize); ArrayResize (bT, populationSize); for (int i = 0; i < populationSize; i++) { ArrayResize (b [i].c, parameters); ArrayResize (b [i].v, parameters); b [i].f = -DBL_MAX; b [i].fLast = -DBL_MAX; ArrayResize (bT [i].c, parameters); ArrayResize (bT [i].v, parameters); } ArrayResize (cB, parameters); } //——————————————————————————————————————————————————————————————————————————————
每次迭代时需要调用的第一个公开方法 — Swim() 或细菌泳动,包括算法的所有主要逻辑。
void C_AO_BFO::Swimming ()
{}
我们详细研究一下该方法。 在第一次迭代中,当评估标志设置为 “false” 时,我们将细菌以均匀分布随机散布在整个搜索空间当中。 在这个阶段,当前的健康状况(适应度)和前值都是未知的。 我们将 DBL_MAX 值分配给相应的变量。 检查随机获得的坐标是否超出边界,并应用更改优化参数的步骤。 在此迭代中,有必要调用 NewVector() 私密方法为每个细菌设置一个单独的位移矢量(我将在下面讨论)。 所有细菌均匀地向前泳动,并与相同的单个矢量呈直线游动,直到满足其变化的条件。
//---------------------------------------------------------------------------- if (!evaluation) { fB = -DBL_MAX; for (int s = 0; s < populationSize; s++) { for (int k = 0; k < parameters; k++) { b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); v [k] = rangeMax [k] - rangeMin [k]; b [s].v [k] = NewVector (k); b [s].f = -DBL_MAX; b [s].fLast = -DBL_MAX; b [s].lifeCNT = 0; } } evaluation = true; }
在第二次、及以后的迭代中,当达到生命极限时,将执行泳动,翻滚,繁衍和消亡细菌的操作。 逻辑中的第一个是繁衍操作(参数中指定的概率)。 这意味着细菌菌落在上一次迭代中按健康值降序排序。
繁衍在算法中执行一个重要函数:通过改善细菌菌落的“基因库”来加速算法的收敛。 该操作是将细菌按想象分裂为两部分,并且只允许菌落的第一部分,较佳的一半允许分离。 菌落的前半部分减半,原始亲本版本放置在菌落的后半部分。 亲本细菌将继续以相同的矢量移动,与其克隆体相反。 克隆体保留在菌落中的位置,并为其分配一个新的运动矢量。 亲本及其克隆将继续从发生分裂的空间点移动。
r = RNDfromCI (0.0, 1.0); //========================================================================== if (r < reproduction) { int st = populationSize / 2; for (int s = 0; s < st; s++) { //bacterium original-------------------------------------------------- for (int k = 0; k < parameters; k++) { b [st + s].v [k] = b [s].v [k]; b [st + s].c [k] = b [s].c [k] + b [s].v [k]; b [st + s].c [k] = SeInDiSp (b [st + s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); b [st + s].fLast = b [s].f; b [st + s].lifeCNT++; } //bacterium clone------------------------------------------------------- for (int k = 0; k < parameters; k++) { b [s].v [k] = NewVector (k); b [s].c [k] = b [s].c [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); b [s].fLast = b [s].f; b [s].lifeCNT = 0; } } }
如果未实现复制概率,则进行检查是否达到细菌生命极限。 在算法的规范版本中,“旧”细菌理应消亡,并创建一个新细菌,替代其在细菌列表内搜索空间的随机位置。 在一般情况下,繁殖和趋化性的操作不足以找到多极端适应度函数的全局最大值,因为
这些程序不允许细菌离开它们发现的局部最小值。 而流动过程旨在克服这一缺陷。 然而,正如运用这种算法和其它算法的验证实践所表明的那样,在这种情况下,简单地改变运动矢量更有效。 生命计数器被重置。 计数器是在给定步数(生命)后改变移动方向的触发器。 由于繁衍和消亡,细菌总数保持不变。
if (b [s].lifeCNT >= lifeCounter) { for (int k = 0; k < parameters; k++) { b [s].v [k] = NewVector (k); b [s].c [k] = b [s].c [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); b [s].fLast = b [s].f; b [s].lifeCNT = 0; } }
如果生命限制尚未用尽,那么我们将检查细菌是否朝着改善适应度函数梯度的方向发展。 换言之,我们检查两个健康值 — 在当前迭代和前一次个迭代时。 如果健康状况有所改善,则保留运动矢量,否则细菌应进行翻滚(改变运动矢量)。
在规范版本中,执行严格的“大于”当前和以前的健康检查,而在我的版本中,应用“大于或等于”,这令细菌即使在所研究表面的完全“水平”部分也能继续移动,那里没有适应度函数梯度,否则细菌会在一个地方无休止地翻滚(健康状况没有变化, 这意味着没有泳动方向)。 在这个阶段,我们还需要检查接收到的新坐标的输出是否超出搜索空间的边界。
else { if (b [s].f >= b [s].fLast) { for (int k = 0; k < parameters; k++) { b [s].c [k] = b [s].c [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); b [s].fLast = b [s].f; b [s].lifeCNT++; } } else { for (int k = 0; k < parameters; k++) { b [s].v [k] = NewVector (k); b [s].c [k] = b [s].c [k] + b [s].v [k]; b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); b [s].fLast = b [s].f; b [s].lifeCNT++; } } }
NewVecror () - 是更改运动矢量(翻滚)的私密方法。 该方法应用于每个坐标。 这里的思路很简单:将相应坐标 v 的搜索边界之间的差异乘以范围 [-1.0;1.0] 中的随机数 r,然后乘以 lambda 比例因子(算法参数之一)。 细菌采用的运动矢量不改变,直到生命极限耗尽(在同一个地方产生新的细菌,但有新的运动矢量),在繁衍期间(克隆体有一个新的矢量)和健康恶化期间(试图找到一个新的更有利的环境)。
//—————————————————————————————————————————————————————————————————————————————— double C_AO_BFO::NewVector (int paramInd) { double r = RNDfromCI (-1.0, 1.0); return lambda * v [paramInd] * r; } //——————————————————————————————————————————————————————————————————————————————
第二个公开的 Evaluation() 方法应在每次迭代时执行,它调用排序方法,检查全局解的更新,将分类菌落中最佳细菌的健康状况与找到的最佳解进行比较。
//—————————————————————————————————————————————————————————————————————————————— void C_AO_BFO::Evaluation () { Sorting (); if (b [0].f > fB) { fB = b [0].f; ArrayCopy (cB, b [0].c, 0, 0, WHOLE_ARRAY); } } //——————————————————————————————————————————————————————————————————————————————
3. 测试结果
BFO 测试台结果:
2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) C_AO_BFO:50;0.01;0.8;100
2023.01.21 12:52:46.501 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) 5 Rastrigin's; Func runs 10000 result: 72.94540549092933
2023.01.21 12:52:48.451 Test_AO_BFO (.US500Cash,M1) Score: 0.90383
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) 25 Rastrigin's; Func runs 10000 result: 54.75744312933767
2023.01.21 12:52:51.778 Test_AO_BFO (.US500Cash,M1) Score: 0.67848
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) 500 Rastrigin's; Func runs 10000 result: 40.668487609790404
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) Score: 0.50391
2023.01.21 12:53:21.197 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) 5 Forest's; Func runs 10000 result: 0.8569098398505888
2023.01.21 12:53:23.211 Test_AO_BFO (.US500Cash,M1) Score: 0.48471
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) 25 Forest's; Func runs 10000 result: 0.37618151461180294
2023.01.21 12:53:26.878 Test_AO_BFO (.US500Cash,M1) Score: 0.21279
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) 500 Forest's; Func runs 10000 result: 0.08748190028975696
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) Score: 0.04948
2023.01.21 12:54:22.339 Test_AO_BFO (.US500Cash,M1) =============================
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) 5 Megacity's; Func runs 10000 result: 4.8
2023.01.21 12:54:28.849 Test_AO_BFO (.US500Cash,M1) Score: 0.40000
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) 25 Megacity's; Func runs 10000 result: 2.216
2023.01.21 12:54:40.089 Test_AO_BFO (.US500Cash,M1) Score: 0.18467
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) 500 Megacity's; Func runs 10000 result: 0.4232
2023.01.21 12:55:24.640 Test_AO_BFO (.US500Cash,M1) Score: 0.03527
现在得出明确的结论还为时过早。 有必要首先分析与其它测试参与者相关的结果。
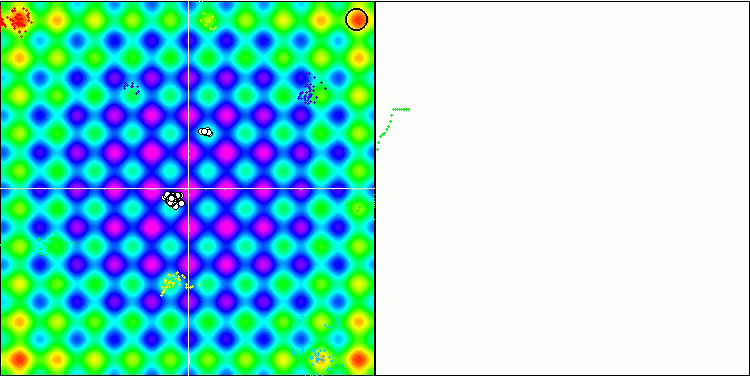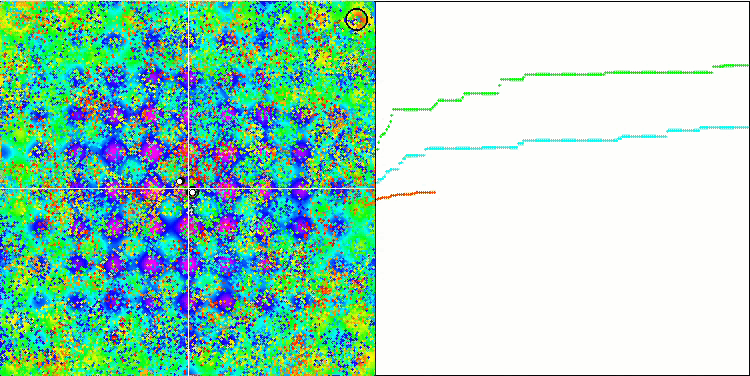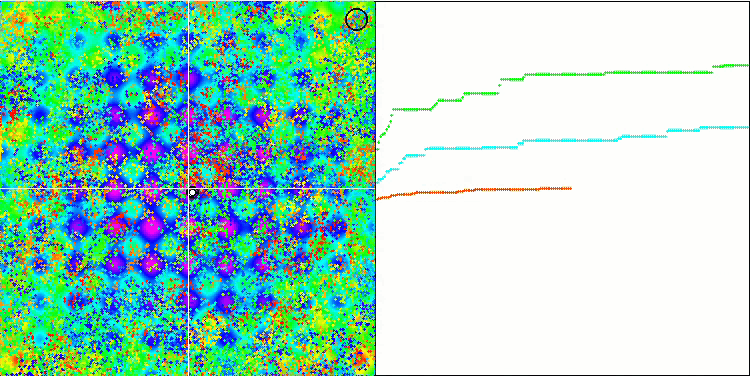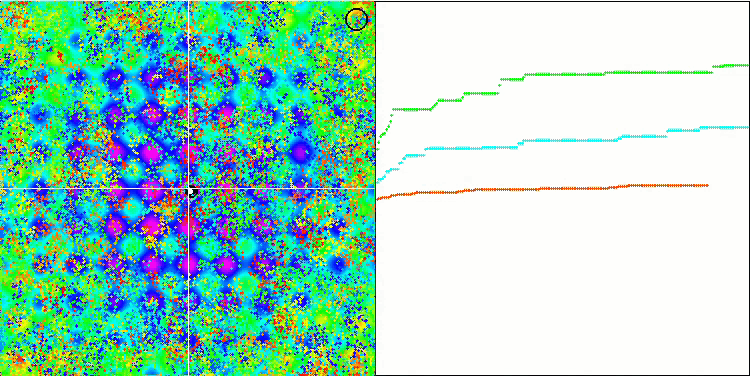
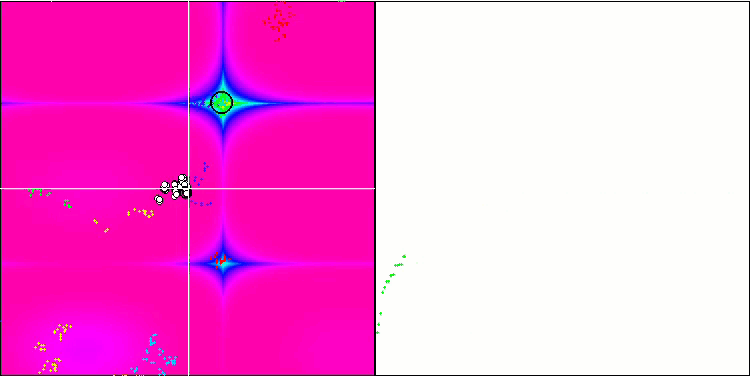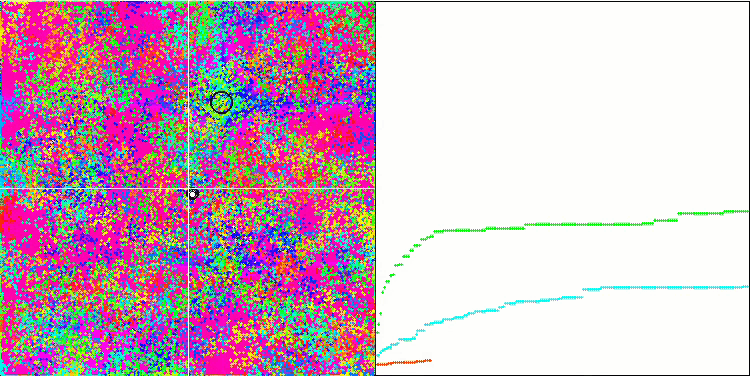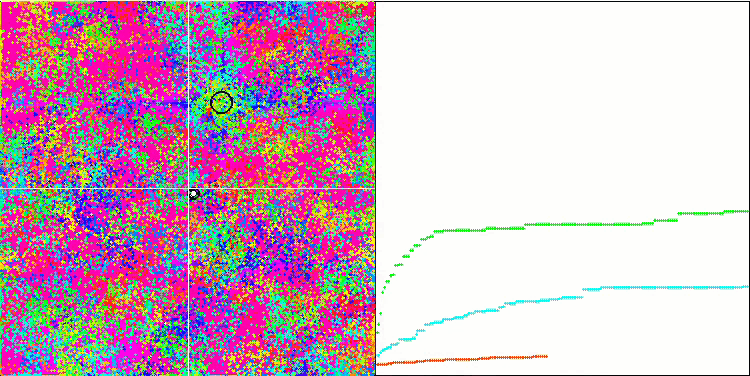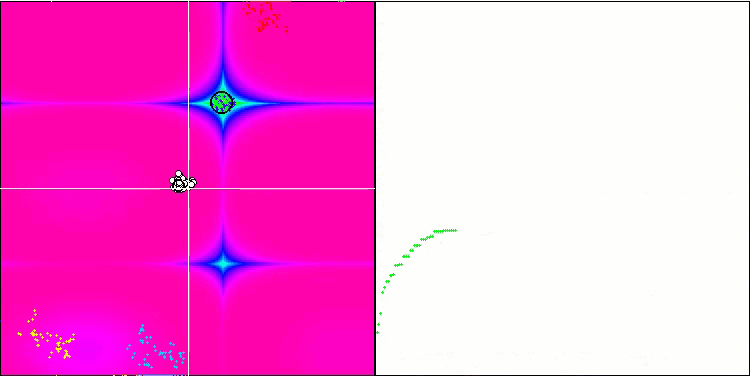
Rastrigin 测试函数上的 BFO
基于 Forest 测试函数的 BFO。
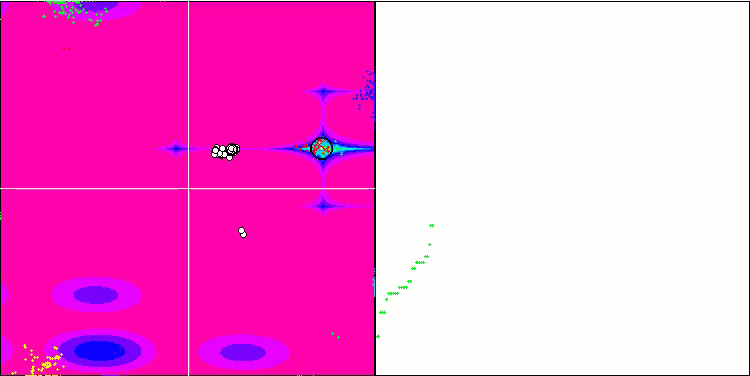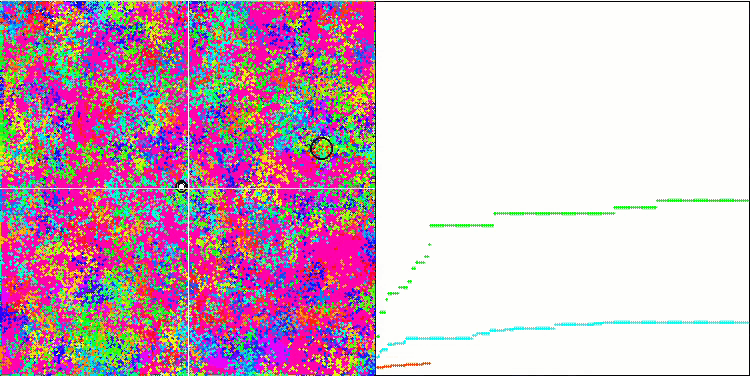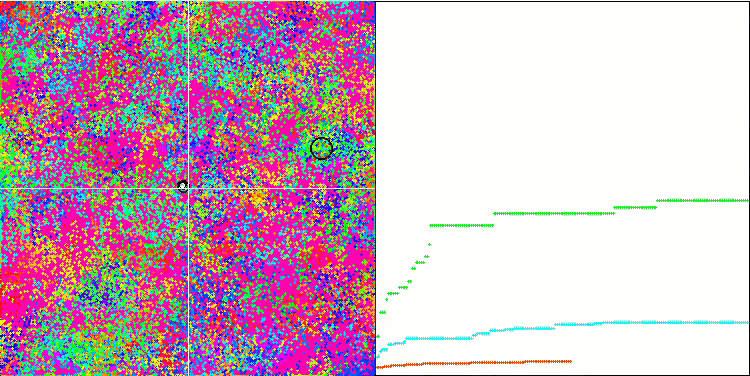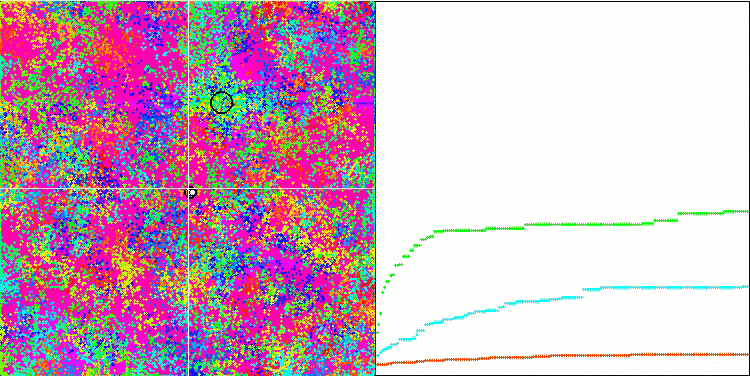
基于 Megacity 测试函数的 BFO。
我们关注测试可视化。 动画证实了在我们的算法中将“大于”算符替换为“大于或等于”的决定的正确性。 这允许细菌继续在测试函数的水平部分中移动。 这在 Forest 和 Megacity 函数中尤其明显。 即使根本没有函数梯度,细菌也会尝试继续前进。 还需要注意细菌菌落在视觉上分成几个单独的菌落的能力,这些菌落在视觉上分为不同的局部极值,这可以明确地被认为是一个积极的特征,尽管该算法不包含任何形成亚菌落的逻辑方法。 一般来说,细菌在搜索空间中的均匀运动是显而易见的,而无需尝试在任何方向上急剧跳跃,这可以通过均匀的增量运动 — 趋化性来解释。
| 算法 | 说明 | Rastrigin | Rastrigin 最终 | Forest | Forest 最终 | Megacity (离散) | Megacity 最终 | 最终结果 | ||||||
| 10 参数 (5 F) | 50 参数 (25 F) | 1000 参数 (500 F) | 10 参数 (5 F) | 50 参数 (25 F) | 1000 参数 (500 F) | 10 参数 (5 F) | 50 参数 (25 F) | 1000 参数 (500 F) | ||||||
| IWO | 入侵杂草优化 | 1.00000 | 1.00000 | 0.33519 | 2.33519 | 0.79937 | 0.46349 | 0.41071 | 1.67357 | 0.75912 | 0.44903 | 0.94088 | 2.14903 | 100.000 |
| ACOm | 蚁群优化 M | 0.36118 | 0.26810 | 0.17991 | 0.80919 | 1.00000 | 1.00000 | 1.00000 | 3.00000 | 1.00000 | 1.00000 | 0.10959 | 2.10959 | 95.996 |
| COAm | 杜鹃优化算法 M | 0.96423 | 0.69756 | 0.28892 | 1.95071 | 0.64504 | 0.34034 | 0.21362 | 1.19900 | 0.67153 | 0.34273 | 0.45422 | 1.46848 | 74.204 |
| FAm | 萤火虫算法 M | 0.62430 | 0.50653 | 0.18102 | 1.31185 | 0.55408 | 0.42299 | 0.64360 | 1.62067 | 0.21167 | 0.28416 | 1.00000 | 1.49583 | 71.024 |
| BA | 蝙蝠算法 | 0.42290 | 0.95047 | 1.00000 | 2.37337 | 0.17768 | 0.17477 | 0.33595 | 0.68840 | 0.15329 | 0.07158 | 0.46287 | 0.68774 | 59.650 |
| ABC | 人工蜂群 | 0.81573 | 0.48767 | 0.22588 | 1.52928 | 0.58850 | 0.21455 | 0.17249 | 0.97554 | 0.47444 | 0.26681 | 0.35941 | 1.10066 | 57.237 |
| BFO | 细菌觅食优化 | 0.70129 | 0.46155 | 0.11627 | 1.27911 | 0.41251 | 0.26623 | 0.26695 | 0.94569 | 0.42336 | 0.34491 | 0.50973 | 1.27800 | 55.516 |
| FSS | 鱼群搜索 | 0.48850 | 0.37769 | 0.11006 | 0.97625 | 0.07806 | 0.05013 | 0.08423 | 0.21242 | 0.00000 | 0.01084 | 0.18998 | 0.20082 | 20.109 |
| PSO | 粒子群优化 | 0.21339 | 0.12224 | 0.05966 | 0.39529 | 0.15345 | 0.10486 | 0.28099 | 0.53930 | 0.08028 | 0.02385 | 0.00000 | 0.10413 | 14.232 |
| RND | 随机 | 0.17559 | 0.14524 | 0.07011 | 0.39094 | 0.08623 | 0.04810 | 0.06094 | 0.19527 | 0.00000 | 0.00000 | 0.08904 | 0.08904 | 8.142 |
| GWO | 灰狼优化器 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.00000 | 0.18977 | 0.04119 | 0.01802 | 0.24898 | 1.000 |
到分析测试结果的时候了。 BFO 位于评级表的中间,在当前参与算法列表中的总体得分刚刚超过 55。 结果并不令人印象深刻,但也不差。 特别是,在具有 10 个变量的 Rastrigin 函数上获得了良好的结果。 在 50 和 1000 个变量的情况下,结果则明显更糟。 此外,该算法在 Forest 函数上表现不佳。 离散 Megacity 函数上相对良好的行为令人惊讶,因为算法中没有处理此类函数的机制。 此外,与其它算法相比,具有良好的可扩展性(测试采用 1000 个参数的 Megacity 进行)。
BFO 是一个具有广泛可能性的科学领域。 一般来说,可以对细菌觅食和动物觅食的许多方面进行建模,以提高优化性能。 对于 BFO 算法,控制参数的自动适应可能特别重要,因为有很多参数,并且可以提高性能,这是进行额外实验的原因。
BFO 具有许多优点,包括在初始化和参数选择期间对坐标初始值的敏感性低,可靠性好,逻辑简单,易于实现,并行化和全局搜索的可能性。 因而,BFO 算法可解决广泛的优化问题。 然而,BFO 也有许多缺点,包括收敛缓慢,在某些情况下无法超越局部最优,以及固定的步长。 BFO 是一种元启发式方法,这意味着它只是一个概念框架,可据其开发算法的各种修改版。 我在这里介绍的 BFO 版本只是众多可能性之一,应该被视为实验的起点,而非关于该主题的最后结语。
算法测试结果的直方图如下。
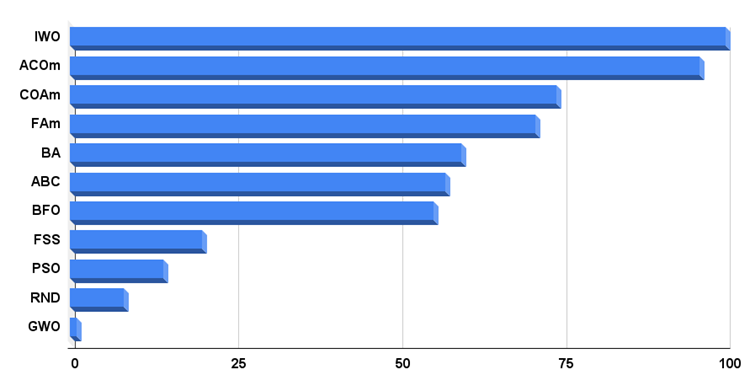
图例 3. 测试算法最终结果的直方图
关于细菌觅食优化(BFO)算法性质的结论:
优点:
1. 高速。
2. 逻辑简单。
3. 收敛贯穿所有迭代,尽管速度很慢。
缺点:
1. 收敛慢。
2. 没有退出局部极值的方法。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/12031
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 MQL5 酷宝书 — 宏观经济事件数据库
MQL5 酷宝书 — 宏观经济事件数据库
1- 这是参数的数量:
这是群体的大小:
3.估计的历元数:
我的代码都正确吗?
1.测试函数是二维的,例如:
指俄语中的 5 个测试函数,因此乘以 2 - 10 个优化参数25 - 50 个优化参数
500 - 1000 个优化参数
2.是
3.是的,没错,估计历元数的目的是使 FF 运行的总次数相同,而不取决于算法中种群规模的选择,也就是说,在不同算法中,不同种群规模参数下的算法测试是公平的。
好的,谢谢。
这一系列文章中的所有算法都是可对等的,其他的还没看吗?我觉得我可以用它,它很有用,只是要优化的函数比较复杂,它有动态的参数数,既有实数参数,也有整数参数,而且范围不同,你必须事后解决问题
我明白了,谢谢。
这一系列文章中的所有算法都是可对等的,其他的还没看吗?我觉得我可以用它,它很有用,只是被优化的函数更复杂,它的参数数量是动态的,既有实数参数,也有整数参数,而且范围不同,你必须事后解决问题。
干得漂亮👏