
Алгоритм голубых обезьян — Blue Monkey (BM) Algorithm
Содержание
Введение
Для поиска наиболее подходящего алгоритма оптимизации для дискретных задач торговых роботов рассмотрим еще один метод и его возможности. В самом сердце африканских джунглей обитают существа, чья жизнь, полная сложных взаимодействий и мудрой иерархии, стала источником вдохновения для создания одного из методов оптимизации. Речь идёт о голубых мартышках, или Cercopithecus mitis — эти маленькие, проворные обитатели древесных крон, чьё поведение, кажущееся хаотичным, на деле подчинено глубоким биологическим законам, породило идею для разработки алгоритма, названного в их честь — Blue Monkey.
Алгоритм был разработан M. Mahmood и B. Al-Khateeb и опубликован в 2019 г. в Periodicals of Engineering and Natural Sciences (PEN) 7(3):1054-1066 DOI:10.21533/pen.v7i3.621.
Эта сложная, но гармоничная экосистема нашла своё отражение в математической абстракции алгоритма Blue Monkey:
- Группы как Команды. Популяция агентов разделяется на независимые команды, каждая из которых имеет своего лидера, подобно доминантному самцу.
- Лидер – Воплощение Совершенства. Лучшая особь в каждой группе, обладающая наивысшей "приспособленностью" (fitness), олицетворяет собой доминантного самца — образец для подражания.
- Детёныши — Новое Поколение. Молодые особи, "детёныши", представляют собой новый виток развития, учащийся и готовый заменить своих старших, привнося свежие идеи и решения.
- Миграция — Обновление Системы. Процесс миграции воплощается в том, что лучшие "детёныши" могут заменить менее приспособленных "взрослых", обеспечивая постоянное обновление и повышение эффективности.
- Социальное Обучение — Путь к Лидеру. Движение "детёнышей" к лидеру группы, управляемое математическими формулами, имитирует процесс социального обучения, когда молодые учатся у опытных.
Реализация алгоритма
Представьте, что вы управляете исследовательской экспедицией в джунглях, которая ищет затерянный город. У вас есть 50 опытных исследователей (взрослые обезьяны) и 15 стажёров-студентов (детёныши — 30% от взрослых).
Организация работы:
- опытных исследователей делим на 5 команд по 10 человек;
- каждая команда исследует свой участок джунглей независимо;
- 5 команд = 5 разных зон поиска: команда А пойдет на север, команда Б отправится на юг, команда В ищет на востоке, команда Г исследует на западе, команда Д остается в центре.
Если затерянный город на севере, команда А найдёт его быстрее, а остальные постепенно подтянутся. Стажёры работают все вместе как учебная группа. Главный механизм 5 команд = 5 разных зон поиска. "Следуй за успешным". В каждой команде определяется лидер — тот, кто нашёл самое правильное направление, остальные корректируют свой маршрут в сторону лидера, но не идут прямо к нему! Сохраняют 70% своего направления + 30% поворачивают к лидеру. Не бросаем сразу свой маршрут (вдруг там тоже что-то есть), но постепенно смещаемся к успешным местам.
Обучение молодых: стажёры делают то же самое, но все следуют за одним лучшим стажёром. Находим худшего в каждой из команд и сравниваем с лучшими стажёрами, и если стажёр лучше — он получает постоянную работу, а неудачник увольняется. Стажёры приносят новые идеи — возможно, опытный исследователь застрял в плохом районе, а молодой случайно нашёл золотую жилу.
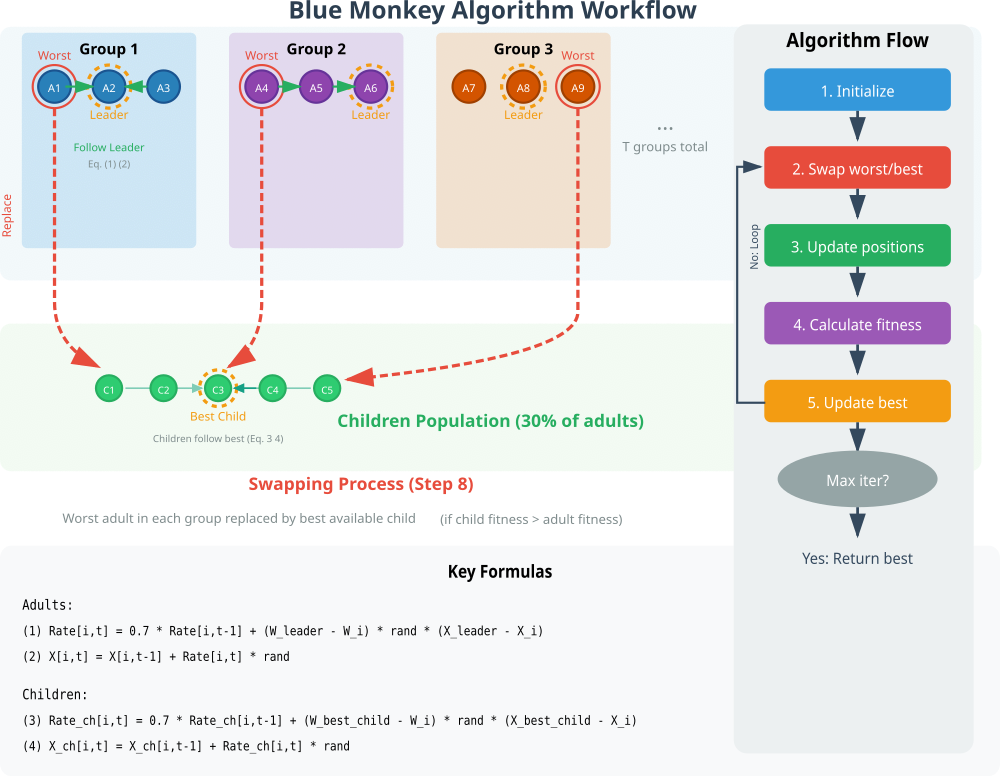
Рисунок 1. Схема работы алгоритма BM
На схеме отображена работа алгоритма BM с разделением логики на два независимых направления для взрослых особей и детенышей с основными формулами. Можем перейти к составлению псевдокода алгоритма BM.
Инициализация:
- Создать популяцию взрослых обезьян (размер N)
- Каждая обезьяна получает случайную позицию в пространстве поиска
- Инициализировать скорость движения нулем
- Присвоить начальный вес от 4 до 6
- Создать популяцию детёнышей (30% от размера взрослых)
- Каждый детёныш получает случайную позицию
- Инициализировать скорость движения нулем
- Присвоить начальный вес от 4 до 6
- Распределить взрослых по группам
- Разделить популяцию на T групп равномерно
- Обезьяна с индексом i попадает в группу (i модуль T)
- Вычислить начальный фитнес
- Оценить качество позиции каждого взрослого
- Оценить качество позиции каждого детёныша
Основной цикл (пока не достигнут критерий остановки):
- Обновить веса на основе фитнеса
- Найти минимальный и максимальный фитнес среди взрослых
- Нормализовать веса: вес = 4 + 2 × (фитнес - мин)/(макс - мин)
- Повторить для детёнышей
- Заменить худших на лучших (начиная со второй итерации)
- Для каждой группы взрослых:
- Найти обезьяну с худшим фитнесом в группе
- Взять следующего лучшего неиспользованного детёныша
- Если фитнес детёныша лучше фитнеса взрослого:
- Заменить взрослого на детёныша
- Создать нового детёныша на освободившееся место
- Для каждой группы взрослых:
- Обновить позиции взрослых обезьян
- Для каждой обезьяны в группе:
- Найти лидера группы (обезьяну с лучшим фитнесом)
- Обновить скорость: новая скорость = 0.7 × старая скорость + (вес лидера - личный вес) × случайное × (позиция лидера - личная позиция)
- Обновить позицию: новая позиция = старая позиция + скорость × случайное
- Ограничить позицию границами пространства поиска
- Для каждой обезьяны в группе:
- Обновить позиции детёнышей
- Найти лучшего детёныша среди всех
- Для каждого другого детёныша:
- Обновить скорость: новая скорость = 0.7 × старая скорость + (вес лучшего - личный вес) × случайное × (позиция лучшего - личная позиция)
- Обновить позицию: новая позиция = старая позиция + скорость × случайное
- Ограничить позицию границами
- Вычислить новый фитнес
- Оценить качество новых позиций всех обезьян
- Оценить качество новых позиций всех детёнышей
- Обновить глобальное лучшее решение
- Если найдено решение лучше текущего рекорда:
- Сохранить его как новый рекорд
- Увеличить счетчик итераций
- Если найдено решение лучше текущего рекорда:
- Проверить критерий остановки
- Если достигнуто максимальное число итераций ИЛИ
- Если достигнута требуемая точность:
- Выйти из цикла
- Иначе: вернуться к шагу 5
Завершение:
- Вернуть результат
- Вернуть лучшую найденную позицию
- Вернуть значение фитнеса в этой позиции
Теперь воплощаем псевдокод в реализацию. Напишем класс "C_AO_BM". Он является наследником класса "C_AO", представляющим собой базовый класс. Класс "C_AO_BM" наследует все публичные и защищенные поля класса "C_AO".
Публичные поля:
Конструктор "C_AO_BM" инициализирует базовые свойства алгоритма и устанавливает начальные параметры алгоритма: "popSize" (размер популяции), "numGroups" (количество групп), "childrenRatio" (доля детёнышей). Настраивает массив "params", который используется для хранения настраиваемых параметров алгоритма. Для каждого параметра указывается его имя и текущее значение. Устанавливает минимальное "minW" и максимальное "maxW" значения для весов, используемых в алгоритме.- SetParams() — метод для установки параметров алгоритма из массива "params". Он считывает значения "val" из "params" и преобразует их в соответствующие типы данных (int или double), присваивая их членам класса.
- Init() — метод инициализации подготавливает алгоритм к работе, используя входные диапазоны (rangeMinP, rangeMaxP, rangeStepP) и количество эпох (epochsP).
- Moving () — метод реализует основную логику перемещения или обновления особей в популяции согласно алгоритму.
- Revision () — метод используется для пересмотра или оценки текущего состояния популяции, возможного отбора и обновления.
- numGroups — количество групп, на которые разбивается популяция.
- childrenRatio — процент популяции, который будет представлен "детёнышами" (новыми особями).
- numChildren — количество "детёнышей" в популяции, рассчитываемое на основе "popSize" и "childrenRatio".
- minW, maxW — минимальные и максимальные значения для весов.
- Массивы для взрослых обезьян:
- monkeyRate — хранит "скорость" для каждой особи в популяции. Размер массива зависит от "popSize" и количества измерений (координат) в пространстве поиска.
- monkeyWeight — хранит "веса" (W) для каждой взрослой особи.
- groupId — массив, указывающий, к какой группе принадлежит каждая взрослая особь.
- Массивы для детёнышей хранят:
- childPos — позиции "детёнышей" в пространстве поиска.
- childRate — "скорость" для "детёнышей".
- childWeight — "веса" для "детёнышей".
- childFitness — значение приспособленности (fitness) для "детёнышей".
- Приватные методы:
- SwapWorstWithBest () — реализует шаг 8 алгоритма, который предполагает замену худшей особи в группе на лучшую.
- UpdatePositions () — реализует шаги 9-10 алгоритма, отвечающие за обновление позиций особей.
- UpdateWeights () — реализует шаг 2 алгоритма и общее обновление весов.
- FindGroupBest () — находит лучшую особь в указанной группе.
- FindGroupWorst () — находит худшую особь в указанной группе.
Алгоритм разделяет популяцию на группы, использует концепции "скорости" (rate) и "весов" (weight) для перемещения особей, а также включает механизмы создания "детёнышей" и обмена худшими особями на лучших в группах. Приватные члены предназначены для внутреннего управления состоянием алгоритма, а публичные члены предоставляют интерфейс для настройки и выполнения оптимизации.
//———————————————————————————————————————————————————————————————————— class C_AO_BM : public C_AO { public: //---------------------------------------------------------- ~C_AO_BM () { } C_AO_BM () { ao_name = "BM"; ao_desc = "Blue Monkey Algorithm"; ao_link = "https://www.mql5.com/ru/articles/19757"; popSize = 50; // размер популяции numGroups = 5; // количество групп T childrenRatio = 0.3; // процент детёнышей от популяции ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "numGroups"; params [1].val = numGroups; params [2].name = "childrenRatio"; params [2].val = childrenRatio; minW = 4.0; maxW = 6.0; } void SetParams () { popSize = (int)params [0].val; numGroups = (int)params [1].val; childrenRatio = params [2].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ int numGroups; // количество групп T double childrenRatio; // процент детёнышей private: //--------------------------------------------------------- int numChildren; // количество детёнышей double minW; double maxW; // Массивы для взрослых обезьян double monkeyRate []; // Rate - скорость изменения [popSize * coords] double monkeyWeight []; // W - веса обезьян int groupId []; // принадлежность к группе // Массивы для детёнышей double childPos []; // позиции детёнышей [numChildren * coords] double childRate []; // Rate для детёнышей double childWeight []; // W для детёнышей double childFitness []; // фитнес детёнышей void SwapWorstWithBest (); // Шаг 8 void UpdatePositions (); // Шаги 9-10 void UpdateWeights (); // Шаг 2 и обновление int FindGroupBest (int groupId); int FindGroupWorst (int groupId); }; //————————————————————————————————————————————————————————————————————
Функция "Init" выполняет следующие действия:
Стандартная инициализация. Сначала вызывается базовая функция инициализации "StandardInit" с переданными параметрами диапазонов (rangeMinP, rangeMaxP, rangeStepP). Если эта базовая инициализация завершается неудачно, функция "Init" также завершается, возвращая "false".
Корректировка параметров:
- Проверяется количество групп (numGroups).
- Рассчитывается количество "детёнышей" (numChildren) на основе размера популяции и доли детёнышей (childrenRatio).
- Изменяется размер массивов, предназначенных для хранения данных "взрослых" особей. Это включает "monkeyRate" (где скорость хранится для каждого измерения), "monkeyWeight" (вес для каждой особи) и "groupId" (принадлежность особи к группе).
- Изменяется размер массивов для "детёнышей", включая их позиции (childPos), скорости (childRate), веса (childWeight) и значения приспособленности (childFitness).
Инициализация скоростей. Массивы "monkeyRate" и "childRate" (которые используются для определения направления движения) инициализируются нулевыми значениями.
Инициализация весов: Веса (monkeyWeight и childWeight) для "взрослых" и "детёнышей" инициализируются случайными значениями в диапазоне от "minW" до "maxW", фактические веса будут пересчитаны после первого вычисления приспособленности.
Распределение по группам:
- Взрослые особи распределяются по группам (groupId) по модулю. То есть, первая особь попадает в группу 0, вторая в группу 1, ..., (numGroups) в группу numGroups -1, (numGroups + 1) снова в группу 0, и так далее.
- Все детёныши будут находиться изначально в одной команде.
Инициализация приспособленности детёнышей: Массив "childFitness" инициализируется минимально возможным значением. Это делается для того, чтобы любое реальное рассчитанное значение приспособленности было больше этого начального значения.
Функция возвращает "true", если инициализация прошла успешно. Таким образом, функция "Init" выполняет всю подготовительную работу: устанавливает необходимые размеры структур данных, задает начальные значения для скорости и весов, распределяет особей по группам и подготавливает их к первому циклу вычислений.
//———————————————————————————————————————————————————————————————————— bool C_AO_BM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Корректировка параметров if (numGroups < 1) numGroups = 1; if (numGroups > popSize) numGroups = popSize; numChildren = (int)(popSize * childrenRatio); if (numChildren < 1) numChildren = 1; // Инициализация массивов для взрослых ArrayResize (monkeyRate, popSize * coords); ArrayResize (monkeyWeight, popSize); ArrayResize (groupId, popSize); // Инициализация массивов для детёнышей ArrayResize (childPos, numChildren * coords); ArrayResize (childRate, numChildren * coords); ArrayResize (childWeight, numChildren); ArrayResize (childFitness, numChildren); // Шаг 2: Initialize Power Rate Rate and Weight W // Rate ∈ [0, 1], W ∈ [4,6] ArrayInitialize (monkeyRate, 0.0); ArrayInitialize (childRate, 0.0); // Веса будут обновлены после первого вычисления фитнеса for (int i = 0; i < popSize; i++) { monkeyWeight [i] = u.RNDfromCI (minW, maxW); } for (int i = 0; i < numChildren; i++) { childWeight [i] = u.RNDfromCI (minW, maxW); } // Шаг 3: Распределение по группам // Взрослые распределяются по T группам for (int i = 0; i < popSize; i++) { groupId [i] = i % numGroups; } // "while all children in one team" - все детёныши в одной команде изначально ArrayInitialize (childFitness, -DBL_MAX); return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" выполняет следующие действия: сначала проверяется флаг "revision" и если "revision" равно "false" (первый запуск):
Инициализация популяции взрослых (Шаг 1). Для каждой взрослой особи "i" от (0 до popSize - 1) и для каждого измерения "j" от (0 до coords - 1) позиция (a [i].c [j]) инициализируется случайным числом в заданном диапазоне (rangeMin [j], rangeMax [j]). Значение позиции затем корректируется с помощью функции "u.SeInDiSp", которая обеспечивает нахождение значения в заданных пределах и с учетом шага (rangeStep [j]).
Инициализация популяции детёнышей (Шаг 1). Для каждого детёныша "i" от (0 до numChildren - 1) и для каждого измерения "j" от (0 до coords - 1) позиция (childPos [i * coords + j]) инициализируется случайным числом в заданном диапазоне (rangeMin, rangeMax). Значение позиции также корректируется функцией "u.SeInDiSp".
Флаг "revision" устанавливается в "true", чтобы при следующих вызовах метода "Moving" выполнялась другая часть логики. Метод завершает выполнение. Если "revision" равно "true" (последующие запуски) происходит обновление позиций, вызывается метод "UpdatePositions ()". Этот метод отвечает за перемещение особей в соответствии с логикой алгоритма "синей обезьяны".
Таким образом, метод "Moving" служит двум основным целям:
- При первом вызове он полностью инициализирует позиции всех взрослой особей и детёнышей в пределах заданных диапазонов.
- При последующих вызовах он делегирует основную работу по перемещению особей согласно метода "UpdatePositions ()", который реализует ядро движения алгоритма.
//———————————————————————————————————————————————————————————————————— void C_AO_BM::Moving () { if (!revision) { // Шаг 1: Инициализация популяции взрослых for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { a [i].c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } // Шаг 1: Инициализация популяции детёнышей for (int i = 0; i < numChildren; i++) { for (int j = 0; j < coords; j++) { childPos [i * coords + j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); childPos [i * coords + j] = u.SeInDiSp (childPos [i * coords + j], rangeMin [j], rangeMax [j], rangeStep [j]); } } revision = true; return; } //------------------------------------------------------------------ UpdatePositions (); } //————————————————————————————————————————————————————————————————————
Метод "Revision" выполняет следующие действия:
Обновление весов. Сначала вызывается метод "UpdateWeights ()". Это означает, что веса каждого индивида пересчитываются на основе их текущих значений приспособленности.Обмен худшего с лучшим. Далее вызывается метод "SwapWorstWithBest ()". Этот метод находит индивида с наихудшим значением приспособленности и замещает его с индивидом, имеющим наилучшее значение приспособленности.
Обновление лучшей особи.Для взрослых особей происходит итерация по всем взрослым особям "i" (от 0 до popSize - 1) и если текущее значение приспособленности взрослой особи (a [i].f) больше, чем лучшее значение приспособленности, которое эта особь когда-либо достигала (a [i].fB), то значение приспособленности особи обновляется. Позиция лучшего достижения особи (a [i].cB) копируется из текущей позиции особи (a [i].c).
Аналогично, если текущее значение приспособленности взрослой особи (a [i].f) больше, чем общее лучшее значение приспособленности во всей популяции (fB), то общее лучшее значение приспособленности (fB) обновляется. Позиция общего лучшего решения (cB) копируется из текущей позиции особи (a [i].c).
Для детёнышей. Происходит итерация по всем детёнышам "i" (от 0 до numChildren - 1). Если приспособленность детёныша (childFitness [i]) больше, чем общее лучшее значение приспособленности (fB), то общее лучшее значение приспособленности (fB) обновляется. Позиция общего лучшего решения (cB) обновляется, копируя координаты детёныша (childPos).В целом, метод "Revision" предназначен для улучшения качества решений путём и отслеживания и сохранения наилучшего решения, найденного как для каждой отдельной особи (личный рекорд), так и для всей популяции в целом (глобальный рекорд), причём учитываются как взрослые особи, так и детёныши.
//———————————————————————————————————————————————————————————————————— void C_AO_BM::Revision () { // Обновляем веса на основе текущего фитнеса UpdateWeights (); // Шаг 8: Swapping SwapWorstWithBest (); // Шаг 12: Update Current Best for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, coords); } if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } // Проверка детёнышей для глобального лучшего for (int i = 0; i < numChildren; i++) { if (childFitness [i] > fB) { fB = childFitness [i]; for (int j = 0; j < coords; j++) { cB [j] = childPos [i * coords + j]; } } } } //————————————————————————————————————————————————————————————————————
Метод "UpdatePositions" класса "C_AO_BM" реализует основную логику движения особей в популяции, следуя определенным математическим уравнениям. Метод разделен на две части: обновление позиций взрослых особей (так называемых "синих обезьян") и обновление позиций детёнышей.
Обновление позиций взрослых особей (синих обезьян):
Метод проходит по каждой взрослой особи "i" (от 0 до popSize - 1). Поиск лидера группы: для каждой текущей особи определяется её группа (groupId [i]) и находится индекс лучшей особи в этой группе (bestIdx = FindGroupBest). Если текущая особь сама является лидером группы или лидер не найден, то переходим к следующей особи. Обновление по уравнениям 1 и 2 (для каждого измерения).
Обновление скорости (Уравнение 1):
- Определяются веса лидера группы "Wleader" и текущей особи "Wi".
- Извлекаются текущие позиции лидера "Xbest" и текущей особи "Xi" в данном измерении.
- Генерируется случайное число "rand1" от 0 до 1.
- Рассчитывается новая скорость "monkeyRate" для текущей особи. Она является комбинацией предыдущей скорости (с коэффициентом 0.9) и влияния разницы весов лидера и текущей особи, умноженного на случайное число и разницу между позициями лидера и текущей особи.
Обновление позиции (Уравнение 2):
Генерируется еще одно случайное число "rand2" от 0 до 1. Новая позиция особи рассчитывается путем добавления к текущей позиции произведения новой скорости "monkeyRate" и случайного числа "rand2". Полученная новая позиция принудительно ограничивается заданными диапазонами (u.SeInDiSp), чтобы она оставалась в пределах допустимой области поиска.
Обновление позиций детёнышей:
- Поиск лучшего детёныша: сначала метод просматривает всех детёнышей "i" от (0 до numChildren - 1), чтобы найти того, у кого наилучшая приспособленность (bestChildFitness) и, соответственно, его индекс (bestChildIdx).
- Обновление по уравнениям 3 и 4 (если лучший детёныш найден):
- Если лучший детёныш найден (bestChildIdx >= 0), метод проходит по всем остальным детёнышам "i" от (0 до numChildren - 1), за исключением самого лучшего.
- Обновление скорости детёныша (Уравнение 3):
- Аналогично взрослым особям, определяются веса лучшего детёныша "Wchleader" и текущего детёныша "Wchi".
- Извлекаются текущие позиции лучшего детёныша "Xchbest" и текущего детёныша "Xchi" в данном измерении.
- Генерируется случайное число "rand1" от 0 до 1.
- Рассчитывается новая скорость (childRate) для текущего детёныша по формуле, аналогичной Уравнению 1.
- Обновление позиции детёныша (Уравнение 4):
- Генерируется случайное число "rand2" от 0 до 1.
- Новая позиция детёныша рассчитывается путем добавления к текущей позиции произведения его новой скорости (childRate) и случайного числа "rand2".
- Ограничение позиции: полученная новая позиция детёныша также ограничивается заданными диапазонами.
Таким образом, метод "UpdatePositions" реализует:
- Модель поведения "синих обезьян": взрослые особи движутся, ориентируясь на лидера своей группы, при этом скорость движения зависит от разницы весов и разницы позиций.
- Модель поведения детёнышей: детёныши движутся, ориентируясь на самого лучшего детёныша, аналогичным образом.
- Поддержание особей в допустимой области поиска с помощью функции "SeInDiSp".
//———————————————————————————————————————————————————————————————————— void C_AO_BM::UpdatePositions () { // Шаг 9: Update position of blue monkeys by Equations 1 and 2 for (int i = 0; i < popSize; i++) { int bestIdx = FindGroupBest (groupId [i]); if (bestIdx < 0 || bestIdx == i) continue; for (int j = 0; j < coords; j++) { // Equation (1): Rate update double Wleader = monkeyWeight [bestIdx]; double Wi = monkeyWeight [i]; double Xbest = a [bestIdx].c [j]; double Xi = a [i].c [j]; double rand1 = u.RNDfromCI (0, 1); // Rate_{i,t} = (0.7*Rate) + (W_leader - W_i) * rand*(X_best-X_i) monkeyRate [i * coords + j] = 0.9 * monkeyRate [i * coords + j] + (Wleader - Wi) * rand1 * (Xbest - Xi); // Equation (2): Position update // X_{i,t} = X_i + Rate_{i,t} * rand double rand2 = u.RNDfromCI (0, 1); a [i].c [j] = a [i].c [j] + monkeyRate [i * coords + j] * rand2; // Ограничение в пределах диапазона a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } // Шаг 10: Update position of children by Equations 3 and 4 // Находим лучшего детёныша int bestChildIdx = -1; double bestChildFitness = -DBL_MAX; for (int i = 0; i < numChildren; i++) { if (childFitness [i] > bestChildFitness) { bestChildFitness = childFitness [i]; bestChildIdx = i; } } if (bestChildIdx >= 0) { for (int i = 0; i < numChildren; i++) { if (i == bestChildIdx) continue; for (int j = 0; j < coords; j++) { // Equation (3): Child rate update double Wchleader = childWeight [bestChildIdx]; double Wchi = childWeight [i]; double Xchbest = childPos [bestChildIdx * coords + j]; double Xchi = childPos [i * coords + j]; double rand1 = u.RNDfromCI (0, 1); childRate [i * coords + j] = 0.9 * childRate [i * coords + j] + (Wchleader - Wchi) * rand1 * (Xchbest - Xchi); // Equation (4): Child position update double rand2 = u.RNDfromCI (0, 1); childPos [i * coords + j] = childPos [i * coords + j] + childRate [i * coords + j] * rand2; childPos [i * coords + j] = u.SeInDiSp (childPos [i * coords + j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } } //————————————————————————————————————————————————————————————————————
Метод "SwapWorstWithBest" выполняет следующие действия:
Подготовка детёнышей. Создается массив "childIndices" для хранения индексов всех детёнышей. Этот массив заполняется индексами от 0 до общего числа детёнышей. Затем происходит сортировка индексов детёнышей по убыванию их значения приспособленности (childFitness). Это делается с помощью простого алгоритма пузырьковой сортировки. В результате "childIndices [0]" будет содержать индекс лучшего детёныша, "childIndices [1]" – индекс второго лучшего, и так далее. Создается булевый массив "childUsed" для отслеживания того, был ли каждый детёныш использован для замены.
Итерация по группам взрослых особей. Метод проходит по каждой группе взрослых особей (от g = 0 до numGroups - 1). Для каждой группы, если все детёныши уже были использованы, дальнейшая обработка прекращается. Внутри каждой группы находится худшая взрослая особь (worstAdultIdx). Выбирается лучший доступный на данный момент детёныш (используя отсортированный массив "childIndices" и счетчик "childIndex"). Проверяется, лучше ли приспособленность выбранного детёныша (childFitness [currentChildIdx]) по сравнению с приспособленностью худшей взрослой особи в группе (a [worstAdultIdx].f).
- Замена (если лучше):
- Если детский лучше:
- Позиция и скорость худшей взрослой особи заменяются позицией и скоростью выбранного детёныша.
- Значение приспособленности взрослой особи обновляется до значения приспособленности детёныша.
- Вес взрослой особи обновляется до веса детёныша.
- Детёныш помечается как использованный (childUsed[currentChildIdx] = true), и счетчик "childIndex" увеличивается для перехода к следующему лучшему детёнышу.
- Если детский лучше:
- Прекращение замены (если хуже):
- Если даже лучший доступный детёныш не лучше, чем худшая взрослая особь в текущей группе, то дальнейшие попытки замены в этой и последующих группах прекращаются. Это связано с тем, что детёныши отсортированы по приспособленности, и если худший из лучших детёнышей не превосходит худшую особь, то и последующие детёныши не дадут выигрыша.
Таким образом, метод "SwapWorstWithBest" выполняет следующую роль: он активно использует лучших детёнышей для замены худших взрослых особей внутри их групп, если это приводит к улучшению, тем самым перенося лучшие из молодых решений в более "взрослые" слои популяции. Детёныши, которые были использованы для замены, затем "перерождаются" с новыми случайными параметрами.
//———————————————————————————————————————————————————————————————————— void C_AO_BM::SwapWorstWithBest () { // Шаг 8: Swapping the worst fitness in each group by the best fitness in children group // Создаем массив индексов детёнышей и сортируем по фитнесу int childIndices []; ArrayResize (childIndices, numChildren); for (int i = 0; i < numChildren; i++) { childIndices [i] = i; } // Сортируем индексы детёнышей по убыванию фитнеса for (int i = 0; i < numChildren - 1; i++) { for (int j = 0; j < numChildren - i - 1; j++) { if (childFitness [childIndices [j]] < childFitness [childIndices [j + 1]]) { int temp = childIndices [j]; childIndices [j] = childIndices [j + 1]; childIndices [j + 1] = temp; } } } // Для отслеживания использованных детёнышей bool childUsed []; ArrayResize (childUsed, numChildren); ArrayInitialize (childUsed, false); // Для каждой группы пытаемся заменить худшего int childIndex = 0; for (int g = 0; g < numGroups; g++) { if (childIndex >= numChildren) break; // Находим худшего в группе int worstAdultIdx = FindGroupWorst (g); if (worstAdultIdx < 0) continue; // Используем лучшего доступного детёныша int currentChildIdx = childIndices [childIndex]; // Проверяем, лучше ли детёныш if (childFitness [currentChildIdx] > a [worstAdultIdx].f) { // Выполняем замену for (int j = 0; j < coords; j++) { a [worstAdultIdx].c [j] = childPos [currentChildIdx * coords + j]; monkeyRate [worstAdultIdx * coords + j] = childRate [currentChildIdx * coords + j]; } a [worstAdultIdx].f = childFitness [currentChildIdx]; monkeyWeight [worstAdultIdx] = childWeight [currentChildIdx]; childUsed [currentChildIdx] = true; childIndex++; } else { // Если лучший детёныш не лучше худшего взрослого, // дальше нет смысла проверять (они отсортированы) break; } } // Генерируем новых детёнышей на место использованных for (int i = 0; i < numChildren; i++) { if (childUsed [i]) { for (int j = 0; j < coords; j++) { childPos [i * coords + j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); childPos [i * coords + j] = u.SeInDiSp (childPos [i * coords + j], rangeMin [j], rangeMax [j], rangeStep [j]); childRate [i * coords + j] = 0.0; } childFitness [i] = -DBL_MAX; childWeight [i] = u.RNDfromCI (minW, maxW); // Новый вес согласно начальным условиям } } } //————————————————————————————————————————————————————————————————————
Функция "UpdateWeights" отвечает за корректировку весов для двух групп сущностей: "обезьян" (родительских особей) и "детёнышей". В основу корректировки весов заложен принцип нормализации и масштабирования на основе приспособленности (fitness) каждой сущности.
Определение диапазона приспособленности. Сначала функция находит минимальное (minFit) и максимальное (maxFit) значения приспособленности среди всех "обезьян" в популяции.
Обработка случая с одинаковой приспособленностью. Если разница между максимальной и минимальной приспособленностью очень мала (меньше, чем 1e-10, что фактически означает, что все приспособленности примерно одинаковы), то всем "обезьянам" присваивается фиксированный вес, равный 5.0 (среднее значение из желаемого диапазона).
Нормализация и масштабирование весов "обезьян". Если диапазон приспособленности достаточен (больше 1e-10), то для каждой "обезьяны" происходит следующее:
- Ее приспособленность (a [i].f) нормализуется в диапазон [0, 1]. Это делается путем вычитания минимальной приспособленности (minFit) и деления на разницу между максимальной и минимальной приспособленностью (maxFit - minFit).
- Полученное нормализованное значение затем масштабируется для получения конечного веса в диапазоне [4, 6]. Это достигается умножением нормализованного значения на 2.0 и прибавлением минимального веса (minW). Таким образом, особи с самой низкой приспособленностью получают вес, близкий к 4.0, а особи с самой высокой приспособленностью — вес, близкий к 6.0.
Обработка весов "детёнышей". После обработки "обезьян", процесс повторяется для "детёнышей". Сначала определяется минимальная (minChildFit) и максимальная (maxChildFit) приспособленность среди всех "детёнышей". При этом игнорируются "детёныши", у которых приспособленность не была инициализирована (предполагается, что неинициализированная приспособленность имеет очень низкое значение, близкое к -DBL_MAX). Аналогично "обезьянам":
- если разница между максимальной и минимальной приспособленностью "детёнышей" мала, всем инициализированным "детёнышам" присваивается вес 5.0;
- если диапазон приспособленности "детёнышей" достаточен, их приспособленность нормализуется в диапазон [0, 1] и затем масштабируется в диапазон [4, 6] аналогично "обезьянам".
В целом, функция "UpdateWeights" преобразует значения приспособленности особей (и "обезьян", и "детёнышей") в веса, которые варьируются от 4 до 6. Это делается для того, чтобы подчеркнуть или уменьшить влияние особей с разной степенью приспособленности на последующие этапы алгоритма. Особи с более высокой приспособленностью получают более высокий вес, что может свидетельствовать об их большей важности.
//———————————————————————————————————————————————————————————————————— void C_AO_BM::UpdateWeights () { double minFit = DBL_MAX, maxFit = -DBL_MAX; for (int i = 0; i < popSize; i++) { if (a [i].f > maxFit) maxFit = a [i].f; if (a [i].f < minFit) minFit = a [i].f; } if (maxFit - minFit > 1e-10) { for (int i = 0; i < popSize; i++) { // Нормализуем в [0,1] и масштабируем в [4,6] double normalized = (a [i].f - minFit) / (maxFit - minFit); monkeyWeight [i] = minW + normalized * 2.0; // Получаем значение в [4,6] } } else { for (int i = 0; i < popSize; i++) { monkeyWeight [i] = 5.0; // Среднее значение } } // Обновление весов детёнышей double minChildFit = DBL_MAX, maxChildFit = -DBL_MAX; for (int i = 0; i < numChildren; i++) { if (childFitness [i] > -DBL_MAX + 1) // Проверка на инициализацию { if (childFitness [i] > maxChildFit) maxChildFit = childFitness [i]; if (childFitness [i] < minChildFit) minChildFit = childFitness [i]; } } if (maxChildFit - minChildFit > 1e-10) { for (int i = 0; i < numChildren; i++) { if (childFitness [i] > -DBL_MAX + 1) { double normalized = (childFitness [i] - minChildFit) / (maxChildFit - minChildFit); childWeight [i] = minW + normalized * 2.0; // В диапазоне [4,6] } } } else { for (int i = 0; i < numChildren; i++) { if (childFitness [i] > -DBL_MAX + 1) { childWeight [i] = 5.0; } } } } //————————————————————————————————————————————————————————————————————
Функция "FindGroupBest" предназначена для поиска лучшей особи в пределах определенной группы. Функция проходит по каждой особи в общей популяции, используя цикл (от 0 до popSize - 1).
- bestFitness обновляется до значения приспособленности текущей особи.
- bestIdx обновляется до индекса текущей особи "i".
После завершения полного прохода по популяции, функция возвращает значение "bestIdx". Это будет индекс особи с наивысшей приспособленностью в указанной группе. Если группа пуста, или в ней нет особей с приспособленностью, превышающей начальное минимальное значение, функция вернет -1.
Таким образом, функция "FindGroupBest" является вспомогательным инструментом для определения лидера или наилучшего решения (особи) в рамках конкретной подгруппы внутри популяции.
//———————————————————————————————————————————————————————————————————— int C_AO_BM::FindGroupBest (int grpId) { int bestIdx = -1; double bestFitness = -DBL_MAX; for (int i = 0; i < popSize; i++) { if (groupId [i] == grpId && a [i].f > bestFitness) { bestFitness = a [i].f; bestIdx = i; } } return bestIdx; } //————————————————————————————————————————————————————————————————————
Функция "FindGroupWorst" проходит по каждой особи, начиная с индекса 0 и заканчивая последней особью в популяции (popSize - 1).
Проверка принадлежности к группе и сравнение приспособленности. Для каждой особи в цикле сначала проверяется, принадлежит ли она к целевой группе, заданной параметром "grpId". Если особь принадлежит к интересующей нас группе, то выполняется сравнение ее значения приспособленности (a [i].f) с текущим наихудшим значением (worstFitness). Если приспособленность текущей особи меньше, чем текущее наихудшее значение (worstFitness), это означает, что мы нашли новую, ещё более плохую особь. В таком случае:
- worstFitness обновляется до значения приспособленности этой новой, более плохой особи;
- worstIdx обновляется, чтобы хранить индекс этой новой, более плохой особи "i".
//———————————————————————————————————————————————————————————————————— int C_AO_BM::FindGroupWorst (int grpId) { int worstIdx = -1; double worstFitness = DBL_MAX; for (int i = 0; i < popSize; i++) { if (groupId [i] == grpId && a [i].f < worstFitness) { worstFitness = a [i].f; worstIdx = i; } } return worstIdx; } //————————————————————————————————————————————————————————————————————
Результаты тестов
Посмотрим на результаты, к сожалению, этого недостаточно, чтобы попасть в турнирную таблицу.BM|Blue Monkey Algorithm|50.0|3.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.6730156841791012
25 Hilly's; Func runs: 10000; result: 0.3811383925125479
500 Hilly's; Func runs: 10000; result: 0.26883473381494066
=============================
5 Forest's; Func runs: 10000; result: 0.6116553050534701
25 Forest's; Func runs: 10000; result: 0.3051920014986885
500 Forest's; Func runs: 10000; result: 0.18691769556662757
=============================
5 Megacity's; Func runs: 10000; result: 0.4384615384615385
25 Megacity's; Func runs: 10000; result: 0.19353846153846152
500 Megacity's; Func runs: 10000; result: 0.1037384615384623
=============================
All score: 3.16249 (35.14%)
На визуализации очень хорошо прослеживается разделение на группы, области концентрации особей.

BM на тестовой функции Hilly

BM на тестовой функции Forest

BM на тестовой функции Megacity
В рейтинговой таблице алгоритм BM представлен ознакомительно.
| AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | |||||||
| DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| BM | blue_monkey _algorithm | 0,67301 | 0,38113 | 0,26883 | 1,32297 | 0,61165 | 0,30519 | 0,18691 | 1,10375 | 0,43846 | 0,19354 | 0,10373 | 0,73573 | 3,162 | 35,14 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 |
Выводы
Алгоритм продемонстрировал работоспособность на тестовых функциях, однако не показал конкурентоспособных результатов для включения в рейтинговую таблицу. Результаты указывают на необходимость дальнейшей оптимизации и доработки ключевых механизмов. Групповая структура обеспечивает параллельное исследование пространства поиска, а механизм смены поколений вносит элемент обновления в популяцию, однако скорость сходимости к оптимальному решению ниже ожидаемой.
Алгоритм Blue Monkey представляет интересный подход к решению оптимизационных задач, основанный на моделировании природных процессов. Несмотря на текущие ограничения производительности, концепция имеет потенциал для развития. Текущая версия может быть рекомендована для образовательных целей и как основа для дальнейших исследований в области метаэвристических алгоритмов оптимизации.
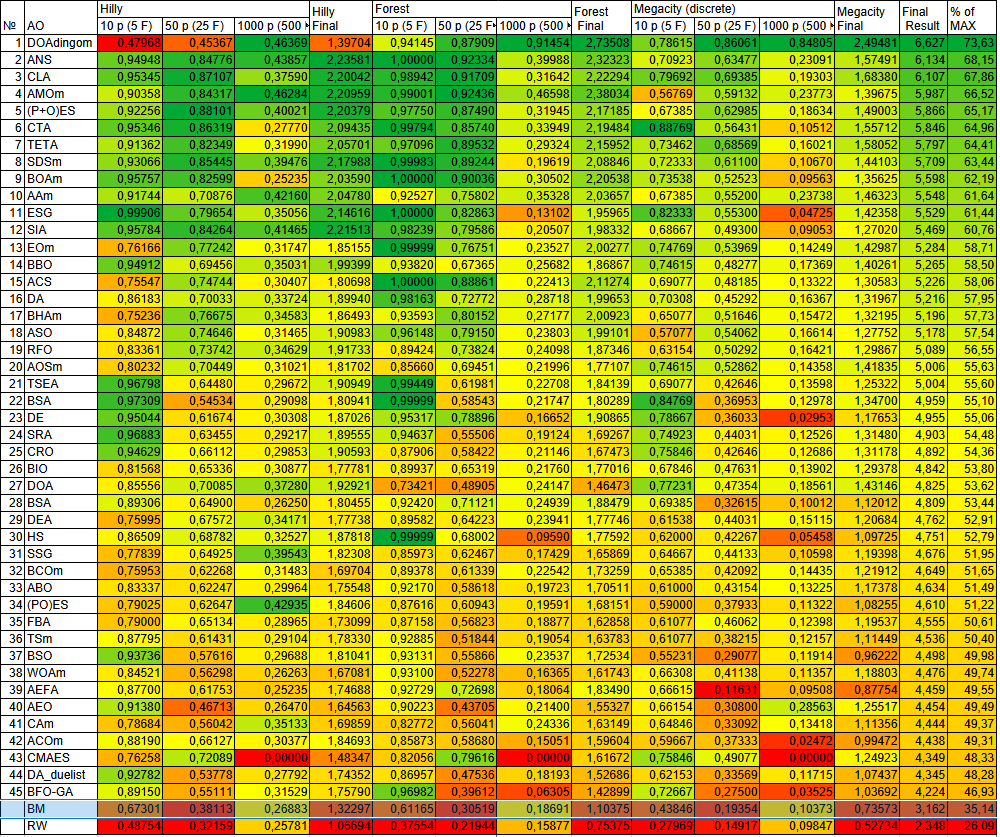
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
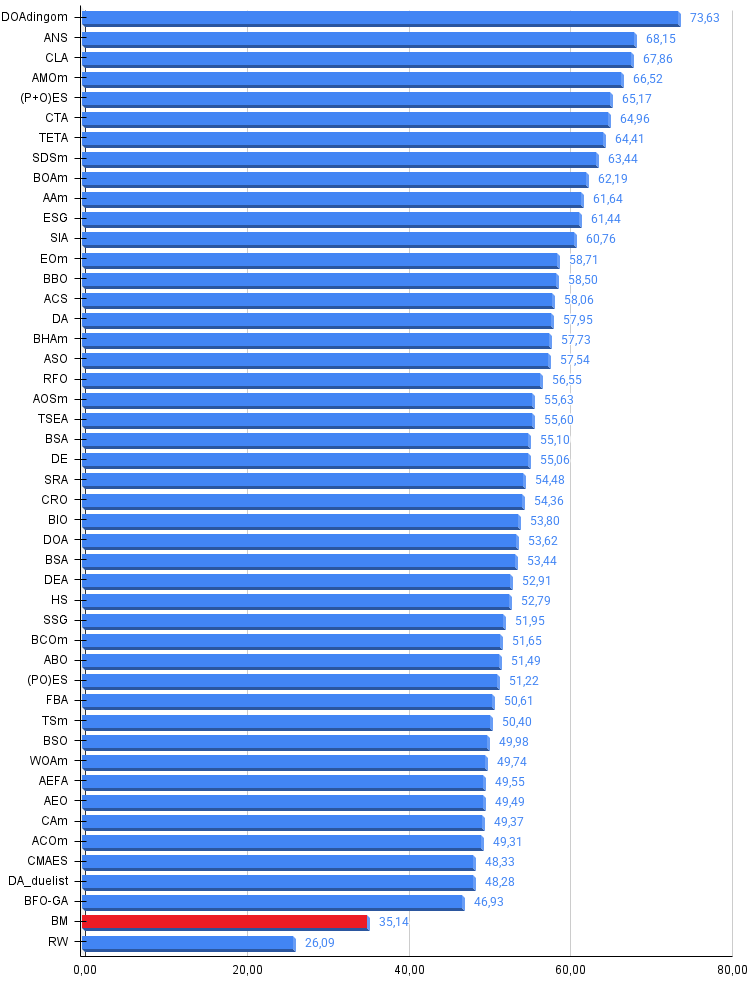
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма BM:
Плюсы:
- Небольшое количество внешних параметров.
Минусы:
- Низкая эффективность на задачах, особенно на дискретных функциях.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_BM.mq5 | Скрипт | Испытательный стенд для BM |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Генеративно-состязательные сети (GAN) для синтетических данных в сфере финансового моделирования (Часть 2): Создание синтетического символа для тестирования
Генеративно-состязательные сети (GAN) для синтетических данных в сфере финансового моделирования (Часть 2): Создание синтетического символа для тестирования
 Автоматизация торговых стратегий на MQL5 (Часть 10): Разработка стратегии Trend Flat Momentum
Автоматизация торговых стратегий на MQL5 (Часть 10): Разработка стратегии Trend Flat Momentum
 Разрабатываем менеджер терминалов (Часть 1): Постановка задачи
Разрабатываем менеджер терминалов (Часть 1): Постановка задачи
 От начального до среднего уровня: Индикатор (I)
От начального до среднего уровня: Индикатор (I)
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования