
Улучшенная оптимизация сталкивающихся тел — Enhanced Colliding Bodies Optimization (ECBO)
Содержание
Введение
На протяжении нескольких статей мы рассматривали алгоритмы оптимизации, которые не могли попасть в нашу рейтинговую таблицу из-за слабых поисковых качеств. В данной статье разберем метод, который подает большие надежды на изменение такого тренда.
Colliding Bodies Optimization (CBO) — это метаэвристический алгоритм оптимизации, разработанный Кавехом и Махдави в 2014 году. Алгоритм черпает вдохновение из физики одномерных столкновений тел, где каждое потенциальное решение задачи оптимизации представляется как физическое тело, обладающее массой и скоростью. Подобно тому, как в реальном мире при столкновении двух объектов происходит обмен импульсом и энергией, в алгоритме CBO кандидаты-решения сталкиваются друг с другом, обмениваясь информацией о своих позициях в пространстве поиска и тем самым направляя поиск к оптимуму.
Физическая метафора алгоритма основана на хорошо известных законах сохранения импульса и энергии. Представим два бильярдных шара: когда движущийся шар ударяет в неподвижный, оба шара после столкновения приобретают новые скорости, зависящие от их масс и начальных скоростей. При этом более тяжёлый шар сложнее сдвинуть с места, а лёгкий шар получает больший импульс. Именно эта интуиция лежит в основе CBO — хорошие решения с высоким значением целевой функции получают большую массу и оказывают большее влияние на направление поиска, притягивая к себе плохие решения.
Реализация алгоритма
Работа алгоритма начинается с инициализации популяции из "n" тел, где "n" должно быть чётным числом. Начальная позиция каждого тела в j-мерном пространстве поиска задаётся случайным образом:
Xij = Xj,min + rand * (Xj,max - Xj,min); где Xij — j-я координата i-го тела, Xj,min и Xj,max — границы пространства поиска по j-й координате, а rand — случайное число, равномерно распределённое в интервале [0, 1].
После вычисления значения целевой функции "Jk" для каждого тела определяется его масса. В алгоритме CBO масса тела обратно пропорциональна значению целевой функции (для задачи минимизации), что означает: чем лучше решение, тем больше его масса:
Mk = (1 / Jk) / sum_{i=1..n} (1 / Ji), k = 1, …, n
Такая нормализация гарантирует, что сумма всех масс равна единице, а относительные массы отражают относительное качество решений.
Рассмотрим работу алгоритма на конкретном примере. Допустим, мы ищем минимум функции на отрезке от 0 до 10, и у нас есть популяция из шести тел с позициями 2, 4, 5, 6, 7 и 9. После вычисления целевой функции для каждой позиции алгоритм сортирует тела по качеству решения. Предположим, что после сортировки порядок стал следующим: 5, 6, 4, 7, 2, 9 — где позиция 5 даёт лучшее значение функции, а позиция 9 — худшее. Теперь популяция делится пополам: первые три тела (5, 6, 4) становятся стационарными объектами, а оставшиеся три (7, 2, 9) — движущимися объектами. Стационарные объекты представляют лучшую половину популяции и остаются неподвижными до столкновения, в то время как движущиеся объекты из худшей половины устремляются к своим стационарным парам.
Парование происходит по принципу соответствия рангов: лучший движущийся объект (позиция 7, четвёртый по качеству) сталкивается с лучшим стационарным (позиция 5, первый по качеству), второй движущийся (позиция 2) — со вторым стационарным (позиция 6), и третий движущийся (позиция 9) — с третьим стационарным (позиция 4). Такое связывание в пары обеспечивает, что худшие решения направляются к лучшим, а не к случайным точкам пространства.
Скорости тел до столкновения определяются следующим образом. Стационарные тела неподвижны:
Vi = 0, i = 1, …, n/2
Скорость движущегося тела направлена к его стационарной паре и равна разности их позиций:
Vi = Xi-(n/2) - Xi, i = n/2 + 1, …, n
В нашем примере для пары (5, 7) скорость движущегося тела равна V = 5 - 7 = -2, что означает движение влево по числовой оси в направлении стационарного партнёра.
После столкновения скорости обоих тел пересчитываются по формулам, основанным на законах сохранения импульса. Для стационарных тел новая скорость вычисляется как:
V'i = (Mi+(n/2) + epsilon * Mi+(n/2)) * Vi+(n/2) / (Mi + Mi+(n/2)), i = 1, …, n/2
Для движущихся тел формула имеет вид:
V'i = (Mi - epsilon * Mi-(n/2)) * Vi / (Mi + Mi-(n/2)), i = n/2 + 1, …, n
где epsilon — коэффициент восстановления, определяющий характер столкновения.
Коэффициент восстановления — это параметр, заимствованный из физики столкновений, определяющий, какая доля кинетической энергии сохраняется после удара. В классической механике он определяется как отношение относительных скоростей тел после и до столкновения:
epsilon = |V'i+1 - V'i| / |Vi+1 - Vi|
В алгоритме CBO этот коэффициент играет ключевую роль в балансировке между исследованием пространства поиска и эксплуатацией найденных решений. Значение коэффициента линейно уменьшается от единицы до нуля на протяжении оптимизации:
epsilon = 1 - iter / iter_max
В начале оптимизации коэффициент восстановления равен единице, что соответствует абсолютно упругому удару с полным сохранением энергии — тела разлетаются далеко, обеспечивая широкое исследование пространства. По мере продвижения оптимизации коэффициент стремится к нулю, что соответствует абсолютно неупругому удару — тела слипаются, концентрируясь вокруг найденных хороших решений и производя тонкую настройку.
После вычисления новых скоростей определяются новые позиции тел. Здесь проявляется важная особенность алгоритма. Стационарные тела обновляют свою позицию относительно текущего положения:
Xinew = Xi + rand * V'i, i = 1, …, n/2
Движущиеся тела обновляют позицию не относительно себя, а относительно своего стационарного партнёра по столкновению:
Xinew = Xi-(n/2) + rand * V'i, i = n/2 + 1, …, n;
где rand — случайный вектор с компонентами, равномерно распределёнными в интервале [-1, 1]. Это ключевой механизм, обеспечивающий притяжение худших решений к лучшим: движущееся тело фактически прыгает в окрестность стационарного тела, а не просто сдвигается в его направлении.
Продолжим наш численный пример. Пусть масса тела в позиции 5 равна 0.3, а масса тела в позиции 7 равна 0.1 (меньше, потому что решение хуже). Коэффициент восстановления на текущей итерации равен 0.8. Скорость движущегося тела до столкновения: V = 5 - 7 = -2. После столкновения стационарное тело в позиции 5 получает скорость:
Vstat' = (0.1 + 0.8 * 0.1) * (-2) / (0.3 + 0.1) = (0.18 * -2) / 0.4 = -0.9.
Движущееся тело получает скорость:
Vmov' = (0.1 - 0.8 * 0.3) * (-2) / (0.3 + 0.1) = (-0.14 * -2) / 0.4 = 0.7.
Затем генерируются случайные числа из [-1, 1], допустим 0.6 и -0.4. Новая позиция стационарного тела:
Xstatnew = 5 + 0.6 * (-0.9) = 4.46.
Новая позиция движущегося тела вычисляется относительно стационарного партнёра:
Xmovnew = 5 + (-0.4) * 0.7 = 4.72.
Как видим, оба тела теперь находятся вблизи позиции 5, которая соответствовала лучшему решению.
Enhanced CBO (ECBO) представляет собой улучшенную версию базового алгоритма, включающую два дополнительных механизма: память столкновений и кроссовер. Память столкновений (Colliding MeMory, CM) — это архив фиксированного размера, хранящий лучшие решения, найденные за всё время работы алгоритма. Перед каждой итерацией худшие решения в текущей популяции заменяются решениями из этого архива. Такой механизм элитизма гарантирует, что качество лучшего решения никогда не ухудшается от итерации к итерации, и предотвращает потерю ценной информации о перспективных областях пространства поиска.
Представим, что на десятой итерации алгоритм нашёл очень хорошее решение в позиции 3.7, но на последующих итерациях случайные возмущения увели популяцию в другую область. Без памяти столкновений это решение могло бы быть утеряно. С памятью столкновений позиция 3.7 сохраняется в архиве и на каждой итерации возвращается в популяцию, замещая худшее текущее решение. Это обеспечивает постоянное присутствие лучших найденных точек в популяции и позволяет алгоритму продолжать исследование их окрестностей.
Механизм кроссовера в ECBO добавляет элемент случайной диверсификации. После обновления позиций для каждого тела выполняется следующая проверка:
Xij = Xj,min + rand * (Xj,max - Xj,min), если RANi < PRO; иначе Xij;
где Xij — случайно выбранная j-я координата i-го тела, PRO — вероятность кроссовера, задаваемая пользователем в диапазоне [0, 1], а RANi — случайное число, генерируемое для каждого тела.
Этот простой механизм помогает алгоритму избегать преждевременной сходимости и застревания в локальных оптимумах, периодически выбрасывая отдельные решения в неисследованные области пространства. Вероятность кроссовера обычно устанавливается небольшой, порядка 0.1–0.3, чтобы не нарушать основную логику алгоритма, но обеспечивать достаточную диверсификацию.
Одним из главных преимуществ CBO и ECBO является минимальное количество настраиваемых параметров. Базовый CBO вообще не требует настройки внутренних параметров — необходимо задать лишь размер популяции, который должен быть чётным числом. Коэффициент восстановления вычисляется автоматически на основе номера текущей итерации. ECBO добавляет два опциональных параметра: размер памяти столкновений и вероятность кроссовера, но оба имеют разумные значения по умолчанию (один элемент памяти и нулевая вероятность кроссовера превращают ECBO в базовый CBO с элитизмом). Такая простота выгодно отличает алгоритм от многих других метаэвристик, требующих тщательной настройки множества гиперпараметров.
Алгоритм демонстрирует естественный баланс между глобальным исследованием и локальной эксплуатацией благодаря адаптивному коэффициенту восстановления. На ранних итерациях, когда "epsilon" близок к единице, тела после столкновений разлетаются на большие расстояния, эффективно исследуя пространство поиска. По мере приближения к концу оптимизации "epsilon" стремится к нулю, и тела начинают концентрироваться вокруг найденных хороших решений, производя их локальное уточнение. Этот механизм не требует никакой настройки и работает автоматически для любой задачи.
Вычислительная сложность одной итерации CBO определяется преимущественно сортировкой популяции, требующей O(n log n) операций, где n — размер популяции. Остальные операции — вычисление масс, скоростей и новых позиций — выполняются за линейное время O(n). Это делает алгоритм вычислительно эффективным и применимым к задачам с дорогостоящими вычислениями целевой функции, где основные затраты приходятся на оценку качества решений, а не на внутреннюю логику оптимизатора. Изобразим на рисунке принцип работы алгоритм CBO.
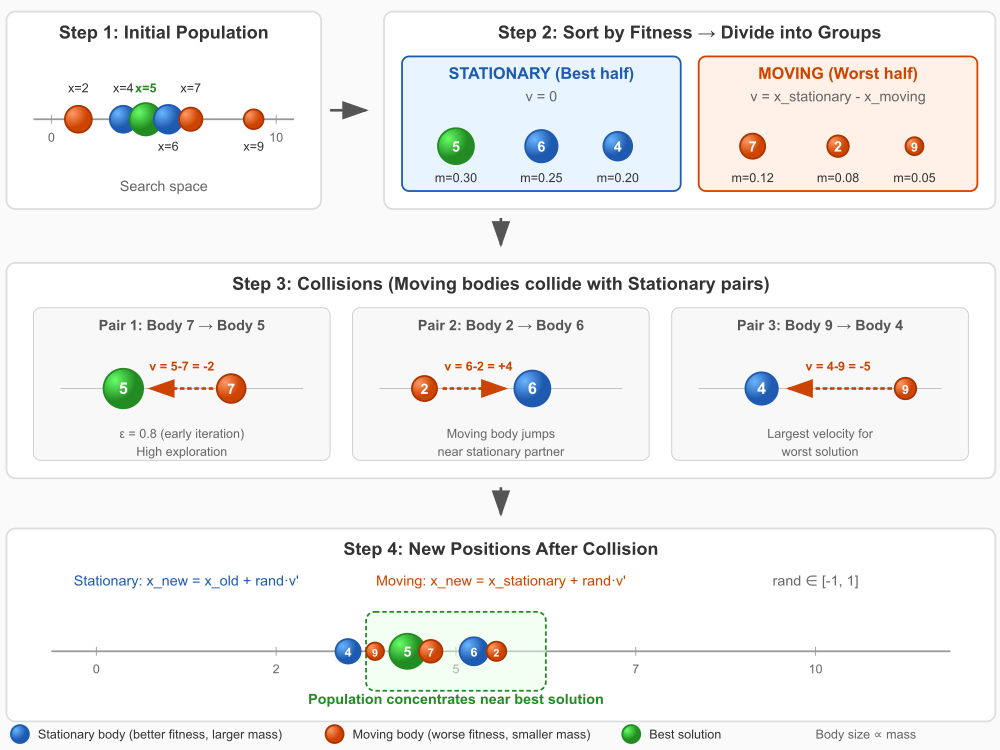
Рисунок 1. Иллюстрация работы алгоритма CBO
Иллюстрация показывает четыре основных этапа работы CBO:
- Step 1 — начальная популяция случайно распределена в пространстве поиска.
- Step 2 — после вычисления фитнеса тела сортируются и делятся на две группы: стационарные (лучшая половина, синие) и движущиеся (худшая половина, оранжевые). Размер тела пропорционален его массе.
- Step 3 — показаны три пары столкновений. Движущиеся тела направлены к своим стационарным партнёрам, скорость равна разности позиций.
- Step 4 — после столкновений вся популяция концентрируется вокруг лучшего решения (зелёная зона). Ключевой момент: движущиеся тела прыгают к позиции стационарного партнёра, а не просто сдвигаются.
Напишем псевдокод алгоритма ECBO (Enhanced Colliding Bodies Optimization) и будем дальше работать с ним, потому что он обещает более продвинутый подход к оптимизации.
-
Задать параметры алгоритма: размер популяции — n, размерность — d, размер памяти — CMsize, вероятность кроссовера — PRO, число итераций — maxIter.
-
Для каждого тела i от 1 до n: для каждой координаты j от 1 до d присвоить случайное значение в пределах границ поиска.
-
Для каждого элемента памяти столкновений m от 1 до CMsize: установить фитнес равным минус бесконечности.
-
Установить глобальный лучший фитнес равным минус бесконечности.
-
Для каждого тела i от 1 до n: вычислить фитнес; если он лучше глобального лучшего, обновить глобальное лучшее решение.
-
Для каждой итерации iter от 1 до maxIter выполнять шаги 7–22.
-
Для каждого тела i от 1 до n: найти худший элемент в памяти столкновений; если фитнес тела лучше, заменить худший элемент памяти текущим телом.
-
Для каждого элемента памяти m от 1 до CMsize: найти худшее тело в популяции; если элемент памяти лучше, заменить худшее тело элементом памяти.
-
Отсортировать популяцию по убыванию фитнеса.
-
Найти минимальный фитнес в популяции.
-
Если минимальный фитнес неположителен, вычислить сдвиг как модуль минимума плюс малая константа; иначе сдвиг равен нулю.
-
Вычислить сумму смещённых фитнесов всех тел.
-
Для каждого тела i от 1 до n: вычислить массу как отношение смещённого фитнеса к сумме.
-
Для каждого тела i от 1 до n: сохранить текущую позицию как старую позицию.
-
Вычислить коэффициент восстановления как единица минус iter делить на maxIter.
-
Для каждого тела i от 1 до n выполнять шаги 17–21.
-
Если i меньше или равно n/2: определить индекс движущегося партнёра как i плюс n/2; вычислить скорость до столкновения — как старая позиция текущего тела минус старая позиция партнёра; вычислить скорость после столкновения по формуле для стационарных тел; вычислить новую позицию — как старая позиция плюс случайное число из минус единицы до единицы умножить на скорость после столкновения.
-
Если i больше n/2: определить индекс стационарного партнёра как i минус n/2; вычислить скорость до столкновения — как старая позиция партнёра минус старая позиция текущего тела; вычислить скорость после столкновения по формуле для движущихся тел; вычислить новую позицию — как старая позиция стационарного партнёра плюс случайное число из минус единицы до единицы умножить на скорость после столкновения.
-
Сгенерировать случайное число; если оно меньше PRO, выбрать случайную координату и присвоить ей случайное значение в пределах границ.
-
Для каждой координаты j от 1 до d: если значение меньше минимума, установить равным минимуму; если больше максимума, установить равным максимуму.
-
Вычислить фитнес тела; если он лучше глобального лучшего, обновить глобальное лучшее решение.
-
Перейти к следующей итерации.
-
Вернуть глобальное лучшее решение и его фитнес.
Теперь можем перейти к самой реализации в коде.
Класс "C_AO_ECBO" наследуется от базового класса "C_AO" и реализует алгоритм Enhanced Colliding Bodies Optimization. Размер популяции по умолчанию устанавливается равным 50 особям, как обычно. Алгоритм имеет три настраиваемых параметра:
- "popSize" — определяет размер популяции и должен быть чётным числом для корректного разделения на стационарные и движущиеся тела;
- "CMsize" — задаёт размер памяти столкновений (Colliding Memory) и по умолчанию равен 20, что означает сохранение двадцати лучших найденных решений;
- "PRO" представляет собой вероятность кроссовера и установлен в 0.7, обеспечивая достаточную диверсификацию поиска.
Среди приватных членов класса присутствуют переменные "epochs" и "epochNow", отслеживающие общее число эпох оптимизации и номер текущей эпохи соответственно — эти значения необходимы для вычисления коэффициента восстановления, линейно убывающего от единицы до нуля. Массив "CM" типа "S_AO_Agent" служит памятью столкновений и хранит лучшие найденные позиции за всё время работы алгоритма. Временный массив "pTemp" используется функцией сортировки для упорядочивания популяции по значению фитнеса. Массив "mass" хранит вычисленные массы всех тел популяции.
//———————————————————————————————————————————————————————————————————— class C_AO_ECBO : public C_AO { public: ~C_AO_ECBO () { } C_AO_ECBO () { ao_name = "ECBO"; ao_desc = "Enhanced Colliding Bodies Optimization"; ao_link = "https://www.mql5.com/ru/articles/21147"; popSize = 50; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "CMsize"; params [1].val = 20; // размер Colliding Memory params [2].name = "PRO"; params [2].val = 0.7; // вероятность кроссовера } void SetParams () { popSize = (int)params [0].val; CMsize = (int)params [1].val; PRO = params [2].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ int CMsize; // размер Colliding Memory double PRO; // вероятность кроссовера private: //————————————————————————————————————————————————————————— int epochs; // общее число эпох int epochNow; // текущая эпоха S_AO_Agent CM []; // Colliding Memory - хранит лучшие позиции S_AO_Agent pTemp []; // временный массив для сортировки double mass []; // массы тел void CalculateMasses (); }; //————————————————————————————————————————————————————————————————————
Метод "Init" выполняет инициализацию алгоритма перед началом оптимизации. Первым делом вызывается "StandardInit" базового класса, который выделяет память под массивы координат, устанавливает границы поиска и инициализирует популяцию агентов. Затем проверяется чётность размера популяции — если "popSize" нечётен, он увеличивается на единицу, поскольку алгоритм требует разделения популяции на две равные группы. Сохраняется общее число эпох из параметра "epochsP", а счётчик текущей эпохи обнуляется.
Далее инициализируется память столкновений: для каждого из "CMsize" элементов выделяется память под координаты и устанавливается начальное значение фитнеса равным минус бесконечности, что гарантирует замещение этих элементов любыми реальными решениями на первых итерациях. Аналогично инициализируется временный массив для сортировки размером "popSize" элементов. Массив "масс" также получает начальные значения — каждая масса устанавливается равной 1/popSize, обеспечивая равномерное распределение до первого вычисления реальных масс.
//———————————————————————————————————————————————————————————————————— bool C_AO_ECBO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // popSize должен быть чётным //------------------------------------------------------------------ if (popSize % 2 != 0) popSize++; epochs = epochsP; epochNow = 0; //------------------------------------------------------------------ // Инициализация Colliding Memory //------------------------------------------------------------------ ArrayResize (CM, CMsize); for (int i = 0; i < CMsize; i++) { CM [i].Init (coords); CM [i].f = -DBL_MAX; } //------------------------------------------------------------------ // Временный массив для сортировки //------------------------------------------------------------------ ArrayResize (pTemp, popSize); for (int i = 0; i < popSize; i++) pTemp [i].Init (coords); //------------------------------------------------------------------ // Массив масс //------------------------------------------------------------------ ArrayResize (mass, popSize); for (int i = 0; i < popSize; i++) mass [i] = 1.0 / popSize; return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" отвечает за перемещение всех тел популяции на новые позиции согласно физике столкновений. В начале метода инкрементируется счётчик эпох "epochNow". Если флаг "revision" равен "false", что означает первую итерацию до получения значений фитнеса, выполняется случайная инициализация всех позиций согласно формуле (1): каждая координата каждого тела получает случайное значение, равномерно распределённое между минимальной и максимальной границами пространства поиска. После дискретизации значения функцией "SeInDiSp" метод завершает работу, оставляя вычисление столкновений для последующих итераций.
На последующих итерациях, когда "revision" равен "true", алгоритм сначала сохраняет текущие позиции всех тел в массив "cP" (previous coordinates). Это критически важный шаг, поскольку при вычислении столкновений необходимо использовать позиции тел до начала обновления, а не уже изменённые значения. Затем вычисляется коэффициент восстановления "epsilon" по формуле . Значение ограничивается диапазоном от нуля до единицы для защиты от выхода за пределы при некорректных значениях счётчиков. Переменная "halfPop" сохраняет половину размера популяции для удобства индексации.
Основной цикл перебирает все тела популяции. Для каждого тела и каждой координаты вычисляется новая позиция на основе физики столкновений. Логика разветвляется в зависимости от принадлежности тела к стационарной или движущейся группе. Тела с индексами от "0" до "halfPop-1" являются стационарными — это лучшая половина популяции после сортировки. Для стационарного тела с индексом "i" его парой является движущееся тело с индексом "i+halfPop". Скорость движущегося тела до столкновения вычисляется как разность позиций стационарного и движущегося тел: vMoving = a[i].cP[c] - a[movingIdx].cP[c].
Скорость стационарного тела после столкновения определяется формулой (5), где в числителе стоит произведение суммы массы движущегося тела и той же массы, умноженной на "epsilon", на скорость движущегося тела, а в знаменателе — сумма масс обоих тел. Новая позиция стационарного тела вычисляется по формуле (8): к старой позиции прибавляется произведение случайного числа из диапазона [-1, 1] на вычисленную скорость.
Тела с индексами от "halfPop" до "popSize-1" являются движущимися — это худшая половина популяции. Для движущегося тела с индексом "i" его стационарной парой является тело с индексом "i-halfPop". Скорость до столкновения вычисляется аналогично, но с учётом правильных индексов. Скорость после столкновения определяется формулой (6), отличающейся от формулы для стационарных тел знаком при epsilon: в числителе стоит разность массы движущегося тела и произведения "epsilon" на массу стационарного. Ключевое отличие в формуле (9) для новой позиции движущегося тела состоит в том, что отсчёт ведётся не от собственной позиции тела, а от позиции стационарного партнёра. Это обеспечивает эффект "прыжка" движущегося тела в окрестность лучшего решения.
После вычисления новой позиции для каждого тела применяется механизм кроссовера, характерный для версии ECBO. Генерируется случайное число "ran_i", и если оно меньше вероятности кроссовера "PRO", выбирается случайная координата "j", которая переинициализируется случайным значением из допустимого диапазона. Этот механизм вносит элемент случайности, помогающий алгоритму избегать застревания в локальных оптимумах. В завершение обработки каждого тела выполняется проверка границ: координаты, вышедшие за пределы пространства поиска, обрезаются до граничных значений, после чего применяется дискретизация.
//———————————————————————————————————————————————————————————————————— void C_AO_ECBO::Moving () { epochNow++; //------------------------------------------------------------------ // Первая итерация - случайная инициализация (формула 1) //------------------------------------------------------------------ if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double r = u.RNDfromCI (0.0, 1.0); a [i].c [c] = rangeMin [c] + r * (rangeMax [c] - rangeMin [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } return; } //------------------------------------------------------------------ // Сохраняем старые позиции //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].cP, a [i].c, 0, 0, coords); } //------------------------------------------------------------------ // Коэффициент восстановления ε (линейно от 1 до 0) // Обеспечивает баланс exploration/exploitation //------------------------------------------------------------------ double epsilon = 1.0 - (double)epochNow / (double)epochs; if (epsilon < 0.0) epsilon = 0.0; if (epsilon > 1.0) epsilon = 1.0; int halfPop = popSize / 2; //------------------------------------------------------------------ // Основной цикл - вычисление столкновений //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double vPrime = 0.0; double newPos = 0.0; if (i < halfPop) { //============================================================ // СТАЦИОНАРНЫЕ ТЕЛА (лучшая половина, индексы 0..halfPop-1) //============================================================ int movingIdx = i + halfPop; // парное движущееся тело //------------------------------------------------------------ // Скорость движущегося тела ДО столкновения (формула 4): // v_moving = x_stationary - x_moving //------------------------------------------------------------ double vMoving = a [i].cP [c] - a [movingIdx].cP [c]; //------------------------------------------------------------ // Скорость стационарного тела ПОСЛЕ столкновения (формула 5): // v'_stat = ((m_mov + ε*m_mov) * v_mov) / (m_stat + m_mov) //------------------------------------------------------------ double mStat = mass [i]; double mMove = mass [movingIdx]; double denominator = mStat + mMove; if (denominator > 1e-10) { vPrime = ((mMove + epsilon * mMove) * vMoving) / denominator; } //------------------------------------------------------------ // Новая позиция стационарного (формула 8): // x_new = x_old + rand * v' // rand ∈ [-1, 1] //------------------------------------------------------------ double rand_c = u.RNDfromCI (-1.0, 1.0); newPos = a [i].cP [c] + rand_c * vPrime; } else { //============================================================ // ДВИЖУЩИЕСЯ ТЕЛА (худшая половина, индексы halfPop..popSize-1) //============================================================ int stationaryIdx = i - halfPop; // парное стационарное тело //------------------------------------------------------------ // Скорость движущегося тела ДО столкновения (формула 4): // v_moving = x_stationary - x_moving //------------------------------------------------------------ double vMoving = a [stationaryIdx].cP [c] - a [i].cP [c]; //------------------------------------------------------------ // Скорость движущегося тела ПОСЛЕ столкновения (формула 6): // v'_mov = ((m_mov - ε*m_stat) * v_mov) / (m_stat + m_mov) //------------------------------------------------------------ double mStat = mass [stationaryIdx]; double mMove = mass [i]; double denominator = mStat + mMove; if (denominator > 1e-10) { vPrime = ((mMove - epsilon * mStat) * vMoving) / denominator; } //------------------------------------------------------------ // Новая позиция движущегося (формула 9): // x_new = x_stationary + rand * v' // ВАЖНО: стартуем от позиции СТАЦИОНАРНОГО тела! //------------------------------------------------------------ double rand_c = u.RNDfromCI (-1.0, 1.0); newPos = a [stationaryIdx].cP [c] + rand_c * vPrime; } a [i].c [c] = newPos; } //---------------------------------------------------------------- // Кроссовер (формула 10) - только для ECBO // С вероятностью PRO случайная координата переинициализируется //---------------------------------------------------------------- if (PRO > 0.0) { double ran_i = u.RNDfromCI (0.0, 1.0); if (ran_i < PRO) { int j = u.RNDminusOne (coords); // случайная координата a [i].c [j] = rangeMin [j] + u.RNDfromCI (0.0, 1.0) * (rangeMax [j] - rangeMin [j]); } } //---------------------------------------------------------------- // Проверка границ //---------------------------------------------------------------- for (int c = 0; c < coords; c++) { if (a [i].c [c] < rangeMin [c]) a [i].c [c] = rangeMin [c]; if (a [i].c [c] > rangeMax [c]) a [i].c [c] = rangeMax [c]; a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" вызывается после вычисления значений фитнеса для всех тел и выполняет несколько ключевых операций. Первым делом обновляется глобальное лучшее решение: цикл по всем телам сравнивает их фитнес с текущим лучшим значением "fB", и при обнаружении лучшего решения сохраняются как значение фитнеса, так и соответствующие координаты в массив "cB".
Следующий этап — обновление памяти столкновений, выполняемое только при "CMsize > 0". Для каждого тела популяции находится худший элемент в "CM" путём линейного поиска минимального фитнеса. Если фитнес текущего тела превышает фитнес худшего элемента "CM", происходит замещение: в "CM" записываются фитнес и координаты текущего тела. Таким образом, "CM" постепенно накапливает лучшие найденные решения за всё время работы алгоритма.
Затем выполняется обратная операция — замещение худших решений в популяции элементами из "CM". Для каждого элемента памяти столкновений находится худшее тело в текущей популяции, и если элемент "CM" лучше этого худшего тела, происходит замена. Этот механизм элитизма гарантирует, что лучшие найденные решения никогда не теряются и постоянно присутствуют в популяции, направляя поиск в перспективные области пространства.
После работы с памятью столкновений популяция сортируется по убыванию фитнеса с помощью функции "u.Sorting". В результате сортировки тела с лучшими значениями фитнеса оказываются в начале массива (индексы 0..halfPop-1) и становятся стационарными на следующей итерации, а тела с худшими значениями перемещаются в конец массива (индексы halfPop..popSize-1) и становятся движущимися.
Завершающим шагом метода "Revision" является вызов "CalculateMasses" для пересчёта масс всех тел на основе их текущих значений фитнеса. Флаг "revision" устанавливается в "true", сигнализируя методу "Moving" о том, что первичная инициализация завершена и можно применять логику столкновений.
//———————————————————————————————————————————————————————————————————— void C_AO_ECBO::Revision () { //------------------------------------------------------------------ // 1. Обновляем глобальное лучшее решение //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } //------------------------------------------------------------------ // 2. Обновляем Colliding Memory (ECBO) // CM хранит лучшие найденные позиции за всё время //------------------------------------------------------------------ if (CMsize > 0) { for (int i = 0; i < popSize; i++) { // Находим худший элемент в CM int worstCMidx = 0; double worstCMf = CM [0].f; for (int m = 1; m < CMsize; m++) { if (CM [m].f < worstCMf) { worstCMf = CM [m].f; worstCMidx = m; } } // Если текущий агент лучше худшего в CM - заменяем if (a [i].f > worstCMf) { CM [worstCMidx].f = a [i].f; ArrayCopy (CM [worstCMidx].c, a [i].c, 0, 0, coords); } } //---------------------------------------------------------------- // 3. Замещаем худшие решения в популяции решениями из CM // Это предотвращает деградацию лучших решений //---------------------------------------------------------------- for (int m = 0; m < CMsize; m++) { // Находим худший элемент в популяции int worstPopIdx = 0; double worstPopF = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f < worstPopF) { worstPopF = a [i].f; worstPopIdx = i; } } // Если элемент CM лучше - заменяем if (CM [m].f > worstPopF) { a [worstPopIdx].f = CM [m].f; ArrayCopy (a [worstPopIdx].c, CM [m].c, 0, 0, coords); } } } //------------------------------------------------------------------ // 4. Сортируем популяцию по убыванию фитнеса // После сортировки: [0..halfPop-1] - стационарные (лучшие) // [halfPop..popSize-1] - движущиеся (худшие) //------------------------------------------------------------------ u.Sorting (a, pTemp, popSize); //------------------------------------------------------------------ // 5. Вычисляем массы тел //------------------------------------------------------------------ CalculateMasses (); revision = true; } //————————————————————————————————————————————————————————————————————
Приватный метод "CalculateMasses" вычисляет массы тел согласно адаптированной формуле (2). Поскольку в нашей реализации выполняется максимизация фитнеса, а не минимизация целевой функции как в оригинальной статье, формула модифицирована: масса пропорциональна значению фитнеса, а не обратно пропорциональна.
Сначала находится минимальное значение фитнеса в популяции. Если это значение неположительно, вычисляется сдвиг "shift", равный модулю минимума плюс малая добавка, гарантирующая строго положительные значения. Затем вычисляется сумма всех смещённых фитнесов. Наконец, масса каждого тела вычисляется как отношение его смещённого фитнеса к общей сумме, что обеспечивает нормализацию: сумма всех масс равна единице. Тела с лучшими значениями фитнеса получают большую массу и, следовательно, оказывают большее влияние на динамику столкновений, притягивая к себе более лёгкие тела с худшими решениями.
//———————————————————————————————————————————————————————————————————— // Вычисление масс тел // Для максимизации: m_k = f_k / sum(f_i) // Чем лучше решение (больше f), тем больше масса //———————————————————————————————————————————————————————————————————— void C_AO_ECBO::CalculateMasses () { //------------------------------------------------------------------ // Находим минимальный фитнес для сдвига (чтобы все значения были > 0) //------------------------------------------------------------------ double minF = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f < minF) minF = a [i].f; } //------------------------------------------------------------------ // Сдвигаем все значения в положительную область //------------------------------------------------------------------ double shift = 0.0; if (minF <= 0.0) shift = MathAbs (minF) + 1e-10; //------------------------------------------------------------------ // Вычисляем сумму смещённых фитнесов //------------------------------------------------------------------ double sumF = 0.0; for (int i = 0; i < popSize; i++) { sumF += a [i].f + shift; } if (sumF < 1e-10) sumF = 1e-10; //------------------------------------------------------------------ // Вычисляем нормализованные массы (формула 2, адаптированная для максимизации) //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { mass [i] = (a [i].f + shift) / sumF; } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Проведённые испытания алгоритма Enhanced Colliding Bodies Optimization на серии тестовых функций продемонстрировали высокую эффективность данного метода оптимизации. Алгоритм набрал 62.43% в общем зачёте и занял восьмое место в рейтинговой таблице, что является весьма достойным результатом среди множества рассмотренных ранее метаэвристик.ECBO|Enhanced Colliding Bodies Optimization|50.0|20.0|0.7|
=============================
5 Hilly's; Func runs: 10000; result: 0.9347970929735123
25 Hilly's; Func runs: 10000; result: 0.7574782134125695
500 Hilly's; Func runs: 10000; result: 0.324717935277771
=============================
5 Forest's; Func runs: 10000; result: 0.9743623825815234
25 Forest's; Func runs: 10000; result: 0.7744615725642837
500 Forest's; Func runs: 10000; result: 0.23037608019234276
=============================
5 Megacity's; Func runs: 10000; result: 0.8892307692307693
25 Megacity's; Func runs: 10000; result: 0.5806153846153848
500 Megacity's; Func runs: 10000; result: 0.15224615384615517
=============================
All score: 5.61829 (62.43%)
Благодаря визуализации работы ECBO, можно отметить склонность алгоритма к застреванию на дискретной функции "Megacity" малой размерности. На остальных тестах стратегия поиска демонстрирует достаточно стабильное последовательное схождение.

ECBO на тестовой функции Hilly

ECBO на тестовой функции Forest

ECBO на тестовой функции Megacity

ECBO на стандартной функции Ackey

ECBO на стандартной функции Shaffer
В рейтинговой таблице лучших популяционных методов оптимизации алгоритм ECBO по результатам тестирования занимает 8 место.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | ECBO | enhanced_colliding_bodies_optimization | 0,93479 | 0,75747 | 0,32471 | 2,01697 | 0,97436 | 0,77446 | 0,23037 | 1,97919 | 0,88923 | 0,58061 | 0,15224 | 1,62208 | 5,618 | 62,43 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | BO | bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| 26 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 27 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 28 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 29 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 30 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 31 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 32 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 33 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 34 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 35 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 36 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 37 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 38 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 39 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 40 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 41 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 42 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 43 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 44 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 45 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Физическая метафора столкновений тел, лежащая в основе алгоритма, оказалась удачным выбором для организации поискового процесса. Механизм разделения популяции на стационарные и движущиеся группы обеспечивает естественное притяжение слабых решений к сильным, при этом лучшие решения также получают возможность улучшить свою позицию за счёт импульса, переданного при столкновении. Адаптивный коэффициент восстановления, линейно убывающий от единицы до нуля, автоматически балансирует глобальное исследование пространства на ранних итерациях и локальную эксплуатацию найденных областей на поздних этапах оптимизации.
Существенный вклад в результативность алгоритма вносят механизмы, добавленные в расширенной версии ECBO. Память столкновений предотвращает потерю лучших найденных решений и обеспечивает элитизм, гарантируя монотонное улучшение или сохранение качества лучшего решения от итерации к итерации. Механизм кроссовера вносит контролируемую случайность, помогая алгоритму выбираться из локальных оптимумов и поддерживая разнообразие популяции на протяжении всего процесса оптимизации.
Отдельно следует отметить высокую скорость работы алгоритма. Вычислительная сложность одной итерации определяется преимущественно операцией сортировки популяции, требующей O(n log n) операций. Остальные вычисления — определение масс, скоростей и новых позиций — выполняются за линейное время. Отсутствие сложных математических операций и простота программной реализации делают ECBO привлекательным выбором для практических задач, где время вычисления целевой функции сопоставимо со временем работы самого оптимизатора.
Важным практическим преимуществом алгоритма является минимальное количество настраиваемых параметров. В отличие от многих метаэвристик, требующих тщательного подбора множества гиперпараметров для каждой новой задачи, ECBO имеет всего три параметра: размер популяции, размер памяти столкновений и вероятность кроссовера. При этом алгоритм демонстрирует устойчивую работу в широком диапазоне значений этих параметров, что снижает трудоёмкость настройки и повышает надёжность применения на практике.
Результаты тестирования показали, что алгоритм хорошо справляется как с гладкими унимодальными функциями, так и со сложными мультимодальными ландшафтами, включая функции с дискретным пространством поиска. Восьмое место в рейтинге среди десятков алгоритмов подтверждает конкурентоспособность ECBO и позволяет рекомендовать его для решения широкого класса оптимизационных задач в области алгоритмической торговли.
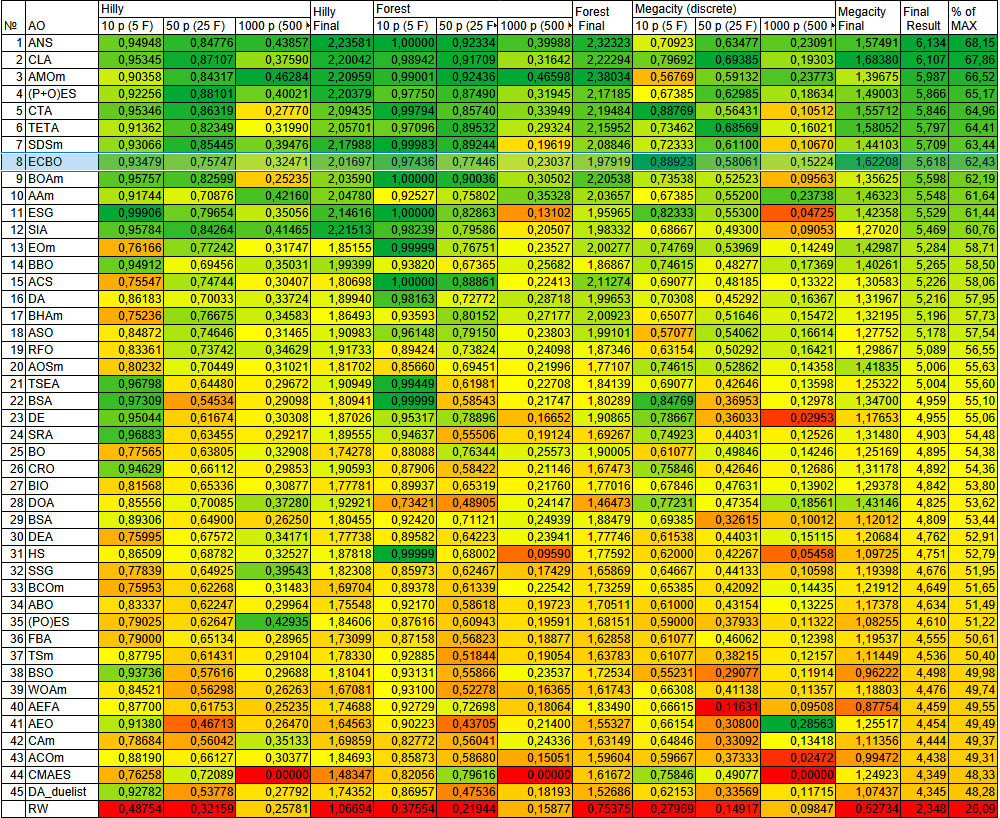
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
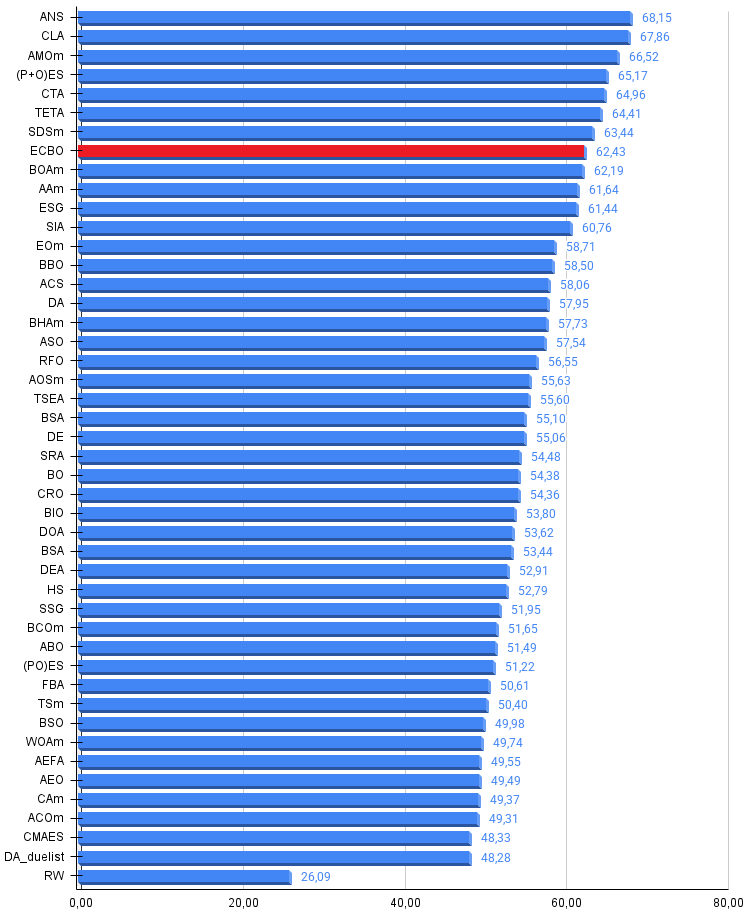
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма ECBO:
Плюсы:
- Хорошие показатели в различных типах задач.
- Мало внешних параметров.
- Быстрый.
Минусы:
- Склонность к застреванию на дискретных задачах малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_ECBO.mq5 | Скрипт | Испытательный стенд для ECBO |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Создание торговой панели администратора на MQL5 (Часть IX): Организация кода (V). Класс AnalyticsPanel
Создание торговой панели администратора на MQL5 (Часть IX): Организация кода (V). Класс AnalyticsPanel
 Инженерия признаков с Python и MQL5 (Часть IV): Распознавание свечных паттернов с помощью UMAP-регрессии
Инженерия признаков с Python и MQL5 (Часть IV): Распознавание свечных паттернов с помощью UMAP-регрессии
 Разработка инструментария для анализа движения цен (Часть 19): ZigZag Analyzer
Разработка инструментария для анализа движения цен (Часть 19): ZigZag Analyzer
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
