Популяционные алгоритмы оптимизации: Гармонический поиск (Harmony Search — HS)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Музыкальная композиция состоит из нескольких составляющих – ритма, мелодии и гармонии. Причем, если ритм с мелодией – это как единое целое музыкального произведения, то гармония – это то, чем будет оно украшено. Пьеса или песня без гармонии – это как нераскрашенная картинка в книжках для детей – она нарисована, но нет цвета, нет красок, яркости, выразительности. Правильно подобранная гармония ласкает слух, облагораживает звучание, представляя нам в полной мере насладиться чудесными звуками пианино, гитары или любого другого музыкального инструмента. Мелодию можно напеть, гармонию – только сыграть. Музыкальная гармония – это свод аккордов, без которых ни одна песня или любое музыкальное произведение не будет полноценным и полнозвучным.

Гармония появляется ровно в тот момент, когда мы соединяем два звука – друг за другом или в одновременном звучании. Более ёмким синонимом будет слово "сочетание". Соединили один звук с другим - получили сочетание, в котором уже по-своему пытается выстроиться иерархия. В музыкальных училищах, колледжах и консерваториях существует специальная дисциплина – гармония, где студенты изучают все существующие в теории музыки аккорды, учатся применять их на практике и даже решают задачи по гармонии.

В процессе музыкальной импровизации определенное количество музыкантов пытаются настроить высоту звука своих инструментов для достижения приятной гармонии (наилучшего состояния). В природе гармония определяется особым соотношением между несколькими звуковыми волнами, которые имеют разные частоты. Качество импровизированной гармонии определяется эстетической оценкой. Чтобы улучшить эстетическую оценку и найти наилучшую гармонию, музыканты проводят практику за практикой. Существует сходство между процессами импровизации музыкантов и оптимизации.

Метод Harmony Search (HS) представляет собой развивающийся метаэвристический алгоритм оптимизации, который использовался для решения многочисленных сложных задач в течение последнего десятилетия. Впервые алгоритм поиска гармонии (Harmony Search algorithm, HS) предложен в 2001 г. Гимом (Z. W. Geem). Метод HS вдохновлен основополагающими принципами импровизации музыкантами и поиском музыкальной гармонии. Сочетания идеальной гармонии звуков алгоритм HS ставит в соответствие глобальному экстремуму в задаче многомерной оптимизации, а процессу импровизации музыканта - процедуру поиска этого экстремума.

В процессе импровизации каждый музыкант на каком-либо такте музыкального произведения воспроизводит звук (в рамках возможностей его музыкального инструмента), так что звуки всех музыкантов оркестра на этом такте образуют один вектор гармонии. Сочетания звуков, образующие "хорошие" гармонии, хранятся в памяти каждого из музыкантов и могут быть ими использованы для формирования ещё более лучших гармоний на следующих тактах произведения.

Как правило, в процессе импровизации музыкант выполняет одно из трех следующих требований: сформировать абсолютно случайный звук из доступного ему диапазона звуков; воспроизвести какой-либо звук из своей памяти гармоний; сыграть смежный вектор гармонии из той же памяти. Основными особенностями алгоритма HS являются возможность его использования для решения задач как непрерывной, так и дискретной оптимизации.

Отличительными чертами HS являются простота алгоритма и эффективность поиска. В силу этого алгоритм привлекает значительное внимание исследователей и быстро развивается как в теоретическом, так и в практическом плане. HS - это метаэвристическая техника, которая обеспечивает высокую стабильность между этапами разведки и эксплуатации в процессе поиска. HS вдохновлен творческими проявлениями человека, метод поиска идеального решения данной проблемы аналогичен методу, который использует музыкант, пытающийся найти приятную для слуха гармонию. Метод, используемый для получения значения фитнес-функции, аналогичен методу получения эталона с помощью высоты тона каждого музыкального инструмента.

2. Описание алгоритма

Работа логики HS аналогична деятельности музыканта при создании идеальной гармонии. Музыкант пытается изменить различные тона, пока не будет найдена идеальная гармония. После этого коллекция найденных гармоний сохраняется в памяти. В задаче оптимизации гармонии претерпевают различные изменения; если результаты вариации благоприятны, то память обновляется добавлением гармонии в память и удалением нежелательного... Так, я уже запутался в терминах авторов алгоритма, что такое гармония? Что такое тона? Попробуем разобраться в алгоритме применяя свои термины.

Что такое музыкальное произведение? Конечно же я не музыкант (жаль), а программист. Но для нас и для написания алгоритма достаточно будет применить понятие "нота". Музыкальное произведение состоит из нот (аккорды). На рисунке 1 схематично представлен "механизм" для построения музыкального произведения, подбор нот на рисунке 1. соответствует одному музыкальному произведению, которое при желании и наличии музыкального слуха (можно без) или музыкальному образованию (можно без), легко определяется, желающие отгадать, можете оставить комментарий к статье.

Процесс оптимизации алгоритма HS заключается в передвижении зеленых планок с нотами поперек синей планки самого произведения. Диапазон зеленой планки - октава, которая состоит из отдельных нот. Произведение (синяя планка) соответствует одному из решений оптимизации. Ноты на зеленой планке - соответствующие оптимизируемые параметры задачи. В памяти музыканта хранится несколько вариантов произведения (несколько вариантов синих планок), это и является популяцией в алгоритме.

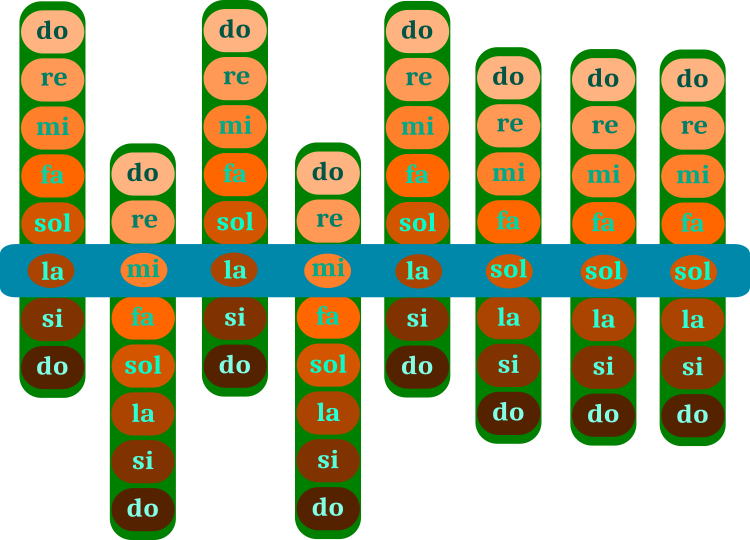
Рисунок 1. Подбор нот в музыкальном произведении (поиск гармонии). Синяя планка - произведение. Зелёные планки - набор нот.

Пример на рисунке 1 соответствует решению дискретной задачи, где шагов в параметре 8 и представлен для простоты понимания работы алгоритма. Однако в произвольной задаче шаг оптимизируемых параметров может быть любым и будут присутствовать промежуточные ноты - полутона. Правильные параметры решения задачи соответствуют правильным нотам в произведении.

Итак, процесс создания музыкального произведения начинается со случайного набора звуков музыкального инструмента, лежащих в диапазоне воспроизводимых частот инструмента. Необходимо создать несколько вариантов произведения для того, чтобы иметь возможность комбинировать отдельные участки нот вариантов. Следующим шагом будет процесс изменения нот в этих вариантах. Для этого мы можем поступить тремя возможными способами:

1. Случайным образом изменить одну из нот в произведении находящуюся в диапазоне музыкального инструмента.
2. Можем взять ноту с соответствующим порядковым номером из других вариантов произведения.
3. Взяв ноту из другого варианта произведения можем немного изменить ее, сделать выше тональностью либо ниже.

Получив таким образом новый набор вариантов музыкального произведения, оценим каждый из вариантов с точки зрения звуковой гармонии, сохраним варианты на их исходное положение в памяти, при условии, что новый вариант лучше своей предыдущей версии. Уникальной особенностью алгоритма является то, что нет необходимости сортировать популяцию, в нашем случае набор произведений: каждый новый лучший вариант заменит старый худший на том же месте. Этот процесс немного напоминает работу генетических алгоритмов, имитирующих эволюцию, когда выживают более приспособленные особи. Кроме того сходство наблюдается также с комбинированием генов в хромосоме.

Исходя из вышесказанного, можем предварительно составить псевдокод алгоритма HS:

1. Генерация случайных гармоний.
2. Замер качества гармоний (вычисление фитнес функции).
3. С вероятностью Eh использовать выбор аккорда выбранной случайным образом гармонии.
  3.1 Изменить аккорд с вероятностью Ep по формуле, если аккорд выбран из какой то гармонии.
    3.1.1 Оставить выбранный аккорд без изменений.
  3.2 Новый аккорд по формуле.
4. Замер качества гармоний (вычисление фитнес функции).
5. повторить с п.3 до выполнения критерия останова.

Итак, перейдем к описанию входных параметров алгоритма, которые немногочисленны и интуитивно понятны.

input int    Population_P = 50;    //Population size
input double Eh_P         = 0.9;   //random selection frequency
input double Ep_P         = 0.1;   //frequency of step-by-step adjustment
input double Range_P      = 0.2;   //range

• Population_P - количество вариантов произведения в памяти музыканта, или, что тоже самое, размер популяции;
• Eh_P - как часто происходит выбор варианта произведения из памяти, влияет на то как часто мы будем обращаться к другим вариантам, чтобы позаимствовать ноту. Более высокое значение означает более высокие комбинаторные свойства алгоритма;
• Ep_P - как часто нужно немного изменить ноту, выше или ниже тоном, если нота была выбрана из другого варианта произведения;
• Range_P - диапазон изменения ноты в редактируемом варианте произведения, если она не была взята из другого варианта. К примеру 0,2 будет означать 20% от диапазона нот музыкального инструмента.
• 
  

Алгоритм HS оперирует гармониями (музыкальными композициями), которые можно описать структурой S_Harmony. Гармония состоит из нот (аккорды), это массив представляющий собой оптимизируемые параметры c []. Лучшие аккорды произведения будем запоминать в массиве cB [], именно в этот массив попадет удачная композиция и именно с этими композициями (гармониями) будем производить комбинаторные перестановки, заимствовать из них ноты. Качество гармонии хранится в переменной h, а лучшая гармония в переменной hB.

//——————————————————————————————————————————————————————————————————————————————
struct S_Harmony //musical composition
{
  double c  []; //chords
  double cB []; //best chords
  double h;     //harmony quality
  double hB;    //best harmony quality
};
//——————————————————————————————————————————————————————————————————————————————

Массив структур гармонии используется в классе C_AO_HS. Объявления в классе методов и членов компактны, поскольку алгоритм отличается необычайной лаконичностью и низкими требованиями к вычислительным ресурсам, здесь мы не увидим сортировку, используемую во многих других алгоритмах оптимизации. Нам понадобится массивы для задания максимума, минимума и шага оптимизируемых параметров (играют роль диапазона и шага аккордов), константные переменные для передачи в них внешних параметров алгоритма, в общем на этом можем остановиться. Переходим к описанию методов, в которых заключена основная логика HS.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_HS
{
  //----------------------------------------------------------------------------
  public: S_Harmony h      []; //harmonies matrix
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best chords
  public: double hB;           //best harmony quality

  public: void Init (const int    chordsNumberP,      //chords number
                     const int    harmoniesNumberP,   //harmonies number
                     const double EhP,                //random selection frequency
                     const double EpP,                //frequency of step-by-step adjustment
                     const double rangeP,             //range
                     const int    maxIterationsP);    //max Iterations

  public: void Moving   (int iter);
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    chordsNumber;      //chords number
  private: int    harmoniesNumber;   //harmonies number
  private: double Eh;                //random selection frequency
  private: double Ep;                //frequency of step-by-step adjustment
  private: double range;             //range
  private: int    maxIterations;
  private: double frequency [];      //frequency range
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Инициализировать алгоритм призван открытый метод Init (). Здесь зададим размер массивам. Показатель качества лучшей найденной гармонии инициализируем минимально возможным числом double, так же поступим с соответствующими переменными массива структур гармоний.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Init (const int    chordsNumberP,      //chords number
                    const int    harmoniesNumberP,   //harmonies number
                    const double EhP,                //random selection frequency
                    const double EpP,                //frequency of step-by-step adjustment
                    const double rangeP,             //range
                    const int    maxIterationsP)     //max Iterations
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  hB       = -DBL_MAX;
  revision = false;

  chordsNumber    = chordsNumberP;
  harmoniesNumber = harmoniesNumberP;
  Eh              = EhP;
  Ep              = EpP;
  range           = rangeP;
  maxIterations   = maxIterationsP;

  ArrayResize (rangeMax,  chordsNumber);
  ArrayResize (rangeMin,  chordsNumber);
  ArrayResize (rangeStep, chordsNumber);
  ArrayResize (frequency, chordsNumber);

  ArrayResize (h, harmoniesNumberP);

  for (int i = 0; i < harmoniesNumberP; i++)
  {
    ArrayResize (h [i].c,  chordsNumber);
    ArrayResize (h [i].cB, chordsNumber);
    h [i].h  = -DBL_MAX;
    h [i].hB = -DBL_MAX;
  }

  ArrayResize (cB, chordsNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Первый обязательный к исполнению на каждой итерации открытый метод Moving (), у которого есть входной параметр iter - текущая итерация. На первой итерации, когда флаг revision равен false, необходимо инициализировать гармонии случайными значениями в диапазоне музыкальных инструментов, что равносильно случайно взятым аккордам музыкантом. Для того, чтобы сократить многократно повторяемые операции, сохраним диапазон звуковых частот соответствующих аккордов (оптимизируемые параметры) в массив frequency [].

//----------------------------------------------------------------------------
if (!revision)
{
  hB = -DBL_MAX;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      h [har].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      h [har].c [c] = SeInDiSp  (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      h [har].h     = -DBL_MAX;
      h [har].hB    = -DBL_MAX;

      frequency [c] = rangeMax [c] - rangeMin [c];
    }
  }

  revision = true;
}

На второй и последующих итерациях происходит импровизация, т.е. последовательное изменение аккордов и их комбинаций. В памяти находится несколько гармоний, которые мы будем изменять и комбинировать. Для каждой новой гармонии последовательно будем перебирать аккорды. Для каждого аккорда есть вероятность быть выбранным случайно взятой из памяти гармонии, т.е. гармония будет выбрана случайно (равновероятно для всех гармоний). Если аккорд взят из памяти гармоний, то также проверяется вероятность его изменения по формуле:

h [har].c [c] = h [har].c [c] + r * B * frequency [c];

где:

r - случайное число в диапазоне от -1 до 1
frequency - диапазон частот инструмента
B - коэффициент, который рассчитывается по формуле:

B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

где:

maxIterations - максимальное количество итераций
iter - текущая итерация
maxB - максимальная граница коэффициента
minB - минимальная граница коэффициента

На рисунке 2 показана зависимость коэффициента B от настроечных параметров алгоритма и текущей итерации.

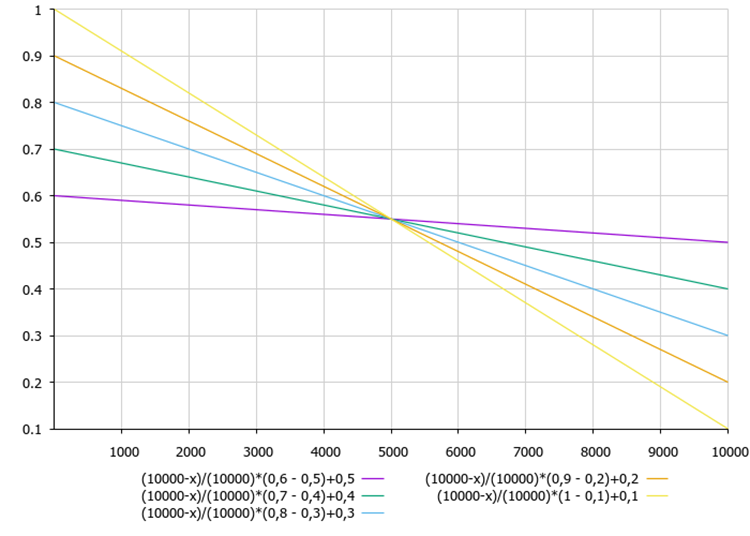
Рисунок 2. Зависимость коэффициента B от настроечных параметров алгоритма maxB, minB и текущей итерации.

Из формулы расчета коэффициента B видим, что с каждой итерацией коэффициент B уменьшается. Таким образом реализуется уточнение найденных экстремумов к концу оптимизации.
В случае, если аккорд не был выбран из памяти гармоний, то будет изменен тот который уже есть в данный момент. Разница в изменении аккорда по сравнении с предыдущим изменением, заключается в фиксированном диапазоне значений звуковых волн.

После того, как процесс изменения аккорда выполнен, проверим полученный аккорд на выход за пределы допустимых значений музыкального инструмента.

//----------------------------------------------------------------------------
else
{
  double r         = 0.0;
  int    harAdress = 0;
  double minB      = 0.0;
  double maxB      = 0.3;
  double B = ((maxIterations - iter) / (double)maxIterations) * (maxB - minB) + minB;

  for (int har = 0; har < harmoniesNumber; har++)
  {
    for (int c = 0; c < chordsNumber; c++)
    {
      r = RNDfromCI (0.0, 1.0);

      if (r <= Eh)
      {
        r = RNDfromCI (0.0, harmoniesNumber - 1);
        harAdress = (int)MathRound (r);
        if (harAdress < 0) harAdress = 0;
        if (harAdress > harmoniesNumber - 1) harAdress = harmoniesNumber - 1;

        h [har].c [c] = h [harAdress].cB [c];

        r = RNDfromCI (0.0, 1.0);

        if (r < Ep)
        {
          r = RNDfromCI (-1.0, 1.0);
          h [har].c [c] = h [har].c [c] + r * B * frequency [c];
        }
      }
      else
      {
        r = RNDfromCI (-1.0, 1.0);
        h [har].c [c] = h [har].cB [c] + r * range * frequency [c];
      }

      h [har].c [c] = SeInDiSp (h [har].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}

Второй открытый метод вызываемый на каждой итерации после вычисления фитнес - функции, Revision (). Его предназначение состоит в том, чтобы обновить найденное глобальное решение. В случае, если гармония лучше своей лучшей версии h > hB, тогда обновим лучшую версию этой гармонии.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_HS::Revision ()
{
  for (int har = 0; har < harmoniesNumber; har++)
  {
    if (h [har].h > hB)
    {
      hB = h [har].h;
      ArrayCopy (cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
    if (h [har].h > h [har].hB)
    {
      h [har].hB = h [har].h;
      ArrayCopy (h [har].cB, h [har].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Внимательно изучив код, мы видим, что в алгоритме поиска гармонии нет принципиально новых идей. Алгоритм поиска гармонии – это заимствование ранее используемых идей эволюционных алгоритмов, включая глобальную равномерную рекомбинацию, равномерную мутацию, гауссову мутацию и замену худшей особи каждое поколение. Некоторые источники указывают на необходимость замены новой гармонией наихудшую в памяти, а в нашем алгоритме гармония может заменить только свое лучшее решение, в этом состоит некоторое отличие данного алгоритма HS от классической версии, потому как мной проведенные исследования указывают, что именно такая реализация алгоритма будет более производительной.

Вклад алгоритма поиска гармонии заключается в двух областях: сочетание данным алгоритмом в себе перечисленных идей, имеет новизну; музыкальная мотивация алгоритма поиска гармонии является новой. Лишь в очень немногих публикациях по поиску гармонии обсуждаются музыкальные мотивы или расширения алгоритма поиска гармонии. Большинство публикаций посвящено гибридизации алгоритма поиска гармонии с другими эволюционными алгоритмами, регулировке параметров поиска гармонии либо применению алгоритма поиска гармонии к конкретным задачам. Если бы к алгоритму HS можно было бы применить более музыкально обусловленные расширения, то это помогло бы выделить его как отдельный эволюционный алгоритм. Такие исследования потребовали бы изучения теории музыки, изучения процесса музыкальной композиции и аранжировки, изучения образовательных теорий музыки и изобретательного применения этих теорий в алгоритме поиска гармонии.

3. Результаты тестов

Распечатка работы HS на тестовом стенде:

2023.02.08 17:30:05.710    Test_AO_HS (EURUSD,M1)    C_AO_HS:50;0.9;0.1;0.2
2023.02.08 17:30:05.711    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.62868417575105
2023.02.08 17:30:07.919    Test_AO_HS (EURUSD,M1)    Score: 0.99903
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 75.85009280972398
2023.02.08 17:30:11.563    Test_AO_HS (EURUSD,M1)    Score: 0.93983
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 50.26867628386793
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    Score: 0.62286
2023.02.08 17:30:45.823    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.7224980742302596
2023.02.08 17:30:47.878    Test_AO_HS (EURUSD,M1)    Score: 0.97433
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    25 Forest's; Func runs 10000 result: 1.0610723369605124
2023.02.08 17:30:51.546    Test_AO_HS (EURUSD,M1)    Score: 0.60020
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.13820341163584177
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    Score: 0.07817
2023.02.08 17:31:31.229    Test_AO_HS (EURUSD,M1)    =============================
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 7.959999999999999
2023.02.08 17:31:34.315    Test_AO_HS (EURUSD,M1)    Score: 0.66333
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 5.112
2023.02.08 17:31:42.862    Test_AO_HS (EURUSD,M1)    Score: 0.42600
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.6492
2023.02.08 17:32:25.172    Test_AO_HS (EURUSD,M1)    Score: 0.05410

Обращая внимание на распечатку результатов тестирования, бросаются в глаза высокие значения тестовых функций, дающие надежду, что результаты в общем зачете тестирования будут выдающимися. Характерной особенностью HS на визуализации является то, что мы не видим никаких структурных образований в виде групп координат, как в случае с некоторыми из предыдущих алгоритмов, визуально незаметно никаких закономерностей в перемещении агентов в пространстве поиска, это похоже на поведение алгоритма оптимизации RND, хотя графики сходимости ведут себя очень уверенно, поступательно приближаясь к решению задачи оптимизации. Застревания в локальных экстремумах не характерны для этого алгоритма.

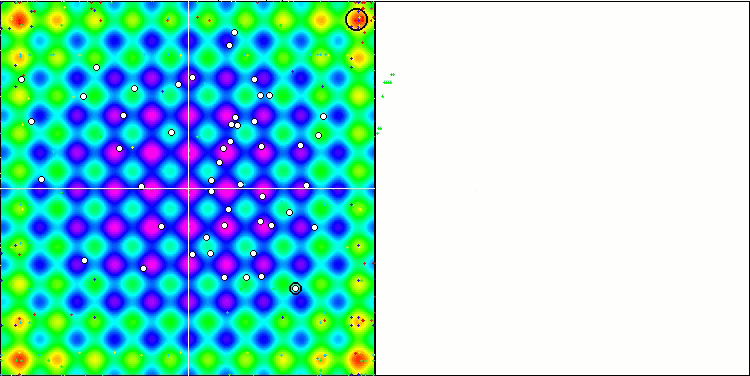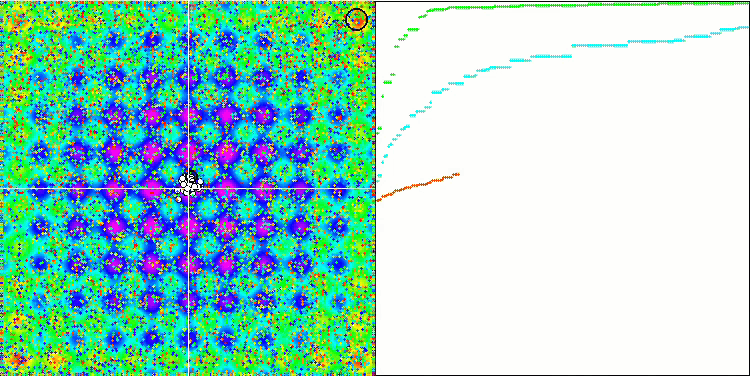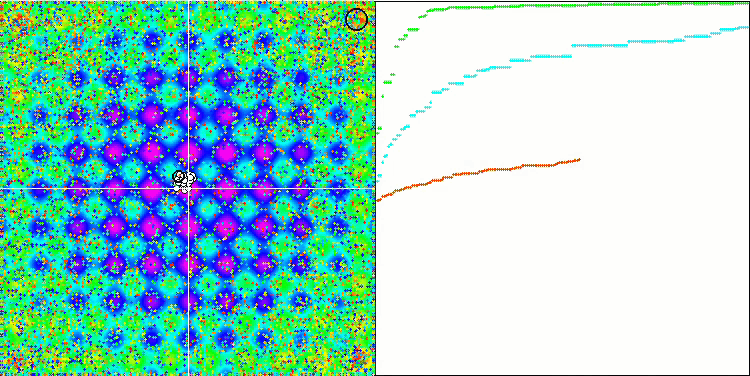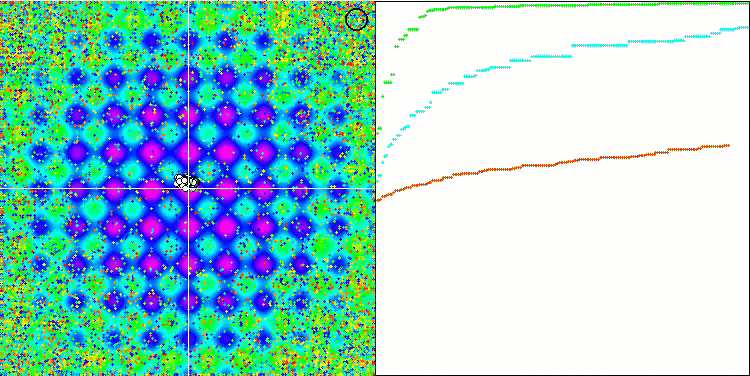
  HS на тестовой функции Rastrigin.

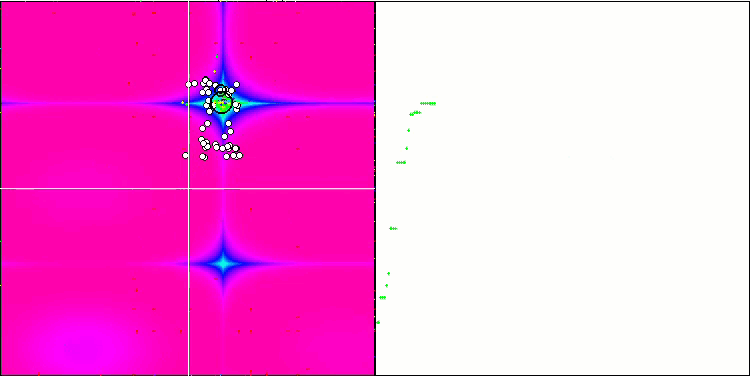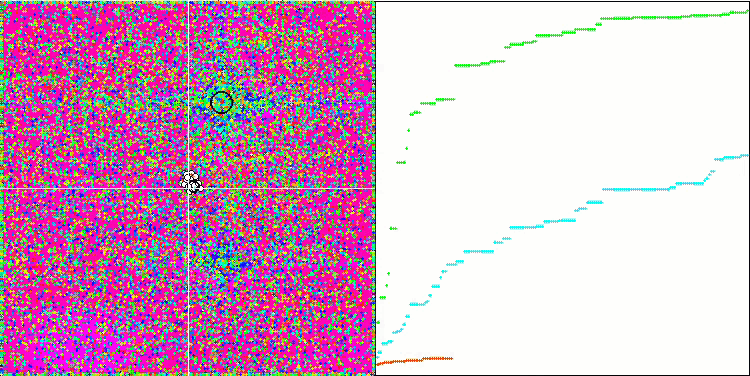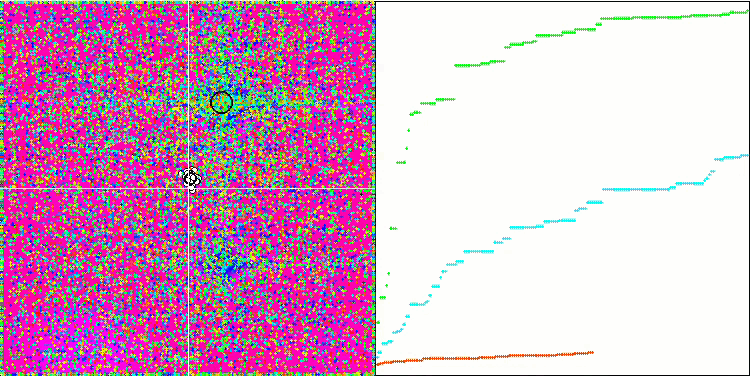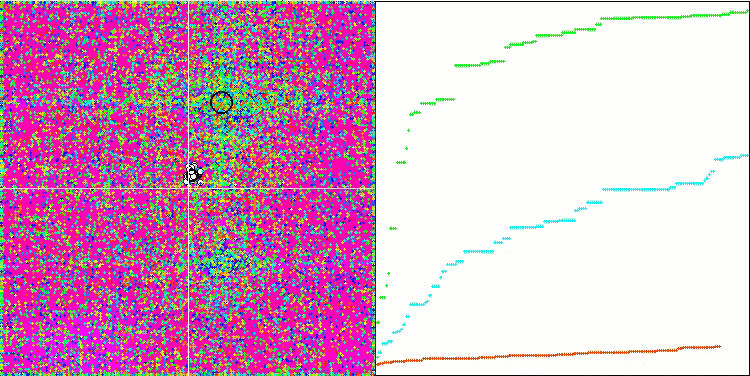
  HS на тестовой функции Forest.

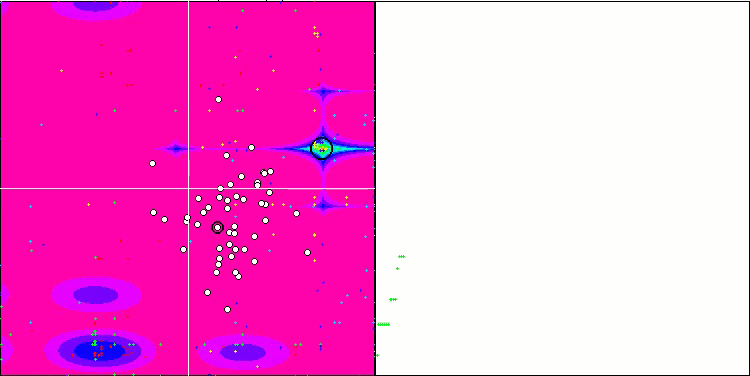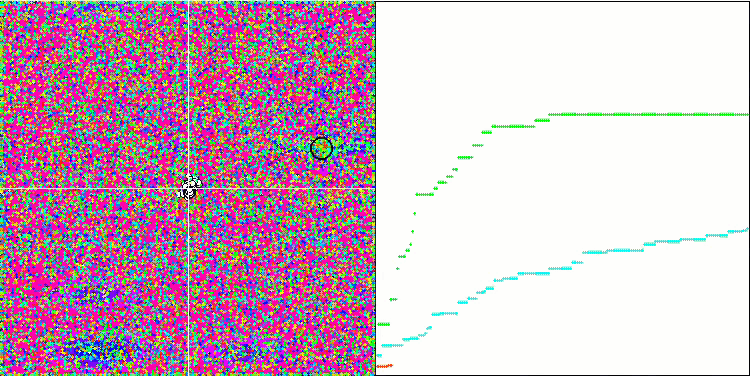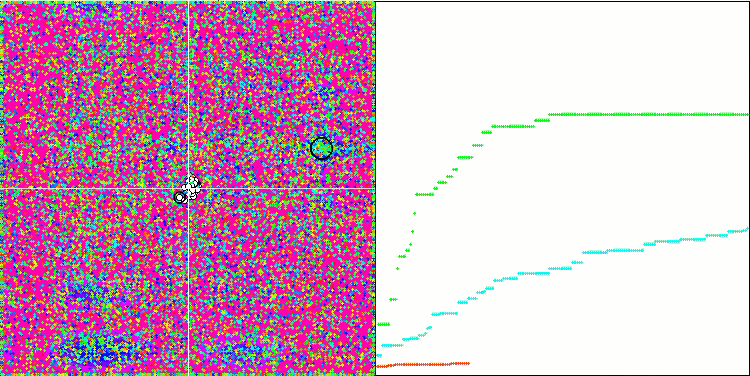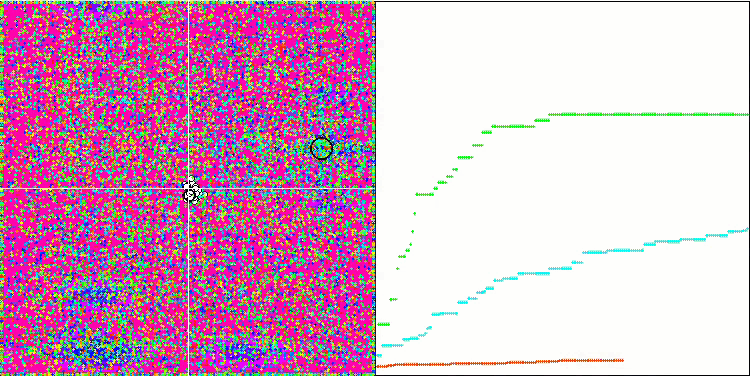
  HS на тестовой функции Megacity.

Пришло время разобрать результаты в таблице и ответить на вопрос в заголовке статьи. В предыдущих статьях я выразил сомнение, сможет ли попасть нам на тестирование алгоритм, который обойдет лидера в рейтинговой таблице на тот момент на дискретной функции. Алгоритм, который визуально выглядит как случайный, смог стать лидером не только на дискретной функции (лучший в трёх тестах), но и на остальных тестовых функциях, в итоге став лучшим в 6 тестах из 9.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
HS	harmony search	1,00000	1,00000	0,57048	2,57048	1,00000	0,98931	0,57917	2,56848	1,00000	1,00000	1,00000	3,00000	100,00000
ACOm	ant colony optimization M	0,34724	0,18876	0,20182	0,73782	0,85966	1,00000	1,00000	2,85966	1,00000	0,88484	0,13497	2,01981	68,094
IWO	invasive weed optimization	0,96140	0,70405	0,35295	2,01840	0,68718	0,46349	0,41071	1,56138	0,75912	0,39732	0,80145	1,95789	67,087
COAm	cuckoo optimization algorithm M	0,92701	0,49111	0,30792	1,72604	0,55451	0,34034	0,21362	1,10847	0,67153	0,30326	0,41127	1,38606	50,422
FAm	firefly algorithm M	0,60020	0,35662	0,20290	1,15972	0,47632	0,42299	0,64360	1,54291	0,21167	0,25143	0,84884	1,31194	47,816
BA	bat algorithm	0,40658	0,66918	1,00000	2,07576	0,15275	0,17477	0,33595	0,66347	0,15329	0,06334	0,41821	0,63484	39,711
ABC	artificial bee colony	0,78424	0,34335	0,24656	1,37415	0,50591	0,21455	0,17249	0,89295	0,47444	0,23609	0,33526	1,04579	38,937
BFO	bacterial foraging optimization	0,67422	0,32496	0,13988	1,13906	0,35462	0,26623	0,26695	0,88780	0,42336	0,30519	0,45578	1,18433	37,651
GSA	gravitational search algorithm	0,70396	0,47456	0,00000	1,17852	0,26854	0,36416	0,42921	1,06191	0,51095	0,32436	0,00000	0,83531	35,937
FSS	fish school search	0,46965	0,26591	0,13383	0,86939	0,06711	0,05013	0,08423	0,20147	0,00000	0,00959	0,19942	0,20901	13,215
PSO	particle swarm optimisation	0,20515	0,08606	0,08448	0,37569	0,13192	0,10486	0,28099	0,51777	0,08028	0,21100	0,04711	0,33839	10,208
RND	random	0,16881	0,10226	0,09495	0,36602	0,07413	0,04810	0,06094	0,18317	0,00000	0,00000	0,11850	0,11850	5,469
GWO	grey wolf optimizer	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,03645	0,06156	0,28778	1,000

Подведем итоги. На гистограмме результатов тестирования алгоритм HS занимает на момент написания статьи лидирующую позицию, с огромным опережением по отношению к другим алгоритмам оптимизации, что говорит о силе и мощи алгоритма и его потенциальных возможностях в области оптимизации решения различной сложности задач.

Фактором, на мой взгляд очень важным, позволяющим демонстрировать впечатляющие результаты на различного вида тестовых функциях, в том числе и очень сложных, является наследование некоторых методов (приемов), присутствующих в других алгоритмах оптимизации: HS не имеет сортировки пула решений, каждое решение обновляет только свое локальное решение - это характерно алгоритму оптимизации поиска с кукушкой, где новый путь развития ветки решений происходит только если яйцо окажется лучше того, что в гнезде; а также методы HS схожи с методами, применяемыми в генетических алгоритмах - комбинаторика элементов решения.

Мощный алгоритм оптимизации HS, который имеет исключительно высокие характеристики может быть с уверенностью рекомендован для решения самых разнообразных сложных задач со многими переменными, как для гладких масштабных функций, так и для сложных дискретных комбинаторных задач. Алгоритм HS уже успешно применяется во многих областях инженерии (оптимизация топологии конструкций и оптимальной формы деталей), электроники и логистики.

Простота реализации алгоритма HS дает простор для исследований, позволяя добавлять и комбинировать различные стратегии оптимизации, это дает основание полагать, что возможности этого алгоритма далеко не полностью реализованы.

Гистограмма результатов тестирования алгоритмов на рисунке 3.

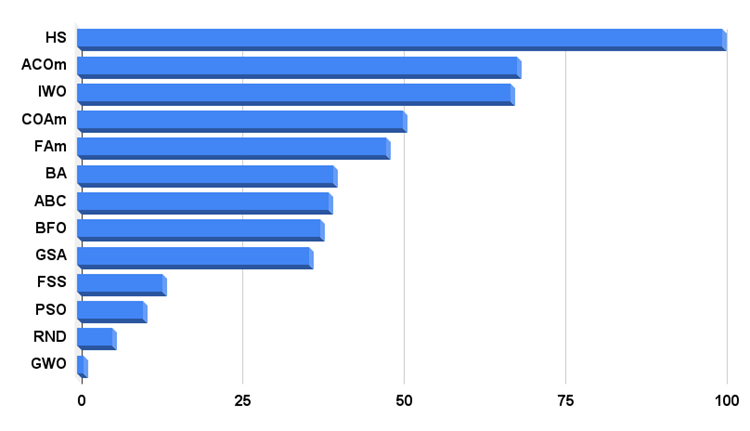
Рисунок 3. Гистограмма итоговых результатов тестирования алгоритмов.

Плюсы и минусы алгоритма гармонического поиска HS:

Плюсы:
1. Простота реализации.
2. Отличная сходимость на всех без исключения типах функций.
3. Впечатляющая масштабируемость.
4. Очень быстрый.
5. Небольшое количество внешних параметров.

Минусы:
Не замечены.

К каждой статье я прикрепляю архив, который содержит обновленные актуальные версии кодов алгоритмов ко всем предыдущим статьям. Статья является накопленным опытом автора и личным мнением, выводы и суждения основаны на проведенных экспериментах.