Алгоритм поисковой оптимизации Эбола — Ebola Optimization Search Algorithm (EOSA)

MetaTrader 5 — Тестер | 20 января 2026, 08:55

Andrey Dik

Содержание

Введение

В данной статье разберем еще один алгоритм оптимизации, скорее перенесем его идею в реализацию, основанную на природном явлении распространения вируса.

Вирус Эбола — один из самых смертоносных патогенов, известных человечеству. Вспышка 2014-2016 годов в Западной Африке продемонстрировала, насколько эффективно вирус может распространяться в популяции. Именно эта мрачная эффективность вдохновила исследователей Oyelade и Ezugwu на создание нового метода оптимизации.

EOSA — это новый био‑вдохновлённый метаэвристический алгоритм оптимизации, основанный на модели распространения вируса Эбола в популяции и опубликованный в 2021 году. Представьте деревню, где появился первый заболевший — "нулевой пациент". Он становится источником инфекции, суперраспространителем. Вирус передаётся двумя путями:

Короткодистанционная передача — через близкий контакт между людьми, такой как рукопожатие, объятие, уход за больным. Заражённый остаётся в своём районе, но активно инфицирует соседей. В терминах оптимизации это эксплуатация — интенсивный поиск в окрестности лучшего решения.
Длиннодистанционная передача — через путешествия и миграцию. Инфицированный садится в автобус и едет в соседний город, неся вирус в новые, ещё не затронутые районы. Это исследование — глобальный поиск в неизведанных областях пространства решений.

Карантин изолирует часть заболевших, предотвращая лавинообразное распространение. В алгоритме это сохраняет разнообразие популяции, не давая всем агентам слиться в одной точке. Что из этого получилось, посмотрим дальше.

Реализация алгоритма

Математическая модель SEIR-HDVQ

Авторы построили сложную эпидемиологическую модель с восемью компартментами (субпопуляциями):

Обозначение	Состояние	Описание
S	Susceptible	Восприимчивые — ещё не заражённые
E	Exposed	Подвергшиеся воздействию — в инкубационном периоде
I	Infected	Инфицированные — активные распространители
H	Hospitalized	Госпитализированные
R	Recovered	Выздоровевшие
D	Dead	Умершие
V	Vaccinated	Вакцинированные
Q	Quarantine	На карантине

Модель описывается системой дифференциальных уравнений (Eq. 6-12), определяющих переходы между состояниями:

(6) ∂S/∂t = π - (β₁I + β₃D + β₄R + β₂(PE)η)S - (τS + ΓI)

(7) ∂I/∂t = (β₁I + β₃D + β₄R + β₂(PE)λ)S - (Γ + γ)I - τS

(8) ∂H/∂t = αI - (γ + ω)H

(9) ∂R/∂t = γI - ΓR

(10) ∂V/∂t = γI - (μ + θ)V

(11) ∂D/∂t = (τS + ΓI) - δD

(12) ∂Q/∂t = (πI - (γR + ΓD)) - ξQ

где π - скорость рекрутирования, β₁-β₄ - коэффициенты контакта, η и λ - коэффициенты затухания, τ - естественная смертность, Γ - смертность от болезни, α - скорость госпитализации, γ - скорость выздоровления, ω - скорость лечения, μ - скорость вакцинации, θ - ответ на вакцину, δ - скорость захоронения, ξ - скорость карантина.

Давайте разберем основные уравнения обновления позиций агентов из оригинальной статьи:

Eq.1 - Обновление позиции: mIᵢᵗ⁺¹ = mIᵢᵗ + ρ × M(I); где ρ - масштабный коэффициент, M(I) - скорость перемещения.

Eq.2 - Эксплуатация (короткая дистанция): M(I) = srate × rand(0,1) + M(Ind_best).

Eq.3 - Исследование (длинная дистанция): M(s) = lrate × rand(0,1) + M(Ind_best).

Eq.4 - Инициализация: individualᵢ = Lᵢ + rand(0,1) × (Uᵢ + Lᵢ).

Проблемы оригинальных формул

При анализе уравнений выявлены критические несоответствия:

Eq.2 и Eq.3 не содержат направленного движения. Формула M(I) = srate × rand(0,1) + M(Ind_best) просто добавляет случайное число к позиции лучшего. Отсутствует вектор направления (target - current), который необходим для движения агента к цели. Без этого компонента агент не перемещается к лучшему решению, а получает позицию, не связанную с его текущим положением.
Eq.4 содержит явную опечатку. Формула L + rand × (U + L) даёт некорректный диапазон. При границах U=10, L=5 результат попадает в интервал [5, 20], что выходит за верхнюю границу. Стандартная формула инициализации: L + rand × (U - L).
Eq.2 и Eq.3 практически идентичны. Единственное отличие — коэффициент srate vs lrate. При этом текстовое описание в статье говорит о движении к лучшему решению (exploitation) и движении через случайного агента-передатчика (exploration), что не отражено в формулах.

Основные уравнения обновления позиций агентов теперь в новом виде:

Eq.2 — Эксплуатация (короткая дистанция): M(I) = srate × rand(0,1) × (IndBest - current). Добавлен вектор направления (Ind_best - current), обеспечивающий движение агента к лучшему решению. Без этого компонента формула не имеет смысла для оптимизации.
Eq.3 — Исследование (длинная дистанция): M(s) = lrate × rand(0,1) × (transmitter - current) + srate × rand(0,1) × (IndBest - current). Добавлен компонент движения к случайному агенту-передатчику (transmitter - current), что соответствует текстовому описанию длиннодистанционной передачи через контакт с другими особями.
Eq.4 — Инициализация: individualᵢ = Lᵢ + rand(0,1) × (Uᵢ - Lᵢ). Исправлена очевидная опечатка: плюс заменён на минус для корректной генерации в заданном диапазоне [L, U].

Псевдокод алгоритма:

1. Инициализировать S, E, I, H, R, V, Q ← ∅
2. Создать начальную популяцию S по Eq.4
3. Выбрать index case (нулевого пациента) → I
4.
5. WHILE epoch ≤ max_epoch AND |I| > 0:
6. Q ← карантинировать часть I по Eq.12
7. fracI ← I \ Q (активные инфицированные)
8.
9. FOR each agent in fracI:
10. IF прошёл инкубационный период:
11. Вычислить neighborhood
12. IF neighborhood < 0.5:
13. Exploitation по Eq.2
14. ELSE:
15. Exploration по Eq.3
16.
17. // Переходы между состояниями:
18. H ← госпитализировать часть I по Eq.8
19. R ← выздоровевшие из I по Eq.9
20. V ← вакцинировать часть H по Eq.10
21. D ← умершие из I по Eq.11
22.
23. I ← I - R - D
24. S ← S + R // выздоровевшие возвращаются
25. S ← S - D + new // умершие заменяются новыми
26.
27. Обновить лучшее решение

Проблема: разрыв между описанием и оптимизацией. При попытке буквально реализовать алгоритм возникли критические проблемы:

Некорректные формулы движения. Оригинальные Eq.2 и Eq.3 не содержат направленного движения к цели. Без вектора (target - current) агенты не могут систематически улучшать свои позиции.
Популяция вымирает. На старте только один агент "index case" — является инфицированным (активным). При высокой смертности (δ = 0.5) и низком заражении популяция быстро сокращается до нуля.
Заморозка агентов. Госпитализированные (H), вакцинированные (V), умершие (D) не участвуют в поиске. Они "выключены" из оптимизации, что резко снижает эффективность.
Слабая генерация новых решений. Формула заражения numNew = β₁ × |I| × srate при малом |I| даёт ноль новых агентов.
Неопределённость "neighborhood". Статья не даёт явной формулы расчёта параметра "neighborhood", от которого зависит выбор стратегии эксплуатации или исследования.

Итоговая реализация

Философия адаптации: мне пришлось сохранить дух эпидемиологической метафоры, но переосмыслить её для оптимизации. Вместо буквального моделирования распространения болезни — используем ключевые механизмы как источник вдохновения. Представьте не саму эпидемию, а информацию о хорошем решении, которая распространяется в популяции подобно вирусу:

близкие к лучшему решению агенты "заражаются" его качеством — уточняют позицию локально;
далёкие агенты совершают "путешествия" — прыжки Леви, в поисках новых перспективных областей.

Введем упрощённую структуру. Вместо восьми состояний — все агенты активны:

Параметр	Значение	Описание
popSize	50	Размер популяции
srate	1.5	Интенсивность эксплуатации
lrate	1.0	Интенсивность исследования
quarantine	0.05	Вероятность пропуска итерации

Механизм выбора стратегии

Параметр "neighborhood" вычисляется случайно с учётом качества агента: neighborhood = rand() × (1 - fitness_ratio × 0.5).

Лучшие агенты чаще попадают в режим эксплуатации, худшие — чаще исследуют. Это интуитивно верно: если вы нашли золотую жилу, копайте глубже; если ваша шахта пуста — ищите новое место.

Эксплуатация: локальный поиск. Когда (neighborhood < 0.5), агент находится в режиме "близкого контакта":

// Целевая точка: смесь глобального и личного лучшего
target = w × gBest + (1-w) × pBest

// Движение к цели с локальным шумом
M = srate × rand() × (target - current)
M += Gaussian_noise × range × 0.05

new_position = current + ρ × M

Проведем аналогию: заражённый в своём районе. Он ходит к соседям (gBest, pBest), но не выходит за пределы квартала. Небольшой гауссов шум — это случайные встречи на улице.

Исследование: глобальный поиск. Когда (neighborhood ≥ 0.5), агент "путешествует". Два варианта. Вариант A — Прыжки Леви (50% случаев):

levy = LevyFlight()  // распределение Леви
step = lrate × levy × range × 0.1
attraction = 0.1 × rand() × (gBest - current)

new_position = current + step + attraction

Пример: инфицированный садится в самолёт и летит в случайный город. Распределение Леви — это много "коротких перелётов + редкие трансконтинентальные рейсы". Именно так распространяются реальные эпидемии в эпоху глобализации.

Вариант B — Передача через агента (50% случаев):

j = random_agent ≠ i

M = lrate × rand() × (agent[j] - current)
M += 0.3 × srate × rand() × (gBest - current)

new_position = current + ρ × M

Пример: заражённый встречает путешественника из другого города и перенимает информацию о тамошней ситуации.

Прыжки Леви, это математика дальних путешествий. Распределение Леви — это тяжелохвостое распределение, характерное для перемещений животных в поисках пищи, миграции людей и распространения эпидемий.

Его особенностью является много мелких шагов, однако изредка — гигантские прыжки.

double LevyFlight()
{
    // Mantegna's algorithm, β = 1.5
    double sigma_u = 0.6966;  // предвычисленная константа
    
    double u = Gaussian() × sigma_u;
    double v = Gaussian();
    
    double step = u / |v|^0.6667;
    
    return clamp(step, -3, 3);
}

Карантин: сохранение разнообразия. С вероятностью 5% агент пропускает итерацию:

if (rand() < quarantine)
    continue;  // агент в изоляции

Зачем? Без карантина все агенты устремляются к лучшему решению и могут слиться в одну точку. Карантин — это "инерция": часть популяции сохраняет свои позиции, обеспечивая разнообразие для будущих итераций.

Личная память (pBest). Каждый агент помнит свою лучшую позицию:

if (current.fitness > pBest.fitness)
    pBest = current;

В режиме эксплуатации агент движется к смеси "gBest" и "pBest". Это предотвращает ситуацию, когда все агенты слепо следуют за одним лидером. Аналогия: вы помните, где было хорошо лично вам, даже если все говорят, что сейчас лучше в другом месте.

Почему были предприняты такие изменения? Оккам и метаэвристики. Сложность эпидемиологической модели не транслируется в качество оптимизации. Восемь состояний и шестнадцать параметров создают большое количество "степеней свободы" и хаотическую динамику, где большинство агентов заморожены в неактивных состояниях. Можно охарактеризовать ситуацию принципом бритвы Оккама: из двух объяснений выбирай простейшее. Из двух алгоритмов — тот, где меньше параметров для настройки и внешней оптимизации.

Levy flights — является научно обоснованной заменой. Оригинальное исследование говорит о "дальних перемещениях", но использует простую линейную комбинацию. Levy flights — это математически обоснованная модель дальних перемещений.

Fitness bias — адаптивный баланс. Вместо фиксированного порога (neighborhood = 0.5) используем адаптивный механизм, когда хорошие решения эксплуатируются, а плохие решения продолжат исследоваться. Это естественно: успешный бизнесмен расширяет то, что работает, а начинающий — пробует разное.
EOSA — является примером того, как биологическая метафора может вдохновить на создание алгоритма оптимизации, но её буквальная реализация не всегда оптимальна и может иметь несколько интерпретаций. В итоге были сохранены ключевые идеи:

два режима поиска (exploitation/exploration) — как аналог короткой/длинной передачи вируса;
карантин — как механизм сохранения разнообразия;
масштабный коэффициент "ρ" — как затухание эпидемии со временем.

Добавлены проверенные техники: "Levy flights" — для глобального исследования, личная память "pBest" — для устойчивости, а "Fitness bias" — для адаптивного баланса стратегий. В результате получился компактный алгоритм с четырьмя параметрами, сохраняющий эпидемиологическую интуицию оригинала. Приведу формулы итоговой реализации:

Инициализация (Eq.4): aᵢ = rangeMin + rand(0,1) × (rangeMax - rangeMin)

Масштабный коэффициент: ρ = 1.0 - epoch/max_epoch × 0.5 (от 1.0 до 0.5)

Exploitation (neighborhood < 0.5):

target = w × gBest + (1-w) × pBest, w ∈ [0.3, 0.7]

M = srate × rand() × (target - aᵢ) + Gaussian() × range × 0.05 × ρ

aᵢ = aᵢ + ρ × M

Exploration — Levy (50%):

step = lrate × LevyFlight() × range × 0.1

attraction = 0.1 × rand() × (gBest - aᵢ)

aᵢ = aᵢ + step + attraction × ρ

Exploration — через агента (50%):

M = lrate × rand() × (aⱼ - aᵢ) + 0.3 × srate × rand() × (gBest - aᵢ)

aᵢ = aᵢ + ρ × M

Levy Flight (β = 1.5):

σᵤ = 0.6966

u = Gaussian() × σᵤ

v = Gaussian()

step = u / |v|^0.6667

return clamp(step, -3, 3)

Можем посмотреть на схему-иллюстрацию для версии реализации алгоритма EOSA.

EOSA

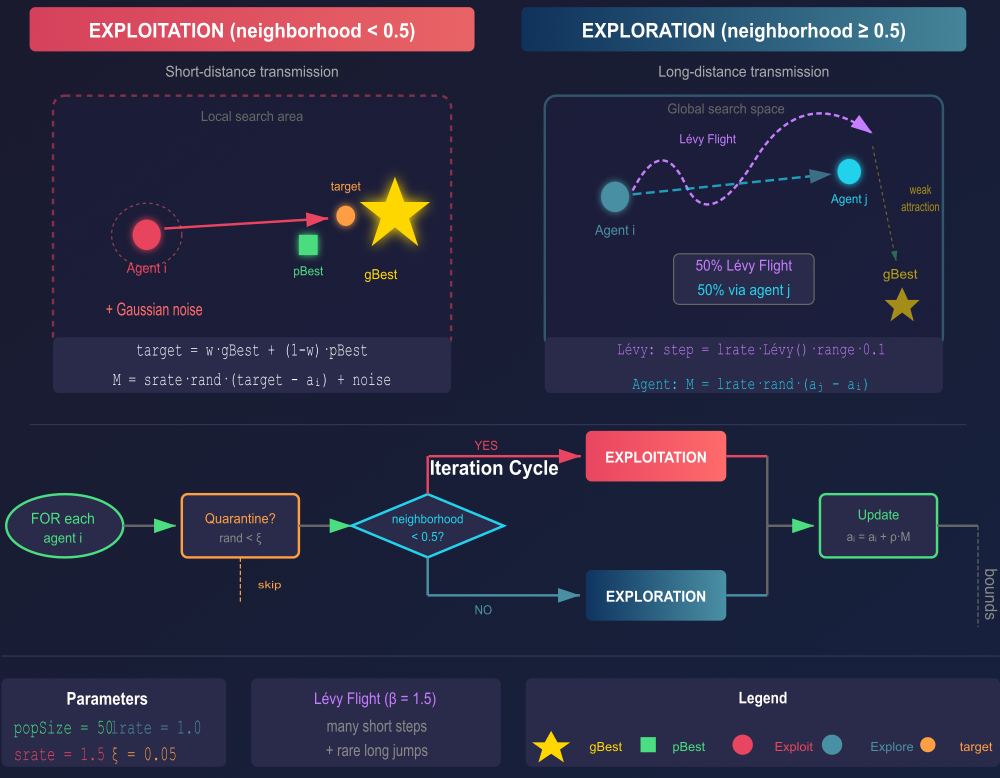
Рисунок 1. Схема-иллюстрация работы алгоритма EOSA

Верхняя часть иллюстрации — два режима работы:

EXPLOITATION (слева): агент движется к target (смесь gBest и pBest) + гауссов шум для локального поиска; EXPLORATION (справа): Lévy flights или передача через случайного агента j (50/50).

Сформируем подробный псевдокод для дальнейшей реализации алгоритма в коде.

Algorithm EOSA
Input: popSize, srate, lrate, ξ, epochs, rangeMin[], rangeMax[]
Output: gBest — best solution found

BEGIN
// Initialization
FOR each agent i DO
a[i] ← random position in [rangeMin, rangeMax]
pBest[i] ← a[i]
END FOR
gBest ← best of population

// Main loop
FOR epoch = 1 TO epochs DO
ρ ← 1.0 − epoch/epochs × 0.5 // scale factor: 1.0 → 0.5

FOR each agent i DO
IF rand() < ξ THEN CONTINUE // quarantine

neighborhood ← rand() × (1 − fitnessBias)

IF neighborhood < 0.5 THEN
//——————————————————————————————————————
// EXPLOITATION: local search
//——————————————————————————————————————
w ← rand(0.3, 0.7)
target ← w·gBest + (1−w)·pBest[i]
M ← srate·rand()·(target − a[i]) + GaussianNoise
a[i] ← a[i] + ρ·M

ELSE
//——————————————————————————————————————
// EXPLORATION: global search
//——————————————————————————————————————
IF rand() < 0.5 THEN
// Lévy flight
step ← lrate · LévyFlight() · range · 0.1
a[i] ← a[i] + step + 0.1·rand()·(gBest − a[i])
ELSE
// Via random agent j
j ← random agent, j ≠ i
M ← lrate·rand()·(a[j] − a[i]) + 0.3·srate·rand()·(gBest − a[i])
a[i] ← a[i] + ρ·M
END IF
END IF

a[i] ← clamp(a[i], rangeMin, rangeMax) // boundary control
END FOR

// Update best solutions
FOR each agent i DO
IF f(a[i]) > f(pBest[i]) THEN pBest[i] ← a[i]
IF f(a[i]) > f(gBest) THEN gBest ← a[i]
END FOR
END FOR

RETURN gBest
END
// Lévy Flight (Mantegna's algorithm, β = 1.5)

Function LévyFlight()
u ← Gaussian() × 0.6966
v ← Gaussian()
RETURN clamp(u / |v|^0.6667, −3, 3)
END
// Default parameters: popSize=50, srate=1.5, lrate=1.0, ξ=0.05

Можем перейти к описанию реализации алгоритма EOSA.

Класс "C_AO_EOSA" реализует алгоритм оптимизации EOSA (Ebola Optimization Search Algorithm), вдохновлённый механизмами распространения вируса Эбола. Класс наследуется от базового класса "C_AO" и содержит четыре настраиваемых параметра: popSize — размер популяции (по умолчанию 50), srate — интенсивность эксплуатации (1.5), lrate — интенсивность исследования с использованием полётов Леви (1.0), и quarantine — вероятность карантина агента (0.05). Внутренние переменные "epochs" и "currentEpoch" отслеживают общее количество итераций и текущую эпоху соответственно.

//————————————————————————————————————————————————————————————————————
class C_AO_EOSA : public C_AO
{
  public:
  ~C_AO_EOSA () { }

  C_AO_EOSA ()
  {
    ao_name = "EOSA";
    ao_desc = "Ebola Optimization Search Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/20932";

    popSize    = 50;
    srate      = 1.5;
    lrate      = 1.0;
    quarantine = 0.05;

    ArrayResize (params, 4);
    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "srate";      params [1].val = srate;      // exploitation intensity
    params [2].name = "lrate";      params [2].val = lrate;      // exploration intensity (Levy)
    params [3].name = "quarantine"; params [3].val = quarantine; // quarantine rate
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    srate      = params      [1].val;
    lrate      = params      [2].val;
    quarantine = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  private: //—————————————————————————————————————————————————————————
  double srate;      // интенсивность эксплуатации
  double lrate;      // интенсивность исследования (Levy)
  double quarantine; // вероятность карантина

  int    epochs;
  int    currentEpoch;

  void   BoundaryControl (int idx);
  double LevyFlight      ();
  double RandGauss       ();
};
//————————————————————————————————————————————————————————————————————

Метод "Init" выполняет инициализацию алгоритма. Он вызывает стандартную инициализацию базового класса, передавая массивы границ поиска "rangeMin", "rangeMax" и шага дискретизации "rangeStep". Затем сохраняет общее число эпох и обнуляет счётчик текущей эпохи. Метод возвращает "true" при успешной инициализации.

//————————————————————————————————————————————————————————————————————
bool C_AO_EOSA::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //------------------------------------------------------------------
  epochs       = epochsP;
  currentEpoch = 0;

  return true;
}
//————————————————————————————————————————————————————————————————————

Метод "Moving" является ядром алгоритма и реализует логику перемещения агентов. На первой итерации, когда флаг "revision" равен "false", метод инициализирует популяцию случайными позициями в заданных границах и завершает работу. На последующих итерациях вычисляется адаптивный масштабный коэффициент "ρ", который линейно уменьшается от 1.0 до 0.5 по мере продвижения оптимизации, обеспечивая постепенный переход от интенсивного исследования к тонкой настройке решений. Для каждого агента сначала проверяется условие карантина — с вероятностью "quarantine" агент пропускает текущую итерацию, что предотвращает преждевременную сходимость и сохраняет разнообразие популяции.

Затем вычисляется параметр "neighborhood", определяющий стратегию поведения агента. Этот параметр представляет собой случайное значение, скорректированное с учётом качества текущего решения агента: лучшие агенты с большей вероятностью попадают в режим эксплуатации, а худшие — в режим исследования. При значении "neighborhood" меньше 0.5 агент выполняет эксплуатацию — локальный поиск вокруг лучших известных решений. Целевая точка формируется как взвешенная комбинация глобального лучшего решения "gBest" и персонального лучшего решения агента "pBest" с весом "w", случайно выбираемым из интервала [0.3, 0.7]. Движение к цели осуществляется с интенсивностью "srate", при этом добавляется гауссов шум для локального исследования окрестности.

При значении "neighborhood" не меньше 0.5 агент выполняет исследование — глобальный поиск с использованием одной из двух стратегий, выбираемых с равной вероятностью. Первая стратегия — полёт Леви, имитирующий дальние перемещения характерные для распространения эпидемий через путешествия и миграцию. Шаг Леви масштабируется коэффициентом "lrate" и добавляется слабое притяжение к глобальному лучшему решению. Вторая стратегия — передача через случайного агента, где текущий агент движется в направлении другого случайно выбранного агента популяции с добавлением притяжения к лучшему решению.

//————————————————————————————————————————————————————————————————————
void C_AO_EOSA::Moving ()
{
  //------------------------------------------------------------------
  // ПЕРВАЯ ИТЕРАЦИЯ: Инициализация популяции
  //------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //------------------------------------------------------------------
  currentEpoch++;

  // Адаптивный масштаб: уменьшается со временем
  double progress = (double)currentEpoch / (double)MathMax (epochs, 1);
  double rho = 1.0 - progress * 0.5;  // 1.0 → 0.5

  //------------------------------------------------------------------
  // Обновление позиций всех агентов
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //================================================================
    // КАРАНТИН: агент в изоляции пропускает итерацию
    // Эпидемиологический смысл: изоляция предотвращает распространение
    //================================================================
    if (u.RNDprobab () < quarantine)
    {
      continue;
    }

    //================================================================
    // Определить neighborhood (близость к "эпицентру" - лучшему решению)
    // Используем случайный выбор с bias на основе fitness
    //================================================================
    double neighborhood = u.RNDprobab ();

    // Bias: лучшие агенты чаще делают exploitation
    double fitnessRatio = 0.5;
    if (fB > -DBL_MAX + 1e10 && a [i].f > -DBL_MAX + 1e10)
    {
      // Нормализуем fitness для bias
      double range_f = MathMax (fB - a [i].f, 1e-10);
      fitnessRatio = MathExp (-range_f / MathMax (MathAbs (fB), 1e-10));
    }

    // Комбинируем случайность с fitness bias
    neighborhood = neighborhood * (1.0 - fitnessRatio * 0.5);

    //================================================================
    // ВЫБОР СТРАТЕГИИ ОБНОВЛЕНИЯ
    //================================================================
    if (neighborhood < 0.5)
    {
      //==============================================================
      // EXPLOITATION: Короткодистанционная передача (Eq.2)
      // Эпидемиология: близкий контакт → локальное распространение
      // Оптимизация: интенсивный поиск вокруг лучших решений
      //==============================================================

      // Выбрать целевую точку: смесь глобального и личного лучшего
      double w = u.RNDfromCI (0.3, 0.7);

      for (int c = 0; c < coords; c++)
      {
        double target;

        // Целевая точка: взвешенная комбинация gBest и pBest
        if (a [i].fB > -DBL_MAX + 1e10)
        {
          target = w * cB [c] + (1.0 - w) * a [i].cB [c];
        }
        else
        {
          target = cB [c];
        }

        // Eq.2 интерпретация: M(I) = srate * rand * direction + noise
        double r1 = u.RNDfromCI (0.0, 1.0);
        double direction = target - a [i].c [c];

        // Движение к цели + локальная случайность
        double M = srate * r1 * direction;

        // Добавить гауссов шум для локального исследования
        double range = rangeMax [c] - rangeMin [c];
        M += RandGauss () * range * 0.05 * rho;

        // Eq.1: обновление позиции
        a [i].c [c] = a [i].c [c] + rho * M;
      }
    }
    else
    {
      //==============================================================
      // EXPLORATION: Длиннодистанционная передача (Eq.3)
      // Эпидемиология: дальний контакт → глобальное распространение
      // Оптимизация: Levy flights для глобального поиска
      //==============================================================

      // Выбрать случайного агента j ≠ i (передатчик)
      int j = u.RNDminusOne (popSize);
      if (j == i) j = (i + 1) % popSize;

      // Решить: Levy flight или движение через передатчика
      if (u.RNDprobab () < 0.5)
      {
        //------------------------------------------------------------
        // LEVY FLIGHT: имитация дальних перемещений
        // В эпидемиологии: путешествия, миграция
        //------------------------------------------------------------
        for (int c = 0; c < coords; c++)
        {
          double range = rangeMax [c] - rangeMin [c];
          double levy = LevyFlight ();  // β = 1.5

          // Levy step от текущей позиции
          double step = lrate * levy * range * 0.1;

          // Слабое притяжение к лучшему
          double attraction = 0.1 * u.RNDfromCI (0.0, 1.0) * (cB [c] - a [i].c [c]);

          a [i].c [c] = a [i].c [c] + step + attraction * rho;
        }
      }
      else
      {
        //------------------------------------------------------------
        // ПЕРЕДАЧА ЧЕРЕЗ АГЕНТА: движение в направлении другого агента
        // В эпидемиологии: заражение через контакт
        //------------------------------------------------------------
        for (int c = 0; c < coords; c++)
        {
          double r1 = u.RNDfromCI (0.0, 1.0);
          double r2 = u.RNDfromCI (0.0, 1.0);

          // Eq.3: M(s) = lrate * rand * (a[j] - a[i]) + attraction_to_best
          double M = lrate * r1 * (a [j].c [c] - a [i].c [c]);

          // Слабое притяжение к лучшему (не доминирует)
          M += 0.3 * srate * r2 * (cB [c] - a [i].c [c]);

          a [i].c [c] = a [i].c [c] + rho * M;
        }
      }
    }

    BoundaryControl (i);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "LevyFlight" генерирует случайный шаг согласно распределению Леви по алгоритму Мантеньи. Используется фиксированное значение параметра β = 1.5, для которого предвычислена константа σ_u = 0.6966. Метод генерирует два гауссовых случайных числа и вычисляет шаг по формуле u/|v|^0.6667, ограничивая результат интервалом [-3, 3] для предотвращения экстремальных выбросов.

//————————————————————————————————————————————————————————————————————
double C_AO_EOSA::LevyFlight ()
{
  // Mantegna's algorithm for Levy distribution
  // beta = 1.5 (fixed)

  // Предвычисленное sigma_u для beta = 1.5:
  // sigma_u = [Γ(2.5)×sin(3π/4) / (Γ(1.25)×1.5×2^0.25)]^(2/3)
  //         = [1.3293×0.7071 / (0.9064×1.5×1.1892)]^0.6667
  //         ≈ 0.6966
  double sigma_u = 0.6966;

  double u_val = RandGauss () * sigma_u;
  double v_val = RandGauss ();

  // Защита от деления на ноль
  if (MathAbs (v_val) < 1e-10) v_val = 1e-10;

  // step = u / |v|^(1/beta) = u / |v|^0.6667 для beta=1.5
  double step = u_val / MathPow (MathAbs (v_val), 0.6667);

  // Ограничить экстремальные значения
  if (step > 3.0)  step = 3.0;
  if (step < -3.0) step = -3.0;

  return step;
}
//————————————————————————————————————————————————————————————————————

Метод "RandGauss" реализует генерацию гауссовой случайной величины с нулевым средним и единичной дисперсией по методу Бокса-Мюллера. Два равномерно распределённых числа преобразуются в нормально распределённое значение через логарифмическое и тригонометрическое преобразования.

//————————————————————————————————————————————————————————————————————
double C_AO_EOSA::RandGauss ()
{
  // Box-Muller transform
  double u1 = u.RNDfromCI (1e-10, 1.0);
  double u2 = u.RNDfromCI (0.0, 1.0);

  return MathSqrt (-2.0 * MathLog (u1)) * MathCos (2.0 * M_PI * u2);
}
//————————————————————————————————————————————————————————————————————

Метод "BoundaryControl" обеспечивает контроль границ поиска методом отражения. В отличие от простого обрезания, отражение сохраняет импульс движения агента: при выходе за нижнюю границу позиция отражается вверх, при выходе за верхнюю — вниз. Если после нескольких отражений позиция остаётся за пределами допустимой области, применяется случайная реинициализация координаты.

//————————————————————————————————————————————————————————————————————
void C_AO_EOSA::BoundaryControl (int idx)
{
  for (int c = 0; c < coords; c++)
  {
    // Отражение от границ вместо обрезки
    double val = a [idx].c [c];
    double min = rangeMin [c];
    double max = rangeMax [c];
    double range = max - min;

    // Отражение
    while (val < min || val > max)
    {
      if (val < min) val = min + (min - val);
      if (val > max) val = max - (val - max);

      // Защита от бесконечного цикла
      if (val < min - range || val > max + range)
      {
        val = min + u.RNDfromCI (0.0, 1.0) * range;
        break;
      }
    }

    a [idx].c [c] = u.SeInDiSp (val, min, max, rangeStep [c]);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "Revision" обновляет лучшие найденные решения. Для каждого агента проверяется, превосходит ли его текущий фитнес персональный рекорд, и при необходимости обновляется "pBest". Одновременно отслеживается лучший агент популяции, и если его фитнес превышает глобальный рекорд, обновляется "gBest". Такая схема обеспечивает сохранение информации о перспективных областях пространства поиска.

//————————————————————————————————————————————————————————————————————
void C_AO_EOSA::Revision ()
{
  //------------------------------------------------------------------
  // Обновить личные и глобального лучших
  //------------------------------------------------------------------
  int    bestIdx = 0;
  double bestFit = -DBL_MAX;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > a [i].fB)
    {
      a [i].fB = a [i].f;
      ArrayCopy (a [i].cB, a [i].c, 0, 0, coords);
    }

    if (a [i].f > bestFit)
    {
      bestFit = a [i].f;
      bestIdx = i;
    }
  }

  //------------------------------------------------------------------
  // Обновить глобального лучшего (Eq.5)
  //------------------------------------------------------------------
  if (bestFit > fB)
  {
    fB = bestFit;
    ArrayCopy (cB, a [bestIdx].c, 0, 0, coords);
  }
}
//————————————————————————————————————————————————————————————————————

Результаты тестов

Теперь можем посмотреть на результаты, не выдающиеся, но с возможностью работы над задачами. Алгоритм EOSA был протестирован на стандартном наборе тестовых функций: Hilly (гладкие многоэкстремальные), Forest (острые пики) и Megacity (дискретные ступенчатые). Тестирование проводилось при размерностях 5, 25 и 500 измерений с ограничением в 10 000 вычислений целевой функции.

Общий результат составил около 38,5% от максимально возможного, что примерно на 10% ниже порога вхождения в таблицу лучших популяционных методов оптимизации.

EOSA|Ebola Optimization Search Algorithm|50.0|3.0|2.0|0.01|
=============================
5 Hilly's; Func runs: 10000; result: 0.710222611733512
25 Hilly's; Func runs: 10000; result: 0.4632808052522758
500 Hilly's; Func runs: 10000; result: 0.29182585953654855
=============================
5 Forest's; Func runs: 10000; result: 0.6237714734740634
25 Forest's; Func runs: 10000; result: 0.38209042951228955
500 Forest's; Func runs: 10000; result: 0.20125437332932763
=============================
5 Megacity's; Func runs: 10000; result: 0.4676923076923078
25 Megacity's; Func runs: 10000; result: 0.2132307692307692
500 Megacity's; Func runs: 10000; result: 0.11516923076923188
=============================
All score: 3.46854 (38.54%)

На визуализации можно заметить, что алгоритм труднее справляется с дискретными функциями типа Megacity, за конечное число итераций. Ступенчатый ландшафт с плоскими плато не даёт градиентной информации, а механизм движения к лучшему решению становится неэффективным, когда множество точек имеют одинаковый фитнес.

Hilly

EOSA на тестовой функции Hilly

Forest

EOSA на тестовой функции Forest

Megacity

EOSA на тестовой функции Megacity

Так же можно посмотреть визуализацию работы алгоритма с более простыми стандартными функциями, на параболической функции тоже есть некоторые проблемы с большой размерностью задачи, сходимость не самая лучшая.

GoldsteinPrice

EOSA на тестовой функции GoldsteinPrice

Paraboloid

EOSA на тестовой функции Paraboloid

В рейтинговой таблице лучших популяционных методов оптимизации алгоритм EOSA представлен ознакомительно.

№	AO	Description	Hilly			Hilly Final	Forest			Forest Final	Megacity (discrete)			Megacity Final	Final Result	% of MAX
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity Final	Final Result	% of MAX
1	DOAdingom	dingo_optimization_algorithm_M	0,47968	0,45367	0,46369	1,39704	0,94145	0,87909	0,91454	2,73508	0,78615	0,86061	0,84805	2,49481	6,627	73,63
2	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
3	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
4	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
5	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
6	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
7	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
8	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
9	BOAm	billiards optimization algorithm M	0,95757	0,82599	0,25235	2,03590	1,00000	0,90036	0,30502	2,20538	0,73538	0,52523	0,09563	1,35625	5,598	62,19
10	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
11	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
12	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
13	EOm	extremal_optimization_M	0,76166	0,77242	0,31747	1,85155	0,99999	0,76751	0,23527	2,00277	0,74769	0,53969	0,14249	1,42987	5,284	58,71
14	BBO	biogeography based optimization	0,94912	0,69456	0,35031	1,99399	0,93820	0,67365	0,25682	1,86867	0,74615	0,48277	0,17369	1,40261	5,265	58,50
15	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
16	DA	dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
17	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
18	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
19	RFO	royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
20	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
21	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
22	BSA	backtracking_search_algorithm	0,97309	0,54534	0,29098	1,80941	0,99999	0,58543	0,21747	1,80289	0,84769	0,36953	0,12978	1,34700	4,959	55,10
23	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
24	SRA	successful restaurateur algorithm (joo)	0,96883	0,63455	0,29217	1,89555	0,94637	0,55506	0,19124	1,69267	0,74923	0,44031	0,12526	1,31480	4,903	54,48
25	BO	bonobo_optimizer	0,77565	0,63805	0,32908	1,74278	0,88088	0,76344	0,25573	1,90005	0,61077	0,49846	0,14246	1,25169	4,895	54,38
26	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
27	BIO	blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
28	DOA	dream_optimization_algorithm	0,85556	0,70085	0,37280	1,92921	0,73421	0,48905	0,24147	1,46473	0,77231	0,47354	0,18561	1,43146	4,825	53,62
29	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
30	DEA	dolphin_echolocation_algorithm	0,75995	0,67572	0,34171	1,77738	0,89582	0,64223	0,23941	1,77746	0,61538	0,44031	0,15115	1,20684	4,762	52,91
31	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
32	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
33	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
34	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
35	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
36	FBA	fractal-based Algorithm	0,79000	0,65134	0,28965	1,73099	0,87158	0,56823	0,18877	1,62858	0,61077	0,46062	0,12398	1,19537	4,555	50,61
37	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
38	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
39	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
40	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
41	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
42	CAm	camel algorithm M	0,78684	0,56042	0,35133	1,69859	0,82772	0,56041	0,24336	1,63149	0,64846	0,33092	0,13418	1,11356	4,444	49,37
43	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
44	CMAES	covariance_matrix_adaptation_evolution_strategy	0,76258	0,72089	0,00000	1,48347	0,82056	0,79616	0,00000	1,61672	0,75846	0,49077	0,00000	1,24923	4,349	48,33
45	DA_duelist	duelist_algorithm	0,92782	0,53778	0,27792	1,74352	0,86957	0,47536	0,18193	1,52686	0,62153	0,33569	0,11715	1,07437	4,345	48,28
	EOSA	ebola_optimization_search_algorithm	0,71022	0,46328	0,29182	1,46532	0,62377	0,38209	0,20125	1,20711	0,46769	0,21323	0,11516	0,79608	3,469	38,54
	RW	random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Выводы

Оригинальная статья предлагает сложную эпидемиологическую модель с восемью состояниями агентов и шестнадцатью параметрами. Однако математический аппарат дифференциальных уравнений, описывающий распространение болезни, не транслируется напрямую в эффективные операторы поиска. Попытка буквальной реализации приводит к вымиранию активной популяции и заморозке большинства агентов в неактивных состояниях. Моя упрощённая реализация сохранила ключевые метафоры — короткую и длинную передачу, карантин, однако потеряла часть потенциального разнообразия механизмов. Возможно, именно в сложных переходах между состояниями скрывался потенциал для более эффективного поиска, который не удалось раскрыть.

Сама концепция "распространения инфекции" как метафоры оптимизации имеет фундаментальное ограничение: в реальной эпидемиологии цель — распространить вирус максимально широко, тогда как в оптимизации цель — сконцентрироваться на лучшем решении. Эти две задачи противоположны по своей природе. Несмотря на скромные практические результаты, алгоритм EOSA представляет значительную ценность как учебный материал. Он наглядно демонстрирует процесс трансформации биологической метафоры в вычислительный алгоритм со всеми сопутствующими трудностями и компромиссами.

На примере EOSA хорошо видна типичная проблема "метафорических" алгоритмов: красивая аналогия не гарантирует эффективности. Сложность исходной модели может оказаться балластом, а не преимуществом. Процесс упрощения и адаптации — неотъемлемая часть разработки метаэвристик.

EOSA — работоспособный алгоритм оптимизации. Его производительность недостаточна для включения в число лучших методов, особенно на дискретных и высокоразмерных задачах. Эпидемиологическая метафора, положенная в основу, оказалась не самой удачной для целей оптимизации, а сложная математическая модель оригинальной статьи потребовала существенного упрощения для получения работающего алгоритма.

Тем не менее EOSA представляет интерес как учебный пример, демонстрирующий весь путь от биологической идеи до программной реализации: анализ исходной концепции, выявление проблем буквальной интерпретации, поиск компромиссов, интеграция проверенных техник и объективная оценка результатов. Этот опыт ценен для понимания природы метаэвристических алгоритмов и развития навыков их разработки.

Tab

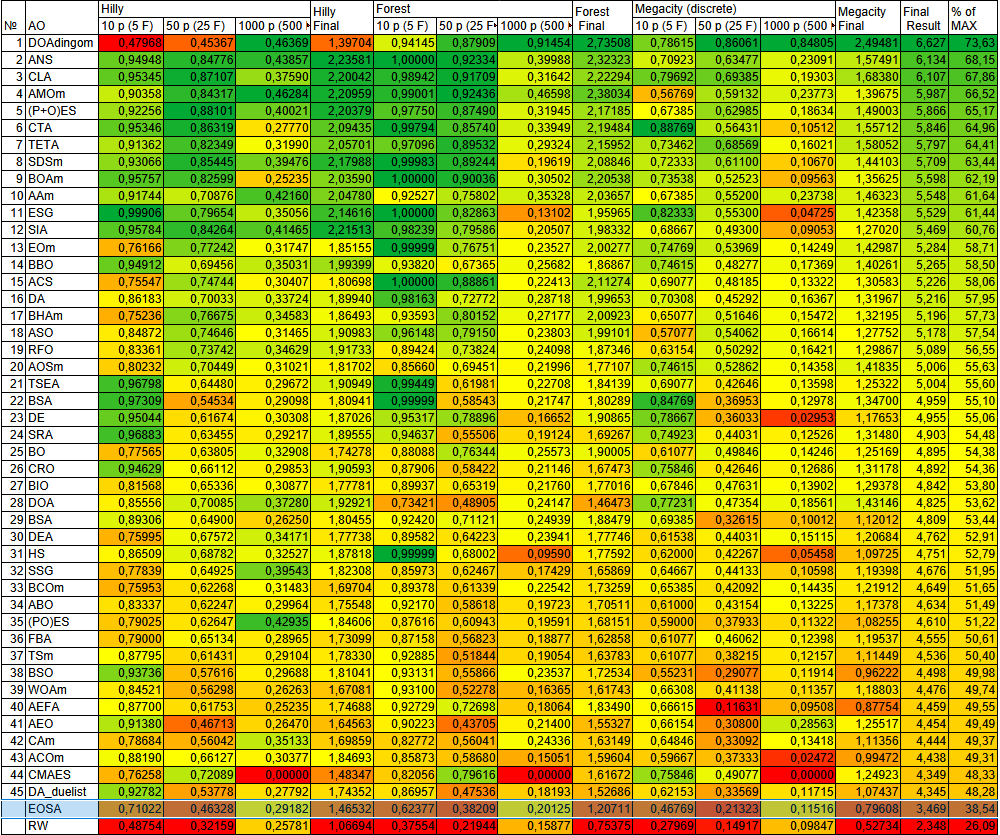
Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам

chart

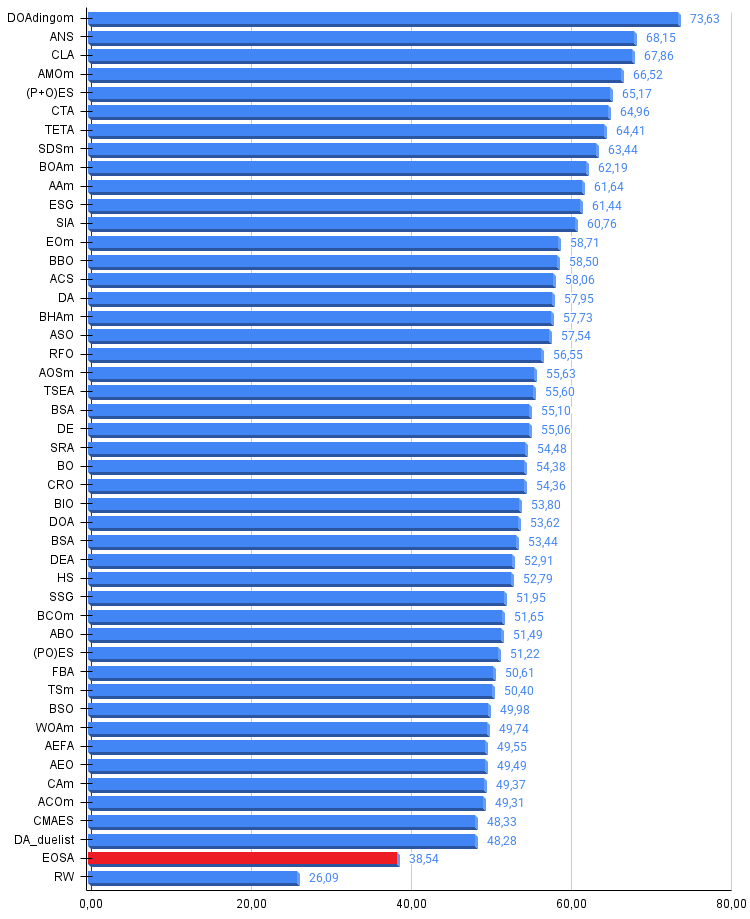
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма EOSA:

Плюсы:

Справляется с некоторым несложным типом задач.

Минусы:

Труднее всего справляется с дискретными функциями.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	TestFunctions.mqh	Включаемый файл	Библиотека тестовых функций
4	TestStandFunctions.mqh	Включаемый файл	Библиотека функций тестового стенда
5	Utilities.mqh	Включаемый файл	Библиотека вспомогательных функций
6	CalculationTestResults.mqh	Включаемый файл	Скрипт для расчета результатов в сравнительную таблицу
7	Testing AOs.mq5	Скрипт	Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8	Simple use of population optimization algorithms.mq5	Скрипт	Простой пример использования популяционных алгоритмов оптимизации без визуализации
9	Test_AO_EOSA.mq5	Скрипт	Испытательный стенд для EOSA

Прикрепленные файлы |

Загрузить ZIP

EOSA.zip (393.85 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Математика волатильности: Почему индикатор GRI достоин возвращения в ваш торговый терминал

Статья посвящена индикатору Gopalakrishnan Range Index (GRI/ROCI), который количественно оценивает "хаотичность" рынка через логарифм диапазона цен закрытия за заданный период. Показано, как реализовать GRI в MetaTrader 5, устранить проблему отрицательных значений с помощью сдвинутого логарифма и привести шкалу к удобным "пунктам" через нормировку на Point. Далее рассматриваются практические сценарии применения GRI как фильтра волатильности и рыночных фаз.

Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (Основные компоненты)

В данной статье представлен практический подход к адаптации современного фреймворка для анализа финансовых потоков средствами MQL5. Рассмотрены ключевые компоненты модели — Depth-Wise свёртки с остаточными связями, конусные Super Kernel Block и модуль глобальной агрегации движения (GMA).

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Машинное обучение и Data Science (Часть 35): NumPy в MQL5 – искусство создания сложных алгоритмов с меньшим объемом кода

Библиотека NumPy лежит в основе практически всех алгоритмов машинного обучения на языке программирования Python. В этой статье мы собираемся реализовать аналогичный модуль, содержащий набор всего сложного кода, который поможет нам создавать сложные модели и алгоритмы любого типа.