Эволюционная стратегия адаптации ковариационной матрицы — Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
Содержание
Введение
В мире оптимизации существует множество алгоритмов, однако мы ищем наиболее сильные для решения оптимизационных задач наших торговых роботов. CMA-ES (Covariance Matrix Adaptation Evolution Strategy) — один из таких редких примеров, где математическая строгость сочетается с биологической интуицией, создавая алгоритм, который не просто решает задачи оптимизации, а учится понимать их структуру.
История CMA-ES началась в конце 1990-х годов в исследовательских лабораториях Германии, где Николаус Хансен и Андреас Остермайер задались фундаментальным вопросом: можно ли создать алгоритм оптимизации, который не просто ищет решение, а адаптируется к геометрии задачи? Традиционные эволюционные алгоритмы генерировали потомство в сферических областях вокруг родительских особей, что работало хорошо для простых функций, но оказывалось неэффективным для сложных, плохо обусловленных задач. Итак, давайте разберем этот интересный алгоритм.
Реализация алгоритма
Представьте себе поиск сокровища на острове неправильной формы. Обычный подход — это искать во всех направлениях одинаково, как будто остров круглый. CMA-ES же постепенно изучает форму острова и начинает искать преимущественно в тех направлениях, где вероятность найти сокровище выше. Более того, он запоминает успешные маршруты и использует эту память для планирования будущих поисков.
В основе CMA-ES лежит обманчиво простое уравнение: x_k ~ N(m, σ²C). Но за этой простотой скрывается глубокая математическая структура. Каждый символ здесь несет важную информацию о состоянии поиска: m — это текущая лучшая догадка о местоположении оптимума, σ — мера того, насколько далеко мы готовы рискнуть отойти от известного, а C — ковариационная матрица, которая кодирует наше понимание геометрии функции. Единственное изменение, которое оправданно внесем, заменим нормальное распределение на степенное, это означает, что реализация будет следовать модифицированной формуле: x_k ~ PowerDist(m, σ²C). Эта модификация меняет характер исследования пространства (более широкие "прыжки"), но сохраняет фундаментальную адаптивную природу алгоритма.
Ковариационная матрица C — это настоящее сердце алгоритма. Она начинает свою жизнь как скромная единичная матрица, представляющая сферическое распределение. Но с каждой итерацией она эволюционирует, вытягиваясь в направлениях быстрого улучшения и сжимаясь там, где прогресс медленный. Постепенно сфера превращается в эллипс, затем в вытянутый эллипсоид, идеально ориентированный вдоль контуров оптимизируемой функции.
Главное нововведение CMA-ES — концепция эволюционных путей. Это своего рода генетическая память алгоритма, которая помнит не только то, где были успешные точки, но и как алгоритм к ним пришел. Эволюционный путь накапливает информацию о последовательных успешных шагах, создавая направленный вектор, который указывает на наиболее перспективные области поиска. Второй эволюционный путь, выполняет более тонкую функцию — он контролирует размер шага. Если последовательные шаги алгоритма коррелированны, то есть каждый следующий шаг продолжает направление предыдущего, то размер шага увеличивается — алгоритм "чувствует", что движется в правильном направлении. Если же шаги случайны и не коррелированны, размер шага уменьшается — возможно, алгоритм уже близок к оптимуму и нужно искать более аккуратно.
За биологической метафорой эволюции в CMA-ES скрывается строгий математический принцип — максимизация правдоподобия. Алгоритм постоянно задается вопросом: какие параметры распределения делают наблюдаемые успешные точки наиболее вероятными? Это превращает эволюционную оптимизацию из эвристики в статистически обоснованный метод.
Каждое обновление ковариационной матрицы C состоит из двух компонентов: rank-one обновления, основанного на эволюционном пути, и rank-μ обновления, использующего информацию от всей выбранной популяции. Rank-one обновление обеспечивает стабильность и способность улавливать долгосрочные тренды, в то время как rank-μ обновление позволяет быстро адаптироваться к новой информации от текущего поколения.
В контексте CMA-ES используется модифицированная функция Хевисайда, которая играет важную роль в механизме обнаружения стагнации алгоритма. Функция сравнивает длину пути эволюции с ожидаемой длиной, если путь слишком короткий — это признак "топтания на месте". Условия деактивации (hsig = 0): алгоритм "блуждает" случайно и шаги отменяют друг друга, тогда вероятно размер шага слишком велик. При стагнации уменьшается влияние rank-one обновления и больше полагаемся на информацию от всей популяции. Условия активации (hsig = 1): алгоритм делает прогресс в определенном направлении, последовательные шаги коррелированны, тогда размер шага адекватен текущей ситуации.
Одно из самых глубоких свойств CMA-ES — его инвариантность к трансформациям пространства поиска. Алгоритм одинаково эффективно решает функцию f(x) и функцию f(Ax + b), где A — любая невырожденная матрица, а b — любой вектор сдвига. Это означает, что CMA-ES не зависит от выбора системы координат. Эта инвариантность не случайна — она является прямым следствием использования принципа максимального правдоподобия и адаптации ковариационной матрицы. Алгоритм автоматически обнаруживает естественную систему координат задачи, где оси совпадают с главными направлениями вариации функции.
Красота теории должна сочетаться с практической применимостью. CMA-ES требует O(n²) памяти для хранения ковариационной матрицы и O(n³) вычислений для ее собственного разложения, что делает алгоритм применимым для задач размерности до нескольких сотен переменных. Для больших размерностей разработаны специализированные модификации sep-CMA-ES ограничивается диагональными ковариационными матрицами, VkD-CMA использует переменную размерность, а LM-CMA применяет принципы ограниченной памяти, реализация этих методов пока выходит за рамки нашей статьи, возможно в последующих статьях будет возможность к ним вернуться.
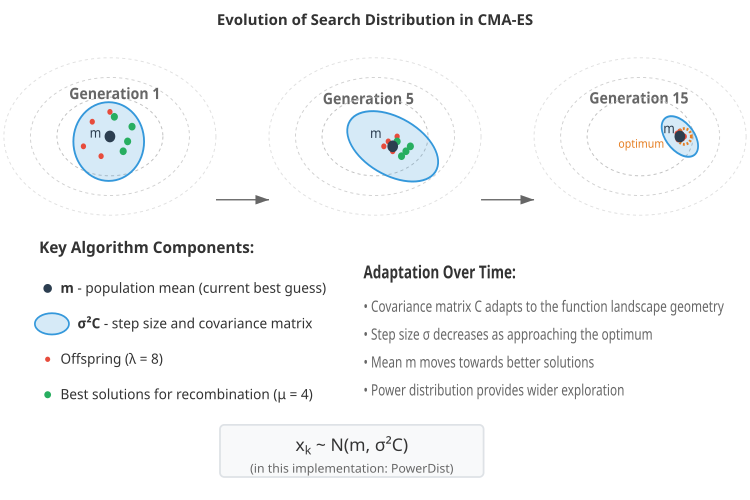
Рисунок 1. Иллюстрация работы алгоритма CMA-ES
На иллюстрации показана эволюция через поколения - три снимка состояния алгоритма (поколения 1, 5 и 15), показывающие как популяция постепенно сходится к оптимуму,
Адаптация ковариационной матрицы - синие эллипсы показывают, как изменяется форма распределения, когда поколение: 1- круглое (единичная матрица), 5 - вытянутое и повернутое, 15 - точно настроенное на локальную геометрию.
Компоненты алгоритма: красные точки - вся популяция (λ потомков), зеленые точки - лучшие решения (μ родителей), черная точка m - среднее популяции, пунктирные круги - изолинии целевой функции.
Ключевая формула внизу с пометкой о модификации степенным распределением. Иллюстрация наглядно демонстрирует, как алгоритм адаптирует свою стратегию поиска к ландшафту оптимизируемой функции, постепенно сужая область поиска и приближаясь к оптимуму.
Переходим к написанию псевдокода алгоритма.
Инициализация
- Установить параметры алгоритма:
- Размер популяции (lambda) = 50
- Количество родителей (mu) = 25
- Скорость обучения для ранг-1 обновления (c1) = 0.01
- Скорость обучения для ранг-μ обновления (cμ) = 0.8
- Демпфирование размера шага = 0.6
- Начальный размер шага (sigma) = 0.3
- Вычислить веса рекомбинации:
- Для каждого из μ родителей вычислить вес как log(μ + 0.5) - log(i + 1)
- Нормализовать веса так, чтобы их сумма равнялась 1
- Вычислить эффективную массу выбора μ_eff
- Инициализировать параметры стратегии:
- Вычислить скорости обучения для путей эволюции (cs, cc)
- Установить ожидаемую норму стандартного нормального распределения (chiN)
- Определить интервал для разложения на собственные значения
- Инициализировать структуры данных:
- Ковариационная матрица C = единичная матрица
- Матрица собственных векторов B = единичная матрица
- Вектор собственных значений D = единичный вектор
- Пути эволюции pc и ps = нулевые векторы
- Среднее значение популяции m = случайная точка в пространстве поиска
- Создать начальную популяцию:
- Сгенерировать lambda случайных точек в пространстве поиска
Основной цикл эволюции
Повторять пока не достигнут критерий остановки:
Этап 1: Генерация потомков
- Для каждого из lambda потомков:
- Сгенерировать случайный вектор z из стандартного нормального распределения
- Применить преобразование: y = B × D × z
- Создать потомка: x_k = m + σ × y
- Применить ограничения пространства поиска к x_k
Этап 2: Оценка и обновление
- Оценить фитнес всех потомков
- Отсортировать популяцию:
- Упорядочить потомков по убыванию фитнеса
- Обновить лучшее найденное решение, если необходимо
- Обновить среднее значение популяции:
- Сохранить старое среднее m_old
- Вычислить новое среднее как взвешенную сумму μ лучших потомков: m_new = Σ(w_i × x_i) для i от 1 до μ
- Обновить пути эволюции:
- Вычислить смещение среднего: y_w = (m_new - m_old) / σ
- Вычислить C^(-1/2) × y_w через разложение на собственные значения
- Обновить путь эволюции для размера шага: ps = (1 - cs) × ps + √(cs × (2 - cs) × μ_eff) × C^(-1/2) × y_w
- Проверить условие стагнации (функция Хевисайда)
- Обновить путь эволюции для ковариационной матрицы: pc = (1 - cc) × pc + индикатор_стагнации × √(cc × (2 - cc) × μ_eff) × y_w
- Обновить ковариационную матрицу:
- Подготовить ранг-1 обновление из внешнего произведения pc
- Подготовить ранг-μ обновление из взвешенной суммы отклонений лучших потомков
- Обновить C: C = (1 - c1 - cμ) × C + c1 × (pc × pc^T) + cμ × Σ(w_i × y_i × y_i^T)
- Обеспечить симметричность матрицы
- Обновить размер шага:
- Вычислить коэффициент адаптации на основе длины пути ps
- Обновить σ: σ = σ × exp((cs/damps) × (||ps||/chiN - 1))
- Ограничить σ в разумных пределах для численной стабильности
- Разложение на собственные значения (при необходимости):
- Если прошло достаточно итераций с последнего разложения:
- Выполнить разложение C = B × D² × B^T методом Якоби
- Отсортировать собственные значения и векторы по убыванию
- Обеспечить положительную определенность матрицы
- Если прошло достаточно итераций с последнего разложения:
- Проверка и коррекция ковариационной матрицы:
- Периодически проверять положительную определенность C
- При необходимости добавить малое значение к диагонали
- Обеспечить симметричность матрицы
Теперь напишем класс "C_AO_CMAES", производный от класса "C_AO", который будет реализовать алгоритм оптимизации CMA-ES.
Публичные поля, метод:
- SetParams () - устанавливает значения параметров CMA-ES из массива "params".
- Init () - инициализирует алгоритм. Принимает минимальные, максимальные значения и размер шага для каждой переменной, а также количество эпох.
- Moving () - реализует основной цикл алгоритма, отвечающий за генерацию новых решений.
- Revision () - оценка новых решений и обновления состояния алгоритма.
Приватные поля:
- Параметры CMA-ES - переменные, содержащие специфичные параметры алгоритма CMA-ES: количество родителей (mu), размер шага (sigma), скорости обучения (learningRateC1, learningRateCMu), фактор демпфирования (stepSizeDamping ) и другие, необходимые для работы алгоритма.
- Структуры данных CMA-ES - массивы, используемые для хранения весов рекомбинации (weights), ковариационной матрицы (covMatrix), собственных векторов (B), собственных значений (D), путей эволюции (pc, ps), а также других вспомогательных данных. Переменные "mu_eff", "counteval", "eigeneval", "chiN", "eigenInterval" используются для контроля и управления ходом алгоритма.
- Переменные для оптимизации производительности предназначены для ускорения вычислений в процессе работы алгоритма такие, как скорости обучения и демпфирование.
- Вспомогательные массивы, используемые в качестве временных хранилищ для векторов и матриц при выполнении различных операций.
- Вспомогательные методы, выполняющие отдельные шаги алгоритма CMA-ES такие, как инициализация распределения, обновление распределения, вычисление собственного разложения, сортировка популяции, вычисление весов, обновление среднего значения, проверка положительной определенности и обеспечение положительной определенности.
В целом, класс "C_AO_CMAES" инкапсулирует логику алгоритма CMA-ES, предоставляя интерфейс для инициализации, настройки параметров и выполнения оптимизации. Он содержит параметры, массивы данных и методы, необходимые для реализации алгоритма. Разделение на публичные и приватные поля обеспечивает контроль доступа к внутренним компонентам класса.
//———————————————————————————————————————————————————————————————————— class C_AO_CMAES : public C_AO { public: //---------------------------------------------------------- ~C_AO_CMAES () { } C_AO_CMAES () { ao_name = "CMAES"; ao_desc = "Covariance Matrix Adaptation Evolution Strategy"; ao_link = "https://www.mql5.com/ru/articles/18227"; // Параметры по умолчанию popSize = 50; // Размер популяции по умолчанию (lambda) mu = 25; // Количество родителей (половина популяции) learningRateC1 = 0.01; // Скорость обучения для ранг-1 обновления learningRateCMu = 0.8; // Скорость обучения для ранг-μ обновления stepSizeDamping = 0.6; // Демпфирование для размера шага // Создание и инициализация массива параметров ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "mu"; params [1].val = mu; params [2].name = "learningRateC1"; params [2].val = learningRateC1; params [3].name = "learningRateCMu"; params [3].val = learningRateCMu; params [4].name = "stepSizeDamping"; params [4].val = stepSizeDamping; } void SetParams () { popSize = (int)params [0].val; mu = (int)params [1].val; learningRateC1 = params [2].val; learningRateCMu = params [3].val; stepSizeDamping = params [4].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // размер шага const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ private: //--------------------------------------------------------- // Специфичные параметры CMA-ES int mu; // Количество родителей (выбранных точек) double sigma; // Размер шага double learningRateC1; // Скорость обучения для ранг-1 обновления double learningRateCMu; // Скорость обучения для ранг-μ обновления double stepSizeDamping; // Фактор демпфирования для обновления размера шага // Специфичные структуры данных CMA-ES double weights []; // Веса рекомбинации double covMatrix []; // Ковариационная матрица (хранится как одномерный массив) double B []; // Собственные векторы C double D []; // Собственные значения (квадратные корни) C double pc []; // Путь эволюции для C double ps []; // Сопряженный путь эволюции для sigma double mu_eff; // Эффективная масса выбора дисперсии int counteval; // Счетчик вычислений функции с последнего разложения int eigeneval; // Счетчик генераций, когда выполнялось разложение double chiN; // Ожидаемая норма N(0,I) int eigenInterval; // Интервал для разложения на собственные значения // Переменные для оптимизации производительности double cs; // Скорость обучения для пути sigma double cc; // Скорость обучения для пути ранг-1 double damps; // Демпфирование для sigma double hsig_threshold; // Порог для функции Хевисайда // Вспомогательные массивы double y_vec []; // Вектор мутации double arindex []; // Массив индексов для сортировки double arfitness []; // Массив фитнеса для сортировки double temp_vec []; // Временный вектор для матричных операций double invsqrtC_times_yw []; // Временное хранилище для C^(-1/2) * y_w // Переменные кэширования для Бокса-Мюллера double cached_normal; bool has_cached; // Вспомогательные методы void InitDistribution (); void UpdateDistribution (); void ComputeEigendecomposition (); double GetChiN (); void SortPopulation (); void ComputeWeights (); void UpdateMean (); bool CheckPositiveDefinite (); void EnforcePositiveDefinite (); }; //————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_CMAES" выполняет инициализацию алгоритма CMA-ES. Он принимает минимальные и максимальные значения параметров, размер шага и количество эпох в качестве входных данных. Сначала вызывается метод "StandardInit" для выполнения стандартной инициализации. Инициализируется флаг "has_cached" в "false", чтобы указать, что кэшированное значение для генерации случайных чисел по методу Бокса-Мюллера отсутствует. Далее инициализируется размер шага "sigma" начальным значением, равным 0.3 (30% от диапазона поиска). Вызывается метод "ComputeWeights" для вычисления весов рекомбинации, вызывается метод "GetChiN" для вычисления ожидаемой нормы N(0, I).
Вычисляются параметры "cs", "cc", "damps" и "hsig_threshold" на основе "mu_eff" (эффективная масса) и количества координат (coords). Эти параметры используются для адаптации стратегии CMA-ES во время работы. Вычисляется и устанавливается "eigenInterval", определяющий частоту выполнения разложения на собственные значения. Этот параметр настраивается для оптимизации производительности.
Выделяется память для массивов, специфичных для CMA-ES, таких, как ковариационная матрица "covMatrix", собственные векторы "B", собственные значения "D", пути эволюции "pc" и "ps", временные векторы "y_vec", "arindex", "arfitness", "temp_vec" и "invsqrtC_times_yw". Массивы пересоздаются только если требуется изменить размерность задачи.
Инициализируются массивы путей эволюции "pc" и "ps" нулями, ковариационная матрица "covMatrix" и матрица собственных векторов "B" единичной матрицей, а массив собственных значений "D" — единицами. Вызывается метод "InitDistribution" для инициализации начального распределения. Затем сбрасываются счетчики вычислений функции "counteval" и "eigeneval". Устанавливается флаг "revision" в "true", чтобы указать, что необходимо пересчитать значения фитнеса. Возвращается "true" при успешной инициализации.
В заключение, метод "Init" выполняет всю необходимую инициализацию для работы алгоритма CMA-ES, включая установку параметров, выделение памяти для массивов и инициализацию начальных значений.
//———————————————————————————————————————————————————————————————————— bool C_AO_CMAES::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // размер шага const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Инициализация кэширования Бокса-Мюллера has_cached = false; // Инициализация специфичных переменных CMA-ES sigma = 0.3; // Начальный размер шага (30% от диапазона поиска) // Вычисление эффективной массы выбора дисперсии ComputeWeights (); // Ожидаемая норма N(0,I) chiN = GetChiN (); // Вычисление и сохранение параметров стратегии cs = (mu_eff + 2.0) / (coords + mu_eff + 5.0); cc = (4.0 + mu_eff / coords) / (coords + 4.0 + 2.0 * mu_eff / coords); damps = 1.0 + 2.0 * MathMax (0.0, MathSqrt ((mu_eff - 1.0) / (coords + 1.0)) - 1.0) + cs; hsig_threshold = 1.4 + 2.0 / (coords + 1.0); // Установка интервала разложения на собственные значения - настройка для производительности eigenInterval = (int)(coords / (10.0 * MathSqrt (learningRateC1 + learningRateCMu))); eigenInterval = MathMax (1, eigenInterval); // Выделение массивов - выделяем только один раз ArrayResize (covMatrix, coords * coords); ArrayResize (B, coords * coords); ArrayResize (D, coords); ArrayResize (pc, coords); ArrayResize (ps, coords); ArrayResize (y_vec, coords); ArrayResize (arindex, popSize); ArrayResize (arfitness, popSize); ArrayResize (temp_vec, coords); ArrayResize (invsqrtC_times_yw, coords); // Инициализация путей эволюции нулями ArrayInitialize (pc, 0); ArrayInitialize (ps, 0); // Быстрая инициализация единичной ковариационной матрицы и разложения ArrayInitialize (covMatrix, 0.0); ArrayInitialize (B, 0.0); for (int i = 0; i < coords; i++) { covMatrix [i * coords + i] = 1.0; B [i * coords + i] = 1.0; D [i] = 1.0; } // Инициализация начального распределения InitDistribution (); // Сброс счетчиков вычислений counteval = 0; eigeneval = 0; // Принудительный пересчет фитнеса revision = true; return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" в классе "C_AO_CMAES" отвечает за генерацию новых потомков (решений) в популяции. Преобразование y = B * D * z: внутри цикла по популяции есть вложенный цикл, который перебирает все координаты "coords" каждой особи. В каждой координате "i" вычисляется значение "y_vec [i]". Это делается путем матричного умножения. Фактически, это умножение вектора случайных чисел "z" на матрицу "B * D", где "B - собственные векторы ковариационной матрицы, а "D" - собственные значения ковариационной матрицы, и "z" - случайные числа, сгенерированные с использованием функции "u.PowerDistribution".
Генерация потомка: для каждой координаты "i" каждого потомка "k" вычисляется значение (a [k].c [i]). Это делается путем добавления к текущему среднему значению "cB [i]" (центр текущего распределения) масштабированного вектора "y_vec [i]". Масштабирование выполняется умножением "y_vec [i]" на размер шага "sigma". Таким образом, a [k].c [i] = cB [i] + sigma * y_vec [i].
Функция "u.SeInDiSp" гарантирует, что значения координат потомков остаются в пределах допустимых диапазонов, определенных "rangeMin [i]", "rangeMax [i]" и "rangeStep [i]". Она может обрезать значения, отражать их от границ и квантовать их к ближайшему допустимому значению шага. После генерации всех потомков устанавливается флаг "revision" в "true", значения фитнес-функции (качества) для сгенерированных потомков должны быть пересчитаны.
В итоге, метод генерирует новую популяцию решений на основе текущего распределения (среднее "cB" и ковариационная матрица, представленная через "B" и "D") и размера шага "sigma". Он использует случайные числа для создания небольших изменений вокруг текущего среднего, чтобы исследовать пространство поиска. Функция "SeInDiSp" обеспечивает, чтобы новые решения оставались в пределах допустимых границ, и флаг "revision" гарантирует, что качество этих решений будет оценено.
//———————————————————————————————————————————————————————————————————— void C_AO_CMAES::Moving () { // Генерация lambda новых потомков for (int k = 0; k < popSize; k++) { // Применение преобразования y = B*D*z for (int i = 0; i < coords; i++) { y_vec [i] = 0.0; for (int j = 0; j < coords; j++) { y_vec [i] += B [i * coords + j] * D [j] * u.PowerDistribution (0.0, -8, 8, 20); } // Генерация потомка: x_k = m + σ * y a [k].c [i] = cB [i] + sigma * y_vec [i]; a [k].c [i] = u.SeInDiSp (a [k].c [i], rangeMin [i], rangeMax [i], rangeStep [i]); } } // Отметка для пересчета фитнеса revision = true; } //————————————————————————————————————————————————————————————————————
Метод "Revision" класса "C_AO_CMAES" отвечает за обновление параметров алгоритма после оценки фитнес-функции для новой популяции. Сначала метод проверяет значение флага "revision". Далее вызывается метод "SortPopulation ()", он сортирует текущую популяцию, чтобы лучшие особи были помещены в начало. Метод "UpdateDistribution ()" обновляет параметры распределения CMA-ES (среднее значение "cB" вектора стратегии, ковариационную матрицу, размер шага "sigma", пути эволюции) на основе информации о лучших особях в популяции. Обновление распределения является ключевым шагом CMA-ES, поскольку оно позволяет алгоритму адаптировать свою стратегию поиска на основе полученных результатов.
В итоге, метод "Revision" представляет собой основной цикл адаптации CMA-ES. Он сортирует популяцию, обновляет параметры распределения на основе лучших особей и увеличивает счетчик вычислений.
//———————————————————————————————————————————————————————————————————— void C_AO_CMAES::Revision () { if (!revision) return; revision = false; // Сортировка популяции по фитнесу SortPopulation (); // Обновление параметров распределения на основе выбранных особей UpdateDistribution (); // Обновление счетчика вычислений counteval++; } //————————————————————————————————————————————————————————————————————
Метод "InitDistribution" класса "C_AO_CMAES" предназначен для инициализации начального распределения поиска решений. Метод определяет начальное среднее значение (cB) для каждой координаты в пространстве поиска. Для каждой координаты "i" значение "cB [i]" устанавливается случайным образом в диапазоне между "rangeMin [i]" и "rangeMax [i]" с помощью функции "u.RNDfromCI ()", начальное среднее значение помещается в центр допустимого диапазона для каждой переменной. Внешний цикл перебирает всю популяцию (popSize особей). Внутри этого цикла находится внутренний цикл, который перебирает все координаты (coords) каждой особи. Для каждого потомка, генерируются его координаты. Сначала они случайным образом выбираются из заданного диапазона "RNDfromCI", а затем округляются до шага дискретизации с помощью "SeInDiSp".
Функция "u.RNDfromCI", генерирует равномерно распределенное случайное число в заданном интервале. Функция "u.SeInDiSp" обеспечивает, что сгенерированные координаты для каждой особи лежат в пределах допустимых границ, определенных rangeMin [i], rangeMax [i] и rangeStep [i].
Метод инициализирует начальную популяцию случайными решениями, равномерно распределенными в пространстве поиска. Центр распределения (cB) так же выбирается случайным образом. Это предоставляет стартовую точку для последующих итераций CMA-ES, в которых алгоритм будет адаптировать стратегию поиска для нахождения оптимального решения.
//+------------------------------------------------------------------+ //| Инициализация распределения поиска | //+------------------------------------------------------------------+ void C_AO_CMAES::InitDistribution () { // Установка начального среднего в центр пространства поиска for (int i = 0; i < coords; i++) { cB [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]); } for (int k = 0; k < popSize; k++) { for (int i = 0; i < coords; i++) { // Генерация равномерно распределенной точки a [k].c [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]); a [k].c [i] = u.SeInDiSp (a [k].c [i], rangeMin [i], rangeMax [i], rangeStep [i]); } } } //————————————————————————————————————————————————————————————————————
Метод "GetChiN" вычисляет математическое ожидание нормы стандартного нормального распределения N (0,I) для заданного числа координат (coords). Результат аппроксимируется на основе размерности пространства поиска.
//+------------------------------------------------------------------+ //| Вычисление ожидаемой нормы N(0,I) | //+------------------------------------------------------------------+ double C_AO_CMAES::GetChiN () { double n = (double)coords; return MathSqrt (n) * (1.0 - 1.0 / (4.0 * n) + 1.0 / (21.0 * n * n)); } //————————————————————————————————————————————————————————————————————
Метод "SortPopulation" предназначен для сортировки популяции решений по их значениям целевой функции (фитнесу) с целью определения наилучшего решения. Сначала, метод копирует значения фитнеса каждой особи из популяции во вспомогательный массив "arfitness". Также создается массив "arindex", который изначально содержит индексы особей. Это необходимо, чтобы после сортировки по фитнесу можно было восстановить соответствие между отсортированным фитнесом и исходной особью в популяции.
Используется алгоритм сортировки вставками (insertion sort). Он проходит по массиву "arfitness", и для каждого элемента вставляет его на правильное место в отсортированной части массива, сдвигая большие элементы вправо. Важно отметить, что сортировка выполняется по убыванию (значение arfitness [j] < tempFitness в цикле while), цель - максимизировать целевую функцию (фитнес). Вместе с "arfitness" синхронно сортируется и "arindex", чтобы отслеживать положение исходных индексов особей.
После сортировки, метод проверяет, является ли фитнес лучшей особи лучше, чем текущее лучшее решение и если это так, "fB" обновляется, и лучшее решение заменяется координатами лучшей особи из популяции. Таким образом, метод не только сортирует популяцию по фитнесу, но и отслеживает лучшее найденное решение на данный момент.
//+------------------------------------------------------------------+ //| Сортировка популяции по фитнесу | //+------------------------------------------------------------------+ void C_AO_CMAES::SortPopulation () { // Копирование значений фитнеса и индексов for (int i = 0; i < popSize; i++) { arindex [i] = i; arfitness [i] = a [i].f; } for (int i = 1; i < popSize; i++) { double tempFitness = arfitness [i]; double tempIndex = arindex [i]; int j = i - 1; // Сортировка по убыванию (для максимизации) while (j >= 0 && arfitness [j] < tempFitness) { arfitness [j + 1] = arfitness [j]; arindex [j + 1] = arindex [j]; j--; } arfitness [j + 1] = tempFitness; arindex [j + 1] = tempIndex; } // Обновление лучшего решения при необходимости if (arfitness [0] > fB) { fB = arfitness [0]; int bestIdx = (int)arindex [0]; ArrayCopy (cB, a [bestIdx].c, 0, 0, coords); } } //————————————————————————————————————————————————————————————————————
Метод "UpdateMean" обновляет среднее значение популяции (cB) путём взвешенной рекомбинации лучших особей. Для каждой координаты новое среднее вычисляется как сумма взвешенных значений координат от лучших особей, где веса заданы в массиве "weights".
//+------------------------------------------------------------------+ //| Обновление среднего с использованием взвешенной рекомбинации | //+------------------------------------------------------------------+ void C_AO_CMAES::UpdateMean () { // Взвешенная рекомбинация: m^(g+1) = Σ w_i * x_{i:λ}^(g+1) for (int j = 0; j < coords; j++) { double meanSum = 0.0; for (int i = 0; i < mu; i++) { int idx = (int)arindex [i]; meanSum += weights [i] * a [idx].c [j]; } cB [j] = meanSum; } } //————————————————————————————————————————————————————————————————————
Метод "ComputeWeights" рассчитывает веса для взвешенной рекомбинации, выделяет массив "weights" размером "mu", вычисляет "log (mu + 0.5)", чтобы использовать его в формуле весов. Для каждого "i" от "0" до "mu-1" присваивает вес как разность log (mu + 0.5) и log (i+1), суммируя эти веса, метод делит все веса на сумму, чтобы сумма была равна 1, и вычисляет сумму квадратов весов, рассчитывает "mu_eff" — эффективность использования весов, что важно для настройки скорости и дисперсии в алгоритме.
Этот метод обеспечивает оптимальные веса для рекомбинации, учитывая вклад лучших решений.
//+------------------------------------------------------------------+ //| Вычисление весов взвешенной рекомбинации | //+------------------------------------------------------------------+ void C_AO_CMAES::ComputeWeights () { // Выделение массива весов ArrayResize (weights, mu); // Предварительное вычисление log(mu + 0.5) double log_mu_plus_half = MathLog (mu + 0.5); // Вычисление положительных весов double sum = 0.0; for (int i = 0; i < mu; i++) { weights [i] = log_mu_plus_half - MathLog (i + 1); sum += weights [i]; } // Нормализация весов double sum_weights = 0.0; double sum_squares = 0.0; for (int i = 0; i < mu; i++) { weights [i] /= sum; sum_weights += weights [i]; sum_squares += weights [i] * weights [i]; } // Вычисление эффективной массы выбора дисперсии mu_eff = sum_weights * sum_weights / sum_squares; } //————————————————————————————————————————————————————————————————————
Метод "UpdateDistribution" обновляет параметры распределения, а именно ковариационную матрицу (covMatrix) и размер шага (sigma) в алгоритме CMA-ES. Если прошло достаточно поколений (counteval - eigeneval > eigenInterval), то вычисляется разложение на собственные значения, сохраняет текущее среднее значение (cB) во временном массиве "oldMean". Метод вызывает "UpdateMean" для вычисления нового среднего значения, вычисляет разницу между новым и старым средним, делённую на "sigma", а так же выполняет умножение "y_w" на C ^ (-1/2), разбитое на несколько шагов с использованием разложения "B" и "D", и сохраняет результат в "invsqrtC_times_yw".
Далее метод обновляет путь эволюции для размера шага "ps", используя "invsqrtC_times_yw", определяет, считать ли прогресс "застрявшим" на основе нормы "ps" и ожидаемой длины, затем обновляет путь эволюции для ковариационной матрицы "pc", используя "y_w" и индикатор прогресса "hsig". Сначала метод вычисляет "ранг-1" матрицу обновления "c1a", потом "ранг-μ" матрицу обновления "cmu" на основе разницы отдельных особей и старого среднего, делённой на "sigma", с использованием весов "weights", делает обновление ковариационной матрицы "covMatrix" с использованием "ранг-1" и "ранг-μ" обновлений и корректирует "c1" при застое прогресса. Периодически вызывается "EnforcePositiveDefinite" для обеспечения положительной определённости ковариационной матрицы. Обновляется размер шага "sigma" на основе нормы "ps" и ограничивается в пределах "min_sigma" и "max_sigma" для численной стабильности.
В целом, "UpdateDistribution" корректирует параметры распределения (ковариационную матрицу и размер шага) на основе истории поиска (пути эволюции) и данных о популяции, чтобы приспособиться к ландшафту целевой функции.
//+------------------------------------------------------------------+ //| Обновление параметров распределения | //+------------------------------------------------------------------+ void C_AO_CMAES::UpdateDistribution () { // Проверка необходимости разложения на собственные значения if (counteval - eigeneval > eigenInterval) { ComputeEigendecomposition (); eigeneval = counteval; } // Сохранение старого среднего double oldMean []; ArrayResize (oldMean, coords); ArrayCopy (oldMean, cB, 0, 0, coords); // Обновление среднего UpdateMean (); // Вычисление смещения среднего double y_w []; ArrayResize (y_w, coords); for (int j = 0; j < coords; j++) { y_w [j] = (cB [j] - oldMean [j]) / sigma; } // Вычисление C^(-1/2) * y_w // Шаг 1: B^T * y_w ArrayInitialize (temp_vec, 0.0); for (int i = 0; i < coords; i++) { for (int j = 0; j < coords; j++) { temp_vec [i] += B [j * coords + i] * y_w [j]; } } // Шаг 2: D^(-1) * (B^T * y_w) for (int i = 0; i < coords; i++) { temp_vec [i] /= D [i]; } // Шаг 3: B * D^(-1) * B^T * y_w ArrayInitialize (invsqrtC_times_yw, 0.0); for (int i = 0; i < coords; i++) { for (int j = 0; j < coords; j++) { invsqrtC_times_yw [i] += B [i * coords + j] * temp_vec [j]; } } // Обновление пути эволюции для sigma double norm_ps_squared = 0.0; for (int i = 0; i < coords; i++) { ps [i] = (1.0 - cs) * ps [i] + MathSqrt (cs * (2.0 - cs) * mu_eff) * invsqrtC_times_yw [i]; norm_ps_squared += ps [i] * ps [i]; } // Функция Хевисайда double norm_ps = MathSqrt (norm_ps_squared); double expected_length = MathSqrt (1.0 - MathPow (1.0 - cs, 2.0 * counteval)) * chiN; bool hsig = norm_ps / expected_length < hsig_threshold; // Обновление пути эволюции для C double delta_hsig = hsig ? 1.0 : 0.0; for (int i = 0; i < coords; i++) { pc [i] = (1.0 - cc) * pc [i] + delta_hsig * MathSqrt (cc * (2.0 - cc) * mu_eff) * y_w [i]; } // Подготовка ранг-1 обновления double c1a []; ArrayResize (c1a, coords * coords); for (int i = 0; i < coords; i++) { for (int j = 0; j <= i; j++) { c1a [i * coords + j] = c1a [j * coords + i] = pc [i] * pc [j]; } } // Подготовка ранг-μ обновления double cmu []; ArrayResize (cmu, coords * coords); ArrayInitialize (cmu, 0.0); for (int k = 0; k < mu; k++) { int idx = (int)arindex [k]; // Вычисление y_i = (x_i - m_old) / sigma for (int i = 0; i < coords; i++) { temp_vec [i] = (a [idx].c [i] - oldMean [i]) / sigma; } // Добавление взвешенного внешнего произведения for (int i = 0; i < coords; i++) { for (int j = 0; j <= i; j++) { double update = weights [k] * temp_vec [i] * temp_vec [j]; cmu [i * coords + j] += update; if (i != j) cmu [j * coords + i] += update; } } } // Обновление ковариационной матрицы C double c1 = learningRateC1; double cmu_rate = learningRateCMu; // Корректировка c1 если hsig false (застой прогресса) if (!hsig) { c1 *= (1.0 - (1.0 - delta_hsig) * cc * (2.0 - cc)); } double one_minus_c1_cmu = 1.0 - c1 - cmu_rate; // Обновление C с ранг-1 и ранг-μ обновлениями for (int i = 0; i < coords; i++) { for (int j = 0; j <= i; j++) { covMatrix [i * coords + j] = one_minus_c1_cmu * covMatrix [i * coords + j] + c1 * c1a [i * coords + j] + cmu_rate * cmu [i * coords + j]; // Сохранение симметрии if (i != j) { covMatrix [j * coords + i] = covMatrix [i * coords + j]; } } } // Обеспечение положительной определенности if (counteval % (10 * eigenInterval) == 0) { EnforcePositiveDefinite (); } // Обновление размера шага sigma double exponent = (cs / damps) * (norm_ps / chiN - 1.0); sigma *= MathExp (exponent); // Ограничение sigma для численной стабильности double min_sigma = 1e-16; double max_eigenvalue = D [0]; // D отсортирован по убыванию double max_sigma = 1e4 * MathMax (1.0, MathSqrt (max_eigenvalue)); if (sigma < min_sigma) sigma = min_sigma; else if (sigma > max_sigma) sigma = max_sigma; } //————————————————————————————————————————————————————————————————————
Метод "ComputeEigendecomposition" выполняет разложение симметричной ковариационной матрицы "covMatrix" на собственные значения и собственные векторы с помощью улучшенного метода Якоби, метод создаёт копию "covMatrix", чтобы не изменять исходные данные. Изначально "B" задаётся как единичная матрица, представляющая начальный базис. Выполняет максимум итераций или пока ненулевые элементы на вне диагонали не станут меньше "tolerance".
Поиск максимального вне диагонального элемента: находит элемент с максимальным по абсолютному значению вне диагонали, чтобы выбрать для поворота. Далее, если максимум меньше "tolerance", цикл прерывается. Метод вычисляет "phi" для проведения поворота Якоби, изменяет элементы "C_copy", применяя поворот, обновляет столбцы матрицы "B" (собственные векторы) в соответствии с поворотом. После итераций метод находит корень квадратный из диагональных элементов (обеспечивая минимальную положительность 1e-14) и упорядочивает по убыванию собственные значения и соответствующие собственные векторы для дальнейшего использования. Таким образом, метод позволяет точно вычислить собственные значения и векторы ковариационной матрицы.
//+------------------------------------------------------------------+ //| Вычисление разложения на собственные значения методом Якоби | //+------------------------------------------------------------------+ void C_AO_CMAES::ComputeEigendecomposition () { // Создание копии ковариационной матрицы для разложения double C_copy []; ArrayResize (C_copy, coords * coords); ArrayCopy (C_copy, covMatrix); // Инициализация B как единичной матрицы for (int i = 0; i < coords; i++) { for (int j = 0; j < coords; j++) { B [i * coords + j] = (i == j) ? 1.0 : 0.0; } } // Улучшенное разложение Якоби на собственные значения int max_iterations = 10; //50 * coords; double tolerance = 0.01; //1e-14 * coords * coords; for (int iter = 0; iter < max_iterations; iter++) { // Поиск наибольшего вне диагонального элемента double max_val = 0.0; int p = 0, q = 1; for (int i = 0; i < coords - 1; i++) { for (int j = i + 1; j < coords; j++) { double val = MathAbs (C_copy [i * coords + j]); if (val > max_val) { max_val = val; p = i; q = j; } } } // Проверка сходимости if (max_val < tolerance) break; // Вычисление угла поворота double app = C_copy [p * coords + p]; double aqq = C_copy [q * coords + q]; double apq = C_copy [p * coords + q]; double phi = 0.5 * MathArctan (2.0 * apq / (aqq - app + 1e-14)); double c = MathCos (phi); double s = MathSin (phi); // Обновление элементов матрицы double app_new = c * c * app - 2 * c * s * apq + s * s * aqq; double aqq_new = s * s * app + 2 * c * s * apq + c * c * aqq; C_copy [p * coords + p] = app_new; C_copy [q * coords + q] = aqq_new; C_copy [p * coords + q] = C_copy [q * coords + p] = 0.0; // Обновление других элементов в строках/столбцах p и q for (int i = 0; i < coords; i++) { if (i != p && i != q) { double aip = C_copy [i * coords + p]; double aiq = C_copy [i * coords + q]; C_copy [i * coords + p] = C_copy [p * coords + i] = c * aip - s * aiq; C_copy [i * coords + q] = C_copy [q * coords + i] = s * aip + c * aiq; } } // Обновление собственных векторов for (int i = 0; i < coords; i++) { double bip = B [i * coords + p]; double biq = B [i * coords + q]; B [i * coords + p] = c * bip - s * biq; B [i * coords + q] = s * bip + c * biq; } } // Извлечение собственных значений и обеспечение положительности double min_eigenvalue = 1e-14; for (int i = 0; i < coords; i++) { D [i] = MathSqrt (MathMax (min_eigenvalue, C_copy [i * coords + i])); } // Сортировка собственных значений и векторов по убыванию for (int i = 0; i < coords - 1; i++) { int max_idx = i; for (int j = i + 1; j < coords; j++) { if (D [j] > D [max_idx]) max_idx = j; } if (max_idx != i) { // Обмен собственных значений double temp = D [i]; D [i] = D [max_idx]; D [max_idx] = temp; // Обмен собственных векторов for (int k = 0; k < coords; k++) { temp = B [k * coords + i]; B [k * coords + i] = B [k * coords + max_idx]; B [k * coords + max_idx] = temp; } } } } //————————————————————————————————————————————————————————————————————
Метод "CheckPositiveDefinite" проверяет, является ли ковариационная матрица положительно определенной. Он быстро проверяет положительность диагональных элементов и сравнивает минимальное собственное значение (из массива "D", отсортированного по убыванию) с небольшим положительным числом 1e-14. Если обе проверки проходят, метод возвращает "true".
//+------------------------------------------------------------------+ //| Проверка положительной определенности ковариационной матрицы | //+------------------------------------------------------------------+ bool C_AO_CMAES::CheckPositiveDefinite () { // Быстрая проверка: все диагональные элементы должны быть положительными for (int i = 0; i < coords; i++) { if (covMatrix [i * coords + i] <= 0) return false; } // Проверка минимального собственного значения на положительность double min_eigenvalue = D [coords - 1]; // D отсортирован по убыванию return min_eigenvalue > 1e-14; } //————————————————————————————————————————————————————————————————————
Метод "EnforcePositiveDefinite" обеспечивает положительную определенность ковариационной матрицы "covMatrix". Он выполняет несколько шагов: находит минимальный элемент на диагонали и добавляет недостающую величину "correction" к диагональным элементам, чтобы минимальный был равен 1e-10, максимизирует симметричность матрицы, усредняя каждый вне диагональный элемент с его транспонированным значением.
Если матрица всё ещё не является положительно определенной, выполняется разложение на собственные значения с помощью "ComputeEigendecomposition", заменяет все собственные значения, менее чем √1e-10, на √1e-10 для обеспечения положительности. Далее метод пересчитывает "covMatrix", используя собственные векторы "B" и исправленные собственные значения "D", чтобы получить скорректированную положительно определенную матрицу. Такой подход гарантирует, что ковариационная матрица станет положительно определенной и пригодной для дальнейших вычислений в алгоритме CMA-ES.
//+------------------------------------------------------------------+ //| Обеспечение положительной определенности ковариационной матрицы | //+------------------------------------------------------------------+ void C_AO_CMAES::EnforcePositiveDefinite () { // Метод 1: Добавление малого значения к диагонали double min_diag = 1e308; // Очень большое число for (int i = 0; i < coords; i++) { if (covMatrix [i * coords + i] < min_diag) { min_diag = covMatrix [i * coords + i]; } } if (min_diag < 1e-10) { double correction = 1e-10 - min_diag; for (int i = 0; i < coords; i++) { covMatrix [i * coords + i] += correction; } } // Метод 2: Обеспечение симметрии for (int i = 0; i < coords; i++) { for (int j = i + 1; j < coords; j++) { double avg = (covMatrix [i * coords + j] + covMatrix [j * coords + i]) * 0.5; covMatrix [i * coords + j] = covMatrix [j * coords + i] = avg; } } // Если все еще не положительно определена, выполнить разложение и исправить if (!CheckPositiveDefinite ()) { ComputeEigendecomposition (); double min_eigenvalue = 1e-10; for (int i = 0; i < coords; i++) { if (D [i] < MathSqrt (min_eigenvalue)) { D [i] = MathSqrt (min_eigenvalue); } } // Восстановление C = B * D^2 * B^T ArrayInitialize (covMatrix, 0.0); for (int i = 0; i < coords; i++) { for (int j = 0; j <= i; j++) { double sum = 0.0; for (int k = 0; k < coords; k++) { sum += B [i * coords + k] * D [k] * D [k] * B [j * coords + k]; } covMatrix [i * coords + j] = covMatrix [j * coords + i] = sum; } } } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Теперь наконец-то, можем посмотреть на результаты. Алгоритм, что можно сразу выделить, прекрасно и быстро справляется с задачами средней размерности, при определенных настройках и с задачами малой размерности, а вот наиболее трудные, многомерные задачи, требуют несоразмерно ресурсам много времени для исполнения, поэтому фактически были исключены из результатов. С чем это связано? Традиционно матричные вычисления в MQL5 представляют серьезную вычислительную проблему. При ручной реализации матричных операций алгоритм демонстрирует неудовлетворительную производительность на задачах высокой размерности, что существенно ограничивает его практическую применимость. Однако с появлением встроенных классов для работы с матрицами ситуация кардинально меняется. Теперь критически важно использовать нативную реализацию матричных операций платформы для всех вычислительно-интенсивных задач.
=============================
5 Hilly's; Func runs: 10000; result: 0.7625797883550075
25 Hilly's; Func runs: 10000; result: 0.7208874560706138
500 Hilly's; Func runs: 10000; result: 0.0
=============================
5 Forest's; Func runs: 10000; result: 0.8205636421348295
25 Forest's; Func runs: 10000; result: 0.7961602627346933
500 Forest's; Func runs: 10000; result: 0.0
=============================
5 Megacity's; Func runs: 10000; result: 0.7584615384615383
25 Megacity's; Func runs: 10000; result: 0.49076923076923074
500 Megacity's; Func runs: 10000; result: 0.0
=============================
All score: 4.34942 (48.33%)
На визуализации можем заметить, что алгоритм работает как "большими прыжками" так и фокусируется на экстремумах функции, тщательно их исследуя.

CMA-ES на тестовой функции Hilly
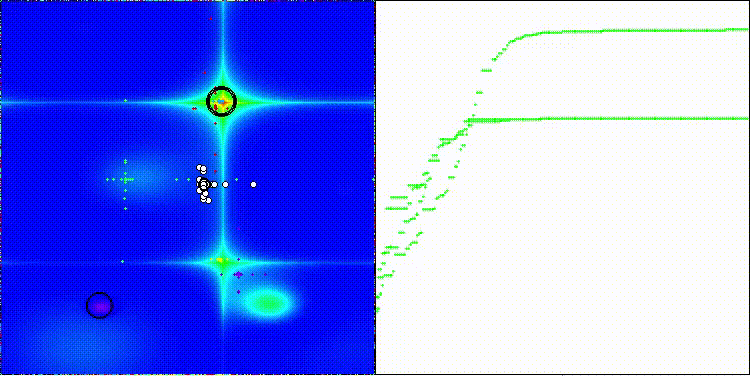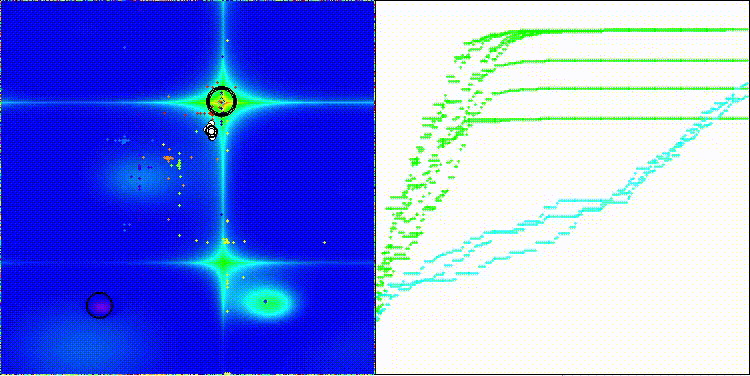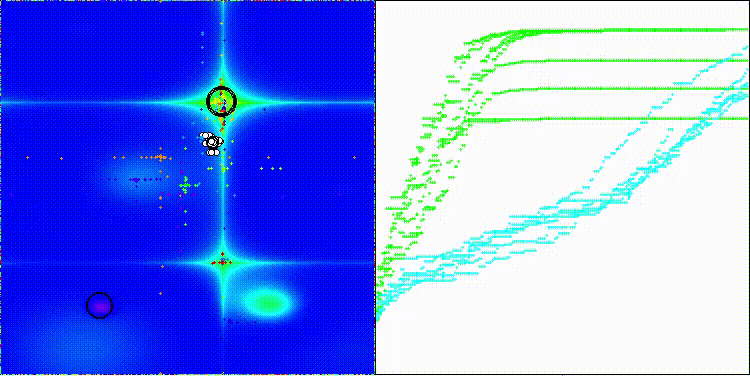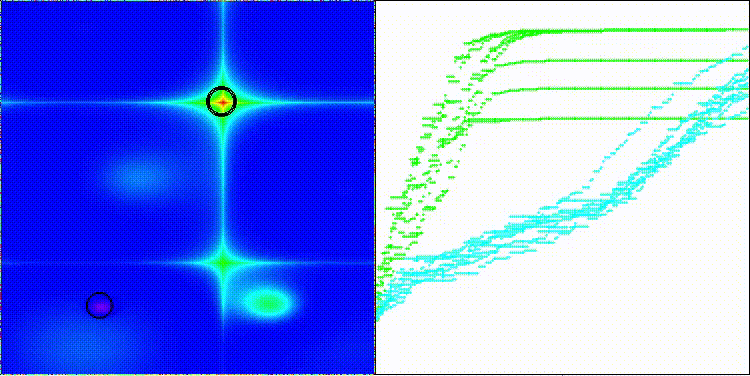
CMA-ES на тестовой функции Forest
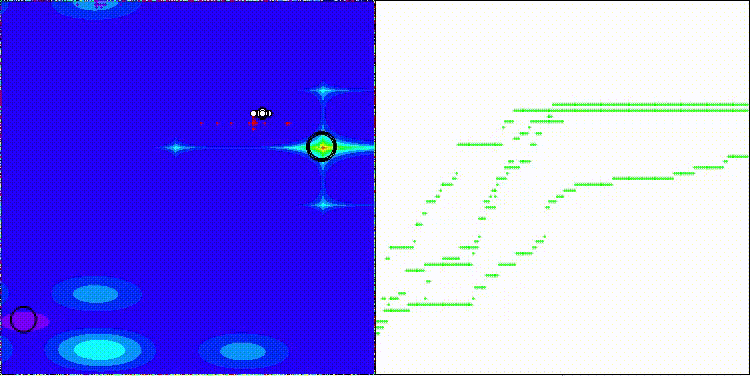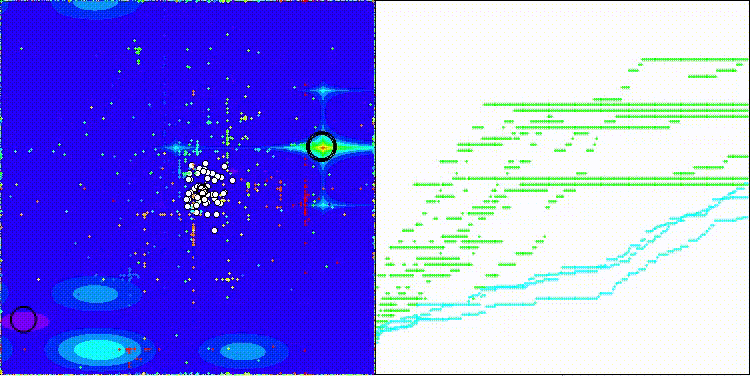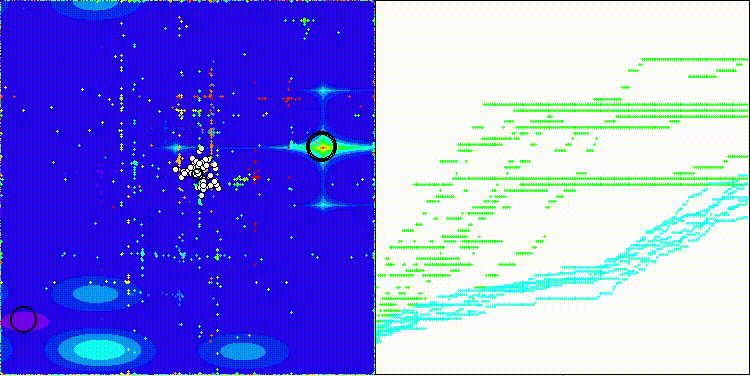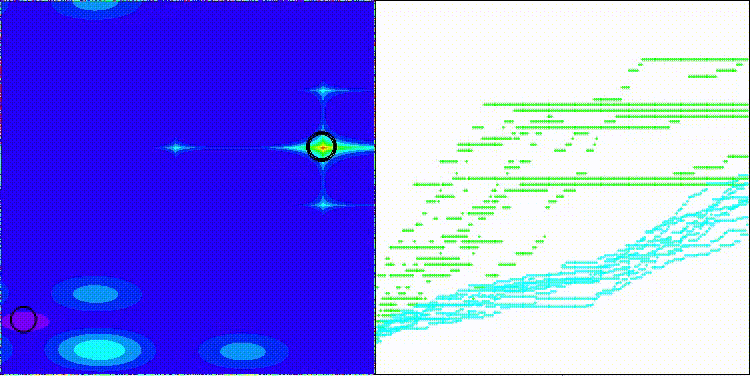
CMA-ES на тестовой функции Megacity
По итогам работы алгоритм CMA-ES занимает 38 место в рейтинге самых сильных популяционных алгоритмов оптимизации.
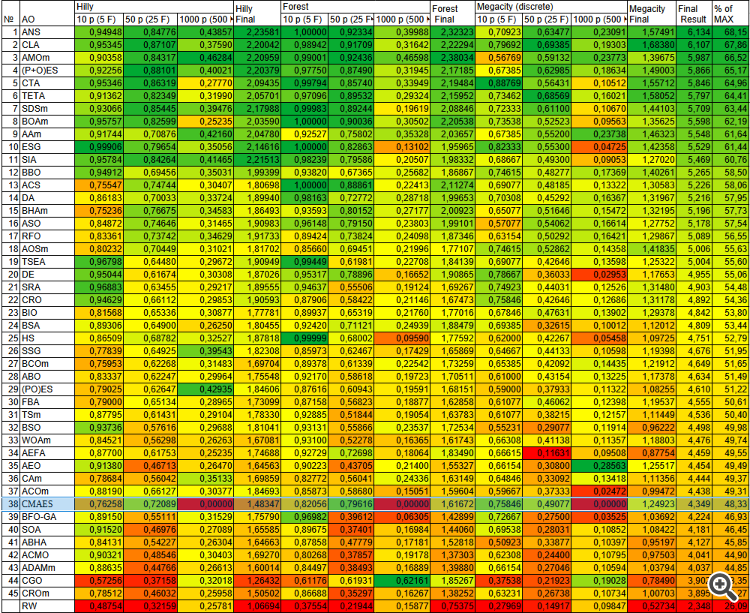
№ | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 13 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 14 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 15 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 16 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 17 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 18 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 19 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 20 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 21 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 22 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 23 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 24 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 25 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 26 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 27 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 28 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 29 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 30 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 31 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 32 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 33 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 34 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 35 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 36 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 37 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 38 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 39 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 40 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 41 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 42 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 43 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 44 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 45 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
CMA-ES способен адаптировать стратегию поиска к локальной геометрии целевой функции делает его практически незаменимым для сложных, плохо обусловленных задач с неизвестной структурой. Тяжелые хвосты степенного распределения позволяют алгоритму совершать "дальние прыжки", что критически важно для выхода из локальных оптимумов. Вычислительная сложность O(n²) по памяти и O(n³) по времени жестко ограничивает применимость алгоритма. Для задач высокой размерности (n > 100) ресурсоемкость становится непропорциональной получаемым преимуществам. Время работы на многомерных функциях растет настолько быстро, что делает алгоритм практически неприменимым для больших n.
CMA-ES работает на зашумленных функциях, справляется с разрывными целевыми функциями, эффективен на многоэкстремальных ландшафтах и секрет этой универсальности кроется в фундаментальной философии алгоритма: вместо того чтобы делать предположения о структуре функции, он осторожно изучает ее, адаптируя свою стратегию поиска на основе накапливаемого опыта. CMA-ES меняет ландшафт эволюционных вычислений, показывая, что биологически инспирированные алгоритмы могут иметь строгие математические основания и адаптация алгоритма — это не просто подстройка параметров, а фундаментальный принцип обучения структуре задачи.
Алгоритм отлично подходит для задач со средними размерностями, это специализированный инструмент, который достойно выглядит альтернативой в своей нише. Алгоритм сочетает математическую элегантность с практической эффективностью, но требует осознанного применения с учетом его вычислительных ограничений. В подобных случаях для расчета матриц разработчиками языка MQL5 недавно были внедрены быстрые матричные операции MQL5, в данной реализации алгоритма были применены обычные последовательные вычисления.
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
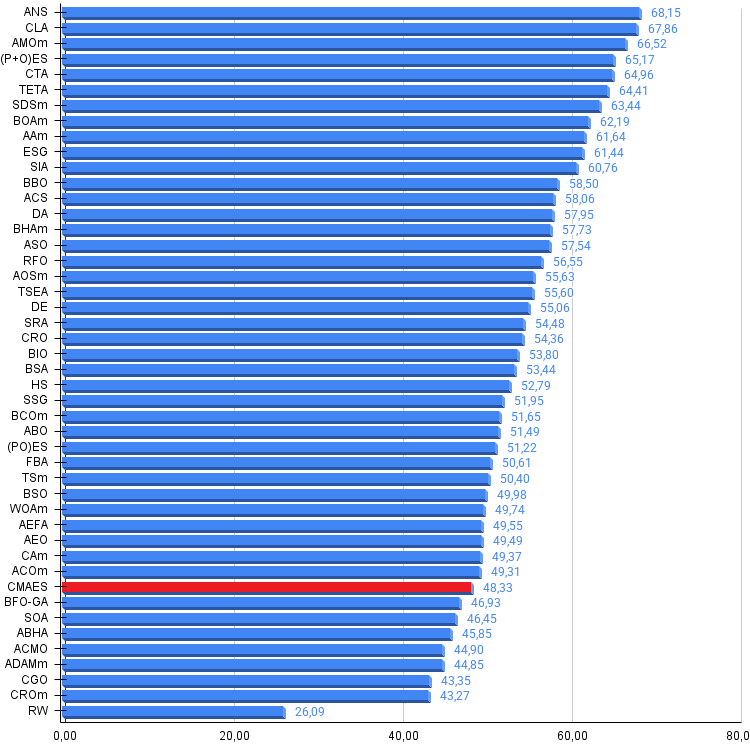
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма CMAES:
Плюсы:
- Хорошая сходимость на функциях средней размерности.
Минусы:
- Разброс результатов на функциях малой размерности.
- Критичная ресурсоемкость на функциях большой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_CMAES.mq5 | Скрипт | Испытательный стенд для CMAES |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 От Python к MQL5: Путешествие в квантовые торговые системы
От Python к MQL5: Путешествие в квантовые торговые системы
 Автоматизация торговых стратегий с помощью MQL5 (Часть 1): Система Profitunity (Торговый хаос Билла Вильямса)
Автоматизация торговых стратегий с помощью MQL5 (Часть 1): Система Profitunity (Торговый хаос Билла Вильямса)
 Нейросети в трейдинге: Адаптивная периодическая сегментация (LightGTS)
Нейросети в трейдинге: Адаптивная периодическая сегментация (LightGTS)
 Подробная информация о торговле на основе объема: Выход за рамки графиков OHLC
Подробная информация о торговле на основе объема: Выход за рамки графиков OHLC
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования