Эко-эволюционный алгоритм — Eco-inspired Evolutionary Algorithm (ECO)

MetaTrader 5 — Трейдинг | 23 января 2026, 11:09

Andrey Dik

Содержание

Введение

В данной статье познакомимся с алгоритмом оптимизации, также решением, подсмотренным у природы. Eco-inspired Evolutionary Algorithm — это метаэвристический метод оптимизации, который использует экологические концепции (местообитание, взаимоотношения видов, экологическая сукцессия) для моделирования поиска решений. Он был предложен в начале 2010‑х годов как расширение идей эволюционных алгоритмов, но с акцентом на экологические процессы.

Природа всегда служила неисчерпаемым источником вдохновения для разработки вычислительных моделей и парадигм. Эволюционные вычисления и роевой интеллект предлагают широкий спектр стратегий оптимизации, основанных на наблюдении за природными процессами: эволюцией видов, поведением социальных групп, динамикой иммунной системы, стратегиями поиска пищи и экологическими взаимоотношениями различных популяций.

Однако до недавнего времени такие фундаментальные экологические концепции, как хабитаты (среды обитания), экологические взаимоотношения и экологическая сукцессия, оставались практически неисследованными в контексте оптимизации. Алгоритм Eco-inspired Evolutionary Algorithm, предложенный Rafael Stubs Parpinelli и Heitor Silvério Lopes в 2011 году, заполняет этот пробел, предлагая принципиально новый взгляд на построение кооперативных алгоритмов поиска.

Реализация алгоритма

В основе ECO лежит экологическая метафора, в которой множество популяций кандидатных решений сосуществуют, взаимодействуют и коэволюционируют друг с другом:

Экологический концепт	Вычислительная интерпретация
Хабитат	Кластер популяций, расположенных в одной области пространства поиска
Популяция	Группа кандидатных решений, эволюционирующих по единой стратегии
Центроид	Точка концентрации особей популяции, определяющая её "регион обитания"
Intra-habitat отношения	Спаривание между особями популяций внутри одного хабитата
Inter-habitat отношения	Миграция лучших особей между хабитатами
Экологическая сукцессия	Итеративный процесс формирования хабитатов и установления связей

Множественные популяции. В отличие от классических эволюционных алгоритмов с единственной популяцией, ECO оперирует несколькими независимыми популяциями, каждая из которых эволюционирует согласно собственной стратегии поиска. Это обеспечивает естественное разделение между интенсификацией (exploiation) и диверсификацией (exploration).

Динамическое формирование хабитатов. На каждой итерации алгоритм вычисляет центроиды популяций и группирует близкие популяции в хабитаты на основе порогового расстояния "ρ". Это позволяет системе самоорганизовываться и адаптироваться к ландшафту целевой функции.

Двухуровневое взаимодействие. "Intra-habitat" взаимодействия (спаривание) усиливают локальный поиск в перспективных регионах, в то время как "inter-habitat" взаимодействия (миграции) обеспечивают обмен генетическим материалом между удалёнными областями пространства поиска.

Коэволюция. Популяции не изолированы друг от друга - они образуют единую экосистему, где успех одной популяции влияет на эволюцию соседних. Это создаёт положительную обратную связь, направляющую поиск к глобальному оптимуму.

Структура алгоритма. Основной цикл ECO (экологическая сукцессия) состоит из следующих этапов:

1. Инициализация популяций в случайных регионах пространства поиска

2. ПОКА не выполнен критерий останова:

2.1. Эволюционный период — каждая популяция независимо эволюционирует.

2.2. Вычисление центроидов популяций.

2.3. Формирование хабитатов на основе близости центроидов.

2.4. Intra-habitat взаимодействия - спаривание между смежными популяциями.

2.5. Inter-habitat взаимодействия - миграция лучших особей между хабитатами.

3. Возврат лучшего найденного решения.

Представьте природную экосистему: на обширной территории обитают несколько стай животных. Каждая стая занимает свой участок — хабитат. Внутри хабитата стаи взаимодействуют друг с другом, обмениваясь особями. Иногда самые сильные особи мигрируют в далёкие хабитаты, принося туда свои гены. Со временем все стаи концентрируются в местах с лучшими условиями для жизни. Именно эту модель воспроизводит алгоритм ECO для поиска оптимальных решений.

Особь — одно кандидатное решение задачи. Например, если мы оптимизируем два параметра торговой стратегии (период скользящей средней и уровень стоп-лосса), то особь — это конкретная пара значений (20, 50).

Популяция — группа особей, живущих рядом и эволюционирующих вместе. Популяция характеризуется своим центром — средним положением всех особей.

Хабитат — объединение близких популяций. Если центры двух популяций находятся недалеко друг от друга, они образуют общий хабитат и начинают обмениваться особями.

Пример: поиск вершины горы. Допустим, пять групп альпинистов ищут высочайшую точку горного массива. Каждая группа стартует в случайном месте:

Высота

▲

│ ∧ ∧∧

│ ╱ ╲ ∧∧ ╱ ╲

│ ╱ ╲ ╱ ╲ ╱ ╲

│ ╱ ╲╱ ╲ ╱ ╲

│╱ ╲╱ ╲

└──────────────────────────────► Позиция

G1 G2 G3 G4 G5

G1-G5 — стартовые позиции групп

Шаг 1: Локальный поиск. Каждая группа исследует свою окрестность, поднимаясь выше.
Шаг 2: Определение хабитатов. Группы G1 и G2 оказались близко — они образуют хабитат. Группы G4 и G5 тоже рядом — другой хабитат. Группа G3 пока одна.
Шаг 3: Обмен внутри хабитата. G1 и G2 делятся информацией о найденных маршрутах. Лучший альпинист из G1 показывает путь участнику из G2.
Шаг 4: Миграция между хабитатами. Лучший альпинист из Хабитата1 отправляется в Хабитат2, принося знания о перспективных направлениях.

Результат: через несколько итераций все группы концентрируются вокруг главной вершины.

Структура алгоритма. Алгоритм работает циклически, повторяя пять основных шагов:

Шаг 1: Эволюция популяций. Каждая особь пытается улучшить свою позицию двумя способами:

случайное исследование — смещение относительно случайного соседа,
притяжение к лидеру — движение к лучшей особи популяции.

Пример для особи с позицией (3, 4): сосед находится в (5, 2), а лидер находится в (7, 8). Случайное смещение: (3,4) - (5,2) = (-2, 2), умножаем на случайный коэффициент. Притяжение к лидеру: (7,8) - (3,4) = (4, 4), умножаем на малый коэффициент. Новая позиция = текущая + смещение + притяжение

Лучшая особь популяции не изменяется — это гарантирует сохранение достигнутого результата.

Шаг 2: Вычисление центроидов. Центроид — это "центр масс" популяции, среднее положение всех особей. Популяция из 4 особей:

5 ┤ ●(2,5)

4 ┤ ●(1,4)

3 ┤ ◉(2,3) ← центроид

2 ┤ ●(3,2)

1 ┤●(1,1)

└─────────────

0 1 2 3 4 5

Центроид = ((1+2+3+1)/4, (1+5+2+4)/4) = (1.75, 3.0) ≈ (2, 3). Центроид показывает, где "живёт" популяция в пространстве поиска.

Шаг 3: Формирование хабитатов. Популяции, чьи центроиды находятся близко друг к другу, объединяются в хабитат. "Близость" определяется порогом "ρ": 5 популяций с центроидами:

Расстояния: P0-P1 = 1.5 (близко); P0-P2 = 3.0 (далеко); P3-P4 = 4.0 (далеко). При пороге "ρ", дающем расстояние 2.0: Хабитат A: {P0, P1} - близкие популяции, Хабитат B: {P2} - одиночная, Хабитат C: {P3} - одиночная, Хабитат D: {P4} - одиночная.

Шаг 4: Спаривание внутри хабитатов. Популяции одного хабитата обмениваются генетическим материалом: Хабитат A содержит популяции P0 и P1.

1. Из P0 выбираем сильную особь (турнирный отбор). Берём 3 случайных особи, выбираем лучшую → Родитель 1: (4, 6).

2. Из P1 аналогично выбираем: → Родитель 2: (8, 2).

3. Создаём потомка (кроссовер): x: между 4 и 8 → случайно выбираем 5.5; y: между 2 и 6 → случайно выбираем 4.0 → Потомок: (5.5, 4.0). Это для равномерного кроссовера, но в нашей реализации будет использоваться uniform crossover (для каждой координаты случайно выбирается один из родителей), а не арифметическое среднее. Потомок (5.5, 4.0) возможен только если для "x" взяли среднее.

4. Потомок заменяет слабую особь в P1. Это усиливает поиск в перспективных регионах.

Шаг 5: Миграция между хабитатами. Лучшие особи путешествуют между хабитатами, распространяя хорошие решения:

Хабитат A Хабитат B

┌─────────────┐ ┌─────────────┐

│ P0: лучшая │ │ P2 │

│ (3, 7) │ ─────────────► │ ? │

│ ★ │ миграция │ ★ │

└─────────────┘ └─────────────┘

Лучшая особь из P0 копируется в P2, заменяя случайную (не лучшую) особь. Миграция предотвращает изоляцию хабитатов и ускоряет распространение найденных решений.

Динамика системы. В начале работы популяции разбросаны по всему пространству поиска - много изолированных хабитатов. По мере оптимизации популяции сходятся к лучшим регионам - хабитаты укрупняются:

Итерация 1: 6 хабитатов (исследование); Итерация 25: 3 хабитата (переход); Итерация 50: 1 хабитат (эксплуатация). Это иллюстративный пример, в реальности зависит от функции и параметра "ρ".

ECO

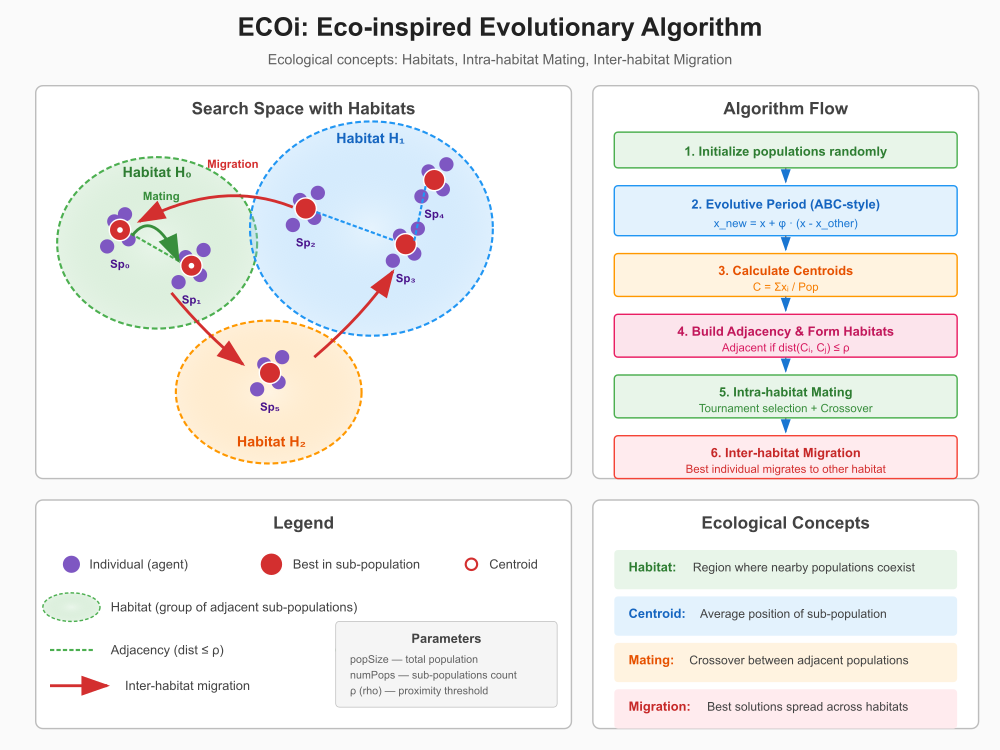
Рисунок 1. Иллюстрация работы алгоритма ECO

Иллюстрация показывает: левая часть — Search Space: 3 хабитата (H₀, H₁, H₂) как цветные области, 6 субпопуляций (Sp₀-Sp₅) с агентами (фиолетовые точки). Лучшие особи выделены красным цветом. Пунктирные линии — смежность между популяциями (dist ≤ ρ). Зелёные стрелки — спаривание внутри хабитата. Красные стрелки — миграции между хабитатами. Правая часть — Algorithm Flow: 6 шагов алгоритма с формулами.

Напишем реализацию алгоритма ECO.

Структура "S_ECO_Coord". Вспомогательная структура для хранения одной координаты центроида. Массив "centroids" хранит центроиды всех субпопуляций в плоском виде размером [numPops × coords], где каждый элемент — одна координата одного центроида.

//————————————————————————————————————————————————————————————————————
struct S_ECO_Coord
{
    double v;
};
//————————————————————————————————————————————————————————————————————

Класс "C_AO_ECOi", основной класс алгоритма, который наследуется от базового класса "C_AO". Этот класс реализует эволюционный алгоритм, вдохновленный экологическими взаимодействиями. Алгоритм разбивает популяцию на подпопуляции, которые имитируют отдельные экосистемы. Эти подпопуляции взаимодействуют друг с другом как на локальном, так и на глобальном уровне, что способствует поиску оптимального решения.

Метод "SetParams" обновляет внутренние параметры алгоритма ECOi на основе значений, хранящихся в массиве "params". Этот метод обычно вызывается после изменений параметров извне.

//————————————————————————————————————————————————————————————————————
class C_AO_ECOi : public C_AO
{
  public:
  ~C_AO_ECOi () { }

  C_AO_ECOi ()
  {
    ao_name = "ECOi";
    ao_desc = "Eco-inspired Evolutionary Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/20608";

    popSize   = 100;   // Total population size
    numPops   = 50;    // Number of sub-populations (N-POP)
    evoStep   = 1;     // Evolutive period iterations (EVO-STEP)
    rho       = 0.3;   // Proximity threshold for habitat formation
    tournSize = 8;     // Tournament selection size (T-SIZE)

    ArrayResize (params, 5);
    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "numPops";   params [1].val = numPops;
    params [2].name = "evoStep";   params [2].val = evoStep;
    params [3].name = "rho";       params [3].val = rho;
    params [4].name = "tournSize"; params [4].val = tournSize;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    numPops   = (int)params [1].val;
    evoStep   = (int)params [2].val;
    rho       = params [3].val;
    tournSize = (int)params [4].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP);

  void Moving   ();
  void Revision ();

  //------------------------------------------------------------------
  int    numPops;       // Number of sub-populations
  int    evoStep;       // Evolutive period
  double rho;           // Proximity threshold
  int    tournSize;     // Tournament size

  private: //—————————————————————————————————————————————————————————
  int         evoCounter;      // Counter for evolutive period
  int         subPopSize;      // Size of each sub-population

  S_ECO_Coord centroids [];    // [numPops * coords] - flattened centroid array
  int         habitat   [];    // Habitat index for each sub-population
  int         numHabitats;
  bool        adjacency [];    // Adjacency matrix [numPops * numPops] - flattened
  int         uniqueHab [];    // Array of unique habitat indices
  double      maxDist;         // Maximum possible distance (for normalization)

  void   CalculateCentroids    ();
  void   BuildAdjacencyMatrix  ();
  void   FormHabitats          ();
  void   IntraHabitatMating    ();
  void   InterHabitatMigration ();
  void   EvolutivePeriod       ();
  int    TournamentSelect      (int popIdx);
  void   Crossover             (int parent1, int parent2, int childIdx);
  double EuclideanDistanceNorm (int pop1, int pop2);
  int    GetBestInPopulation   (int popIdx);
  int    GetRandomInPopulation (int popIdx, int excludeIdx);
  void   BoundaryControl       (int idx);
  int    GetPopStart           (int popIdx);
  int    GetPopEnd             (int popIdx);
};
//————————————————————————————————————————————————————————————————————

Метод "Init" — инициализация алгоритма перед запуском оптимизации. Метод вызывает "StandardInit" базового класса для инициализации общих структур. Сбрасывается счётчик эволюционного периода, корректируется "numPops", если оно превышает "popSize" или меньше 1. Вычисляется subPopSize = popSize / numPops. Выделяется память под массивы: centroids, habitat, adjacency, uniqueHab. Вычисляется "maxDist" — длина диагонали пространства поиска для нормализации расстояний. Инициализируются хабитаты: каждая субпопуляция изначально образует свой хабитат.

//————————————————————————————————————————————————————————————————————
bool C_AO_ECOi::Init (const double &rangeMinP  [],
                      const double &rangeMaxP  [],
                      const double &rangeStepP [],
                      const int     epochsP)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //------------------------------------------------------------------
  evoCounter = 0;

  // Ensure numPops doesn't exceed popSize
  if (numPops > popSize) numPops = popSize;
  if (numPops < 1) numPops = 1;

  subPopSize = popSize / numPops;
  if (subPopSize < 1) subPopSize = 1;

  // Allocate arrays
  ArrayResize (centroids, numPops * coords);
  ArrayResize (habitat,   numPops);
  ArrayResize (adjacency, numPops * numPops);
  ArrayResize (uniqueHab, numPops);

  // Calculate maximum distance for normalization
  maxDist = 0.0;
  for (int c = 0; c < coords; c++)
  {
    double width = rangeMax [c] - rangeMin [c];
    maxDist += width * width;
  }
  maxDist = MathSqrt (maxDist);
  if (maxDist < 1e-10) maxDist = 1.0;

  // Initialize habitats - each population is its own habitat
  for (int p = 0; p < numPops; p++)
  {
    habitat [p] = p;
  }
  numHabitats = numPops;

  return true;
}
//————————————————————————————————————————————————————————————————————

Метод "Moving". Назначение: основной метод, выполняющий один шаг алгоритма. Вызывается на каждой итерации и управляет процессом поиска. Первая итерация (отсутствие ревизии). Метод инициализирует всю популяцию случайными значениями, распределенными по нормальному закону вокруг случайных центров в пределах заданных диапазонов.

Последующие итерации: инкрементирует счетчик эволюционных итераций (evoCounter). Вызывает метод "EvolutivePeriod" для проведения локального поиска внутри каждой субпопуляции. После завершения эволюционного периода (достижение evoStep): вызывается "CalculateCentroids" для определения центров каждой субпопуляции, "BuildAdjacencyMatrix" — для построения матрицы смежности на основе расстояний между центроидами, "FormHabitats" — для формирования экологических местообитаний на основе матрицы смежности, "IntraHabitatMating" — для проведения обмена генетической информацией (скрещивания) между соседними популяциями в пределах одного местообитания, и "InterHabitatMigration" — для выполнения "великих миграций" (переноса лучших особей между разными местообитаниями).

Сбрасывается счетчик эволюционных итераций (evoCounter) в ноль.

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::Moving ()
{
  //------------------------------------------------------------------
  // First iteration: random initialization of all populations
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        // Initialize with normal distribution around random center (Box-Muller)
        double center = u.RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = u.GaussDistribution (center, rangeMin [c], rangeMax [c], 2.0);
        a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //------------------------------------------------------------------
  evoCounter++;

  //==================================================================
  // Evolutive Period: Simple evolution for each sub-population
  // Using ABC-inspired local search (employed bee phase)
  //==================================================================
  EvolutivePeriod ();

  //==================================================================
  // After evoStep iterations, perform ecological interactions
  //==================================================================
  if (evoCounter >= evoStep)
  {
    // Step 5: Calculate centroids for each population (Eq. 1)
    CalculateCentroids ();

    // Step 6: Build adjacency matrix and form habitats
    BuildAdjacencyMatrix ();
    FormHabitats ();

    // Step 7-8: Intra-habitat interactions (mating)
    IntraHabitatMating ();

    // Step 9-10: Inter-habitat interactions (great migrations)
    InterHabitatMigration ();

    evoCounter = 0;
  }
}
//————————————————————————————————————————————————————————————————————

Метод "EvolutivePeriod". Назначение: эволюционный период — локальный поиск внутри каждой субпопуляции. Реализует ABC-подобную стратегию (фаза employed bee). Метод перебирает каждую особь в общей популяции и случайным образом выбирает одну из координат для изменения, определяет, к какой субпопуляции принадлежит данная особь, выбирает другую случайную особь из той же субпопуляции. Генерирует новую позицию для текущей особи, используя формулу, схожую с ABC: x_new = x_i + phi * (x_i - x_k), где "phi" - случайный коэффициент. Применяет новую позицию к особи и выполняет контроль границ (BoundaryControl).

Примечание: жадная селекция (сравнение с предыдущим значением) не выполняется — фитнес пересчитывается внешним кодом после "Moving".

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::EvolutivePeriod ()
{
  // Simple evolution: Each individual explores neighborhood
  // Inspired by ABC employed bee phase
  for (int i = 0; i < popSize; i++)
  {
    // Select a random dimension to modify
    int dim = u.RNDminusOne (coords);

    // Determine which sub-population this individual belongs to
    int popIdx = i / subPopSize;
    if (popIdx >= numPops) popIdx = numPops - 1;

    // Select a random different individual from same sub-population
    int otherIdx = GetRandomInPopulation (popIdx, i);

    // Generate new position using ABC-style equation:
    // x_new = x_i + phi * (x_i - x_k)
    double phi    = u.RNDfromCI (-1.0, 1.0);
    double newVal = a [i].c [dim] + phi * (a [i].c [dim] - a [otherIdx].c [dim]);

    // Apply new value
    a [i].c [dim] = newVal;
    BoundaryControl (i);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "CalculateCentroids". Назначение: вычисление центроидов (геометрических центров) для каждой субпопуляции. Формула (Equation 1 из статьи): C = Σxi / Pop. Логика работы для каждой субпопуляции: инициализируются координаты центроида нулями, суммируются координаты всех особей в данной субпопуляции, затем делится полученная сумма на количество особей в субпопуляции, чтобы получить среднее значение (центроид).

Результат: заполненный массив "centroids".

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::CalculateCentroids ()
{
  // Calculate centroid for each sub-population
  // C = sum(xi) / Pop  (Equation 1 from paper)

  for (int p = 0; p < numPops; p++)
  {
    int startIdx = GetPopStart (p);
    int endIdx   = GetPopEnd (p);
    int count    = endIdx - startIdx;
    if (count < 1) count = 1;

    // Initialize centroid to zero
    for (int c = 0; c < coords; c++)
    {
      centroids [p * coords + c].v = 0.0;
    }

    // Sum all positions
    for (int i = startIdx; i < endIdx; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        centroids [p * coords + c].v += a [i].c [c];
      }
    }

    // Divide by population count
    for (int c = 0; c < coords; c++)
    {
      centroids [p * coords + c].v /= count;
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "BuildAdjacencyMatrix". Осуществляется построение матрицы смежности субпопуляций на основе расстояния между их центроидами. Критерий смежности: две субпопуляции смежны, если нормализованное евклидово расстояние между их центроидами ≤ ρ (rho).

Логика работы метода для каждой пары субпопуляций: вычисляется нормализованное евклидово расстояние между их центроидами, используя метод "EuclideanDistanceNorm", если расстояние меньше или равно заданному порогу "rho", устанавливается соответствующий элемент матрицы смежности в "true" (что означает, что они соседние), иначе в "false". Результат: заполненная матрица "adjacency".

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::BuildAdjacencyMatrix ()
{
  // Build adjacency matrix based on normalized Euclidean distance
  // Two populations are adjacent if distance <= rho

  for (int i = 0; i < numPops; i++)
  {
    for (int j = 0; j < numPops; j++)
    {
      if (i == j)
      {
        adjacency [i * numPops + j] = false;
      }
      else
      {
        double dist = EuclideanDistanceNorm (i, j);
        adjacency [i * numPops + j] = (dist <= rho);
      }
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "EuclideanDistanceNorm" — вычисление нормализованного евклидова расстояния между центроидами двух субпопуляций. Параметры: pop1, pop2 — индексы субпопуляций. Метод возвращает расстояние в диапазоне [0, 1], где 1 — максимально возможное расстояние (диагональ пространства).

Формула: dist = sqrt(Σ(c1[i] - c2[i])²) / maxDist. Делится полученное расстояние на максимальное возможное расстояние (maxDist) для нормализации.

//————————————————————————————————————————————————————————————————————
double C_AO_ECOi::EuclideanDistanceNorm (int pop1, int pop2)
{
  // Calculate normalized Euclidean distance between two population centroids
  double dist = 0.0;

  for (int c = 0; c < coords; c++)
  {
    double diff = centroids [pop1 * coords + c].v - centroids [pop2 * coords + c].v;
    dist += diff * diff;
  }

  dist = MathSqrt (dist);

  // Normalize by maximum possible distance
  return dist / maxDist;
}
//————————————————————————————————————————————————————————————————————

Метод "FormHabitats". Формирование хабитатов — групп смежных субпопуляций. Алгоритм: Union-Find (объединение множеств) на основе матрицы смежности.

Изначально каждая субпопуляция считается отдельным местообитанием. Используя матрицу смежности, субпопуляции, которые являются соседними (находятся друг к другу в пределах rho), объединяются в одно местообитание. Это делается путем последовательного слияния местообитаний. После формирования всех местообитаний, собирается список уникальных индексов местообитаний (uniqueHab) и подсчитывается их общее количество (numHabitats).

Результат: habitat — индекс хабитата для каждой субпопуляции, uniqueHab — список уникальных индексов хабитатов и numHabitats — количество хабитатов.

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::FormHabitats ()
{
  // Form habitats using union-find approach on adjacency matrix
  // Initially each population is its own habitat

  for (int p = 0; p < numPops; p++)
  {
    habitat [p] = p;
  }

  // Merge adjacent populations into same habitat
  for (int i = 0; i < numPops; i++)
  {
    for (int j = i + 1; j < numPops; j++)
    {
      if (adjacency [i * numPops + j])
      {
        // Merge habitats: all populations in j's habitat join i's habitat
        int oldHab = habitat [j];
        int newHab = habitat [i];

        if (oldHab != newHab)
        {
          for (int p = 0; p < numPops; p++)
          {
            if (habitat [p] == oldHab)
            {
              habitat [p] = newHab;
            }
          }
        }
      }
    }
  }

  // Collect unique habitat indices
  numHabitats = 0;
  for (int p = 0; p < numPops; p++)
  {
    int h = habitat [p];
    bool found = false;

    for (int k = 0; k < numHabitats; k++)
    {
      if (uniqueHab [k] == h)
      {
        found = true;
        break;
      }
    }

    if (!found)
    {
      uniqueHab [numHabitats] = h;
      numHabitats++;
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "IntraHabitatMating". Внутрихабитатное спаривание — обмен генетическим материалом между смежными субпопуляциями одного хабитата. Экологическая аналогия: репродуктивные связи между популяциями в пределах одного местообитания. Перебираются все пары субпопуляций. Если две субпопуляции находятся в одном местообитании и являются соседними (согласно матрице смежности), тогда с использованием турнирного отбора (TournamentSelect) выбираются два родителя из этих двух субпопуляций. Выбирается случайная особь в одной из субпопуляций (исключая лучшую особь), которая будет заменена потомком. Выполняется скрещивание (Crossover) двух родителей для создания потомка. Потомок заменяет выбранную особь в целевой субпопуляции.

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::IntraHabitatMating ()
{
  // Mating between adjacent populations within the same habitat
  // For each pair of adjacent populations: tournament select parents, crossover, replace random individual

  for (int p = 0; p < numPops; p++)
  {
    for (int q = p + 1; q < numPops; q++)
    {
      // Check if in same habitat and adjacent
      if (habitat [p] == habitat [q] && adjacency [p * numPops + q])
      {
        // Tournament selection from population p
        int parent1 = TournamentSelect (p);

        // Tournament selection from population q
        int parent2 = TournamentSelect (q);

        // Select a random individual (not the best) from population q to replace
        int bestQ    = GetBestInPopulation (q);
        int childIdx = GetRandomInPopulation (q, bestQ);

        // Perform crossover - child replaces selected individual
        Crossover (parent1, parent2, childIdx);
      }
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "InterHabitatMigration". Назначение: межхабитатная миграция — перенос лучших решений между хабитатами. Экологическая аналогия: "Великие миграции" — лучшие особи мигрируют в другие местообитания. Для каждого местообитания выбирается случайная субпопуляция из данного местообитания, находится лучшая особь в этой субпопуляции (GetBestInPopulation), выбирается случайное другое местообитание (отличное от исходного), далее выбирается случайная субпопуляция в целевом местообитании. Выбирается случайная особь в целевой субпопуляции (исключая лучшую) для замены. Лучшая особь из исходной субпопуляции копируется на место выбранной, для замены особи в целевой субпопуляции.

Примечание: фитнес мигрировавшего агента будет пересчитан внешним кодом.

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::InterHabitatMigration ()
{
  // Great migrations: best individual from one habitat migrates to another
  // For each habitat, select random population, migrate best to another habitat

  if (numHabitats < 2) return;

  // For each habitat, perform migration
  for (int hIdx = 0; hIdx < numHabitats; hIdx++)
  {
    int srcHab = uniqueHab [hIdx];

    // Find populations in this habitat
    int popsInHab [];
    ArrayResize (popsInHab, 0);

    for (int p = 0; p < numPops; p++)
    {
      if (habitat [p] == srcHab)
      {
        int size = ArraySize (popsInHab);
        ArrayResize (popsInHab, size + 1);
        popsInHab [size] = p;
      }
    }

    if (ArraySize (popsInHab) == 0) continue;

    // Select random population from this habitat
    int srcPopIdx = popsInHab [u.RNDminusOne (ArraySize (popsInHab))];

    // Get best individual from this population
    int bestIdx = GetBestInPopulation (srcPopIdx);

    // Select random destination habitat (different from source)
    int destHabIdx = u.RNDminusOne (numHabitats);
    int attempts = 0;
    while (uniqueHab [destHabIdx] == srcHab && attempts < numHabitats)
    {
      destHabIdx = (destHabIdx + 1) % numHabitats;
      attempts++;
    }

    if (uniqueHab [destHabIdx] == srcHab) continue; // No other habitat available

    int destHab = uniqueHab [destHabIdx];

    // Find populations in destination habitat
    int popsInDestHab [];
    ArrayResize (popsInDestHab, 0);

    for (int p = 0; p < numPops; p++)
    {
      if (habitat [p] == destHab)
      {
        int size = ArraySize (popsInDestHab);
        ArrayResize (popsInDestHab, size + 1);
        popsInDestHab [size] = p;
      }
    }

    if (ArraySize (popsInDestHab) == 0) continue;

    // Select random population in destination habitat
    int destPopIdx = popsInDestHab [u.RNDminusOne (ArraySize (popsInDestHab))];

    // Select random individual (not the best) in destination population to replace
    int bestDest  = GetBestInPopulation (destPopIdx);
    int targetIdx = GetRandomInPopulation (destPopIdx, bestDest);

    // Copy best individual to target position (migration)
    for (int c = 0; c < coords; c++)
    {
      a [targetIdx].c [c] = a [bestIdx].c [c];
    }
    // Note: fitness will be recalculated externally after Moving()
  }
}
//————————————————————————————————————————————————————————————————————

Метод "TournamentSelect". Турнирная селекция — выбор агента с лучшим фитнесом среди случайной выборки.
Параметр: "popIdx" — индекс субпопуляции. Метод выполняет турнирный отбор внутри одной субпопуляции. Случайным образом выбирает "tournSize" особей из указанной субпопуляции. Возвращается индекс особи с наилучшей приспособленностью (наибольшим значением "f") среди выбранных.

//————————————————————————————————————————————————————————————————————
int C_AO_ECOi::TournamentSelect (int popIdx)
{
  // Tournament selection within a sub-population
  int startIdx = GetPopStart (popIdx);
  int endIdx   = GetPopEnd   (popIdx);
  int popCount = endIdx - startIdx;

  if (popCount <= 0) return startIdx;

  int    bestIdx = startIdx + u.RNDminusOne (popCount);
  double bestFit = a [bestIdx].f;

  for (int t = 1; t < tournSize && t < popCount; t++)
  {
    int idx = startIdx + u.RNDminusOne (popCount);
    if (a [idx].f > bestFit)
    {
      bestFit = a [idx].f;
      bestIdx = idx;
    }
  }

  return bestIdx;
}
//————————————————————————————————————————————————————————————————————

Метод "Crossover". Назначение: равномерный (uniform) кроссовер двух родителей. Метод реализует равномерное скрещивание между двумя родителями для создания потомка. Для каждой координаты потомка с вероятностью 0.5 выбирается соответствующая координата от первого родителя. В противном случае выбирается координата от второго родителя. После создания потомка выполняется контроль границ (BoundaryControl).

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::Crossover (int parent1, int parent2, int childIdx)
{
  // Uniform crossover between two parents
  for (int c = 0; c < coords; c++)
  {
    if (u.RNDbool ())
    {
      a [childIdx].c [c] = a [parent1].c [c];
    }
    else
    {
      a [childIdx].c [c] = a [parent2].c [c];
    }
  }

  BoundaryControl (childIdx);
}
//————————————————————————————————————————————————————————————————————

Метод "GetBestInPopulation". Описание: находит и возвращает индекс лучшей особи в указанной субпопуляции. Перебирает всех особей в заданной субпопуляции и находит ту, у которой значение приспособленности (f) наибольшее.

//————————————————————————————————————————————————————————————————————
int C_AO_ECOi::GetBestInPopulation (int popIdx)
{
  int startIdx = GetPopStart (popIdx);
  int endIdx   = GetPopEnd (popIdx);

  int    bestIdx = startIdx;
  double bestFit = a [startIdx].f;

  for (int i = startIdx + 1; i < endIdx; i++)
  {
    if (a [i].f > bestFit)
    {
      bestFit = a [i].f;
      bestIdx = i;
    }
  }

  return bestIdx;
}
//————————————————————————————————————————————————————————————————————

Метод "GetRandomInPopulation". Назначение: выбор случайного агента из субпопуляции, исключая указанный индекс. Параметры: popIdx —индекс субпопуляции, excludeIdx — индекс агента, который нужно исключить. Метод возвращает индекс случайной особи из указанной субпопуляции, с возможностью исключить определенную особь.

Выбирает случайную особь из субпопуляции, если выбранная особь совпадает с исключаемой (excludeIdx), происходит повторный выбор (с ограничением попыток), чтобы избежать возвращения исключенной особи.

//————————————————————————————————————————————————————————————————————
int C_AO_ECOi::GetRandomInPopulation (int popIdx, int excludeIdx)
{
  int startIdx = GetPopStart (popIdx);
  int endIdx   = GetPopEnd (popIdx);
  int popCount = endIdx - startIdx;

  if (popCount <= 1) return startIdx;

  int idx = startIdx + u.RNDminusOne (popCount);
  int attempts = 0;

  while (idx == excludeIdx && attempts < 10)
  {
    idx = startIdx + u.RNDminusOne (popCount);
    attempts++;
  }

  return idx;
}
//————————————————————————————————————————————————————————————————————

Метод "GetPopStart". Вычисление границ субпопуляции в общем массиве агентов. Возвращается индекс первого агента субпопуляции.

//————————————————————————————————————————————————————————————————————
int C_AO_ECOi::GetPopStart (int popIdx)
{
  int start = popIdx * subPopSize;
  if (start >= popSize) start = popSize - 1;
  return start;
}
//————————————————————————————————————————————————————————————————————

Метод "GetPopEnd". Возвращается индекс после последнего агента субпопуляции. Для последней субпопуляции end = popSize (получает "остаток" агентов).

//————————————————————————————————————————————————————————————————————
int C_AO_ECOi::GetPopEnd (int popIdx)
{
  int end = (popIdx + 1) * subPopSize;
  if (end > popSize) end = popSize;
  if (popIdx == numPops - 1) end = popSize; // Last population gets remaining
  return end;
}
//————————————————————————————————————————————————————————————————————

Метод "BoundaryControl". Назначение: контроль границ — возврат координат агента в допустимый диапазон. Для каждой координаты особи, если координата выходит за пределы допустимого диапазона (min, max), применяется механизм отражающих границ (отражение от границы), если отражение не помогло (координата все еще вне диапазона после нескольких попыток), устанавливается случайное значение в пределах допустимого диапазона.

Результат дополнительно обрабатывается методом "SeInDiSp", который корректирует значение с учетом шага (rangeStep).

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::BoundaryControl (int idx)
{
  for (int c = 0; c < coords; c++)
  {
    double val = a [idx].c [c];
    double min = rangeMin [c];
    double max = rangeMax [c];

    // Reflection boundary handling
    int iter = 0;
    while ((val < min || val > max) && iter < 10)
    {
      if (val < min) val = min + (min - val);
      if (val > max) val = max - (val - max);
      iter++;
    }

    // If reflection fails, use random position
    if (val < min || val > max)
    {
      val = u.RNDfromCI (min, max);
    }

    a [idx].c [c] = u.SeInDiSp (val, min, max, rangeStep [c]);
  }
}
//————————————————————————————————————————————————————————————————————

Метод "Revision" находит глобально лучшую особь среди всей популяции и обновляет лучшую найденную ранее (если текущая лучше). Перебирает всех особей в общей популяции. Сравнивает приспособленность текущей лучшей особи (fB) с приспособленностью найденной на данной итерации.

Если найдена новая лучшая особь, ее приспособленность и координаты сохраняются.

//————————————————————————————————————————————————————————————————————
void C_AO_ECOi::Revision ()
{
  // Find and update global best
  int    bestIdx = 0;
  double bestFit = a [0].f;

  for (int i = 1; i < popSize; i++)
  {
    if (a [i].f > bestFit)
    {
      bestFit = a [i].f;
      bestIdx = i;
    }
  }

  if (bestFit > fB)
  {
    fB = bestFit;
    ArrayCopy (cB, a [bestIdx].c, 0, 0, coords);
  }
}
//————————————————————————————————————————————————————————————————————

Результаты тестов

Алгоритм ECOi (Eco-inspired Evolutionary Algorithm) показал результат 48% на тестовом наборе функций. Это значение находится на границе попадания в таблицу лучших алгоритмов оптимизации — совсем немного не хватило для включения в рейтинг.

Алгоритм использует разнообразные механизмы: ABC-подобный локальный поиск, формирование хабитатов, внутрихабитатное спаривание с турнирной селекцией и кроссовером, межхабитатные миграции. Такое разнообразие обеспечивает баланс между эксплуатацией и исследованием.

Концепция хабитатов позволяет динамически группировать субпопуляции по близости их центроидов, что теоретически должно способствовать эффективному обмену информацией между перспективными регионами.

Адаптивная структура популяции. Разбиение на субпопуляции с динамическим формированием хабитатов создаёт естественную нишевую структуру, потенциально полезную для мультимодальных задач.

ECOi|Eco-inspired Evolutionary Algorithm|100.0|50.0|1.0|0.3|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8454991049506774
25 Hilly's; Func runs: 10000; result: 0.5348563688609891
500 Hilly's; Func runs: 10000; result: 0.29261342860799167
=============================
5 Forest's; Func runs: 10000; result: 0.8820344476464197
25 Forest's; Func runs: 10000; result: 0.46479689499361054
500 Forest's; Func runs: 10000; result: 0.19211609956835546
=============================
5 Megacity's; Func runs: 10000; result: 0.6553846153846152
25 Megacity's; Func runs: 10000; result: 0.348
500 Megacity's; Func runs: 10000; result: 0.12630769230769343
=============================
All score: 4.34161 (48.24%)

Визуализация работы алгоритма ECO на наших тестовых функциях и, как пример, на стандартных тестовых функциях, которые можно выбрать из предложенного списка функций в программе.

Hilly

ECOi на тестовой функции Hilly

Forest

ECOi на тестовой функции Forest

Megacity

ECOi на тестовой функции Megacity

Shaffer

ECOi на тестовой функции Shaffer

GoldsteinPrice

ECOi на тестовой функции GoldsteinPrice

Алгоритма ECO представлен ознакомительно в рейтинговой таблице лучших популяционных методов оптимизации.

Description	Hilly			Hilly Final	Forest			Forest Final	Megacity (discrete)			Megacity Final	Final Result	% of MAX
Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity Final	Final Result	% of MAX
dingo_optimization_algorithm_M	0,47968	0,45367	0,46369	1,39704	0,94145	0,87909	0,91454	2,73508	0,78615	0,86061	0,84805	2,49481	6,627	73,63
across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
billiards optimization algorithm M	0,95757	0,82599	0,25235	2,03590	1,00000	0,90036	0,30502	2,20538	0,73538	0,52523	0,09563	1,35625	5,598	62,19
archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
extremal_optimization_M	0,76166	0,77242	0,31747	1,85155	0,99999	0,76751	0,23527	2,00277	0,74769	0,53969	0,14249	1,42987	5,284	58,71
biogeography based optimization	0,94912	0,69456	0,35031	1,99399	0,93820	0,67365	0,25682	1,86867	0,74615	0,48277	0,17369	1,40261	5,265	58,50
artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
backtracking_search_algorithm	0,97309	0,54534	0,29098	1,80941	0,99999	0,58543	0,21747	1,80289	0,84769	0,36953	0,12978	1,34700	4,959	55,10
differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
successful restaurateur algorithm (joo)	0,96883	0,63455	0,29217	1,89555	0,94637	0,55506	0,19124	1,69267	0,74923	0,44031	0,12526	1,31480	4,903	54,48
bonobo_optimizer	0,77565	0,63805	0,32908	1,74278	0,88088	0,76344	0,25573	1,90005	0,61077	0,49846	0,14246	1,25169	4,895	54,38
chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
dream_optimization_algorithm	0,85556	0,70085	0,37280	1,92921	0,73421	0,48905	0,24147	1,46473	0,77231	0,47354	0,18561	1,43146	4,825	53,62
bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
dolphin_echolocation_algorithm	0,75995	0,67572	0,34171	1,77738	0,89582	0,64223	0,23941	1,77746	0,61538	0,44031	0,15115	1,20684	4,762	52,91
harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
fractal-based Algorithm	0,79000	0,65134	0,28965	1,73099	0,87158	0,56823	0,18877	1,62858	0,61077	0,46062	0,12398	1,19537	4,555	50,61
tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
camel algorithm M	0,78684	0,56042	0,35133	1,69859	0,82772	0,56041	0,24336	1,63149	0,64846	0,33092	0,13418	1,11356	4,444	49,37
ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
covariance_matrix_adaptation_evolution_strategy	0,76258	0,72089	0,00000	1,48347	0,82056	0,79616	0,00000	1,61672	0,75846	0,49077	0,00000	1,24923	4,349	48,33
duelist_algorithm	0,92782	0,53778	0,27792	1,74352	0,86957	0,47536	0,18193	1,52686	0,62153	0,33569	0,11715	1,07437	4,345	48,28
eco-inspired_evolutionary_algorithm	0,84549	0,53485	0,29261	1,67295	0,88203	0,46479	0,19211	1,53893	0,65538	0,34800	0,12630	1,12968	4,342	48,24
random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Выводы

Возможная причина недостаточно высоких результатов, которые ожидались: избыточная сложность алгоритма. Множество взаимодействующих операторов (эволюционный период, вычисление центроидов, формирование хабитатов, спаривание, миграции) создаёт значительные вычислительные накладные расходы. При ограниченном бюджете вычислений фитнес-функции часть ресурсов тратится на "организационные" операции вместо непосредственного поиска.

Слабый локальный поиск. ABC-подобная формула x_new = x + φ·(x - x_other) модифицирует только одно измерение за итерацию. Для функций с сильными межпараметрическими зависимостями это может быть недостаточно эффективно.

Потеря хороших решений. При кроссовере и миграции потомок заменяет случайного агента (не худшего), что может приводить к потере неплохих решений. Отсутствие жадной селекции в эволюционном периоде также может замедлять сходимость.

Чувствительность к параметрам. Порог близости "ρ" критически влияет на формирование хабитатов. При неоптимальном значении либо все популяции объединяются в один хабитат (теряется разнообразие), либо остаются изолированными (теряется обмен информацией).

Редкие экологические взаимодействия. Спаривание и миграции происходят только каждые evoStep итераций. Если этот период слишком длинный, полезная информация распространяется медленно; если слишком короткий — популяции не успевают локально сойтись.

Алгоритм ECO демонстрирует интересный подход к оптимизации, вдохновлённый экологическими концепциями. Результат 48% — вполне приемлемый, особенно учитывая оригинальность идеи. Однако сложность архитектуры с множеством операторов не трансформировалась в пропорционально высокую эффективность. Возможно, некоторое упрощение алгоритма (меньше операторов, но более агрессивных) или усиление локального поиска могли бы улучшить результаты. Также стоит отметить, что экологическая метафора лучше подходит для задач с явной мультимодальной структурой, где концепция хабитатов может проявить свои преимущества в полной мере.

tab

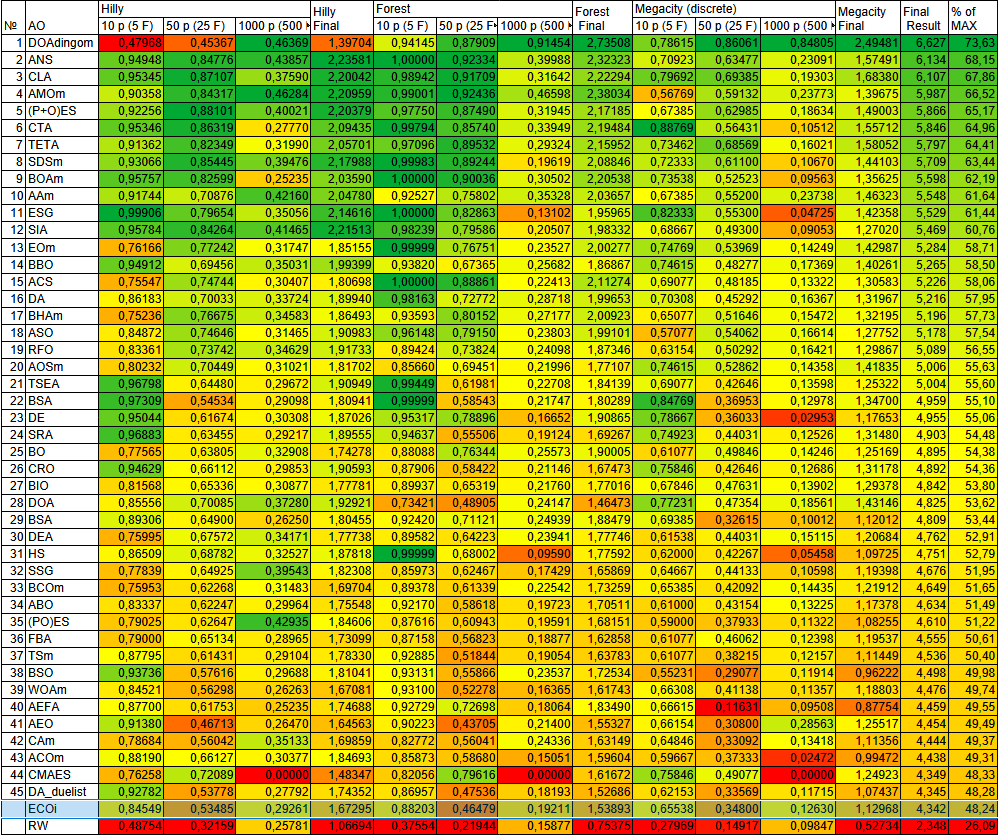
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам

chart

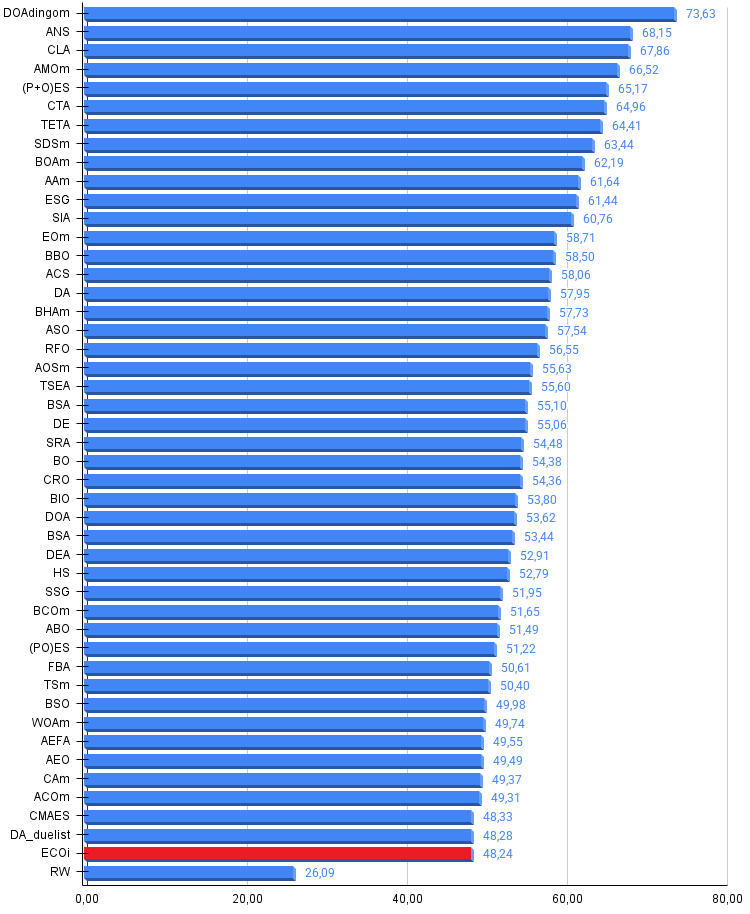
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма ECO:

Плюсы:

Хорошая сходимость на функциях высокой и средней размерности (не самые худшие результаты в таблице).

Минусы:

На задачах малой размерности низкая сходимость.
Много внешних параметров.
Много различных операторов модификации решений, что усложняет отладку и настройку алгоритма.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	TestFunctions.mqh	Включаемый файл	Библиотека тестовых функций
4	TestStandFunctions.mqh	Включаемый файл	Библиотека функций тестового стенда
5	Utilities.mqh	Включаемый файл	Библиотека вспомогательных функций
6	CalculationTestResults.mqh	Включаемый файл	Скрипт для расчета результатов в сравнительную таблицу
7	Testing AOs.mq5	Скрипт	Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8	Simple use of population optimization algorithms.mq5	Скрипт	Простой пример использования популяционных алгоритмов оптимизации без визуализации
9	Test_AO_ECOi.mq5	Скрипт	Испытательный стенд для EGOi

Прикрепленные файлы |

Загрузить ZIP

ECOi.zip (399.28 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (Окончание)

В статье представлена адаптация фреймворка P-SSE для задач анализа финансовых рынков. Реализованные решения обеспечивают последовательную обработку локальных событий, аккумулируя их в согласованное представление рыночной динамики. Подход позволяет прогнозировать изменения рынка на заданный горизонт планирования, сохраняя высокую чувствительность к микроимпульсам и минимизируя вычислительные затраты.

Возможности Мастера MQL5, которые вам нужно знать (Часть 58): Обучение с подкреплением (DDPG) совместно с паттернами скользящей средней и стохастика

Скользящая средняя и стохастический осциллятор — очень распространенные индикаторы, совместные паттерны которых мы исследовали в предыдущей статье с помощью сети обучения с учителем, чтобы понять, какие из них работают. В этой статье мы сделаем следующий шаг, рассмотрев влияние обучения с подкреплением, используемого с обученной нейронной сетью, на производительность. Наши испытания проводились в течение очень ограниченного промежутка времени. Тем не менее, мы продолжим использовать возможности, предоставляемые Мастером MQL5.

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Нейросети в трейдинге: Возмущённые модели пространства состояний для анализа рыночной динамики (модуль E-TROF)

В статье показан механизм превращения потока тиков или баров в устойчивое контекстное представление рынка, пригодное для онлайн-торговли без лишних вычислений. Инкрементальная обработка, стековое накопление состояния и расширенное пространство признаков позволяют выявлять направленные движения и локальные корреляции там, где классические методы видят лишь шум.