Экстремальная оптимизация — Extremal Optimization (EO)
Содержание
Введение
Многие реальные задачи, а в частности трейдерские, характеризуются сложными дискретными ландшафтами целевой функции с множественными локальными экстремумами, разрывами и недифференцируемыми областями, что делает классические градиентные методы неприменимыми. Для решения таких задач разработано множество метаэвристических алгоритмов, и каждый подход имеет свои преимущества и недостатки в балансе между исследованием (exploration) и эксплуатацией (exploitation) пространства поиска.
Extremal Optimization (EO) — это метаэвристический алгоритм оптимизации, вдохновленный моделью Бака-Снеппена (Bak-Sneppen). Алгоритм был разработан Стефаном Бётчером (Stefan Boettcher) и Аллоном Перкусом (Allon Percus) в 1999 году как метод, вдохновленный концепцией самоорганизованной критичности, которые естественным образом эволюционируют к критическому состоянию, где происходят лавинообразные изменения различных масштабов. Population-based EO был разработан для решения задач непрерывной оптимизации, используя популяционные итерационные операции.
Реализация алгоритма
Модель Бака-Снеппена была разработана для описания эволюции экосистем и демонстрации явления самоорганизованной критичности. Это простая модель коэволюции, которая показывает, как локальные взаимодействия могут привести к глобальным критическим явлениям.
Принципы модели Бака-Снеппена
Экосистема видов:
- N видов расположены в цепочке (или на решетке)
- Каждому виду i присвоено значение fitness fi ∈ [0,1]
- Fitness представляет приспособленность вида к окружающей среде
Динамика эволюции
На каждом шаге времени: 1. Найти вид с минимальным fitness: fmin = min{fi} 2. Заменить fitness этого вида и его соседей новыми случайными значениями 3. Повторять процессСамоорганизованная критичность
- Система самоорганизуется к критическому состоянию
- Возникает пороговое значение fc ≈ 0.67
- Виды с fitness < fc вымирают лавинообразно
- Размеры лавин подчиняются степенному закону
Длительные периоды стагнации, когда мало изменений сменяются внезапными лавинообразными изменениями различных масштабов при отсутствии внешнего управления — система самоорганизуется. Степенные изменения затрагивают размеры лавин: P(s) ~ s^(-τ), где времена жизни видов подчиняются степенному закону при отсутствии характерного масштаба. Изменение одного вида влияет на соседей. Глобальная динамика возникает из локальных взаимодействий.
Бёттчер и Перкус адаптировали принципы модели Бака-Снеппена для создания алгоритма оптимизации. Вместо улучшения лучших, улучшаем худшие. Фокус на худших элементах — это против интуиции, но эффективно для выхода из локальных оптимумов. В модели Бака-Снеппена эволюция происходит через "прерывистое равновесие" — длительные периоды стазиса прерываются внезапными изменениями. EO использует этот принцип: когда изменяются только плохие компоненты, и когда изменение одного компонента драматически улучшает решение, улучшение одного компонента может сделать другие компоненты "плохими".
Extremal Optimization переносит принципы самоорганизованной критичности из физики экосистем в область оптимизации. Ключевая инновация — использование естественной тенденции сложных систем к самоорганизации для автоматического баланса между исследованием и эксплуатацией пространства поиска, так ли это, проверим при практических задачах. Перейдем к написанию псевдокода алгоритма.
Инициализация:
- Создать популяцию из popSize агентов
- Инициализировать параметры
- Создать массивы для ранжирования агентов и компонентов
Первый запуск (инициализация популяции):
- Для каждого агента в популяции:
- Для каждого компонента (координаты):
- присвоить случайное значение в допустимом диапазоне
- применить дискретизацию если необходимо
- Для каждого компонента (координаты):
Основной цикл оптимизации:
Для каждого агента в популяции выполнить:
- Ранжирование агентов:
- создать список всех агентов с их fitness
- отсортировать агентов по fitness (худшие в начале для максимизации)
- Выбор целевого агента:
- использовать степенное распределение P(n) ∝ n^(-τ)
- выбрать ранг согласно этому распределению
- определить агента с выбранным рангом как целевого
- Ранжирование компонентов целевого агента:
- Для каждого компонента вычислить его fitness:
- fitness = 1 - (нормализованное отклонение от лучшего известного значения)
- Отсортировать компоненты по fitness (худшие в начале)
- Для каждого компонента вычислить его fitness:
- Выбор и мутация компонента:
- использовать степенное распределение для выбора ранга компонента
- заменить выбранный компонент на новое случайное значение
- проверить границы и применить дискретизацию
Обновление результатов:
- Отсортировать всю популяцию по fitness (лучшие в начале)
- Обновить глобальное лучшее решение если найдено улучшение
Реализуем алгоритм в коде. Напишем класс, который будет представлять реализацию алгоритма EO, основанного на методе оптимизации с использованием принципа удаления худших элементов для поиска решений. Класс наследуется от базового класса "C_AO" и дополнительно включает параметры и методы, специфичные для алгоритма. Конструктор и деструктор: инициализация параметров и освобождение ресурсов соответственно. Основные параметры:
- popSize — размер популяции, количество агентов в работе;
- tau — параметр степенного распределения, определяющего вероятности выбора элементов;
- greedyStart — доля агентов с инициализацией по жадному принципу;
- eliteUpdate — доля агентов, участвующих в обновлении за итерацию.
- SetParams — извлекает текущие значения параметров из массива и применяет их;
- Init — инициализация популяции с учетом диапазонов параметров и количества эпох;
- Moving — выполнение одного шага алгоритма, обновление состояния популяции;
- Revision — пересчет оценок или подготовка к следующему этапу.
- RankedComponent — структура для хранения ранжирования компонент агента по их качеству (Fitness);
- RankedAgent — структура для хранения ранжирования самих агентов по их итоговому уровню пригодности.
- compRanks и agentRanks — массивы структур для хранения отсортированных компонентов и агентов;
- tau, greedyStart, eliteUpdate позволяют управлять поведением алгоритма.
- ApplyExtremalOptimization — основной механизм для выбора и обновления элементов на основе их рангов с учетом распределения степенного закона.
- CalculateComponentFitness — вычисление фитнеса компонента агента.
- SelectRankByPowerLaw — выбор ранга компонента или агента с использованием распределения со степенным законом, что позволяет сосредоточиться на худших элементах.
Класс предназначен для применения алгоритма экстремальной оптимизации, особенно в задачах, требующих поиска качественного решения за счет последовательного устранения наименее подходящих компонентов в популяции.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_EO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ ArrayResize (compRanks, coords); ArrayResize (agentRanks, popSize); return true; } //————————————————————————————————————————————————————————————————————
Метод инициализации класса EO отвечает за подготовку начальных условий для дальнейшей работы алгоритма. Он принимает параметры диапазонов минимальных и максимальных значений для переменных, а также размеры шагов для их изменения, а также количество эпох (итераций), если это необходимо.
Первым делом метод вызывает стандартную процедуру инициализации, которая занимается настройкой базовых параметров и подготовкой общих структур данных. Если эта процедура завершается неудачей, инициализация метода прекращается.
Если инициализация прошла успешно, внутри метода происходит изменение размеров массивов, предназначенных для хранения ранжированных компонентов и агентов. Размер массива компонентов устанавливается в соответствии с числом координат или переменных задачи, а массив агентов — в соответствии с заданным размером популяции. По завершении этих шагов метод возвращает результат успешной инициализации.
//———————————————————————————————————————————————————————————————————— //--- Основной цикл алгоритма void C_AO_EO::Moving () { // Начальная инициализация популяции if (!revision) { int greedyCount = (int)(popSize * greedyStart); for (int i = 0; i < popSize; i++) { // Случайная инициализация для остальных for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } // Применяем Extremal Optimization --------------------------------- ApplyExtremalOptimization (); } //————————————————————————————————————————————————————————————————————
Метод "ApplyExtremalOptimization" реализует основной цикл работы алгоритма EO для обновления популяции агентов. Его цель — улучшать решения путем модификации компонентов агентов, основываясь на принципах EO. Определяется количество агентов для обновления за одну итерацию, беря во внимание параметр "eliteUpdate" (доля обновляемых агентов) и размер популяции. Агенты сортируются на основе их общего качества. Алгоритм ранжирует агентов от худших к лучшим, чтобы алгоритм работал на поиск максимумов. Используя степенное распределение вероятности, выбирается агент, который будет подвергнут изменениям.
Для выбранного агента, производится ранжирование его компонентов. Каждому компоненту присваивается значение пригодности "fitness", чтобы оценивать его вклад в общее качество агента. Компоненты сортируются от худших к лучшим на основе их "fitness". Используется степенное распределение вероятности для выбора одного из компонентов агента для модификации. Это делается для того, чтобы с большей вероятностью выбирать компоненты с худшим рангом.
Выбранный компонент агента заменяется случайным значением в пределах допустимого диапазона, который задается параметрами "rangeMin" и "rangeMax". Происходит проверка на допустимость получившегося значения, чтобы гарантировать соответствие заданным границам и размерам шага.Метод повторяет эти шаги для каждого агента, подлежащего обновлению, реализуя ключевую логику алгоритма EO: выбор компонентов с худшими характеристиками и их случайная замена с целью улучшить общее качество решений.
//———————————————————————————————————————————————————————————————————— //--- Применение Extremal Optimization void C_AO_EO::ApplyExtremalOptimization () { // Количество агентов для обновления на этой итерации int numUpdates = MathMax (1, (int)(popSize * eliteUpdate)); // Обновляем выбранных агентов по принципу EO //for (int update = 0; update < numUpdates; update++) for (int update = 0; update < popSize; update++) { // Шаг 1: Выбираем агента для модификации // Используем ранжирование по общему fitness int targetAgent; // Ранжируем агентов по fitness (от худшего к лучшему для максимизации) for (int i = 0; i < popSize; i++) { agentRanks [i].idx = i; agentRanks [i].fitness = a [i].f; } // Сортировка (худшие в начале для максимизации) for (int i = 0; i < popSize - 1; i++) { for (int j = i + 1; j < popSize; j++) { if (agentRanks [i].fitness > agentRanks [j].fitness) { RankedAgent temp = agentRanks [i]; agentRanks [i] = agentRanks [j]; agentRanks [j] = temp; } } } // Выбираем агента согласно степенному распределению int rank = SelectRankByPowerLaw (popSize); targetAgent = agentRanks [rank].idx; // Шаг 2: Ранжируем компоненты выбранного агента for (int c = 0; c < coords; c++) { compRanks [c].agentIdx = targetAgent; compRanks [c].componentIdx = c; compRanks [c].fitness = CalculateComponentFitness (targetAgent, c); } // Сортировка компонентов (худшие в начале) for (int i = 0; i < coords - 1; i++) { for (int j = i + 1; j < coords; j++) { if (compRanks [i].fitness > compRanks [j].fitness) { RankedComponent temp = compRanks [i]; compRanks [i] = compRanks [j]; compRanks [j] = temp; } } } // Шаг 3: Выбираем компонент для изменения согласно P(n) ∝ n^(-τ) int compRank = SelectRankByPowerLaw (coords); int compIdx = compRanks [compRank].componentIdx; // Шаг 4: Заменяем выбранный компонент новым случайным значением // Это ключевой принцип EO - безусловная замена на случайное a [targetAgent].c [compIdx] = u.RNDfromCI (rangeMin [compIdx], rangeMax [compIdx]); // Проверка границ a [targetAgent].c [compIdx] = u.SeInDiSp (a [targetAgent].c [compIdx], rangeMin [compIdx], rangeMax [compIdx], rangeStep [compIdx]); } } //————————————————————————————————————————————————————————————————————
Метод "CalculateComponentFitness" вычисляет значение пригодности "fitness" для отдельного компонента агента. Эта функция играет важную роль в алгоритме Extremal Optimization (EO), оценивая вклад каждого компонента в общее качество решения. Алгоритм использует простую метрику, основанную на расчёте "fitness", как относительного вклада компонента в общее качество.
Вначале "fitness" инициализируется нулём. Далее вычисляется диапазон значений компонента (range). Если этот диапазон больше нуля, рассчитывается нормализованное отклонение "deviation". Отклонение вычисляется как абсолютное значение разницы между значением компонента агента и базовым значением "cB", нормированное на диапазон значений компонента. Приспособленность рассчитывается путем вычитания "deviation" из 1.0. Это делает "fitness" обратно пропорциональным отклонению: чем меньше отклонение компонента от целевого значения, тем выше его "fitness".
Таким образом, функция возвращает оценку пригодности конкретного компонента, которая показывает, насколько хорошо текущее значение компонента соответствует целевому значению, что необходимо для дальнейшего ранжирования компонентов.
//———————————————————————————————————————————————————————————————————— //--- Расчет fitness компонента double C_AO_EO::CalculateComponentFitness (int agentIdx, int componentIdx) { // Для общей задачи оптимизации используем простую метрику // λi = относительный вклад компонента в общее качество double fitness = 0.0; double range = rangeMax [componentIdx] - rangeMin [componentIdx]; if (range > 0) { // Нормализованное отклонение double deviation = MathAbs (a [agentIdx].c [componentIdx] - cB [componentIdx]) / range; fitness = 1.0 - deviation; // Инвертируем, чтобы больше = лучше } return fitness; } //————————————————————————————————————————————————————————————————————
Метод "SelectRankByPowerLaw" реализует выбор позиции (ранга) элемента из списка на основе степенного распределения вероятностей. Этот метод является ключевым для алгоритма EO, так как именно через него производится выбор агентов и компонентов для модификации. Метод принимает на вход "maxRank", который определяет максимальный ранг элемента.
В основе метода лежит принцип обратного преобразования для получения случайного значения, следуя степенному закону P(n) ∝ n^(-τ), где: n - ранг элемента; τ (tau) — параметр, определяющий форму степенного распределения.
В зависимости от значения параметра "tau", реализуются два сценария:
Общий случай (τ ≠ 1.0):
- вычисляется нормализующий множитель "norm", который обеспечивает правильное масштабирование вероятностей;
- генерируется случайное число "r" в диапазоне [0, 1) с помощью "u.RNDprobab ()";
- используется формула обратного преобразования для вычисления ранга "rank" на основе "r", "norm" и "τ";
- ранг ограничивается в пределах [0, maxRank - 1], чтобы избежать выхода за пределы массива.
Специальный случай (τ = 1.0):
- вычисляется нормализующий множитель "norm" для случая τ = 1.0;
- используется специальная формула для вычисления ранга "rank";
- ранг ограничивается в пределах [0, maxRank - 1].
В итоге метод возвращает целое число "rank", которое указывает на выбранную позицию элемента в ранжированном списке. Этот выбор вероятностный, то есть, элементы с меньшим рангом (худшие) имеют большую вероятность быть выбранными, в соответствии с принципами EO.
//———————————————————————————————————————————————————————————————————— //--- Выбор ранга согласно степенному распределению int C_AO_EO::SelectRankByPowerLaw (int maxRank) { // P(n) ∝ n^(-τ), где n - ранг от 1 до maxRank // Используем метод обратного преобразования double r = u.RNDprobab (); if (tau != 1.0) { // Общий случай: обратное преобразование для P(n) ∝ n^(-τ) double norm = (1.0 - MathPow (maxRank + 1.0, 1.0 - tau)) / (1.0 - tau); double x = r * norm; int rank = (int)MathPow ((1.0 - tau) * x + 1.0, 1.0 / (1.0 - tau)) - 1; if (rank >= maxRank) rank = maxRank - 1; if (rank < 0) rank = 0; return rank; } else { // Специальный случай τ = 1: P(n) ∝ 1/n double norm = MathLog (maxRank + 1.0); int rank = (int)(MathExp (r * norm) - 1.0); if (rank >= maxRank) rank = maxRank - 1; if (rank < 0) rank = 0; return rank; } } //————————————————————————————————————————————————————————————————————
Метод "Revision" предназначен для обновления информации о лучших найденных решениях в процессе работы алгоритма EO. Его задача —определить текущее наилучшее решение и обновить глобальные переменные, хранящие информацию о нём. Создаётся временный массив "aT" для хранения отсортированных агентов. Популяция агентов "a" сортируется, используя встроенную функцию "u.Sorting". Сортировка выполняется для максимизации, то есть лучшие агенты (те, у которых значение функции пригодности "f" больше) оказываются в начале массива "a" (является основной структурой данных), содержащей информацию об агентах, включая значения их компонент "c" и значение функции пригодности "f".
После сортировки проверяется, является ли значение функции пригодности "f" самого лучшего агента (то есть a [0]) больше, чем текущее лучшее значение "fB" (хранит значение функции пригодности лучшего решения, найденного на данный момент). Если текущий лучший агент лучше, чем глобальное лучшее решение, то значения компонент лучшего агента (a [0].c) копируются в массив "cB", который вероятно хранит компоненты лучшего решения, а "fB" обновляется до значения функции пригодности лучшего агента (a [0].f).
Таким образом, функция "Revision" обновляет информацию о лучшем решении, сохраняя его компоненты и значение функции пригодности, а также сортирует популяцию, чтобы лучшие решения всегда были доступны в начале массива.
//———————————————————————————————————————————————————————————————————— //--- Обновление лучших решений void C_AO_EO::Revision () { // Сортировка популяции для МАКСИМИЗАЦИИ static S_AO_Agent aT []; ArrayResize (aT, popSize); // Используем встроенную функцию сортировки u.Sorting (a, aT, popSize); // Обновление глобального лучшего решения if (a [0].f > fB) { ArrayCopy (cB, a [0].c, 0, 0, WHOLE_ARRAY); fB = a [0].f; } } //————————————————————————————————————————————————————————————————————
Результаты тестов
После тестирования, алгоритм не показал хороших результатов, поэтому я решил пересмотреть все оригинальные методы и сделать модифицированную версию, направленную на улучшение сходимости алгоритма.EO|Extremal Optimization (Boettcher-Percus)|50.0|1.4|0.5|0.3|
=============================
5 Hilly's; Func runs: 10000; result: 0.5146369337195529
25 Hilly's; Func runs: 10000; result: 0.29089804555433085
500 Hilly's; Func runs: 10000; result: 0.25192095557138877
=============================
5 Forest's; Func runs: 10000; result: 0.367128650332966
25 Forest's; Func runs: 10000; result: 0.19477408852361866
500 Forest's; Func runs: 10000; result: 0.15367465708144543
=============================
5 Megacity's; Func runs: 10000; result: 0.2584615384615384
25 Megacity's; Func runs: 10000; result: 0.12707692307692314
500 Megacity's; Func runs: 10000; result: 0.09413846153846227
=============================
All score: 2.25271 (25.03%)
Ниже представлена моя собственная интерпретация данного метода оптимизации. Реализуем новый класс, являющийся наследником базового класса оптимизации.
В конструкторе устанавливаются начальные параметры алгоритма: размер популяции, количество худших решений, которые подлежат повышению (улучшению), вероятность мутации и степени распределения для отбора и мутации. Параметры сохранены в массиве структур для дальнейшего изменения и настройки.
Метод "SetParams" обновляет внутренние переменные класса на основе значений из массива параметров. Объявлены методы для инициализации алгоритма, выполнения шагов движения (обновления состояния) и пересмотра (для оценки и коррекции решений). В закрытой части класса хранятся переменные, отслеживающие текущую и общую эпохи выполнения алгоритма. Определён метод для мутации конкретного компонента решения в популяции, что является ключевой частью реализуемого алгоритма.
//———————————————————————————————————————————————————————————————————— class C_AO_EOm : public C_AO { public: //---------------------------------------------------------- ~C_AO_EOm () { } C_AO_EOm () { ao_name = "EOm"; ao_desc = "Extremal Optimization M"; ao_link = "https://www.mql5.com/ru/articles/18755"; popSize = 50; // Размер популяции popRaising = 3; // Повышение самых худших mutationRate = 0.1; // Вероятность мутации powCh = 2.0; // Степень закона распределения отбора powMut = 8.0; // Степень закона распределения мутации ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "popRaising"; params [1].val = popRaising; params [2].name = "mutationRate"; params [2].val = mutationRate; params [3].name = "powCh"; params [3].val = powCh; params [4].name = "powMut"; params [4].val = powMut; } void SetParams () { popSize = (int)params [0].val; popRaising = (int)params [1].val; mutationRate = params [2].val; powCh = params [3].val; powMut = params [4].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ int popRaising; // Повышение самых худших double mutationRate; // Вероятность мутации double powCh; // Степень закона распределения отбора double powMut; // Степень закона распределения мутации private: //--------------------------------------------------------- int currentEpoch; // текущая эпоха int totalEpochs; // общее количество эпох void MutateComponent (int agentIdx, int componentIdx); }; //————————————————————————————————————————————————————————————————————
Метод "Init" отвечает за инициализацию алгоритма. Функция принимает на вход массивы с минимальными, максимальными значениями и шагом для параметров оптимизации, а также общее количество эпох (циклов) работы алгоритма.
Внутри метода сначала вызывается функция "StandardInit", из базового класса "C_AO". Эта функция, выполняет общую инициализацию, выделение памяти или установку базовых параметров, связанных с диапазонами и шагами для параметров оптимизации.
Если "StandardInit" завершается неудачно, то функция "Init" также завершает работу, возвращая "false". Если "StandardInit" прошла успешно, то метод инициализирует переменные "currentEpoch" (текущая эпоха) в "0" и "totalEpochs" (общее количество эпох) значением, полученным в параметре "epochsP".
В конце метод возвращает "true", сигнализируя об успешной инициализации. Таким образом, метод подготавливает алгоритм к работе, задавая начальные параметры и счетчики эпох.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_EOm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ currentEpoch = 0; totalEpochs = epochsP; return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" представляет собой основной цикл работы алгоритма экстремальной оптимизации. Он отвечает за эволюцию популяции решений в процессе поиска оптимального решения. Инкремент эпохи: увеличивается счетчик "currentEpoch". Инициализация популяции (только в первую эпоху): если флаг "revision" (указывающий на необходимость пересмотра решений) равен "false" (т.е. в первом цикле работы алгоритма), происходит инициализация популяции.
Для каждого "агента" (решения) в популяции, для каждой "координаты" (параметра решения) генерируется случайное значение в заданном диапазоне (rangeMin, rangeMax) для текущей координаты. Применяется дискретизация "SeInDiSp" чтобы значения параметров соответствовали заданным шагам. После инициализации "revision" устанавливается в "true", чтобы этот блок кода выполнялся только один раз. Метод завершает свою работу.
Применение экстремальной оптимизации (в последующих эпохах): создается временный массив "aT" для хранения новых (мутировавших) решений. Для каждого агента в популяции инициализируется структура "aT [i]". Для каждой координаты решения генерируется случайное число, возводится в степень "powCh". Это используется для отбора "родителя".
Случайное число масштабируется для выбора индекса родителя в популяции "ind". Определяется тип мутации: если случайное число меньше "mutationRate" (мутация включается с вероятностью "mutationRate"), то применяется мутация по закону степенного распределения "PowerDistribution" к значению координаты родителя. В противном случае, происходит "направленное движение" к лучшему решению с добавлением случайного шума. Новое значение вычисляется как сумма значения координаты родителя, случайного числа, и разницы между "cB [c]" (лучшая найденная координата) и координатой родителя. Применяется дискретизация "SeInDiSp". После мутации, все координаты из временного массива "aT" копируются в основной массив популяции "a".
Таким образом, метод реализует цикл эволюции, где на каждом шаге (эпохе) решения мутируют (изменяются), используя механизмы отбора, случайной мутации и направленного поиска, с целью улучшить свои значения (минимизируя или максимизируя целевую функцию), чтобы в итоге найти оптимальное решение.
//———————————————————————————————————————————————————————————————————— //--- Основной цикл алгоритма void C_AO_EOm::Moving () { currentEpoch++; // Начальная инициализация популяции if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //Apply Extremal Optimization--------------------------------------- static S_AO_Agent aT []; ArrayResize (aT, popSize); for (int i = 0; i < popSize; i++) { aT [i].Init (coords); for (int c = 0; c < coords; c++) { double rnd = u.RNDprobab (); rnd = pow (rnd, powCh); int ind = (int)u.Scale (rnd, 0.0, 1.0, 0, popSize - 1); // Выбор типа мутации double mutType = u.RNDprobab (); if (mutType < mutationRate) { aT [i].c [c] = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], powMut); } else { // Направленное движение к лучшему с шумом aT [i].c [c] = a [ind].c [c] + u.RNDprobab () * (cB [c] - a [ind].c [c]); } // Проверка границ aT [i].c [c] = u.SeInDiSp (aT [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, aT [i].c); } //————————————————————————————————————————————————————————————————————
Этот метод отвечает за обновление информации о лучших решениях в процессе работы алгоритма.
Сортировка популяции: создается временный массив "aT" для хранения копии популяции. Популяция "a" сортируется по значению целевой функции. Для сортировки используется метод "u.Sorting".
Обновление глобального лучшего решения: проверяется, лучше ли значение целевой функции "f" первого элемента популяции (т.е. самого лучшего решения) текущего глобального лучшего значения "fB". Если текущее лучше, то "cB" копируются из координат первого элемента "a [0].c", а "fB" обновляется значением "f" лучшего решения.
Обновление худшего решения: "fW" обновляется значением функции последнего элемента популяции.
"Поднятие" (Raising) худших решений: в цикле, выполняющемся "popRaising" раз, происходит "поднятие" худших решений в популяции: для "popRaising" худших агентов (расположенных в конце отсортированного массива "a"), значение целевой функции "f" пересчитывается как случайное значение, расположенное между "fW" (худший текущий результат) и "fB" (лучший текущий результат). Это сделано для внесения разнообразия или смещения худших решений в лучшую сторону.
Пересортировка популяции: популяция "a" пересортировывается, используя метод "u.Sorting". Это необходимо, чтобы снова привести популяцию в порядок после внесения изменений в значения "f".
//———————————————————————————————————————————————————————————————————— //--- Обновление лучших решений void C_AO_EOm::Revision () { // Сортировка популяции -------------------------------------------- static S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); // Обновление глобального лучшего решения if (a [0].f > fB) { ArrayCopy (cB, a [0].c, 0, 0, WHOLE_ARRAY); fB = a [0].f; } fW = a [popSize - 1].f; //------------------------------------------------------------------ for (int i = 0; i < popRaising; i++) { a [popSize - 1 - i].f = u.RNDfromCI (fW, fB); } u.Sorting (a, aT, popSize); } //————————————————————————————————————————————————————————————————————
Теперь алгоритм, в некотором смысле наследующий идеи EO, но измененный, использует степенное распределение для выбора доноров (не обязательно плохих).
a [popSize - 1 - i].f = u.RNDfromCI (fW, fB);Мною добавлена особенность, не встречающаяся в описаниях EO, алгоритм фактически "воскрешает" худших агентов, присваивая им случайный fitness в диапазоне от самого худшего до самого лучшего по популяции. PowerDistribution для мутации — это интерпретация "мутации на основе степенного распределения". Направленное движение к лучшему (при mutType >= mutationRate ) — дополнение для ускорения сходимости.
Теперь можем посмотреть на результаты работы модифицированной версии. Такие результаты можем занести в нашу рейтинговую таблицу.
EOm|Extremal Optimization Mod|50.0|3.0|0.1|2.0|8.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.7616651321732368
25 Hilly's; Func runs: 10000; result: 0.7724295992586084
500 Hilly's; Func runs: 10000; result: 0.3174703398632668
=============================
5 Forest's; Func runs: 10000; result: 0.9999936711143977
25 Forest's; Func runs: 10000; result: 0.7675163269928252
500 Forest's; Func runs: 10000; result: 0.23527203643380376
=============================
5 Megacity's; Func runs: 10000; result: 0.7476923076923077
25 Megacity's; Func runs: 10000; result: 0.5396923076923076
500 Megacity's; Func runs: 10000; result: 0.14249230769230903
=============================
All score: 5.28422 (58.71%)
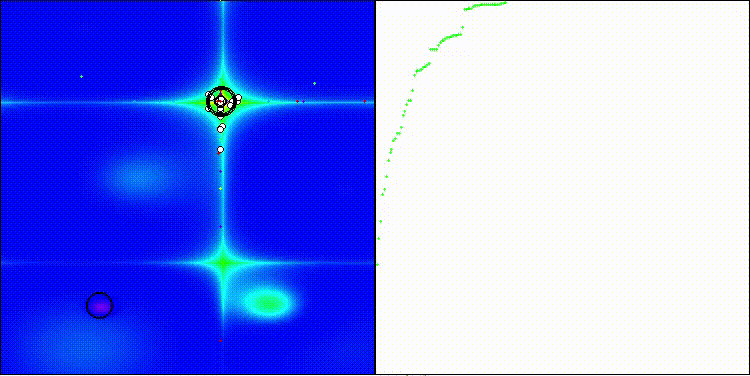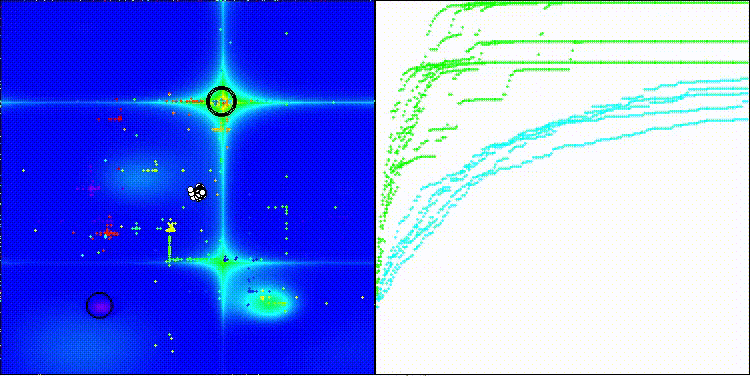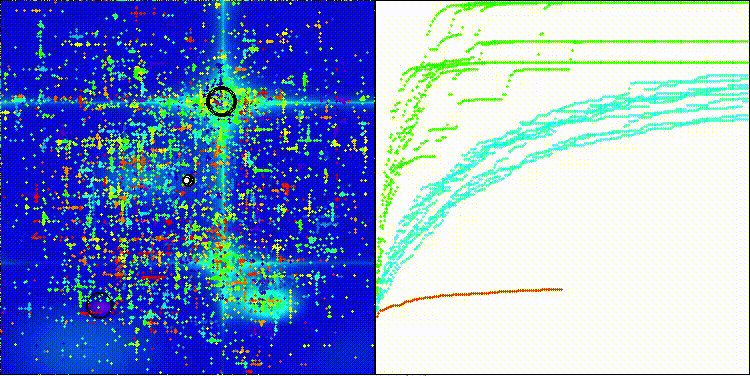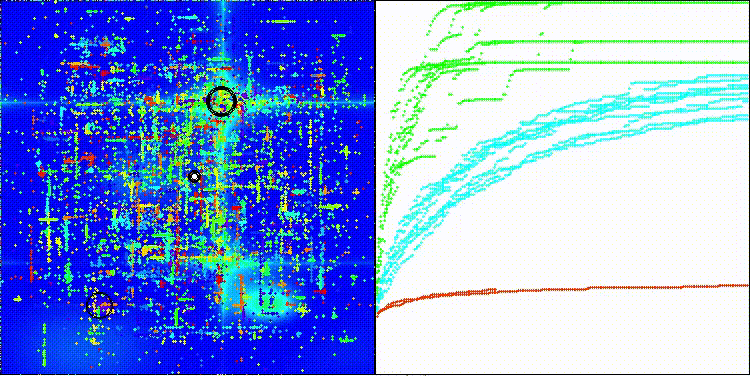
На визуализации заметен большой разброс результатов на функциях малой размерности (зеленые линии).
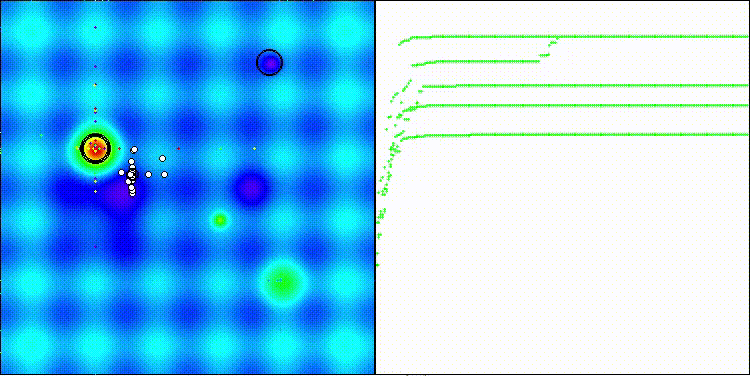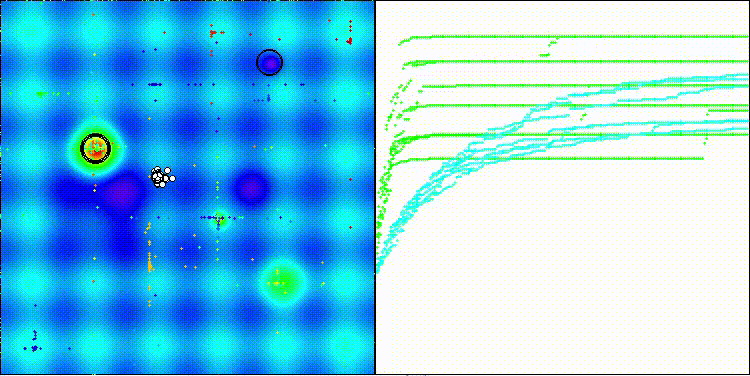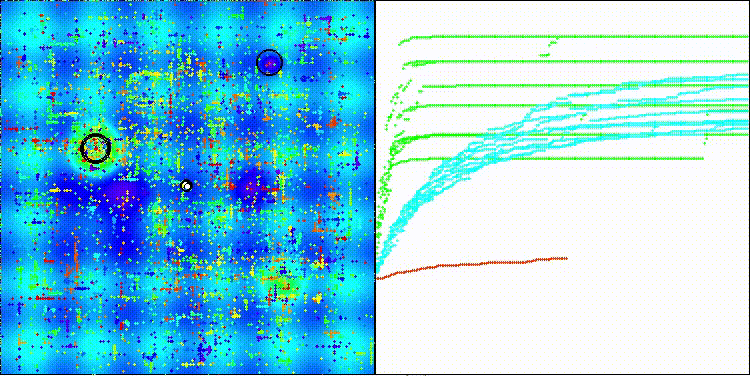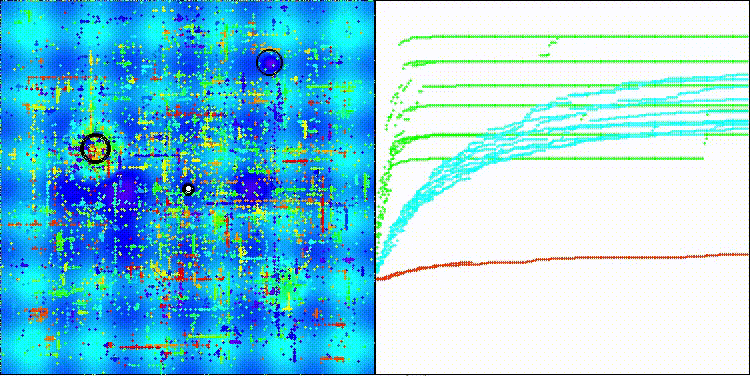
EOm на тестовой функции Hilly
EOm на тестовой функции Forest
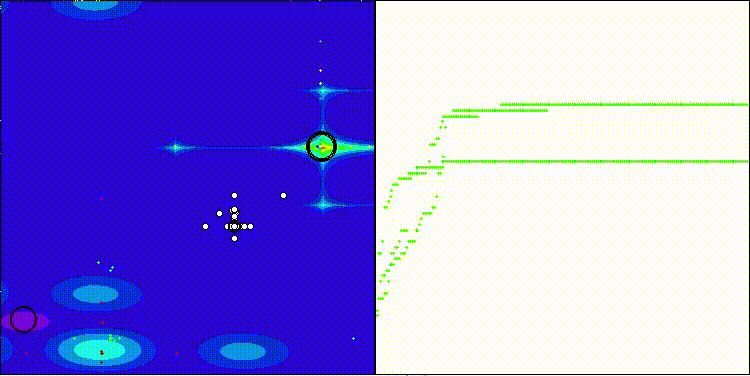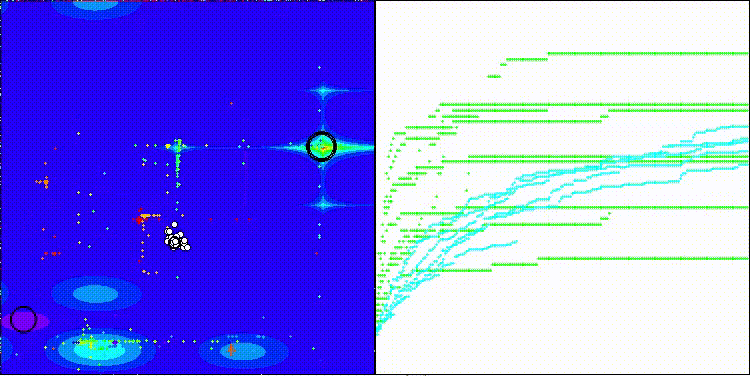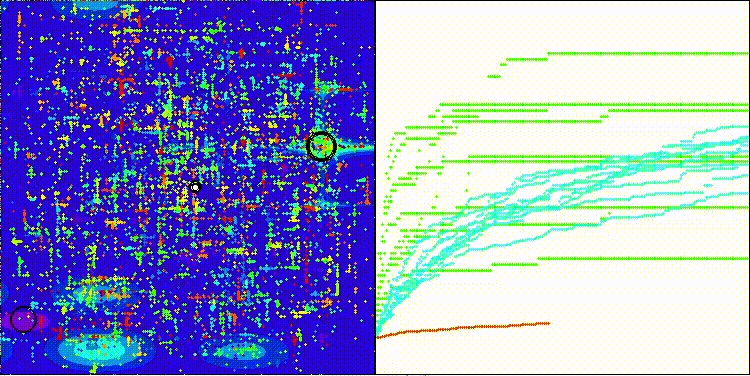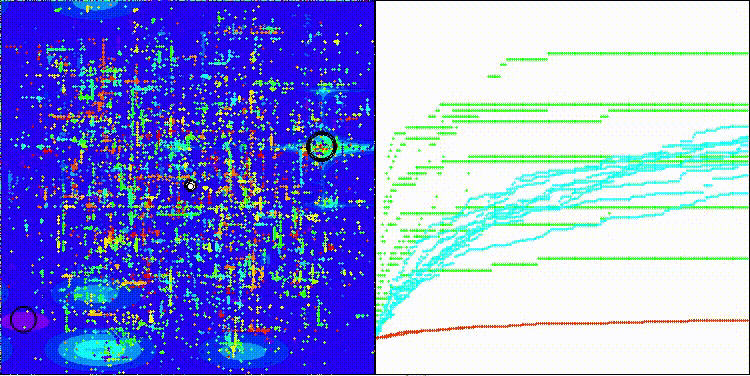
EOm на тестовой функции Megacity
После проведенного тестирования, алгоритм EOm в нашей рейтинговой таблице занимает 12 место.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 13 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 14 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 15 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 16 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 17 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 18 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 19 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 20 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 21 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 22 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 23 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 24 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 25 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 26 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 27 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 28 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 29 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 30 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 31 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 32 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 33 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 34 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 35 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 36 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 37 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 38 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 39 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 40 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 41 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 42 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 43 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 44 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 45 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Представленная компактная модифицированная реализация EOm демонстрирует интересный пример в области метаэвристической оптимизации: значительное отклонение от теоретических принципов может привести к улучшению практических результатов. Алгоритм, занявший 12-е место среди 45 популяционных методов, фактически представляет собой гибрид, сохранивший лишь ключевую идею степенного распределения из оригинального EO.
Механизм "воскрешения" худших агентов предотвращает преждевременную сходимость, поддерживает разнообразие популяции, создает дополнительные возможности для исследования. Упрощение вычислительной схемы: отказ от покомпонентной оценки снижает вычислительную сложность, а прямая работа с решениями ускоряет сходимость.
Успех модифицированной версии EO подтверждает важный принцип в разработке метаэвристик: эффективность алгоритма определяется не верностью исходной идее, а балансом между исследованием и эксплуатацией пространства поиска. Представленная реализация, несмотря на отход от классических принципов Extremal Optimization, демонстрирует высокую скорость сходимости, конкурентоспособные результаты, простоту реализации и настройки.
Это делает её полезным инструментом в арсенале методов популяционной оптимизации, особенно для задач, где важен баланс между качеством решения и вычислительными затратами.
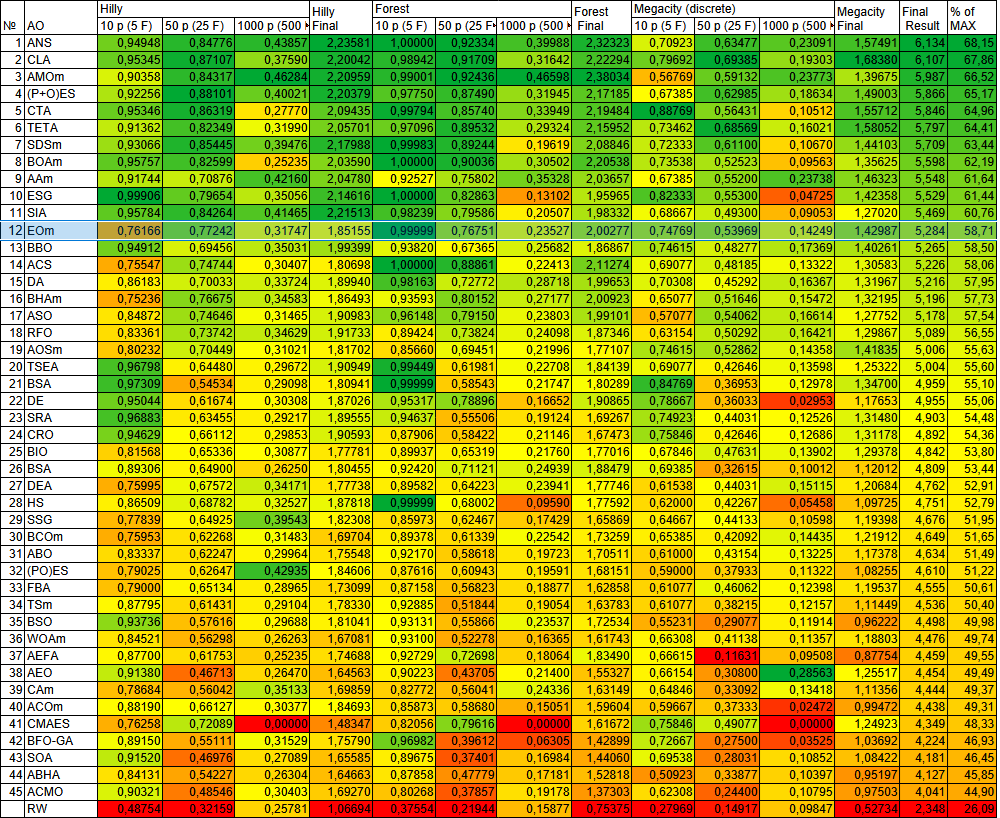
Рисунок 1. Цветовая градация алгоритмов по соответствующим тестам
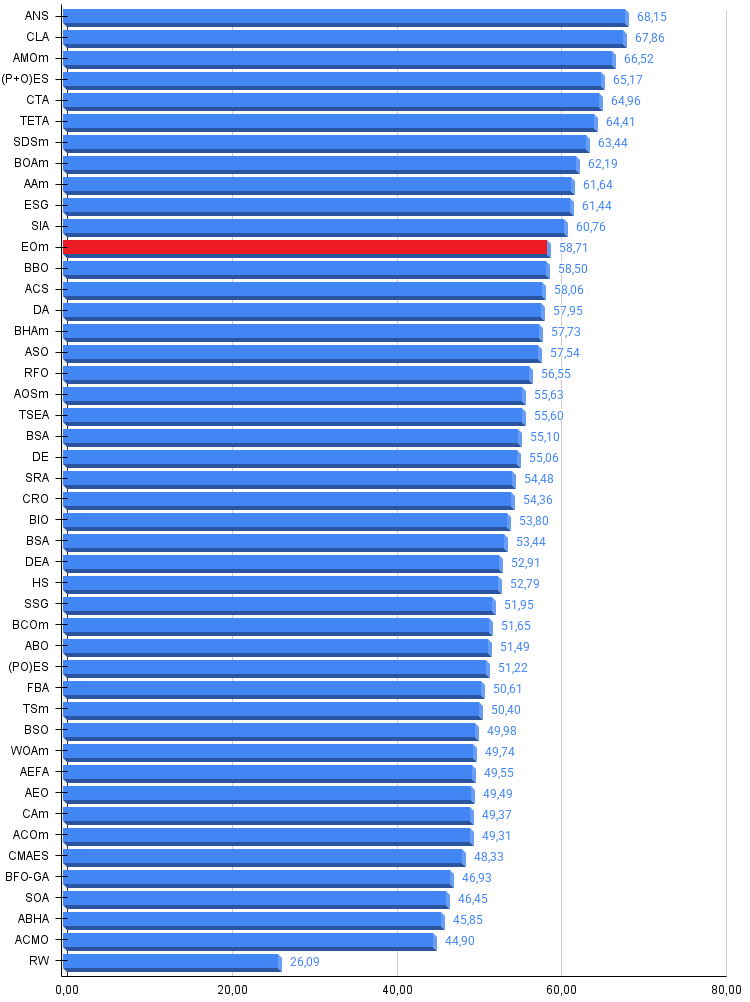
Рисунок 2. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма EOm:
Плюсы:
- Простая реализация
- Быстрый и производительный
- Хорошие результаты на дискретных задачах
Минусы:
- Большой разброс результатов на функциях малой размерности
- Средние результаты на "гладких" задачах малой размерности
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_EOm.mq5 | Скрипт | Испытательный стенд для EOm |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Знакомство с кривыми рабочих характеристик приемника (ROC-кривыми)
Знакомство с кривыми рабочих характеристик приемника (ROC-кривыми)
 Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (GinAR)
Нейросети в трейдинге: Сквозная многомерная модель прогнозирования временных рядов (GinAR)
 Автоматизация торговых стратегий на MQL5 (Часть 6): Поиск ордер-блоков для торговли по концепции Smart Money
Автоматизация торговых стратегий на MQL5 (Часть 6): Поиск ордер-блоков для торговли по концепции Smart Money
 Механизмы гейтинга в ансамблевом обучении
Механизмы гейтинга в ансамблевом обучении
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования