Популяционные алгоритмы оптимизации: Гибридный алгоритм оптимизации бактериального поиска с генетическим алгоритмом (Bacterial Foraging Optimization - Genetic Algorithm, BFO-GA)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Гибридный алгоритм оптимизации BFO-GA объединяет два различных алгоритма оптимизации: алгоритм оптимизации поиска пищи (BFO) и генетический алгоритм (GA). Этот гибридный алгоритм был создан с целью улучшить эффективность оптимизации и преодолеть некоторые недостатки каждого из отдельных алгоритмов.

BFO (Bacterial Foraging Optimization) — это алгоритм оптимизации, вдохновленный поведением бактерий при поиске пищи. Он был предложен в 2002 году Рахулом К. Куджуром. BFO моделирует движение бактерий, используя три основных механизма: переходы, диффузию и обновление позиции. Каждая бактерия в алгоритме представляет решение оптимизационной задачи, а пища соответствует оптимальному решению. Бактерии перемещаются в пространстве поиска с целью найти наилучшую пищу.

Генетический алгоритм (GA) - это алгоритм оптимизации, вдохновленный принципами естественного отбора и генетики. Он был разработан Джоном Холландом в 1970-х годах. GA работает с популяцией индивидов, представляющих решения оптимизационной задачи. Индивиды подвергаются операциям скрещивания (комбинирования генетической информации) и мутации (случайным изменениям генетической информации) для создания новых поколений. Через несколько поколений GA стремится найти оптимальное решение.

Гибридный алгоритм BFO-GA объединяет преимущества обоих алгоритмов. BFO обладает хорошей способностью к локальному поиску и быстрому сходимости, но может затрудняться в глобальном поиске. С другой стороны, GA имеет хорошую способность к глобальному поиску, но может быть медленным в сходимости и склонным к застреванию в локальных оптимумах. Гибридный алгоритм BFO-GA пытается преодолеть эти ограничения, используя BFO для глобального поиска и GA для уточнения локальных оптимумов.

Гибридный алгоритм BFO-GA (Bacterial Foraging Optimization - Genetic Algorithm) был предложен в 2007 году в работе Д. Н. Кима, А. Абрахама и Чоу. Этот алгоритм комбинирует принципы оптимизации, основанные на поведении роющихся бактерий, с генетическими операторами отбора, скрещивания и мутации.

BFO-GA использует бактериальный алгоритм в качестве основы, но расширяет его с помощью генетических операторов отбора, скрещивания и мутации. Этот алгоритм использует роение бактерий для поиска оптимального решения.

В качестве оператора отбора BFO-GA использует алгоритм на основе метода рулетки. Этот метод выбирает родительские бактерии с вероятностями, пропорциональными их приспособленности. Таким образом, более приспособленные бактерии имеют большую вероятность быть выбранными для скрещивания.

Скрещивание в алгоритме BFO-GA реализовано с помощью оператора арифметического кроссовера. Он комбинирует генетическую информацию двух родительских бактерий, создавая новое потомство с новыми комбинациями генов.

Мутация в BFO-GA выполняется с помощью неравномерного мутатора Михалевича. Этот мутатор изменяет генетическую информацию внутри бактерий, внося случайные изменения. Неравномерность мутации означает, что вероятность мутации может изменяться в зависимости от различных факторов.

Указанные модифицирующие операторы выполняются после завершения процедур хемотаксиса и репродукции бактериального алгоритма перед процедурами ликвидации и рассеивания этого алгоритма. То есть после того, как бактерии совершили движение в сторону оптимального решения и произвели потомство, применяются генетические операторы для разнообразия и улучшения решений.

2. Описание алгоритма

Алгоритм BFO-GA использует моделирование поведения роющихся бактерий для поиска оптимального решения задачи оптимизации. Он имитирует движение бактерий в пространстве параметров, где каждая бактерия представляет собой потенциальное решение задачи. Бактерии перемещаются в пространстве параметров, выполняя два основных типа движений: движение в направлении пищевого градиента и движение в случайном направлении.

В алгоритме BFO-GA используются следующие шаги:

1. Инициализация: Создание начальной популяции бактерий, каждая из которых представляет собой потенциальное решение задачи. Каждая бактерия имеет свои параметры, которые могут быть изменены в процессе оптимизации.
2. Оценка пищевого градиента: Вычисление значения функции приспособленности для каждой бактерии в популяции и дальнейшее сравнение двух последних значений, и эта разница значений определяет качество решения, представляемого каждой бактерией.
3. Движение в направлении градиента: Каждая бактерия перемещается в направлении пищевого градиента, что позволяет ей двигаться в сторону более оптимальных решений с постоянным вектором изменения положения.
4. Движение в случайном направлении: Часть бактерий также выполняет случайное движение, чтобы избежать застревания в локальных оптимумах. Это движение основано на случайном изменении параметров бактерии в случае предыдущего неудачного перемещения.
5. Генетические операторы: Применение генетических операторов - отбор, скрещивание и мутация, к популяции бактерий. Это позволяет создавать новые комбинации параметров и улучшать качество решений.
6. Повторение шагов 2-5: Повторение шагов движения в направлении градиента, движения в случайном направлении и применения генетических операторов до достижения критерия остановки, например, достижения максимального числа итераций или достижения определенного значения функции приспособленности.

Теоретически, гибридный алгоритм BFO-GA должен иметь ряд преимуществ перед BFO, которые стоит упомянуть:

1. Эксплорация и эксплуатация: BFO-GA обладает способностью к эксплорации пространства параметров, благодаря случайному движению бактерий, и эксплуатация, благодаря движению в направлении пищевого градиента. Это позволяет алгоритму находить оптимальные решения, избегая локальные оптимумы и сходясь к глобальному.
2. Адаптивность: BFO-GA обладает способностью адаптироваться к изменяющимся условиям оптимизации. В процессе работы алгоритма параметры бактерий могут изменяться, что позволяет адаптироваться к новым условиям и находить более оптимальные решения.
3. Отcутсвие необходимости в тюнинге параметров: Как и у любого оптимизационного алгоритма, у BFO-GA есть набор параметров, которые могут быть настроены для достижения лучших результатов. Это включает параметры, связанные с размером популяции бактерий, шагами движения в направлении градиента и случайного движения, вероятностями генетических операторов и другими. Изменение параметров не оказывает существенного влияния на результат.
   

Рисунок 1. Наследование родительских "генов" дочерней бактерией.

Переходим от теоретических основ к практической реализации.

Во-первых, я отказался от селекции по методу рулетки (метод был использован в алгоритме искусственной пчелиной колонии), экспериментально были получены более высокие результаты в BFO-GA с помощью простого случайного отбора среди популяции родителей.

Во-вторых, было мной решено заменить неравномерный мутатор Михалевича на мутацию по степенному закону (в некоторых источниках упоминается как разновидность степенного мутатора), а по сути генерация случайного числа со степенным распределением, упомянутом в статье об Умном Головастике.

В-третьих, оператор арифметического кроссовера заменен на простое случайное наследование генов от различных родительских особей, выбранных случайным образом по равномерному закону распределения.

Для описания бактерии напишем структуру S_Bacteria, содержащая следующие поля:

• c: массив координат бактерии, представляет текущие координаты бактерии в пространстве параметров, размер массива "c" зависит от числа переменных в задаче оптимизации.
• cLast: массив предыдущих координат бактерии, используется для хранения предыдущего положения бактерии в пространстве параметров, от которых производится расчёт нового положения.
  
• v: массив векторов бактерии, представляет текущее направление движения бактерии в пространстве параметров, размер массива "v" зависит от числа переменных в задаче оптимизации.
• f: текущее значение здоровья (приспособленности) бактерии, определяет качество текущего положения бактерии в пространстве параметров, чем больше значение "f", тем лучше.
• fLast: предыдущее значение здоровья бактерии, используется для отслеживания предыдущего качества положения бактерии и использования в определении пишевого градиента.
  
• lifeCNT: счетчик жизни бактерии, отслеживает количество итераций, которые бактерия провела в текущем положении, используется для ограничения количества шагов перемещения бактерий в одном направлении.
  

//——————————————————————————————————————————————————————————————————————————————
struct S_Bacteria
{
  double c     []; //coordinates
  double cLast []; //coordinates
  double v     []; //vector
  double f;        //current health
  double fLast;    //previous health
  double lifeCNT;  //life counter
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс C_AO_BFO_GA, который реализует алгоритм BFO-GA (Bacterial Foraging Optimization - Genetic Algorithm). Давайте разберем каждое поле и метод класса:

Поля класса:

• b: массив бактерий, каждый элемент массива является объектом типа "S_Bacteria", представляющим бактерию в алгоритме.
• rangeMax: массив максимальных значений диапазона поиска для каждой переменной в задаче оптимизации.
• rangeMin: массив минимальных значений диапазона поиска для каждой переменной.
• rangeStep: массив шагов поиска для каждой переменной.
• cB: массив лучших координат, найденных алгоритмом.
• fB: значение фитнес-функции для лучших координат.

Методы класса:

• Init: Инициализирует параметры алгоритма BFO-GA, такие как количество оптимизируемых параметров "paramsP", размер популяции "populationSizeP", параметр "lambda" - длина перемещения бактерий, вероятность размножения "reproductionP", счетчик жизни "lifeCounterP" - по завершению количества жизней бактерии совершают кувырок, и сила мутации "powerMutP".
• Swimming: осуществляет движение бактерий в пространстве параметров.
• Evaluation: выполняет ревизию популяции и обновление глобального решения.
  

Приватные методы класса:

• NewVector: генерирует новый вектор для указанного параметра "paramInd" бактерии.
• PowerDistribution: применяет степенное распределение к входному значению "In" с заданными параметрами "outMin", "outMax", "power".
• Sorting: cортирует бактерии в популяции по их значениям фитнес-функции в порядке убывания.
• SeInDiSp: производит нормирование входного значения "In" в интервале [InMin, InMax] с шагом "Step".
• RNDfromCI: генерирует случайное число в заданном интервале [min, max].
• Scale: масштабирует входное значение "In" из интервала [InMIN, InMAX] в интервал [OutMIN, OutMAX].
  

//——————————————————————————————————————————————————————————————————————————————
class C_AO_BFO_GA
{
  //----------------------------------------------------------------------------
  public: S_Bacteria b     []; //bacteria
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    paramsP,         //number of opt. parameters
                     const int    populationSizeP, //population size
                     const double lambdaP,         //lambda
                     const double reproductionP,   //probability of reproduction
                     const int    lifeCounterP,    //life counter
                     const double powerMutP);      //mutation power

  public: void Swimming   ();
  public: void Evaluation ();

  //----------------------------------------------------------------------------
  private: double NewVector (int paramInd);
  private: S_Bacteria bT []; //bacteria
  private: double v      [];
  private: int    ind    [];
  private: double val    [];

  private: int    populationSize; //population size
  private: int    parameters;     //number of optimized parameters
  private: double lambda;         //lambda
  private: double reproduction;   //probability of reproduction
  private: int    lifeCounter;    //life counter
  private: double powerMut;       //mutation power
  private: bool   evaluation;

  private: double PowerDistribution (const double In, const double outMin, const double outMax, const double power);
  private: void   Sorting           ();
  private: double SeInDiSp          (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI         (double min, double max);
  private: double Scale             (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Для инициализации класса служит метод "Init", который инициализирует параметры алгоритма BFO-GA.

Входные параметры метода:

• paramsP: количество оптимизируемых параметров.
• populationSizeP: размер популяции.
• lambdaP: параметр lambda, определяющий дальность перемещения бактерий на каждом шаге.
  
• reproductionP: вероятность размножения.
• lifeCounterP: счетчик жизни.
• powerMutP: сила мутации.

Внутри метода происходит инициализация полей класса C_AO_BFO_GA начальными значениями и задаются размеры массивов.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO_GA::Init (const int    paramsP,         //number of opt. parameters
                        const int    populationSizeP, //population size
                        const double lambdaP,         //lambda
                        const double reproductionP,   //probability of reproduction
                        const int    lifeCounterP,    //life counter
                        const double powerMutP)       //mutation power
{
  fB = -DBL_MAX;
  evaluation = false;

  parameters      = paramsP;
  populationSize  = populationSizeP;
  lambda          = lambdaP;
  reproduction    = reproductionP;
  lifeCounter     = lifeCounterP;
  powerMut        = powerMutP;

  ArrayResize (rangeMax,  parameters);
  ArrayResize (rangeMin,  parameters);
  ArrayResize (rangeStep, parameters);
  ArrayResize (v,         parameters);

  ArrayResize (ind,       populationSize);
  ArrayResize (val,       populationSize);

  ArrayResize (b,  populationSize);
  ArrayResize (bT, populationSize);

  for (int i = 0; i < populationSize; i++)
  {
    ArrayResize (b [i].c,     parameters);
    ArrayResize (b [i].cLast, parameters);
    ArrayResize (b [i].v,     parameters);
    b [i].f     = -DBL_MAX;
    b [i].fLast = -DBL_MAX;

    ArrayResize (bT [i].c,     parameters);
    ArrayResize (bT [i].cLast, parameters);
    ArrayResize (bT [i].v,     parameters);
  }

  ArrayResize (cB, parameters);
}
//——————————————————————————————————————————————————————————————————————————————

Для осуществления хемитаксиса бактерий, их репликации, отбора, наследования признаков и мутации напишем метод "Swimming":

void Swimming ()
{
}

На первой итерации флаг "evalution" равен "false", распределим бактерии по всему пространству поиска случайно с равномерным распределением. На этом этапе текущее здоровье и предыдущее не известны, поэтому присвоим соответствующим переменным значение "-DBL_MAX", так же добавим к новосозданным бактериям случайный вектор перемещения.

Полученные координаты положения бактерий проверяем на выход за границы и применяем шаг изменения оптимизируемых параметров. Вектор перемещения каждой бактерии позволяет им плавать равномерно поступательно.

if (!evaluation)
{
  fB = -DBL_MAX;

  for (int s = 0; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);

      v [k] = rangeMax [k] - rangeMin [k];

      b [s].v [k] = NewVector (k);

      b [s].f     = -DBL_MAX;
      b [s].fLast = -DBL_MAX;

      b [s].lifeCNT = 0;
    }
  }

  evaluation = true;
  return;
}

На второй и последующих итерациях сначала выполняется проверка выполнения вероятности репродукции (репликации) бактерий. Если вероятность репродукции исполнена, то происходит следующее:

• "bacterium original": лучшая половина отсортированной популяции бактерий продолжает своё движение в том же направлении, для этого к координатам предыдущего положения прибавляем индивидуальный для каждой бактерии вектор движения.
  
•  "bacterium clone": вторая половина популяции заполняется дочерними бактериями, каждая из которых получается из "генов" (координат) разных родительских бактерий, осуществляется тем самым наследование признаков и выполняется комбинаторная способность алгоритма, рисунок 1 выше.
  
• клонированные бактерии, унаследовавшие гены разных родителей, наследуют к тому же компонент вектора движения родителя, а наследованный ген подвергается мутации по степенному закону распределения.

Таким образом, клонированные бактерии наследуют признаки различных родителей. При этом гены изменяются с высокой вероятностью в их окрестностях, а с ненулевой вероятностью - вдали от значений родительского гена. Это позволяет комбинировать удачные свойства родителей, поскольку гены могут передавать наследникам только лучшие члены популяции. Кроме того, унаследованные компоненты вектора движения приводят к тому, что дочерние бактерии начинают двигаться на следующей итерации в соответствии с лучшими компонентами векторов своих родителей.

В идеальном случае это должно напоминать движение стаи рыб, однако такая аналогия не всегда подтверждается из-за воздействия множества случайных факторов на движение бактерий. Среди таких факторов - ландшафт фитнес-функции, замещение более удачливыми членами популяции и неизбежное изменение вектора движения из-за ограничения количества жизней.

Счетчик жизней бактерий в лучшей половине колонии увеличивается на единицу, а у клонированных - сбрасывается.

double r = RNDfromCI (0.0, 1.0);

if (r < reproduction)
{
  int st = populationSize / 2;

  //bacterium original--------------------------------------------------------
  for (int s = 0; s < st; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      b [s].c [k] = b [s].cLast [k] + b [s].v [k];
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
    b [s].lifeCNT++;
  }

  //bacterium clone-----------------------------------------------------------
  for (int s = st; s < populationSize; s++)
  {
    for (int k = 0; k < parameters; k++)
    {
      int i = (int)RNDfromCI (0, st);
      if (i >= st) i = st - 1;

      b [s].c [k] = b [i].cLast [k];

      b [s].c [k] = PowerDistribution (b [s].c [k], rangeMin [k], rangeMax [k], powerMut);
      b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
    }
    b [s].lifeCNT = 0;
  }
}

Далее, если вероятность репродукции не выполнена, в цикле для всей популяции:

for (int s = 0; s < populationSize; s++)

Сначала выполняется проверка на достижение лимита жизней бактерии. Достигшие лимита жизней бактерии совершают кувырок и начинают двигаться в новом направлении, изменив вектор своего движения. Счетчик жизней при этом сбрасывается.

После проверки на достижение лимита жизней бактерии те, кто его достиг, мутируют, а на следующей итерации начинают двигаться в новом направлении, изменив свой вектор движения, при этом счетчик жизней сбрасывается.

if (b [s].lifeCNT >= lifeCounter)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].v [k] = NewVector (k);

    b [s].c [k] = PowerDistribution (b [s].cLast [k], rangeMin [k], rangeMax [k], powerMut);
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
  }
  b [s].lifeCNT = 0;
}

Если у бактерии ещё не исчерпан лимит жизней, мы проводим проверку наличия положительного хемотаксиса, то есть на то, движется ли бактерия в сторону увеличения пищевого градиента. Движение бактерии считается верным, если значения приспособленности на двух предыдущих итерациях равны. Почему именно равны? Потому что на следующем этапе, в методе "Evaluation", мы проводим проверку на положительное изменение здоровья бактерий. Если изменения оказываются положительными, то текущее состояние присваивается предыдущему состоянию. Именно поэтому, если состояния здоровья на двух последних итерациях одинаковы, это говорит о верности направления движения бактерии в поисках увеличения пищи. Таким образом, бактерия может двигаться только в сторону ещё большего количества пищи. В противном случае бактерия начинает кувыркаться на месте. Впрочем, это не является проблемой, поскольку рано или поздно застрявшая бактерия либо мутирует в новое состояние, либо унаследует гены более удачливых родителей и их вектор движения.

Счетчик жизней бактерий, двигающихся в верном направлении, постепенно увеличивается. Это означает, что рано или поздно даже успешные бактерии подвергнутся мутациям, о чем было упомянуто в предыдущем блоке кода.

if (b [s].f == b [s].fLast)
{
  for (int k = 0; k < parameters; k++)
  {
    b [s].c [k] = b [s].cLast [k] + b [s].v [k];
    b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
  }
  b [s].lifeCNT++;
}

И, если положительного хемотаксиса не наблюдается у бактерии, то такая бактерия меняет вектор движения, совершив кувырок. Счётчик жизней таких бактерий тоже продолжает тикать, тут возникла идея увеличивать значение счетчика жизней подобных малоуспешных бактерий более интенсивно, хотя, я эту догадку не проверял.

Если у бактерии отсутствует положительный хемотаксис, она изменяет вектор движения, совершая кувырок. Счетчик жизней таких бактерий продолжает тикать; на момент написания этой строки статьи у меня возникла идея более интенсивно увеличивать значение счетчика жизней таких малоуспешных бактерий, но данное предположение я не проверял в дальнейшем.

for (int k = 0; k < parameters; k++)
{
  b [s].v [k] = NewVector (k);
  b [s].c [k] = b [s].cLast [k] + b [s].v [k];
  b [s].c [k] = SeInDiSp (b [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]);
}
b [s].lifeCNT++;

Для осуществления кувырка бактерий, то есть, изменения вектора движения, служит метод "NewVector", который выполняется для оптимизируемого параметра с индексом "paramInd":

• генерируется случайное число "r" с равномерным распределением в интервале [-1.0, 1.0] с использованием функции "RNDfromCI".
• вычисляется новое значение компонента вектора путем умножения допустимого диапазона значений "v" оптимизируемого параметра на коэффициент "lambda" и случайное число "r".

//——————————————————————————————————————————————————————————————————————————————
double C_AO_BFO_GA::NewVector (int paramInd)
{
  double r = RNDfromCI (-1.0, 1.0);
  return lambda * v [paramInd] * r;
}
//——————————————————————————————————————————————————————————————————————————————

Для организации процесса конкуренции между бактериями и обновления глобального решения используется метод "Evaluation".

В начале этого метода каждая бактерия в популяции проходит проверку на наличие положительного хемотаксиса: если текущее значение функции приспособленности "b[s].f" больше предыдущего значения "b[s].fLast", происходит обновление предыдущей приспособленности и обновление предыдущих координат, от которых бактерии будут двигаться в будущем.

Затем популяция сортируется с помощью метода "Sorting" в порядке убывания значений функции приспособленности, используя значение "fLast" бактерий.

После этого происходит обновление глобального решения.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_BFO_GA::Evaluation ()
{
  for (int s = 0; s < populationSize; s++)
  {
    if (b [s].f > b [s].fLast)
    {
      b [s].fLast = b [s].f;
      ArrayCopy (b [s].cLast, b [s].c, 0, 0, WHOLE_ARRAY);
    }
  }

  Sorting ();

  if (b [0].fLast > fB)
  {
    fB = b [0].fLast;
    ArrayCopy (cB, b [0].cLast, 0, 0, WHOLE_ARRAY);
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы гибридного алгоритма BFO-GA на тестовом стенде:

C_AO_BFO_GA:50;0.01;0.8;50;10.0
=============================
5 Hilly's; Func runs: 10000; result: 0.8914957961234459
25 Hilly's; Func runs: 10000; result: 0.5511088047221568
500 Hilly's; Func runs: 10000; result: 0.31529201642392934
=============================
5 Forest's; Func runs: 10000; result: 0.9698155977381523
25 Forest's; Func runs: 10000; result: 0.39612322805995287
500 Forest's; Func runs: 10000; result: 0.06304955092899359
=============================
5 Megacity's; Func runs: 10000; result: 0.7266666666666667
25 Megacity's; Func runs: 10000; result: 0.275
500 Megacity's; Func runs: 10000; result: 0.035250000000000004
=============================
All score: 4.22380 (46.93%)

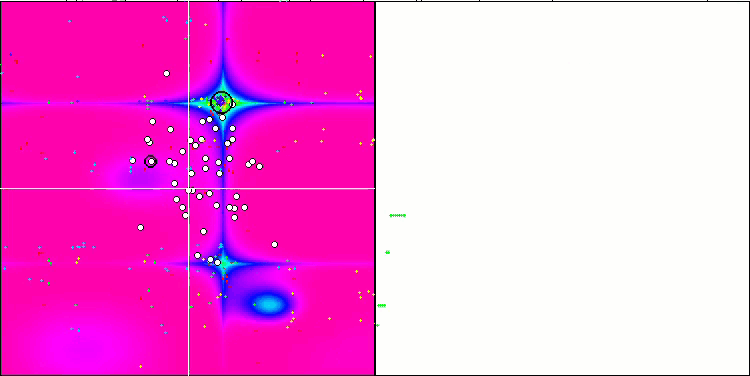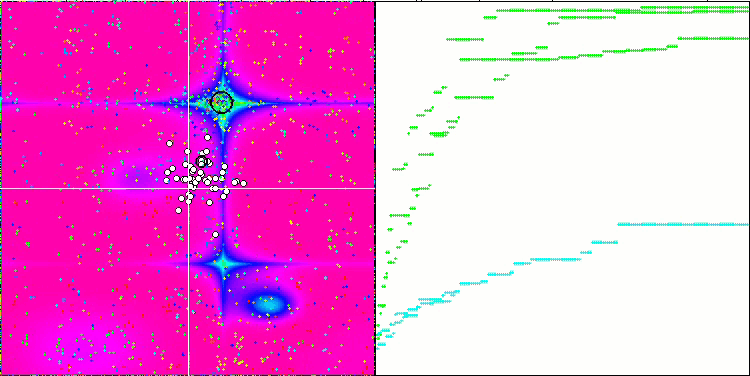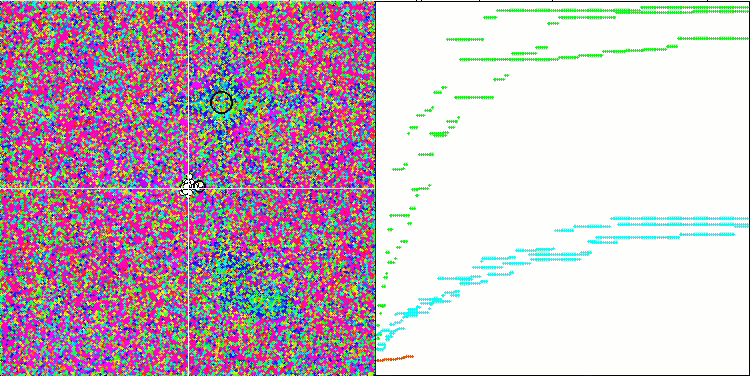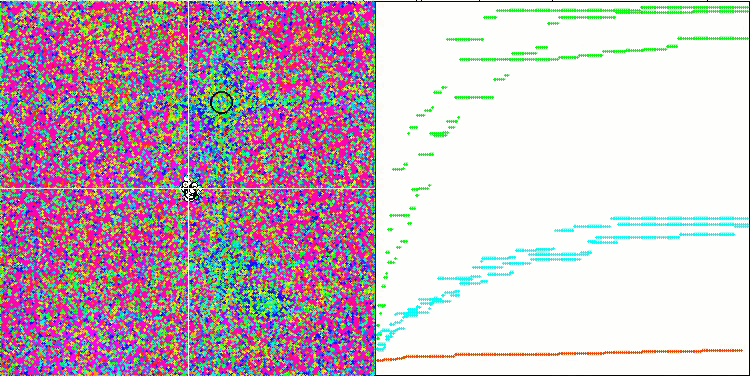
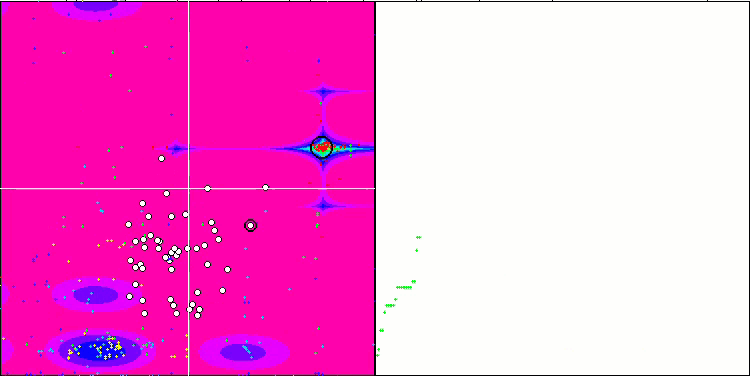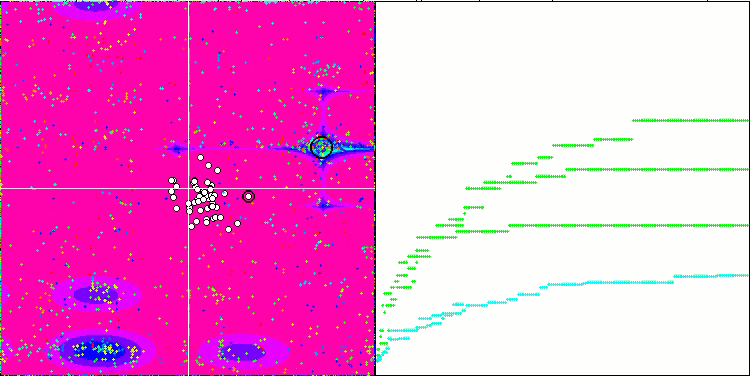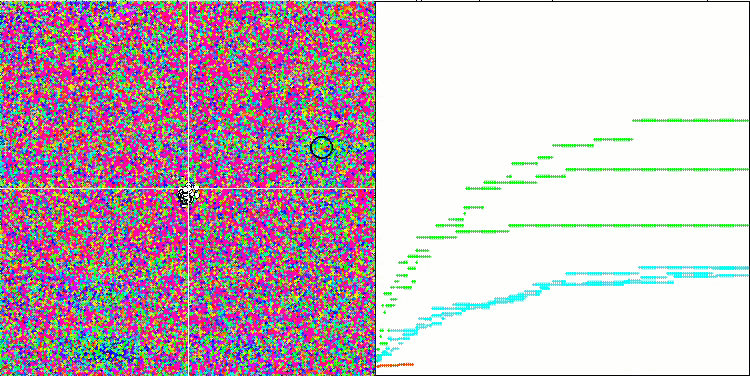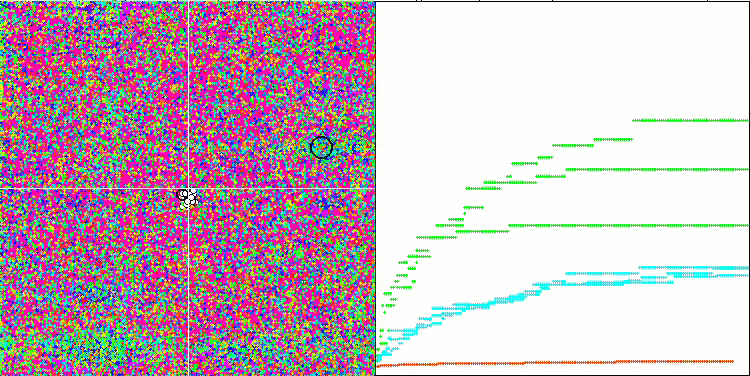
Визуальный анализ работы тестового стенда позволяет заметить, что алгоритм BFO-GA быстро обнаруживает область глобального экстремума, при этом уделяя меньше внимания на проработку локальных экстремумов, что потенциально может привести к застреванию, если глобальный экстремум окажется мнимым (ошибочным). В целом, алгоритм сходится достаточно уверенно, хотя и несколько медленно. Наблюдается некоторое "роение", что является хорошим признаком, при этом отсутствует полная связь между бактериями, и они ведут себя как самостоятельные единицы популяции.

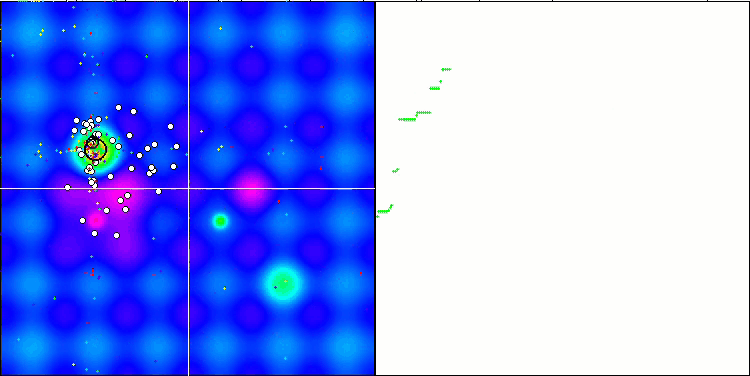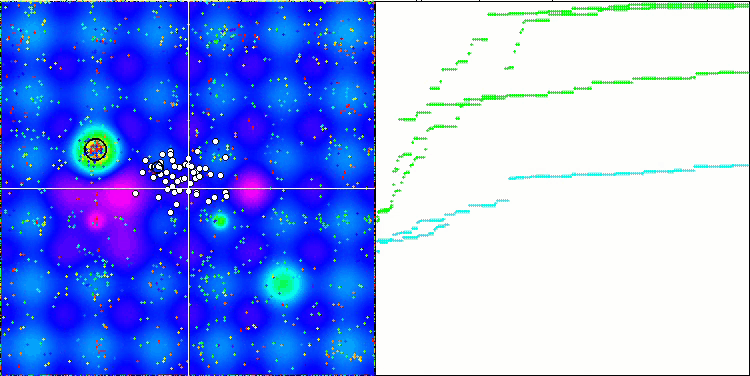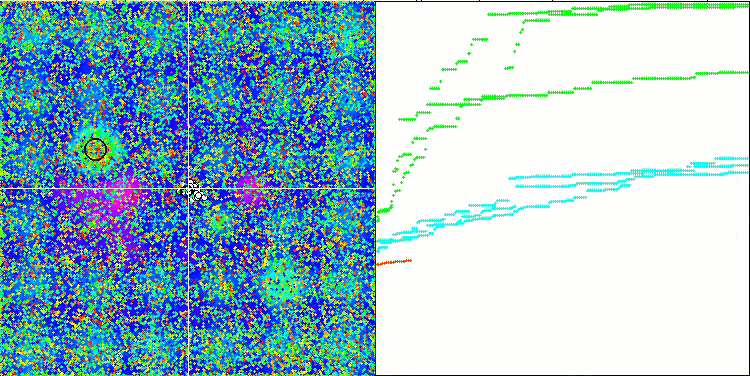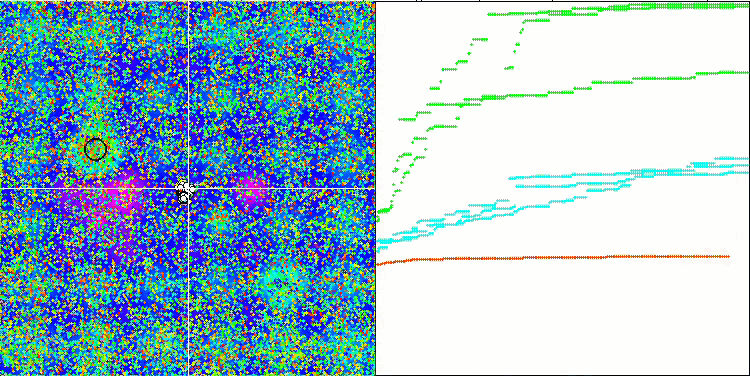
  BFO-GA на тестовой функции Hilly.

  BFO-GA на тестовой функции Forest.

  BFO-GA на тестовой функции Megacity.

В общей рейтинговой таблице можно увидеть алгоритм BFO-GA на 9-м месте, что говорит о достаточно высоком результате. Это свидетельствует о том, что преобразования, внесенные при добавлении операторов генетического алгоритма к оригинальному алгоритму BFO, оказались не напрасными и привели к соответствующим результатам. Преимущественно лучшие результаты этот алгоритм продемонстрировал на тестовых функциях с небольшим количеством переменных, превзойдя большинство других алгоритмов.

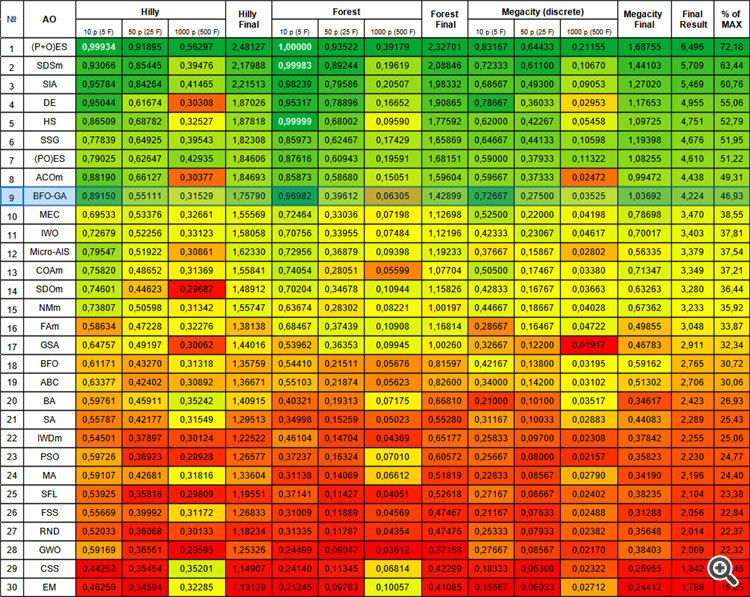
№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	(P+O)ES	(P+O) evolution strategies	0,99934	0,91895	0,56297	2,48127	1,00000	0,93522	0,39179	2,32701	0,83167	0,64433	0,21155	1,68755	6,496	72,18
2	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
3	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
4	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
5	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
6	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
7	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
8	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
9	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
10	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
11	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
12	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
13	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
14	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
15	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
16	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
17	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
18	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
19	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
20	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
21	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
22	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
23	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
24	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
25	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
26	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
27	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
28	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
29	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
30	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Выводы

Мы видим явные улучшения в результатах BFO-GA по сравнению с оригинальным алгоритмом BFO, что обусловлено использованием операторов генетического алгоритма: селекции, мутации и наследования. BFO ранее не имел механизмов выхода из локальных экстремумов, и теперь эта проблема отсутствует. Алгоритм представляет огромные возможности для экспериментирования, комбинирования порядка компонентов стратегии бактериального поиска и операторов ГА, многие из которых я еще не испробовал.

В алгоритме BFO ранее мной была допущена ошибка в подсчете количества жизней бактерий, однако эта ошибка была исправлена. BFO немного улучшил результаты и поднялся на строку выше ABC. Хочу отметить, что при написании алгоритмов оптимизации сложно обнаруживать ошибки в коде и логике стратегии поиска. Даже при наличии ошибок алгоритм практически всегда продолжает поиск. Ошибки не всегда ухудшают результаты; бывает так, что результаты значительно улучшаются, и "ошибка" становится частью стратегии. Стоит всегда помнить, что в алгоритмах оптимизации большие изменения в логике не всегда приводят к значительным улучшениям результатов, а мелкие изменения порой могут приводить к кардинальным улучшениям. Исправленная версия BFO находится в архиве к статье.

Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам.

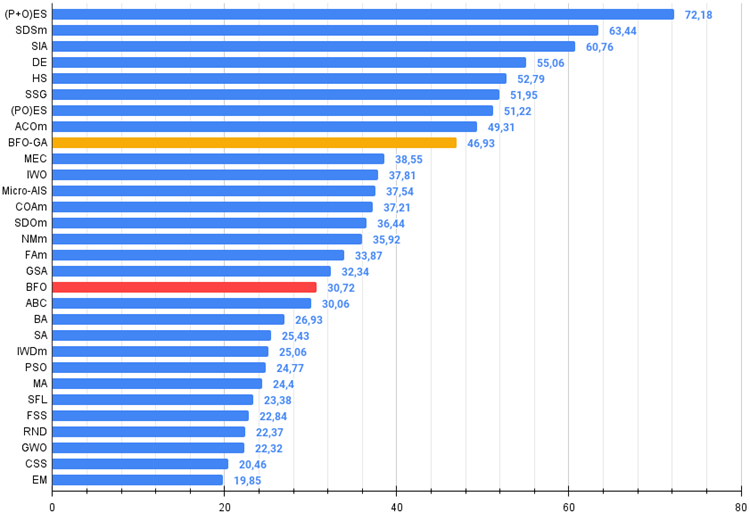
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы).

Плюсы и минусы гибридного алгоритма оптимизации бактериального поиска с генетическим алгоритмом (BFO-GA):

Плюсы:

1. Высокая скорость работы алгоритма.
   
2. Простая реализация.
3. Хорошая сходимость на функциях с небольшим количеством параметров.
   

Минусы:

1. Невысокая сходимость на задачах с большим пространством поиска.
   

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.