Алгоритм оптимизации бабочек — Butterfly Optimization Algorithm (BOA)

MetaTrader 5 — Трейдинг | 9 февраля 2026, 10:24

Andrey Dik

Содержание

Введение

Рассмотрим в статье один из новых алгоритмов оптимизации, подсмотренный у природы. Бабочки — одни из самых удивительных созданий, чья жизнь неразрывно связана с поиском: поиском пищи, партнёра, места для откладывания яиц. В отличие от многих других насекомых, бабочки обладают уникальной системой химической коммуникации, основанной на восприятии и испускании ароматических веществ — феромонов. Именно эта особенность легла в основу алгоритма оптимизации бабочек Butterfly Optimization Algorithm, BOA, предложенного индийскими исследователями С. Аророй и С. Сингхом в 2019 году.

В природе бабочки используют специализированные хеморецепторы, расположенные на антеннах, для обнаружения химических сигналов на поразительно больших расстояниях. Самцы некоторых видов способны улавливать феромоны самки за несколько километров. Интенсивность воспринимаемого запаха зависит от двух факторов: силы источника аромата и расстояния до него. Согласно закону Стивенса, описывающему психофизическое восприятие стимулов у живых организмов, воспринимаемая величина ощущения связана с физической интенсивностью стимула степенной зависимостью. Этот принцип авторы алгоритма формализовали в виде уравнения аромата: f = c·I^a, где f — воспринимаемая величина аромата, "I" — интенсивность стимула (связанная с качеством источника пищи), "c" — сенсорная модальность (способность бабочки воспринимать запахи), а показатель степени "a" определяет характер зависимости восприятия от интенсивности.

Поведение бабочек при поиске пищи можно разделить на две фазы. Когда бабочка улавливает сильный аромат цветка с обильным нектаром, она целенаправленно летит к источнику — это глобальный поиск, ориентация на лучший известный ресурс. Однако если явного лидера нет или бабочка находится в облаке смешанных запахов от нескольких цветков, она совершает локальные перемещения между ближайшими источниками, исследуя окрестности — это локальный поиск. Вероятность выбора между глобальным и локальным поиском определяется параметром переключения — p.

Важная особенность химической коммуникации бабочек — затухание аромата с расстоянием. Молекулы феромонов рассеиваются в воздухе, поглощаются препятствиями, разрушаются под действием ультрафиолета. Параметр "a" в формуле аромата моделирует именно этот эффект поглощения: при "a" близком к нулю, аромат распространяется практически без потерь и может быть воспринят из любой точки пространства, что способствует глобальному исследованию; при "a" близком к единице, аромат быстро затухает, и бабочки ориентируются преимущественно на ближайшие источники, что усиливает локальную эксплуатацию найденных решений.

Ещё одна характерная черта поведения бабочек — они сами являются источниками аромата. Каждая бабочка испускает феромоны, привлекающие других особей. Чем лучше место, которое она нашла (больше нектара, лучше условия), тем интенсивнее её феромонный сигнал. В алгоритме это моделируется связью интенсивности стимула "I" со значением целевой функции: бабочки с лучшим фитнесом испускают более сильный аромат и сильнее влияют на движение популяции.

Таким образом, рой виртуальных бабочек в алгоритме BOA представляет собой самоорганизующуюся систему, где каждая особь одновременно является и искателем, и маяком для других.

Реализация алгоритма

При реализации алгоритма оптимизации бабочек BOA я столкнулся с серьёзной проблемой: оригинальные формулы из научной статьи приводили к некорректному поведению алгоритма. Популяция бабочек вместо движения к оптимуму систематически схлопывалась к началу координат, а на многомерных функциях алгоритм показывал результаты хуже случайного поиска. Детальный математический анализ выявил причину этого явления.

В оригинальной статье формула глобального поиска записана как x_new = x + (r²·g - x)·f*, где x — текущая позиция бабочки, g* — лучшее найденное решение, r — случайное число из [0,1], а f — аромат бабочки. На первый взгляд формула выглядит логично: бабочка должна двигаться к лучшему решению. Однако при внимательном рассмотрении выражения в скобках, (r²·g - x)* становится очевидной проблемой.

Рассмотрим конкретный пример: пусть лучшее решение g* = 10, текущая позиция x = 5, случайное число r = 0.7 (тогда r² = 0.49), аромат f = 0.5. Подставляя значения, получаем: x_new = 5 + (0.49·10 - 5)·0.5 = 5 + (4.9 - 5)·0.5 = 5 + (-0.1)·0.5 = 4.95. Бабочка сместилась не к оптимуму g* = 10, а в противоположную сторону — к нулю! Это происходит потому, что выражение r²·g* при r < 1 всегда даёт значение меньше g*, и разность (r²·g* - x) направлена не к g*, а к точке r²·g*, которая ближе к нулю.

Аналогичная проблема присутствует в формуле локального поиска x_new = x + (r²·x_j - x_k)·f. Выражение (r²·x_j - x_k) не создаёт осмысленного направления между двумя бабочками j и k. Вместо этого оно генерирует вектор, систематически смещённый к началу координат из-за множителя r² < 1 перед x_j.

Интересно отметить, что оригинальные формулы могут давать приемлемые результаты на стандартных тестовых функциях (Sphere, Rastrigin, Ackley и других), глобальный оптимум которых находится именно в точке (0, 0, ..., 0). В этом случае смещение к началу координат случайно совпадает с движением к оптимуму, что маскирует ошибку в логике алгоритма. Однако на реальных задачах оптимизации, где оптимум может находиться в произвольной точке пространства поиска, алгоритм демонстрирует полную неработоспособность.

Для исправления ситуации пришлось изменить расстановку скобок в формулах, сохранив при этом все оригинальные компоненты алгоритма. Скорректированная формула глобального поиска будет иметь вид x_new = x + r²·(g - x)·f*. Теперь выражение (g* - x) представляет собой вектор направления от текущей позиции к лучшему решению, что соответствует биологической метафоре: бабочка летит на аромат лучшего цветка. Множитель r² масштабирует длину шага, а аромат f определяет интенсивность движения. Проверим на том же примере: x_new = 5 + 0.49·(10 - 5)·0.5 = 5 + 0.49·5·0.5 = 5 + 1.225 = 6.225. Теперь бабочка корректно движется от x = 5 в сторону g* = 10.

Формула локального поиска была скорректирована аналогично: x_new = x + r²·(x_j - x_k)·f. Выражение (x_j - x_k) теперь представляет разностный вектор между двумя случайными бабочками, задающий направление локального исследования. Это создаёт случайное блуждание в пределах текущего распределения популяции, что соответствует локальному поиску пищи бабочками в ограниченной области.

Математическая запись формул в научных статьях может содержать неоднозначности или ошибки, и просто копирование уравнений без понимания их геометрического смысла чревато получением неработающего алгоритма. При реализации любого оптимизационного метода необходимо анализировать физический или биологический смысл каждой операции и проверять корректность работы на задачах с известным расположением оптимума в различных точках пространства поиска.

BOA_Illustration

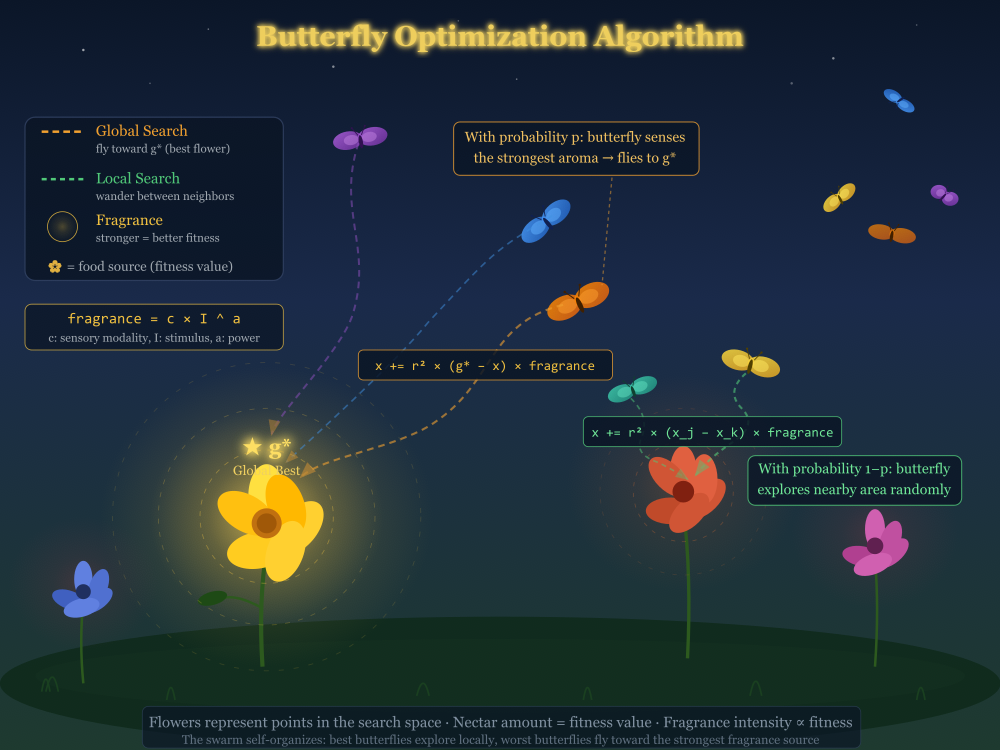
Иллюстрация работы алгоритма BOA

Иллюстрация показывает ночную поляну с цветами и бабочками. Лучший цветок (g*) — крупный жёлтый с золотым ореолом аромата и концентрическими волнами распространения. Три бабочки (оранжевая, синяя, фиолетовая) летят к нему по пунктирным оранжевым траекториям — глобальный поиск. Две другие (жёлтая, бирюзовая) зигзагообразно исследуют область вокруг второго цветка по зелёным траекториям — локальный поиск.

Напишем псевдокод алгоритма BOA.

ВХОД:

N — размер популяции
c — сенсорная модальность, [0, 1]
aStart — начальный показатель поглощения
p — вероятность переключения глобальный/локальный поиск
T — общее число эпох
D — размерность пространства поиска
min[d], max[d] — границы поиска по каждой координате d

ВЫХОД:
g* — лучшая найденная позиция
fB — лучшее значение целевой функции

//-----------------------------------------------------------------------------
// Инициализация
//-----------------------------------------------------------------------------
1. aCurrent ← aStart
2. fB ← −∞
3. ДЛЯ КАЖДОЙ бабочки i = 1..N:
4. fragrance[i] ← c
5. intensity[i] ← 0.5
6. ДЛЯ КАЖДОЙ координаты d = 1..D:
7. x[i][d] ← min[d] + rand(0,1) × (max[d] − min[d])
8. f[i] ← FitnessFunction(x[i])

//-----------------------------------------------------------------------------
// Основной цикл
//-----------------------------------------------------------------------------
9. ДЛЯ КАЖДОЙ эпохи t = 1..T:

//--- Обновление лучшего глобального решения ---
10. ДЛЯ КАЖДОЙ бабочки i = 1..N:
11. ЕСЛИ f[i] > fB:
12. fB ← f[i]
13. g* ← x[i]

//--- Нормализация интенсивности стимула ---
14. fMin ← min(f[1..N])
15. fMax ← max(f[1..N])
16. range ← fMax − fMin
17. ДЛЯ КАЖДОЙ бабочки i = 1..N:
18. ЕСЛИ range < ε:
19. intensity[i] ← 0.5
20. ИНАЧЕ:
21. intensity[i] ← 0.1 + 0.9 × (f[i] − fMin) / range

//--- Обновление показателя поглощения ---
22. aCurrent ← aStart + (t / T) × (1.0 − aStart)
23. ЕСЛИ aCurrent > 1.0: aCurrent ← 1.0

//--- Вычисление аромата (Формула 1) ---
24. ДЛЯ КАЖДОЙ бабочки i = 1..N:
25. fragrance[i] ← c × intensity[i] ^ aCurrent

//--- Перемещение бабочек ---
26. ДЛЯ КАЖДОЙ бабочки i = 1..N:
27. rnd ← rand(0,1)

28. ЕСЛИ rnd < p:
//--- Глобальный поиск (Формула 2) ---
29. ДЛЯ КАЖДОЙ координаты d = 1..D:
30. r ← rand(0,1)
31. r² ← r × r
32. direction ← g*[d] − x[i][d]
33. x[i][d] ← x[i][d] + r² × direction × fragrance[i]

34. ИНАЧЕ:
//--- Локальный поиск (Формула 3) ---
35. j ← случайная бабочка из [1..N]
36. k ← случайная бабочка из [1..N], k ≠ j
37. ДЛЯ КАЖДОЙ координаты d = 1..D:
38. r ← rand(0,1)
39. r² ← r × r
40. direction ← x[j][d] − x[k][d]
41. x[i][d] ← x[i][d] + r² × direction × fragrance[i]

//--- Проверка границ ---
42. ДЛЯ КАЖДОЙ координаты d = 1..D:
43. ЕСЛИ x[i][d] < min[d]: x[i][d] ← min[d]
44. ЕСЛИ x[i][d] > max[d]: x[i][d] ← max[d]

//--- Вычисление фитнеса ---
45. f[i] ← FitnessFunction(x[i])

46. ВЕРНУТЬ g*, fB

Переходим к реализации алгоритма BOA.

Класс "C_AO_BOA" наследуется от базового класса "C_AO" и реализует алгоритм оптимизации бабочек. В конструкторе задаются имя алгоритма, его описание и ссылка на статью, а также значения параметров по умолчанию: размер популяции, сенсорная модальность, начальный показатель поглощения, вероятность переключения между глобальным и локальным поиском.

Массив "params" содержит четыре элемента, каждый из которых хранит имя и значение соответствующего параметра. Публичные поля "sensorModC", "aStart" и "switchP" доступны извне для прямого задания значений перед инициализацией. Приватная часть класса содержит текущий показатель поглощения "aCurrent", общее число эпох "epochs", счётчик текущей эпохи "epochNow", а также два массива, "fragrance" для хранения вычисленного аромата каждой бабочки и "intensity" для хранения нормализованной интенсивности стимула. Метод "SetParams" считывает значения из массива "params" и присваивает их соответствующим полям класса.

//————————————————————————————————————————————————————————————————————
class C_AO_BOA : public C_AO
{
  public:
  ~C_AO_BOA () { }

  C_AO_BOA ()
  {
    ao_name = "BOA";
    ao_desc = "Butterfly Optimization Algorithm";
    ao_link = "https://www.mql5.com/ru/articles/21209";

    popSize    = 50;
    sensorModC = 0.9;
    aStart     = 0.5;
    switchP    = 0.8;

    ArrayResize (params, 4);
    params [0].name = "popSize";    params [0].val = popSize;
    params [1].name = "sensorModC"; params [1].val = sensorModC; // сенсорная модальность [0, 1]
    params [2].name = "aStart";     params [2].val = aStart;     // начальный показатель поглощения
    params [3].name = "switchP";    params [3].val = switchP;    // вероятность переключения (switch probability)
  }

  void SetParams ()
  {
    popSize    = (int)params [0].val;
    sensorModC = params      [1].val;
    aStart     = params      [2].val;
    switchP    = params      [3].val;
  }

  bool Init (const double &rangeMinP  [],
             const double &rangeMaxP  [],
             const double &rangeStepP [],
             const int     epochsP = 0);

  void Moving   ();
  void Revision ();

  //------------------------------------------------------------------
  double sensorModC;  // сенсорная модальность c (sensory modality)
  double aStart;      // начальный показатель поглощения
  double switchP;     // вероятность переключения p (switch probability)

  private: //—————————————————————————————————————————————————————————
  double aCurrent;    // текущий показатель поглощения
  int    epochs;      // общее число эпох
  int    epochNow;    // текущая эпоха

  double fragrance []; // аромат каждой бабочки
  double intensity []; // интенсивность стимула (нормализованный фитнес)

  void CalculateFragrance ();
  void NormalizeIntensity ();
};
//————————————————————————————————————————————————————————————————————

Метод "Init" принимает массивы минимальных и максимальных границ пространства поиска, массив шагов дискретизации и общее число эпох. Сначала вызывается метод "StandardInit" базового класса, который выполняет стандартную инициализацию: выделение памяти под популяцию, копирование границ и шагов поиска, определение числа координат. Если стандартная инициализация завершилась неудачно, метод возвращает "false".

Затем запоминается общее число эпох, счётчик текущей эпохи обнуляется, текущий показатель поглощения устанавливается равным начальному значению "aStart". После этого выделяется память под массивы аромата и интенсивности размером "popSize", и каждому элементу аромата присваивается начальное значение "sensorModC", а каждому элементу интенсивности — значение 0.5. Это означает, что до первой оценки фитнеса все бабочки считаются одинаковыми по привлекательности, а их начальный аромат определяется только сенсорной модальностью.

//————————————————————————————————————————————————————————————————————
bool C_AO_BOA::Init (const double &rangeMinP  [],
                     const double &rangeMaxP  [],
                     const double &rangeStepP [],
                     const int     epochsP = 0)
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //------------------------------------------------------------------
  epochs   = epochsP;
  epochNow = 0;
  aCurrent = aStart;

  //------------------------------------------------------------------
  // Инициализация массивов аромата и интенсивности
  //------------------------------------------------------------------
  ArrayResize (fragrance, popSize);
  ArrayResize (intensity, popSize);

  for (int i = 0; i < popSize; i++)
  {
    fragrance [i] = sensorModC;
    intensity [i] = 0.5;
  }

  return true;
}
//————————————————————————————————————————————————————————————————————

Метод "Moving" реализует перемещение всех бабочек на текущей итерации. В начале увеличивается счётчик эпох "epochNow". Если флаг "revision" установлен в "false", что означает первую итерацию, каждой бабочке назначается случайная позиция: для каждой координаты генерируется случайное число из равномерного распределения на отрезке от нуля до единицы, и позиция вычисляется как линейная интерполяция между минимальной и максимальной границей с последующей дискретизацией функцией "SeInDiSp". После инициализации флаг "revision" устанавливается в "true", и метод завершается.

На всех последующих итерациях сначала вызывается метод "CalculateFragrance", вычисляющий аромат каждой бабочки на основе текущей интенсивности стимула и показателя поглощения. Затем для каждой бабочки "i" генерируется случайное число и сравнивается с вероятностью переключения "switchP". Если случайное число меньше "switchP", выполняется глобальный поиск: для каждой координаты "d" генерируется случайное число "r", вычисляется его квадрат "r²", определяется направление как разность между координатой лучшего глобального решения "cB" и текущей координатой бабочки, после чего позиция обновляется прибавлением произведения "r²", направления и аромата данной бабочки. Таким образом бабочка смещается в сторону лучшего найденного решения, причём величина шага пропорциональна расстоянию до цели, случайному множителю и силе аромата.

Если случайное число больше или равно "switchP", выполняется локальный поиск. Случайным образом выбираются две различные бабочки "j" и "k" из популяции. Для каждой координаты "d" аналогично генерируется "r²", вычисляется направление как разность координат бабочек "j" и "k", и позиция обновляется прибавлением произведения "r²", направления и аромата. Этот механизм создаёт случайное блуждание, масштаб которого определяется текущим разбросом популяции.

Дополнительно после локального поиска с вероятностью 0.2 одна случайно выбранная координата бабочки заменяется значением, сгенерированным по нормальному распределению с центром в соответствующей координате лучшего решения "cB" и границами, совпадающими с границами пространства поиска. Этот приём отсутствует в оригинальном алгоритме и служит для предотвращения застревания популяции в локальных экстремумах путём внесения контролируемого шума вблизи лучшего известного решения.

В завершение для каждой координаты каждой бабочки вызывается функция "SeInDiSp", которая одновременно ограничивает значение допустимым диапазоном и выполняет дискретизацию с заданным шагом.

//————————————————————————————————————————————————————————————————————
void C_AO_BOA::Moving ()
{
  epochNow++;

  //------------------------------------------------------------------
  // Первая итерация - случайная инициализация популяции
  // Позиции бабочек генерируются случайно в пространстве поиска
  //------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int d = 0; d < coords; d++)
      {
        double rnd = u.RNDfromCI (0.0, 1.0);
        a [i].c [d] = rangeMin [d] + rnd * (rangeMax [d] - rangeMin [d]);
        a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]);
      }
    }
    revision = true;
    return;
  }

  //------------------------------------------------------------------
  // Вычисление аромата для каждой бабочки (формула 1)
  // f = c * I^a
  //------------------------------------------------------------------
  CalculateFragrance ();

  //------------------------------------------------------------------
  // Основной цикл - движение бабочек
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (u.RNDprobab () < switchP)
    {
      //==============================================================
      // ГЛОБАЛЬНЫЙ ПОИСК (формула 2, скорректированная)
      // x_i(t+1) = x_i(t) + r² × (g - x_i(t)) × f_i
      // Бабочка движется к лучшему глобальному решению g
      //
      // Логика: направление (g - x) указывает от текущей позиции к лучшей,
      // шаг масштабируется r² (случайность) и f (аромат/фитнес)
      //==============================================================
      for (int d = 0; d < coords; d++)
      {
        double r = u.RNDprobab ();
        double r2 = r * r;

        // Направление от текущей позиции к лучшей
        double direction = cB [d] - a [i].c [d];

        // Шаг: r² × направление × аромат
        double step = r2 * direction * fragrance [i];

        a [i].c [d] = a [i].c [d] + step;
      }
    }
    else
    {
      //==============================================================
      // ЛОКАЛЬНЫЙ ПОИСК (формула 3, скорректированная)
      // x_i(t+1) = x_i(t) + r² × (x_j(t) - x_k(t)) × f_i
      // Случайное блуждание: направление определяется разницей между
      // двумя случайными бабочками j и k
      //
      // Логика: (x_j - x_k) даёт случайное направление в пространстве,
      // определяемое текущим распределением популяции
      //==============================================================

      // Выбираем две случайные бабочки j и k
      int j = u.RNDminusOne (popSize);
      int k = u.RNDminusOne (popSize);

      // Убеждаемся, что j и k различны
      while (k == j) k = u.RNDminusOne (popSize);

      for (int d = 0; d < coords; d++)
      {
        double r = u.RNDprobab ();
        double r2 = r * r;

        // Случайное направление между двумя бабочками
        double direction = a [j].c [d] - a [k].c [d];

        // Шаг: r² × направление × аромат
        double step = r2 * direction * fragrance [i];

        a [i].c [d] = a [i].c [d] + step;
      }

      //==============================================================
      // Добавление шума к координатам лучшего решения
      // для предотвращения застревания в локальных экстремумах
      // этого нет в оригинальном BOA
      //==============================================================
      if (u.RNDprobab () < 0.2)
      {
        int ind = u.RNDminusOne (coords);
        a [i].c [ind] = u.GaussDistribution (cB [ind], rangeMin [ind], rangeMax [ind], 1);
      }
    }

    //----------------------------------------------------------------
    // Проверка границ и дискретизация
    //----------------------------------------------------------------
    for (int d = 0; d < coords; d++)
    {
      a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]);
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "Revision" выполняет три операции после того, как все бабочки были перемещены и их фитнес вычислен. Первая операция — обновление глобального лучшего решения: для каждой бабочки "i" проверяется, превышает ли её значение фитнеса текущее лучшее значение "fB", и если да, "fB" обновляется и позиция бабочки копируется в массив лучших координат "cB". Вторая операция — вызов метода "NormalizeIntensity", который пересчитывает интенсивность стимула для каждой бабочки на основе текущих значений фитнеса.

Третья операция — обновление показателя поглощения "aCurrent" путём линейной интерполяции от начального значения "aStart" до единицы в зависимости от отношения текущей эпохи к общему числу эпох. Если вычисленное значение превышает единицу, оно ограничивается сверху. Нарастание показателя поглощения от малых значений к единице означает, что в начале оптимизации аромат всех бабочек примерно одинаков и поиск ведётся равномерно, а к концу бабочки с высоким фитнесом получают существенно больший аромат, что усиливает эксплуатацию найденных перспективных областей.

//————————————————————————————————————————————————————————————————————
void C_AO_BOA::Revision ()
{
  //------------------------------------------------------------------
  // 1. Обновляем глобальное лучшее решение
  //------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ArrayCopy (cB, a [i].c, 0, 0, coords);
    }
  }

  //------------------------------------------------------------------
  // 2. Нормализуем интенсивность стимула (I)
  //    Интенсивность I пропорциональна фитнесу f(x)
  //------------------------------------------------------------------
  NormalizeIntensity ();

  //------------------------------------------------------------------
  // 3. Обновляем показатель поглощения a
  //    Согласно псевдокоду: "Update the value of a"
  //    a линейно возрастает от aStart до 1.0
  //    Это постепенно уменьшает влияние интенсивности на аромат
  //------------------------------------------------------------------
  if (epochs > 0)
  {
    aCurrent = aStart + (double)epochNow / (double)epochs * (1.0 - aStart);
    if (aCurrent > 1.0) aCurrent = 1.0;
  }
}
//————————————————————————————————————————————————————————————————————

Метод "NormalizeIntensity" отвечает за приведение значений фитнеса к единой шкале интенсивности стимула. Сначала определяются минимальное и максимальное значения фитнеса среди всех бабочек текущей популяции. Если разница между максимальным и минимальным фитнесом пренебрежимо мала — меньше 10⁻¹⁰, что означает практическое равенство всех значений фитнеса, — всем бабочкам присваивается одинаковая интенсивность 0.5.

В противном случае для каждой бабочки интенсивность вычисляется по формуле линейного отображения значения фитнеса в диапазон от 0.1 до 1.0: I = 0.1 + 0.9 × (f − fMin) / (fMax − fMin). Бабочка с наихудшим фитнесом получает интенсивность 0.1, с наилучшим — 1.0. Нижняя граница 0.1 выбрана ненулевой намеренно: даже худшие бабочки должны иметь ненулевой аромат, чтобы сохранять способность участвовать в поисковом процессе и не превращаться в полностью пассивных агентов.

//————————————————————————————————————————————————————————————————————
// Нормализация интенсивности стимула
// Согласно статье: "Stimulus Intensity I at x is determined by f(x)"
// I пропорционален фитнесу
//————————————————————————————————————————————————————————————————————
void C_AO_BOA::NormalizeIntensity ()
{
  //------------------------------------------------------------------
  // Находим минимальный и максимальный фитнес
  //------------------------------------------------------------------
  double minF = a [0].f;
  double maxF = a [0].f;

  for (int i = 1; i < popSize; i++)
  {
    if (a [i].f < minF) minF = a [i].f;
    if (a [i].f > maxF) maxF = a [i].f;
  }

  //------------------------------------------------------------------
  // Нормализуем интенсивность в диапазон [0.1, 1.0]
  // Нижняя граница 0.1 предотвращает слишком малый аромат у худших бабочек
  //------------------------------------------------------------------
  double range = maxF - minF;

  if (range < 1e-10)
  {
    // Все фитнесы примерно равны
    for (int i = 0; i < popSize; i++)
    {
      intensity [i] = 0.5;
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      intensity [i] = 0.1 + 0.9 * (a [i].f - minF) / range;
    }
  }
}
//————————————————————————————————————————————————————————————————————

Метод "CalculateFragrance" вычисляет аромат каждой бабочки по основной формуле алгоритма: fragrance = c × I^a, где "c" — сенсорная модальность "sensorModC", "I" — нормализованная интенсивность стимула "intensity", "a" — текущий показатель поглощения "aCurrent". Эта формула основана на законе Стивенса из психофизики, описывающем связь между физической интенсивностью стимула и субъективным восприятием.

При малых значениях показателя "a", характерных для начала оптимизации, возведение интенсивности в малую степень даёт значения близкие к единице для всех бабочек независимо от их фитнеса, и аромат всех бабочек оказывается примерно равным сенсорной модальности "c", что обеспечивает равномерное исследование пространства. По мере роста "a" к единице различия в интенсивности всё сильнее проявляются в аромате: бабочки с высоким фитнесом получают аромат близкий к "c", а бабочки с низким фитнесом — существенно меньший, что направляет поиск в сторону наиболее перспективных областей.

//————————————————————————————————————————————————————————————————————
// Вычисление аромата по формуле 1: f = c * I^a
// где:
// c - сенсорная модальность (определяет базовую величину шага)
// I - интенсивность стимула (нормализованный фитнес)
// a - показатель степени поглощения
//
// При малом a (начало): I^a → 1 для всех I, аромат ≈ c (равномерный поиск)
// При большом a (конец): I^a → I, лучшие бабочки имеют больший аромат
//————————————————————————————————————————————————————————————————————
void C_AO_BOA::CalculateFragrance ()
{
  for (int i = 0; i < popSize; i++)
  {
    // Формула 1: fragrance = c * I^a
    fragrance [i] = sensorModC * MathPow (intensity [i], aCurrent);
  }
}
//————————————————————————————————————————————————————————————————————

Результаты тестов

Будет важным отметить, что без вот этого небольшого участка кода ниже, недостаточным является разнообразие в популяции для мотыльков. Этот фрагмент реализует механизм стохастической мутации, отсутствующий в оригинальном описании алгоритма BOA и добавленный для компенсации его структурной слабости. Проблема заключается в том, что локальный поиск в оригинальной идее авторов целиком зависит от разности позиций двух случайных бабочек (x_j − x_k). По мере схождения популяции расстояния между бабочками уменьшаются, разности стремятся к нулю, и шаги локального поиска становятся микроскопическими. Популяция теряет способность покинуть окрестность текущего лучшего решения, даже если оно является локальным оптимумом.

Добавленный механизм работает следующим образом: с вероятностью 0.2, то есть примерно для каждой пятой бабочки при локальном поиске, случайным образом выбирается одна координата из всех доступных, и её значение заменяется числом, сгенерированным по нормальному распределению с центром в соответствующей координате лучшего глобального решения "cB". Параметр сигма равен 1, а значения ограничены допустимым диапазоном координаты. Это создаёт контролируемое возмущение: новое значение с высокой вероятностью окажется вблизи лучшего решения, но с некоторой вероятностью может оказаться достаточно далеко, чтобы вытолкнуть бабочку в новую область пространства поиска.

Важно, что мутации подвергается только одна координата из всех, а не весь вектор позиции. Это сохраняет большую часть накопленной информации о перспективной области и одновременно вносит разнообразие по одному измерению. Также существенно, что центром распределения служит координата лучшего решения, а не текущая позиция бабочки — таким образом мутация не является слепым случайным блужданием, а представляет собой направленное исследование окрестности лучшей найденной точки.

//==============================================================
      // Добавление шума к координатам лучшего решения
      // для предотвращения застревания в локальных экстремумах
      // этого нет в оригинальном BOA
      //==============================================================
      if (u.RNDprobab () < 0.2)
      {
        int ind = u.RNDminusOne (coords);
        a [i].c [ind] = u.GaussDistribution (cB [ind], rangeMin [ind], rangeMax [ind], 1);
      }
    }

    //----------------------------------------------------------------

Вот такие результаты без этого возмущения.

BOA|Butterfly Optimization Algorithm|50.0|0.9|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.6635729348082547
25 Hilly's; Func runs: 10000; result: 0.3933240668190092
500 Hilly's; Func runs: 10000; result: 0.2670951838030907
=============================
5 Forest's; Func runs: 10000; result: 0.5030842340559138
25 Forest's; Func runs: 10000; result: 0.31195194496509265
500 Forest's; Func runs: 10000; result: 0.1922137682213402
=============================
5 Megacity's; Func runs: 10000; result: 0.32461538461538464
25 Megacity's; Func runs: 10000; result: 0.16953846153846158
500 Megacity's; Func runs: 10000; result: 0.10381538461538553
=============================
All score: 2.92921 (32.55%)

А такие получаем, когда добавляем шум к координатам лучшего решения.

BOA|Butterfly Optimization Algorithm|50.0|0.9|0.5|0.8|
=============================
5 Hilly's; Func runs: 10000; result: 0.7293075035168879
25 Hilly's; Func runs: 10000; result: 0.5005498140056686
500 Hilly's; Func runs: 10000; result: 0.2754406215727097
=============================
5 Forest's; Func runs: 10000; result: 0.94839177748601
25 Forest's; Func runs: 10000; result: 0.45575888873544235
500 Forest's; Func runs: 10000; result: 0.19904714403024765
=============================
5 Megacity's; Func runs: 10000; result: 0.5
25 Megacity's; Func runs: 10000; result: 0.24523076923076922
500 Megacity's; Func runs: 10000; result: 0.10603076923077022
=============================
All score: 3.95976 (44.00%)

Визуализация работы алгоритма на наших тестовых функциях, а также на стандартных тестовых функциях, представленных в программе для свободного выбора и тестирования.

Hilly

BOA на тестовой функции Hilly

Forest

BOA на тестовой функции Forest

Megacity

BOA на тестовой функции Megacity

Ackley

BOA на стандартной функции Ackey

Shaffer

BOA на стандартной функции Shaffer

В рейтинговой таблице лучших популяционных методов оптимизации алгоритм BOA по результатам тестирования представлен ознакомительно.

№	AO	Description	Hilly			Hilly Final	Forest			Forest Final	Megacity (discrete)			Megacity Final	Final Result	% of MAX
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Hilly Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest Final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity Final	Final Result	% of MAX
1	ANS	across neighbourhood search	0,94948	0,84776	0,43857	2,23581	1,00000	0,92334	0,39988	2,32323	0,70923	0,63477	0,23091	1,57491	6,134	68,15
2	CLA	code lock algorithm (joo)	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	AMOm	animal migration ptimization M	0,90358	0,84317	0,46284	2,20959	0,99001	0,92436	0,46598	2,38034	0,56769	0,59132	0,23773	1,39675	5,987	66,52
4	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
5	CTA	comet tail algorithm (joo)	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
6	TETA	time evolution travel algorithm (joo)	0,91362	0,82349	0,31990	2,05701	0,97096	0,89532	0,29324	2,15952	0,73462	0,68569	0,16021	1,58052	5,797	64,41
7	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
8	ECBO	enhanced_colliding_bodies_optimization	0,93479	0,75747	0,32471	2,01697	0,97436	0,77446	0,23037	1,97919	0,88923	0,58061	0,15224	1,62208	5,618	62,43
9	BOAm	billiards optimization algorithm M	0,95757	0,82599	0,25235	2,03590	1,00000	0,90036	0,30502	2,20538	0,73538	0,52523	0,09563	1,35625	5,598	62,19
10	AAm	archery algorithm M	0,91744	0,70876	0,42160	2,04780	0,92527	0,75802	0,35328	2,03657	0,67385	0,55200	0,23738	1,46323	5,548	61,64
11	ESG	evolution of social groups (joo)	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
12	SIA	simulated isotropic annealing (joo)	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
13	EOm	extremal_optimization_M	0,76166	0,77242	0,31747	1,85155	0,99999	0,76751	0,23527	2,00277	0,74769	0,53969	0,14249	1,42987	5,284	58,71
14	BBO	biogeography based optimization	0,94912	0,69456	0,35031	1,99399	0,93820	0,67365	0,25682	1,86867	0,74615	0,48277	0,17369	1,40261	5,265	58,50
15	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
16	DA	dialectical algorithm	0,86183	0,70033	0,33724	1,89940	0,98163	0,72772	0,28718	1,99653	0,70308	0,45292	0,16367	1,31967	5,216	57,95
17	BHAm	black hole algorithm M	0,75236	0,76675	0,34583	1,86493	0,93593	0,80152	0,27177	2,00923	0,65077	0,51646	0,15472	1,32195	5,196	57,73
18	ASO	anarchy society optimization	0,84872	0,74646	0,31465	1,90983	0,96148	0,79150	0,23803	1,99101	0,57077	0,54062	0,16614	1,27752	5,178	57,54
19	RFO	royal flush optimization (joo)	0,83361	0,73742	0,34629	1,91733	0,89424	0,73824	0,24098	1,87346	0,63154	0,50292	0,16421	1,29867	5,089	56,55
20	AOSm	atomic orbital search M	0,80232	0,70449	0,31021	1,81702	0,85660	0,69451	0,21996	1,77107	0,74615	0,52862	0,14358	1,41835	5,006	55,63
21	TSEA	turtle shell evolution algorithm (joo)	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
22	BSA	backtracking_search_algorithm	0,97309	0,54534	0,29098	1,80941	0,99999	0,58543	0,21747	1,80289	0,84769	0,36953	0,12978	1,34700	4,959	55,10
23	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
24	SRA	successful restaurateur algorithm (joo)	0,96883	0,63455	0,29217	1,89555	0,94637	0,55506	0,19124	1,69267	0,74923	0,44031	0,12526	1,31480	4,903	54,48
25	BO	bonobo_optimizer	0,77565	0,63805	0,32908	1,74278	0,88088	0,76344	0,25573	1,90005	0,61077	0,49846	0,14246	1,25169	4,895	54,38
26	CRO	chemical reaction optimisation	0,94629	0,66112	0,29853	1,90593	0,87906	0,58422	0,21146	1,67473	0,75846	0,42646	0,12686	1,31178	4,892	54,36
27	BIO	blood inheritance optimization (joo)	0,81568	0,65336	0,30877	1,77781	0,89937	0,65319	0,21760	1,77016	0,67846	0,47631	0,13902	1,29378	4,842	53,80
28	DOA	dream_optimization_algorithm	0,85556	0,70085	0,37280	1,92921	0,73421	0,48905	0,24147	1,46473	0,77231	0,47354	0,18561	1,43146	4,825	53,62
29	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
30	DEA	dolphin_echolocation_algorithm	0,75995	0,67572	0,34171	1,77738	0,89582	0,64223	0,23941	1,77746	0,61538	0,44031	0,15115	1,20684	4,762	52,91
31	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
32	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
33	BCOm	bacterial chemotaxis optimization M	0,75953	0,62268	0,31483	1,69704	0,89378	0,61339	0,22542	1,73259	0,65385	0,42092	0,14435	1,21912	4,649	51,65
34	ABO	african buffalo optimization	0,83337	0,62247	0,29964	1,75548	0,92170	0,58618	0,19723	1,70511	0,61000	0,43154	0,13225	1,17378	4,634	51,49
35	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
36	FBA	fractal-based Algorithm	0,79000	0,65134	0,28965	1,73099	0,87158	0,56823	0,18877	1,62858	0,61077	0,46062	0,12398	1,19537	4,555	50,61
37	TSm	tabu search M	0,87795	0,61431	0,29104	1,78330	0,92885	0,51844	0,19054	1,63783	0,61077	0,38215	0,12157	1,11449	4,536	50,40
38	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
39	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
40	AEFA	artificial electric field algorithm	0,87700	0,61753	0,25235	1,74688	0,92729	0,72698	0,18064	1,83490	0,66615	0,11631	0,09508	0,87754	4,459	49,55
41	AEO	artificial ecosystem-based optimization algorithm	0,91380	0,46713	0,26470	1,64563	0,90223	0,43705	0,21400	1,55327	0,66154	0,30800	0,28563	1,25517	4,454	49,49
42	CAm	camel algorithm M	0,78684	0,56042	0,35133	1,69859	0,82772	0,56041	0,24336	1,63149	0,64846	0,33092	0,13418	1,11356	4,444	49,37
43	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
44	CMAES	covariance_matrix_adaptation_evolution_strategy	0,76258	0,72089	0,00000	1,48347	0,82056	0,79616	0,00000	1,61672	0,75846	0,49077	0,00000	1,24923	4,349	48,33
45	BOA	butterfly_optimization_algorithm	0,72930	0,50054	0,27544	1,50528	0,94839	0,45575	0,19904	1,60318	0,50000	0,24523	0,10603	0,85126	3,960	44,00
	RW	random walk	0,48754	0,32159	0,25781	1,06694	0,37554	0,21944	0,15877	0,75375	0,27969	0,14917	0,09847	0,52734	2,348	26,09

Выводы

В основе алгоритма BOA лежит идея: каждая бабочка одновременно является и искателем, и источником аромата, сила которого определяется качеством найденного решения. Формула аромата, основанная на законе Стивенса из психофизики, обеспечивает плавный переход от равномерного исследования пространства на ранних итерациях к целенаправленной эксплуатации перспективных областей на поздних.

В ходе работы над алгоритмом была обнаружена и исправлена ошибка в оригинальных формулах движения, опубликованных авторами. Неверная расстановка скобок в выражениях глобального и локального поиска приводила к систематическому смещению популяции в сторону начала координат вместо движения к оптимуму. Эта ошибка оставалась незамеченной, поскольку стандартные тестовые функции, как правило, имеют оптимум именно в начале координат, и дефект формул случайно совпадал с направлением к решению. После исправления скобок, алгоритм стал корректно работать на задачах с произвольным расположением оптимума в пространстве поиска.

Тем не менее даже с исправленными формулами алгоритм продемонстрировал склонность к преждевременной сходимости. По мере схождения популяции разности между позициями бабочек уменьшаются, шаги локального поиска становятся пренебрежимо малыми, и популяция утрачивает способность покинуть окрестность текущего лучшего решения. Для компенсации этого недостатка был добавлен механизм стохастической мутации, отсутствующий в оригинальном описании: с небольшой вероятностью одна координата бабочки заменяется значением, сгенерированным по нормальному распределению с центром в лучшем найденном решении. Это позволило поднять результативность алгоритма с 32.5% до 44% на тестовом наборе функций.

Несмотря на улучшение, достигнутый результат не позволяет алгоритму войти в рейтинговую таблицу. Основная причина заключается в архитектурных ограничениях самого подхода. Механизм перемещения бабочек опирается всего на два режима — глобальный, направленный к единственному лучшему решению, и локальный, определяемый разностью позиций двух случайных агентов. Оба режима порождают шаги, масштабируемые квадратом случайного числа r² со средним значением около 0.33, что в сочетании с аромат-множителем порядка 0.5 даёт типичный шаг около 12% от расстояния до цели. Такая динамика слишком консервативна для эффективного исследования многомерных пространств с множеством локальных оптимумов.

В целом алгоритм оптимизации бабочек следует оценивать как работоспособную, но не выдающуюся метаэвристику. Его сильной стороной является простота реализации. Слабой стороной остаётся недостаточное разнообразие поисковых стратегий и склонность к затуханию шагов при схождении популяции.

tab

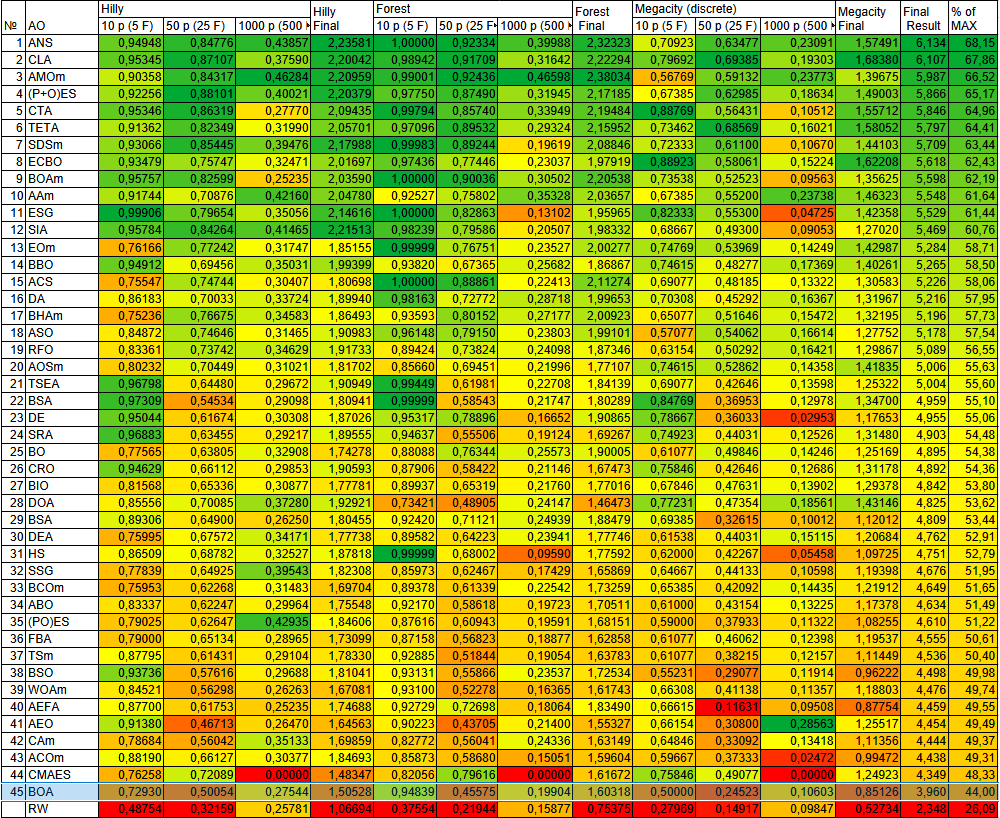
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам

chart

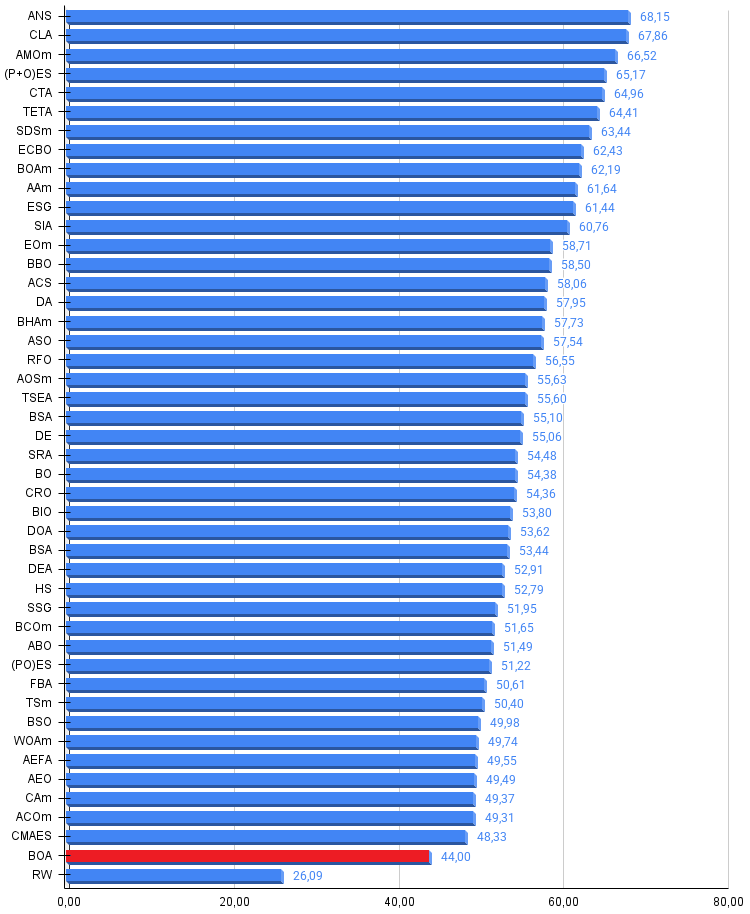
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)

Плюсы и минусы алгоритма BOA:

Плюсы:

Неплохие показатели на задачах типа Forest (гладкие с "острыми" экстремумами).

Минусы:

Склонность к застреванию.

К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

Обновления в едином испытательном стенде - поправил енумератор выбора алгоритмов (исправил выбор этих алгоритмов):

AO_CryStAlm (Crystal Structure Algorithm M)
AO_CoSO (Community of Scientist Optimization)

github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5

Программы, используемые в статье

#	Имя	Тип	Описание
1	#C_AO.mqh	Включаемый файл	Родительский класс популяционных алгоритмов оптимизации
2	#C_AO_enum.mqh	Включаемый файл	Перечисление популяционных алгоритмов оптимизации
3	TestFunctions.mqh	Включаемый файл	Библиотека тестовых функций
4	TestStandFunctions.mqh	Включаемый файл	Библиотека функций тестового стенда
5	Utilities.mqh	Включаемый файл	Библиотека вспомогательных функций
6	CalculationTestResults.mqh	Включаемый файл	Скрипт для расчета результатов в сравнительную таблицу
7	Testing AOs.mq5	Скрипт	Единый испытательный стенд для всех популяционных алгоритмов оптимизации
8	Simple use of population optimization algorithms.mq5	Скрипт	Простой пример использования популяционных алгоритмов оптимизации без визуализации
9	Test_BOA.mq5	Скрипт	Испытательный стенд для BOA

Прикрепленные файлы |

Загрузить ZIP

BOA.zip (411.27 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Машинное обучение и Data Science (Часть 36): Работа с несбалансированными финансовыми рынками

Финансовые рынки не находятся в идеальном равновесии. Некоторые рынки демонстрируют бычий тренд, другие — медвежий, а третьи — флэт. Эта несбалансированная информация, используемая для обучения моделей машинного обучения, может вводить в заблуждение, поскольку рынки часто меняют направление. В этой статье мы обсудим несколько способов решения этой проблемы.

Знакомство с языком MQL5 (Часть 29): Освоение API и функции WebRequest в языке MQL5 (III)

В этой статье мы продолжаем осваивать API и WebRequest в языке MQL5, получая свечные данные из внешнего источника. Мы разберем ответ сервера, очистим данные и извлечем ключевые элементы – время открытия и значения OHLC для нескольких дневных свечей, подготовив все для дальнейшего анализа.

Особенности написания экспертов

Написание и тестирование экспертов в торговой системе MetaTrader 4.

Разрабатываем мультивалютный советник (Часть 30): От торговой стратегии — к запуску мультивалютного советника

Статья показывает полный цикл работы по созданию мультивалютного советника с использованием библиотеки Adwizard для MetaTrader 5: от подготовки окружения для создания проектов оптимизации до получения итоговых мультивалютных советников, объединяющих много экземпляров простой торговой стратегии. Разбираем настройку нужных входных параметров, соглашения об удобных именах файлов и запуск трёх экземпляров итоговых советников на разных торговых счетах с разными параметрами.