Популяционные алгоритмы оптимизации: Муравьиная Колония (Ant Colony Optimization - ACO)
Великая тайна любого поведения – это общественное поведение…
Ф. Бартлетт
Содержание:
1. Введение
2. Принципы алгоритма
3. Модифицированная версия
4. Результаты тестов
1. Введение
Бельгийский исследователь Марко Дориго создал математическую модель, научно описывающую процесс коллективного интеллекта в колонии муравьев. Он опубликовал её в докторской диссертации в 1992 году и реализовал в виде алгоритма. Оптимизация колоний муравьев (ACO) — это основанный на популяции метод стохастического поиска для решения широкого круга задач комбинаторной оптимизации. В основе ACO лежит концепция стигмергии. В 1959 году Пьер-Поль Грассе изобрел теорию стигмергии, чтобы объяснить поведение термитов при строительстве гнезд. Стигмергия состоит из двух греческих слов: стигма — знак и ергон — действие.
Каноническим определением считается непрямой тип взаимодействия между членами популяции, протяжённый во времени, через взаимодействие с окружающей средой. Т.е. один из агентов оставляет след или как-то видоизменяет локаль, чтобы, при входе в её область, другой агент получил некую информацию. Для муравьёв стигмергией является феромоны. Примером стигмергии является общение муравьев в процессе поиска пищи: муравьи косвенно общаются друг с другом, оставляя следы феромонов на земле и тем самым влияя на процессы принятия решений другими муравьями. Эта простая форма общения между отдельными муравьями порождает сложное поведение и возможности колонии в целом.
Муравьи — общественные насекомые, они живут колониями. Поведение муравьев контролируется целью поиска пищи. Во время поиска они бродят по своим колониям. Муравей неоднократно прыгает с одного места на другое в поисках еды и во время движения он откладывает на землю органическое соединение, называемое феромоном. Таким образом муравьи общаются друг с другом с помощью феромонных следов.
Когда муравей находит какое-то количество еды, он несет столько, сколько может унести. При возвращении он откладывает феромоны на пути в зависимости от количества и качества пищи. Муравей чувствует запах феромона. Вследствии этого другие муравьи могут учуять этот запах и следовать по этому маршруту. Чем выше уровень феромона, тем выше вероятность выбора именно этого пути, и чем больше муравьев проходит конкретный путь, тем количество феромона также будет увеличиваться на этом маршруте.
Давайте посмотрим это на примере. Предположим, что есть два пути добраться до еды из колонии. Сначала на земле нет феромона. Итак, вероятность выбора этих двух путей равна, что означает 50%. Предположим, что два муравья выбирают два разных пути к еде, так как вероятность выбора этих путей равна пятьдесят на пятьдесят. Расстояния этих двух путей различны. Муравей, следующий более коротким путем, доберется до еды раньше, чем другой. Найдя пищу, он уносит немного еды с собой и возвращается в колонию. Когда он отслеживает обратный путь, он откладывает феромон на землю. Муравей, идущий по более короткому пути, раньше достигнет колонии.
Когда третий муравей захочет выйти на поиски пищи, он пойдет по пути, имеющему более короткое расстояние в зависимости от уровня феромона на земле. Поскольку на более коротком пути больше феромонов, чем на более длинном, третий муравей будет следовать по пути, имеющему больше феромонов. К тому времени, когда муравей, следующий более длинным путем, вернулся в колонию, больше муравьев уже прошли путь с большим уровнем феромонов. Затем, когда другой муравей попытается добраться до пункта назначения (еды) из колонии, он обнаружит, что каждый путь имеет одинаковый уровень феромона. Таким образом, он случайным образом выбирает один. Повторяя этот процесс снова и снова, через некоторое время более короткий путь имеет больший уровень феромонов, чем другие, и имеет более высокую вероятность следовать по этому пути, и все муравьи в следующий раз пойдут по более короткому пути.
Алгоритм ACO — это своего рода алгоритм роевого интеллекта. Путем моделирования процесса поиска пищи муравьиной колонией кратчайший путь в различных средах устанавливается с использованием внутреннего механизма передачи информации муравьиной колонии. В процессе деятельности муравьи будут оставлять феромон, а последующие муравьи могут выбирать путь по феромону, оставленному предыдущими муравьями. Чем выше концентрация оставшегося на пути феромона, тем выше вероятность того, что муравей выберет этот путь. В то же время концентрация феромона со временем улетучивается. Следовательно, благодаря поведению муравьиной колонии муравьи постоянно учатся и оптимизируются с помощью механизма обратной связи, чтобы определить кратчайший путь поиска пищи. Согласно характеристикам алгоритма ACO, он широко используется при планировании пути.
2. Принципы алгоритма
В ACO набор программных агентов, называемых искусственными муравьями, ищет хорошие решения для данной задачи оптимизации. Для применения ACO задача оптимизации трансформируется в задачу поиска наилучшего пути на взвешенном графе. Искусственные муравьи (далее муравьи) постепенно строят решения, перемещаясь по графу. Процесс построения решения является стохастическим и зависит от модели феромонов, то есть набора параметров, связанных с компонентами графа (узлами или ребрами), значения которых изменяются муравьями во время выполнения.
Рассмотрим алгоритм к задаче коммивояжера. Задан набор местоположений (например, городов) и расстояния между ними. Задача состоит в том, чтобы найти замкнутый путь минимальной длины, который посещает каждый город только один раз. Граф, определенный путем связывания набора городов с набором вершин графа. Этот граф называется строительным графом. Так как можно переехать из любого заданного города в любой другой город, строительный граф является полносвязным, а количество вершин равно количеству городов. Мы устанавливаем длины ребер между вершинами пропорциональными расстояниям между городами, представленными этими вершинами, и связываем значения феромонов и эвристические значения с ребрами графа. Значения феромонов изменяются во время выполнения и представляют собой совокупный опыт муравьиной колонии, в то время как эвристические значения являются значениями, зависящими от проблемы.
Муравьи строят решения следующим образом. Каждый муравей начинает со случайно выбранного города (вершины графа построения). Затем на каждом шаге построения он перемещается по ребрам графа. Каждый муравей хранит память своего пути, а на последующих шагах выбирает среди ребер, не ведущих к уже посещенным вершинам. Муравей построил решение, как только он посетил все вершины графа. На каждом шаге построения муравей вероятностно выбирает ребро, которому нужно следовать, среди тех, которые ведут к еще не посещенным вершинам. Вероятностное правило основано на значениях феромонов и эвристической информации: чем выше феромон и эвристическое значение, связанное с ребром, тем выше вероятность того, что муравей выберет именно это ребро. Как только все муравьи завершили свой путь, феромоны на краях обновляются. Каждое из значений феромона изначально уменьшается на определенный процент. Эта процедура применяется повторно до тех пор, пока не будет удовлетворен критерий завершения.
Коммуникация на основе феромонов является одним из наиболее эффективных способов коммуникации, широко распространенных в природе. Феромон используется общественными насекомыми, такими как пчелы, муравьи и термиты для связи между агентами. Из-за своей осуществимости искусственные феромоны были приняты в многороботных и роевых роботизированных системах.
Как понять, что наши муравьи нашли действительно кратчайший маршрут. Для этого есть отличный тестовый пример: точки, расположенные по кругу. Для них кратчайший путь будет всегда один — окружность.
Первый ACO-алгоритм назывался муравьиной системой и был нацелен на решение задачи коммивояжера, цель которой — найти кратчайший путь туда и обратно, чтобы связать ряд городов. Общий алгоритм относительно прост и основан на наборе муравьев, каждый из которых совершает одно из возможных обходов городов. На каждом этапе муравей выбирает путь из одного города в другой по некоторым правилам:
- Он должен посетить каждый город ровно один раз;
- У отдаленного города меньше шансов быть выбранным (видимость);
- Чем интенсивнее феромонный след, проложенный на границе между двумя городами, тем больше вероятность того, что эта граница будет выбрана;
- Завершив свой путь, муравей откладывает больше феромонов на все пройденные им ребра, если путь короткий;
- После каждой итерации следы феромонов испаряются.

Рисунок 1. Пример возможных путей в пяти узловых точках.
3. Модифицированная версия
Известно несколько самых популярных вариантов алгоритмов ACO. Перечислим их:
Муравьиная система (AS).
Система муравьев — это первый алгоритм ACO.
Система колоний муравьев (ACS).
В алгоритме системы муравьиной колонии исходная система муравьев была изменена в трех аспектах:
1. Выбор края смещен в сторону эксплуатации (т.е. в пользу вероятности выбора самых коротких краев с большим количеством феромона);
2. При построении решения муравьи изменяют уровень феромонов на ребрах, которые они выбирают, применяя локальное правило обновления феромонов;
3. В конце каждой итерации только лучший муравей может обновлять следы, применяя модифицированное глобальное правило обновления феромонов.
Элитная муравьиная система.
В этом алгоритме глобальное лучшее решение откладывает феромон на своем следе после каждой итерации (даже если этот след не посещался повторно) вместе со всеми остальными муравьями. Цель элитарной стратегии состоит в том, чтобы направить поиск всех муравьев на построение решения, содержащего ссылки текущего наилучшего маршрута.
Муравьиная система макс-мин (MMAS).
Этот алгоритм контролирует максимальное и минимальное количество феромонов на каждом следе. Только лучший глобальный тур или лучший тур повторения могут добавлять феромоны в свой след. Во избежание стагнации алгоритма поиска диапазон возможных количеств феромонов на каждом следе ограничен интервалом [τ max ,τ min]. Все ребра инициализируются значением τ max, чтобы ускорить исследование решения. Следы повторно инициализируются до τ max при приближении к стагнации.
Система муравьев на основе рангов (Asrank).
Все решения ранжированы в соответствии с их длиной. Только фиксированное количество лучших муравьев в этой итерации может обновлять свои испытания. Количество осажденного феромона взвешивается для каждого раствора, так что растворы с более короткими путями откладывают больше феромона, чем растворы с более длинными путями.
Параллельная оптимизация муравьиной колонии (PACO).
Разработана система колонии муравьев (ACS) с коммуникативными стратегиями.
Искусственные муравьи разделены на несколько групп. Предлагаются семь методов коммуникации для обновления уровня феромонов между группами в ACS, которые работают над проблемой коммивояжера.
Непрерывная ортогональная муравьиная колония (COAC).
Механизм отложения феромонов COAC позволяет муравьям совместно и эффективно искать решения. Используя метод ортогонального проектирования, муравьи в допустимой области могут быстро и эффективно исследовать выбранные ими области с расширенными возможностями и точностью глобального поиска. Метод ортогонального проектирования и метод адаптивной настройки радиуса также могут быть распространены на другие алгоритмы оптимизации для обеспечения более широких преимуществ при решении практических задач.
Рекурсивная оптимизация муравьиной колонии.
Это рекурсивная форма муравьиной системы, которая делит всю область поиска на несколько поддоменов и решает задачу в этих поддоменах. Результаты всех поддоменов сравниваются, и несколько лучших из них переходят на следующий уровень. Подобласти, соответствующие выбранным результатам, далее подразделяются, и процесс повторяется до тех пор, пока не будет получен результат желаемой точности. Этот метод был проверен на некорректных задачах геофизической инверсии и работает хорошо.
Рассмотренные выше алгоритмы муравьиной колонии изначально разрабатывались для решения задач оптимизации на графах, в такие алгоритмы задача интегрирована, а условия задачи подаются в виде параметров алгоритма - координаты узлов графов, поэтому алгоритмы, основанные на принципах ACO, узкоспециализированные. Для наших задач такие алгоритмы неприменимы, потому что мы не используем фиксированные координаты, они у нас могут быть любыми, в том числе одинаковыми. Для решения широкого спектра задач оптимизации в области торговли финансовыми инструментами, в том числе для обучения нейронных сетей, нам понадобится разработать новый алгоритм, универсальный, чтобы он мог проходить и наши специальные тесты, т.е. это должен быть совершенно новый, не имеющий аналогов ACO.
Продумаем основную концепцию алгоритма. Так же, как и в каноническом варианте, у нас будет колония муравьев. Мы не можем помечать феромонами пройденные пути, они могут проходить где угодно в многомерном пространстве, запоминать и сохранять маршруты, тем более с непрерывным шагом не представляется целесообразным, потому что вероятность пройти по тому же маршруту стремится к нулю. К тому же нет необходимости вообще запоминать узлы, поскольку нет задачи последовательного прохождения без повторений - необходимо вынести задачу из алгоритма. Так как же быть? На этом этапе совершенно не понятно, учитывая вышесказанное, в каком направлении двигаться в разработке концепции.
Хорошо, тогда ещё раз для себя отметим главные моменты, которые отличают наш новый алгоритм от канонического:
1. Нет фиксированных точек в пространстве.
2. Нет необходимости проходить путь только в определённом порядке.
3. Поскольку нет путей, то и нечего помечать феромонами.
Тогда, по порядку, выясним, что имеем, держа в голове идею муравьиной колонии. Мы можем помечать феромоном сами точки, где были муравьи, а не путь ими пройденный. Примем значение фитнес функции за количество феромонов в точке местонахождения муравья на данный момент итерации. Тогда муравьи должны будут двигаться в сторону координат, где больше всего феромона. Но мы можем столкнуться с проблемой, когда все муравьи просто сбегутся в одну точку, в ту, которая имеет больше всего феромона, а это вовсе необязательно лучшее решение задачи, имея в виду, что точки это и есть переменные оптимизируемой функции. Мы помним, что в классическом ACO так же имеет значение длина пути до узла, чем короче выбранный путь, тем лучше. Таким образом, мы должны рассчитывать расстояние от текущего местоположения до того, куда должен перейти муравей. А следующее место, это то, где находятся другие муравьи, т.е. принимаем концепцию, при которой муравьи перемещаются друг к другу с определенной долей случайности.
Какую мы можем добавить случайность в перемещении?
- Во-первых, добавим коэффициент случайности при выборе следующей позиции PheromoneEffect_P.
- Во-вторых, добавим коэффициент случайности с учетом расстояния до следующей позиции PathLengthEffect_P (чем меньше расстояние, тем предпочтительнее выбор).
Итак, имеем два критерия выбора следующей позиции, количество феромона в каждой конкретной позиции, где находятся муравьи и расстояние между всеми этими точками попарно. Однако, если мы даже сделаем это, используя только эти два критерия выбора, то муравьи будут перемещаться в пространстве по неким ребрам воображаемой фигуры, узлами которой находится их собственное местоположение и никакого прогресса в поисках лучшего места не будет.
Добавим в таком случае радиус влияния феромона PheromoneRadius_P (коэффициент от расстояния между точками), в пределах которого муравьи могут его чувствовать, тогда муравьи смогут проскочить дальше точки, в которую он двигался. Это даст дополнительную степень свободы муравьям при движении в многомерном пространстве.
А для того, чтобы муравьи могли исследовать новые области, им нужно позволить отклоняться от вектора направления по любой из координат, введём коэффициент PathDeviation_P, который даст отклонение от приращения по конкретной координате. Поскольку у нас многомерное пространство, то следуя вектору перемещения, одни координаты могут иметь положительное приращение, а другие отрицательное, к тому же приращения могут иметь разное значение по модулю. Этот коэффициент как раз и даст возможность учитывать эти моменты и даст некоторую степень свободы муравьям в поиске пищи (экстремума функции).
Итак, что представляет собой вектор перемещения и как мы измерим расстояние, которое предстоит пройти муравью? Для этого воспользуемся формулой для расчета расстояния между двумя точками в трехмерном пространстве:
![]()
Визуальное представление о векторе перемещения можно получить, посмотрев на рисунок 2.
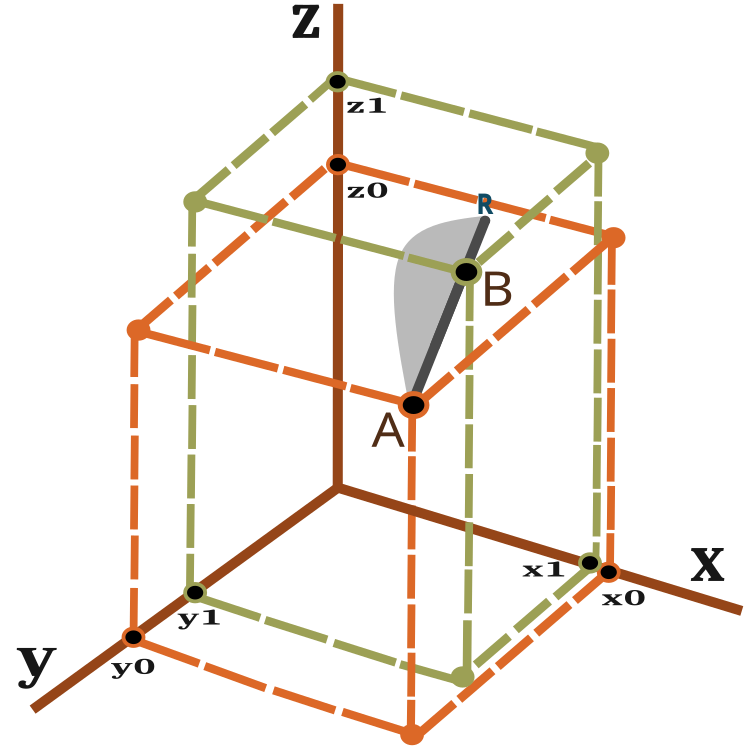
Рисунок 2. Вектор перемещения муравья.
Для n-мерных пространств расчет аналогичный.
Муравей за одну итерацию(эпоху) перемещается из точки А в точку В с возможным проскальзыванием до точки R. Расстояние до точки R от точки B зависит от коэффициента PheromoneRadius_P и может быть рассчитано так: BR = AB x PheromoneRadius_P.
Вероятность нового местоположения на линии AR схематично (без соблюдения масштаба) показана на рисунке 2 в виде серой зоны. Таким образом новое местоположение муравья с большей вероятностью стремится в окрестности точки В. Принцип смещения вероятности рассмотрен в предыдущей статье.
Алгоритм включает в себя следующие шаги на каждой итерации:
1) Случайное расположение муравьёв в пространстве.
2) Определение значения количества феромона (фитнес функция) для муравьёв.
3) Расчет расстояния от каждого муравья к каждому.
4) Расчет выбора предпочитаемой точки, куда будет двигаться муравей.
5) Расчет вероятности точки на векторе AR.
6) Расчет координат точки, полученной на векторе AR.
7) Повторять с пункта 2) до выполнения условия останова.
Перейдем к описанию кода алгоритма. Первым делом напишем структуру, содержащую в себе описание муравья, где:
- c [] - его координаты,
- cLast [] - предыдущие координаты,
- cB [] - лучшие координаты за все итерации,
- f - текущее значение феромона,
- fB - максимальное значение феромона, достигнутое за все итерации.
В конструкторе структуры муравья значение f и fB инициализируем минимально возможным значением, которое может быть представлено типом double.
//—————————————————————————————————————————————————————————————————————————————— struct S_Ants { double cLast []; //last coordinates double c []; //coordinates double cB []; //best coordinates double f; //pheromone of the current coordinates double fB; //pheromone of the best coordinates S_Ants () { f = -DBL_MAX; fB = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Нам понадобится структура, массив которой позволит нам хранить попарно расстояния между всеми муравьями.
struct S_Paths { double a []; };
Наш модифицированный алгоритм ACO запишем в виде класса, в котором всё также лишь три публичных метода, достаточных и необходимых в рамках разработанной концепцией построения алгоритмов оптимизации, рассмотренной в предыдущих статьях, InitAnts (), Preparation (), и Dwelling (). Появляются приватные методы GenerateRNDants () и AntsMovement (), и ставшими уже стандартными для наших алгоритмов остальные приватные методы. Массив структур ants [] - колония муравьёв.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ACO { public: //---------------------------------------------------------------------------- S_Ants ants []; //ants double rangeMax []; //maximum search range double rangeMin []; //manimum search range double rangeStep []; //step search double cB []; //best coordinates double fB; //pheromone of the best coordinates void InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP); void Preparation (); void Dwelling (); private: //---------------------------------------------------------------------------- S_Paths paths []; int coordinates; //number of coordinates int antHillSize; //ant hill size double goals []; double pheromoneEffect; double pathLengthEffect; double pheromoneRadius; double pathDeviation; bool dwelling; void GenerateRNDants (); void AntsMovement (); double SeInDiSp (double in, double inMin, double inMax, double step); double RNDfromCI (double min, double max); double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers); }; //——————————————————————————————————————————————————————————————————————————————
В методе инициализации назначим начальные значения переменным и размер массивов.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::InitAnts (const int coordinatesP, //number of opt. parameters const int antHillSizeP, double pheromoneEffectP, double pathLengthEffectP, double pheromoneRadiusP, double pathDeviationP) { fB = -DBL_MAX; coordinates = coordinatesP; antHillSize = antHillSizeP; pheromoneEffect = pheromoneEffectP; pathLengthEffect = pathLengthEffectP; pheromoneRadius = pheromoneRadiusP; pathDeviation = pathDeviationP; ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); dwelling = false; ArrayResize (ants, antHillSize); ArrayResize (paths, antHillSize); for (int i = 0; i < antHillSize; i++) { ArrayResize (ants [i].c, coordinates); ArrayResize (ants [i].cLast, coordinates); ArrayResize (ants [i].cB, coordinates); ArrayResize (paths [i].a, antHillSize); } ArrayResize (cB, coordinates); ArrayResize (goals, antHillSize); } //——————————————————————————————————————————————————————————————————————————————
Первым на каждой итерации вызывается метод Preparation ().
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Preparation () { if (!dwelling) { fB = -DBL_MAX; GenerateRNDants (); dwelling = true; } else AntsMovement (); } //——————————————————————————————————————————————————————————————————————————————
За создание случайной колонии муравьев отвечает метод GenerateRNDants (), координаты муравьев назначаем случайным образом в заданных пределах.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::GenerateRNDants () { for (int s = 0; s < antHillSize; s++) { for (int k = 0; k < coordinates; k++) { ants [s].c [k] = RNDfromCI (rangeMin [k], rangeMax [k]); ants [s].c [k] = SeInDiSp (ants [s].c [k], rangeMin [k], rangeMax [k], rangeStep [k]); ants [s].cLast [k] = ants [s].c [k]; ants [s].cB [k] = ants [s].c [k]; } } } //——————————————————————————————————————————————————————————————————————————————
Запомним текущие координаты муравьев в методе Dwelling (), а заодно обновим максимальные значения феромона, полученные на момент текущей итерации.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::Dwelling () { for (int i = 0; i < antHillSize; i++) { ArrayCopy (ants [i].cLast, ants [i].c, 0, 0, WHOLE_ARRAY); //remember the best coordinates for the ant if (ants [i].f > ants [i].fB) { ants [i].fB = ants [i].f; ArrayCopy (ants [i].cB, ants [i].c, 0, 0, WHOLE_ARRAY); } //remember the best coordinates for the anthill if (ants [i].f > fB) { fB = ants [i].f; ArrayCopy (cB, ants [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
Основной метод алгоритма AntsMovement (). В нем выполняются действия: расчет расстояния от каждого муравья к каждому, расчет выбора предпочитаемой точки, куда будет двигаться муравей, расчет вероятности точки на векторе AR. Расчет координат точки, полученной на векторе AR.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ACO::AntsMovement () { double rndPh; double rndPt; double summCoordinates = 0.0; double scores []; ArrayResize (scores, antHillSize); double maxPh = -DBL_MAX; double minPh = DBL_MAX; double maxPt = -DBL_MAX; double minPt = DBL_MAX; double goal; double goalBest = -DBL_MAX; int goalInd = 0; //measure the distance between all the ants----------------------------------- for (int i = 0; i < antHillSize; i++) { for (int k = 0; k < antHillSize; k++) { if (i == k) { paths [i].a [k] = DBL_MAX; continue; } for (int c = 0; c < coordinates; c++) summCoordinates += pow (ants [i].cLast [c] - ants [k].cLast [c], 2.0); paths [i].a [k] = pow (summCoordinates, 0.5); if (maxPt < paths [i].a [k]) maxPt = paths [i].a [k]; if (minPt > paths [i].a [k]) minPt = paths [i].a [k]; } } //---------------------------------------------------------------------------- for (int i = 0; i < antHillSize; i++) { maxPh = -DBL_MAX; minPh = DBL_MAX; for (int k = 0; k < antHillSize; k++) { if (i != k) { if (maxPh < ants [k].f) maxPh = ants [k].f; if (minPh > ants [k].f) minPh = ants [k].f; } } goalBest = -DBL_MAX; goalInd = 0; for (int k = 0; k < antHillSize; k++) { if (i != k) { rndPh = RNDfromCI (0.0, pheromoneEffect); rndPt = RNDfromCI (0.0, pathLengthEffect); goal = Scale (ants [k].f, minPh, maxPh, 0.0, 1.0, false) * rndPh * Scale (paths [i].a [k], minPt, maxPt, 0.0, 1.0, true) * rndPt; if (goalBest < goal) { goalBest = goal; goalInd = k; } } } double wayToGoal = paths [i].a [goalInd]; double radiusNearGoal = wayToGoal * pheromoneRadius; double endWay = wayToGoal + radiusNearGoal; double x = RNDfromCI (-1.0, 1.0); double y = x * x; if (x > 0.0) y = Scale (y, 0.0, 1.0, wayToGoal, endWay, false); else y = Scale (y, 0.0, 1.0, 0.0, wayToGoal, true); for (int j = 0; j < coordinates; j++) { double incrementFactor = y / wayToGoal; double coordDistance = ants [goalInd].cLast [j] - ants [i].cLast [j]; ants [i].c [j] = ants [i].cLast [j] + (coordDistance * incrementFactor); double w = coordDistance * RNDfromCI (-1.0, 1.0) * pathDeviation; ants [i].c [j] += w; ants [i].c [j] = SeInDiSp (ants [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } } //——————————————————————————————————————————————————————————————————————————————
Стоит уделить внимание функции масштабирования числа из одного числового диапазона в другой. Мы уже встречались с ней в предыдущих статьях, в этот раз расширим ее функционал. Входным параметром revers меняем направление масштабирования, как представлено на рисунке ниже.
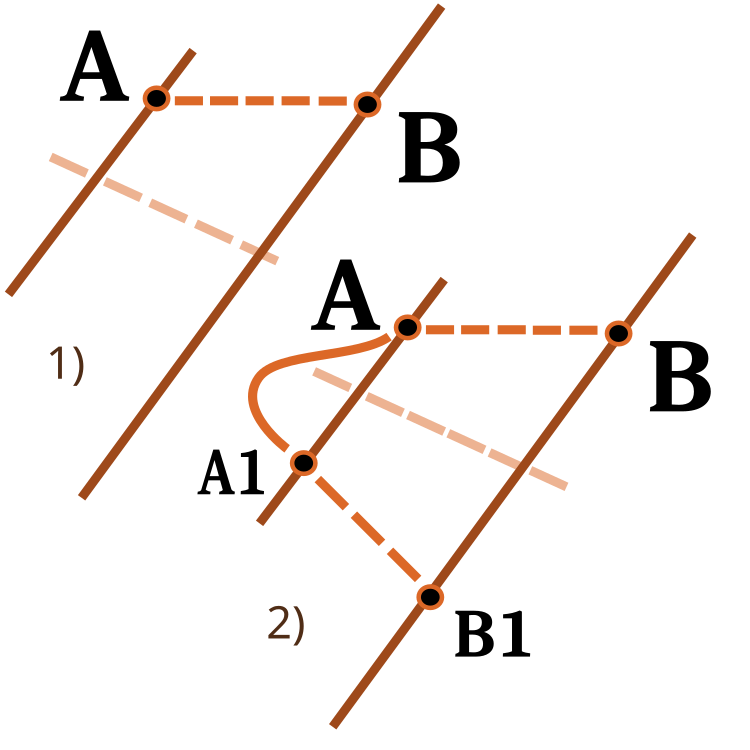
Рисунок 3. Пример масштабирования числа из одного числового диапазона в другой.
1) Прямое масштабирование; 2) Реверсное масштабирование.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ACO::Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool revers) { if (OutMIN == OutMAX) return (OutMIN); if (InMIN == InMAX) return (double((OutMIN + OutMAX) / 2.0)); else { if (In < InMIN) return revers ? OutMAX : OutMIN; if (In > InMAX) return revers ? OutMIN : OutMAX; double res = (((In - InMIN) * (OutMAX - OutMIN) / (InMAX - InMIN)) + OutMIN); if (!revers) return res; else return OutMAX - res; } } //——————————————————————————————————————————————————————————————————————————————
4. Результаты тестов
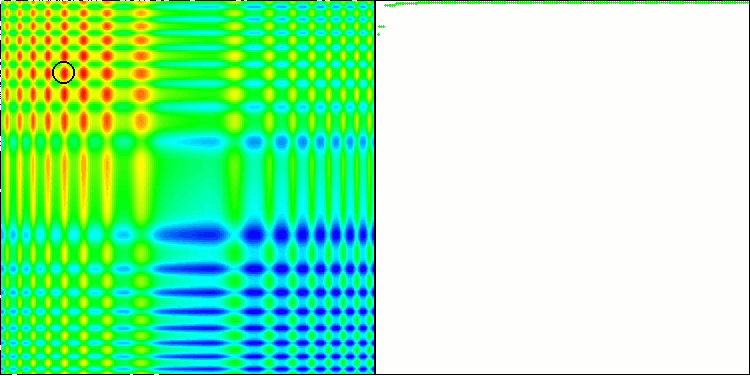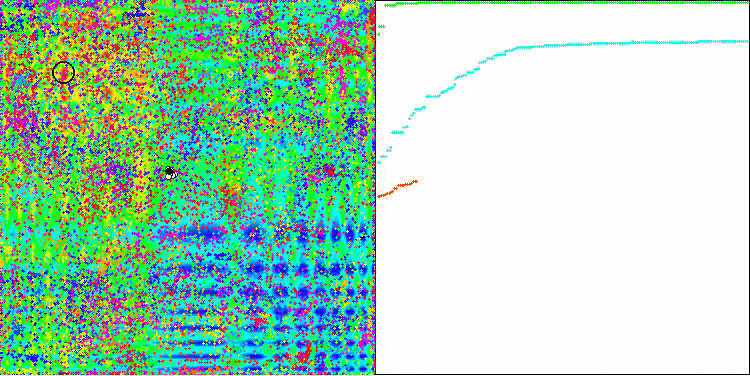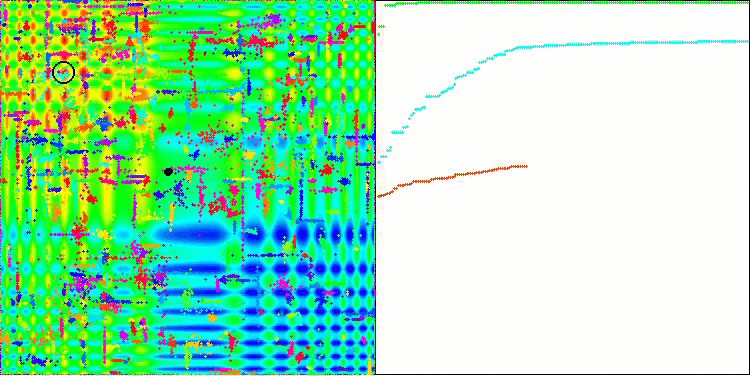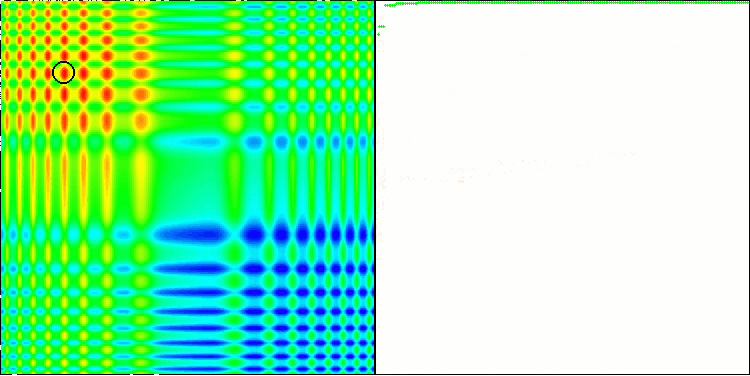
ACO на тестовой функции Skin.
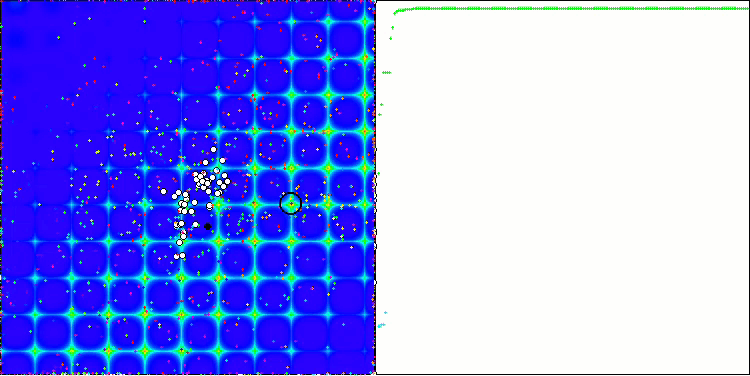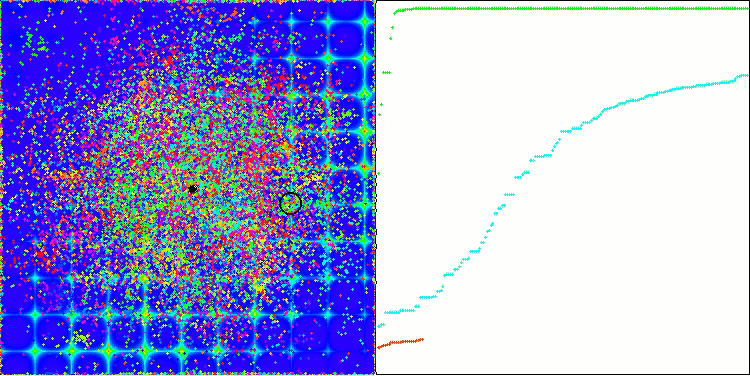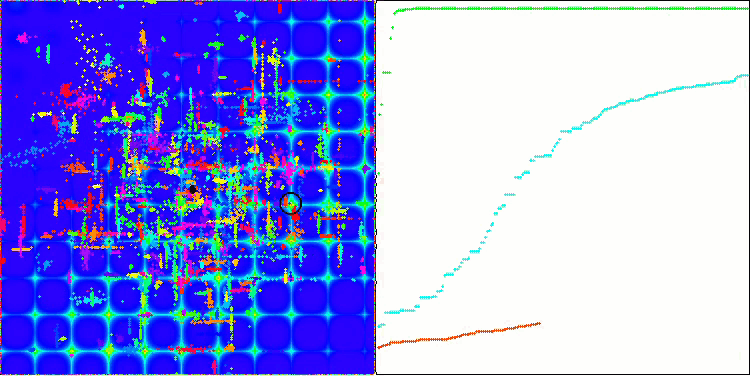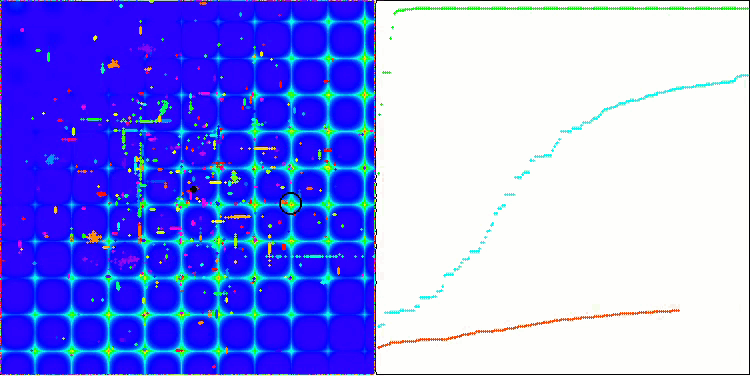
ACO на тестовой функции Forest.
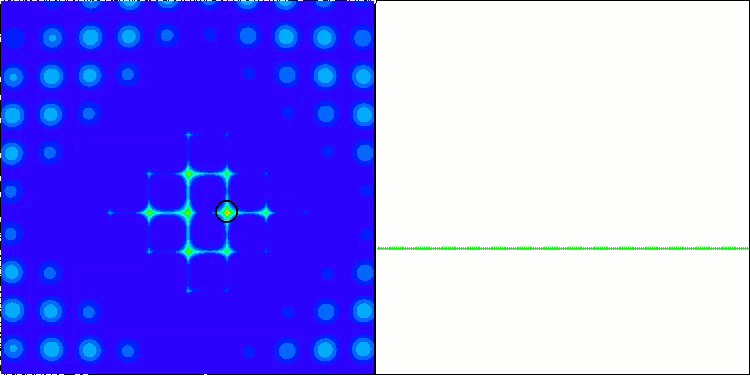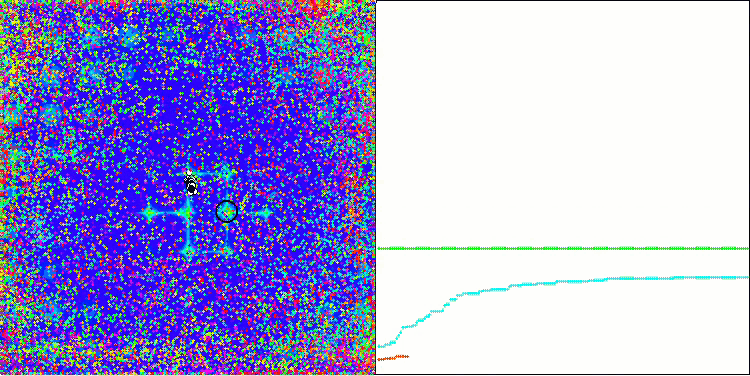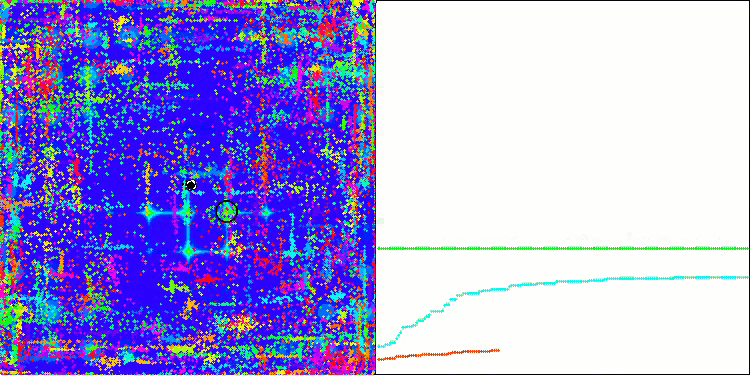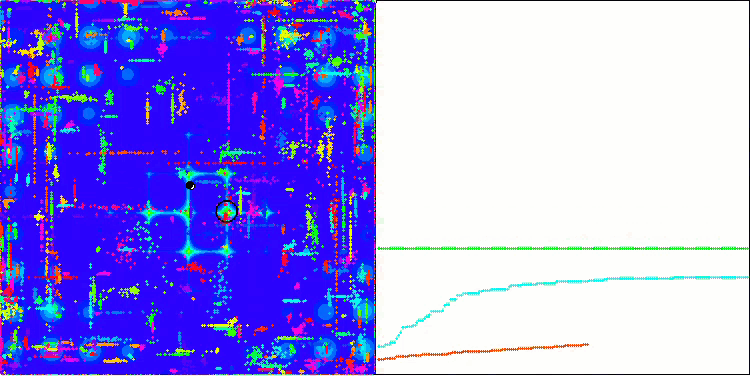
ACO на тестовой функции Megacity.
Итак, пора подводить итоги. С одной стороны, классический алгоритм Муравьиной колонии не применим к задачам оптимизации для торговли финансовыми инструментами и его можно было не рассматривать. Однако, некоторый полёт фантазии всё же позволил избежать ограничений классического варианта и написать новую оригинальную версию. Вы стали свидетелем появления совершенно новой концепции алгоритма Муравьиной колонии, в рамках которой возможно направление дальнейшего развития ACO. Такой алгоритм уже можно применять для широкого спектра задач, в том числе и для той же задачи комивояжера.
Кроме того мы получили нового лидера рейтинговой таблицы. Рассмотрим результаты более подробно. Для начала обратим внимание на результаты работы тестового стенда:
2022.10.27 16:46:28.678 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) 1 Skin's; Func runs 1000 result: 13.969156176320473; Func runs 10000 result: 13.986949123110085 2022.10.27 16:46:50.599 Test_AO_ACO (EURUSD,M1) Score1: 0.99502; Score2: 0.99599 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) 20 Skin's; Func runs 1000 result: 8.514904198298202; Func runs 10000 result: 11.56159524595023 2022.10.27 16:47:12.424 Test_AO_ACO (EURUSD,M1) Score1: 0.69826; Score2: 0.86403 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) 500 Skin's; Func runs 1000 result: 4.962716036996786; Func runs 10000 result: 6.488619274853463 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) Score1: 0.50498; Score2: 0.58800 2022.10.27 16:48:04.200 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) 1 Forest's; Func runs 1000 result: 15.805601165115196; Func runs 10000 result: 15.839944455892518 2022.10.27 16:48:25.999 Test_AO_ACO (EURUSD,M1) Score1: 0.99087; Score2: 0.99302 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) 20 Forest's; Func runs 1000 result: 3.568897096569507; Func runs 10000 result: 10.45940001108266 2022.10.27 16:48:47.897 Test_AO_ACO (EURUSD,M1) Score1: 0.22374; Score2: 0.65571 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) 500 Forest's; Func runs 1000 result: 1.3412234994286016; Func runs 10000 result: 2.7822130728041756 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) Score1: 0.08408; Score2: 0.17442 2022.10.27 16:49:41.855 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) 1 Megacity's; Func runs 1000 result: 11.8; Func runs 10000 result: 11.8 2022.10.27 16:50:03.740 Test_AO_ACO (EURUSD,M1) Score1: 0.78667; Score2: 0.78667 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) 20 Megacity's; Func runs 1000 result: 1.75; Func runs 10000 result: 3.9200000000000004 2022.10.27 16:50:26.002 Test_AO_ACO (EURUSD,M1) Score1: 0.11667; Score2: 0.26133 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) 500 Megacit 's; Func runs 1000 result: 0.6335999999999999; Func runs 10000 result: 1.2312 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) Score1: 0.04224; Score2: 0.08208 2022.10.27 16:49:41.075 Test_AO_ACO (EURUSD,M1) ============================= 2022.10.27 16:51:21.075 Test_AO_ACO (EURUSD,M1) All score for C_AO_ACO: 0.5468768583006471
Алгоритм хорошо показал себя на гладкой функции Skin, продемонстрировав отличную сходимость и хорошие возможности для масштабирования, особенно заметно опережая в тестах на 20 и 500 функций. На гладкой фунции Forest с острыми изломами, отрыв еще заметнее, алгоритм продолжает поиск даже попадая в локальные экстремумы. На дискретной функции Megacity алгоритм уступил случайному алгоритму RND только на задаче с 500 функциями.
| AO | Runs | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| 1000 | 0,99502 | 0,69826 | 0,50498 | 0,99087 | 0,22374 | 0,08408 | 0,78667 | 0,11667 | 0,04224 | 0,54688 | |
| 10000 | 0,99599 | 0,86403 | 0,58800 | 0,99302 | 0,65571 | 0,17442 | 0,78667 | 0,26133 | 0,08208 | ||
| 1000 | 0,98744 | 0,61852 | 0,49408 | 0,89582 | 0,19645 | 0,14042 | 0,77333 | 0,19000 | 0,14283 | 0,51254 | |
| 10000 | 0,99977 | 0,69448 | 0,50188 | 0,98181 | 0,24433 | 0,14042 | 0,88000 | 0,20133 | 0,14283 | ||
| 1000 | 0,98436 | 0,72243 | 0,65483 | 0,71122 | 0,15603 | 0,08727 | 0,53333 | 0,08000 | 0,04085 | 0,47695 | |
| 10000 | 0,99836 | 0,72329 | 0,65483 | 0,97615 | 0,19640 | 0,09219 | 0,82667 | 0,10600 | 0,04085 | ||
| 1000 | 0,96678 | 0,64727 | 0,57654 | 0,80616 | 0,13388 | 0,06800 | 0,53333 | 0,08067 | 0,04211 | 0,45144 | |
| 10000 | 0,99505 | 0,64986 | 0,57654 | 0,90401 | 0,18194 | 0,07104 | 0,74667 | 0,10400 | 0,04211 | ||
Выводы
Настроек у алгоритма достаточно много, поэтому есть возможность получить еще более лучшие результаты. Возможность настройки под конктреные типы задач. Можно на этом остановиться более подробно. Первый параметр PheromoneEffect_P непосредственно влияет на скорость сходимости, особенно это хорошо для гладких монотонных функций, например парабола, сходимость будет 100%, но это будет одновременно способствовать к застреванию в локальных экстремамах на дискретных функциях если его ставить большим.
Второй параметр PathLengthEffect_P, показывает степень ленивости муравьев, при высоком значении этого параметра, будут выбираться более близкие цели для перемещения. Необходимо данный параметр сбалансировать с первым параметром, для получения наилучшего результата. Этот параметр и создан для обеспечения противовеса желанию муравья идти к точке где больше пищи, вместо этого иногда выбирать ближайшие цели для более детального обследования небольших участков, что может быть очень полезным как на примере функции Forest, где наилучшая точка может находиться неожиданно совсем рядом.
Самое главное достижение - удалось избавится от основной проблемы канонического ACO: способности решать только дискретные комбинаторные задачи. Теперь алгоритм Муравьиной колонии вполне можно использовать для обучения нейронныйх сетей.
Визуально тестовый стенд наблюдать очень любопытно благодаря определённой кластеризации, муравьи сосредотачиваются в измерениях многомерной функции определённым образом, выделяя характерные группы локальных экстремумов. Возможно, этот эффект можно использовать для решения специфических задач, но для этого потребуются дополнительные исследования.
У алгоритма замечено интересное свойство: при решении задачи с двумя переменными вероятность застревания в локальном экстремуме несколько выше, чем при оптимизации 40-а переменных. Алгоритм продолжает поиск решений когда переменных много, предполагаю, что это эффект использования вектора, как средство связывающее все координаты пространства поиска. В качестве примера, если муравей перешёл в новое лучшее место, то изменились пространственно все координаты в лучшую сторону, а не какие то по отдельности.
Созданный алгоритм новый и неисследованный детально, поэтому я буду благодарен, если кто-то в коментариях к статье поделится настройками алгоритма, при которых тестовый стенд покажет итоговое значение больше 0,6 и я обновлю результаты таблицы. Впрочем, эта просьба так же относится и к предыдущим ранее рассмотренным алгоритмам.
1. Алгоритм достаточно быстрый.
2. Универсальность. Может быть использован в самых различных задачах оптимизации.
3. Способность не сосредотачиваться только на локальных экстремумах.
4. Достаточно хорошая сходимость как для гладких так и дискретных функций.
5. Масштабируем.
Минусы:
1. Возможно требуется большее количество итераций для сходимости, чем у того же PSO для гладких функций, однако это частично компенсируется способностью продолжать поиск даже там, где PSO уже остановился.
2. Сильное влияние параметров алгоритма на результат.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торговой системы на основе индекса силы быков Bulls Power
Разработка торговой системы на основе индекса силы быков Bulls Power
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Эти статьи о метаэвристических методах оптимизации просто потрясающие. Вы делаете огромную работу, Андрей, это умопомрачительно, как много опыта вы делитесь с нами, спасибо!
@METAQUOTES, пожалуйста, рассмотрите возможность внедрения этих целей метаэвристической оптимизации в оптимизатор! Это было бы здорово для программного обеспечения.
Что-то простое, что пользователь может установить внутри OnTester() как:
Привет из Бразилии