Популяционные алгоритмы оптимизации: Алгоритм растущих деревьев (Saplings Sowing and Growing up — SSG)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Все живые организмы в природе подчинены определенным законам, это помогает представителям флоры и фауны выживать в изменчивых условиях окружающей среды. Существуют различные варианты приспособленности растений к среде обитания. Некоторые из них способны переносить сезонные изменения, другие — адаптироваться к нехватке влаги, высоким или низким температурам, отсутствию опылителей. Одними из самых устойчивых организмов среди растений являются деревья, отдельные выды которых способны жить более 50 тысяч лет образуя колонии.

Природа - это неисчерпаемое поле вдохновения для многих эффективных идей в области разработки и изобретения вычислительных методов. Фактически, эволюционные вычисления - это проекция эволюции в моделировании на компьютере. Существует множество методов оптимизации, которые были вдохновлены процессами происходящими в природе, такие как эволюционные вычисления, искусственная иммунология, популяционные методы и другие. SSG в основном определяется как итеративные процессы генерации и комбинирования, работающие с садом потенциальных решений, называемых саженцами.  Алгоритм растущих деревьев (Saplings Sowing and Growing up, SSG) был предложен Карчи (А. Karci) с соавторами в 2002 г. Алгоритм вдохновлен эволюцией растущих деревьев и моделирует рост и ветвление деревьев.

2. Описание алгоритма

Алгоритм растущих деревьев один из немногих, который не имеет четкого описания авторами (высказаны лишь общие положения и идеи). Представленные авторами операторы алгоритма также не являются готовыми инструкциями для алгоритмической реализации программы, не имеется четких указаний о дочерних и родительских деревьях и их взаимодействии. Требований к очерёдности выполнения операторов нет и любой пользователь может изменить их порядок с целью получения лучшего саженца.

В широком понимании SSG не является алгоритмом оптимизации, это общий набор правил, который предназначен дополнить другие алгоритмы для повышения качества оптимизации, то есть SSG - надстройка для любых эволюционных популяционных алгоритмов, поэтому у меня имеется простор для фантазии и возможность экспериментировать с конкретной реализацией алгоритма оптимизации. Я применил некоторые собственные соображения и накопленный опыт в процессе написания предыдущих алгоритмов и воспользовался ими для работы с SSG, результаты экспериментов представлены на суд читателя ниже.

Для начала понимания алгоритма нужно представить себе дерево как агента оптимизации. Дерево - решение задачи оптимизации, где каждая ветвь является оптимизируемым параметром задачи. Весьма абстрактно и, я бы сказал, художественно, можно иллюстрировать дочернее дерево и родительское (алгоритм оперирует этими двумя понятиями) на рисунке 1. Ствол дерева - набор оптимизируемых параметров. Каждая ветвь - отдельный оптимизируемый параметр, где длина ветви ограничена допустимым диапазоном значений соответствующего параметра. Направление ветвей не имеет значения и на рисунке представлены только для того, что бы показать что они отличаются.

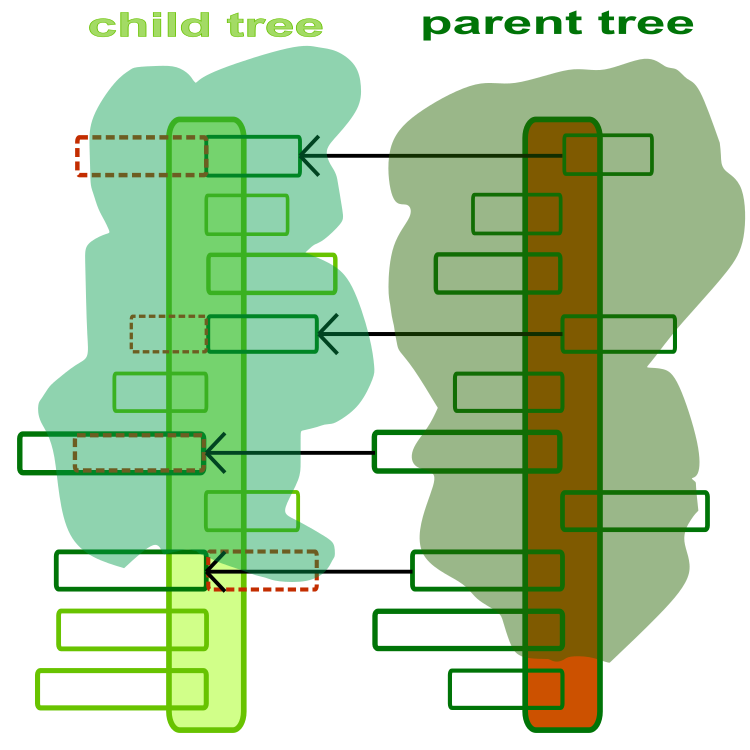
Рисунок 1. Дочернее и родительское дерево. Пунктирной линией обозначены дочерние ветви заменяемые родительскими.

Таким образом ветви деревьев - это координаты деревьев в пространстве поиска.

Алгоритм SSG состоит из операторов вариации, генерирующих новые решения - кандидаты в общий пул решений. Основными операторами вариации являются скрещивание, ветвление и вакцинация. Посадка саженцев должна осуществляться на равноудалённом расстоянии в каждом направлении друг от друга (запад, восток, север, юг), и это начальный этап метода. Когда координат (оптимизируемых параметров) гораздо больше трёх, то "равномерная" посадка - это простое случайное распределение саженцев по пространству поиска. Затем саженцы подрастают, они скрещиваются, ветвятся и происходит процесс вакцинации.

Рассмотрим шаги и операторы алгоритма SSG:

1) Посадка саженцев.

Пространство поиска можно рассматривать как сад саженцев, и, следовательно, все саженцы должны быть равномерно разбросаны по саду. Если фермер хочет посеять саженцы, он просто высеет их на равном расстоянии друг от друга, чтобы саженцы быстрее выросли не мешая друг другу. Чтобы решить проблему, имитируя выращивание саженцев, произвольные решения, которые должны быть сгенерированы изначально, должны быть равномерно распределены в допустимом пространстве поиска.

Когда координат две или три, то нет проблем равномерно распределить саженцы, но когда координат гораздо больше трёх, то проще использовать случайное распределение. Но практически, при небольшом количестве координат, нет необходимости заботиться о равномерном распределении саженцев, так как задача не представляет собой большую проблему и заведомо известно, что решение будет получено с высокой точностью, поэтому независимо от количества координат в алгоритме будем использовать случайное распределение саженцев по саду. 

2) Выращивание саженцев (деревьев), три оператора, выполняемые последовательно.

2.1) Скрещивание.

Целью оператора "скрещивание" является создание нового саженца из существующих в настоящее время саженцев путем обмена информацией между ними. Скрещивание по сути - пересадка копии ветви от родительского дерева дочернему (рисунок 1). Для каждой пары саженцев используется свой коэффициент скрещивания, который является вероятностью скрещивания. Вероятность скрещивания зависит от расстояния между саженцами в паре, чем больше расстояние, тем ниже вероятность скрещивания. Оператор скрещивания - очень важный метод алгоритма, обеспечивающий комбинаторные механизмы, комбинирование информации между агентами позволяет значительно повысить в целом качества алгоритма оптимизации.

2.2) Ветвление.

Оператор моделирует рост ветвей, причем рост может быть как положительный (удлинение), так и отрицательный (отсыхание). "Для того, чтобы вырастить ветвь в любой точке тела саженца, там не будет ни одной ближней ветви, ранее возникшей там." - примерно так звучит описание оператора "ветвление" у авторов алгоритма. На самом деле этот процесс проще и понятнее, чем может показаться на первый взгляд, и представляет собой модификацию существующих ветвей у дочернего дерева (конкретный способ модификации не уточняется).

Модификация каждой отдельной ветви тем вероятнее, чем больше прошло итераций между текущей итерацией и той, на которой производилась последняя модификация ветви. Мои эксперименты показали неэффективность этого оператора, к тому же отсутствует прямые указания на использование способа модификации и я позволил себе проявить инициативу в этом вопросе и применил изменение длины ветви по закону распределения полётов Леви. Модификация будет производиться с вероятностью и интенсивностью, указанными как внешние параметры алгоритма.   

2.3) Вакцинация.

Процесс вакцинации происходит между двумя разными саженцами в случае сходства саженцев. Сходство саженцев влияет на успех процесса вакцинации и пропорционально среднеарифметическому взвешенному расстоянию. Оператор похож на оператор скрещивания и заключается в обмене ветвями, представляя алгоритму дополнительный способ комбинирования информации между агентами. Оператор в статье будет освещён, но в исходных кодах этот оператор закомментирован и результаты тестов представлены без его участия, так как вакцинация ухудшает результаты, к сожалению.

3) Вычисление приспособленности деревьев.

4) Высадка новых саженцев в сад.

Полученные с помощью операторов скрещивания, ветвления и вакцинации саженцы представляют собой временные решения (дочерний сад). На этом этапе необходимо отобрать n - лучших саженцев (внешний параметр алгоритма) и поместить в сад, заменив n худших по саду деревьев. Надо отметить, что замена саженцами произойдет в любом случае, даже если они хуже худших деревьев по саду.

Настало подходящее время для рассмотрения кода алгоритма растущих деревьев, неуклонно приближая нас к волнующей кульминации настоящего исследования - рассмотрению результатов тестирования.

Итак, каждое дерево удобно представить в виде структуры Garden, которая послужит нам основой для создания цветущего сада. Нет ничего проще в этом алгоритме чем сущность "дерево", которой необходимо только два компонента: координаты с [] и значение приспособленности f.

//——————————————————————————————————————————————————————————————————————————————
struct S_Garden
{
  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Класс C_AO_SSG алгоритма SG не представляет собой ничего особенного, здесь всё очень привычное нам по рассмотренным ранее алгоритмам. В классе объявим члены и методы для оперирования родительским и дочерним садами, временный сад для функционирования метода сортировки, ведь нам понадобится сортировать как дочерний, так и родительский сад. Объявим массив лучших координат решения в целом и лучшее значение приспособленности, а также константные переменные для хранения внешних параметров алгоритма.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_SSG
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Garden pGarden []; //parent's garden
  public: S_Garden cGarden []; //child's garden
  public: S_Garden gardenT []; //temp garden
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP); //Power branching operator

  public: void Sowing      (int iter);
  public: void Germination ();


  //============================================================================
  private: void   Sorting        (S_Garden &garden []);
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];               //Vector
  private: int    ind [];
  private: double val [];
  private: double r;

  private: bool   sowing;               //Sowing
  private: int    coordinates;          //Coordinates number
  private: int    numberTrees;          //Number of trees
  private: int    seedlingsReplacement; //Seedlings replacement
  private: double probabMatingOperator; //Probability mating operator
  private: double probabBranchOperator; //Probability branching operator
  private: double powerBranchOperator;  //Power branching operator
};
//——————————————————————————————————————————————————————————————————————————————

В методе инициализации Init () распределим память под массивы и назначим константам - параметрам значения. Так как параметр seedlingsReplacementP задается в долях от размера сада (от 0.0 до 1.0), отвечающий за количество дочерних саженцев для посадки в родительский сад, то его нужно пересчитать в целочисленное представление от размера сада. Сбросим флаг первоначального засева сада и инициализируем переменную глобального решения минимально возможным значением double.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_SSG::Init (const int    coordinatesP,          //Number of coordinates
                     const int    numberTreesP,          //Number of trees
                     const double seedlingsReplacementP, //Seedlings replacement
                     const double probabMatingOperatorP, //Probability mating operator
                     const double probabBranchOperatorP, //Probability branching operator
                     const double powerBranchOperatorP)  //Power branching operator
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberTrees    = numberTreesP;

  if (seedlingsReplacementP >= 1.0)
  {
    seedlingsReplacement = numberTreesP;
  }
  else
  {
    if (seedlingsReplacementP <= 0.0)
    {
      seedlingsReplacement = 1;
    }
    else seedlingsReplacement = int(numberTreesP * seedlingsReplacementP);
  }

  probabMatingOperator = probabMatingOperatorP;
  probabBranchOperator = probabBranchOperatorP;
  powerBranchOperator  = powerBranchOperatorP;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);


  ArrayResize (pGarden,  numberTrees);
  ArrayResize (cGarden,  numberTrees);
  ArrayResize (gardenT,  numberTrees);
  ArrayResize (ind,      numberTrees);
  ArrayResize (val,      numberTrees);

  for (int i = 0; i < numberTrees; i++)
  {
    ArrayResize (pGarden  [i].c, coordinates);
    ArrayResize (cGarden  [i].c, coordinates);
    ArrayResize (gardenT  [i].c, coordinates);
    cGarden [i].f = -DBL_MAX;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Первый открытый метод, обязательно вызываемый на каждой итерации, Sowing () - посев. На первой итерации, когда алгоритм только запущен, раскидаем саженцы по саду (пространство поиска) случайным образом с равномерным распределением. Тут мы видим, что координаты генерируются случайно в допустимом диапазоне между min и max оптимизируемых параметров, производим проверку на выход из допустимого диапазона, далее приводим значения координат в соответствие с шагом оптимизации.

На этом этапе приспособленность саженцев минимальная. Зададим вектор vec[], он нам понадобится для масштабирования приращений ветвей в операторе ветвления, а так же рассчитаем максимально возможное евклидово расстояние r в пространстве поиска, оно пригодится в операторе скрещивания для определения вероятности, зависящей от расстояния между парами деревьев.

//the first planting of trees-------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;
  r = 0.0;

  for (int t = 0; t < numberTrees; t++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      cGarden [t].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    cGarden [t].f = -DBL_MAX;
  }

  for (int c = 0; c < coordinates; c++)
  {
    vec [c] = rangeMax [c] - rangeMin [c];
    r += vec [c] * vec [c];
  }

  r = sqrt (r);

  return;
}

Далее, в методе Sowing () на второй и последующих итерациях выполняются операторы скрещивания, ветвления и вакцинации. Вот в этом основном цикле выполняются последовательно операторы:

//tree growth-----------------------------------------------------------------
int child, parent;
double rnd;
double ed; //euclidean distance
double eM;
double u;
double temp;

for (int t = 0; t < numberTrees; t++)

При выполнении операторов понятия "дочерний" и "родительский" очень условны, на самом деле это просто источники базовой информации для создания нового саженца. Новый саженец копирует все ветви (а ветви, как мы помним, и есть оптимизируемые параметры) от дочернего дерева, а от родительского получит новые.

Для каждого нового саженца индивидуально выбираются из сада два дерева, дочернее и родительское случайным образом, равновероятно для всех деревьев сада, то есть, участие в создании нового саженца могут принимать все деревья с равной вероятностью и независимо от своей приспособленности. Таким образом child и parent это просто индексы исходных двух деревьев в массиве родительского сада.

ed = 0.0;

rnd = RNDfromCI (0.0, numberTrees - 1);
child = (int)MathRound (rnd);
if (child < 0) child = 0;
if (child > numberTrees - 1) child = numberTrees - 1;

rnd = RNDfromCI (0.0, numberTrees - 1);
parent = (int)MathRound (rnd);
if (parent < 0) parent = 0;
if (parent > numberTrees - 1) parent = numberTrees - 1;

if (child == parent) parent++;
if (parent > numberTrees - 1) parent = 0;

ArrayCopy (cGarden [t].c, pGarden [child].c, 0, 0, WHOLE_ARRAY);

Первый оператор - скрещивание, или сопряжение (mating). Для выполнения оператора скрещивания над саженцем с индексом t необходимо посчитать евклидово пространство между дочерним и родительскими деревьями с индексами child и parent:

//mating operator-----------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  temp = pGarden [child].c [c] - pGarden [parent].c [c];
  ed += temp * temp;
}

ed = sqrt (ed);

Евклидово расстояние участвует в формуле расчета вероятности скрещивания через нормирование на максимально возможное евклидово расстояние r в пространстве поиска:

eM = 1.0 - (ed / r);

Генерируем случайное число в диапазоне [0.0;1.0] и если полученное число попадает в вычисленную вероятность eM, то выполняем скрещивание - копирование ветвей с родительского дерева с вероятностью probabMatingOperator для каждой ветви. Если вероятность eM не выполнена, то саженец перейдет к выполнению следующего оператора со всеми изначальными ветвями дочернего дерева.

rnd = RNDfromCI (0.0, 1.0);

if (rnd <= eM)
{
  for (int c = 0; c < coordinates; c++)
  {
    rnd = RNDfromCI (0.0, 1.0);

    if (rnd <= probabMatingOperator) cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Далее выполняется оператор ветвления. Ветвление обеспечивает вариацию ветвей - удлинение и укорачивание, это основной оператор создающий ветви новой длины, а остальные операторы выполняют только комбинаторную роль и не создают новые уникальные ветви. Для каждой ветви генерируем случайное число в диапазоне [0.0;1.0] и если вероятность probabBranchOperator выполнена, то осуществляем ветвление - изменение длины ветви по закону распределения полетов Леви, рассмотренного здесь.

Как видим, далеко не все ветви саженца будут изменены, причем будут изменены независимо от того, была ли ветвь скопирована от родительского дерева на предыдущем операторе, или это изначальная дочерняя ветвь. После модификации ветви проверим на выход за пределы допустимых значений и приведём в соответствие с шагом оптимизации.

//branching operator--------------------------------------------------------
for (int c = 0; c < coordinates; c++)
{
  rnd = RNDfromCI (0.0, 1.0);

  if (rnd < probabBranchOperator)
  {
    double r1 = RNDfromCI (0.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);

    cGarden [t].c [c] = cGarden [t].c [c] + r1 * vec [c] * powerBranchOperator * pow (r2, -2.0);
    cGarden [t].c [c] = SeInDiSp (cGarden [t].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Третий оператор - вакцинация. Оператор вакцинации был задуман авторами, судя по всему, как комбинаторный оператор, и должен выполняться для копирования ветвей от родительского дерева в том случае, когда ветви дочернего и родительского дерева отличались более чем средняя разница по всем ветвям пары. Звучит это очень сложно, но пользы от этого оператора мало и поэтому в исходных файлах этот оператор закомментирован. В данном случае не могу выступать в качестве эксперта в последней инстанции, а потому допускаю возможность неправильного понимания мною этого оператора.

//vaccinating operator------------------------------------------------------
u = 0.0;
    
for (int c = 0; c < coordinates; c++)
{
  u += fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c];
}

u /= coordinates;

for (int c = 0; c < coordinates; c++)
{
  if (fabs (cGarden [t].c [c] - pGarden [parent].c [c]) / vec [c] >= u)
  {
    cGarden [t].c [c] = pGarden [parent].c [c];
  }
}

Сажали мы сажали саженцы, скрещивали и ветвили, и даже иногда вакцинировали. Настал черед заключительной по исполнению, но не последней по важности, операции алгоритма - прорастание, то есть выполняем второй обязательный к исполнению на каждой итерации открытый метод Germination ().

Если подходит к концу первая итерация, а это мы непременно узнаем по флагу sowing, то это означает что родительский сад пуст, посадим в родительский сад все саженцы из дочернего сада, просто скопировав поочередно все молодые деревья. После этого выполним сортировку родительского сада по значению приспособленности с помощью метода Sorting (). А если деревья отсортированы, то у дерева с индексом 0 будет наилучшая приспособленность, и мы можем обновить лучшее глобальное решение, если оно уже не является лучшим.

if (!sowing)
{
  for (int t = 0; t < numberTrees; t++) pGarden [t] = cGarden [t];

  Sorting (pGarden);

  if (pGarden [0].f > fB)
  {
    fB = pGarden [0].f;

    ArrayCopy (cB, pGarden [0].c, 0, 0, WHOLE_ARRAY);
  }
  
  sowing = true;
  return;
}

Далее по коду мы попадём только на второй и последующих итерациях в алгоритме, поскольку флагу sowing предусмотрительно назначили значение true. На второй и последующих итерациях нужно отсортировать дочерний сад, прежде чем перенести саженцы в родительский сад и заменить худшие деревья. Проверим факт улучшения глобального решения, а затем скопируем n лучших экземпляров саженцев в конец родительского сада.

В заключение осталось только отсортировать родительский сад, новые члены садового деревянного общества смогут заменить деревья старших поколений что бы радовать нас цветением результатами решения задач оптимизации.

//planting some part from all child trees-------------------------------------
Sorting (cGarden);

if (cGarden [0].f > fB)
{
  fB = cGarden [0].f;

  ArrayCopy (cB, cGarden [0].c, 0, 0, WHOLE_ARRAY);
}

for (int t = 0; t < seedlingsReplacement; t++) pGarden [numberTrees - seedlingsReplacement + t] = cGarden [t];

Sorting (pGarden);

3. Результаты тестов

Распечатка работы алгоритма растущих деревьев на тестовом стенде:

2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    C_AO_SSG:50;0.3;0.5;0.4;0.1
2023.03.09 12:50:37.207    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    5 Rastrigin's; Func runs 10000 result: 80.7052793572295
2023.03.09 12:50:45.954    Test_AO_SSG (GBPUSD,M1)    Score: 0.99998
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    25 Rastrigin's; Func runs 10000 result: 77.3972262608643
2023.03.09 12:50:59.290    Test_AO_SSG (GBPUSD,M1)    Score: 0.95900
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    500 Rastrigin's; Func runs 10000 result: 52.24518909141432
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    Score: 0.64735
2023.03.09 12:52:25.368    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    5 Forest's; Func runs 10000 result: 1.331178589711503
2023.03.09 12:52:31.419    Test_AO_SSG (GBPUSD,M1)    Score: 0.75298
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    25 Forest's; Func runs 10000 result: 1.019329018074209
2023.03.09 12:52:42.575    Test_AO_SSG (GBPUSD,M1)    Score: 0.57658
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    500 Forest's; Func runs 10000 result: 0.25410121872226443
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    Score: 0.14373
2023.03.09 12:53:48.922    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    5 Megacity's; Func runs 10000 result: 6.4
2023.03.09 12:53:57.201    Test_AO_SSG (GBPUSD,M1)    Score: 0.53333
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    25 Megacity's; Func runs 10000 result: 4.504
2023.03.09 12:54:08.004    Test_AO_SSG (GBPUSD,M1)    Score: 0.37533
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    500 Megacity's; Func runs 10000 result: 1.2336
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    Score: 0.10280
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    =============================
2023.03.09 12:56:07.061    Test_AO_SSG (GBPUSD,M1)    All score: 5.09109

Можно сказать, что параметров у SSG не слишком много, хотя это следствие моей самодеятельности в написании алгоритма (у авторов параметров SSG меньше), но они (параметры) заслуживают исключительного внимания и следует обсудить их значение. Вот эти параметры использовались в тестах, напомню, в каждой статье я привожу наилучшие параметры алгоритмов в том смысле, что параметры должны обеспечить максимально возможный результат в тестах.

C_AO_SSG:50;0.3;0.5;0.4;0.1

input int NumberTrees_P = 50;  - количество деревьев в саду, с этим параметром я не эксперементировал, оставил значение по умолчанию (по умолчанию в моих эксперементах), со значением 100 алгоритм выдаёт результаты в совокупности ещё лучше, но падает способность к масштабированию, из-за уменьшения количества допустимых итераций на сад с учетом размера сада, сад с большим количеством ветвей не успевает эволюционировать.

input double SeedlingsReplacement_P = 0.3; - доля саженцев от дочернего сада, подлежащая переносу в родительский сад.
input double ProbabMatingOperator_P = 0.5; - вероятность скрещивания (копирования ветвей от родительского дерева) если вероятность, учитывающая расстояние между парой деревьев, выполнена.
input double ProbabBranchOperator_P = 0.4; - вероятность ветвления (роста/усыхания ветвей), важный параметр значительно влияющий на результативность алгоритма (впрочем, все параметры важны).
input double PowerBranchOperator_P  = 0.1; - сила ветвления, это масштабный коэффициент в размерности оптимизируемых параметров, 1.0 и более будет означает рост ветвей до границ сада, 0.0 - отсутствие роста ветвей, то есть новые размеры ветвей не будут возникать и алгоритм вырождается в простой инструмент комбинаторики (отличная идея применения SSG, кстати, не проводил исследований в этом направлении).

Если обратить внимание на анимации работы алгоритма SSE на тестовых функциях, то можно заметить отсутствие каких-либо паттернов передвижения деревьев по саду, заметно лишь некоторое "кучкование" в локальных экстремумах. Однако заметно сразу высокое качество сходимости если сравнивать с предыдущими ранее рассмотренными алгоритмами. Обращает на себя также стабильная воспроизводимость результатов.

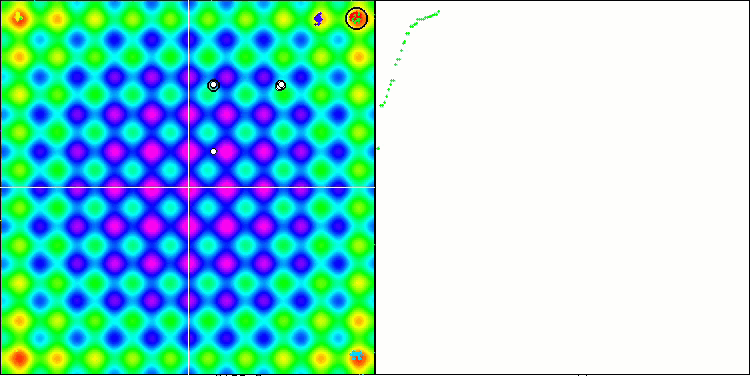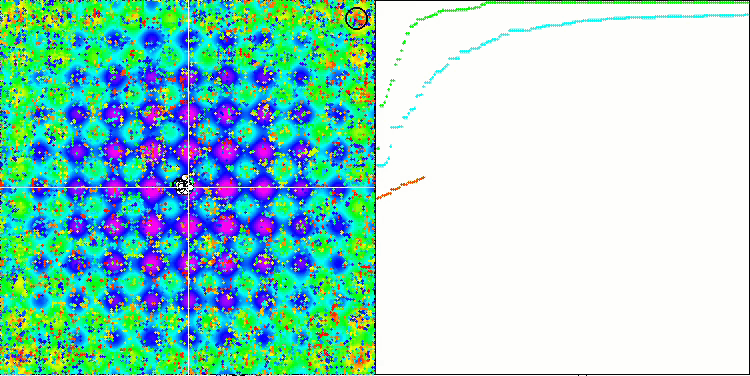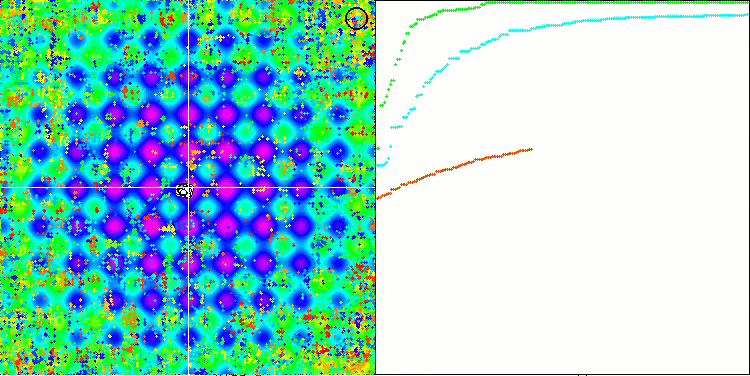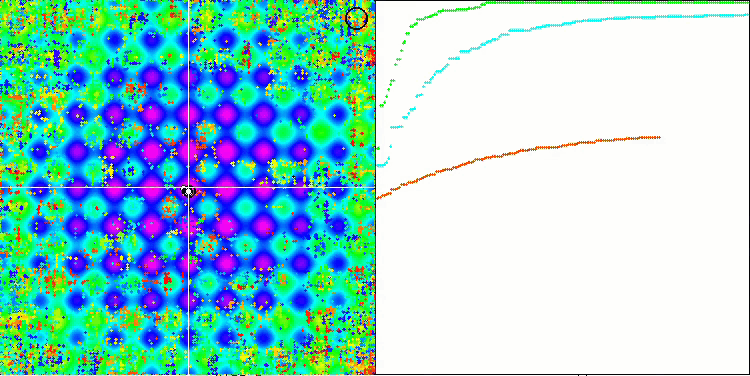
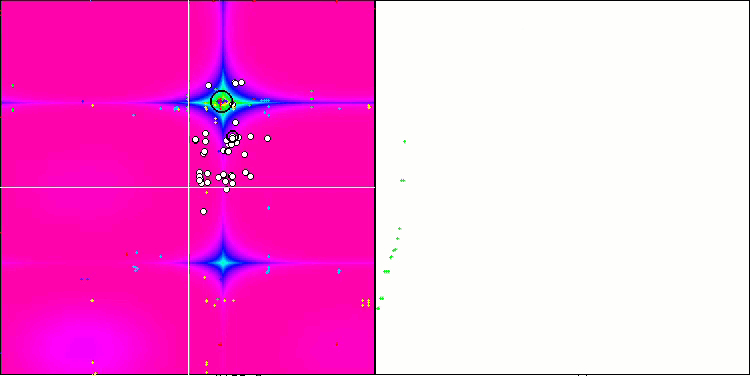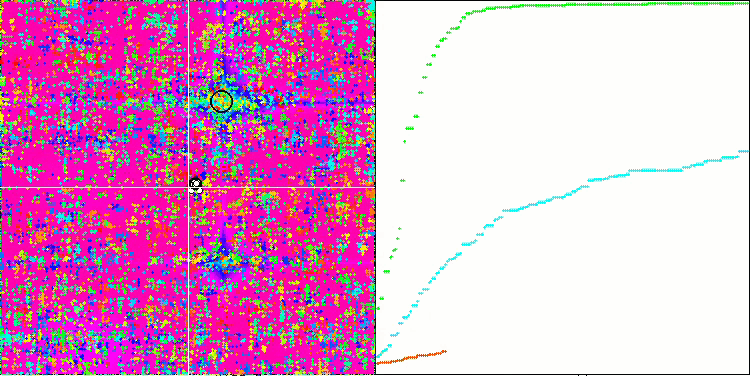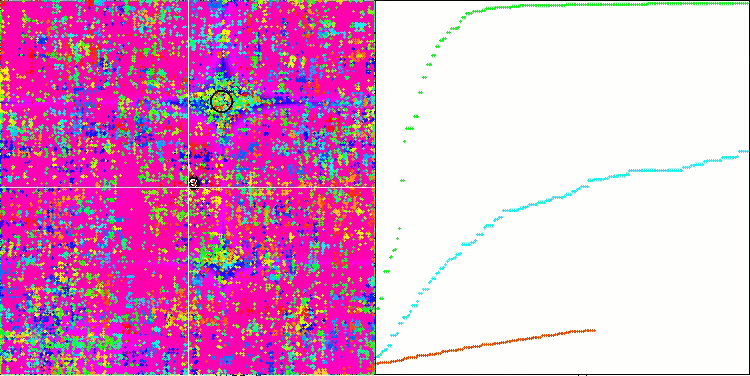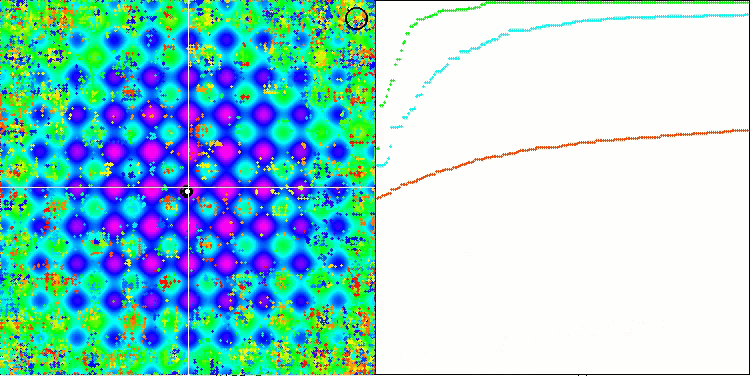
  SSG на тестовой функции Rastrigin.

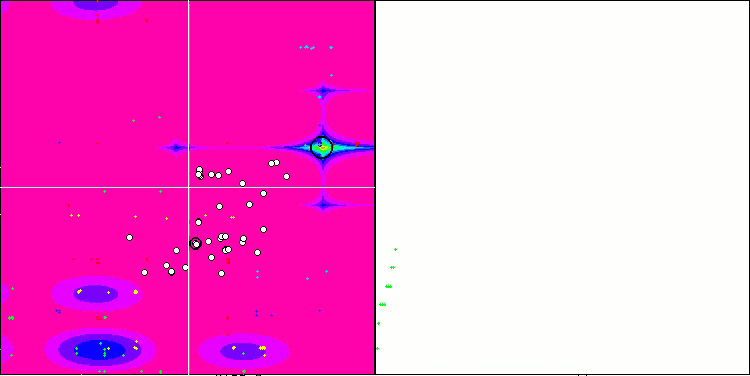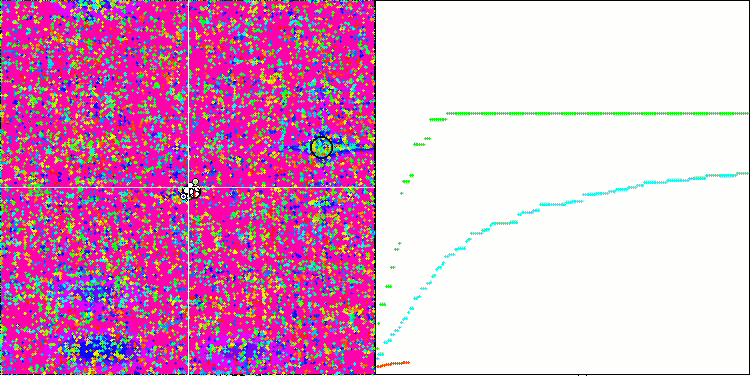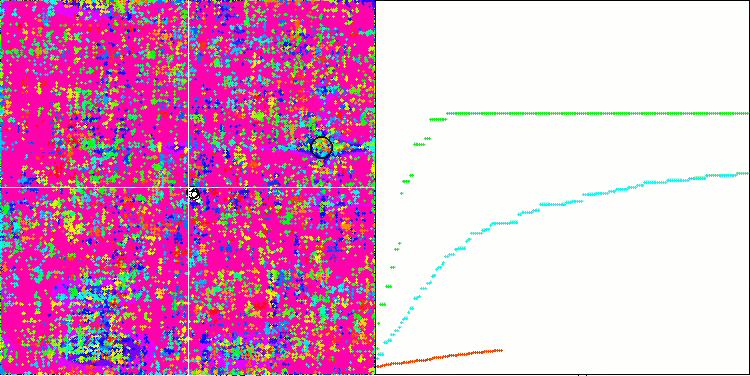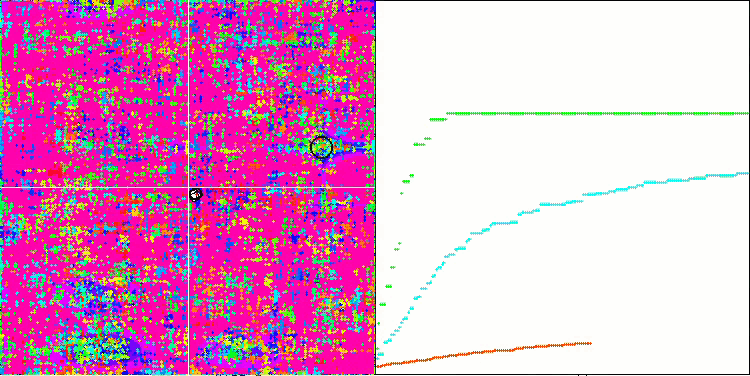
  SSG на тестовой функции Forest.

  SSG на тестовой функции Megacity.

Переходим к обсуждению результатов алгоритма SSG, а тут определённо есть о чем поговорить. Алгоритм растущих деревьев триумфально разместился в первой строчке рейтинга, от соперников только щепки летят! Алгоритм не использует знание о приспособленности непосредственно для модификации деревьев (решений), приспособленность нужна лишь для сортировки дочернего сада и родительского сада, поэтому тем более удивительно, что алгоритм смог показать такие замечательные результаты в тестировании.

Это то же самое, как если бы команда незрячих победила в ориентировании на местности команду зрячих. Алгоритм опередил участников таблицы в четырёх тестах из шести, не намного отставая в тестах, где он не является лидером. Самый впечатляющий отрыв от соперников SSG продемонстрировал на дискретной функции Megacity, опередив ближайшего конкурента HS почти на 60%! - что демонстрирует прекрасную масштабируемость алгоритма. Лучший результат масштабируемости и на "острой" тестовой функции Forest, опередив лучшего соперника в этом тесте ACOm почти на 30%.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
SSG	saplings sowing and growing	1,00000	1,00000	0,65914	2,65914	0,70823	0,94522	1,00000	2,65345	0,71532	0,85412	1,00000	2,56944	100,000
HS	harmony search	0,99676	0,95282	0,57048	2,52006	1,00000	0,98931	0,44806	2,43736	1,00000	1,00000	0,41537	2,41537	93,370
ACOm	ant colony optimization M	0,34611	0,17985	0,20182	0,72778	0,85966	1,00000	0,77362	2,63327	1,00000	0,88484	0,05606	1,94090	66,407
IWO	invasive weed optimization	0,95828	0,67083	0,35295	1,98207	0,68718	0,46349	0,31773	1,46840	0,75912	0,39732	0,33289	1,48933	61,691
COAm	cuckoo optimization algorithm M	0,92400	0,46794	0,30792	1,69987	0,55451	0,34034	0,16526	1,06012	0,67153	0,30326	0,17083	1,14561	48,226
FAm	firefly algorithm M	0,59825	0,33980	0,20290	1,14095	0,47632	0,42299	0,49790	1,39721	0,21167	0,25143	0,35258	0,81568	41,042
ABC	artificial bee colony	0,78170	0,32715	0,24656	1,35541	0,50591	0,21455	0,13344	0,85390	0,47444	0,23609	0,13926	0,84979	37,204
BA	bat algorithm	0,40526	0,63761	1,00000	2,04287	0,15275	0,17477	0,25989	0,58741	0,15329	0,06334	0,17371	0,39034	36,703
GSA	gravitational search algorithm	0,70167	0,45217	0,00000	1,15384	0,26854	0,36416	0,33204	0,96475	0,51095	0,32436	0,00000	0,83531	35,834
BFO	bacterial foraging optimization	0,67203	0,30963	0,13988	1,12154	0,35462	0,26623	0,20652	0,82736	0,42336	0,30519	0,18932	0,91786	34,700
MA	monkey algorithm	0,33192	0,33451	0,17340	0,83983	0,03684	0,07891	0,08932	0,20508	0,05838	0,00383	0,10720	0,16941	13,185
FSS	fish school search	0,46812	0,25337	0,13383	0,85532	0,06711	0,05013	0,06516	0,18240	0,00000	0,00959	0,08283	0,09242	12,089
PSO	particle swarm optimisation	0,20449	0,08200	0,08478	0,37127	0,13192	0,10486	0,21738	0,45415	0,08028	0,02110	0,01957	0,12095	9,696
RND	random	0,16826	0,09743	0,09495	0,36065	0,07413	0,04810	0,04715	0,16938	0,00000	0,00000	0,04922	0,04922	4,916
GWO	grey wolf optimizer	0,00000	0,00000	0,02672	0,02672	0,00000	0,00000	0,00000	0,00000	0,18977	0,03645	0,02557	0,25179	1,000

Выводы

Особенности SSG: нет требований к дифференцируемости и непрерывности оптимизируемой функции, нет никаких ограничений на тип используемого представления и кодировок, алгоритм не использует информацию приспособленности отдельных агентов и лучшего решения в целом. Благодаря этим особенностям SSG может быть легко применен к различным задачам оптимизации, в том числе очень сложным, SSG с уверенностью может быть рекомендован к использованию в задачах трейдеров и машинном обучении. На момент написания этой статьи алгоритм растущих деревьев бесспорный лидер по качеству сходимости, устойчивости результатов и масштабируемости.

Гистограмма результатов тестирования алгоритмов на рисунке 2.

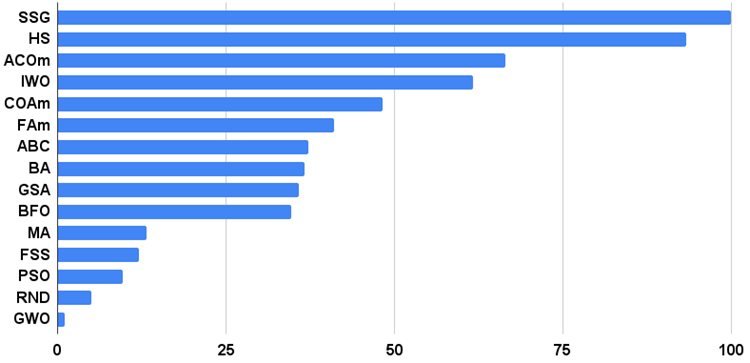
Рисунок 2. Гистограмма итоговых результатов тестирования алгоритмов.

Плюсы и минусы алгоритма растущих деревьев (SSG):

Плюсы:
1. Простота реализации.
2. Отличная сходимость на всех без исключения типах функций.
3. Впечатляющая масштабируемость.

Минусы:
1. Большое количество настроечных параметров, хотя параметры интуитивно понятны.

К каждой статье я прикрепляю архив, который содержит обновленные актуальные версии кодов алгоритмов ко всем предыдущим статьям. Статья является накопленным опытом автора и личным мнением, выводы и суждения основаны на проведенных экспериментах.