Популяционные алгоритмы оптимизации: Алгоритм имитации изотропного отжига (Simulated Isotropic Annealing, SIA). Часть II

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

В первой части статьи мы рассмотрели каноническую версию алгоритма имитации отжига Simulated Annealing (SA). Алгоритм основан на трех основных концепциях: применение случайности, принятие худших решений и постепенное уменьшение вероятности принятия худших решений. Применение случайности позволяет исследовать различные области пространства поиска и избегать застревания в локальных оптимумах. Принятие худших решений с некоторой вероятностью позволяет алгоритму временно "выскочить" из локальных оптимумов и искать лучшие решения в других местах пространства поиска, что позволяет сначала исследовать пространство поиска более широко, а затем сосредоточиться на улучшении решения.

В основе идеи алгоритма SA лежит аналогия с процессом отжига металла. Предварительно разогретый металл постепенно охлаждается, что приводит к изменению его структуры. Аналогично, алгоритм имитации отжига начинает с высокой температуры (высокой вероятности принятия худшего решения) и постепенно уменьшает температуру (уменьшает вероятность принятия худшего решения), что предположительно должно помочь алгоритму сходиться к оптимальному решению.

Алгоритм начинает свою работу с исходного решения, которое может быть случайным или полученным из предыдущих итераций. Затем применяются операции изменения состояния решения, которые могут быть случайными или управляемыми, чтобы получить новое состояние, даже если оно хуже текущего. Вероятность принятия худшего решения определяется функцией "охлаждения", которая со временем уменьшает вероятность принятия худшего решения.

Для описания процесса имитации отжига используются несколько простых формул. Формула для вычисления изменения энергии позволяет определить разницу значений фитнес-функции на двух последовательных итерациях. Формула для вычисления вероятности принятия худшего решения определяет вероятность принятия нового состояния с учетом разницы в энергии и текущей температуре.

Важными параметрами, которые нужно настроить при использовании алгоритма имитации отжига, являются начальная температура и коэффициент охлаждения. Настройка этих параметров может оказать значительное влияние на производительность и качество решения и является одной из слабых сторон алгоритма - сложность в выборе параметров из-за неочевидного их влияния на результативность. К тому же оба этих параметра взаимно влияют друг на друга: увеличение температуры практически равнозначно может быть заменено уменьшением коэффициента снижения температуры.

В первой части статьи мы выявили основные проблемы алгоритма:

• Настройка параметров: параметры алгоритма SA, такие, как начальная температура и коэффициент охлаждения, могут существенно влиять на его производительность и эффективность. Настройка этих параметров может быть сложной задачей, и требуется экспериментирование для достижения оптимальных значений.

• Проблема застревания в локальных экстремумах: для преодоления этой проблемы можно использовать различные стратегии, такие как выбор наиболее подходящего распределения случайной величины при генерации новых решений в сочетании с имеющимся инструментарием стратегии алгоритма, а также рассмотрение возможных решений для повышений комбинаторных возможностей.

• Улучшение скорости сходимости: для ускорения сходимости можно применить модификации функции охлаждения, которые позволят более быстро (или с иной формой функции охлаждения) снижать температуру системы. Также можно пересмотреть в алгоритме методы выбора следующего состояния, которые учитывают информацию о ранее пройденных состояниях.

• Улучшение эффективности алгоритма SA при большом количестве переменных: это одна из самых сложных проблематик для подавляющего большинства алгоритмов, поскольку с ростом количества переменных сложность пространства поиска растёт гораздо быстрее, чем это можно учесть с помощью специальных методик в стратегиях поиска. 

Одной из главных проблем в многомерных пространствах является комбинаторный взрыв возможных комбинаций переменных. При увеличении числа переменных экспоненциально возрастает количество возможных состояний системы, которые нужно исследовать. Это приводит к тому, что алгоритмы оптимизации сталкиваются с проблемой пространственной сложности.

Пространственная сложность означает, что объем пространства поиска растет экспоненциально с увеличением числа переменных. Например, если у нас есть 10 переменных, каждая из которых может принимать 10 значений, то общее количество возможных комбинаций будет равно 10^10, что равно 10 миллиардам, и это при том, у нас всего лишь 10 тысяч попыток (количество запусков фитнес-функции). Поиск оптимального решения среди такого количества комбинаций становится крайне сложной задачей. Отдельно стоит отметить, что в наших тестах мы проводим оптимизацию параметров функций с шагом 0, это означает немыслимо сложные условия для алгоритмов, и те из них, которые справляются удовлетворительно на подобных сложнейших тестовых задачах, будут практически гарантированно лучше работать на менее сложных (при прочих равных) реальных задачах.

2. Описание алгоритма

Алгоритм имитации отжига настолько прост, что поистине сложно представить, как его можно еще улучшить. Это подобно превращению стакана с водой в чарующее вино — словно акт волшебства. И действительно, что можно усовершенствовать, если генерация новых значений равномерно распределена, а идея принимать худшее решение полностью нарушает обычную логику построения алгоритмов оптимизации.

Для наглядного сравнения последующих результатов экспериментов с начальным эталонным результатом оригинального алгоритма имитации отжига (SA) приведём здесь распечатку результатов из предыдущей статьи:

C_AO_SA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 65.78409729002105
Score: 0.81510
25 Rastrigin's; Func runs 10000 result: 52.25447043222567
Score: 0.64746
500 Rastrigin's; Func runs 10000 result: 40.40159931988021
Score: 0.50060
=============================
5 Forest's; Func runs 10000 result: 0.5814827554067439
Score: 0.32892
25 Forest's; Func runs 10000 result: 0.23156336186841173
Score: 0.13098
500 Forest's; Func runs 10000 result: 0.06760002887601002
Score: 0.03824
=============================
5 Megacity's; Func runs 10000 result: 2.92
Score: 0.24333
25 Megacity's; Func runs 10000 result: 1.256
Score: 0.10467
500 Megacity's; Func runs 10000 result: 0.33840000000000003
Score: 0.02820
=============================
All score: 2.83750

Итак, поехали. Попытаемся улучшить результаты, заменим равномерное распределение случайных величин на нормальное при генерации новых состояний системы.

Будем использовать класс алгоритма имитации отжига как основу для нового алгоритма SIA, поэтому не будем приводить описание методов и функционала этого класса, так как все уже было представлено в первой части статьи.

Тогда для генерации случайного числа с нормальным распределением можно использовать метод обратной функции. Предположим, что мы хотим сгенерировать число "x" с нормальным распределением, mu (среднее значение) и sigma (стандартное отклонение). Тогда можно использовать следующую формулу:

x = z0 * sigma + mu

где:

• z0 - вычисляем по формуле:

z0 = sqrt (-2 * log (u1)) * cos(2 * Pi * u2)

где:

• u1* - случайное число в диапазоне (0.0;1.0] (здесь min не входит в диапазон)
  

• u2** - случайное число в диапазоне [0.0;1.0]

• * и ** - два независимых случайных числа с равномерным распределением
  

В предыдущей статье мы добавили к алгоритму SA параметр коэффициента диффузии, который ограничивает область генерации случайных чисел. Именно в этой области мы и должны сгенерировать случайные числа.

Напишем метод класса C_AO_SIA, имитирующий диффузию - "Diffusion". Метод генерирует случайное число с нормальным распределением до двух стандартных отклонений. Выходящие за эти границы значения мы заворачиваем "внутрь" без потери формы распределения (рассмотрим подробнее в одной из следующих статей).

Зная значение стандартного отклонения (sigma), мы можем перевести этот диапазон значений в наш требуемый диапазон, имитирующий диффузию, для этого используем функцию масштабирования "Scale".

//——————————————————————————————————————————————————————————————————————————————
double C_AO_SIA::Diffusion (const double value, const double rMin, const double rMax, const double step)
{
  double logN = 0.0;
  double u1   = RNDfromCI (0.0, 1.0);
  double u2   = RNDfromCI (0.0, 1.0);

  logN = u1 <= 0.0 ? 0.000000000000001 : u1;

  double z0 = sqrt (-2 * log (logN))* cos (2 * M_PI * u2);

  double sigma = 2.0;//Sigma > 8.583864105157389 ? 8.583864105157389 : Sigma;

  if (z0 >=  sigma) z0 = RNDfromCI (0.0,    sigma);
  if (z0 <= -sigma) z0 = RNDfromCI (-sigma, 0.0);

  double dist = d * (rMax - rMin);

  if (z0 >= 0.0) return Scale (z0, 0.0,    sigma, value,        value + dist, false);
  else           return Scale (z0, -sigma, 0.0,   value - dist, value,        false);
}
//——————————————————————————————————————————————————————————————————————————————

В методе "Moving" будем использовать метод "Diffusion" так:

for (int i = 0; i < popSize; i++)
{
   for (int c = 0; c < coords; c++)
   {
     a [i].c [c] = Diffusion (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
     a [i].c [c] = SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
   } 
}

После выполнения тестов с внесёнными изменениями (заменили равномерное на нормальное распределение) получили такие результаты:

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 60.999013617749895
Score: 0.75581
25 Rastrigin's; Func runs 10000 result: 47.993562806349246
Score: 0.59467
500 Rastrigin's; Func runs 10000 result: 40.00575378955945
Score: 0.49569
=============================
5 Forest's; Func runs 10000 result: 0.41673083215719087
Score: 0.23572
25 Forest's; Func runs 10000 result: 0.16700842421505407
Score: 0.09447
500 Forest's; Func runs 10000 result: 0.049538421252065555
Score: 0.02802
=============================
5 Megacity's; Func runs 10000 result: 2.7600000000000002
Score: 0.23000
25 Megacity's; Func runs 10000 result: 0.9039999999999999
Score: 0.07533
500 Megacity's; Func runs 10000 result: 0.28
Score: 0.02333
=============================
All score: 2.53305

Когда мы меняем распределение случайной величины в алгоритме имитации отжига, впрочем, как и в любом другом алгоритме, это обязательно повлияет на его работу и результаты. В исходной формуле алгоритма используется равномерное распределение для генерации случайных шагов исследования пространства решений. Это распределение обеспечивает равные вероятности для всех возможных шагов.

Когда мы заменили равномерное распределение на нормальное распределение, вероятностные свойства алгоритма поменялись. Нормальное распределение имеет пик вокруг среднего значения и уменьшается по мере удаления от среднего. Это означает, что случайные шаги, генерируемые с использованием нормального распределения, будут сконцентрированы вокруг среднего значения, и маловероятными становятся шаги, находящиеся на большом удалении от среднего. В нашем случае "среднее значение" на исходном значении координаты, которое мы хотим улучшить.

Такое изменение распределения, очевидно, приводит к менее разнообразным шагам исследования пространства решений. Похоже, алгоритм становится более локальным и менее способным исследовать более удаленные или менее вероятные регионы пространства решений.

Из представленных выше тестов следует, что в данном случае использование нормального распределения привело к незначительному, но статистически значимому ухудшению итоговых результатов по сравнению с равномерно распределенной случайной величиной (как отражено в первой части статьи). Эти результаты были получены при использовании двух стандартных отклонений, и увеличение значения сигмы (стандартного отклонения) приводит к дальнейшему статистически значимому ухудшению результатов.

Отсюда делаем вывод, изменение формы распределения к более острой, в данном конкретном случае ухудшает результаты.

Теперь, когда мы осознали, что "заострение" формы распределения в исходном алгоритме не приносит пользы, давайте рассмотрим другой подход. Предположим, что в исходном алгоритме молекулам в металле, а можно сказать, целым кристаллам в пределах зоны диффузии, не хватает возможности обмениваться энергией, чтобы равномерно распределить ее по всему объему металла. В таком случае мы можем предложить следующую идею: позволить кристаллам обмениваться молекулами в процессе обмена энергией.

Этот процесс обмена молекулами между кристаллами с разной энергией позволит передавать координаты между агентами. Таким образом, молекулы станут некими переносчиками энергии, способными сгладить энергетическое распределение по всему объему металла. В результате такого взаимодействия кристаллической решетки и молекул, энергия будет более равномерно распределена, что позволит достичь более стабильной и оптимальной конфигурации системы. То есть, постараемся увеличить изотропность в структуре металла.

Изотропность — это свойство объекта или системы сохранять одинаковые характеристики или свойства во всех направлениях. В более простых терминах, объект или система является изотропным, если они выглядят и ведут себя одинаково в любом направлении. Таким образом, изотропность подразумевает отсутствие предпочтительного направления или ориентации, и объект или система считается одинаковым или однородным во всех направлениях.

Для реализации имитации выравнивания свойств в металле по всем направлениям (повышение изотропности) нам понадобится внести изменения в методе "Moving".

Логика кода заключается в следующем: происходит итерация по каждому элементу популяции "popSize" и каждой координате "coords":

• генерируется случайное целое число "r" в диапазоне от 0 до "popSize" с помощью функции RNDfromCI, тем самым выбираем случайно агента в популяции
  
• выполняется проверка условия: если значение фитнес-функции выбранного агента больше значения приспособленности изменяемого агента, то копируем координату лучшего, в противном случае координата агента не меняется
  
• генерируется случайное число "rnd" в диапазоне [-0.1;0.1] с помощью функции RNDfromCI
• значение координаты обновляется путем добавления к нему произведения "rnd", (rangeMax[c] - rangeMin[c]) и "d", то есть добавляем случайное приращение в диффузионном диапазоне
• полученную координату проверяем с помощью функции SeInDiSp, чтобы она находилось в пределах допустимого диапазона и с требуемым шагом
  

int    r   = 0;
double rnd = 0.0;

for (int i = 0; i < popSize; i++)
{
  for (int c = 0; c < coords; c++)
  {
      
    r = (int)RNDfromCI (0, popSize);
    if (r >= popSize) r = popSize - 1;

    if (a [r].fPrev > a [i].fPrev)
    {
      a [i].c [c] = a [r].cPrev [c];
    }
    else
    {
      a [i].c [c] = a [i].cPrev [c];
    }
      
    rnd = RNDfromCI (-0.1, 0.1);
    a [i].c [c] = a [i].c [c] + rnd * (rangeMax [c] - rangeMin [c]) * d;
    a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Результаты отжига с теми же параметрами с равномерным распределением и с добавлением изотропности:

C_AO_SIA:50:1000.0:0.1:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.52391137534615
Score: 0.99774
25 Rastrigin's; Func runs 10000 result: 77.70887543197314
Score: 0.96286
500 Rastrigin's; Func runs 10000 result: 57.43358792423487
Score: 0.71163
=============================
5 Forest's; Func runs 10000 result: 1.5720970326889474
Score: 0.88926
25 Forest's; Func runs 10000 result: 1.0118351454323513
Score: 0.57234
500 Forest's; Func runs 10000 result: 0.3391169587652742
Score: 0.19182
=============================
5 Megacity's; Func runs 10000 result: 6.76
Score: 0.56333
25 Megacity's; Func runs 10000 result: 5.263999999999999
Score: 0.43867
500 Megacity's; Func runs 10000 result: 1.4908
Score: 0.12423
=============================
All score: 5.45188

Использование процесса повышения изотропности, в котором происходит обмен молекулами между кристаллами с разной энергией, привел к значительному улучшению результатов работы алгоритма, это заявка на лидерство.

Выводы, которые можно сделать, мотивируясь описанным процессом:

• Передача координат между агентами: обмен молекулами между кристаллами с разной энергией позволяет передавать информацию о координатах между агентами в алгоритме. Это способствует более эффективному и быстрому поиску оптимального решения, так как информация о хороших решениях передается другим агентам
• Сглаживание энергетического распределения: процесс обмена молекулами между кристаллами с разной энергией позволяет сгладить энергетическое распределение по всему объему металла. Это означает, что энергия будет более равномерно распределена, что помогает избежать локальных минимумов и достичь более стабильной и оптимальной конфигурации системы

Теперь, после значительного улучшения результатов с помощью добавления изотропности, попробуем снова добавить нормальное распределение (сначала выполняем операцию повышения изотропности и к полученным значениям прибавляем приращение с нормальным распределением).

Результаты отжига с добавлением повышения изотропности + нормальное распределение:

C_AO_SIA:50:1000.0:0.1:0.05
=============================
5 Rastrigin's; Func runs 10000 result: 78.39172420614801
Score: 0.97132
25 Rastrigin's; Func runs 10000 result: 66.41980717898778
Score: 0.82298
500 Rastrigin's; Func runs 10000 result: 47.62039509425823
Score: 0.59004
=============================
5 Forest's; Func runs 10000 result: 1.243327107341557
Score: 0.70329
25 Forest's; Func runs 10000 result: 0.7588262864735575
Score: 0.42923
500 Forest's; Func runs 10000 result: 0.13750740782669305
Score: 0.07778
=============================
5 Megacity's; Func runs 10000 result: 6.8
Score: 0.56667
25 Megacity's; Func runs 10000 result: 2.776
Score: 0.23133
500 Megacity's; Func runs 10000 result: 0.46959999999999996
Score: 0.03913
=============================
All score: 4.43177

Результаты значительно ухудшились.

Предположение, что если простая генерация приращений с нормальным распределением в алгоритме имитации отжига улучшений не принесла, то может быть после применения повышения изотропности приращение с нормальным распределением даст ожидаемый эффект? Ожидания не подтвердились. Это может быть объяснено тем, что после применения повышения изотропности по-прежнему равномерное распределение обеспечивает более равномерное исследование пространства решений, позволяя алгоритму изучать различные области без сильных искажений в предпочтениях. Попытка уточнять имеющиеся координаты с помощью нормального распределения не увенчалась успехом, это ограничивает более широкое исследование областей алгоритму.

Проведем последний эксперимент, чтобы окончательно сделать выводы в пользу равномерного распределения приращений случайной величины после применения повышения изотропности. Попытаемся ещё более точно исследовать окрестности известных координат, будем использовать для этого квадратичное распределение. Если случайная величина с равномерным распределением возводится во вторую степень, то полученное распределение будет называться распределением случайной величины в квадрате или квадратичным распределением.

Результаты алгоритма имитации отжига с теми же параметрами с добавлением повышения изотропности + острое квадратичное распределение:

C_AO_SIA:50:1000.0:0.1:0.2
=============================
5 Rastrigin's; Func runs 10000 result: 70.23675927985173
Score: 0.87027
25 Rastrigin's; Func runs 10000 result: 56.86176837508631
Score: 0.70455
500 Rastrigin's; Func runs 10000 result: 43.100825665204596
Score: 0.53404
=============================
5 Forest's; Func runs 10000 result: 0.9361317757226002
Score: 0.52952
25 Forest's; Func runs 10000 result: 0.25320813586138297
Score: 0.14323
500 Forest's; Func runs 10000 result: 0.0570263375476293
Score: 0.03226
=============================
5 Megacity's; Func runs 10000 result: 4.2
Score: 0.35000
25 Megacity's; Func runs 10000 result: 1.296
Score: 0.10800
500 Megacity's; Func runs 10000 result: 0.2976
Score: 0.02480
=============================
All score: 3.29667

Результаты возведения в квадрат равномерно распределенной случайной величины также не дали положительного эффекта, спад производительности даже сильнее, чем с применением нормального распределения.

Теперь, избавимся ещё от одного недостатка алгоритма имитации отжига - трудность в выборе настроек и сочетания температуры и коэффициента снижения температуры, так как оба этих параметров взаимно влияют друг на друга. Для того, чтобы увязать вместе эти два параметра, объединим функцию снижения температуры и функцию вероятностного принятия худших решений. Применим функцию гиперболического арккосинуса:

(1 - delta) * (acosh (-(x^3 - 3))) / 1,765

где:

• delta - нормированная в диапазон [0.0;1.0] разница значений фитнес-функции на двух последних итерациях
• x - нормированные шаги эпох алгоритма

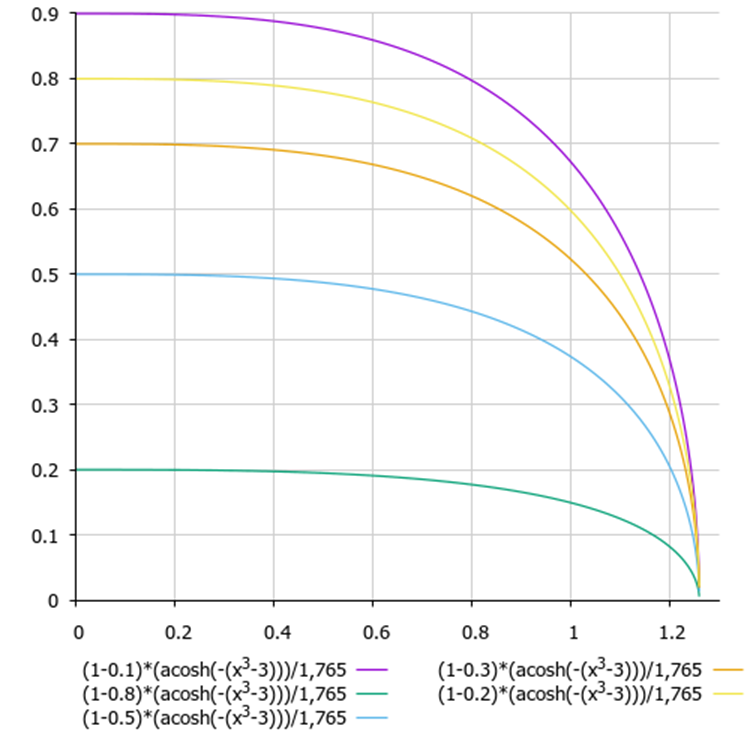
Рисунок 1. График зависимости принятия худшего решения от разницы энергий и номера текущей эпохи (y - разница энергий, x - эпохи).

3. Результаты тестов

Распечатка работы итоговой версии алгоритма имитации изотропного отжига (SIA) на тестовом стенде:

C_AO_SIA:100:0.01:0.1
=============================
5 Rastrigin's; Func runs 10000 result: 80.49732910930824
Score: 0.99741
25 Rastrigin's; Func runs 10000 result: 78.48411039606445
Score: 0.97246
500 Rastrigin's; Func runs 10000 result: 56.26829697982381
Score: 0.69720
=============================
5 Forest's; Func runs 10000 result: 1.6491133508905373
Score: 0.93282
25 Forest's; Func runs 10000 result: 1.3608802086313785
Score: 0.76978
500 Forest's; Func runs 10000 result: 0.31584037846210056
Score: 0.17866
=============================
5 Megacity's; Func runs 10000 result: 8.6
Score: 0.71667
25 Megacity's; Func runs 10000 result: 6.152
Score: 0.51267
500 Megacity's; Func runs 10000 result: 1.0544
Score: 0.08787
=============================
All score: 5.86552

Впечатляющие результаты, при этом, если вы заметили, параметров стало на один меньше.

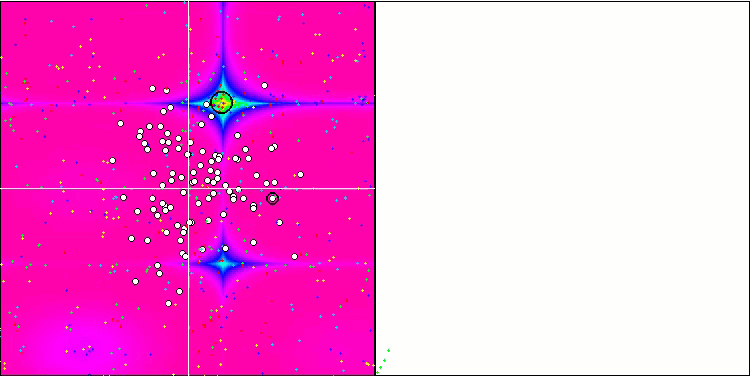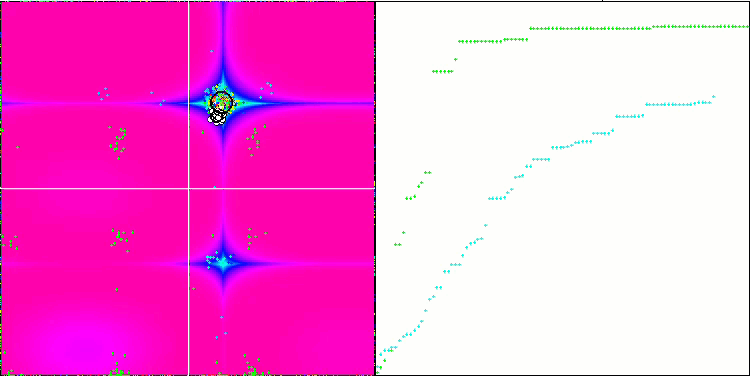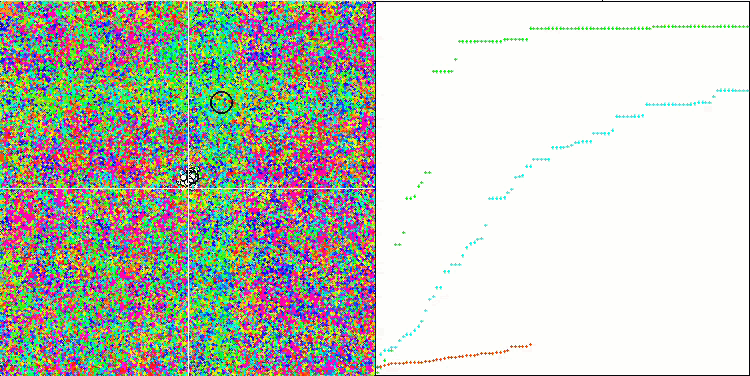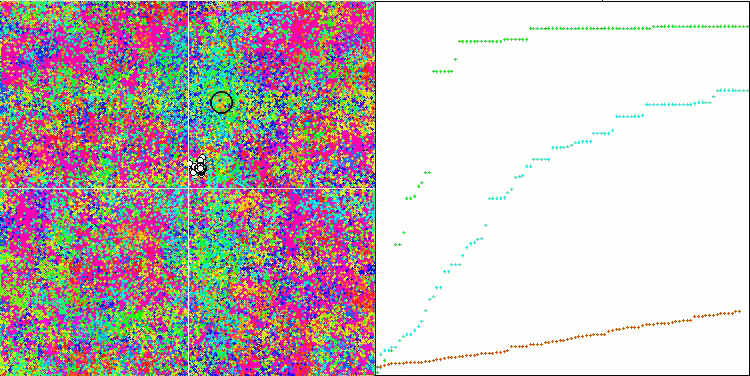
Визуализация работы алгоритма демонстрирует отчетливое разделение на отдельные кластеры агентов, при этом все значимые локальные экстремумы охвачены. Картинка напоминает реальную кристаллизацию застывающего металла. Обращает на себя внимание отличная сходимость на всех тестах, в том числе, что очень важно, и со многими переменными.

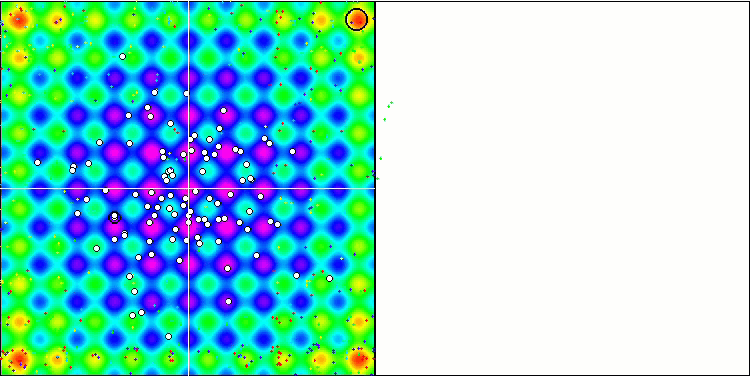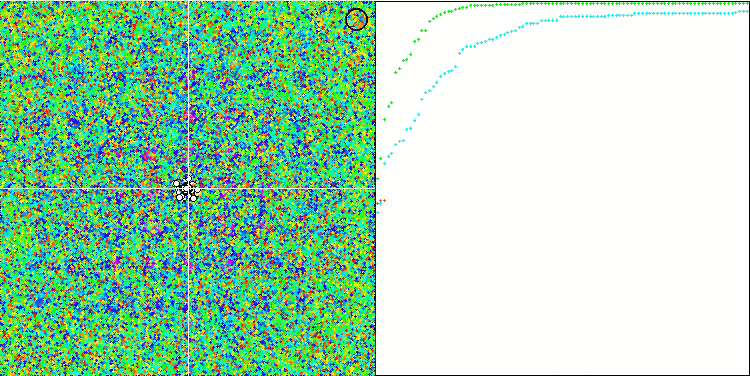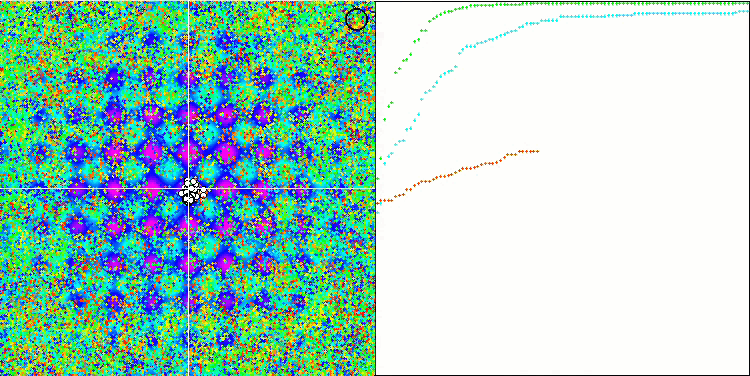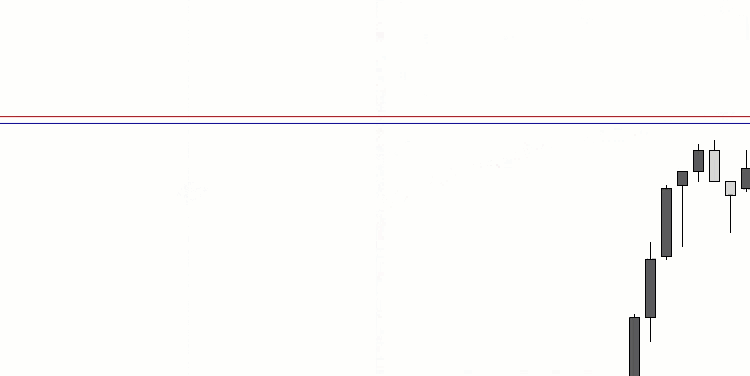
SIA на тестовой функции Rastrigin.

SIA на тестовой функции Forest.

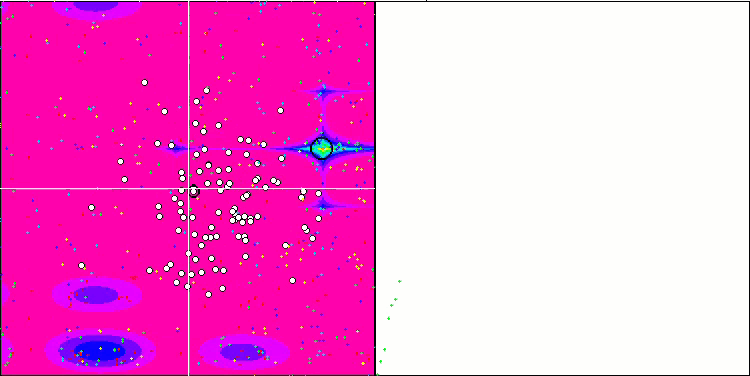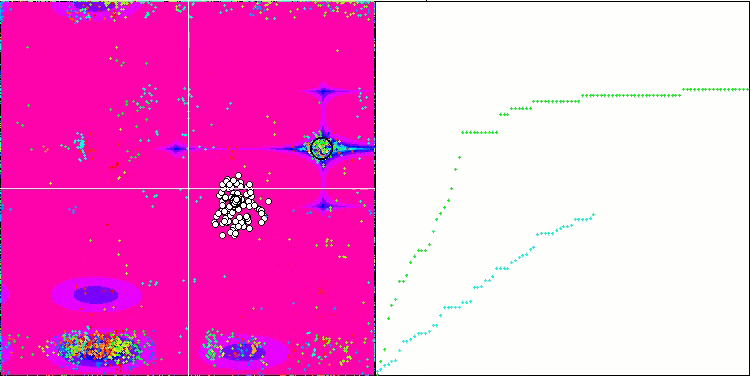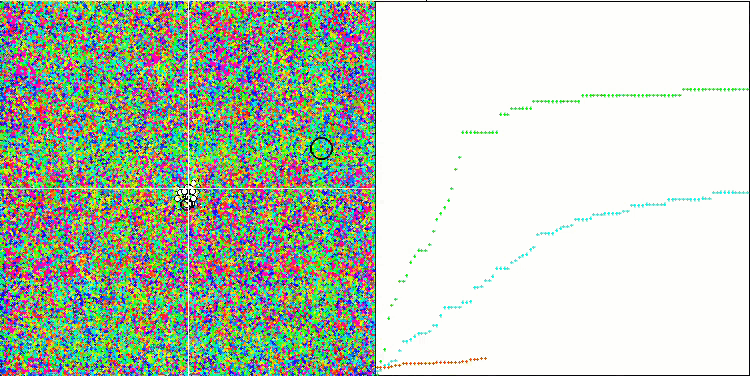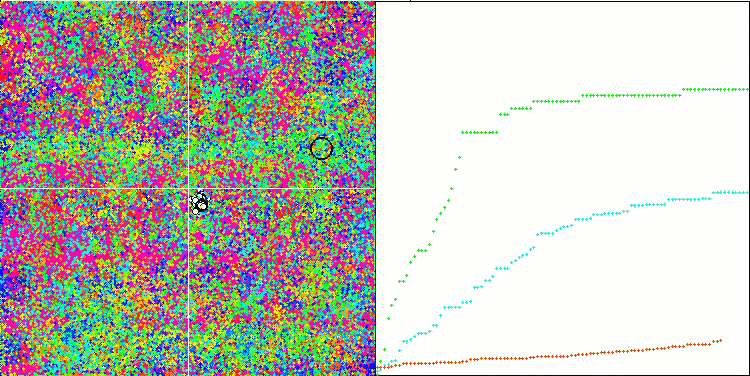
  SIA на тестовой функции Megacity.

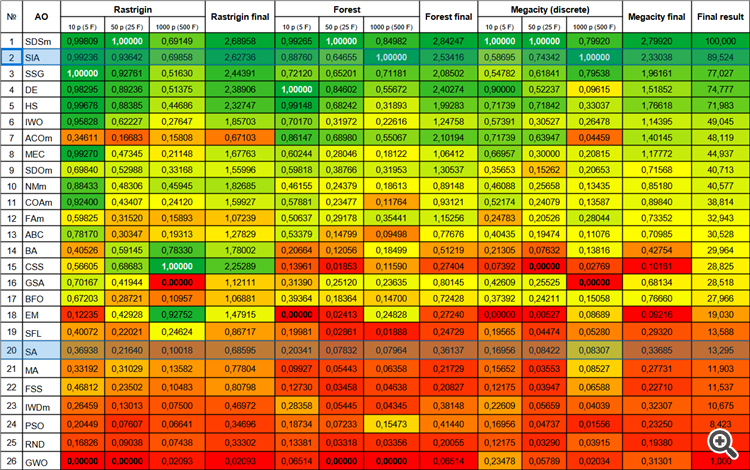
Новый алгоритм имитации изотропного отжига (SIA, 2023 г), занял второе место в рейтинговой таблице, при этом отобрал лидерство у SDSm в двух труднейших тестах (на острой Forest и дискретной Megacity с 1000 переменных).

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	0,99265	1,00000	0,84982	2,84247	1,00000	1,00000	0,79920	2,79920	100,000
2	SIA	simulated isotropic annealing	0,99236	0,93642	0,69858	2,62736	0,88760	0,64655	1,00000	2,53416	0,58695	0,74342	1,00000	2,33038	89,524
3	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72120	0,65201	0,71181	2,08502	0,54782	0,61841	0,79538	1,96161	77,027
4	DE	differential evolution	0,98295	0,89236	0,51375	2,38906	1,00000	0,84602	0,55672	2,40274	0,90000	0,52237	0,09615	1,51852	74,777
5	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99148	0,68242	0,31893	1,99283	0,71739	0,71842	0,33037	1,76618	71,983
6	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70170	0,31972	0,22616	1,24758	0,57391	0,30527	0,26478	1,14395	49,045
7	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86147	0,68980	0,55067	2,10194	0,71739	0,63947	0,04459	1,40145	48,119
8	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60244	0,28046	0,18122	1,06412	0,66957	0,30000	0,20815	1,17772	44,937
9	SDOm	spiral dynamics optimization M	0,69840	0,52988	0,33168	1,55996	0,59818	0,38766	0,31953	1,30537	0,35653	0,15262	0,20653	0,71568	40,713
10	NMm	Nelder-Mead method M	0,88433	0,48306	0,45945	1,82685	0,46155	0,24379	0,18613	0,89148	0,46088	0,25658	0,13435	0,85180	40,577
11	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,57881	0,23477	0,11764	0,93121	0,52174	0,24079	0,13587	0,89840	38,814
12	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,50637	0,29178	0,35441	1,15256	0,24783	0,20526	0,28044	0,73352	32,943
13	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53379	0,14799	0,09498	0,77676	0,40435	0,19474	0,11076	0,70985	30,528
14	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20664	0,12056	0,18499	0,51219	0,21305	0,07632	0,13816	0,42754	29,964
15	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,13961	0,01853	0,11590	0,27404	0,07392	0,00000	0,02769	0,10161	28,825
16	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31390	0,25120	0,23635	0,80145	0,42609	0,25525	0,00000	0,68134	28,518
17	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39364	0,18364	0,14700	0,72428	0,37392	0,24211	0,15058	0,76660	27,966
18	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,24828	0,27240	0,00000	0,00527	0,08689	0,09216	19,030
19	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,19981	0,02861	0,01888	0,24729	0,19565	0,04474	0,05280	0,29320	13,588
20	SA	simulated annealing	0,36938	0,21640	0,10018	0,68595	0,20341	0,07832	0,07964	0,36137	0,16956	0,08422	0,08307	0,33685	13,295
21	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,09927	0,05443	0,06358	0,21729	0,15652	0,03553	0,08527	0,27731	11,903
22	FSS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12730	0,03458	0,04638	0,20827	0,12175	0,03947	0,06588	0,22710	11,537
23	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28358	0,05445	0,04345	0,38148	0,22609	0,05659	0,04039	0,32307	10,675
24	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18734	0,07233	0,15473	0,41440	0,16956	0,04737	0,01556	0,23250	8,423
25	RND	random	0,16826	0,09038	0,07438	0,33302	0,13381	0,03318	0,03356	0,20055	0,12175	0,03290	0,03915	0,19380	5,097
26	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06514	0,00000	0,00000	0,06514	0,23478	0,05789	0,02034	0,31301	1,000

Выводы

На основании проведенных экспериментов и анализа результатов можно сделать следующие выводы:

1. Новый алгоритм имитации изотропного отжига (SIA) демонстрирует впечатляющие результаты в оптимизации функций с множеством переменных. Это указывает на эффективность алгоритма в поиске оптимальных решений в пространствах высокой размерности.
2. Алгоритм показывает особенно хорошие результаты на функциях с острыми и дискретными особенностями. Это может быть связано с тем, что SIA позволяет равномерно исследовать пространство решений и находить оптимальные точки, даже в сложных и нерегулярных областях.
3. В целом, новый алгоритм SIA является мощным инструментом оптимизации. Благодаря успешной комбинации стратегий поиска алгоритм обладает качественно новыми свойствами и демонстрирует высокую эффективность в поиске оптимальных решений.

В новом алгоритме SIA, помимо размера популяции, есть только два параметра, температура и коэффициент диффузии, вместо трёх как было в SA. Кроме того, теперь параметр температуры очень прост в понимании и выражен в частях от некой абстрактной температуры и по умолчанию равен 0.01.

На основании проведенных исследований и анализа результатов, можно с полной уверенностью рекомендовать алгоритм SIA для использования в обучении нейронных сетей, в трейдерских задачах со многими параметрами и сложных задач комбинаторики.

Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам.

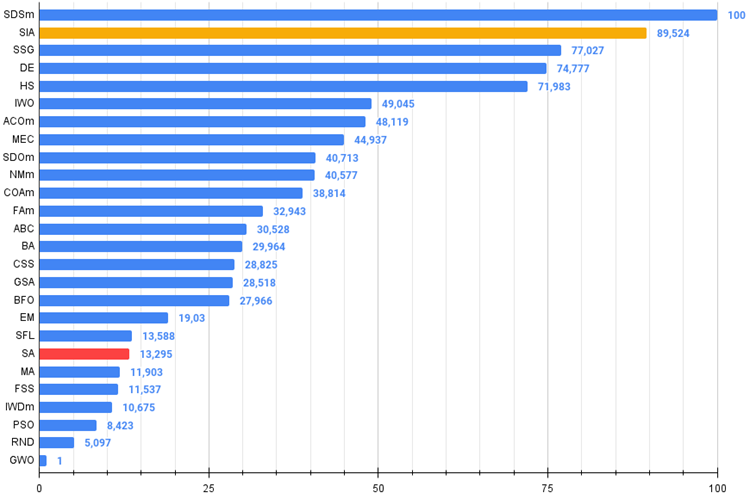
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье).

Плюсы и минусы алгоритма имитации изотропного отжига (SIA):

Плюсы:

1. Минимальное количество внешних параметров.
2. Высокая эффективность при решении разнообразных задач.
3. Низкая нагрузка на вычислительные ресурсы.
4. Легкость в реализации алгоритма.
5. Устойчивость к застреванию.
6. Высокие результаты как на гладких, так и на сложных дискретных функциях.
7. Высокая сходимость.

Минусы:

1. Не замечены.

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.