
Алгоритм сверчков — Cricket Algorithm (CA)
Содержание
Введение
Разберем для целей оптимизации еще один достаточно новый алгоритм. Алгоритм сверчков (Cricket Algorithm, CA) — это метаэвристический метод, разработанный Canayaz и Karci в 2015 году и опубликованный в журнале Applied Intelligence. Алгоритм черпает вдохновение из поведения сверчков в природе, в частности из их способности общаться с помощью звука и ориентироваться на сородичей с наиболее громким стрекотанием. В основу алгоритма положены физические законы распространения звука в атмосфере, что придаёт ему уникальную связь с реальным миром.
Алгоритм объединяет элементы трёх известных метаэвристик: алгоритма летучих мышей (Bat Algorithm), роевой оптимизации частиц (Particle Swarm Optimization) и алгоритма светлячков (Firefly Algorithm). От алгоритма летучих мышей заимствован механизм обновления скорости и позиции на основе частоты, от роевой оптимизации — концепция движения к лучшему решению, а от алгоритма светлячков — притяжение к более «ярким» (в данном случае — более громким) особям.
Реализация алгоритма
Сверчки — насекомые, известные своим характерным стрекотанием в тёплые летние дни. Звук производится преимущественно самцами путём трения надкрылий друг о друга — этот процесс называется стридуляцией. С помощью издаваемых звуков сверчки привлекают самок для спаривания, отпугивают непрошеных гостей от своих нор и предупреждают сородичей об опасности. Слуховые органы сверчков расположены на передних лапках, что позволяет им точно определять направление на источник звука и двигаться к сверчку с наиболее громким стрекотанием.
Американский физик А. Долбир в 1897 году обнаружил связь между частотой стрекотания сверчков и температурой воздуха. Согласно закону Долбира, количество стрекотаний в минуту напрямую зависит от температуры окружающей среды: в тёплую погоду сверчки стрекочут чаще, чем в холодную. Эта зависимость используется в алгоритме для моделирования вариативности поведения агентов. Поскольку сверчки общаются посредством звука, в алгоритме применяются физические законы акустики для моделирования взаимодействия между агентами. Рассмотрим основные формулы.
Скорость звука в воздухе зависит от температуры и вычисляется по формуле:
V = 20.1 × √(273 + C); где V - скорость звука в метрах в секунду, C - температура воздуха в градусах Цельсия. При температуре 20°C скорость звука составляет примерно 343 м/с.
Частота звука связана со скоростью распространения и длиной волны соотношением:
f = V / λ; где f - частота в герцах, V - скорость звука, λ - длина волны. В контексте алгоритма длина волны интерпретируется как расстояние между сверчком и лучшим решением в популяции.
Интенсивность звука убывает обратно пропорционально квадрату расстояния от источника (закон обратных квадратов):
I = W / (4πr²); где I - интенсивность звука в Вт/м², W - мощность источника в ваттах, r - расстояние от источника в метрах. Отсюда мощность звука выражается как: W = I × 4πr².
Уровень звукового давления на определённом расстоянии от источника рассчитывается по формуле:
Lp = Lw + 10 × log₁₀[Q / (4πr²)]; где Lp - уровень звукового давления в децибелах, Lw - уровень звуковой мощности источника, Q - коэффициент направленности (принимается равным 1 для неровной местности и 2 для плоской), r - расстояние от источника.
При распространении звука в атмосфере происходит его поглощение воздухом. Величина атмосферного поглощения вычисляется согласно стандарту ISO 9613-1:
A_atm = 7.4 × (f² × r / Ø) × 10⁻⁸; где A_atm - коэффициент поглощения, f - частота звука в герцах, r - расстояние в метрах, Ø - относительная влажность воздуха в процентах. Реальный уровень звукового давления с учётом атмосферного поглощения составляет: Lp' = Lp − A_atm.
Эти физические формулы используются в алгоритме для расчёта коэффициента притяжения между агентами, что позволяет моделировать реалистичное затухание «слышимости» сверчков с расстоянием.
Алгоритм сверчков представляет собой популяционный метод оптимизации. На каждой итерации все агенты (сверчки) обновляют свои позиции в пространстве поиска, стремясь найти глобальный оптимум целевой функции. Алгоритм состоит из нескольких ключевых этапов: генерация параметров стрекотания, обновление скорости и позиции по аналогии с алгоритмом летучих мышей, выбор стратегии поиска на основе коэффициента поглощения звука, и притяжение к более громким сверчкам по аналогии с алгоритмом светлячков.
На этапе инициализации создаётся популяция из "n" агентов, каждый из которых представляет потенциальное решение задачи оптимизации. Позиции агентов инициализируются случайным образом в пределах допустимой области поиска. Для каждого агента вычисляется значение целевой функции, и определяется лучшее решение в популяции.
На каждой итерации для каждого сверчка выполняется следующая последовательность действий. Сначала генерируется случайное число стрекотаний "N" в диапазоне от 0 до 120. По закону Долбира это число преобразуется в температуру воздуха. Формула для температуры в градусах Цельсия имеет вид:
T_C = 10 + (N − 40) / 7. При N = 0 температура составляет примерно 4.3°C, при N = 120 - около 21.4°C. Таким образом, случайное число стрекотаний определяет «индивидуальную» температуру для каждого сверчка на данной итерации.
Далее вычисляется скорость звука при полученной температуре:
V_i = 20.1 × √(273 + T_C). Значение скорости звука варьируется примерно от 335 до 345 м/с в зависимости от температуры. Затем определяется расстояние "λ" от текущего сверчка до лучшего решения в популяции. Это расстояние вычисляется как евклидова норма разности координат:
λ = ‖x_i − x*‖; где x_i - позиция текущего сверчка, x* - позиция лучшего решения. В реализации расстояние нормализуется делением на диагональ пространства поиска, чтобы получить безразмерную величину в диапазоне от 0 до 1.
На основе скорости звука и расстояния вычисляется максимальная частота:
f_max = V_i / λ. Чем ближе сверчок к лучшему решению (меньше λ), тем выше частота, что усиливает притяжение. Чем дальше сверчок (больше λ), тем ниже частота, что позволяет ему более свободно исследовать пространство.
Индивидуальная частота каждого сверчка определяется по формуле из алгоритма летучих мышей:
f_i = f_min + (f_max − f_min) × β; где f_min = 0, а β - случайное число в диапазоне [0, 1]. Таким образом, частота f_i принимает случайное значение от нуля до f_max.
После вычисления частоты обновляются скорость и позиция сверчка. Формула обновления скорости:
v_i^t = v_i^(t−1) + (x* − x_i) × f_i + V_i; где v_i^t - новая скорость, v_i^(t−1) - скорость на предыдущей итерации, (x* − x_i) - направление к лучшему решению, f_i - частота, V_i - скорость звука, добавляющая стохастический импульс. В отличие от оригинального алгоритма летучих мышей, здесь добавляется слагаемое V_i, что является уникальной особенностью алгоритма сверчков.
Новая позиция вычисляется как:
x_i^t = x_i^(t−1) + v_i^t. Важно отметить, что обновление скорости и позиции выполняется для всех сверчков на каждой итерации, независимо от последующего выбора стратегии.
После обновления позиции алгоритм выбирает одну из двух стратегий дальнейшего поиска. Выбор осуществляется на основе коэффициента поглощения звука "γ", который вычисляется с использованием формулы атмосферного поглощения. Генерируется случайное число r в диапазоне [0, 1], и если r > γ, выполняется фаза притяжения к более громким сверчкам (аналог алгоритма светлячков). В противном случае сверчок совершает случайное блуждание вблизи лучшего решения.
Коэффициент "γ" зависит от частоты и расстояния: при высокой частоте и большом расстоянии поглощение звука больше, что повышает вероятность случайного блуждания. Это создаёт адаптивный баланс между глобальным исследованием пространства и локальной эксплуатацией найденных решений.
Фаза притяжения (Firefly-подобная). Если случайное число превышает коэффициент поглощения, сверчок выполняет фазу притяжения к более громким сородичам. Для этого перебираются все остальные сверчки в популяции, и для каждого сверчка "j", чей звук громче (значение целевой функции лучше), чем у текущего сверчка "i", выполняется притяжение.
Сначала вычисляется расстояние между сверчками:
r_ij = ‖x_i − x_j‖. Затем по формулам акустики рассчитываются мощность звука, уровень звукового давления, атмосферное поглощение и реальный уровень звукового давления. На основе этих величин определяется коэффициент притяжения:
K = K_0 × exp(−γ × r_ij²); где K_0 - базовый коэффициент, зависящий от реального уровня звукового давления, γ - параметр затухания притяжения с расстоянием.
Позиция сверчка обновляется по формуле:
x_i = x_i + K × (x_j − x_i) + α × ε; где первое слагаемое - притяжение к более громкому сверчку "j", а второе - случайный шум с амплитудой "α" и случайным вектором "ε". Параметр "α" уменьшается со временем по формуле α = α_0 × 0.95^t, где t - номер итерации, что обеспечивает переход от исследования к эксплуатации.
Существенной особенностью алгоритма является то, что притяжение выполняется последовательно ко всем более громким сверчкам в популяции, а не только к одному. Это означает, что если в популяции из 50 сверчков 30 имеют лучшее значение целевой функции, текущий сверчок испытает притяжение от всех 30, что создаёт усреднённое движение к области хороших решений.
Если случайное число не превышает коэффициент поглощения, сверчок выполняет случайное блуждание вблизи лучшего решения:
x_i = x* + 0.01 × rand(0, 1); где x* - позиция лучшего решения, а случайное число масштабирует отклонение. Эта стратегия обеспечивает локальный поиск в окрестности лучшего найденного решения. При случайном блуждании скорость сверчка обнуляется, что позволяет ему начать заново из новой точки.
После обновления позиций всех сверчков вычисляются значения целевой функции для новых позиций. Если какой-либо сверчок нашёл решение лучше текущего глобального лучшего, глобальное лучшее обновляется. Алгоритм продолжает работу до достижения заданного числа итераций.
Алгоритм использует следующие параметры: размер популяции "n" (типичное значение 50), начальный коэффициент шума α_0 = 0.5, коэффициент затухания притяжения γ = 1.0, относительная влажность воздуха Ø = 50%, коэффициент направленности Q = 2. Параметр "α" уменьшается на каждой итерации умножением на 0.95, что обеспечивает постепенный переход от глобального исследования к локальной оптимизации.
При практической реализации алгоритма необходимо учитывать масштабирование величин. Физические формулы оперируют размерными величинами (метры, герцы, децибелы), тогда как пространство поиска может иметь произвольный масштаб. Для корректной работы алгоритма расстояния нормализуются делением на диагональ пространства поиска, скорость звука нормализуется относительно референсного значения 340 м/с, а частота ограничивается разумными пределами для предотвращения численной нестабильности.
Коэффициент поглощения звука также требует нормализации для получения значений в диапазоне [0, 1], что обеспечивает осмысленное вероятностное переключение между стратегиями поиска. Без нормализации формула атмосферного поглощения может давать значения, многократно превышающие единицу, что приводит к вырождению алгоритма в чистое случайное блуждание.
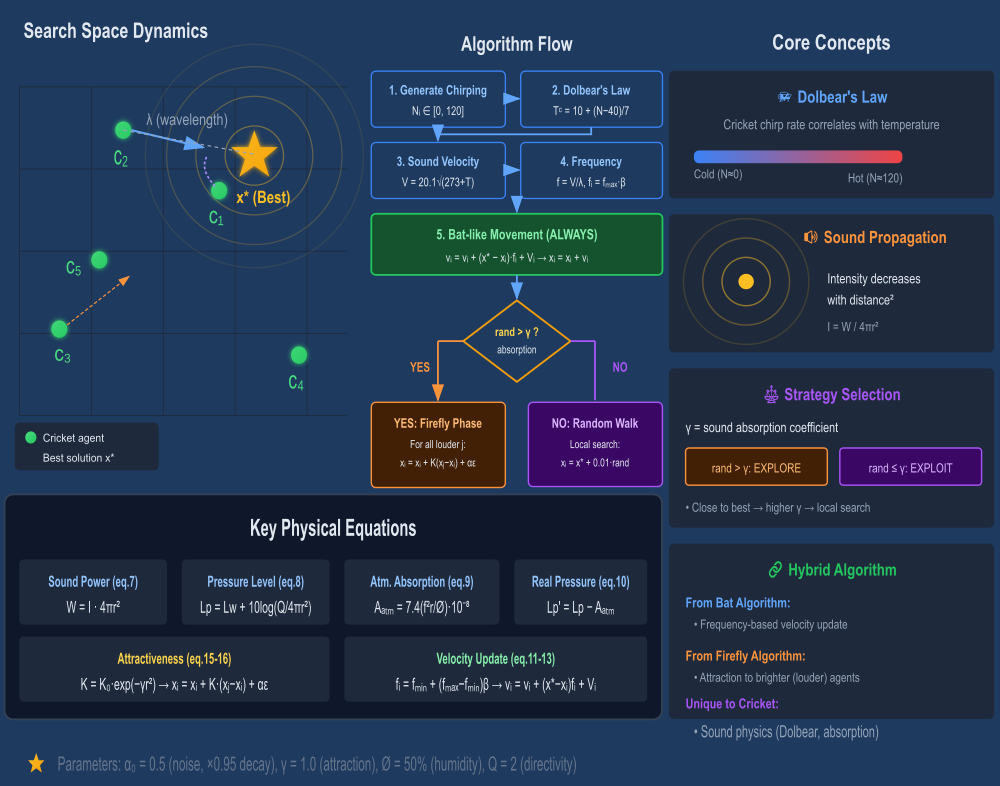
Рисунок 1. Иллюстрация работы алгоритма CA-Cricket
Иллюстрация включает Search Space Dynamics (левая панель): визуализация агентов-сверчков в пространстве поиска; звуковые волны от лучшего решения; стрелки движения (velocity, attraction); обозначение λ (wavelength/distance to best).
Algorithm Flow (центральная панель): пошаговая блок-схема алгоритма этапы 1-5 с формулами; ветвление (rand > γ ?) YES: Firefly Phase, NO: Random Walk. Key Physical Equations (нижняя панель): eq.7-10: звуковые уравнения; eq.11-13: обновление скорости; eq.15-16: коэффициент притяжения. Core Concepts (правая панель): Dolbear's Law с температурной шкалой; Sound Propagation с inverse square lawAdaptive; Strategy SelectionHybrid; Algorithm nature (Bat + Firefly + unique Cricket features)
Напишем псевдокод алгоритма CA-Cricket:
// Инициализация
FOR i = 1 TO n DO
xᵢ ← случайная позиция в пределах bounds
vᵢ ← 0
fᵢ ← ЦелеваяФункция(xᵢ)
END FOR
x* ← позиция агента с лучшим f
f* ← лучшее значение f
diagonal ← диагональ пространства поиска
α ← α₀
// Основной цикл
FOR iter = 1 TO MaxIter DO
α ← α₀ × 0.95^iter
IF α < 0.01 THEN α ← 0.01
FOR i = 1 TO n DO
// Генерация параметров стрекотания
N ← случайное число из [0, 120]
T ← 10 + (N - 40) / 7
V ← 20.1 × √(273 + T)
// Вычисление частоты
λ ← ‖xᵢ - x*‖ / diagonal
f_max ← (V / 340) / λ
fᵢ ← f_max × случайное число из [0, 1]
// Обновление скорости и позиции (выполняется всегда)
FOR каждой координаты c DO
направление ← (x*[c] - xᵢ[c]) / диапазон[c]
импульс ← (V/340 - 1) × 0.1 × случайное из [-1, 1]
vᵢ[c] ← vᵢ[c] + направление × fᵢ × диапазон[c] × 0.1 + импульс × диапазон[c]
vᵢ[c] ← ограничить(vᵢ[c], -0.3 × диапазон[c], 0.3 × диапазон[c])
xᵢ[c] ← xᵢ[c] + vᵢ[c]
END FOR
// Выбор стратегии
γ ← 0.1 + 0.4 × (1 - λ)
r ← случайное число из [0, 1]
IF r > γ THEN
// Фаза притяжения (Firefly)
FOR j = 1 TO n DO
IF fⱼ > fᵢ THEN
r_ij ← ‖xᵢ - xⱼ‖ / diagonal
K ← вычислить коэффициент притяжения по формулам акустики
FOR каждой координаты c DO
xᵢ[c] ← xᵢ[c] + K × (xⱼ[c] - xᵢ[c]) + α × диапазон[c] × случайное из [-0.5, 0.5]
END FOR
END IF
END FOR
ELSE
// Случайное блуждание
FOR каждой координаты c DO
xᵢ[c] ← x*[c] + α × 0.2 × диапазон[c] × случайное из [-1, 1]
vᵢ[c] ← 0
END FOR
END IF
// Ограничение координат
xᵢ ← привести к границам bounds
// Обновление лучшего решения
fᵢ ← ЦелеваяФункция(xᵢ)
IF fᵢ > f* THEN
f* ← fᵢ
x* ← xᵢ
END IF
END FOR
END FOR
RETURN x*, f*
КОНЕЦ
Теперь можем приступить к самой реализации алгоритма. Вспомогательная структура "S_CA_Velocity" будет предназначена для хранения вектора скорости отдельного агента. Структура содержит единственное поле - динамический массив "v", размерность которого соответствует количеству координат в пространстве поиска. Использование отдельной структуры для хранения скоростей позволит нам организовать массив скоростей всех агентов популяции и обеспечит удобный доступ к компонентам скорости каждого агента по индексу координаты.
//———————————————————————————————————————————————————————————————————— struct S_CA_Velocity { double v []; }; //————————————————————————————————————————————————————————————————————
Класс "C_AO_CA_Cricket" реализует алгоритм сверчков и наследуется от базового класса "C_AO". Класс содержит публичные и приватные члены, обеспечивающие полную функциональность алгоритма.
Публичные члены класса включают два настраиваемых параметра алгоритма. Параметр "alpha0" определяет начальное значение коэффициента шума, используемого в формулах обновления позиций агентов. Параметр "gammaFirefly" задаёт коэффициент затухания притяжения в фазе взаимодействия агентов по аналогии с алгоритмом светлячков. Оба параметра доступны для изменения через массив "params" базового класса, что позволяет настраивать поведение алгоритма без перекомпиляции.
Приватные члены класса хранят внутреннее состояние алгоритма. Переменная "alpha" содержит текущее значение коэффициента шума, которое уменьшается с каждой итерацией. Переменная "currentEpoch" отслеживает номер текущей итерации алгоритма. Константа "humidity" задаёт относительную влажность воздуха в процентах и используется в формуле атмосферного поглощения звука. Константа "Q" определяет коэффициент направленности звука, принимающий значение 2 для плоской местности. Массив "vel" типа "S_CA_Velocity" хранит векторы скоростей всех агентов популяции. Константа "pi" содержит значение числа пи для тригонометрических вычислений. Переменная "V_ref" задаёт референсную скорость звука 340 м/с, относительно которой нормализуются вычисляемые скорости. Переменная "maxDiagonal" хранит длину диагонали пространства поиска и используется для нормализации расстояний между агентами.
Метод "SetParams" предназначен для применения параметров, заданных пользователем через массив "params". Метод извлекает значения из массива и присваивает их соответствующим переменным класса: "popSize" получает целочисленное значение первого элемента, "alpha0" - значение второго элемента, "gammaFirefly" — значение третьего элемента. Вызов этого метода необходим после изменения значений в массиве "params" для актуализации внутренних переменных алгоритма.
//———————————————————————————————————————————————————————————————————— class C_AO_CA_Cricket : public C_AO { public: //---------------------------------------------------------- ~C_AO_CA_Cricket () { } C_AO_CA_Cricket () { ao_name = "CA_Cricket"; ao_desc = "Cricket Algorithm"; ao_link = "https://www.mql5.com/ru/articles/21058"; popSize = 50; alpha0 = 0.5; gammaFirefly = 1.0; ArrayResize (params, 3); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha0"; params [1].val = alpha0; params [2].name = "gammaFirefly"; params [2].val = gammaFirefly; } void SetParams () { popSize = (int)params [0].val; alpha0 = params [1].val; gammaFirefly = params [2].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP); void Moving (); void Revision (); //------------------------------------------------------------------ double alpha0; double gammaFirefly; private://---------------------------------------------------------- double alpha; int currentEpoch; double humidity; double Q; S_CA_Velocity vel []; double pi; double V_ref; // Референсная скорость звука (340 м/с) double maxDiagonal; // Диагональ пространства поиска }; //————————————————————————————————————————————————————————————————————
Метод "Init" выполняет полную инициализацию алгоритма перед началом оптимизации. Метод принимает четыре параметра: массивы "rangeMinP" и "rangeMaxP" определяют границы пространства поиска по каждой координате, массив "rangeStepP" задаёт шаг дискретизации для каждой координаты, параметр "epochsP" указывает максимальное число итераций.
В начале метода вызывается "StandardInit" базового класса, выполняющий стандартную инициализацию популяции и внутренних структур данных. После успешной стандартной инициализации устанавливаются начальные значения внутренних переменных. Текущий коэффициент шума "alpha" получает значение "alpha0". Счётчик итераций "currentEpoch" обнуляется. Константы среды инициализируются фиксированными значениями: влажность "humidity" - 50 %, коэффициент направленности Q - 2.0, число пи - 3.14, референсная скорость звука "V_ref" - 340 м/с.
Далее вычисляется диагональ пространства поиска "maxDiagonal". Для этого суммируются квадраты диапазонов по каждой координате, после чего извлекается квадратный корень из суммы. Если вычисленная диагональ оказывается меньше 10⁻¹⁰, она принудительно устанавливается равной единице для предотвращения деления на ноль при последующей нормализации расстояний.
Завершающим этапом инициализации является создание массива скоростей. Массив "vel" изменяет размер до "popSize" элементов. Для каждого агента создаётся вектор скорости размерностью "coords", все компоненты которого инициализируются нулями. Метод возвращает "true" при успешном завершении инициализации.
//———————————————————————————————————————————————————————————————————— bool C_AO_CA_Cricket::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ alpha = alpha0; currentEpoch = 0; humidity = 50.0; Q = 2.0; pi = 3.14; V_ref = 340.0; // Вычисляем диагональ пространства для нормализации maxDiagonal = 0.0; for (int c = 0; c < coords; c++) { double rangeC = rangeMax [c] - rangeMin [c]; maxDiagonal += rangeC * rangeC; } maxDiagonal = sqrt (maxDiagonal); if (maxDiagonal < 1e-10) maxDiagonal = 1.0; ArrayResize (vel, popSize); for (int i = 0; i < popSize; i++) { ArrayResize (vel [i].v, coords); for (int c = 0; c < coords; c++) { vel [i].v [c] = 0.0; } } return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" реализует основную логику перемещения агентов в пространстве поиска и вызывается на каждой итерации алгоритма. Метод не принимает параметров и не возвращает значений, модифицируя позиции агентов непосредственно в массиве "a" базового класса.
При первом вызове метода, когда флаг "revision" имеет значение "false", выполняется начальная инициализация позиций агентов. Для каждого агента и каждой координаты генерируется случайное значение в пределах допустимого диапазона с помощью функции "RNDfromCI", после чего значение приводится к сетке дискретизации функцией "SeInDiSp". Компоненты скорости агента обнуляются. После инициализации всех агентов флаг "revision" устанавливается в "true", и метод завершает работу.
При последующих вызовах метода выполняется полный цикл обновления позиций. В начале инкрементируется счётчик итераций "currentEpoch" и пересчитывается коэффициент шума "alpha" по формуле экспоненциального затухания: "alpha" умножается на 0.95 в степени номера итерации. Если "alpha" становится меньше 0.01, значение фиксируется на этом минимальном уровне для сохранения минимальной стохастичности поиска.
Далее для каждого агента популяции выполняется последовательность вычислений согласно псевдокоду алгоритма. Генерируется случайное число стрекотаний "Ni" в диапазоне от 0 до 120. По закону Долбира вычисляется температура воздуха в градусах Цельсия. На основе температуры рассчитывается скорость звука "Vi".
Вычисляется расстояние "lambda_raw" от текущего агента до лучшего решения "cB" как евклидова норма разности координат. Расстояние нормализуется делением на диагональ пространства "maxDiagonal", результат ограничивается диапазоном от 0.001 до 1.0 для численной стабильности.
Скорость звука нормализуется делением на референсное значение "V_ref", давая "Vi_norm" около единицы. Максимальная частота "f_max" вычисляется как отношение "Vi_norm к lambda", ограничиваясь диапазоном от 0.01 до 10.0. Индивидуальная частота "fi" определяется как произведение "f_max" на случайное число "beta" из диапазона от 0 до 1.
Обновление скорости выполняется для каждой координаты агента. Вычисляется нормализованное направление к лучшему решению как разность координат, делённая на диапазон. Импульс "V_impulse" рассчитывается на основе отклонения "Vi_norm" от единицы с добавлением случайного множителя. Новая скорость складывается из предыдущей скорости, произведения направления на частоту и диапазон с коэффициентом 0.1, и импульса, умноженного на диапазон. Скорость ограничивается по модулю значением 0.3 от диапазона координаты. Позиция агента обновляется добавлением вектора скорости к текущим координатам.
Коэффициент поглощения "gammaAbsorption" вычисляется по упрощённой формуле: 0.1 плюс 0.4, умноженное на разность единицы и "lambda". Таким образом, агенты, находящиеся близко к лучшему решению, имеют больший коэффициент и чаще выполняют локальный поиск, тогда как удалённые агенты чаще участвуют в глобальном исследовании.
Генерируется случайное число, и если оно превышает "gammaAbsorption", выполняется фаза притяжения к более громким сверчкам. Для каждого другого агента "j" с лучшим значением целевой функции вычисляется нормализованное расстояние "r_ij". По формулам акустики рассчитываются мощность звука "Ps", уровень звукового давления "Lp", атмосферное поглощение "A_atm" и реальный уровень давления "R_Lp". Коэффициент притяжения "K_0" определяется через сигмоидную функцию от R_Lp, а итоговый коэффициент K_i учитывает экспоненциальное затухание с расстоянием. Позиция агента смещается в направлении агента "j" пропорционально K_i с добавлением случайного шума, масштабированного коэффициентом "alpha". Притяжение выполняется последовательно ко всем более громким агентам без прерывания цикла.
Если случайное число не превышает "gammaAbsorption", выполняется случайное блуждание вблизи лучшего решения. Новая позиция вычисляется как координаты лучшего решения "cB" плюс случайное отклонение, масштабированное произведением "alpha", коэффициента 0.2 и диапазона координаты. Скорость агента обнуляется. В завершение цикла по агентам координаты каждого агента приводятся к допустимому диапазону и сетке дискретизации функцией "SeInDiSp".
//———————————————————————————————————————————————————————————————————— void C_AO_CA_Cricket::Moving () { //------------------------------------------------------------------ if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); vel [i].v [c] = 0.0; } } revision = true; return; } //------------------------------------------------------------------ currentEpoch++; alpha = alpha0 *pow (0.95, currentEpoch); if (alpha < 0.01) alpha = 0.01; //================================================================== for (int i = 0; i < popSize; i++) { //================================================================ // N_i ∈ [0, 120] //================================================================ double Ni = u.RNDfromCI (0.0, 120.0); //================================================================ // eq. 3: T_C = 10 + (N - 40) / 7 //================================================================ double T_C = 10.0 + (Ni - 40.0) / 7.0; //================================================================ // eq. 4: V = 20.1 * sqrt(273 + C) //================================================================ double Vi = 20.1 * MathSqrt (273.0 + T_C); //================================================================ // λ — НОРМАЛИЗОВАННОЕ расстояние до лучшего [0, 1] //================================================================ double lambda_raw = 0.0; for (int c = 0; c < coords; c++) { double diff = a [i].c [c] - cB [c]; lambda_raw += diff * diff; } lambda_raw = MathSqrt (lambda_raw); // Нормализация к [0, 1] double lambda = lambda_raw / maxDiagonal; if (lambda < 0.001) lambda = 0.001; if (lambda > 1.0) lambda = 1.0; //================================================================ // eq. 5: f = V / λ // Нормализуем Vi относительно V_ref, получаем f ∈ [0, ~2] //================================================================ double Vi_norm = Vi / V_ref; // ≈ [0.98, 1.02] double f_max = Vi_norm / lambda; // Теперь разумные значения // Ограничиваем f_max для стабильности if (f_max > 10.0) f_max = 10.0; if (f_max < 0.01) f_max = 0.01; //================================================================ // eq. 11: f_i = f_min + (f_max - f_min) * β //================================================================ double beta = u.RNDprobab (); double f_min = 0.0; double fi = f_min + (f_max - f_min) * beta; //================================================================ // eq. 12: v_i = v_i + (x* - x_i) * f_i + V_i (нормализованное) //================================================================ for (int c = 0; c < coords; c++) { double rangeC = rangeMax [c] - rangeMin [c]; // Нормализованное направление double diff_to_best = (cB [c] - a [i].c [c]) / rangeC; // V_i как нормализованный импульс double V_impulse = (Vi_norm - 1.0) * 0.1 * u.RNDfromCI (-1.0, 1.0); // eq. 12: v = v + direction * f + V vel [i].v [c] = vel [i].v [c] + diff_to_best * fi * rangeC * 0.1 + V_impulse * rangeC; // Ограничение скорости double maxVel = rangeC * 0.3; vel [i].v [c] = MathMax (-maxVel, MathMin (maxVel, vel [i].v [c])); } //================================================================ // eq. 13: x_i = x_i + v_i //================================================================ for (int c = 0; c < coords; c++) { a [i].c [c] = a [i].c [c] + vel [i].v [c]; } //================================================================ // γ — нормализованный коэффициент поглощения // Используем упрощённую формулу для получения γ ∈ [0.1, 0.5] //================================================================ // Чем ближе к лучшему (малое lambda) → больше γ → больше local search // Чем дальше (большое lambda) → меньше γ → больше global search double gammaAbsorption = 0.1 + 0.4 * (1.0 - lambda); //================================================================ // if rand[0,1] > γ //================================================================ double rnd = u.RNDprobab (); if (rnd > gammaAbsorption) { //-------------------------------------------------------------- // FIREFLY ФАЗА: притяжение к более громким //-------------------------------------------------------------- for (int j = 0; j < popSize; j++) { if (j != i && a [j].f > a [i].f) { //---------------------------------------------------------- // r_ij — НОРМАЛИЗОВАННОЕ расстояние [0, 1] //---------------------------------------------------------- double r_ij_raw = 0.0; for (int c = 0; c < coords; c++) { double diff = a [i].c [c] - a [j].c [c]; r_ij_raw += diff * diff; } r_ij_raw = MathSqrt (r_ij_raw); double r_ij = r_ij_raw / maxDiagonal; if (r_ij < 0.001) r_ij = 0.001; //---------------------------------------------------------- // eq. 7: Ps = I * 4πr² (нормализованное) //---------------------------------------------------------- double I_j = 1.0; // Нормализованная интенсивность double Ps = I_j * 4.0 * pi * r_ij * r_ij; //---------------------------------------------------------- // eq. 8: Lp = Lw + 10*log[Q / (4πr²)] //---------------------------------------------------------- double Lw = 10.0 * MathLog10 (Ps + 1e-10); double Lp = Lw + 10.0 * MathLog10 (Q / (4.0 * pi * r_ij * r_ij + 1e-10)); //---------------------------------------------------------- // eq. 9: A_atm = 7.4 * (f²r / Ø) * 10⁻⁸ // Для нормализованных значений масштабируем //---------------------------------------------------------- double A_atm = 7.4 * (fi * fi * r_ij / humidity) * 0.01; //---------------------------------------------------------- // eq. 10: R_Lp = Lp - A_atm //---------------------------------------------------------- double R_Lp = Lp - A_atm; //---------------------------------------------------------- // eq. 15, 16: K = K_0 * exp(-γ * r²) //---------------------------------------------------------- double K_0 = 1.0 / (1.0 + MathExp (-R_Lp / 5.0)); double K_i = K_0 * MathExp (-gammaFirefly * r_ij * r_ij); //---------------------------------------------------------- // eq. 17: x_i = x_i + K * direction + α * ε //---------------------------------------------------------- for (int c = 0; c < coords; c++) { double rangeC = rangeMax [c] - rangeMin [c]; double direction = a [j].c [c] - a [i].c [c]; double attraction = K_i * direction; double epsilon = u.RNDfromCI (-0.5, 0.5); double noise = alpha * rangeC * epsilon; a [i].c [c] = a [i].c [c] + attraction + noise; } // Нет break — притяжение ко всем более громким } } } else { //-------------------------------------------------------------- // eq. 14: random walk // x_i = x_best + ε * scale // // Масштаб зависит от alpha (уменьшается со временем) //-------------------------------------------------------------- for (int c = 0; c < coords; c++) { double rangeC = rangeMax [c] - rangeMin [c]; double eps = u.RNDfromCI (-1.0, 1.0); // Адаптивный масштаб: больше в начале, меньше в конце double scale = alpha * 0.2; // 0.1 в начале, уменьшается a [i].c [c] = cB [c] + eps * scale * rangeC; vel [i].v [c] = 0.0; } } //================================================================ // Ограничение координат и приведение к шагу //================================================================ for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" выполняет обновление лучшего найденного решения на основе результатов вычисления целевой функции для всех агентов. Метод вызывается после "Moving" и после внешнего вычисления значений целевой функции для новых позиций агентов.
Метод начинается с инициализации переменных для поиска лучшего агента: "bestIdx" устанавливается в 0, "bestFit" получает значение целевой функции первого агента. Далее выполняется проход по всем агентам начиная со второго. Если значение целевой функции текущего агента превышает "bestFit", обновляются обе переменные: "bestFit" получает новое лучшее значение, "bestIdx" — индекс агента.
После определения лучшего агента в текущей популяции выполняется сравнение с глобальным лучшим решением "fB". Если найденное значение "bestFit" превосходит "fB", глобальное лучшее обновляется. Таким образом, метод "Revision" обеспечивает сохранение лучшего найденного решения на протяжении всего процесса оптимизации.
//———————————————————————————————————————————————————————————————————— void C_AO_CA_Cricket::Revision () { int bestIdx = 0; double bestFit = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f > bestFit) { bestFit = a [i].f; bestIdx = i; } } if (bestFit > fB) { fB = bestFit; ArrayCopy (cB, a [bestIdx].c, 0, 0, coords); } } //————————————————————————————————————————————————————————————————————
Результаты тестов
По результатам тестирования на стандартном наборе тестовых функций алгоритм продемонстрировал относительно скромную производительность, набрав около 34% от максимально возможного результата в рейтинговой таблице алгоритмов оптимизации. Данный показатель позиционирует алгоритм сверчков в нижней части списка рассмотренных метаэвристик, что указывает на необходимость дополнительной работы по его настройке и модификации.
=============================
5 Hilly's; Func runs: 10000; result: 0.5836480537501225
25 Hilly's; Func runs: 10000; result: 0.4394651273931123
500 Hilly's; Func runs: 10000; result: 0.3106533980628491
=============================
5 Forest's; Func runs: 10000; result: 0.5352980150573591
25 Forest's; Func runs: 10000; result: 0.3114351845482898
500 Forest's; Func runs: 10000; result: 0.18345680555353047
=============================
5 Megacity's; Func runs: 10000; result: 0.40307692307692317
25 Megacity's; Func runs: 10000; result: 0.19846153846153847
500 Megacity's; Func runs: 10000; result: 0.11247692307692414
=============================
All score: 3.07797 (34.20%)
Визуализация работы алгоритма на наших тестовых функциях и пример работы на стандартных тестовых функциях.

CA_Cricket на тестовой функции Hilly

CA_Cricket на тестовой функции Forest

CA_Cricket на тестовой функции Megacity

CA_Cricket на тестовой функции Rastrigin

CA_Cricket на тестовой функции Paraboloid
По результатам тестирования, алгоритм CA-Cricket, представлен в рейтинговой таблице лучших популяционных методов оптимизации только ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 5 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 6 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 7 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 8 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | BO | bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| 26 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 27 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 28 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 29 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 30 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 31 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 32 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 33 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 34 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 35 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 36 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 37 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 38 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 39 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 40 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 41 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 42 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 43 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 44 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 45 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| CA_Cricket | cricket_algorithm | 0,58364 | 0,43946 | 0,31065 | 1,33375 | 0,53529 | 0,31143 | 0,18346 | 1,03018 | 0,40307 | 0,19846 | 0,11247 | 0,71400 | 3,078 | 34,20 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Наблюдение за динамикой работы алгоритма позволяет отметить его своеобразный характер исследования пространства поиска. Сочетание bat-подобного механизма обновления скорости с firefly-подобным притяжением создаёт интересную картину движения популяции, где агенты одновременно стремятся к глобальному лучшему решению и притягиваются к локально лучшим соседям. Физические формулы распространения звука добавляют дополнительный уровень сложности взаимодействиям, хотя их влияние на итоговую производительность требует более детального исследования.
Полученные результаты свидетельствуют о том, что алгоритм сверчков в его текущей реализации нуждается в дополнительной настройке для достижения конкурентоспособных показателей. Потенциальные направления улучшения включают корректировку коэффициентов в формулах обновления скорости и позиции, модификацию механизма вычисления коэффициента поглощения для более сбалансированного переключения между глобальным исследованием и локальной эксплуатацией, а также возможный пересмотр логики притяжения к множественным источникам. Представляется перспективным исследование влияния отдельных компонентов алгоритма на его производительность с целью выявления наиболее значимых факторов и их оптимальной настройки.
Несмотря на текущие ограничения в производительности, алгоритм сверчков представляет интерес как пример интеграции физических законов акустики в метаэвристический метод оптимизации. Уникальное сочетание закона Долбира, формул распространения и поглощения звука с классическими механизмами роевого интеллекта создаёт концептуально богатый алгоритм, потенциал которого может быть раскрыт при надлежащей калибровке параметров и возможной модификации отдельных формул. Дальнейшие исследования могут быть направлены на выявление оптимальных значений параметров для различных классов задач, а также на разработку адаптивных механизмов настройки, учитывающих характеристики конкретной оптимизационной задачи.
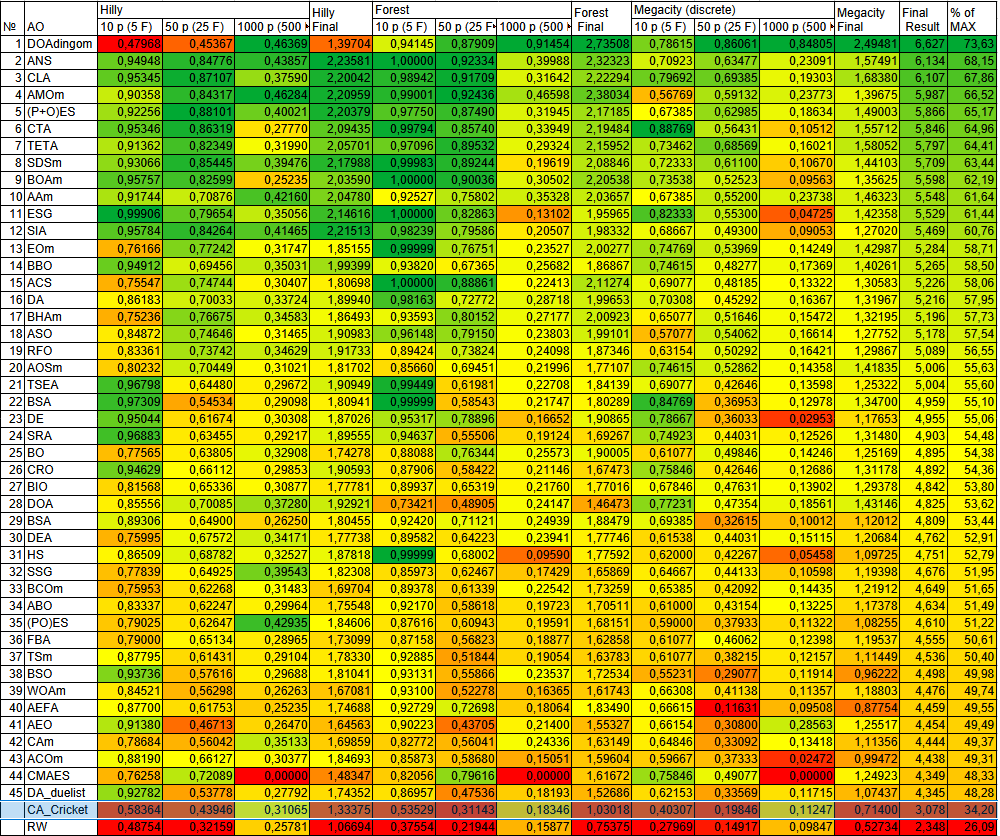
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
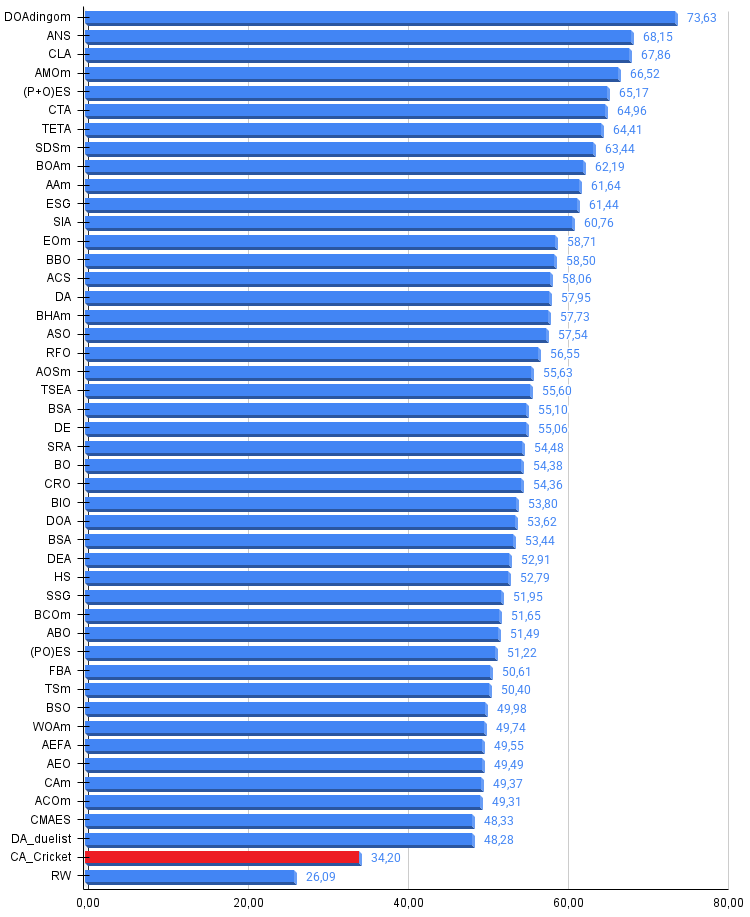
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма CA_Cricket:
Плюсы:
- Лучше себя показывает на функциях средней и большой размерностей.
Минусы:
- Недостаточно хорошо справляется с функциями малой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_CA_Cricket.mq5 | Скрипт | Испытательный стенд для CA_Cricket |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Асинхронная обработка событий в потоковых моделях (Основные компоненты)
Нейросети в трейдинге: Асинхронная обработка событий в потоковых моделях (Основные компоненты)
 Нейросети в трейдинге: Асинхронная обработка событий в потоковых моделях (EVA-Flow)
Нейросети в трейдинге: Асинхронная обработка событий в потоковых моделях (EVA-Flow)
 Забытая классика объёма: индикатор "Finite Volume Elements" для современных рынков
Забытая классика объёма: индикатор "Finite Volume Elements" для современных рынков
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
