MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português
preview
Популяционные алгоритмы оптимизации: Алгоритмы эволюционных стратегий (Evolution Strategies, (μ,λ)-ES и (μ+λ)-ES)

Популяционные алгоритмы оптимизации: Алгоритмы эволюционных стратегий (Evolution Strategies, (μ,λ)-ES и (μ+λ)-ES)

MetaTrader 5 — Примеры | 21 декабря 2023, 12:11
1 394 2
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Замена тестовой функции
4. Результаты тестов
5. Выводы


1. Введение

Алгоритмы эволюционных стратегий (Evolution Strategies) являются методами оптимизации, основанными на принципах, наблюдаемых в природе. Они имитируют процесс естественного отбора, где лучшие решения выживают и передают свои характеристики следующему поколению. Эти алгоритмы широко применяются в решении задач оптимизации, особенно в областях машинного обучения и искусственного интеллекта и были разработаны в 1960-х годах профессором Инго Рейхертом (Ingo Rechenberg) и его коллегами в Германии для решения оптимизационных задач в промышленности и технике.

Основная идея эволюционных стратегий заключается в создании популяции решений и их последующем улучшении с помощью операторов мутации и селекции, аналогичных тем, которые используются в естественной эволюции. Эволюционные стратегии используют вещественные векторы для представления решений. Это позволяет более гибко и точно описывать пространство решений и искать оптимальные значения, в отличие от классического генетического алгоритма, который оперирует бинарными строками.

Существует несколько различных вариантов эволюционных стратегий, которые отличаются способом генерации и обработки популяции, а также используемыми операторами мутации и селекции. Некоторые из наиболее распространенных вариантов включают:

  1. (1+1)-ES: В этом варианте создается только один потомок для каждого родителя, и лучшее решение из двух становится родителем для следующего поколения. Этот простой и быстрый метод может быть эффективным для некоторых задач, но менее эффективным при оптимизации сложных задач. Алгоритм (1+1)-ES был создан в 1960-х годах и является одним из простейших методов оптимизации через эволюционные стратегии. Он заключается в генерации случайного вектора, который затем изменяется на случайный шаг. Если измененный вектор оказывается лучше, он заменяет исходный, иначе исходный вектор остается неизменным. Этот процесс повторяется до достижения оптимума.
  1. (μ,λ)-ES: В этом алгоритме создается популяция родителей размера μ, которые порождают λ потомков, и лучшие потомки заменяют родителей. Может быть эффективным для различных задач оптимизации. Алгоритм (μ,λ)-ES был создан Райнхардом Шпайгельманном в 1965 году. После оценки потомков оставляются только лучшие μ решений, которые становятся родителями для следующего поколения, таким образом родители полностью заменяются потомками на каждой эпохе.
  1. (μ+λ)-ES: В этом варианте создается λ потомков, лучшие из них совместно с родителями участвуют в создании следующего поколения. В этом методе, родители и потомки конкурируют между собой, что является важным отличием от (μ,λ)-ES. Алгоритм (μ+λ)-ES был создан в 1970-х годах Йоханнесом Райхенбахером и Ханс-Паулем Швефелем и является методом оптимизации через эволюционные стратегии. Этот метод позволяет более полно исследовать пространство решений и может быть более эффективным для сложных задач.

Существуют и другие варианты эволюционных стратегий, но в данной статье мы рассмотрим только (μ,λ)-ES и (μ+λ)-ES. Вариант (1+1)-ES является простым и не подходит для решения многомерных задач. В связи с трудностями в использовании букв греческого алфавита и специальных символов в названиях файлов и имён переменных в коде, в дальнейшем мы будем использовать написание PO и P_O соответственно, где P - parents (родители) и O - offsprings (отпрыски, потомки).

Эволюционные стратегии в компьютерных науках позволяют моделировать процессы эволюции и естественного отбора для решения сложных задач оптимизации. Они используют принципы, аналогичные естественному отбору, чтобы искать оптимальные решения в пространстве параметров.

Эти алгоритмы могут быть особенно полезны в задачах, где нет явного аналитического решения или когда пространство поиска очень большое. Они могут эффективно искать оптимальные решения, применяя операции, вдохновленные эволюцией, такие как скрещивание, мутации и селекция.

Важно отметить, что название "Эволюционные стратегии" может ввести в заблуждение, что это общее название для класса эволюционных алгоритмов. Однако это не так. Фактически, это конкретная группа алгоритмов, которые используют идеи эволюции для решения задач оптимизации.


2. Описание алгоритма

(μ,λ)-ES означает, что на каждой итерации алгоритма выбирается μ родителей и генерируется λ потомков. Затем из λ потомков выбираются лучшие μ, которые становятся родителями для следующей итерации. Таким образом, в (μ,λ)-ES новые потомки полностью заменяют родителей и участвуют в создании следующего поколения.

(μ+λ)-ES работает похожим образом, но вместо того, чтобы выбирать лучших потомков из λ, они объединяются с родителями, чтобы образовать новую популяцию размером μ+λ. Затем из этой комбинированной популяции выбираются лучшие μ особей, которые становятся родителями для следующей итерации. Таким образом, в (μ+λ)-ES новые потомки работают вместе с родителями для формирования следующей популяции и конкурируют между собой.

Основное отличие между (μ,λ)-ES и (μ+λ)-ES заключается в том, как новые потомки конкурируют с родителями за место в следующей популяции. В (μ,λ)-ES новые потомки конкурируют с родителями за ограниченное количество мест, что может привести к преждевременной сходимости к локальному оптимуму. В (μ+λ)-ES новые потомки работают вместе с родителями, что приводит к более широкому исследованию пространства решений.

Оба алгоритма эволюционной стратегии основаны на комбинации генетических операторов: мутации и селекции. На каждой итерации алгоритма выбирается особь из текущей популяции и к ней применяется оператор мутации, после чего вычисляются приспособленности для полученной особи, и наиболее приспособленная из них помещается в следующую популяцию. Для генерации начальной популяции задается интервал для каждой компоненты вектора варьируемых параметров, а начальные значения компонентов полагаются равномерно распределенными в указанном интервале. Алгоритм может использовать различные условия останова, такие как достижение заданного числа поколений, определенного состояния популяции или заданного уровня сходимости. В случае (μ+λ) - алгоритма в популяцию включаются все особи, а в случае (μ,λ) - алгоритма - только потомки. Для (μ+λ) - алгоритма доказана сходимость по вероятности, а для (μ,λ) - алгоритма вопрос о сходимости остается открытым.

Сравнение (μ+λ) - алгоритма и (μ,λ) - алгоритма показывает, что (μ+λ) - алгоритм более экономичен в использовании высокоприспособленных особей, оставляя их для конкуренции с потомками. Это повышает интенсивность поиска, но может привести к преждевременной сходимости к локальному экстремуму. Оператор мутации в каноническом алгоритме эволюционной стратегии является единственным эволюционным оператором и использует алгоритм гауссовой мутации.

Классический алгоритм (μ,λ)-ES может быть описан следующим псевдокодом:

1. Инициализировать начальную популяцию случайными особями.
2. Повторять до достижения критерия остановки:
2.1. Каждый из μ родителей порождает λ потомков в текущую популяцию используя оператор мутации.
2.2. Выбрать лучшие μ потомков для формирования следующей популяции.
3. Вернуть лучшую особь из последней популяции.

Классический алгоритм (μ+λ)-ES может быть описан следующим псевдокодом::

1. Инициализировать начальную популяцию случайными особями.
2. Повторять до достижения критерия остановки:
2.1. Каждый из μ родителей порождает λ потомков в текущую популяцию используя оператор мутации.
2.2. Объединить родителей и потомков, чтобы получить комбинированную популяцию размером μ+λ.
2.3. Выбрать лучшие μ особей из комбинированной популяции для формирования следующей популяции.
3. Вернуть лучшую особь из последней популяции.

Выше мы рассмотрели классические варианты двух основных алгоритмов "Эволюционных стратегий". В обоих случаях родители порождают λ-потомков, используя только свою генетическую информацию. Это приводит к звездообразному ветвлению, где каждый потомок развивается независимо от других. Обмен информацией между родителями также отсутствует, что исключает возможность комбинирования их генетических свойств. В итоге комбинаторные качества полностью отсутствуют.

Результаты тестирования показали, что оба этих варианта ES имеют низкую эффективность, для повышения которой мной предпринята попытка использовать рекомбинацию.

Рекомбинация позволяет комбинировать генетический материал разных особей и создавать новые комбинации, которые могут иметь лучшие свойства или признаки. Этот процесс способствует разнообразию в популяции.

Рекомбинация (или скрещивание) — это процесс комбинирования генетического материала родительских особей для создания потомка. Этот процесс имитирует естественное скрещивание в биологической эволюции. Во время рекомбинации гены родителей сочетаются, чтобы создать новый генетический материал для потомка. Рекомбинация обычно осуществляется на уровне генов или генетических признаков. Гены представляют собой участки информации в геноме, которые кодируют определенные свойства или характеристики организма.

После рекомбинации гены потомка будут изменены с помощью оператора мутации, который вносит случайные изменения в гены. Это помогает введению новых вариантов исследования в популяцию и способствует разнообразию в генетическом материале.

Поэтому для каждого гена потомка будем использовать гены случайно выбранных родителей, где ген - соответствующая координата родителя. Таким образом потомки будут наследовать признаки всех родителей в популяции.


Алгоритм (μ,λ)-ES.

Переходим к рассмотрению кода и начнем с более простого алгоритма (μ,λ)-ES, модифицированного добавлением рекомбинации (наследование генов от множества родителей).

Для родителя и потомка, выступающих в роли агента, хорошо подойдет структура S_Agent, которая содержит массив координат "c" и переменную "f" - значение приспособленности. Функция "Init" инициализирует агента, изменяя размер массива "c" и устанавливая значение "f" в "-DBL_MAX" (наихудшее из возможных значений приспособленности).

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }

  double c []; //coordinates
  double f;    //fitness
};
//——————————————————————————————————————————————————————————————————————————————

Для описания алгоритма (μ,λ)-ES объявим класс C_AO_POES,

Класс содержит следующие элементы:
  • Публичные переменные "cB", "fB", "a", "rangeMax", "rangeMin", "rangeStep": эти переменные используются для хранения лучшей координаты, соответствующего значения функции приспособленности, агентов, максимальных и минимальных значений поиска и шага поиска соответственно.
  • Публичная "Init()": эта функция инициализирует алгоритм оптимизации. Она принимает несколько аргументов, таких как количество координат, размер популяции, количество родительских агентов, силу мутации и значение сигмы. Внутри функции происходит инициализация переменных и массивов, используемых в алгоритме.
  • Публичные функции "Moving()" и "Revision()": эти функции используются для выполнения движения агентов и ревизии популяции соответственно.
  • Приватные переменные "coords", "popSize", "parentsNumb", "mutationPower", "sigmaM", "revision": эти переменные используются для хранения количества координат, размера популяции, количества родительских агентов, силы мутации, значения сигмы и флага ревизии соответственно.
  • Приватные массивы "parents", "ind", "val", "pTemp": эти массивы используются для хранения информации о родительских агентах, индексов, значений и временных переменных соответственно.
  • Приватные функции GaussDistribution(), SeInDiSp(), RNDfromCI(), Scale(), Sorting(): эти функции используются для выполнения генерации случайных чисел, масштабирования значений и сортировки массивов.
//——————————————————————————————————————————————————————————————————————————————
class C_AO_POES
{
  //----------------------------------------------------------------------------
  public: double  cB [];  //best coordinates
  public: double  fB;     //FF of the best coordinates
  public: S_Agent a  [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,          //coordinates number
                     const int    popSizeP,         //population size
                     const int    parentsP,         //number of parents, < Population size
                     const double mutationPowerP,   //mutation power
                     const double sigmaP);          //sigma

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    parentsNumb;   //number of parents
  private: double mutationPower; //mutation power
  private: double sigmaM;
  private: bool   revision;

  private: S_Agent parents [];  //parents
  private: int     ind     [];
  private: double  val     [];
  private: S_Agent pTemp   [];

  private: double GaussDistribution   (const double In, const double outMin, const double outMax, const double sigma);
  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
  private: double Scale     (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
  private: void   Sorting   (S_Agent &p [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

Для инициализации алгоритма оптимизации служит функция "Init" класса C_AO_POES. Функция принимает несколько аргументов: количество координат, размер популяции, количество родительских агентов, силы мутации и значение сигмы.

Внутри функции происходит инициализация переменных и массивов, используемых в алгоритме. Функция выполняет следующие действия:

  • сброс генератора случайных чисел и установка значения переменной "fB" в "-DBL_MAX". 
  • установка значений переменных "coords", "popSize", "parentsNumb", "mutationPower" и "sigmaM". 
  • изменение размеров массивов "ind", "val", "pTemp", "a", "parents", "rangeMax", "rangeMin", "rangeStep" и "cB" с помощью функции "ArrayResize". 
  • массивы "a" и "parents" инициализируются с помощью функции "Init" класса "S_Agent", которая инициализирует координаты агента и устанавливает значение переменной "f" в "-DBL_MAX". 
//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Init (const int    coordsP,          //coordinates number
                      const int    popSizeP,         //population size
                      const int    parentsP,         //number of parents, < Population size
                      const double mutationPowerP,   //mutation power
                      const double sigmaP)           //sigma
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  parentsNumb   = parentsP;
  mutationPower = mutationPowerP;
  sigmaM        = sigmaP;

  ArrayResize (ind,   popSize);
  ArrayResize (val,   popSize);
  ArrayResize (pTemp, popSize);
  ArrayResize (a,     popSize);
  for (int i = 0; i < popSize; i++) a [i].Init (coords);

  ArrayResize (parents, parentsNumb);
  for (int i = 0; i < parentsNumb; i++) parents [i].Init (coords);

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Для перемещения агентов в пространстве поиска предназначен метод "Moving".

Функция содержит два блока кода, разделенных условием "if (!revision)".

  1. В первом блоке происходит генерация случайных координат для каждого агента в случае, если флаг ревизии "revision" равен "falsе". Для каждой координаты генерируется случайное число с равномерным распределением в диапазоне между "rangeMin" и "rangeMax", затем это число нормируется с помощью функции "SeInDiSp", которая устанавливает значение координаты в ближайшее значение, кратное "rangeStep".
  2. Во втором блоке происходит выполнение движения агентов в случае, если флаг ревизии "revision" равен "true". Для каждого агента выбирается случайный родительский агент из массива "parents". Затем для каждой координаты агента вычисляется значение мутации "dist", которое зависит от силы мутации "mutationPower" и диапазона поиска "rangeMin" и "rangeMax". Значение координаты агента изменяется с помощью функции "GaussDistribution", которая генерирует случайное число с нормальным распределением вокруг родительского значения координаты, используя значение сигмы "sigmaM". Затем значение координаты нормируется с помощью функции "SeInDiSp". 
//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Moving ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    for (int i = 0; i < popSize; i++)
    {
      for (int c = 0; c < coords; c++)
      {
        a [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
        a [i].c [c] = SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  int    indx = 0;
  double min  = 0.0;
  double max  = 0.0;
  double dist = 0.0;

  for (int i = 0; i < popSize; i++)
  {
    for (int c = 0; c < coords; c++)
    {
      indx = (int)RNDfromCI (0, parentsNumb);
      if (indx >= parentsNumb) indx = parentsNumb - 1;

      a [i].c [c] = parents [indx].c [c];

      dist = (rangeMax [c] - rangeMin [c]) * mutationPower;

      min = a [i].c [c] - dist; if (min < rangeMin [c]) min = rangeMin [c];
      max = a [i].c [c] + dist; if (max > rangeMax [c]) max = rangeMax [c];

      a [i].c [c] = GaussDistribution (a [i].c [c], min, max, sigmaM);
      a [i].c [c] = SeInDiSp  (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Ревизию популяции выполняет метод "Revision", который используется для ревизии текущего состояния агентов в алгоритме оптимизации.

Функция содержит два блока кода.

  1. В первом блоке происходит поиск лучшего агента в массиве "a" с помощью цикла "for". Если найден агент с более высоким значением приспособленности, чем текущий лучший агент "fB", то индекс этого агента сохраняется в переменной "indx". Затем значение "fB" и координаты "cB" текущего лучшего агента обновляются в соответствии с новым лучшим агентом.
  2. Во втором блоке происходит сортировка массива "a" по убыванию приспособленности с помощью функции "Sorting", а затем копирование "parentsNumb" лучших агентов из массива "a" в массив "parents".


Таким образом функция "Revision" позволяет обновлять текущее состояние агентов и сохранять лучших агентов в массиве "parents", где лучшие потомки полностью заменяют всех родителей.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_POES::Revision ()
{
  //----------------------------------------------------------------------------
  int indx = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB) indx = i;
  }

  if (indx != -1)
  {
    fB = a [indx].f;
    ArrayCopy (cB, a [indx].c, 0, 0, WHOLE_ARRAY);
  }

  //----------------------------------------------------------------------------
  Sorting (a, popSize);
  for (int i = 0; i < parentsNumb; i++)
  {
    parents [i] = a [i];
  }
}
//——————————————————————————————————————————————————————————————————————————————


Алгоритм (μ+λ)-ES.

Изменения начинаются с добавления продолжительности жизни особи в виде параметра "yearsNumber". Это позволит контролировать максимальный возраст в популяции и избежать "забивания" ее очень старыми особями, которые могут препятствовать изучению новых горизонтов бесконечного жизненного пространства и совершению новых открытий. Надеемся, это будет полезным в данном алгоритме.

Почему этого счетчика нет в алгоритме "(μ,λ)-ES?" - Потому что так было задумано: полностью заменять родителей потомками. Это также имеет смысл, как и в случае с семелогами в животном мире, когда некоторые виды размножаются только один раз в жизни. Примеры таких видов включают лососевых рыб, агавы, бамбук, крабов-кокосовых и цикад. Однако, в нашем алгоритме мы дадим возможность особям размножаться несколько раз, жить бесконечно долго или умереть, как гордый бамбук. Продолжительность жизни может быть регулируемым внешним параметром, и в рамках нашего тестирования была экспериментально найдена оптимальная продолжительность в 10 лет.

Кроме того, счетчик жизней может помочь избежать "переобучения" модели, когда популяция начинает "запоминать" и накапливать конкретные решения, а не находить новые удачные решения в других местах пространства поиска. Ограничение времени жизни особей позволяет сохранить разнообразие популяции и продолжать искать более оптимальные решения.

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
    yearsNumber = 0;
  }

  double c []; //coordinates
  double f;    //fitness
  int yearsNumber;
};
//——————————————————————————————————————————————————————————————————————————————

В методе "Init" мы увеличим размер родительской популяции на количество потомков, это позволит совместно сортировать родителей и потомков, хотя, как и в алгоритме (μ,λ)-ES, в последующем будет использоваться только μ - часть совместной популяции для генерации новых потомков. Если в предыдущем алгоритме количество родителей обязательно должно было быть меньше либо равно популяции потомков, то в этом алгоритме это не имеет значения и размер популяции родителей может быть задан любым, в том числе и очень большим, это никак не влияет на количество эпох. Экспериментально обнаружено, что оптимально при размере популяции 100 потомков (больше нельзя - уменьшается количество эпох) родительская популяция 150. Дальнейшее увеличение популяции родителей приводит к слишком большому разнообразию генофонда и алгоритм начинает хуже сходиться (это интересно само по себе).

ArrayResize (ind,   popSize + parentsNumb);
ArrayResize (val,   popSize + parentsNumb);
ArrayResize (pTemp, popSize + parentsNumb);
ArrayResize (a,     popSize);
for (int i = 0; i < popSize; i++) a [i].Init (coords);

ArrayResize (parents, popSize + parentsNumb);
for (int i = 0; i < popSize + parentsNumb; i++) parents [i].Init (coords);

В методе "Moving" при создании новых потомков устанавливаем счетчик лет особи равным 1.

a [i].yearsNumber = 1;

Изменения коснулись и метода "Revision", в котором учитывая изменения код выполняет следующее:

  • Увеличивает значение "yearsNumber" каждого родителя на 1.
  • Если значение "yearsNumber" превышает заданный предел (lifespan), то устанавливает значение приспособленности "f" для соответствующего родителя в "-DBL_MAX", что означает удаление особи из популяции.
  • Копирует новых потомков из массива "a" в массив родителей "parents".
  • Сортирует массив "parents" по значению приспособленности "f".
//----------------------------------------------------------------------------
for (int i = 0; i < parentsNumb; i++)
{
  parents [i].yearsNumber++;

  if (parents [i].yearsNumber > lifespan)
  {
    parents [i].f = - DBL_MAX;
  }
}

for (int i = parentsNumb; i < parentsNumb + popSize; i++)
{
  parents [i] = a [i - parentsNumb];
}

Sorting (parents, parentsNumb + popSize);



3. Замена тестовой функции

Ранее мы использовали функцию Rastrigin в качестве тестовой функции для оценки алгоритмов оптимизации. Однако, функция Rastrigin не является идеальным выбором для таких целей. Она обладает строгой периодичностью и сбалансированными минимумами и максимумами, что может быть относительно просто обнаружено некоторыми алгоритмами. Таким образом, в функции Rastrigin проявляются закономерности, которые могут повлиять на способность алгоритма определить экстремумы функции.

Для более надежного и объективного тестирования алгоритмов оптимизации рекомендуется использовать функции с разнообразными и непредсказуемыми свойствами. Такие функции обычно не обладают явными закономерностями или балансом между минимумами и максимумами. Примерами таких функций могут быть шумовые функции, функции с нелинейными зависимостями или функции с большим числом локальных экстремумов. Такой выбор функций позволяет более точно оценить способности алгоритмов к обнаружению и сходимости к глобальным оптимумам в различных условиях.

Условно все функции можно разделить на "простые" и "сложные". К простым функциям относятся те, большая часть поверхности которых находится выше средней линии между max и min, и чем больше площади поверхности лежит ближе к max, тем она проще для алгоритмов оптимизации. Так, если простым случайным образом разместить точки по всей поверхности в области определения функции, то мы получим ложное представление о "высоких" результатах оптимизации, поскольку результаты будут близки к абсолютному глобальному максимуму. Примером такой простой функции может послужить схематический рисунок гипотетической функции на рис.1.

false success

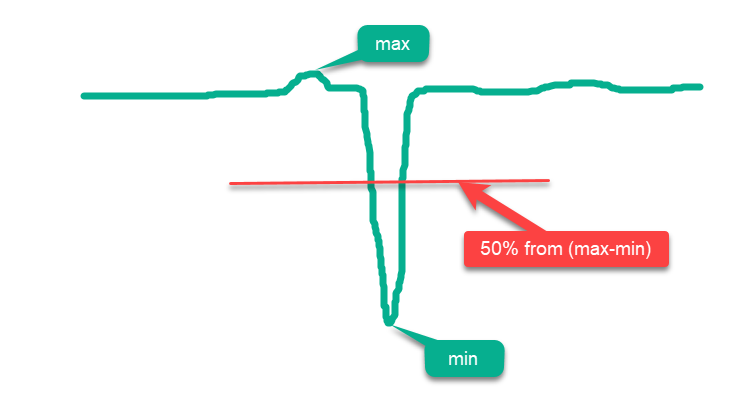
Рисунок 1. Пример "простой" функции для алгоритмов оптимизации.

Ввиду вышесказанного, функцию "Rastrigin" можно отнести к категории простых функций, которые могут вызывать завышенные результаты у некоторых алгоритмов оптимизации. Это связано с особенностями поисковой стратегии этих алгоритмов, которые могут размещать своих агентов рассредоточено по всей поверхности функции.

Особенно заметное влияние проявляется на функции "Rastrigin" с большим числом переменных, например, 1000. В то время как некоторые алгоритмы "честно" пытаются найти глобальный экстремум, другие могут просто размещать агентов равномерно по всей поверхности функции. Такой подход не говорит о способности алгоритма оптимизации к точному поиску, но вызывает лишь иллюзию способности делать это.

Функция "Rastrigin" была значительно изменена, чтобы создать более сложное и вызывающее трудности окружение для алгоритмов оптимизации. В новой версии функции были добавлены несколько "холмов" и "впадин", сохраняя при этом периодичность в той части поверхности, которая не помогает в поиске глобального экстремума. Эти изменения создают дополнительные препятствия, отвлекая агентов и выполняя роль "ловушек".

Теперь нельзя просто прыжками по ступенькам, имеющими периодичность, достичь глобального экстремума, как это было в классической версии "Rastrigin". Кроме того, глобальный оптимум был смещен от края, что затрудняет его поиск при наличии артефактов в алгоритмах, которые часто сосредоточены на границах определения функции.

Новая функция получила название "Hilly" (рис. 2) и, так же как "Forest" и "Megacity", относится к сложным тестовым функциям. У этих трех функций площадь поверхности, лежащей выше 50% от максимальной высоты, примерно одинакова и составляет около 20% от общей площади функции.

Функции "Hilly", "Forest" и "Megacity" представляют собой сложные и реалистичные сценарии оптимизации, которые могут помочь оценить производительность алгоритмов в сложных и разнообразных условиях. При использовании этих функций в качестве комплексного тестирования алгоритмов оптимизации можно получить более полное представление о их способности находить глобальные оптимумы и преодолевать локальные "ловушки".

Кроме того, в методику тестирования внесены изменения. Теперь проводится 10-кратное тестирование вместо 5-кратного (количество повторных запусков процесса оптимизации), для уменьшения случайных "выбросов" в результатах.


Hilly2

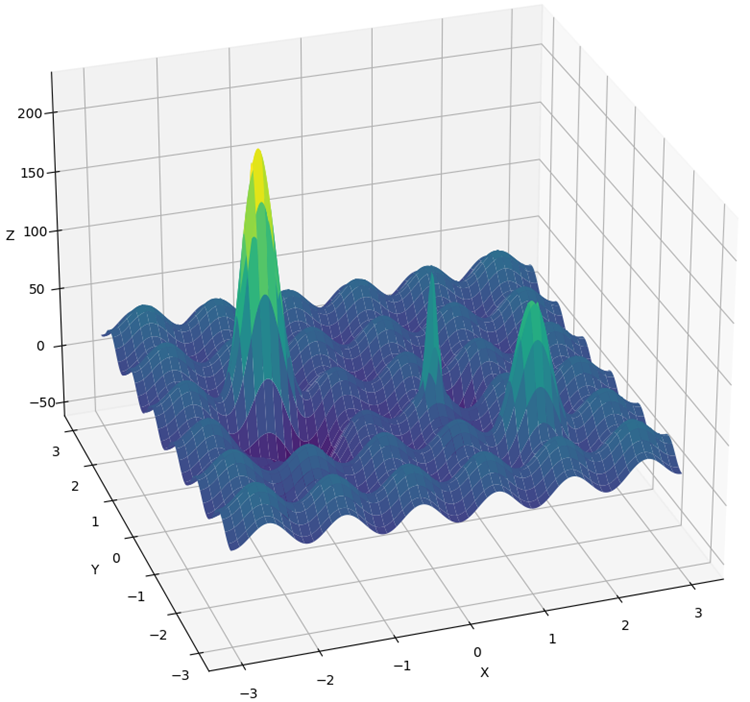
Рисунок 2. Тестовая функция "Hilly" (холмистый).

4. Результаты тестов

Распечатка работы алгоритма (μ,λ)-ES на тестовом стенде:

C_AO_(PO)ES:100:10:0.025:8.0
=============================
5 Hilly's; Func runs: 10000; result: 0.7902459324049909
25 Hilly's; Func runs: 10000; result: 0.6264667539839893
500 Hilly's; Func runs: 10000; result: 0.42934981087827656
=============================
5 Forest's; Func runs: 10000; result: 0.8761631782479373
25 Forest's; Func runs: 10000; result: 0.6094343681829253
500 Forest's; Func runs: 10000; result: 0.19591138782930953
=============================
5 Megacity's; Func runs: 10000; result: 0.5900000000000001
25 Megacity's; Func runs: 10000; result: 0.37933333333333336
500 Megacity's; Func runs: 10000; result: 0.11321666666666666
=============================
All score: 4.61012

Распечатка работы алгоритма (μ+λ)-ES на тестовом стенде:

C_AO_(P_O)ES:100:150:0.02:8.0:10
=============================
5 Hilly's; Func runs: 10000; result: 0.9993447297882565
25 Hilly's; Func runs: 10000; result: 0.9189524317647721
500 Hilly's; Func runs: 10000; result: 0.562968579605404
=============================
5 Forest's; Func runs: 10000; result: 1.0
25 Forest's; Func runs: 10000; result: 0.9352215748931851
500 Forest's; Func runs: 10000; result: 0.3917923122543615
=============================
5 Megacity's; Func runs: 10000; result: 0.8316666666666664
25 Megacity's; Func runs: 10000; result: 0.6443333333333332
500 Megacity's; Func runs: 10000; result: 0.21155000000000007
=============================
All score: 6.49583

Визуализация ниже приведена для алгоритма (μ+λ)-ES, который демонстрирует отличную проработку пространства поиска, не оставляя без внимания потенциально перспективные области.

Hilly

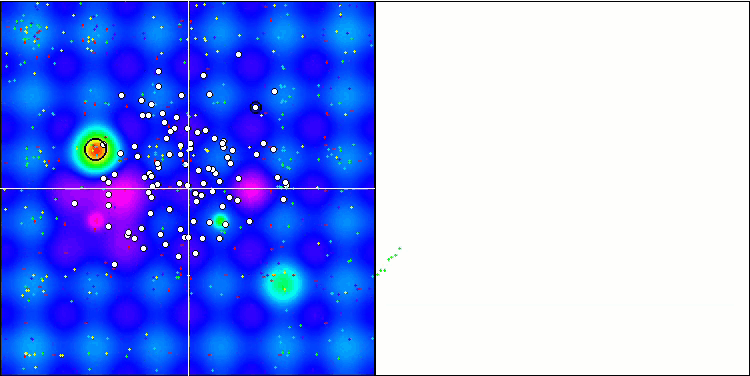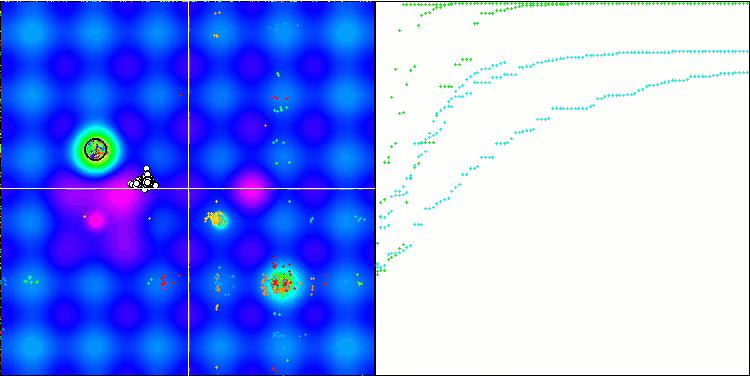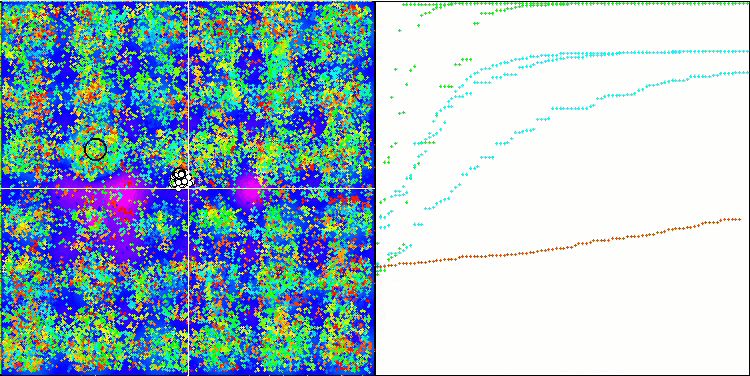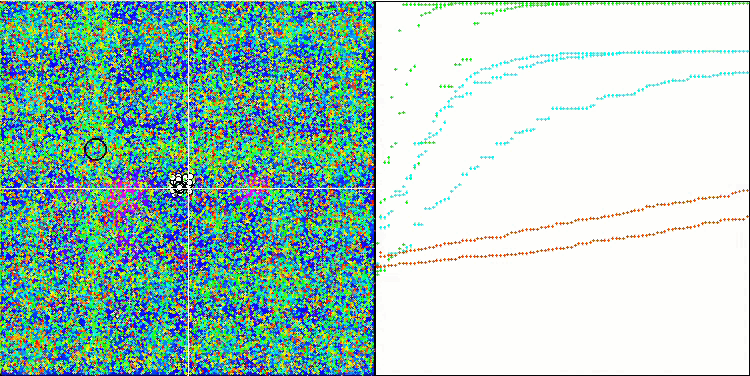
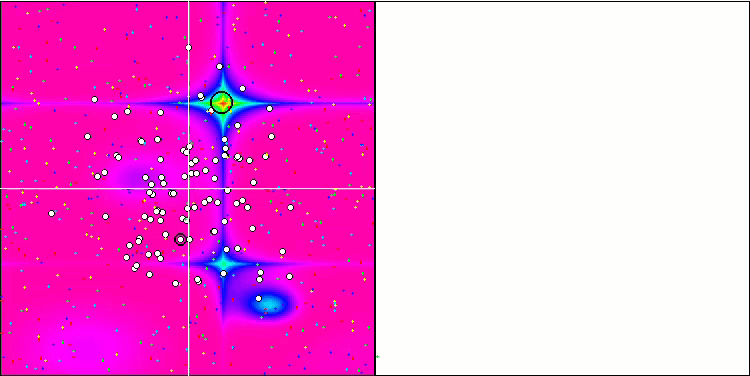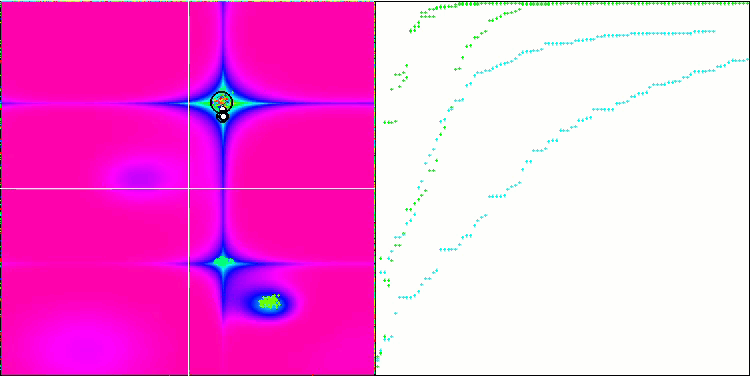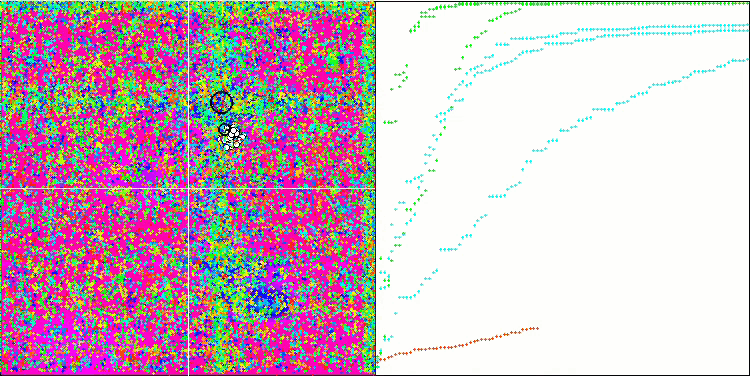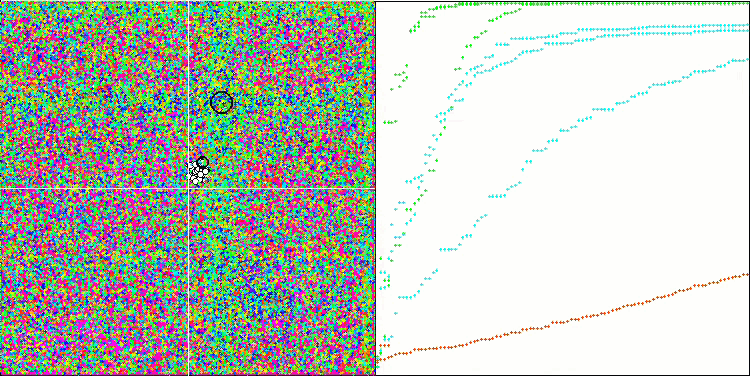
(μ+λ)-ES на тестовой функции Hilly.

Forest

  (μ+λ)-ES на тестовой функции Forest.

Megacity

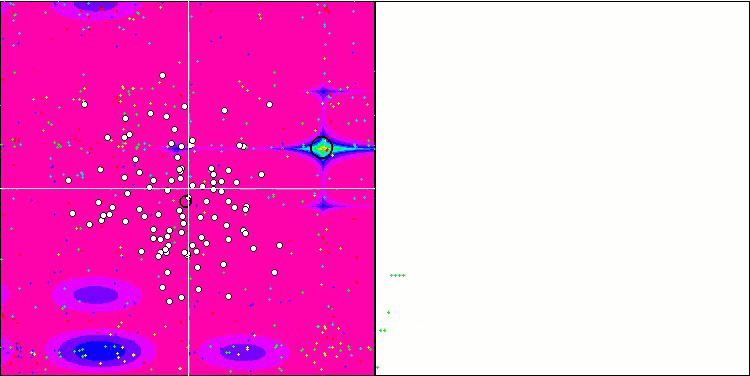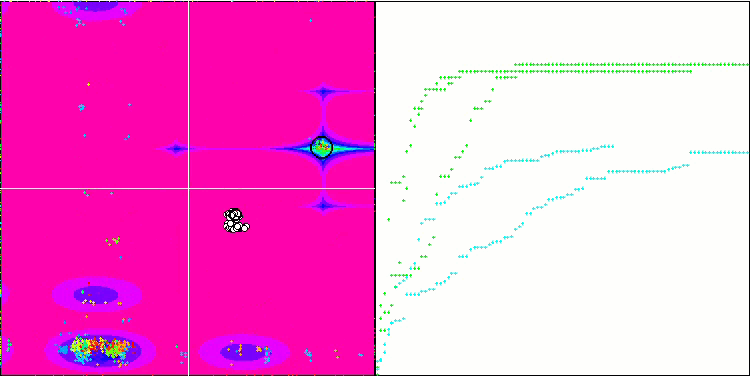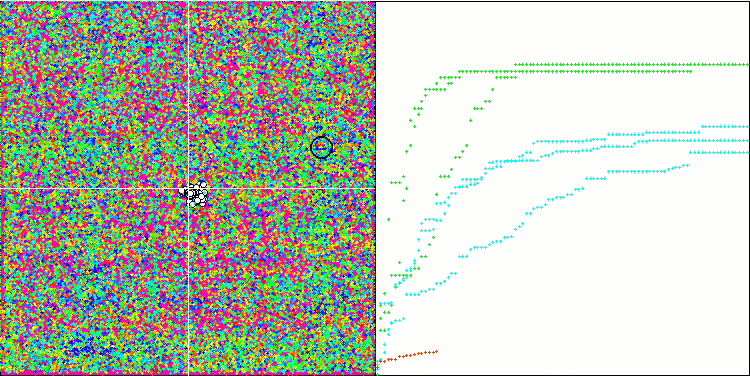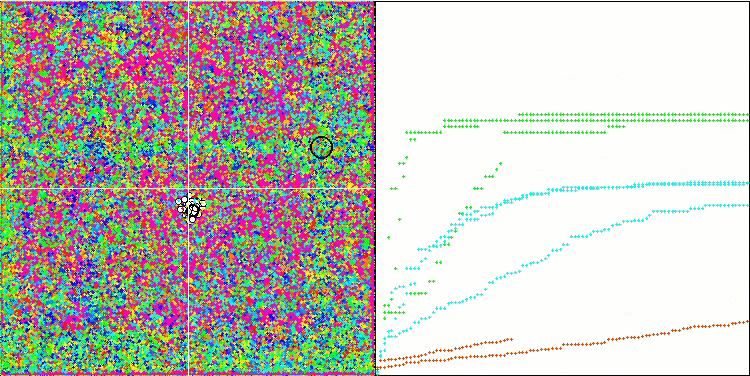
  (μ+λ)-ES на тестовой функции Megacity.


Было решено вернуться к абсолютным значениям результатов тестов и отказаться от относительных. Для этого были изменены тестовые функции таким образом, чтобы они возвращали значения в диапазоне от 0.0 до 1.0. Теперь, если результат равен 1.0, это означает 100% сходимость, а, например, результат 0.32527 означает 32.5% от глобального максимума тестовой функции. Таким образом, поскольку общее количество тестов составляет 9, теоретически алгоритмы могут показать максимально возможный суммарный результат по всем тестам не более 9.0 в случае 100% сходимости алгоритма на каждом тесте в столбце "Final result" таблицы. Дополнительно был добавлен столбец "% of MAX", показывающий процент от максимально возможного результата.


Теперь цифры результатов не будут изменяться при добавлении новых алгоритмов в таблицу, так как они представлены в абсолютных значениях.

Итак, переходим к результатам рассмотренных алгоритмов, прежде всего (μ+λ)-ES. Этот алгоритм действительно поразил меня своими феноменальными результатами: он набрал в общей сложности 72.18% от теоретически возможного результата. Чтобы убедиться в таких впечатляющих результатах, было проведено 20-кратное тестирование специально для этого алгоритма. И каждый из 20 запусков показал 100% сходимость на сложной функции "Forest" - это просто грандиозно! Кроме того, результаты на остальных функциях также были замечательными.

Теперь немного хороших слов о (μ,λ)-ES. Этот алгоритм продемонстрировал стабильные и хорошие результаты. В цветовой таблице он равномерно "зеленый", без резких изменений цвета.

№

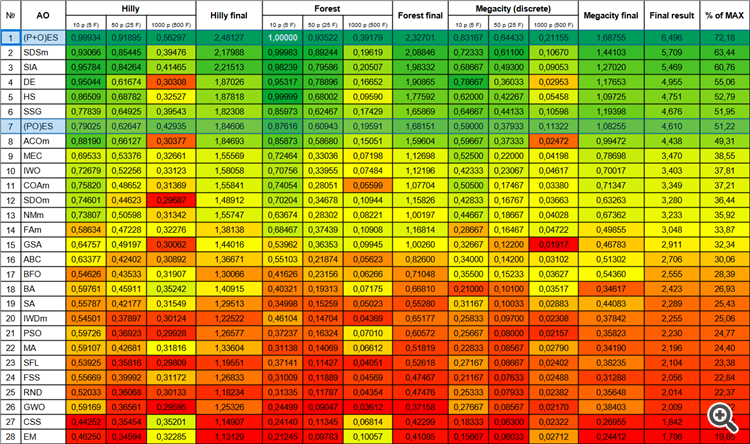
AO

Description

Hilly

Hilly final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

% of MAX

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

10 p (5 F)

50 p (25 F)

1000 p (500 F)

1

(P+O)ES

(P+O) evolution strategies

0,99934

0,91895

0,56297

2,48127

1,00000

0,93522

0,39179

2,32701

0,83167

0,64433

0,21155

1,68755

6,496

72,18

2

SDSm

stochastic diffusion search M

0,93066

0,85445

0,39476

2,17988

0,99983

0,89244

0,19619

2,08846

0,72333

0,61100

0,10670

1,44103

5,709

63,44

3

SIA

simulated isotropic annealing

0,95784

0,84264

0,41465

2,21513

0,98239

0,79586

0,20507

1,98332

0,68667

0,49300

0,09053

1,27020

5,469

60,76

4

DE

differential evolution

0,95044

0,61674

0,30308

1,87026

0,95317

0,78896

0,16652

1,90865

0,78667

0,36033

0,02953

1,17653

4,955

55,06

5

HS

harmony search

0,86509

0,68782

0,32527

1,87818

0,99999

0,68002

0,09590

1,77592

0,62000

0,42267

0,05458

1,09725

4,751

52,79

6

SSG

saplings sowing and growing

0,77839

0,64925

0,39543

1,82308

0,85973

0,62467

0,17429

1,65869

0,64667

0,44133

0,10598

1,19398

4,676

51,95

7

(PO)ES

(PO) evolution strategies

0,79025

0,62647

0,42935

1,84606

0,87616

0,60943

0,19591

1,68151

0,59000

0,37933

0,11322

1,08255

4,610

51,22

8

ACOm

ant colony optimization M

0,88190

0,66127

0,30377

1,84693

0,85873

0,58680

0,15051

1,59604

0,59667

0,37333

0,02472

0,99472

4,438

49,31

9

MEC

mind evolutionary computation

0,69533

0,53376

0,32661

1,55569

0,72464

0,33036

0,07198

1,12698

0,52500

0,22000

0,04198

0,78698

3,470

38,55

10

IWO

invasive weed optimization

0,72679

0,52256

0,33123

1,58058

0,70756

0,33955

0,07484

1,12196

0,42333

0,23067

0,04617

0,70017

3,403

37,81

11

COAm

cuckoo optimization algorithm M

0,75820

0,48652

0,31369

1,55841

0,74054

0,28051

0,05599

1,07704

0,50500

0,17467

0,03380

0,71347

3,349

37,21

12

SDOm

spiral dynamics optimization M

0,74601

0,44623

0,29687

1,48912

0,70204

0,34678

0,10944

1,15826

0,42833

0,16767

0,03663

0,63263

3,280

36,44

13

NMm

Nelder-Mead method M

0,73807

0,50598

0,31342

1,55747

0,63674

0,28302

0,08221

1,00197

0,44667

0,18667

0,04028

0,67362

3,233

35,92

14

FAm

firefly algorithm M

0,58634

0,47228

0,32276

1,38138

0,68467

0,37439

0,10908

1,16814

0,28667

0,16467

0,04722

0,49855

3,048

33,87

15

GSA

gravitational search algorithm

0,64757

0,49197

0,30062

1,44016

0,53962

0,36353

0,09945

1,00260

0,32667

0,12200

0,01917

0,46783

2,911

32,34

16

ABC

artificial bee colony

0,63377

0,42402

0,30892

1,36671

0,55103

0,21874

0,05623

0,82600

0,34000

0,14200

0,03102

0,51302

2,706

30,06

17

BFO

bacterial foraging optimization

0,54626

0,43533

0,31907

1,30066

0,41626

0,23156

0,06266

0,71048

0,35500

0,15233

0,03627

0,54360

2,555

28,39

18

BA

bat algorithm

0,59761

0,45911

0,35242

1,40915

0,40321

0,19313

0,07175

0,66810

0,21000

0,10100

0,03517

0,34617

2,423

26,93

19

SA

simulated annealing

0,55787

0,42177

0,31549

1,29513

0,34998

0,15259

0,05023

0,55280

0,31167

0,10033

0,02883

0,44083

2,289

25,43

20

IWDm

intelligent water drops M

0,54501

0,37897

0,30124

1,22522

0,46104

0,14704

0,04369

0,65177

0,25833

0,09700

0,02308

0,37842

2,255

25,06

21

PSO

particle swarm optimisation

0,59726

0,36923

0,29928

1,26577

0,37237

0,16324

0,07010

0,60572

0,25667

0,08000

0,02157

0,35823

2,230

24,77

22

MA

monkey algorithm

0,59107

0,42681

0,31816

1,33604

0,31138

0,14069

0,06612

0,51819

0,22833

0,08567

0,02790

0,34190

2,196

24,40

23

SFL

shuffled frog-leaping

0,53925

0,35816

0,29809

1,19551

0,37141

0,11427

0,04051

0,52618

0,27167

0,08667

0,02402

0,38235

2,104

23,38

24

FSS

fish school search

0,55669

0,39992

0,31172

1,26833

0,31009

0,11889

0,04569

0,47467

0,21167

0,07633

0,02488

0,31288

2,056

22,84

25

RND

random

0,52033

0,36068

0,30133

1,18234

0,31335

0,11787

0,04354

0,47476

0,25333

0,07933

0,02382

0,35648

2,014

22,37

26

GWO

grey wolf optimizer

0,59169

0,36561

0,29595

1,25326

0,24499

0,09047

0,03612

0,37158

0,27667

0,08567

0,02170

0,38403

2,009

22,32

27

CSS

charged system search

0,44252

0,35454

0,35201

1,14907

0,24140

0,11345

0,06814

0,42299

0,18333

0,06300

0,02322

0,26955

1,842

20,46

28

EM

electroMagnetism-like algorithm

0,46250

0,34594

0,32285

1,13129

0,21245

0,09783

0,10057

0,41085

0,15667

0,06033

0,02712

0,24412

1,786

19,85

rating table

Рисунок 3. Цветовая градация алгоритмов по соответствующим тестам.

chart

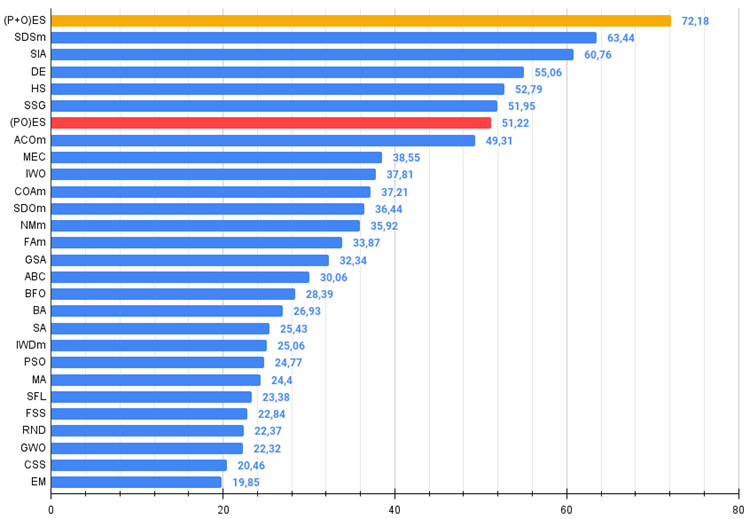
Рисунок 4. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы).


5. Выводы

Использование эволюционных стратегий открывает новые возможности в различных областях, включая оптимизацию параметров в машинном обучении, проектирование роботов и управление сложными системами. Они позволяют нам получить лучшие решения, основанные на биологических принципах эволюции.

У нас новый безусловный лидер в таблице на данный момент, опережающий ближайшего конкурента SDSm почти на 10%.


Плюсы и минусы алгоритма эволюционной стратегии (μ,λ)-ES:

Плюсы:
  1. Малое количество внешних параметров.
  2. Высокая эффективность при решении разнообразных задач.
  3. Легкость в реализации алгоритма.
  4. Устойчивость к застреванию.
  5. Высокие результаты как на гладких, так и на сложных дискретных функциях.
  6. Высокая сходимость.
Минусы:
  1. Большой разброс результатов на дискретных функциях.

Плюсы и минусы алгоритма эволюционной стратегии (μ+λ)-ES:

Плюсы:
  1. Малое количество внешних параметров.
  2. Высокая эффективность при решении разнообразных задач.
  3. Легкость в реализации алгоритма.
  4. Устойчивость к застреванию.
  5. Высокие результаты как на гладких, так и на сложных дискретных функциях.
  6. Высокая сходимость.
Минусы:
  1. Большой разброс результатов на дискретных функциях (хотя при этом это лучшие результаты на данный момент).

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

Прикрепленные файлы |
Загрузить ZIP
28_The_world_of_AO_ES.ZIP (1580.39 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (2)
fxsaber
fxsaber | 25 дек. 2023 в 17:17
Уж очень сильный рывок!
Andrey Dik
Andrey Dik | 25 дек. 2023 в 17:27
fxsaber #:
Уж очень сильный рывок!

Да, неожиданный рывок.

Можно было бы списать на то, что заменена одна из функций, но нет, с Растригином он так же лучший. Только что общая сложность тестов возросла и некоторые алгоритмы спустились вниз, а те что были в топе так и остались там.

Теория категорий в MQL5 (Часть 18): Квадрат естественности Теория категорий в MQL5 (Часть 18): Квадрат естественности
Статья продолжает серию о теории категорий, представляя естественные преобразования, которые являются ключевым элементом теории. Мы рассмотрим сложное на первый взгляд определение, затем углубимся в примеры и способы применения преобразований в прогнозировании волатильности.
Индикатор исторических позиций на графике в виде диаграммы их прибыли/убытка Индикатор исторических позиций на графике в виде диаграммы их прибыли/убытка
В статье рассмотрим вариант получения информации о закрытых позициях по истории их сделок. Создадим простой индикатор, отображающий в виде диаграммы приблизительный профит/убыток позиций на каждом баре.
Нейросети — это просто (Часть 69): Ограничение политики поведения на основе плотности офлайн данных (SPOT) Нейросети — это просто (Часть 69): Ограничение политики поведения на основе плотности офлайн данных (SPOT)
В оффлайн обучении мы используем фиксированный набор данных, что ограничивает покрытие разнообразия окружающей среды. В процессе обучения наш Агент может генерировать действия вне этого набора. При отсутствии обратной связи от окружающей среды корректность оценок таких действий вызывает вопросы. Поддержание политики Агента в пределах обучающей выборки становится важным аспектом для обеспечения надежности обучения. Об этом мы и поговорим в данной статье.
Тесты на перестановку Монте-Карло в MetaTrader 5 Тесты на перестановку Монте-Карло в MetaTrader 5
В статье рассматриваются тесты на перестановку на основе перетасованных тиковых данных на любом советнике исключительно силами MetaTrader 5.