
Алгоритм обратного поиска — Backtracking Search Algorithm (BSA)
Содержание
Введение
В бесконечном лабиринте возможностей, где каждый поворот может вести как к триумфу, так и к тупику, мудрый путешественник оставляет за собой невидимые следы — нечто эфемерное, но в то же время более надежное: память о пройденных путях. Эта древняя мудрость — оглянуться, чтобы увидеть будущее — легла в основу алгоритма оптимизации. Каждый шаг в неизведанное делается с оглядкой на опыт прошлого, где история становится компасом, а воспоминания — картой.
В данной статье рассмотрим алгоритм, который мне показался очень интересным, благодаря своей идее поиска. Backtracking Se arch Algorithm (BSA) — это новый эволюционный алгоритм (EA) для решения численных оптимизационных задач с действительными значениями, предложенный Pinar Civicioglu в 2013 году. Это метод поиска лучшего решения, который умеет "учиться на прошлом опыте".
Реализация алгоритма
BSA работает по принципу эволюционных алгоритмов, но имеет уникальные особенности, используя две популяции:- текущая популяция (P) — активно эволюционирующая популяция
- историческая популяция (oldP) — случайно выбранная популяция из прошлых поколений
BSA использует случайную стратегию мутации, которая выдает только одно направляющее решение для каждого целевого индивида. Формула мутации:
Mutant = P + F × (oldP - P)
где F — фактор амплитуды, контролирующий размер шага поиска.
Процесс кроссовера BSA включает два шага. Первая стратегия использует "mixrate". Вторая стратегия позволяет мутировать только одному случайно выбранному индивиду в каждой пробе. Представьте, что вы с друзьями (это наша популяция) ищете лучшую пиццерию в городе.
Начальная ситуация:
- у вас есть 10 друзей (размер популяции),
- каждый начинает поиск в случайном районе города,
- у каждого есть смартфон с картой прошлых походов (историческая память).
День 1: все разошлись по городу. Первый друг нашел пиццерию с рейтингом 7/10, второй друг нашел пиццерию с рейтингом 5/10, а третий нашел пиццерию с рейтингом 8/10...и так далее.
День 2: используем накопленный опыт.
Шаг 1: "вспоминаем прошлое" (Selection-I). Алгоритм: "Бросаем монетку!", если выпал орел, тогда "Запомним, где все были вчера" (обновляем историю), если выпала решка, "Используем старые воспоминания" (не обновляем), затем "Перемешаем воспоминания" (как колоду карт).
Шаг 2: "Идем по следам" (Mutation). Каждый друг думает: "Где я сейчас? (текущая позиция), а где я был раньше?" (историческая позиция). Тогда формула движения будет: Новое место = Текущее место + Случайный шаг × (Старое место - Текущее место). Например: первый друг сейчас на улице А., 10, его "призрак из прошлого" был на улице Б., 20, случайный шаг = 2. Новое место = А.,10 + 2 × (Б.,20 - А.,10) = движение в сторону улицы Б, но в 2 раза дальше!
"Корректируем маршрут" (Crossover). Алгоритм бросает монетку и выбирает стратегию. Стратегия А: "Частичное изменение". Первый друг планировал идти на какой-то адрес, но алгоритм говорит: "Измени только улицу, дом оставь, как был". Результат: хорошо, меняем улицу, а дом оставляем. Стратегия Б: "Минимальное изменение". Первый друг планировал идти на какой-то адрес, однако алгоритм говорит: "Оставайся на старом месте, но измени только номер дома". Результат: хорошо, меняем номер дома.
"Проверяем общий результат" (Selection-II). Друг 1 пришел в новое место:
- Если новая пиццерия лучше (рейтинг 9/10): "Отлично, остаюсь здесь!"
- Если хуже (рейтинг 4/10): "Нет, возвращаюсь!"
Рассмотрим иллюстрацию работы алгоритма на рисунке ниже.
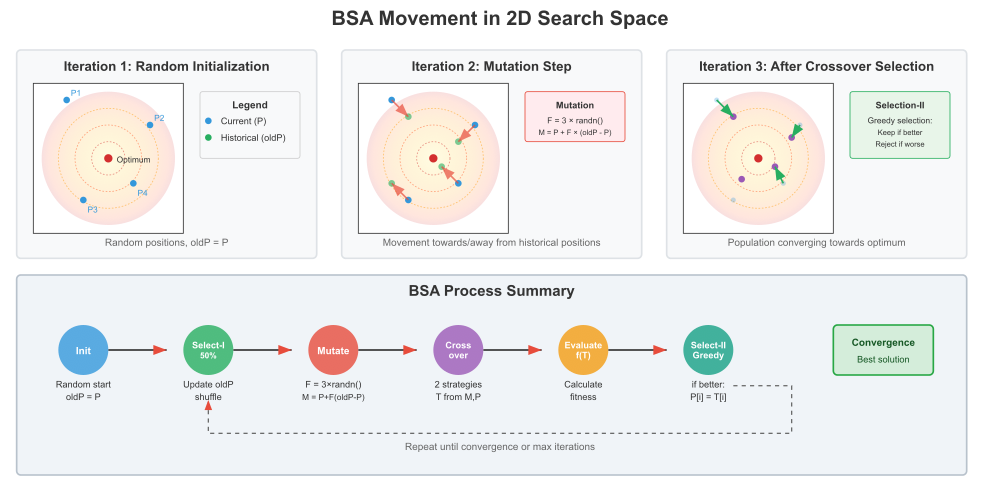
Рисунок 1. Иллюстрация работы фаз алгоритма BSA.
Эта иллюстрация показывает, как алгоритм BSA ищет оптимальное решение в двумерном пространстве. Представьте, что вы смотрите на топографическую карту сверху, где цель — найти самую высокую точку (красный центр).
Иллюстрация разделена на три панели, показывающие эволюцию поиска: Iteration 1 — Random Initialization. Квадратное поле поиска с контурными линиями (как на топографической карте), красная точка в центре — это глобальный оптимум (лучшее решение), 4 синие точки (P1, P2, P3, P4) — начальные случайные позиции "исследователей". Алгоритм случайно размещает 4 агента по пространству поиска, на этом этапе oldP = P (историческая популяция копирует текущую) и это стартовая точка поиска.
Iteration 2 - Mutation Step. Синие точки — текущие позиции агентов, зеленые полупрозрачные точки — позиции из исторической памяти (перемешанные), красные стрелки — направления движения при мутации.
Ключевые элементы: красные стрелки показывают формулу мутации в действии: M = P + F × (oldP - P). Каждый агент движется относительно своей "исторической пары". Некоторые стрелки направлены к историческим позициям, другие — от них (зависит от знака F). Формула в красной рамке: F = 3 × randn(); M = P + F × (oldP - P). Это ключевая формула мутации BSA.
Iteration 3 - After Crossover & Selection. Фиолетовые точки — новые позиции после кроссовера (Trial population), полупрозрачные синие точки — предыдущие позиции (для сравнения) и зеленые стрелки — показывают только улучшения (где новая позиция лучше старой). Кроссовер: алгоритм скомбинировал информацию из мутантной и текущей популяций. Жадный отбор оставил только те перемещения, которые улучшили решение. Популяция приблизилась к оптимуму (красному центру).
BSA Process Summary, полный цикл алгоритма в виде последовательности цветных кругов:- Init (синий) — случайный старт
- Select-I (зеленый) — обновление памяти с вероятностью 50%
- Mutate (красный) — применение формулы мутации
- Crossover (фиолетовый) — комбинирование решений
- Evaluate (оранжевый) — вычисление качества
- Select-II (бирюзовый) — жадный отбор лучших
Пунктирная стрелка показывает, что процесс повторяется до сходимости. Эта иллюстрация наглядно демонстрирует, почему BSA эффективен: он "помнит" где был раньше и использует эту информацию для более умного поиска, чем простое случайное блуждание.
Переходим к написанию псевдокод алгоритма BSA.
Подготовка к работе
Начальные параметры:
- Установить размер популяции
- Установить параметр кроссовера mixrate
- Создать пустые контейнеры для:
- текущей популяции
- исторической популяции
- мутантной популяции
- пробной популяции
- карт кроссовера для каждой особи
Инициализация:
- Разместить все особи исторической популяции случайным образом в пространстве поиска
- Учесть дискретизацию, если задан шаг
- Установить флаг "нужен отбор" в положение "нет"
Основной цикл алгоритма
ШАГ 1: Первый запуск
Если это первая итерация:
- Разместить текущую популяцию случайным образом
- Применить дискретизацию к координатам
- Пометить, что инициализация выполнена
- Выйти и дождаться вычисления приспособленности
ШАГ 2: Жадный отбор (если требуется)
Если флаг "нужен отбор" установлен:
- Для каждой особи сравнить:
- если новое решение хуже сохраненного → вернуть старые координаты и приспособленность
- если лучше → оставить новое
- Сбросить флаг отбора
ШАГ 3: Сохранение текущего состояния
Для каждой особи:
- Запомнить текущую приспособленность
- Сохранить копию текущих координат
ШАГ 4: Обновление исторической памяти (Selection-I)
- Бросить монетку (вероятность 50%)
- Если выпал "орел":
- скопировать всю текущую популяцию в историческую память
- сохранить их приспособленности
- Перемешать историческую популяцию, как колоду карт:
- идти от последней особи к первой
- для каждой выбрать случайную позицию для обмена
- поменять местами
ШАГ 5: Мутация
- Сгенерировать фактор движения F из нормального распределения
- среднее = 0, границы от -3 до +3
- типа бросок кости, но с колоколообразным распределением
- Для каждой особи и каждой координаты:
- Новая позиция = Текущая + F × (Историческая - Текущая)
- если F положительный → движение к исторической позиции
- если F отрицательный → движение от исторической позиции
ШАГ 6: Кроссовер
- Скопировать мутантную популяцию в пробную
- Бросить взвешенную монетку (40% / 60%)
Если выпало 40% (Стратегия 1):
Для каждой особи:
- определить сколько координат изменить (от 0 до всех, используя mixrate)
- случайно выбрать какие именно координаты
- для выбранных координат взять значения из текущей популяции
- остальные оставить из мутантной
Если выпало 60% (Стратегия 2):
Для каждой особи:
- выбрать только одну случайную координату
- заменить её значением из текущей популяции
- все остальные оставить из мутантной
ШАГ 7: Контроль границ
Для каждой особи пробной популяции:
- Проверить каждую координату
- Если вышла за границы:
- бросить монетку (50/50)
- если "орел" → сгенерировать новое случайное значение в границах
- если "решка" → поставить на ближайшую границу
- Применить дискретизацию, если задан шаг
ШАГ 8: Подготовка к оценке
- Скопировать пробную популяцию в основную для оценки
- Установить флаг "нужен отбор" в положение "да"
- Передать управление для вычисления приспособленности
После вычисления приспособленности
- Найти особь с лучшей приспособленностью
- Если нашли лучше глобального рекорда:
- обновить глобальный рекорд
- сохранить координаты лучшего решения
Повторение
Вернуться к ШАГУ 2 и продолжать, пока:
- не достигнута сходимость
- или не исчерпан лимит итераций
Основные моменты теперь нам понятны, приступим к написанию кода алгоритма. Класс "C_AO_BSA_Backtracking" будет представлять собой реализацию алгоритма обратного поиска BSA для решения задач оптимизации. Он будет являться наследником базового класса "C_AO", который определяет общий интерфейс для алгоритмов оптимизации.
Основные характеристики и назначение:
Параметры оптимизации:- popSize — размер популяции, количество "агентов" или "решений", которые алгоритм одновременно рассматривает.
- mixrate — параметр кроссовера, контролирует степень "смешивания" информации между агентами при создании новых решений.
- Конструктор класса инициализирует базовые параметры и добавляет "popSize" и "mixrate" в массив "params", который используется для управления параметрами алгоритма.
- Метод "SetParams" позволяет обновить внутренние параметры алгоритма на основе значений, полученных из массива "params". Он также включает базовые проверки на корректность значений.
- Init — для первоначальной настройки алгоритма, включая установку диапазонов изменения переменных (минимальные, максимальные значения и шаги) и количества эпох оптимизации.
- Moving — описывает основную итерацию алгоритма, отвечающую за генерацию новых "кандидатов" или "подвижных" решений на основе текущей популяции.
- Revision — выполняет оценку сгенерированных решений и обновление популяции на основе их качества.
- oldP — массив, представляющий "историческую" или предыдущую популяцию агентов.
- M — массив для популяции, которая получается в результате мутации.
- T — массив для "пробной" популяции, используется для сравнения с текущей популяцией перед принятием решений.
- F — фактор амплитуды для мутации, влияющий на величину изменения при мутации.
- needSelection — флаг, указывающий на необходимость выполнения второй стадии селекции.
- prevFitness — массив для хранения значений пригодности (fitness) агентов с предыдущей итерации.
- S_Map — вспомогательная структура, содержащая бинарную карту, используется в процессе кроссовера для определения, какие переменные агента будут "смешаны" от разных родителей.
- map — массив этих бинарных карт, по одной для каждого агента.
- SelectionI — первая стадия селекции, отвечающая за выбор агентов для создания новых решений.
- Mutation — применяет операцию мутации к выбранным агентам.
- Crossover — выполняет операцию кроссовера (смешивания) между агентами для создания новых "пробных" решений.
- BoundaryControl — проверяет, чтобы значения параметров агента оставались в заданных пределах (минимальных и максимальных).
- ShufflePopulation — метод для случайного перемешивания популяции.
Таким образом, класс "C_AO_BSA_Backtracking" реализует эволюционный алгоритм оптимизации, который использует концепции популяции, мутации, и кроссовера, а также специфические для BSA-механизмы, такие как обратный поиск, для решения оптимизационных задач.
//———————————————————————————————————————————————————————————————————— class C_AO_BSA_Backtracking : public C_AO { public: //---------------------------------------------------------- ~C_AO_BSA_Backtracking () { } C_AO_BSA_Backtracking () { ao_name = "BSA"; ao_desc = "Backtracking Search Algorithm"; ao_link = "https://www.mql5.com/ru/articles/18568"; popSize = 10; // размер популяции mixrate = 1.0; // параметр кроссовера ArrayResize (params, 2); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "mixrate"; params [1].val = mixrate; } void SetParams () { popSize = (int)params [0].val; mixrate = params [1].val; // Проверка корректности параметров //if (popSize < 2) popSize = 2; if (mixrate < 0.0) mixrate = 0.0; if (mixrate > 1.0) mixrate = 1.0; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //------------------------------------------------------------------ double mixrate; // параметр кроссовера private: //--------------------------------------------------------- S_AO_Agent oldP []; // историческая популяция S_AO_Agent M []; // мутантная популяция (Mutant) S_AO_Agent T []; // пробная популяция (Trial) double F; // фактор амплитуды для мутации bool needSelection; // флаг необходимости выполнения Selection-II double prevFitness []; // массив для хранения предыдущих fitness // Вспомогательные структуры для кроссовера struct S_Map { int val []; // бинарная карта для кроссовера void Init (int size) { ArrayResize (val, size); ArrayInitialize (val, 0); } }; S_Map map []; // массив бинарных карт для каждого агента // Методы алгоритма void SelectionI (); void Mutation (); void Crossover (); void BoundaryControl (S_AO_Agent &agent); void ShufflePopulation (S_AO_Agent &pop []); }; //————————————————————————————————————————————————————————————————————
Метод "Init" отвечает за подготовку алгоритма к работе перед началом оптимизации. В первую очередь, вызывается базовая функция инициализации, которая устанавливает основные параметры, связанные с диапазонами значений переменных (минимальные, максимальные значения и шаг изменения). Если этот базовый этап не проходит успешно, метод прерывается и возвращает неудачу.
Далее происходит выделение и подготовка внутренних структур данных, специфичных для алгоритма BSA. В частности, создаются и приводятся к нужному размеру массивы популяций: историческая популяция "oldP", мутантная популяция "M", пробная популяция "T", а также массив бинарных карт для кроссовера "map" и массив для хранения предыдущих значений фитнеса каждого агента "prevFitness". Флаг необходимости дополнительной селекции изначально устанавливается в ложное состояние.
После этого, для каждого агента в популяции вызываются методы инициализации, которые готовят внутренние структуры каждого агента в соответствии с количеством параметров задачи.
Затем происходит заполнение исторической популяции начальными значениями. Для каждого агента и каждого параметра в его наборе генерируется случайное значение в пределах заданного диапазона, после чего это значение корректируется в соответствии с заданным шагом изменения. При успешном выполнении всех этих шагов, метод возвращает значение, свидетельствующее об успешной инициализации объекта алгоритма и готовности к дальнейшему выполнению оптимизации.
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_BSA_Backtracking::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ // Инициализация дополнительных структур BSA ArrayResize (oldP, popSize); ArrayResize (M, popSize); ArrayResize (T, popSize); ArrayResize (map, popSize); ArrayResize (prevFitness, popSize); needSelection = false; for (int i = 0; i < popSize; i++) { oldP [i].Init (coords); M [i].Init (coords); T [i].Init (coords); map [i].Init (coords); } // Инициализация исторической популяции oldP for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { oldP [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); oldP [p].c [c] = u.SeInDiSp (oldP [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" описывает основной шаг алгоритма оптимизации BSA и отвечает за генерацию новых кандидатов решений в популяции. При первом вызове метода, когда флаг "revision" ложен, происходит первоначальное заполнение активной популяции "a". Для каждого агента в популяции и для каждого его параметра генерируется случайное значение в пределах заданного диапазона (минимум и максимум). Затем это случайное значение корректируется согласно заданному шагу изменения параметра. После инициализации флаг "revision" устанавливается в истинное значение (чтобы этот блок не выполнялся при последующих вызовах), а флаг "needSelection" сбрасывается. Метод завершается.
Выполнение жадного отбора (Selection-II) (выполняется, если требуется): если флаг "needSelection" истинен, это означает, что на предыдущем шаге была сгенерирована новая популяция, и теперь нужно сравнить ее фитнес (пригодность) с фитнесом предыдущих решений. Происходит итерация по каждому агенту в популяции. Сравнивается текущее значение фитнеса агента "a [i].f" (которое было вычислено для "пробного" решения) с его фитнесом на предыдущем шаге, сохраненным в "prevFitness [i]". Если "пробное" решение "a [i]" оказалось хуже предыдущего, то значения координат текущего агента "a [i].c" восстанавливаются из "a [i].cP" (координат агента на предыдущем шаге), и его фитнес "a [i].f" также восстанавливается до "prevFitness [i]". Это гарантирует, что популяция не ухудшается. После выполнения отбора флаг "needSelection" сбрасывается.
Основные шаги алгоритма BSA (после инициализации или отбора): перед генерацией новых решений, текущие значения фитнеса всех агентов из "a" сохраняются в "prevFitness" для последующего использования в "Selection-II" и текущие координаты агентов из "a [i].c" копируются в "a [i].cP", чтобы иметь возможность отката, если новые решения окажутся хуже.
Вызывается внутренний метод "SelectionI". Этот шаг отвечает за выбор или подготовку "архивной" популяции "oldP", которая будет использоваться для мутации. Вызывается внутренний метод "Mutation". На этом шаге генерируется "мутантная" популяция "M" на основе активной и/или архивной популяций. Вызывается внутренний метод "Crossover". На этом шаге происходит смешивание мутантной популяции "M" с текущей активной популяцией "a", в результате чего формируется "пробная" популяция "T".
Координаты агентов из сгенерированной пробной популяции "T" копируются в активную популяцию "a". Теперь "a" содержит новые "пробные" решения, фитнес которых предстоит вычислить. Флаг "needSelection" устанавливается в "true". Это сигнализирует о том, что на следующем вызове "Moving" (после того, как фитнес новых решений в "a" будет вычислен), должен быть выполнен жадный отбор (Selection-II).
Таким образом, метод "Moving" инкапсулирует одну полную итерацию или "эпоху" алгоритма BSA, включая инициализацию, селекцию, мутацию, кроссовер и подготовку к сравнению результатов.
//———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма void C_AO_BSA_Backtracking::Moving () { // Начальная инициализация популяции if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; needSelection = false; return; } // Если нужно выполнить жадный отбор после вычисления fitness if (needSelection) { // Selection-II: Жадный отбор for (int i = 0; i < popSize; i++) { // Если текущее решение (из T) хуже предыдущего, возвращаем предыдущее if (a [i].f < prevFitness [i]) { ArrayCopy (a [i].c, a [i].cP, 0, 0, WHOLE_ARRAY); a [i].f = prevFitness [i]; } } needSelection = false; } //--- Основные шаги BSA: // Сохраняем текущие fitness перед генерацией новой популяции for (int i = 0; i < popSize; i++) { prevFitness [i] = a [i].f; ArrayCopy (a [i].cP, a [i].c, 0, 0, WHOLE_ARRAY); } // 1. Selection-I SelectionI (); // 2. Mutation Mutation (); // 3. Crossover Crossover (); // 4. Копируем пробную популяцию T в основную популяцию a для вычисления fitness for (int i = 0; i < popSize; i++) { ArrayCopy (a [i].c, T [i].c, 0, 0, WHOLE_ARRAY); } // Устанавливаем флаг для выполнения Selection-II после вычисления fitness needSelection = true; } //————————————————————————————————————————————————————————————————————
Метод "SelectionI" реализует первый этап селекции в алгоритме BSA и отвечает за выбор исторической популяции, которая впоследствии используется для мутации.
Вероятностное обновление исторической популяции: с вероятностью 50% (или, проще говоря, с равной вероятностью) историческая популяция "oldP" обновляется текущей популяцией "a". Если генерируется случайное число меньше заданного порога (0.5), то происходит копирование содержимого ("c", координаты) каждого агента из текущей популяции "a" в соответствующего агента в исторической популяции "oldP", также копируется фитнес "f" агента.
Перемешивание исторической популяции: независимо от того, была ли обновлена историческая популяция на предыдущем шаге или нет, метод "ShufflePopulation (oldP)" вызывается для перемешивания агентов в исторической популяции. Это делается для внесения случайности в процесс мутации. Перемешивание гарантирует, что агенты в исторической популяции будут выбираться в случайном порядке, а не в том порядке, в котором они изначально располагались.
Таким образом, "SelectionI" либо обновляет архивную популяцию текущими кандидатами решений, либо сохраняет ее прежнее состояние, а затем, в любом случае перемешивает агентов в архивной популяции, что позволяет разнообразить поиск при последующей мутации.
//———————————————————————————————————————————————————————————————————— //--- Selection-I: выбор исторической популяции void C_AO_BSA_Backtracking::SelectionI () { // С вероятностью 50% обновляем историческую популяцию if (u.RNDprobab () < 0.5) // эквивалент if (a < b) где a,b ~ U(0,1) { // Копируем текущую популяцию в историческую for (int i = 0; i < popSize; i++) { ArrayCopy (oldP [i].c, a [i].c, 0, 0, WHOLE_ARRAY); oldP [i].f = a [i].f; } } // Перемешиваем историческую популяцию ShufflePopulation (oldP); } //————————————————————————————————————————————————————————————————————
Метод "ShufflePopulation" предназначен для случайного перемешивания элементов в заданной популяции агентов (представленных структурой "S_AO_Agent"). Он принимает на вход массив агентов "pop []" и выполняет перемешивание на месте, то есть изменяет порядок элементов непосредственно в переданном массиве.
Алгоритм перемешивания: метод использует алгоритм тасования Фишера-Йетса (Fisher-Yates shuffle) для случайного перемешивания элементов в популяции, алгоритм гарантирует, что каждая перестановка (порядок) элементов имеет равную вероятность.
Цикл "for" начинается с последнего элемента массива (popSize - 1) и идет в обратном порядке до второго элемента (индекс 1). Первый элемент (индекс 0) не нуждается в перемешивании, так как к тому моменту он уже будет "перемещен" по ходу алгоритма. Для каждого элемента с индексом "i" выбирается случайный индекс "j" в диапазоне от "0" до "i" включительно. Это делается с помощью функции "u.RNDminusOne (i + 1)", которая возвращает случайное целое число в указанном диапазоне (включая "0" и исключая "i + 1").
Элементы с индексами "i" и "j" меняются местами. Для этого используется временная переменная "temp" типа "S_AO_Agent". Поскольку "S_AO_Agent" содержит массив "c" (координаты), производится копирование этого массива. Также копируется значение фитнеса "f". Значения координат и фитнеса элемента "pop [i]" сохраняются во временной переменной "temp", также значения координат и фитнеса элемента "pop [j]" копируются в "pop [i]". Сохраненные значения из "temp" (исходное значение "pop [i]") копируются в "pop [j]". В итоге после завершения цикла, порядок элементов в массиве "pop []" будет случайным.
//———————————————————————————————————————————————————————————————————— //--- Перемешивание популяции void C_AO_BSA_Backtracking::ShufflePopulation (S_AO_Agent &pop []) { for (int i = popSize - 1; i > 0; i--) { int j = u.RNDminusOne (i + 1); // Обмен местами элементов i и j S_AO_Agent temp; temp.Init (coords); ArrayCopy (temp.c, pop [i].c, 0, 0, WHOLE_ARRAY); temp.f = pop [i].f; ArrayCopy (pop [i].c, pop [j].c, 0, 0, WHOLE_ARRAY); pop [i].f = pop [j].f; ArrayCopy (pop [j].c, temp.c, 0, 0, WHOLE_ARRAY); pop [j].f = temp.f; } } //————————————————————————————————————————————————————————————————————
Метод "Mutation" отвечает за генерацию мутантной популяции, которая является ключевым этапом в алгоритме BSA. Он базируется на различии между текущей популяцией и исторической популяцией.
Сначала генерируется случайный фактор амплитуды "F", который определяет величину воздействия исторической популяции на текущую. Затем, для каждого агента в популяции и для каждой координаты внутри этого агента вычисляется новое значение координаты в мутантной популяции. Это делается путем добавления к текущей координате произведения фактора амплитуды "F" и разности между соответствующей координатой в исторической популяции и текущей координатой. Таким образом, мутантная популяция создается путем смещения текущей популяции в направлении, определяемом исторической популяцией, с амплитудой, зависящей от фактора "F".
//———————————————————————————————————————————————————————————————————— //--- Mutation: генерация мутантной популяции void C_AO_BSA_Backtracking::Mutation () { // Генерируем фактор амплитуды F = u.GaussDistribution (0.0, -3.0, 3.0, 2); // Применяем мутацию: M = P + F * (oldP - P) for (int i = 0; i < popSize; i++) { for (int j = 0; j < coords; j++) { M [i].c [j] = a [i].c [j] + F * (oldP [i].c [j] - a [i].c [j]); } } } //————————————————————————————————————————————————————————————————————
Метод "Crossover" занимается формированием пробной популяции на основе текущей мутантной популяции, используя выбранную стратегию кроссовера. Этот процесс направлен на комбинирование особенностей наследуемых решений для поиска более оптимальных вариантов.
Первоначально, пробная популяция копируется из мутантной, чтобы была база для дальнейших модификаций. Затем происходит выбор стратегии кроссинговера: с вероятностью 40% используется первая стратегия, или же в противном случае — вторая.
Если выбран первый вариант, осуществляется стратегия, называемая "mixrate". В этом случае для каждого агента определяется число элементов (в пределах координат), которые будут взяты из текущего агента, с учетом заданного коэффициента "mixrate". Эти элементы выбираются случайным образом, без повторений. После этого, у выбранных индексов в агента пробной популяции копируются соответствующие координаты из текущего решения.
Если выбрана вторая стратегия, то для каждого агента выбирается один случайный элемент (координата), и в пробной популяции в соответствующей позиции происходит замена этого элемента на его значение из текущего решения.
После завершения кроссинговера проводится контроль границ для каждого агента пробной популяции, чтобы убедиться, что все решения валидны и соответствуют требованиям по диапазонам значений.
//———————————————————————————————————————————————————————————————————— //--- Crossover: генерация пробной популяции void C_AO_BSA_Backtracking::Crossover () { // Инициализируем пробную популяцию как копию мутантной for (int i = 0; i < popSize; i++) { ArrayCopy (T [i].c, M [i].c, 0, 0, WHOLE_ARRAY); } // Выбираем стратегию кроссовера if (u.RNDprobab () < 0.4) { //--- СТРАТЕГИЯ 1: Использование mixrate for (int i = 0; i < popSize; i++) { // Сброс карты ArrayInitialize (map [i].val, 0); // Определяем количество элементов для кроссовера int numElements = (int)MathCeil (mixrate * u.RNDprobab () * coords); // Генерируем уникальные индексы для кроссовера for (int n = 0; n < numElements; n++) { int idx; do { idx = u.RNDminusOne (coords); } while (map [i].val [idx] == 1); // пока не найдем неиспользованный индекс map [i].val [idx] = 1; } // Применяем кроссовер for (int j = 0; j < coords; j++) { if (map [i].val [j] == 1) { T [i].c [j] = a [i].c [j]; } } } } else { //--- СТРАТЕГИЯ 2: Мутация только одного элемента for (int i = 0; i < popSize; i++) { // Выбираем один случайный элемент int randomIndex = u.RNDminusOne (coords); T [i].c [randomIndex] = a [i].c [randomIndex]; } } // Контроль границ для всех агентов пробной популяции for (int i = 0; i < popSize; i++) { BoundaryControl (T [i]); } } //————————————————————————————————————————————————————————————————————
Метод "BoundaryControl" предназначен для проверки и корректировки значений решений агента, чтобы они оставались в допустимых границах, а также для приведения решений к нужному дискретному формату.
Для каждого элемента координат агента происходит проверка: если значение выходит за установленные минимальные или максимальные границы, то осуществляется обработка этого выхода в соответствии с выбранной стратегией. В случае, если вероятность случайным образом выбирается ниже 50%, происходит случайная регенерация значения внутри допустимого диапазона. В противном случае, значение устанавливается на ближайшую границу — либо минимальную, либо максимальную.
После этого, каждое значение координаты подвергается дискретизации — то есть, превращается в ближайшее допустимое значение, соответствующее заданному диапазону и шагу дискретизации. Это обеспечивает, что решение соответствует требованиям по типу данных и диапазонам.
//———————————————————————————————————————————————————————————————————— //--- Контроль границ void C_AO_BSA_Backtracking::BoundaryControl (S_AO_Agent &agent) { for (int j = 0; j < coords; j++) { if (agent.c [j] < rangeMin [j] || agent.c [j] > rangeMax [j]) { // Выбор стратегии обработки границ if (u.RNDprobab () < 0.5) { // Случайная регенерация agent.c [j] = u.RNDfromCI (rangeMin [j], rangeMax [j]); } else { // Установка на границу if (agent.c [j] < rangeMin [j]) agent.c [j] = rangeMin [j]; else agent.c [j] = rangeMax [j]; } } // Дискретизация agent.c [j] = u.SeInDiSp (agent.c [j], rangeMin [j], rangeMax [j], rangeStep [j]); } } //————————————————————————————————————————————————————————————————————
Метод "Revision" отвечает за выбор и обновление лучшего найденного решения в текущей популяции. Проходя по всем решениям, он ищет то, у которого значение функции оценки (фитнеса) является максимальным. Если такое решение обнаружено, оно сохраняется как текущий лучший результат, и его координаты копируются в отдельный массив, предназначенный для хранения лучшего решения на данный момент. Таким образом, этот метод обеспечивает постоянное отслеживание и обновление оптимального решения, найденного в ходе итераций алгоритма.
//———————————————————————————————————————————————————————————————————— //--- Selection-II и обновление лучшего решения void C_AO_BSA_Backtracking::Revision () { int bestIND = -1; for (int i = 0; i < popSize; i++) { // Обновляем глобальное лучшее решение if (a [i].f > fB) { fB = a [i].f; bestIND = i; } } // Копируем координаты лучшего решения if (bestIND != -1) { ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY); } } //————————————————————————————————————————————————————————————————————
Метод "GaussDistribution" генерирует случайное число с Гауссовым (нормальным) распределением, центрированным вокруг заданного входного значения и ограниченного определённым диапазоном, используя метод Бокса-Мюллера для получения нормально распределённых случайных величин.
Сначала он генерирует две равномерно распределённые случайные величины. Затем, на основе этих величин, вычисляется стандартная нормально распределённая случайная величина, которая может быть использована для получения Гауссова распределения.
Далее метод проверяет, находится ли сгенерированное значение в пределах заданного диапазона отклонений, определяемого параметром сигма. Если сгенерированное значение выходит за эти пределы, метод рекурсивно вызывается снова, чтобы сгенерировать новое значение, пока оно не попадёт в допустимый диапазон.
Наконец, сгенерированное нормально распределённое отклонение масштабируется таким образом, чтобы оно соответствовало заданному выходному диапазону (от "outMin" до "outMax") относительно входного значения "In". Это позволяет смещать и масштабировать распределение, чтобы оно соответствовало желаемым параметрам. Результатом является число, распределённое по Гауссу, с центром в "In", но с учётом ограничений на минимальное и максимальное выходное значение.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_Utilities :: GaussDistribution (const double In, const double outMin, const double outMax, const double sigma) { double logN = 0.0; double u1 = 2.0 * MathRand () / 32767.0 - 1.0;//RNDfromCI (0.0, 1.0); double u2 = 2.0 * MathRand () / 32767.0 - 1.0;//RNDfromCI (0.0, 1.0); logN = u1 <= 0.0 ? 0.000000000000001 : u1; double z0 = sqrt (-2 * log (logN)) * cos (2 * M_PI * u2); double sigmaN = sigma > 8.583864105157389 ? 8.583864105157389 : sigma; // Если z0 выходит за пределы [-sigmaN, sigmaN], генерируем заново if (z0 >= sigmaN || z0 <= -sigmaN) { return GaussDistribution(In, outMin, outMax, sigma); // Рекурсивный вызов } if (z0 >= 0.0) z0 = Scale (z0, 0.0, sigmaN, 0.0, outMax - In, false); else z0 = -Scale (fabs (z0), 0.0, sigmaN, 0.0, In - outMin, false); return In + z0; } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
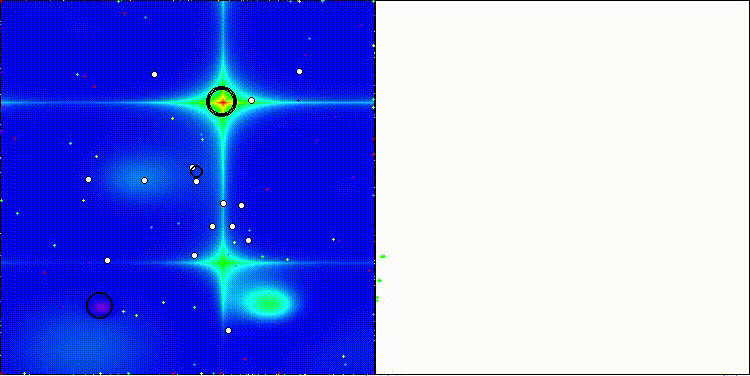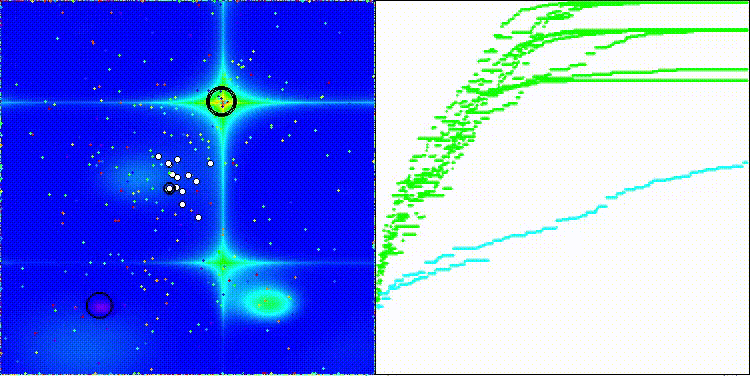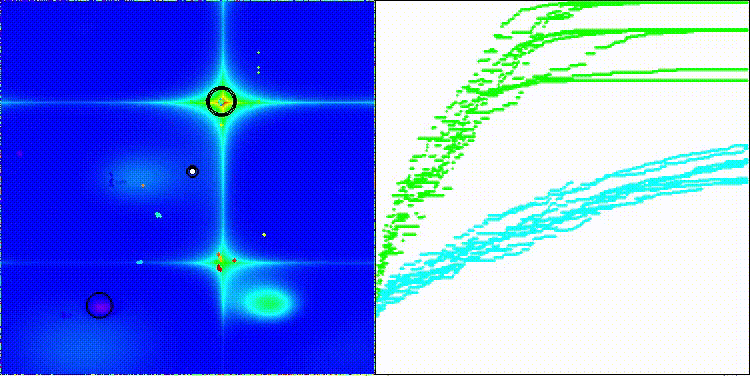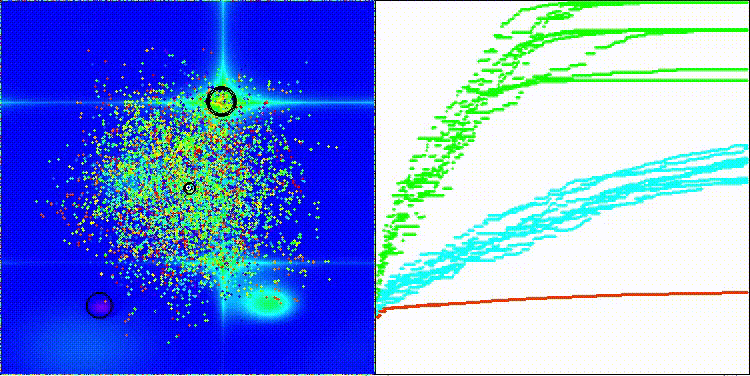
Результаты работы алгоритма BSA очень хорошие.
=============================
5 Hilly's; Func runs: 10000; result: 0.9730917210619289
25 Hilly's; Func runs: 10000; result: 0.5453406317593932
500 Hilly's; Func runs: 10000; result: 0.2909827609772065
=============================
5 Forest's; Func runs: 10000; result: 0.9999986842258451
25 Forest's; Func runs: 10000; result: 0.5854340780208712
500 Forest's; Func runs: 10000; result: 0.21747482800959225
=============================
5 Megacity's; Func runs: 10000; result: 0.8476923076923077
25 Megacity's; Func runs: 10000; result: 0.3695384615384615
500 Megacity's; Func runs: 10000; result: 0.12978461538461658
=============================
All score: 4.95934 (55.10%)
На визуализации работы алгоритма BSA можно заметить разброс значений по результатам на функциях малой и средней размерности, однако, с увеличением в параметрах размера популяции разброс уменьшается, но для лучшей сходимости необходимо увеличивать количество итераций.
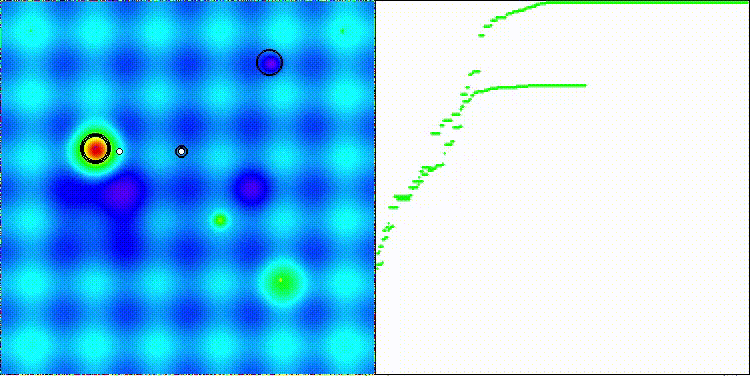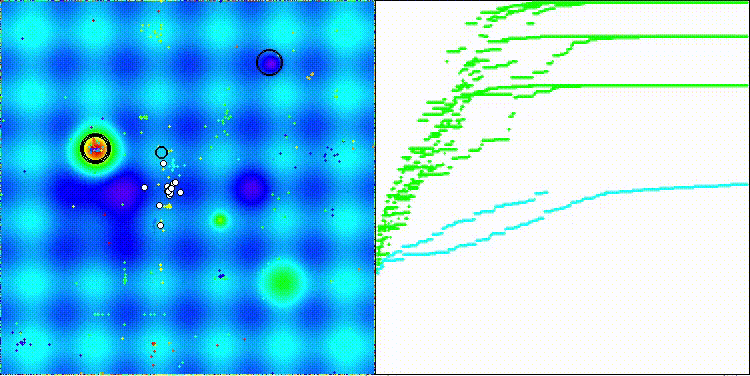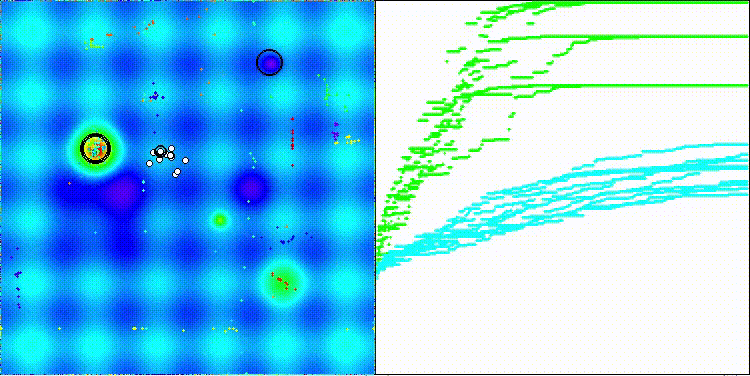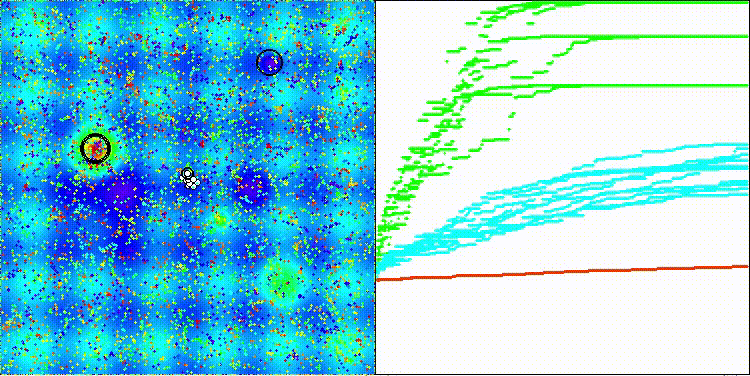
BSA на тестовой функции Hilly
BSA на тестовой функции Forest
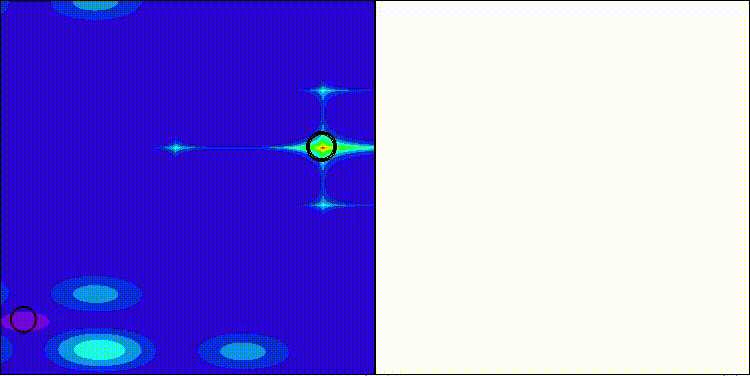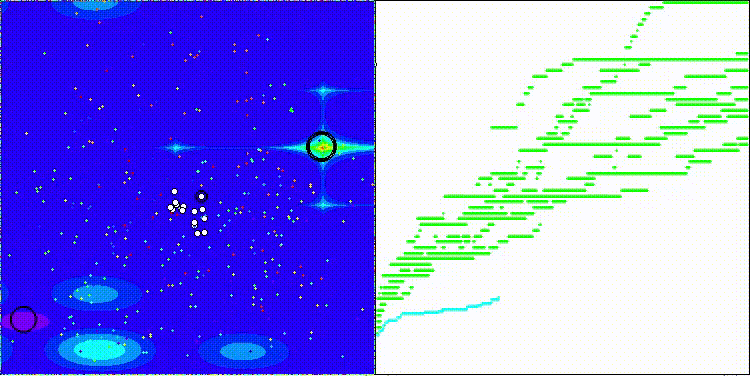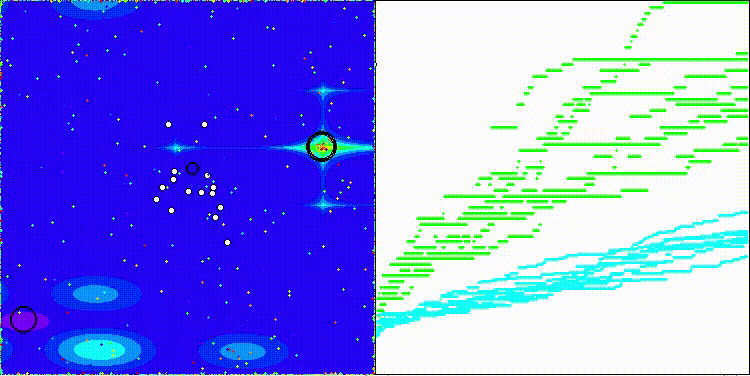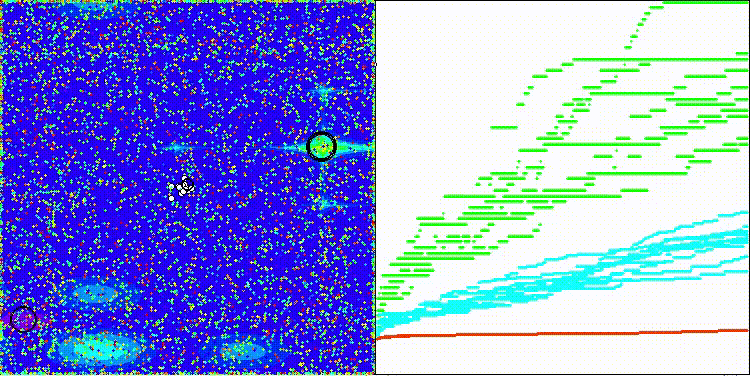
BSA на тестовой функции Megacity
Алгоритм BSA занимает 20 место в рейтинговой таблице популяционных алгоритмов оптимизации.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 13 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 14 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 15 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 16 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 17 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 18 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 19 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 20 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 21 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 22 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 23 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 24 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 25 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 26 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 27 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 28 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 29 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 30 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 31 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 32 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 33 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 34 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 35 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 36 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 37 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 38 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 39 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 40 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 41 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 42 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 43 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 44 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 45 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
BSA представляет собой компромисс между простотой реализации и эффективностью поиска, занимая устойчивую позицию в середине рейтинговой таблицы популяционных алгоритмов оптимизации. Его главное преимущество — интересная концепция исторической памяти — позволяет алгоритму избегать преждевременной сходимости без усложнения вычислительной схемы. В отличие от многих современных метаэвристик, перегруженных параметрами и сложными операторами, BSA обходится минимальным набором настроек, что делает его привлекательным выбором для практиков, не желающих тратить время на тонкую настройку внешних параметров.
Единственный существенный параметр "mixrate" интуитивно понятен и не требует глубокого понимания внутренней механики алгоритма. При этом BSA демонстрирует стабильную производительность на широком классе задач — от простых унимодальных функций до сложных многоэкстремальных ландшафтов с множеством локальных оптимумов. Алгоритм не претендует на звание чемпиона по скорости сходимости или точности решения, но его надежность и предсказуемость делают его рабочей лошадкой. Особенно ценно то, что при растущей популяции BSA слабо подвержен стагнации — механизм случайного обновления исторической популяции обеспечивает постоянный приток разнообразия даже на поздних стадиях поиска.
Его позиция в середине рейтинга — это не признак посредственности, а скорее свидетельство универсальности и практичности, ведь не всегда для решения реальных задач нужен самый сложный и современный инструмент. Иногда достаточно надежного алгоритма с понятной логикой работы, который дает хорошие результаты без необходимости в экспертной настройке, и BSA успешно заполняет эту нишу.
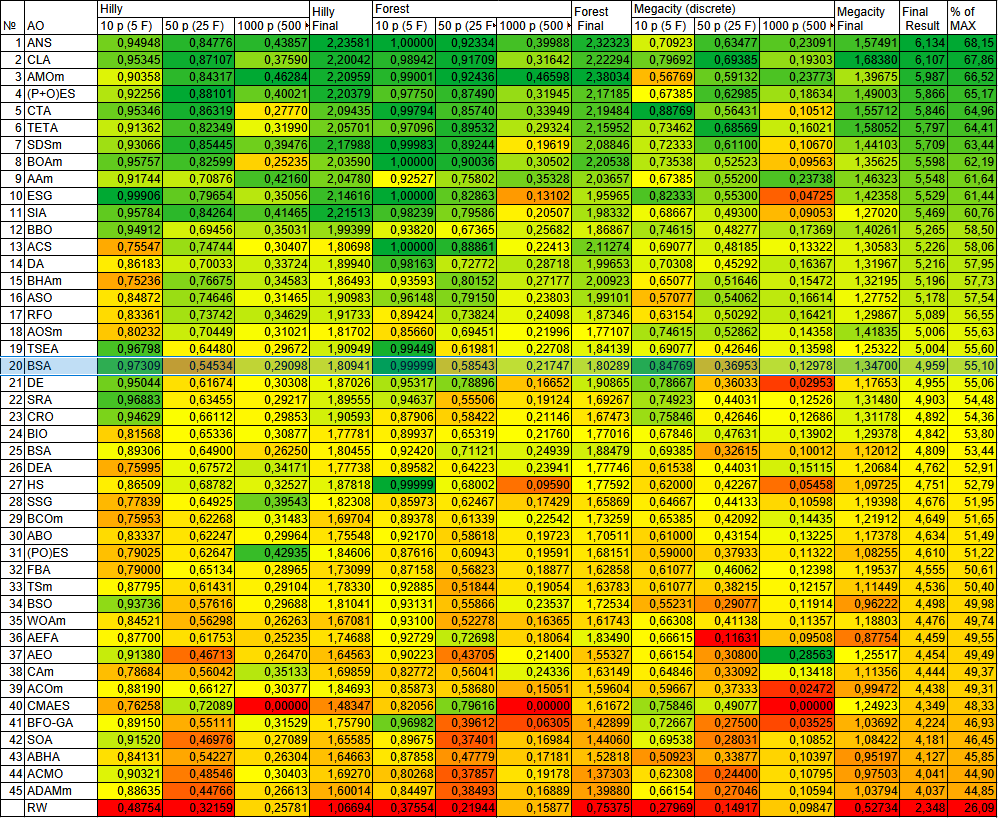
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
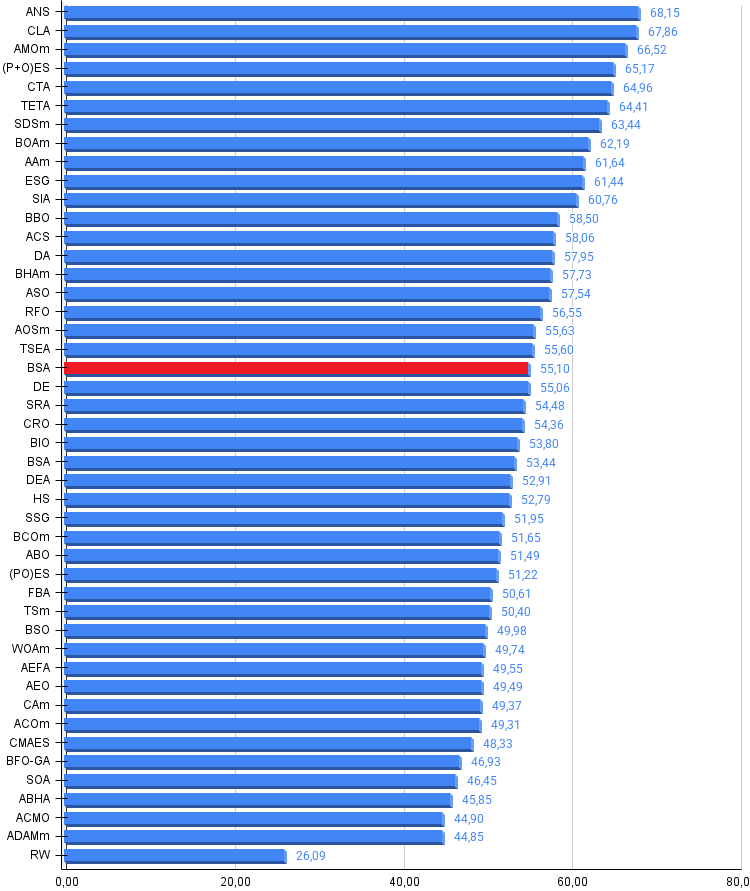
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма BSA:
Плюсы:
- Хорошая сходимость на функциях.
- Кроме размера популяции, всего лишь один дополнительный внешний параметр.
Минусы:
- Присутствует некоторая склонность к застреванию на задачах малой размерности при небольшой популяции.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_BSA.mq5 | Скрипт | Испытательный стенд для BSA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Торговая стратегия "Захват ликвидности" (Liquidity Grab)
Торговая стратегия "Захват ликвидности" (Liquidity Grab)
 Строим и оптимизируем торговую систему, основанную на объемах торгов (Chaikin Money Flow - CMF)
Строим и оптимизируем торговую систему, основанную на объемах торгов (Chaikin Money Flow - CMF)
 Нейросети в трейдинге: Адаптивная периодическая сегментация (Окончание)
Нейросети в трейдинге: Адаптивная периодическая сегментация (Окончание)
 Модель портфельного риска с использованием критерия Келли и моделирования по методу Монте-Карло
Модель портфельного риска с использованием критерия Келли и моделирования по методу Монте-Карло
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования