
Оптимизация Роем Жуков — Beetle Swarm Optimization (BSO)
Содержание
Введение
Исследуем еще один из современных алгоритмов оптимизации, черпающий вдохновение у природы. Жуки-усачи (Cerambycidae) — одно из крупнейших семейств жуков, насчитывающее более 35 000 видов. Их отличительная черта — чрезвычайно длинные усики-антенны, нередко превышающие длину тела в три-четыре раза. Эти антенны — не просто украшение: они представляют собой сложнейшую сенсорную систему, объединяющую хеморецепцию, механорецепцию и даже элементы слуха. С помощью антенн жуки находят пищу, обнаруживают партнёров, выбирают места для кладки яиц и уклоняются от хищников. По существу, длинноусый жук — это живой навигатор, который непрерывно "ощупывает" окружающее пространство, сравнивая интенсивность химических градиентов на правом и левом усике, и поворачивает в сторону более сильного сигнала.
Именно этот принцип двухантенного поиска лёг в основу алгоритма BAS (Beetle Antennae Search), предложенного Jiang X. и соавторами. Идея BAS элегантна: один виртуальный жук перемещается в пространстве решений, выставляя "правый" и "левый" усик по обе стороны от текущей позиции. Сравнивая значения целевой функции в точках, соответствующих кончикам усиков, жук определяет направление улучшения и делает шаг. Алгоритм не требует вычисления градиента, работает с функциями произвольной формы и отличается предельной простотой — в нём всего одна особь.
Однако именно простота BAS оказалась его ограничением. Единственный агент сильно зависит от начальной позиции, легко застревает в локальных оптимумах и плохо справляется с многомерными ландшафтами, где структура целевой функции неоднородна. Эти наблюдения подтолкнули исследователей к следующему логичному шагу — объединению антенного механизма BAS с коллективной динамикой роя частиц (PSO). Так появился алгоритм BSO (Beetle Swarm Optimization) — Оптимизация Роем Жуков.
Beetle Swarm Optimization Algorithm расширяет популяцию до группы жуков, каждый из которых сохраняет двухантенный механизм обнаружения, но при этом обменивается информацией с сородичами по правилам, заимствованным из PSO. Позиция каждого жука обновляется как взвешенная комбинация двух компонент: PSO-компонента направляет жука к личному и глобальному лучшим решениям, а BAS-компонента корректирует движение на основе локального градиента, оценённого парой антенн. Коэффициент "λ" управляет балансом между "социальным знанием" роя и "личным восприятием" каждой особи.
В данной статье мы рассмотрим математический аппарат алгоритма BSO, разберём все ключевые формулы, представим подробный псевдокод и реализацию на языке MQL5 в рамках стандартного тестового стенда для сравнения метаэвристических алгоритмов.
Реализация алгоритма
Представьте поляну, залитую разнообразными запахами. Одинокий жук-усач, выставив длинные антенны, пытается найти источник самого сильного аромата. Он поворачивает голову: если правый усик улавливает запах сильнее левого — жук разворачивается вправо, и наоборот. Это суть алгоритма BAS — один разведчик, два "датчика", простое правило.
А теперь представьте, что на поляну вышла целая колония жуков. Каждый по-прежнему ощупывает пространство своими усиками, но теперь жуки могут ориентироваться не только на собственные ощущения — они замечают, куда устремляются сородичи, помнят свои лучшие находки и знают о лучшей находке всей колонии. Это и есть BSO — Beetle Swarm Optimization.
Популяция состоит из "n" жуков в S-мерном пространстве поиска. Каждый i-й жук описывается:
- позицией Xi = (x_i1, x_i2, …, x_iS) — точка в пространстве решений,
- скоростью Vi = (v_i1, v_i2, …, v_iS) — направление и величина движения,
- личным лучшим Pi — лучшая позиция, которую этот жук когда-либо посещал,
- глобальным лучшим Pg — лучшая позиция, найденная любым жуком в колонии.
Допустим, мы ищем максимум функции f(x, y) на плоскости (S = 2), и у нас 3 жука (n = 3). Начальное состояние:
Жук; Позиция X;Скорость V;f(X)
1 (2.0, 3.0) (0.5, -0.3) 7.2
2 (5.0, 1.0) (-0.2, 0.4) 4.8
3 (1.0, 4.0) (0.3, 0.1) 8.5
Личный лучший Pi каждого жука совпадает с его текущей позицией (первая итерация). Глобальный лучший Pg = (1.0, 4.0) с f = 8.5 (жук №3).
Шаг 1. Каждый жук выставляет правый и левый усик на расстояние d/2 от текущей позиции. Направление усиков определяется нормализованным вектором скорости жука — усики расположены вдоль линии движения.
Позиции антенн (формула 10 в статье):
- Xrs = X + V · d/2 (правый усик)
- Xls = X - V · d/2 (левый усик)
Пример для жука №1 (X = (2.0, 3.0), V = (0.5, -0.3), d = 0.5):
- Xrs = (2.0 + 0.5·0.25, 3.0 + (-0.3)·0.25) = (2.125, 2.925)
- Xls = (2.0 - 0.5·0.25, 3.0 - (-0.3)·0.25) = (1.875, 3.075)
Жук нюхает в двух точках. Допустим, f(Xrs) = 7.0, f(Xls) = 7.6. Левый усик обнаружил лучшее значение.
Шаг 2. На основе разницы фитнеса антенн вычисляется BAS-инкремент ξ (формула 9): ξ = δ · V · sign(f(Xrs) - f(Xls))
Функция "sign" возвращает: +1, если правая антенна лучше; -1, если левая; 0, если одинаково.
Продолжение примера для жука №1 (δ = 1.0): sign(7.0 - 7.6) = sign(-0.6) = -1
- ξx = 1.0 · 0.5 · (-1) = -0.5
- ξy = 1.0 · (-0.3) · (-1) = 0.3
Отрицательный знак по "x" и положительный по "y" — жук понял, что нужно двигаться в сторону левого усика (где запах сильнее), то есть уменьшить "x" и увеличить "y".
Шаг 3. Одновременно работает PSO-механизм: скорость обновляется с учётом инерции, притяжения к личному лучшему и глобальному лучшему (формула 7):
Vnew = ω · V + c₁ · r₁ · (Pi - X) + c₂ · r₂ · (Pg - X); где:
- ω — инерционный вес (насколько жук помнит своё прежнее направление),
- c₁, c₂ — когнитивный и социальный коэффициенты,
- r₁, r₂ — случайные числа в [0, 1].
Продолжение примера для жука №1 (ω = 0.8, c₁ = 1.5, c₂ = 1.5, r₁ = 0.6, r₂ = 0.4):
Личный лучший P1 = (2.0, 3.0), глобальный лучший Pg = (1.0, 4.0).
- Vnewx = 0.8·0.5 + 1.5·0.6·(2.0-2.0) + 1.5·0.4·(1.0-2.0) = 0.4 + 0 + (-0.6) = -0.2
- Vnewy = 0.8·(-0.3) + 1.5·0.6·(3.0-3.0) + 1.5·0.4·(4.0-3.0) = -0.24 + 0 + 0.6 = 0.36
Скорость повернулась: жук теперь движется в сторону глобального лучшего решения (влево и вверх), что совпадает с направлением, подсказанным антеннами.
Шаг 4. Новая позиция вычисляется как сумма текущей позиции, PSO-компоненты и BAS-компоненты с коэффициентом баланса "λ" (формула 6):
Xnew = X + λ · Vnew + (1 - λ) · ξ
Параметр λ ∈ [0, 1] управляет вкладом каждого механизма:
- λ = 1 — чистый PSO (антенны игнорируются),
- λ = 0 — чистый BAS (роевой интеллект игнорируется),
Продолжение примера для жука №1 (λ = 0.5):
- Xnewx = 2.0 + 0.5·(-0.2) + 0.5·(-0.5) = 2.0 - 0.1 - 0.25 = 1.65
- Xnewy = 3.0 + 0.5·0.36 + 0.5·0.3 = 3.0 + 0.18 + 0.15 = 3.33
Xnew = (1.65, 3.33)
Жук переместился из (2.0, 3.0) в (1.65, 3.33) — ближе к глобальному оптимуму. Оба механизма согласились, что нужно двигаться влево и вверх, и их комбинация дала уверенный шаг.
Шаг 5. На протяжении оптимизации два ключевых параметра адаптируются автоматически.
Инерционный вес "ω" линейно убывает (формула 8):
ω = ωmax - (ωmax - ωmin) / K · k; где K — общее число итераций, k — текущая итерация.
Пример для K = 100:
- k = 1: ω = 0.9 - 0.5/100·1 = 0.895 (широкое исследование),
- k = 50: ω = 0.9 - 0.5/100·50 = 0.65 (умеренное движение),
- k = 100: ω = 0.9 - 0.5/100·100 = 0.4 (точная настройка).
Высокий "ω" в начале позволяет жукам быстро разлетаться по пространству, а низкий в конце — тщательно исследовать окрестности лучшего найденного решения.
Размер шага антенн "δ" экспоненциально затухает (формула 4):
δ^(k+1) = η · δ^k, η ≈ 0.95
а расстояние между антеннами пропорционально шагу (формула 5):
d = δ / c₂
Пример для δ₀ = 1.0, η = 0.95:
- k = 0: δ = 1.0, d = 0.5 (усики широко расставлены),
- k = 20: δ = 0.95²⁰ ≈ 0.358, d ≈ 0.179 (усики сближаются),
- k = 60: δ = 0.95⁶⁰ ≈ 0.046, d ≈ 0.023 (тонкое обнюхивание).
В начале жуки ощупывают большие участки пространства, в конце — проводят точечный анализ. Это обеспечивает плавный переход от глобальной разведки к локальной эксплуатации.
Шаг 6. После оценки новой позиции каждого жука:
- Если f(Xnew) лучше личного лучшего Pi — обновляем Pi.
- Если f(Xnew) лучше глобального лучшего Pg — обновляем Pg.
Пример. Жук №1 переместился в (1.65, 3.33) и получил f = 8.9. Это лучше его предыдущего личного лучшего (7.2) и лучше глобального лучшего (8.5). Обновляем оба: P1 = (1.65, 3.33), Pg = (1.65, 3.33). Теперь все жуки в колонии знают о новом лучшем решении и будут притягиваться к нему.
Сводная таблица формул алгоритма BSO.
| Формула | Описание | |
|---|---|---|
| 6 | X^(k+1) = X^k + λ·V^(k+1) + (1-λ)·ξ^k | Обновление позиции (PSO + BAS) |
| 7 | V^(k+1) = ω·V^k + c₁·r₁·(P_i - X) + c₂·r₂·(P_g - X) | Обновление скорости (PSO) |
| 8 | ω = ωmax - (ωmax - ωmin)/K · k | Линейное убывание инерционного веса |
| 9 | ξ = δ · V · sign(f(X_rs) - f(X_ls)) | BAS-инкремент (реакция на антенны) |
| 10 | X_rs = X + V·d/2, X_ls = X - V·d/2 | Позиции правой и левой антенн |
| 4 | δ^(k+1) = η · δ^k | Экспоненциальное затухание шага |
| 5 | d = δ / c₂ | Расстояние между антеннами |
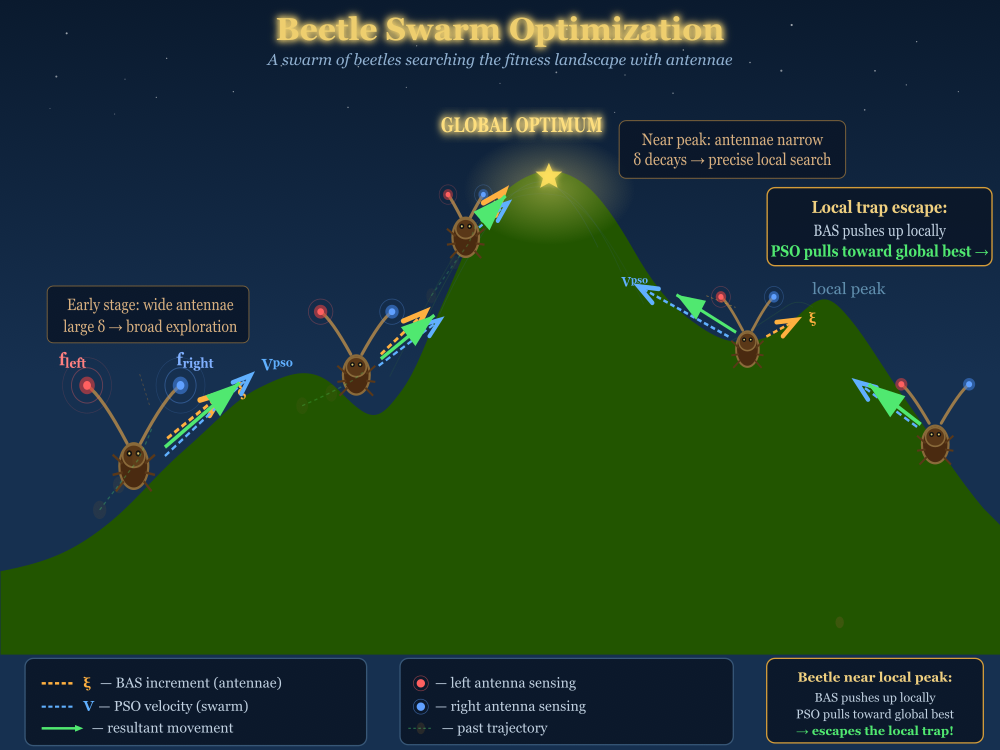
Рисунок 1. Иллюстрация работы алгоритма BSO
На иллюстрации изображена сцена поиска на фитнес-ландшафте с холмами: 5 жуков в разных стадиях поиска — от раннего исследователя слева до жука вблизи глобального пика, у каждого жука видны красная (left) и синяя (right) антенны с волнами поиска, причём у жука у вершины антенны сближены (δ затухает). Три типа стрелок: оранжевая пунктирная ξ (BAS — антенны подсказывают направление), синяя пунктирная V (PSO — рой тянет к лучшему), зелёная сплошная — результирующее движение.
Напишем псевдокод алгоритма BSO.
n — размер популяции (popSize)
S — размерность пространства (coords)
K_total — общий бюджет вызовов Moving/Revision (epochsP)
λ — баланс PSO/BAS [0, 1]
c₁, c₂ — когнитивный и социальный коэффициенты PSO
ω_max, ω_min — диапазон инерционного веса
η — коэффициент затухания шага (≈ 0.95)
δ₀ — начальный размер шага BAS
c₂_bas — делитель расстояния антенн
ИНИЦИАЛИЗАЦИЯ (Init):
Для каждого измерения s = 1..S:
Vmax[s] = (rangeMax[s] − rangeMin[s]) / 2
Для каждого жука i = 1..n:
cP[i] = случайная позиция в области поиска // реальная позиция
V[i] = случайная скорость в [−Vmax, Vmax] // начальная скорость
δ = δ₀ // текущий шаг BAS
d = δ / c₂_bas // расстояние антенн
K = (K_total − 1) / 3 // число BSO-итераций
k = 0 // счётчик итераций
phase = −1 // начальная фаза
ОСНОВНОЙ ЦИКЛ (чередование Moving → оценка фитнеса → Revision):
┌─ Moving (phase = −1):
Для каждого жука i:
c[i] = дискретизировать(cP[i]) // выставить позиции для оценки
├─ Revision (phase = −1):
Для каждого жука i:
cB[i] = c[i], fB[i] = f[i] // личный лучший = начальная позиция
Если f[i] > fB_global:
fB_global = f[i], cB_global = c[i] // обновить глобальный лучший
phase = 0
┌─── ЦИКЛ BSO-ИТЕРАЦИЙ (повторять пока k < K): ───────────────────┐
Moving (phase = 0): // ПРАВАЯ АНТЕННА
Для каждого жука i:
c[i] = дискретизировать(cP[i] + V[i] · d/2)
Revision (phase = 0):
Для каждого жука i:
fR[i] = f[i] // запомнить f правой
phase = 1
Moving (phase = 1): // ЛЕВАЯ АНТЕННА
Для каждого жука i:
c[i] = дискретизировать(cP[i] − V[i] · d/2)
Revision (phase = 1):
Для каждого жука i:
fL[i] = f[i] // запомнить f левой
ω = ω_max − (ω_max − ω_min)/K · (k+1) // формула (8)
ω = max(ω, ω_min) // защитный клемп
Для каждого жука i:
sign = знак(fR[i] − fL[i])
Для каждого измерения s:
ξ = δ · V[i,s] · sign // формула (9)
r₁, r₂ = случайные из [0, 1]
V[i,s] = ω·V[i,s]
+ c₁·r₁·(cB[i,s] − cP[i,s])
+ c₂·r₂·(cB_global[s] − cP[i,s]) // формула (7)
V[i,s] = ограничить(V[i,s], −Vmax[s], Vmax[s])
cP[i,s] = cP[i,s] + λ·V[i,s] + (1−λ)·ξ // формула (6)
cP[i,s] = ограничить(cP[i,s], rangeMin[s], rangeMax[s])
δ = η · δ // формула (4)
d = δ / c₂_bas // формула (5)
k = k + 1
phase = 2
Moving (phase = 2): // ПОЗИЦИЯ ЖУКА
Для каждого жука i:
c[i] = дискретизировать(cP[i])
Revision (phase = 2):
Для каждого жука i:
Если f[i] > fB[i]:
fB[i] = f[i], cB[i] = c[i] // обновить личный лучший
Если f[i] > fB_global:
fB_global = f[i], cB_global = c[i] // обновить глобальный
phase = 0 // начать новую итерацию
└───────────────────────────────────────────────────────────────────┘
ВЫХОД: cB_global, fB_global
Переходим к реализации. Класс "C_AO_BSO_Beetle" наследуется от базового класса "C_AO" и реализует алгоритм Beetle Swarm Optimization — гибрид роевой оптимизации частицами (PSO) и антенного поиска жуков (BAS). Наследование от "C_AO" обеспечивает совместимость со стандартным тестовым стендом: внешний код в цикле вызывает Moving(), затем оценивает фитнес, затем вызывает Revision(), и алгоритм должен укладываться в эту двухтактную схему. Особенность BSO в том, что каждая логическая итерация требует трёх оценок фитнеса — для правой антенны, левой антенны и собственно позиции жука, — поэтому реализация использует внутреннюю машину состояний на основе переменной "phase".
Класс содержит девять настраиваемых параметров. Параметр "lambda" управляет балансом между PSO-компонентой и BAS-компонентой при обновлении позиции: при "lambda" равном единице алгоритм превращается в чистый PSO, при нуле — в чистый BAS, рекомендуемое значение 0.5. Параметры "c1_pso" и "c2_pso" — когнитивный и социальный коэффициенты PSO, определяющие силу притяжения к личному и глобальному лучшему решению соответственно. Параметры "omega_max" и "omega_min" задают диапазон линейного убывания инерционного веса: в начале оптимизации высокий инерционный вес стимулирует широкое исследование пространства, в конце низкий обеспечивает точную настройку.
Параметр "eta" — множитель экспоненциального затухания шага антенного поиска, обычно 0.95: на каждой итерации размер шага "δ" умножается на "eta", что постепенно сужает зону ощупывания антеннами. Параметр "delta0" — начальное значение шага "δ". Параметр "c2_bas" — делитель, определяющий расстояние между антеннами: d = δ / c2_bas. Все параметры объявлены в секции "public" и дублируются в массиве "params" для единообразного доступа из тестового стенда.
В секции "private" объявлены четыре массива, не имеющие аналога в родительском классе. Массив "V" хранит скорости всех жуков по всем измерениям в плоском формате. Массивы "fR" и "fL" хранят значения фитнеса, вычисленные на позициях правой и левой антенны соответственно — по одному значению на жука. Массив "Vmax" хранит максимально допустимую скорость по каждому измерению, вычисляемую как половина ширины диапазона поиска.
Переменная "delta" хранит текущий размер шага BAS, который уменьшается на каждой итерации. Переменная "d_ant" хранит текущее расстояние между антеннами, пересчитываемое синхронно с "delta". Переменная "omega" хранит текущий инерционный вес, пересчитываемый на каждой BSO-итерации. Переменная "phase" принимает значения от минус единицы до двух и определяет, какое действие выполняется в текущем такте Moving/Revision. Переменная "totalBSOepochs" содержит общее число полных BSO-итераций, доступных в рамках выделенного бюджета оценок, а "bsoEpoch" — счётчик выполненных итераций.
Вспомогательный метод "Idx" принимает номер жука и номер координаты и возвращает линейный индекс для доступа к плоскому массиву скоростей "V". Метод "Clamp" ограничивает значение "val" рамками от "minV" до "maxV": если значение меньше минимума, возвращает минимум, если больше максимума — максимум, иначе возвращает исходное значение.
//———————————————————————————————————————————————————————————————————— class C_AO_BSO_Beetle : public C_AO { public: //---------------------------------------------------------- ~C_AO_BSO_Beetle () { } C_AO_BSO_Beetle () { ao_name = "BSO(Beetle)"; ao_desc = "Beetle Swarm Optimization"; ao_link = "https://www.mql5.com/ru/articles/21292"; popSize = 50; lambda = 0.5; c1_pso = 4.0; c2_pso = 1.5; omega_max = 0.9; omega_min = 0.4; eta = 0.95; delta0 = 1.0; c2_bas = 2.0; ArrayResize (params, 9); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lambda"; params [1].val = lambda; params [2].name = "c1"; params [2].val = c1_pso; params [3].name = "c2"; params [3].val = c2_pso; params [4].name = "omega_max"; params [4].val = omega_max; params [5].name = "omega_min"; params [5].val = omega_min; params [6].name = "eta"; params [6].val = eta; params [7].name = "delta0"; params [7].val = delta0; params [8].name = "c2_bas"; params [8].val = c2_bas; } void SetParams () { popSize = (int)params [0].val; lambda = params [1].val; c1_pso = params [2].val; c2_pso = params [3].val; omega_max = params [4].val; omega_min = params [5].val; eta = params [6].val; delta0 = params [7].val; c2_bas = params [8].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //------------------------------------------------------------------ double lambda; // баланс PSO/BAS [0,1] double c1_pso; // когнитивный коэффициент PSO double c2_pso; // социальный коэффициент PSO double omega_max; // макс инерционный вес double omega_min; // мин инерционный вес double eta; // коэффициент затухания шага BAS double delta0; // начальный размер шага BAS double c2_bas; // d = delta / c2_bas private: //--------------------------------------------------------- double V []; // скорости жуков [popSize * coords] double fR []; // фитнес правой антенны [popSize] double fL []; // фитнес левой антенны [popSize] double Vmax []; // макс скорость [coords] double delta; double d_ant; double omega; int phase; int totalBSOepochs; int bsoEpoch; int Idx (int i, int c) { return i * coords + c; } double Clamp (double val, double minV, double maxV) { if (val < minV) return minV; if (val > maxV) return maxV; return val; } }; //————————————————————————————————————————————————————————————————————
Метод "Init" принимает массивы границ поиска "rangeMinP", "rangeMaxP" и шагов дискретизации "rangeStepP", а также целое число "epochsP" — количество вызовов "Moving", которое будет совершено за весь цикл оптимизации. В начале вызывается "StandardInit" из родительского класса, который инициализирует генератор случайных чисел, запоминает размерность пространства, создаёт массив агентов размером "popSize" и вызывает S_AO_Agent::Init для каждого агента, устанавливая фитнесы в минус бесконечность и выделяя память под массивы координат.
После стандартной инициализации метод выделяет память под четыре кастомных массива: "V" размером (popSize * coords), "fR" и "fL" размером "popSize", "Vmax" размером "coords". Затем вычисляет максимальные скорости: для каждого измерения "Vmax" равен половине ширины диапазона поиска.
Далее для каждого жука генерируется случайная начальная позиция (a [i].cP) в пределах области поиска и случайная начальная скорость "V" в пределах от минус "Vmax" до плюс "Vmax". Поля (a [i].fB) уже установлены в минус бесконечность вызовом S_AO_Agent::Init, поэтому дополнительная инициализация не требуется.
Устанавливается начальный размер шага "delta" равный "delta0" и расстояние между антеннами "d_ant" равное (delta / c2_bas). Вычисляется общее число BSO-итераций по формуле (epochsP − 1) / 3: единица вычитается потому, что первый вызов Moving/Revision занят фазой инициализации (phase = −1), а каждая полная BSO-итерация требует трёх вызовов (фазы 0, 1, 2). Если результат меньше единицы, он принудительно устанавливается в единицу. Счётчик "bsoEpoch" обнуляется, "phase" устанавливается в минус единицу.
//———————————————————————————————————————————————————————————————————— bool C_AO_BSO_Beetle::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //--- кастомные массивы (только то, чего нет в родительском классе) ArrayResize (V, popSize * coords); ArrayResize (fR, popSize); ArrayResize (fL, popSize); ArrayResize (Vmax, coords); //--- Vmax --------------------------------------------------------- for (int c = 0; c < coords; c++) { Vmax [c] = (rangeMax [c] - rangeMin [c]) * 0.5; } //------------------------------------------------------------------ for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].cP [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); V [Idx (i, c)] = u.RNDfromCI (-Vmax [c], Vmax [c]); } } //--- параметры BAS ------------------------------------------------ delta = delta0; d_ant = delta / c2_bas; //--- подсчёт итераций BSO ----------------------------------------- totalBSOepochs = (epochsP - 1) / 3; if (totalBSOepochs < 1) totalBSOepochs = 1; bsoEpoch = 0; phase = -1; return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" вызывается внешним кодом для получения координат, на которых нужно вычислить фитнес. Поведение метода полностью определяется текущей фазой.
В фазе минус один выполняется начальная расстановка: для каждого жука координаты из "cP" дискретизируются функцией "SeInDiSp" и записываются в (a [i].c). Функция "SeInDiSp" привязывает непрерывное значение к ближайшему допустимому шагу сетки в пределах границ, обеспечивая совместимость с задачами, где параметры принимают дискретные значения.
В фазе ноль вычисляются позиции правых антенн по формуле (10): для каждого жука и каждого измерения координата правой антенны равна (cP + V * d_ant / 2). Результат дискретизируется и записывается в (a [i].c). Функция "SeInDiSp" автоматически выполняет ограничение в пределы допустимого диапазона, поэтому дополнительный "Clamp" не требуется.
В фазе один аналогично вычисляются позиции левых антенн: координата равна (cP − V * d_ant / 2). Результат дискретизируется и записывается в (a [i].c).
В фазе два обновлённые позиции жуков из "cP" дискретизируются и записываются в (a [i].c) для финальной оценки фитнеса. Код фаз минус один и два идентичен: оба копируют "cP" → c через дискретизацию, но выполняются в разные моменты жизненного цикла.
//———————————————————————————————————————————————————————————————————— void C_AO_BSO_Beetle::Moving () { //--- ФАЗА -1: начальные позиции из cP → c для первой оценки ------- if (phase == -1) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].cP [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } return; } //--- ФАЗА 0: правая антенна — X_rs = cP + V * d/2 ----------------- if (phase == 0) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double xrs = a [i].cP [c] + V [Idx (i, c)] * d_ant / 2.0; a [i].c [c] = u.SeInDiSp (xrs, rangeMin [c], rangeMax [c], rangeStep [c]); } } return; } //--- ФАЗА 1: левая антенна — X_ls = cP - V * d/2 ------------------ if (phase == 1) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { double xls = a [i].cP [c] - V [Idx (i, c)] * d_ant / 2.0; a [i].c [c] = u.SeInDiSp (xls, rangeMin [c], rangeMax [c], rangeStep [c]); } } return; } //--- ФАЗА 2: позиции жуков — cP → c для оценки -------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].cP [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } return; } } //————————————————————————————————————————————————————————————————————
Метод "Revision" вызывается после того, как внешний код вычислил фитнес на координатах, выставленных в "Moving". Поведение определяется текущей фазой.
В фазе минус один выполняется однократная начальная обработка: для каждого жука фитнес начальной позиции (a [i].f) записывается в (a [i].fB), а дискретизированные координаты (a [i].c) копируются в (a [i].cB) — так формируются начальные личные лучшие. Одновременно проверяется, не лучше ли текущий фитнес глобального лучшего "fB", и при необходимости обновляются "fB" и "cB". После обработки всех жуков "phase" переключается на ноль — начинается основной цикл.
В фазе ноль значение (a [i].f) для каждого жука записывается в массив "fR" — это фитнес правых антенн. Никаких обновлений лучших позиций не происходит, фитнес антенн не должен влиять на личные и глобальные лучшие. "Phase" переключается на единицу.
В фазе один выполняется основная вычислительная работа BSO-итерации. Сначала фитнес левых антенн (a [i].f) записывается в массив "fL". Затем вычисляется инерционный вес "omega" по формуле (8): omega = omega_max − (omega_max − omega_min) / totalBSOepochs * (bsoEpoch + 1). Используется bsoEpoch + 1, потому что на первой итерации bsoEpoch равен нулю, а формула предполагает k от 1 до K. Дополнительный клемп гарантирует, что omega не опустится ниже omega_min из-за погрешностей деления.
Далее для каждого жука вычисляется знак разности фитнеса антенн: signVal = sign(fR[i] − fL[i]). Если правая антенна дала лучший фитнес, "signVal" равен плюс единице, если левая — минус единице, при равенстве — нулю. Затем для каждого измерения последовательно вычисляются три величины. BAS-инкремент "xi" по формуле (9): xi = delta * V[idx] * signVal — это произведение текущего шага, текущей скорости и знака, использующее старые значения "V" и "delta" до их обновления. Новая скорость "vNew" по формуле (7): vNew = omega * V[idx] + c1_pso * r1 * (a [i].cB[c] − a [i].cP[c]) + c2_pso * r2 * (cB [c] − a [i].cP [c]), где "r1" и "r2" — независимые случайные числа из отрезка от нуля до единицы, a [i].cB [c] — личная лучшая позиция жука, cB [c] — глобальная лучшая позиция. Скорость ограничивается диапазоном от минус "Vmax" до плюс "Vmax". Новая позиция "xNew" по формуле (6): xNew = a [i].cP [c] + lambda * vNew + (1 − lambda) * xi — взвешенная сумма PSO-компоненты и BAS-компоненты. Позиция ограничивается границами поиска. Обновлённые скорость и позиция записываются обратно в (V [idx]) и (a [i].cP [c]).
После обработки всех жуков выполняется затухание параметров BAS: "delta" умножается на eta по формуле (4), "d_ant" пересчитывается как (delta / c2_bas) по формуле (5). Инкрементируется счётчик "bsoEpoch", "phase" переключается на два.
В фазе два для каждого жука проверяется, улучшился ли фитнес по сравнению с личным лучшим. Обратите внимание, что в "cB" копируются дискретизированные координаты (a [i].c), а не непрерывные (a [i].cP), поскольку фитнес был вычислен именно на дискретизированных координатах. Аналогично проверяется глобальный лучший: если (a [i].f > fB), обновляются "fB" и "cB" класса "C_AO". "Phase" переключается обратно на ноль, начиная новую BSO-итерацию.
Последовательность операций внутри фазы один имеет принципиальное значение и не может быть изменена. Сначала вычисляется BAS-инкремент "xi" на основе старой скорости "V" и старого шага "delta" — это гарантирует, что антенный сигнал использует то же направление, в котором жук двигался при зондировании. Затем вычисляется новая скорость "vNew" по PSO-формуле с текущим "omega". Затем вычисляется новая позиция как комбинация старой позиции, новой скорости и старого BAS-инкремента. И только после обработки всех жуков выполняется затухание "delta" и "d_ant". Если бы "delta" затухала до вычисления "xi", или скорость обновлялась до вычисления "xi", результат был бы некорректен, потому что BAS-инкремент должен соответствовать тем же условиям, при которых антенны оценивали фитнес.
Одна полная BSO-итерация потребляет три вызова Moving/Revision: фаза 0 (правая антенна), фаза 1 (левая антенна + вычисления), фаза 2 (позиция жука). Каждый вызов "Moving" выставляет "popSize" точек для оценки, поэтому одна BSO-итерация расходует 3 * popSize оценок целевой функции. При стандартном бюджете в 10 000 оценок и popSize = 50 это даёт приблизительно 66 полных BSO-итераций — втрое меньше, чем получил бы стандартный PSO при том же бюджете. Дополнительная стоимость оправдана тем, что антенный механизм предоставляет информацию о локальном градиенте без численного дифференцирования, что позволяет каждому шагу быть более точным.
//———————————————————————————————————————————————————————————————————— void C_AO_BSO_Beetle::Revision () { //--- ФАЗА -1: инициализация личных и глобального лучших ----------- if (phase == -1) { for (int i = 0; i < popSize; i++) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, coords); if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } phase = 0; return; } //--- ФАЗА 0: сохранить фитнес правых антенн ----------------------- if (phase == 0) { for (int i = 0; i < popSize; i++) fR [i] = a [i].f; phase = 1; return; } //--- ФАЗА 1: сохранить фитнес левых антенн + обновить ξ, V, cP ---- if (phase == 1) { for (int i = 0; i < popSize; i++) fL [i] = a [i].f; // Формула (8): ω omega = omega_max - (omega_max - omega_min) / (double)totalBSOepochs * (double)(bsoEpoch + 1); if (omega < omega_min) omega = omega_min; for (int i = 0; i < popSize; i++) { double signVal = 0.0; if (fR [i] > fL [i]) signVal = 1.0; else if (fR [i] < fL [i]) signVal = -1.0; for (int c = 0; c < coords; c++) { int idx = Idx (i, c); // Формула (9): ξ = δ * V * sign(fR - fL) double xi = delta * V [idx] * signVal; // Формула (7): V_new = ω*V + c1*r1*(cB_i - cP) + c2*r2*(cB_g - cP) double r1 = u.RNDfromCI (0.0, 1.0); double r2 = u.RNDfromCI (0.0, 1.0); double vNew = omega * V [idx] + c1_pso * r1 * (a [i].cB [c] - a [i].cP [c]) + c2_pso * r2 * (cB [c] - a [i].cP [c]); vNew = Clamp (vNew, -Vmax [c], Vmax [c]); // Формула (6): X_new = X + λ*V_new + (1-λ)*ξ double xNew = a [i].cP [c] + lambda * vNew + (1.0 - lambda) * xi; xNew = Clamp (xNew, rangeMin [c], rangeMax [c]); V [idx] = vNew; a [i].cP [c] = xNew; } } // Формула (4): δ = η*δ, Формула (5): d = δ/c2_bas delta = eta * delta; d_ant = delta / c2_bas; bsoEpoch++; phase = 2; return; } //--- ФАЗА 2: оценка позиций, обновление лучших -------------------- if (phase == 2) { for (int i = 0; i < popSize; i++) { if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, coords); } if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, coords); } } phase = 0; return; } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Алгоритм BSO показал на стандартном тестовом наборе результат 43%, что соответствует среднему общему уровню среди большинства метаэвристик, однако это не позволяет ему войти в рейтинговую таблицу, нижняя граница которой составляет выше 48%.BSO(Beetle)|Beetle Swarm Optimization|50.0|0.5|4.0|1.5|0.9|0.4|0.95|1.0|2.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.863284721848441
25 Hilly's; Func runs: 10000; result: 0.4419698960521393
500 Hilly's; Func runs: 10000; result: 0.2695211726191594
=============================
5 Forest's; Func runs: 10000; result: 0.8504590892687588
25 Forest's; Func runs: 10000; result: 0.4483586443765045
500 Forest's; Func runs: 10000; result: 0.21373784941636523
=============================
5 Megacity's; Func runs: 10000; result: 0.4338461538461539
25 Megacity's; Func runs: 10000; result: 0.2572307692307692
500 Megacity's; Func runs: 10000; result: 0.11098461538461646
=============================
All score: 3.88939 (43.22%)
Визуализация работы алгоритма BSO.

BSO на тестовой функции Hilly

BSO на тестовой функции Forest

BSO на тестовой функции Megacity

BSO на стандартной функции Ackey

BSO на стандартной функции Rastrigin
Ниже наглядно видно на наших стандартных тестовых задачах как алгоритм ведёт себя при увеличении числа итераций. Я решил показать это, чтобы продемонстрировать: даже при 100 000 запусков фитнес-функции (обычно в тестах используем 10 000 запусков) алгоритм застревает и не достигает полной (100%) сходимости.

BSO на стандартных функциях Hilly, Forest, Megacity
По результатам тестирования алгоритм BSO представлен в нашей рейтинговой таблице только ознакомительно.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | ECBO | enhanced_colliding_bodies_optimization | 0,93479 | 0,75747 | 0,32471 | 2,01697 | 0,97436 | 0,77446 | 0,23037 | 1,97919 | 0,88923 | 0,58061 | 0,15224 | 1,62208 | 5,618 | 62,43 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | BO | bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| 26 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 27 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 28 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 29 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 30 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 31 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 32 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 33 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 34 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 35 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 36 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 37 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 38 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 39 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 40 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 41 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 42 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 43 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 44 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 45 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| BSO_beetle | beetle_swarm_optimization | 0,86328 | 0,44196 | 0,26952 | 1,57476 | 0,85045 | 0,44836 | 0,21373 | 1,51254 | 0,43384 | 0,25723 | 0,11098 | 0,80205 | 3,889 | 43,22 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Основная идея BSO — объединить коллективный интеллект роя (PSO) с локальным зондированием антеннами (BAS) — выглядит привлекательно на уровне концепции. Два механизма действительно дополняют друг друга: PSO обеспечивает глобальную ориентацию, а антенный поиск добавляет информацию о локальном градиенте без численного дифференцирования. Однако практическая реализация этого симбиоза выявила ряд ограничений.
Главная структурная проблема — тройной расход бюджета. Каждая итерация BSO потребляет три оценки целевой функции на агента (правая антенна, левая антенна, позиция жука). Дополнительная информация от антенн не компенсирует трёхкратное сокращение числа итераций — каждый шаг точнее, но шагов слишком мало для полноценной конвергенции.
Анализ сходимости показал характерную картину стагнации к концу оптимизации. Экспоненциальное затухание шага "δ" с коэффициентом η = 0.95 приводит к тому, что к 50-й итерации "δ" уменьшается примерно в 13 раз, а расстояние между антеннами сужается до значений, при которых разница фитнеса правой и левой антенны становится пренебрежимо малой. BAS-инкремент "ξ" фактически обнуляется, и алгоритм вырождается в PSO с уменьшенным бюджетом. Более того, при малом "δ" даже формально ненулевой "ξ" настолько мал, что его вклад подавляется PSO-компонентой. Таким образом, антенный механизм, составляющий суть алгоритма, работает преимущественно на начальных итерациях и затухает задолго до завершения оптимизации.
На тестовых функциях малой размерности наблюдается разброс результатов. Это объясняется совокупностью факторов: малое число итераций (из-за тройного расхода), зависимость знаковой функции sign(fR − fL) от стохастических флуктуаций фитнеса антенн, и высокая чувствительность BAS-компоненты к направлению вектора скорости — на малом числе измерений каждый компонент скорости вносит существенный вклад, и ошибка в определении направления антеннами сильнее влияет на траекторию.
Параметр "λ", управляющий балансом PSO и BAS, является ключевой, но трудно настраиваемой характеристикой. При λ = 1 алгоритм превращается в PSO с тройным расходом бюджета (худший вариант), при λ = 0 — в рой независимых BAS-агентов без коллективного обмена (тоже неэффективно). Оптимальное значение зависит от ландшафта целевой функции и не может быть определено заранее, что снижает робастность алгоритма на разнородных тестовых наборах.
Следует отметить, что BSO обладает потенциалом для модификаций: адаптивное управление "λ" в зависимости от стадии поиска, более медленное затухание "δ", или гибридная стратегия, при которой антенные оценки выполняются не на каждой итерации, а периодически — всё это могло бы повысить эффективность. Однако в базовом варианте, описанном в оригинальной статье, алгоритм демонстрирует средние показатели.
BSO занимает позицию ниже рейтинговой таблицы с результатом 43%, что ставит его в один ряд с другими алгоритмами, чьи оригинальные концепции интересны, но практическая эффективность ограничена конструктивными особенностями.
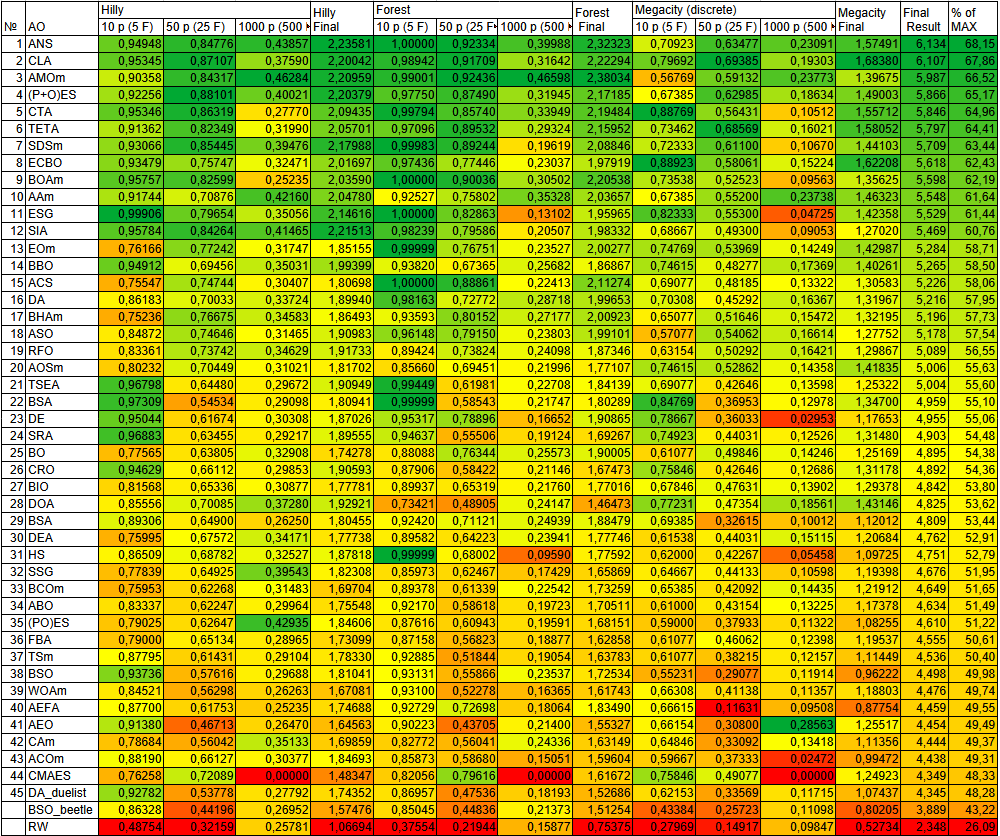
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
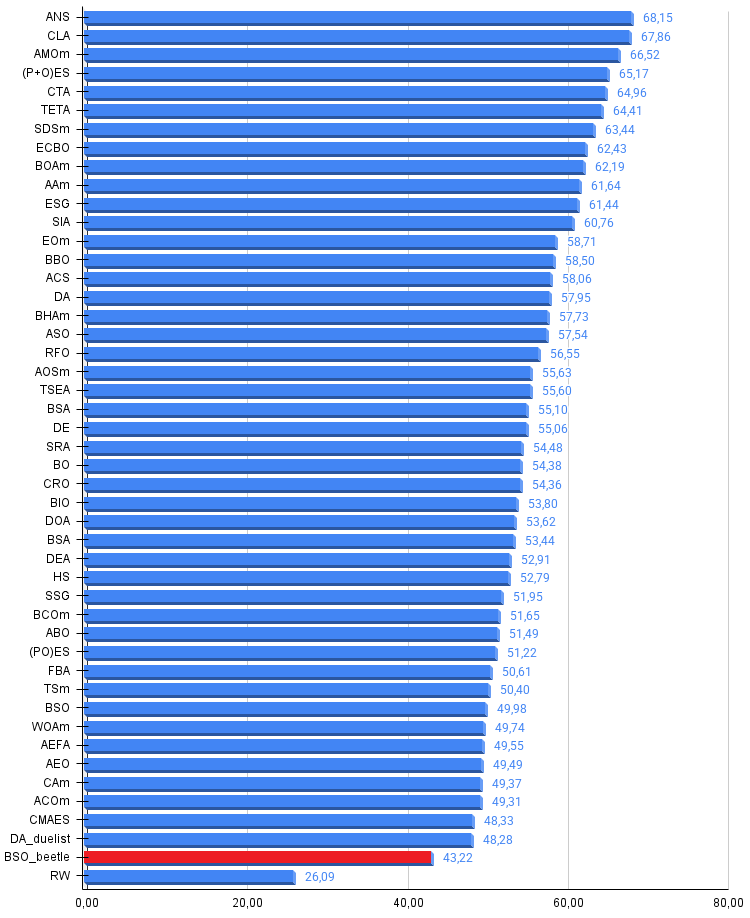
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма BSO_beetle:
Плюсы:
- Не обнаружено.
Минусы:
- Большое количество параметров.
- Застревает.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_BSO_beetle.mq5 | Скрипт | Испытательный стенд для BSO_beetle |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Особенности написания Пользовательских Индикаторов
Особенности написания Пользовательских Индикаторов
 Разрабатываем мультивалютный советник (Часть 31): Секреты шага создания проекта оптимизации (I)
Разрабатываем мультивалютный советник (Часть 31): Секреты шага создания проекта оптимизации (I)
 Возможности Мастера MQL5, которые вам нужно знать (Часть 62): Использование паттернов ADX и CCI с обучением с подкреплением TRPO
Возможности Мастера MQL5, которые вам нужно знать (Часть 62): Использование паттернов ADX и CCI с обучением с подкреплением TRPO
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
