
Алгоритм эхолокации дельфинов — Dolphin Echolocation Algorithm (DEA)
Содержание
Введение
С каждой новой статьей мы становимся все ближе к нашей цели — поиску достойного алгоритма для решения оптимизационных задач нашими торговыми роботами. Исследуем еще один новый алгоритм, подсмотренный у природы, основой которого является возможность эхолокации у некоторых морских животных.
Представьте себе дельфина, охотящегося в темных глубинах океана. Видимость практически нулевая, но это не мешает ему успешно находить добычу. Секрет кроется в удивительной способности — дельфин издает серию щелчков и по отраженному эху создает точную картину окружающего пространства. Интересный факт, частота этих щелчков меняется: редкие щелчки при общем поиске и частые — когда цель близка. Именно эта необычная стратегия легла в основу алгоритма оптимизации DEA (Dolphin Echolocation Algorithm).
В мире оптимизации мы часто сталкиваемся с похожей задачей — нужно найти лучшее решение в огромном пространстве возможностей, не имея полной картины. Как дельфин в океане, мы начинаем с широкого поиска и постепенно фокусируемся на наиболее перспективных областях.
Реализация алгоритма
Чтобы лучше понять принцип работы алгоритма, представим себе следующую ситуацию. Вы с друзьями ищете золото на большом пляже, вооружившись металлоискателями. В начале поиска логично разойтись по всей территории — так больше шансов наткнуться на что-то интересное. Но как только кто-то из вас слышит сильный сигнал, он сообщает остальным, и постепенно вся команда начинает концентрироваться в перспективных местах. К концу поиска все копают рядом с самым сильным сигналом. Это и есть суть алгоритма эхолокации дельфинов.
В алгоритме роль дельфинов играют поисковые агенты — точки в пространстве решений. Каждый такой "дельфин" представляет собой потенциальное решение задачи. Например, если мы ищем минимум простой функции y = x², то один дельфин может находиться в точке x = -3 (где y = 9), другой в точке x = 1 (где y = 1), а третий случайно окажется в точке x = 0 (где y = 0) — это и будет наш чемпион.
Но как дельфины обмениваются информацией? Здесь вступает в игру концепция эффективного радиуса, обозначаемого как "Re". Подумайте, как далеко распространяется свет от фонарика. При Re = 1 у нас узкий луч, освещающий только ближайшую область. При Re = 3 свет распространяется шире, охватывая больше пространства. А при Re = 5 и выше мы получаем практически прожектор. В контексте алгоритма это означает, что информация о хорошем решении распространяется на соседние области, причем, сила этого влияния убывает с расстоянием.
Вся эта информация накапливается в виде "карты перспективности", которую алгоритм называет накопленной пригодностью "AF". Представьте тепловую карту города, где "горячие" зоны показывают места с высокой активностью. В нашем случае "горячие" зоны — это области, где дельфины нашли хорошие решения (добычу). Чем больше успешных находок в определенной области, тем "горячее" она становится, привлекая других дельфинов.
Однако, алгоритм умнее простого скопления в одном месте. Он использует параметр, называемый предопределенной вероятностью "PP", который контролирует баланс между исследованием новых территорий и эксплуатацией уже найденных хороших мест. В начале, когда "PP" низкий, около 0.1 алгоритм экспериментирует, а далее, когда "PP" около 0.5 он уже больше полагается на проверенные подходы, и уже перед "PP" приближающимся к 1 использует только самые эффективные методы.
Рассмотрим конкретный пример работы алгоритма. Допустим, мы ищем самую высокую точку в холмистой местности. В начале поиска наши дельфины случайно разбросаны по всей территории — кто-то в долине, кто-то на склонах, а кому-то повезло оказаться на вершине холма. После оценки высоты каждой позиции алгоритм определяет, что дельфин на вершине нашел лучшее место. Теперь происходит интересное: область вокруг этого удачливого дельфина становится более привлекательной для остальных, но — и это ключевой момент — сама точка, где находится лидер, временно "обнуляется". Это заставляет других дельфинов исследовать соседние области, а не скапливаться в одной точке. Такой подход помогает избежать преждевременной сходимости и найти другие потенциально хорошие решения.
По мере работы алгоритма картина меняется. На 50-й итерации мы видим, что дельфины начинают группироваться в холмистых областях, но все еще сохраняют некоторое разнообразие. К 100-й итерации большинство из них сосредоточено в самых высоких точках местности, а к финалу все дельфины собираются в глобальном максимуме. Эффективность работы алгоритма зависит от правильной настройки параметров.
Выбор эффективного радиуса "Re" важен для баланса между локальным и глобальным поиском. При Re = 1 мы получаем очень точный, но узконаправленный поиск — как если бы искали иголку в стоге сена с помощью лупы. Увеличение "Re" до 3-4 дает сбалансированный подход, похожий на поиск с фонариком. А при "Re" больше 5 алгоритм работает как прожектор, охватывая большие области, но теряя в точности.
Параметр "Power" определяет, насколько резко алгоритм переходит от исследования к эксплуатации. При Power = 1 этот переход плавный и постепенный. Значение Power = 2 (рекомендуемое) дает более выраженный переход, а при Power = 3 и выше переход становится резким, что может быть полезно для определенных типов задач.
Начальная вероятность "PP1" задает стартовый баланс между исследованием и эксплуатацией. Низкое значение (0.05) означает агрессивное исследование пространства, стандартное значение 0.1 обеспечивает хороший баланс, а высокое значение (0.5) приводит к быстрой концентрации на найденных решениях.
Основное преимущество DEA заключается в его адаптивности — алгоритм автоматически регулирует баланс между исследованием новых областей и углублением в перспективные зоны. При этом он остается относительно простым, требуя настройки всего четырех параметров. Механизм распространения информации через накопленную пригодность позволяет эффективно использовать знания о пространстве поиска, а обнуление AF для лучших позиций помогает избегать застревания в локальных оптимумах.
Конечно, у алгоритма есть и некоторые ограничения. Он требует дополнительной памяти для хранения накопленной пригодности всех альтернатив, что может быть проблемой для очень больших пространств поиска. И пожалуй, еще одно — эффективность алгоритма зависит от правильного выбора эффективного радиуса "Re". Ниже представлена схематичная иллюстрация работы алгоритма.
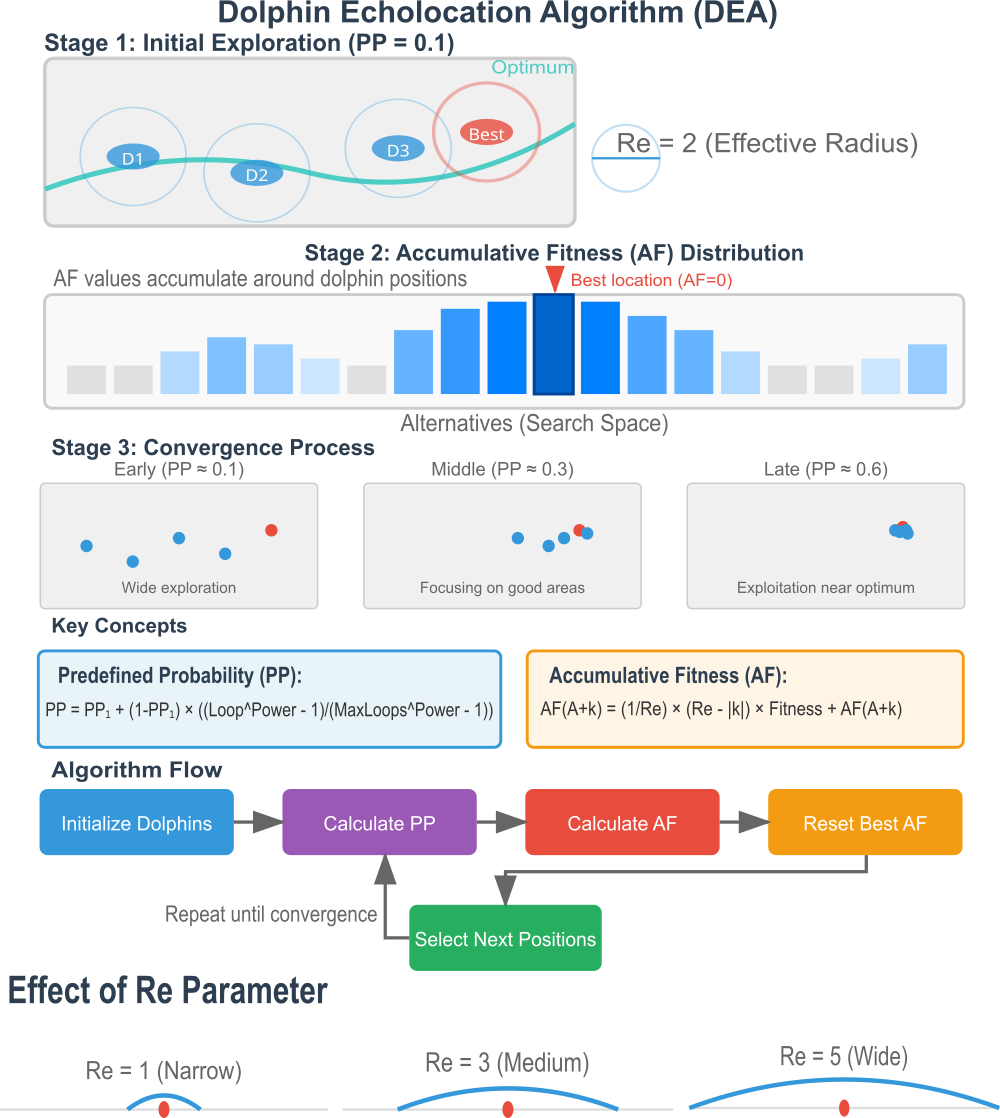
Рисунок 1. Иллюстрация работы алгоритма DEA.
Основные этапы работы алгоритма DEA, изображенные на рисунке:
- Начальное исследование — дельфины (агенты поиска) в случайных позициях с радиусом эхолокации "Re".
- Распределение накопленной пригодности (AF) — как "AF" накапливается вокруг позиций дельфинов.
- Процесс сходимости — три под этапа показывающие переход от исследования к эксплуатации.
Иллюстрация помогает понять, как дельфины используют эхолокацию для поиска оптимума, каким образом информация распространяется через накопленную пригодность, как параметр "Re" влияет на ширину поиска, и как "PP" контролирует баланс между исследованием и эксплуатацией. Ключевые концепции — формулы для PP (предопределенной вероятности) и AF. Блок-схема алгоритма — основные шаги с циклом. Влияние параметра "Re" — визуализация узкого, среднего и широкого радиуса влияния.
Цветовая схема на рисунке: синий - обычные дельфины, красный - лучшее решение, градиенты синего - уровни накопленной пригодности, серый - пространство поиска.
Теперь, имея некоторое представление об алгоритме, можем перейти к написанию детального псевдокода.
Входные параметры:
- Количество дельфинов (поисковых агентов)
- Эффективный радиус эхолокации
- Степень кривой сходимости
- Начальная предопределенная вероятность
- Границы пространства поиска и шаг дискретизации для каждого измерения
Инициализация:
Создание пространства альтернатив:
- Для каждого измерения пространства поиска создать набор возможных альтернатив
- Если задан шаг дискретизации, создать альтернативы с этим шагом от минимума до максимума
- Если шаг не задан, создать 500 равномерно распределенных альтернатив
- Проверить эффективный радиус: он не должен превышать четверть количества альтернатив
Начальное размещение дельфинов:
- Случайно разместить всех дельфинов в пространстве поиска
- Для каждого дельфина вычислить качество его позиции (fitness)
- Инициализировать накопленную пригодность нулями для всех альтернатив
Основной цикл оптимизации:
Повторять заданное количество итераций:
Этап 1. Вычисление предопределенной вероятности
Рассчитать вероятность сохранения лучшей позиции на текущей итерации. В начале процесса эта вероятность равна начальному значению, затем постепенно растет по степенной функции до единицы к концу оптимизации.
Этап 2. Расчет динамического коэффициента адаптации
Вычислить коэффициент, определяющий баланс между локальным и глобальным поиском. Коэффициент равен отношению разницы между лучшим и худшим решениями к сумме отклонений всех решений от лучшего. Когда популяция разнообразна, коэффициент высокий, когда сходится — низкий.
Этап 3. Накопление информации о пригодности
Для каждого дельфина:
- Нормализовать его fitness относительно текущего диапазона в популяции
- Для каждой координаты найти ближайшую альтернативу к позиции дельфина
- Распространить информацию о качестве в радиусе эхолокации вокруг этой альтернативы
- Сила влияния убывает линейно с расстоянием от центра
- На границах пространства применить отражение для сохранения информации
- Добавить малое значение ко всем накопленным пригодностям для избежания нулевых вероятностей
Этап 4. Обнуление информации для лучшей позиции
Найти дельфина с лучшим решением и обнулить накопленную пригодность для альтернатив, соответствующих его координатам. Это предотвращает чрезмерную концентрацию поиска в одной точке.
Этап 5. Выбор новых позиций
Для каждого дельфина и каждой его координаты:
- Если это лучший дельфин, и выпадает вероятность сохранения позиции, оставить координату без изменений
- Иначе, если есть накопленная информация о пригодности, выбрать новую альтернативу пропорционально этой информации методом рулетки
- Если накопленная информация отсутствует или недостаточна:
- с вероятностью, равной динамическому коэффициенту, выполнить локальный поиск в радиусе эхолокации
- иначе, выполнить глобальный поиск, выбрав случайную альтернативу
- Применить ограничения пространства поиска и дискретизацию
Этап 6. Оценка новых позиций
Вычислить качество решения для каждого дельфина в его новой позиции.
Этап 7. Обновление глобальной информации
Обновить записи о лучшем и худшем решениях в популяции. Если найдено решение лучше текущего глобального оптимума, сохранить его.
Завершение:
После выполнения всех итераций вернуть лучшее найденное решение и его качество.
Переходим непосредственно к формированию кода алгоритма DEA.
Напишем структуру "S_Alternative". Она будет предназначена для хранения информации об альтернативе в процессе принятия решений для оптимизации и содержит "value" — значение, характеризующее эту альтернативу, оценку эффективности и "AF" — накопленную пригодность (Accumulated Fitness) для данной альтернативы, это необходимо для оценки "хорошести" альтернативы, когда требуется применять итеративный процесс.
//———————————————————————————————————————————————————————————————————— struct S_Alternative { double value; // значение альтернативы double AF; // накопленная пригодность для этой альтернативы }; //————————————————————————————————————————————————————————————————————
Структура "S_Coordinate" предназначена для представления набора альтернатив, связанных с определенной координатой, "alt" — массив альтернатив, каждая из которых соответствует координате, "count" — переменная, указывающая текущее количество альтернатив, фактически хранящихся в массиве "alt".
//———————————————————————————————————————————————————————————————————— struct S_Coordinate { S_Alternative alt []; // массив альтернатив для данной координаты int count; // количество альтернатив }; //————————————————————————————————————————————————————————————————————
Далее переходим к описанию класса, который реализует непосредственно алгоритм оптимизации (DEA). Класс "C_AO_DEA" является наследником базового класса "C_AO". При создании объекта класса происходит инициализация основных параметров алгоритма:
- popSize — инициализируется размер популяции (количество "дельфинов" или локаций).
- Re — устанавливается начальное значение эффективного радиуса поиска.
- Power — задается степень кривой сходимости.
- PP1 — инициализируется фактор сходимости для первой итерации.
Метод "SetParams" предназначен для обновления внутренних параметров алгоритма на основе значений, записанных в массиве "params". После извлечения "popSize", "Re", "Power", "PP1" значений выполняется проверка корректности.
Методы:
- Init — предназначен для инициализации алгоритма, принимающий минимальные, максимальные значения и шаги для каждого параметра, а также общее количество эпох (итераций).
- Moving — отвечает за перемещение "дельфинов" в пространстве поиска, это часть основного цикла оптимизации.
- Revision — выполняет корректировку позиций и параметров популяции после перемещения.
Следующие поля используются внутренне для работы алгоритма и не доступны извне класса.
- PP — число с плавающей точкой, представляющее предопределенную вероятность для текущей итерации, используемую для стохастических решений, currentEpoch — значение, отслеживающее текущую эпоху (итерацию) алгоритма.
- totalEpochs — значение, хранящее общее запланированное количество эпох.
- coeffA — динамический коэффициент, используемый для выбора позиций.
- coordData — массив структур, где каждая "S_Coordinate" содержит массив альтернатив и их количество для определенной координаты.
- CalculatePP — предназначен для вычисления значения "PP" (предопределенной вероятности) на текущей итерации.
- CalculateAccumulativeFitness — вычисляет накопленную пригодность для каждой альтернативы.
- ResetAFforBestLocation — сбрасывает значения накопленной пригодности для наилучших локаций.
- SelectNextLocations — выбирает следующие позиции для "дельфинов" на основе текущего состояния.
- FindNearestAlternative — ищет ближайшую альтернативу по заданным координатам и значению.
- CalculateCoefficientA — вычисляет динамический коэффициент "coeffA".
В целом, данный класс "C_AO_DEA" готов к использованию для поиска решений в многомерном пространстве. Он имеет открытые методы для инициализации и выполнения основных шагов оптимизации, а также закрытые методы и данные, реализующие внутреннюю логику алгоритма.
//———————————————————————————————————————————————————————————————————— class C_AO_DEA : public C_AO { public: //---------------------------------------------------------- ~C_AO_DEA () { } C_AO_DEA () { ao_name = "DEA"; ao_desc = "Dolphin Echolocation Algorithm"; ao_link = "https://www.mql5.com/ru/articles/18495"; popSize = 100; // NL - количество локаций (дельфинов) Re = 2; // эффективный радиус поиска Power = 2.0; // степень кривой сходимости PP1 = 1.0; // фактор сходимости первой итерации ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "Re"; params [1].val = Re; params [2].name = "Power"; params [2].val = Power; params [3].name = "PP1"; params [3].val = PP1; } void SetParams () { popSize = (int)params [0].val; Re = (int)params [1].val; Power = params [2].val; PP1 = params [3].val; // Проверка корректности параметров if (Re < 0) Re = 0; if (PP1 < 0.0) PP1 = 0.0; if (PP1 > 1.0) PP1 = 1.0; if (Power < 0.1) Power = 0.1; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //------------------------------------------------------------------ int Re; // эффективный радиус поиска double Power; // степень кривой сходимости double PP1; // фактор сходимости первой итерации private: //--------------------------------------------------------- double PP; // предопределенная вероятность для текущей итерации int currentEpoch; // текущая эпоха int totalEpochs; // общее количество эпох double coeffA; // динамический коэффициент для выбора позиций S_Coordinate coordData []; // данные по координатам (альтернативы и AF) void CalculatePP (); void CalculateAccumulativeFitness (); void ResetAFforBestLocation (); void SelectNextLocations (); int FindNearestAlternative (int coord, double value); void CalculateCoefficientA (); }; //————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_DEA" выполняет инициализацию алгоритма (DEA). Он принимает в качестве входных параметров минимальные и максимальные значения для каждой переменной, шаги изменения каждой переменной, и общее количество эпох для оптимизации. Сначала метод вызывает базовый метод "StandardInit" для выполнения стандартной инициализации общих параметров алгоритма и, если эта инициализация не удалась, возвращает "false". Затем инициализируются переменные, отслеживающие текущую и общую эпохи выполнения алгоритма.
После этого, создается структура данных "coordData" для хранения информации о каждой координате (переменной) пространства поиска. Для каждой координаты определяется число возможных альтернативных значений. Если для координаты задан шаг изменения, количество альтернатив вычисляется на основе границ и шага. Если шаг не задан (равен нулю), полагается, что координата непрерывная, и для нее устанавливается фиксированное количество альтернатив.
Затем выполняется проверка и, при необходимости, корректировка параметра "Re" (радиус поиска), чтобы он не превышал четверть от количества альтернатив для каждой координаты. После этого, выделяется память для хранения альтернативных значений для каждой координаты.
В конце, цикл заполняет массив альтернативных значений для каждой координаты, равномерно распределяя их между минимальным и максимальным значениями. Если шаг задан, альтернативные значения вычисляются с использованием этого шага. Если шаг не задан, используется дискретизация пространства между заданными границами. Также, для каждой альтернативы инициализируется связанное с ней значение "AF" ("Accumulative Fitness" — накопленная пригодность) нулем. Если все этапы инициализации успешно завершены, метод возвращает "true".
//———————————————————————————————————————————————————————————————————— //--- Инициализация bool C_AO_DEA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ currentEpoch = 0; totalEpochs = epochsP; // Инициализация структуры данных для координат ArrayResize (coordData, coords); // Создаем альтернативы для каждой координаты for (int c = 0; c < coords; c++) { if (rangeStep [c] != 0) { coordData [c].count = (int)((rangeMax [c] - rangeMin [c]) / rangeStep [c]) + 1; } else { coordData [c].count = 500; } // Проверяем, что Re не слишком большой для количества альтернатив if (Re > coordData [c].count / 4) Re = coordData [c].count / 4; ArrayResize (coordData [c].alt, coordData [c].count); // Заполняем альтернативы for (int i = 0; i < coordData [c].count; i++) { if (rangeStep [c] != 0) { coordData [c].alt [i].value = rangeMin [c] + i * rangeStep [c]; } else { coordData [c].alt [i].value = rangeMin [c] + (rangeMax [c] - rangeMin [c]) * i / (coordData [c].count - 1); } coordData [c].alt [i].AF = 0.0; } } return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" реализует один основной шаг алгоритма (DEA), соответствующий определенной итерации процесса оптимизации. Если это первая итерация, выявляется с помощью флага "revision", происходит начальное случайное присвоение координат популяции. Для каждого участка (элемента популяции) и для каждой переменной в диапазоне задаются случайные значения. Эти значения проходят коррекцию с учетом границ и шага изменения для обеспечения допустимых решений. После этого устанавливается флаг, инициализация выполнена, и метод завершает работу в этом цикле.
Когда инициализация уже произведена, счетчик текущей эпохи (итерации) увеличивается на единицу. Затем выполняются ключевые этапы алгоритма: определяются показатели эффективности для каждого решения в текущей популяции, которые показывают, насколько хорошо они соответствуют задаче. Рассчитывается коэффициент "a". На основе показателей качества определяется обобщенная мера пригодности каждого решения и для него сбрасывается индекс "AF", что позволяет сосредоточить поиск в области наилучших решений. На основе текущей информации и расчетных коэффициентов выбираются следующие расположения (позиции) для представления и перемещения решений в пространстве поиска.
В целом, метод "Moving" реализует один цикл итерации алгоритма DEA, последовательно выполняя ключевые шаги обновления и улучшения решений в процессе поиска оптимума.
//———————————————————————————————————————————————————————————————————— //--- Основной шаг алгоритма (согласно Algorithm 1) void C_AO_DEA::Moving () { // Начальная инициализация if (!revision) { for (int p = 0; p < popSize; p++) { for (int c = 0; c < coords; c++) { a [p].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [p].c [c] = u.SeInDiSp (a [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); a [p].cB [c] = a [p].c [c]; } } revision = true; return; } // Увеличиваем счетчик эпох currentEpoch++; // Шаги алгоритма DEA согласно Algorithm 1: // 1. Вычисляем PP для текущей итерации CalculatePP (); // 2. Рассчитываем динамический коэффициент a CalculateCoefficientA (); // 3. Вычисляем накопленную пригодность CalculateAccumulativeFitness (); // 4. Находим лучшую локацию и сбрасываем для нее AF ResetAFforBestLocation (); // 5. Выбираем следующие позиции SelectNextLocations (); } //————————————————————————————————————————————————————————————————————
Следующий метод "CalculatePP" отвечает за расчет предопределенной вероятности (PP), используется в процессе принятия решений внутри алгоритма. Если общее число эпох (итераций) равно единице или меньше, то вероятность устанавливается равной заранее заданному начальному значению (PP1). В этом случае, дальнейший расчет не требуется, и метод завершается.
Если же число эпох больше одного, то значение "PP" вычисляется на основе заданной формулы, которая учитывает текущую эпоху и включает следующую логику: рассчитывается степень, являющаяся функцией текущей эпохи, возведенной в степень (Power), и из этого вычитается единица, аналогично вычисляется степень для общего числа эпох.
Значение "PP" обновляется по формуле, которая постепенно стремится к 1, с учетом текущего прогресса по эпохам. Конкретно, добавляется к начальному значению "PP1" часть, пропорциональная прогрессу, скорректированному с помощью степени и заданных параметров "Power" и "totalEpochs". Если общий показатель степени не равен нулю, происходит деление, чтобы получить текущую вероятность; иначе значение остается равным начальному "PP1".
В итоге, метод динамически изменяет значение вероятности в ходе выполнения алгоритма, обеспечивая баланс между начальным и более «прогрессивным» значением по мере продвижения эпох.
//———————————————————————————————————————————————————————————————————— //--- Вычисление предопределенной вероятности (согласно формуле 5) void C_AO_DEA::CalculatePP () { if (totalEpochs <= 1) { PP = PP1; return; } // PP = PP1 + (1 - PP1) * ((Loop^Power - 1) / (LoopsNumber^Power - 1)) double iterPower = MathPow ((double)currentEpoch, Power) - 1.0; double totalPower = MathPow ((double)totalEpochs, Power) - 1.0; if (totalPower != 0) { PP = PP1 + (1.0 - PP1) * iterPower / totalPower; } else { PP = PP1; } } //————————————————————————————————————————————————————————————————————
Далее представленный метод "CalculateCoefficientA" предназначен для вычисления динамического коэффициента "a", который используется в алгоритме DEA для регулирования процесса поиска. Метод проходится по всей текущей популяции решений и для каждого решения вычисляет разницу между максимально возможной пригодностью "fB" и текущей пригодностью конкретного решения (a[i].f). Эти разницы аккумулируются в сумму.
После накопления суммы значений, коэффициент "a" получают как отношение разности между "fB" и минимальной пригодностью "fW" к полученной сумме. Это позволяет определить динамический коэффициент, который адаптируется в зависимости от текущего состояния популяции и помогает сбалансировать скорость сходимости или исследование пространства поиска.Таким образом, этот метод создает масштабный параметр, который учитывает распределение пригодностей решений и влияет на стратегию их обновления и перемещения в последующих итерациях алгоритма.
//———————————————————————————————————————————————————————————————————— //--- Расчет динамического коэффициента a void C_AO_DEA::CalculateCoefficientA () { double sumFitness = 0.0; for (int i = 0; i < popSize; i++) { sumFitness += fB - a [i].f; } coeffA = (fB - fW) / sumFitness; } //————————————————————————————————————————————————————————————————————
Метод "FindNearestAlternative" предназначен для поиска ближайшей альтернативы заданному значению в рамках конкретной координат и принимает два аргумента: индекс координаты "coord" и значение "value", для которого требуется найти ближайшую альтернативу. Инициализируются и устанавливаются начальные значения для "nearest" (индекс ближайшей альтернативы) и "minDist" (минимальное расстояние).
Цикл проходит по всем альтернативам, связанным с заданной координатой "coord". Для каждой альтернативы вычисляется расстояние между заданным значением "value" и значением альтернативы (coordData[coord].alt[i].value) и если вычисленное расстояние меньше текущего минимального расстояния (minDist), то "minDist" обновляется новым, меньшим значением расстояния, а "nearest" обновляется индексом текущей альтернативы.
После завершения цикла возвращается индекс альтернативы, которая оказалась ближайшей к заданному значению "value" в рамках заданной координаты. Таким образом, метод определяет, какая из доступных альтернатив для указанной координаты наиболее близка к заданному вещественному значению.
//———————————————————————————————————————————————————————————————————— //--- Поиск ближайшей альтернативы int C_AO_DEA::FindNearestAlternative (int coord, double value) { int nearest = 0; double minDist = DBL_MAX; for (int i = 0; i < coordData [coord].count; i++) { double dist = MathAbs (value - coordData [coord].alt [i].value); if (dist < minDist) { minDist = dist; nearest = i; } } return nearest; } //————————————————————————————————————————————————————————————————————
Метод "CalculateAccumulatetiveFitness" предназначен для вычисления накопленной пригодности (AF) для альтернатив, согласно "Algorithm 2". Перед началом расчетов все значения накопленной пригодности для каждой альтернативы в каждой координате очищаются и устанавливаются в ноль. Обнаруживается диапазон пригодностей в текущей популяции решений, вычисляемый как разность между максимальной возможной пригодностью (fB) и минимальной (fW).
Затем ,для каждого агента (дельфина) происходит нормализация его пригодности относительно диапазона, и для каждой координаты поиска определяется ближайшая альтернатива, а в радиусе "Re" вокруг этой альтернативы происходит обновление накопленной пригодности для альтернативы, с учетом отражательного характера границ. Это делается путем взвешенного добавления вкладов, где веса формируются на основе расстояния от ближайшей альтернативы (учитывая границы с отражением), и включают коэффициент, связанный с текущим шагом в радиусе "Re".
В результате работы метода для каждой альтернативы в каждой координате формируются накопленные значения пригодности, учитывающие вклад соседних альтернатив.
//———————————————————————————————————————————————————————————————————— //--- Вычисление накопленной пригодности (согласно Algorithm 2) void C_AO_DEA::CalculateAccumulativeFitness () { // Очищаем накопленную пригодность для всех альтернатив for (int c = 0; c < coords; c++) { for (int i = 0; i < coordData [c].count; i++) { coordData [c].alt [i].AF = 0.0; } } double rangeFF = fB - fW; if (rangeFF == 0.0) rangeFF = DBL_EPSILON; // Для каждого агента (дельфина) for (int i = 0; i < popSize; i++) { // Нормализуем fitness для данного агента double normalizedFitness = (a [i].f - fW) / rangeFF; for (int c = 0; c < coords; c++) { // Находим ближайшую альтернативу для текущей координаты int nearestAlt = FindNearestAlternative (c, a [i].c [c]); // Обновляем накопленную пригодность в радиусе Re // Согласно Algorithm 2: AF(A+k)j = (1/Re) * (Re - |k|) * fitness(i) + AF(A+k)j for (int k = -Re; k <= Re; k++) { int altIndex = nearestAlt + k; // Проверка границ с учетом отражения (reflective characteristic) if (altIndex < 0) { altIndex = -altIndex; // отражение от нижней границы } else if (altIndex >= coordData [c].count) { altIndex = 2 * (coordData [c].count - 1) - altIndex; // отражение от верхней границы } if (altIndex >= 0 && altIndex < coordData [c].count) { double weight = (1.0 / (double)(Re + 1)) * (Re - MathAbs (k) + 1); coordData [c].alt [altIndex].AF += weight * normalizedFitness; } } } } // Добавляем малое значение epsilon ко всем AF для избежания нулевых вероятностей double epsilon = 0.0001; for (int c = 0; c < coords; c++) { for (int i = 0; i < coordData [c].count; i++) { coordData [c].alt [i].AF += epsilon; } } } //————————————————————————————————————————————————————————————————————
Метод "ResetAFforBestLocation" предназначен для сброса накопленной пригодности (AF) для альтернатив, соответствующих местоположению наилучшего решения (агента) в популяции. Сначала метод определяет индекс лучшего решения (агента) в текущей популяции. Он перебирает все решения, находя решение с максимальным значением пригодности (fitness). Индекс решения с максимальной пригодностью сохраняется в переменной "bestIndex".
Для каждой координаты "c" лучшего решения метод определяет ближайшую альтернативу значению координаты лучшего решения в этой координате, используя функцию "FindNearestAlternative", и если найденная альтернатива существует (индекс находится в пределах допустимых значений), то значение накопленной пригодности "AF" для этой конкретной альтернативы обнуляется.
Таким образом, метод сбрасывает "AF" только для тех альтернатив, которые наиболее точно соответствуют координатам лучшего решения. Это делается, чтобы уменьшить влияние этих альтернатив на последующие этапы поиска, потенциально стимулируя исследование других областей пространства поиска.
В результате, пригодность тех координат, что наиболее соответствуют лучшему решению, "обнуляются/сбрасываются", чтобы стимулировать поиск других, возможно более оптимальных решений.
//———————————————————————————————————————————————————————————————————— //--- Сброс AF для лучшей локации (согласно Algorithm 3) void C_AO_DEA::ResetAFforBestLocation () { // Находим индекс лучшего решения int bestIndex = 0; double bestFitness = a [0].f; // Ищем решение с максимальным fitness (т.к. мы всегда максимизируем нормализованный fitness) for (int i = 1; i < popSize; i++) { if (a [i].f > bestFitness) { bestFitness = a [i].f; bestIndex = i; } } // Обнуляем AF для ВСЕХ альтернатив, соответствующих координатам лучшего решения for (int c = 0; c < coords; c++) { // Находим ближайшую альтернативу к координате лучшего решения int nearestAlt = FindNearestAlternative (c, a [bestIndex].c [c]); // Обнуляем AF только для этой альтернативы if (nearestAlt >= 0 && nearestAlt < coordData [c].count) { coordData [c].alt [nearestAlt].AF = 0.0; } } } //————————————————————————————————————————————————————————————————————
Метод "SelectNextLocations" предназначен для выбора следующей позиции для каждого решения в популяции (для каждого дельфина), исходя из вероятностных соображений и с учетом как накопленной пригодности (AF), так и стратегии сохранения лучшей позиции. Метод сначала определяет наилучшее решение в текущей популяции по значению его пригодности. Индекс лучшего решения сохраняется для дальнейшего использования.
Для каждого решения и каждой его координаты выполняется следующий набор действий: если текущее решение является лучшим, и случайное число меньше вероятности "PP", текущая координата этого решения сохраняется без изменений. Это сохраняет предыдущее лучшее решение, однако, если текущее решение не является лучшим и вероятность "PP" не сработала, тогда суммируются все значения "AF" для альтернатив в текущей координате и, если общая сумма "AF" больше небольшого числа (эпсилон), что указывает на наличие ненулевых значений пригодности, выполняется рулетка: случайное число выбирается пропорционально сумме "AF", и координата решения выбирается на основе кумулятивной суммы "AF" альтернатив, что позволяет решениям двигаться к местам с большей пригодностью.
Если же сумма "AF" близка к нулю (все значения "AF" очень малы), выполняется локальный поиск, если случайное число меньше динамического коэффициента "coeffA". В этом случае, выбирается случайное смещение (-Re...+Re) относительно текущего значения, и координата обновляется ближайшим значением. Границы при этом учитываются.
Глобальный поиск (случайный выбор), если случайное число больше "coeffA". В этом случае, выбирается совершенно случайная альтернатива для координаты. В конце работы метода полученное значение координаты ограничивается допустимым диапазоном (rangeMin, rangeMax) и дискретизируется с заданным шагом "rangeStep", чтобы гарантировать, что значение находится в допустимых пределах и соответствует допустимым значениям.
В результате этого метода, координаты каждого решения обновляются с учетом вероятностных весов на основе накопленной пригодности, стратегии "PP" (сохранения лучших), динамического локального и глобального поиска, что позволяет алгоритму эффективно исследовать пространство поиска и искать оптимальные решения.
//———————————————————————————————————————————————————————————————————— //--- Выбор следующих позиций на основе вероятностей void C_AO_DEA::SelectNextLocations () { // Сначала находим индекс лучшего решения int bestIndex = 0; double bestFitness = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f > bestFitness) { bestFitness = a [i].f; bestIndex = i; } } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Для лучшей позиции применяем PP if (i == bestIndex && u.RNDprobab () < PP) { // Сохраняем текущее значение координаты лучшего решения с вероятностью PP continue; } // Выбираем на основе накопленной пригодности double totalAF = 0.0; for (int alt = 0; alt < coordData [c].count; alt++) { totalAF += coordData [c].alt [alt].AF; } if (totalAF > DBL_EPSILON) // Проверяем, что есть ненулевые AF { // Выбор альтернативы на основе рулетки double rnd = u.RNDprobab () * totalAF; double cumSum = 0.0; for (int alt = 0; alt < coordData [c].count; alt++) { cumSum += coordData [c].alt [alt].AF; if (cumSum >= rnd) { a [i].c [c] = coordData [c].alt [alt].value; break; } } } else { // Если все AF практически нулевые, используем случайный выбор // с динамическим коэффициентом coeffA для вероятности локального поиска if (u.RNDprobab () < coeffA) // Используем динамический коэффициент { // Локальный поиск - остаемся рядом с текущей позицией int currentAlt = FindNearestAlternative (c, a [i].c [c]); int shift = u.RNDminusOne (2 * Re + 1) - Re; // случайное смещение в пределах Re int newAlt = currentAlt + shift; // Проверка границ if (newAlt < 0) newAlt = 0; if (newAlt >= coordData [c].count) newAlt = coordData [c].count - 1; a [i].c [c] = coordData [c].alt [newAlt].value; } else { // Глобальный поиск - полностью случайный выбор int randAlt = u.RNDminusOne (coordData [c].count); a [i].c [c] = coordData [c].alt [randAlt].value; } } // Проверка границ и дискретизация a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //————————————————————————————————————————————————————————————————————
Метод "Revision" служит для обновления информации о лучшем и худшем решениях в текущей популяции. Задается индекс лучшего решения, а переменной, хранящей лучший фитнес, присваивается значение худшего из текущего. Это создаёт начальный статус для поиска новых экстремумов. Происходит перебор всех решений в текущей популяции: определяется решение с максимальным значением фитнеса (лучшее решение). Его значение сохраняется, а запомненный индекс обновляется. Также ищется решение с минимальным значением фитнеса (худшее решение). Если было найдено действительно лучшее решение, его координаты копируются в специальный массив или переменную, предназначенную для хранения текущего лучшего решения.
В результате выполнения метода, в текущий момент времени точно известны координаты лучшего и худшего решений в популяции. Это позволяет алгоритму отслеживать динамику поиска и использовать эти данные при принятии решений для улучшения процесса поиска оптимальных решений.
//———————————————————————————————————————————————————————————————————— //--- Обновление лучшего решения void C_AO_DEA::Revision () { int bestIND = -1; fW = fB; // Находим лучшее и худшее решения в текущей популяции for (int i = 0; i < popSize; i++) { // Обновляем лучшее решение if (a [i].f > fB) { fB = a [i].f; bestIND = i; } // Обновляем худшее решение if (a [i].f < fW) { fW = a [i].f; } } // Копируем координаты лучшего решения if (bestIND != -1) { ArrayCopy (cB, a [bestIND].c, 0, 0, WHOLE_ARRAY); } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Теперь посмотрим на результаты. Можно сразу выделить, что алгоритм прекрасно и быстро справляется с различными типами задач.
DEA|Dolphin Echolocation Algorithm|100.0|2.0|2.0|1.0|
=============================5 Hilly's; Func runs: 10000; result: 0.7599517883429889
25 Hilly's; Func runs: 10000; result: 0.6757192867862007
500 Hilly's; Func runs: 10000; result: 0.34170057553968197
=============================
5 Forest's; Func runs: 10000; result: 0.8958173952258406
25 Forest's; Func runs: 10000; result: 0.6422393144820473
500 Forest's; Func runs: 10000; result: 0.23940903266305935
=============================
5 Megacity's; Func runs: 10000; result: 0.6153846153846154
25 Megacity's; Func runs: 10000; result: 0.4403076923076923
500 Megacity's; Func runs: 10000; result: 0.15115384615384736
=============================
All score: 4.76168 (52.91%)
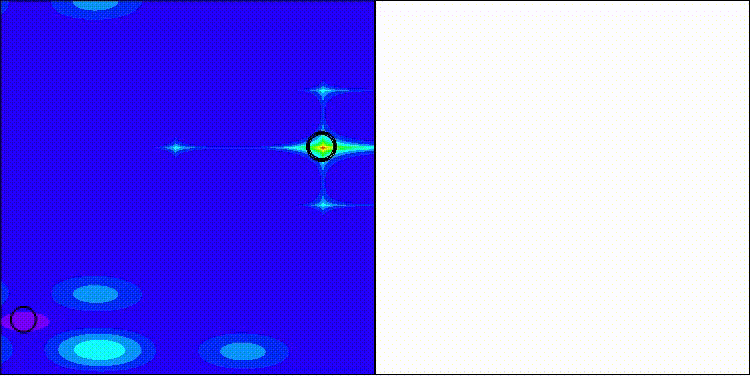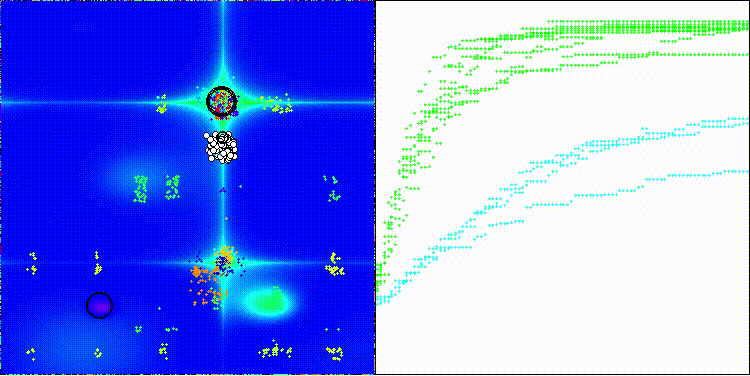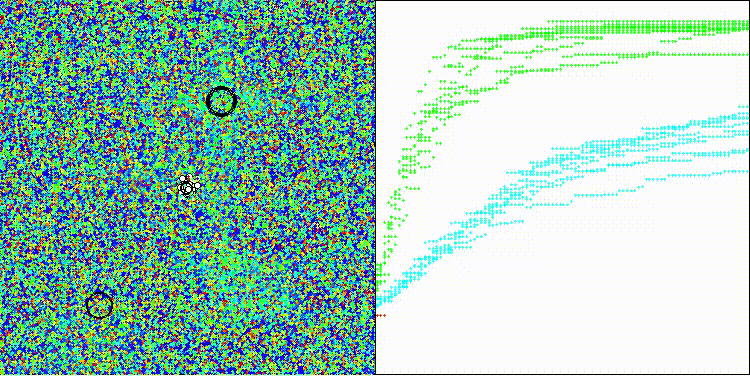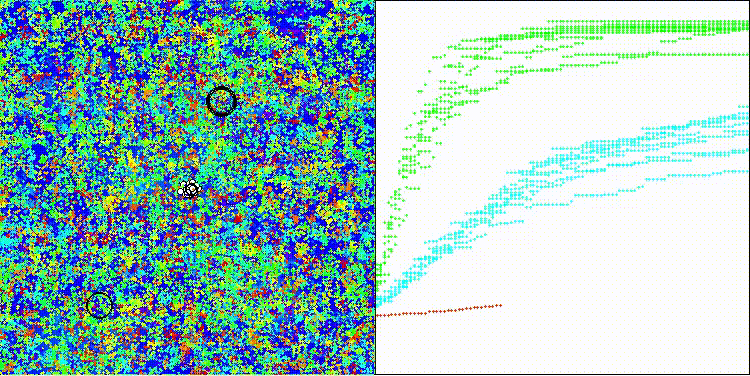
На визуализации заметен разброс результатов на функциях малой размерности (зеленый), хорошие результаты на функциях средней размерности (синий).
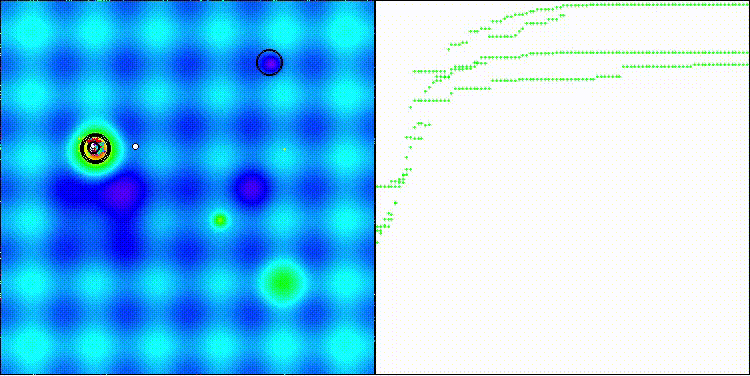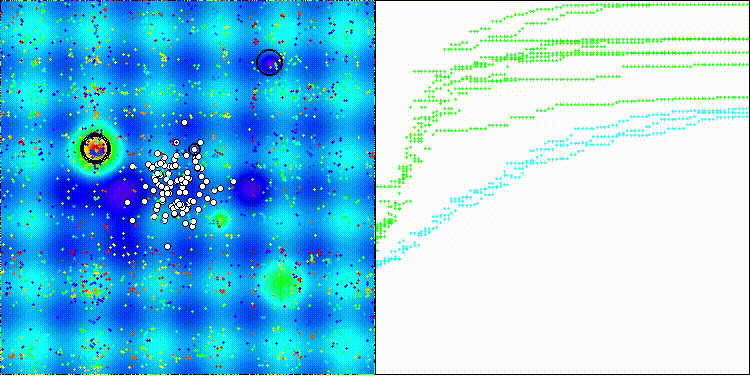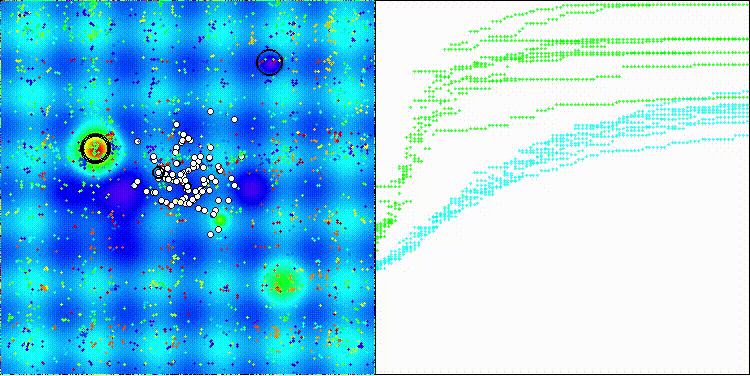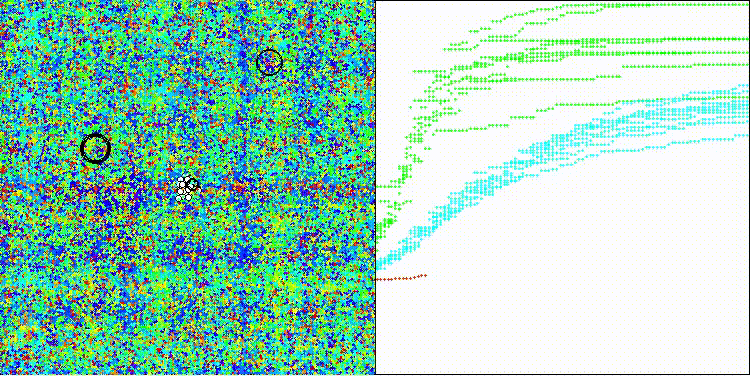
DEA на тестовой функции Hilly
DEA на тестовой функции Forest
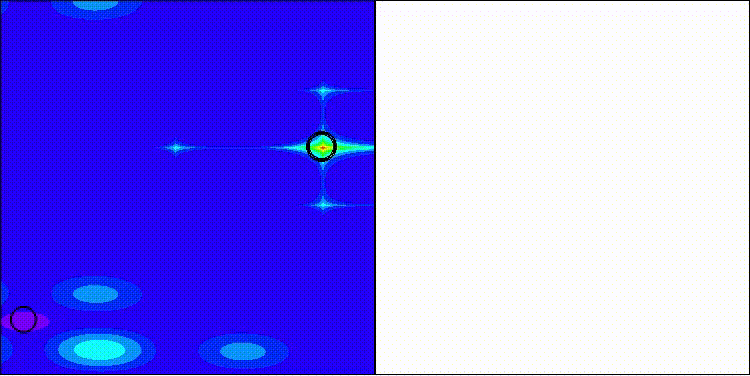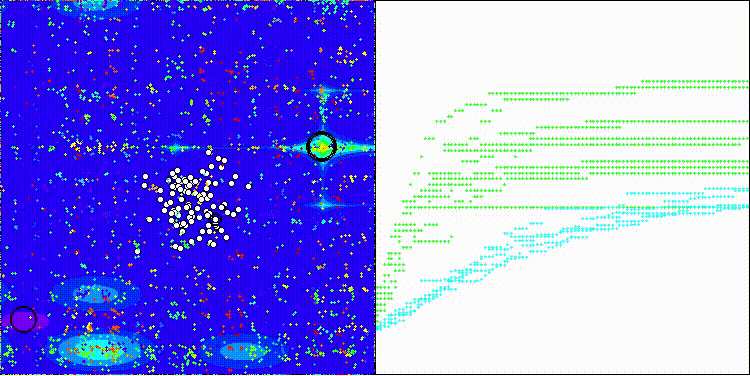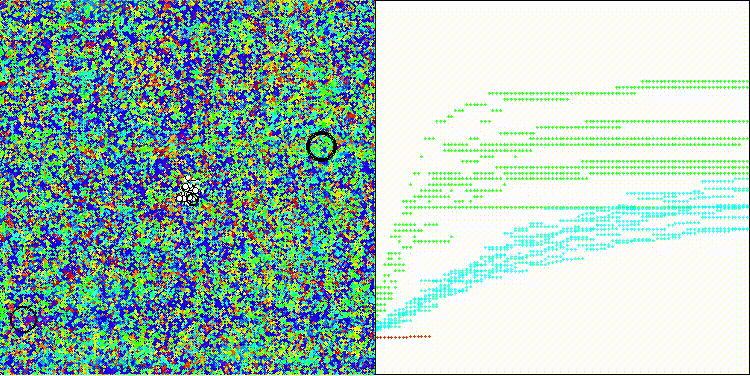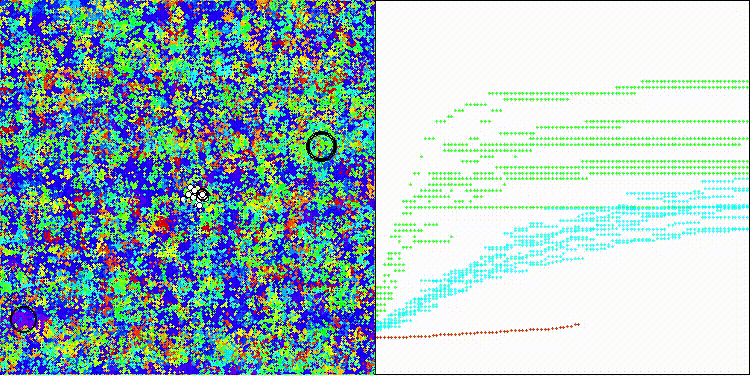
DEA на тестовой функции Megacity
По результатам работы алгоритм DEA занимает 25 место в рейтинговой таблице.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 13 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 14 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 15 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 16 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 17 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 18 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 19 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 20 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 21 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 22 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 23 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 24 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 25 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 26 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 27 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 28 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 29 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 30 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 31 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 32 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 33 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 34 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 35 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 36 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 37 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 38 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 39 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 40 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 41 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 42 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 43 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 44 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 45 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Основными преимуществами алгоритма стали: адаптивное управление поиском: предопределенная вероятность постепенно увеличивается, смещая баланс от исследования к эксплуатации, динамическая адаптация, коллективная память: накопленная пригодность сохраняет и распространяет информацию о перспективных областях, механизм разнообразия: обнуление информации для лучших позиций стимулирует исследование новых областей.
Сила алгоритма кроется в его адаптивной природе. Динамический коэффициент делает его "живым" — он чувствует пульс популяции и подстраивается под ритм задачи. Когда дельфины рассеяны по океану поиска, алгоритм поощряет локальное исследование. Когда они начинают сходиться к цели, он толкает их к новым горизонтам, не давая застрять в иллюзии локального успеха.
Накопленная пригодность — это коллективная память стаи, где каждое открытие оставляет эхо в пространстве решений. Но в отличие от простого накопления, алгоритм умеет забывать — обнуление лучших позиций парадоксальным образом ведет к еще лучшим находкам.
Это не просто метафора — это философия оптимизации, где каждый щелчок эхолокатора несет информацию о пространстве возможностей.
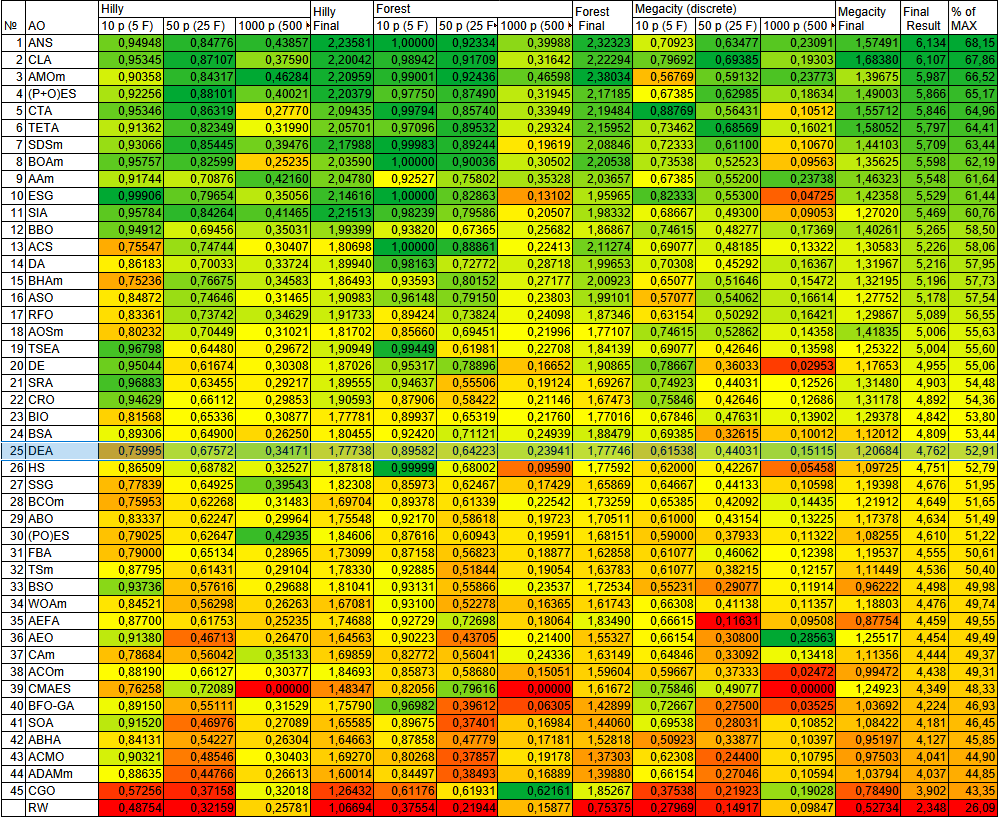
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
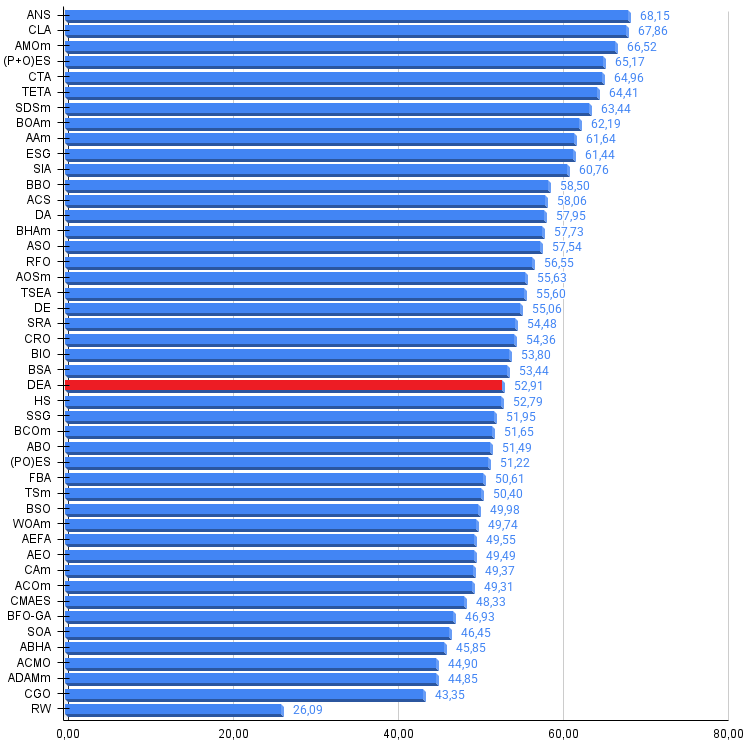
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DEA:
Плюсы:
- Хорошая сходимость на функциях средней и высокой размерности.
- Малое количество внешних параметров.
Минусы:
- Присутствует некоторая склонность к застреванию на задачах малой размерности.
- Ресурсоемкость на функциях большой размерности.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DEA.mq5 | Скрипт | Испытательный стенд для DEA |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Возможности Мастера MQL5, которые вам нужно знать (Часть 48): Аллигатор Билла Вильямса
Возможности Мастера MQL5, которые вам нужно знать (Часть 48): Аллигатор Билла Вильямса
 От начального до среднего уровня: Перегрузка
От начального до среднего уровня: Перегрузка
 Анализ временных разрывов цен в MQL5 (Часть I): Создаем базовый индикатор
Анализ временных разрывов цен в MQL5 (Часть I): Создаем базовый индикатор
 Подробная информация о торговле на основе объема: Подтверждение тренда
Подробная информация о торговле на основе объема: Подтверждение тренда
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования