Популяционные алгоритмы оптимизации: Оптимизация инвазивных сорняков (Invasive Weed Optimization - IWO)

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Метаэвристический алгоритм инвазивных сорняков — это алгоритм оптимизации на основе популяции, который находит общий оптимум оптимизируемой функции путем имитации совместимости и случайности колонии сорняков.
Сорняковый алгоритм оптимизации относится к популяционным алгоритмам, вдохновленным природой, и отражает поведение сорняков на ограниченной территории в борьбе за выживание в течение ограниченного количества времени.

Сорняки — это мощные травы, которые своим наступательным ростом представляют серьезную угрозу для сельскохозяйственных культур. Они показали себя очень устойчивыми и адаптируемыми к изменениям окружающей среды. Поэтому, учитывая их характеристики, получается мощный алгоритм оптимизации. Этот алгоритм пытается имитировать устойчивость, приспособляемость и случайность сообщества сорняков в природе.

Что же такого особенного в сорняках, что дает им преимущество? Сорняки, как правило, являются первопроходцами, распространяясь повсюду с помощью множества механизмов. Таким образом, они редко попадают в категорию вымирающих по виду,
если коротко сформулировать, основные восемь способов, согласно которым происходит адаптация и выживание сорняков в природе:

1. Универсальный генотип. Из проведенных исследований выявлена реакция сорных растений на изменение климата, в большинстве из которых зафиксировано наличие эволюционных изменений у растений.

2. Стратегии жизненного цикла, плодовитость. Сорняки демонстрируют широкий спектр стратегий жизненного цикла, поэтому по мере изменения систем управления обработки почвы, сорняки, ранее не представлявшие серьезную проблему в данной системе земледелия, показывают себя более жизнестойкими. Например, сокращенные системы обработки почвы способствует особенно развитию сорняков многолетников с разными стратегиями жизненного цикла. Кроме того, изменение климата начинает вызывать появление новых ниш для видов или генотипов сорняков, чья история жизни лучше приспособлена к меняющимся условиям. В результате ответа на увеличение выброса в атмосферу углекислого газа сорняки становятся выше и крупнее, и сильнее, а это означает, что смогут производить больше семян и распространять их дальше от более высоких растений из-за аэродинамических свойств. Их плодовитость огромна: например, осот полевой образует до 19000 семян.

3. Быстрая эволюция (всхожесть, неприхотливость роста, конкурентоспособность, селекционная система, производство семян и особенности распространения). Повышенная способность к рассеянию семян и сопутствующее рассредоточение, неприхотливость произрастания дает возможности к выживанию. Сорняки крайне неприхотливы к почвенным условиям, стойко выдерживают резкие колебания температуры и влаги.

4. Эпигенетика. Помимо быстрой эволюции, многие инвазивные растения обладают способностью быстро реагировать на меняющиеся факторы окружающей среды, изменяя экспрессию своих генов. В постоянно меняющейся среде растениям необходимо быть гибкими, чтобы выдерживать такие стрессы, как колебания освещённости, температуры, наличия воды и уровня соли в почве. Чтобы быть гибкими, растения способны самостоятельно подвергаться эпигенетической модификации.

5. Гибридизация. Гибридные виды сорняков часто проявляют гибридную силу, также известную как гетерозис, когда потомство демонстрирует улучшенную биологическую функцию по сравнению с обоими родительскими видами. Как правило, гибрид будет демонстрировать более агрессивный рост с улучшенной способностью распространяться на новые территории и конкурировать в пределах вторгшихся территорий.

6. Устойчивость и толерантность к гербицидам. Отмечен резкий рост случаев устойчивости к гербицидам за последние несколько десятилетий у большинства сорняков.

7. Совместная эволюция сорняков, связанная с деятельностью человека. Благодаря методам борьбы с сорняками, такими как применение гербицидов и пропалывание, сорняки выработали механизмы устойчивости. Они меньше страдают от внешних повреждений при обработке почвы, чем культурные растения. Напротив, эти повреждения часто оказываются даже полезными для распространения сорняков, размножающихся вегетативным путем (например, частями корня, корневищ).

8. Всё более частые климатические перепады предоставляют возможность сорнякам быть более жизнеспособными по сравнению с "тепличными" культурными растениями. Сорняки наносят огромный вред сельскому хозяйству. Менее требовательные к условиям произрастания, они опережают культурные растения в росте и развитии. Поглощая влагу, питательные вещества, солнечный свет, сорняки резко снижают урожай, затрудняют уборку полевых культур, их обмолот, ухудшают качество продукции.

2. Описание алгоритма

Алгоритм инвазийных сорняков вдохновлён процессом роста сорняков в природе. Этот метод был представлен Мехрабианом и Лукасом в 2006 году. Естественно, сорняки сильно разрослись, и этот сильный рост представляет серьезную угрозу для полезных растений. Важной характеристикой сорняков является их устойчивость и высокая приспособляемость в природе, что является основой оптимизации алгоритма IWO. Этот алгоритм можно использовать в качестве основы для эффективных подходов к оптимизации.

IWO — это непрерывный стохастический численный алгоритм, который имитирует колонизирующее поведение сорняков. Во-первых, популяция исходных семян случайным образом распределяется по всему пространству поиска. Эти сорняки, наконец, вырастут и выполнят дальнейшие шаги алгоритма. Алгоритм состоит из семи шагов, которые можно представить в виде псевдо-кода:

1. Посеять семена случайным образом
2. Вычислить FF
3. Посеять семена от сорняков
4. Вычислить FF
5. Объединить дочерние сорняки с родительскими
6. Сортировать все сорняки
7. повторить п.3. до выполнения условия останова

Блок-схема представляет собой работу алгоритма на одной итерации. IWO начинает свою работу с процесса инициализации посевных семян, которые рассеиваются на "поле" пространства поиска случайно и равномерно. После этого предполагаем, что семена проросли и образовали взрослые растения, которые необходимо оценить функцией пригодности.

На следующем этапе, зная приспособленность каждого растения, можем позволить сорнякам размножиться посредством семян, где количество семян пропорционально приспособленности. После этого объединяем проросшие семена с родительскими растениями и сортируем. В целом алгоритм инвазивных сорняков можно считать простым для написания кода, модификации и применения совместно со сторонними приложениями.

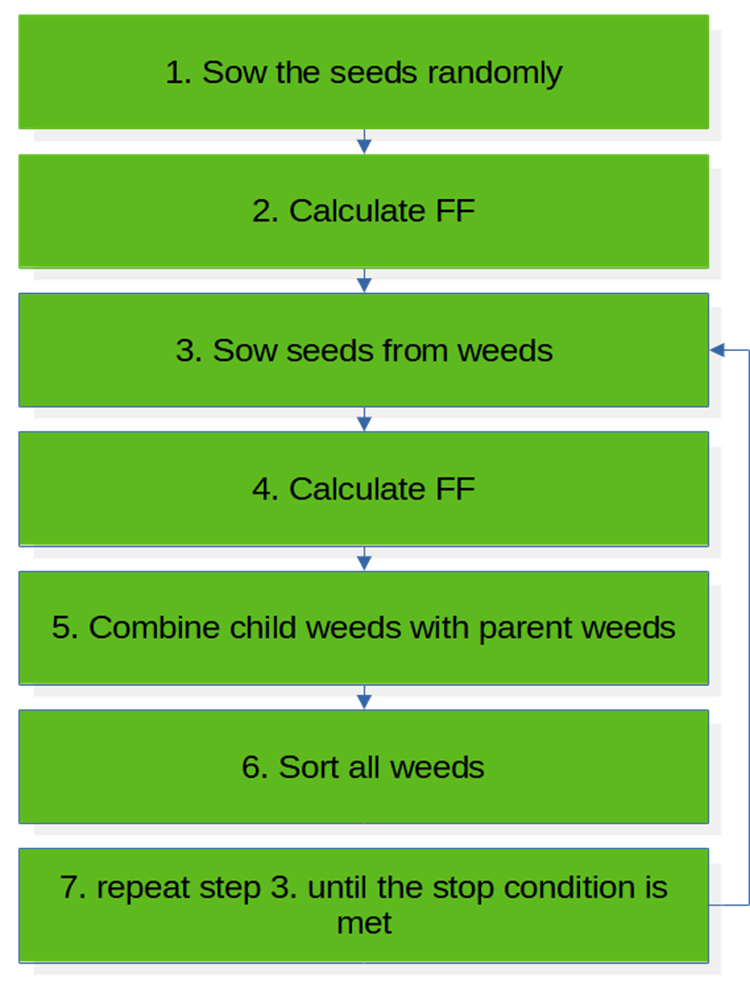
Рисунок 1. Блок-схема алгоритма IWO.

Перейдем к рассмотрению особенностей сорнякового алгоритма. Многие возможности чрезвычайной приспособленности к выживанию сорняков реализованы в алгоритме. Отличительной особенностью колонии сорняков, в отличии от таких алгоритмов, как генетический, пчелиный и некоторые другие, является гарантированный посев семян всеми без исключения растениями колонии. Это обеспечивает возможность оставить потомков даже теми растениями, которые приспособлены хуже всего, так как всегда существует ненулевая вероятность того, что самый худший может находиться ближе всего к глобальному экстремуму.

Каждый из сорняков как мы уже сказали, оставит семена в количестве от минимально возможного до максимально возможного (внешние параметры алгоритма). Естественно, при таких условиях, когда каждое растение оставит как минимум одно или больше семян, дочерних растений получится больше, чем родительских - эта особенность интересно реализована в коде и будет рассмотрена ниже. В общем алгоритм визуально представлен на рисунке 2. Родительские растения разбрасывают семена в количестве пропорционально своей приспособленности.

Так лучшее растение под номером 1 посеяло 6 семян, а растение под номером 6 посеяло только одно семя (одно гарантированное). Проросшие семена дают растения, которые в последствии сортируются вместе с родительскими: это имитация выживания. Из всей отсортированной группы будут отобраны новые родительские растения и жизненный цикл повторится на следующей итерации. Еще одной особенностью того, что существует максимальное и минимальное количество семян, допустимое для каждого растения, в алгоритме есть механизм, позволяющий решить проблему "перенаселения" или не полностью реализованной возможности посева семян.

Для примера возьмем количество семян, один из параметров алгоритма, равным 50, а количество родительских растений 5, минимальное количество семян 1, а максимальное 6. Тогда 5 * 6 = 30 что меньше 50. Как видим из данного примера, возможности посева не реализованы полностью. В этом случае право оставить потомка переходит к следующему по списку, пока разрешённое максимальное количество потомков не будет достигнуто у всех родительских растений. При достижении конца списка право переходит к первому в списке и ему всё же будет разрешено оставить потомка больше, чем ограничено лимитом. 

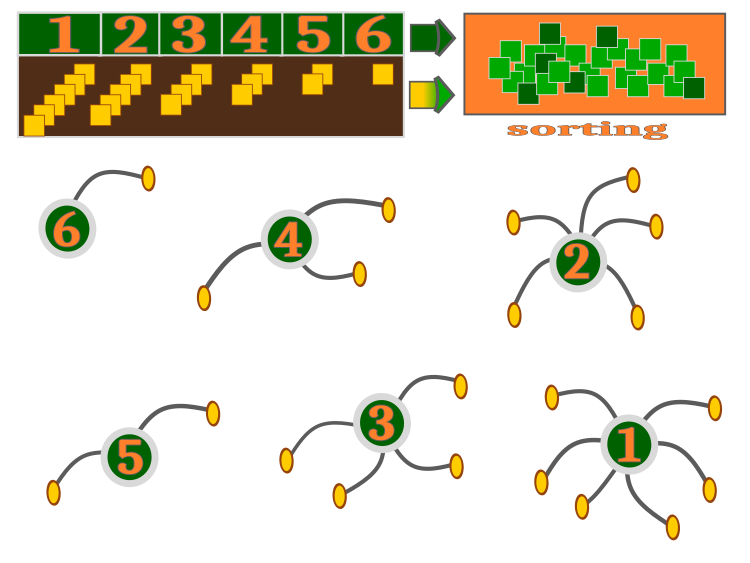
Рисунок 2. Принцип работы алгоритма IWO. Количество потомков пропорционально приспособленности родителя.

Следующим моментом, которому стоит уделить внимание является дисперсия посева. Дисперсия посева в алгоритме — линейная убывающая функция, пропорциональная количеству итераций. Внешними параметрами дисперсии являются нижняя и верхняя граница разброса семян. Таким образом с ростом итераций радиус посева убывает и обеспечивается уточнение найденных экстремумов. Распределение посева по рекомендации авторов алгоритма следует применять нормальное, однако я упростил вычисления и применил кубическую функцию. Функцию дисперсии от количества итераций можно увидеть на рисунке 3.

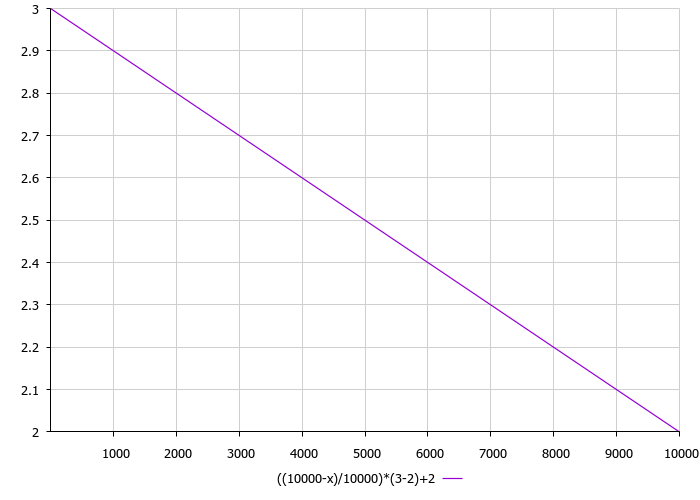
Рисунок 3. Зависимость дисперсии от количества итераций, где 3 максимальная граница а 2 минимальная.

Переходим к рассмотрению кода алгоритма оптимизации инвазивных сорняков — IWO. Код отличается простотой и скоростью исполнения.

Простейшей единицей (агентом) алгоритма является "сорняк", он же и будет описывать семена сорняка, это позволит нам использовать нам однотипные данные для последующей сортировки. Структура состоит из массива координат, переменная для хранения значения фитнесс функции и счетчик количества семян (потомки). Этот счетчик позволит нам контролировать минимальное и максимально допустимое количество семян для каждого растения.

//——————————————————————————————————————————————————————————————————————————————
struct S_Weed
{
  double c []; //coordinates
  double f;    //fitness
  int    s;    //number of seeds
};
//——————————————————————————————————————————————————————————————————————————————

Нам понадобится структура для реализации функции вероятности выбора родителей пропорционально их приспособленности. В данном случае применяется принцип рулетки, который мы уже встречали в алгоритме пчелиной колонии. Переменные start и end отвечают за начало и окончание поля вероятности.

//——————————————————————————————————————————————————————————————————————————————
struct S_WeedFitness
{
  double start;
  double end;
};
//——————————————————————————————————————————————————————————————————————————————

Объявим класс сорнякового алгоритма. Внутри него объявим все необходимые переменные, которые нам понадобятся, здесь как обычно границы и шаг оптимизируемых параметров, массив, описывающий сорняки, а также массив семян, массив лучших глобальных координат и лучшее достигнутое алгоритмом значение фитнесс функции. Также нам понадобится флаг первой итерации sowing и константные переменные параметров алгоритма.

//——————————————————————————————————————————————————————————————————————————————
class C_AO_IWO
{
  //============================================================================
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search
  public: S_Weed weeds     []; //weeds
  public: S_Weed weedsT    []; //temp weeds
  public: S_Weed seeds     []; //seeds
  public: double cB        []; //best coordinates
  public: double fB;           //fitness of the best coordinates

  public: void Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP);    //Maximum iterations

  public: void Sowing      (int iter);
  public: void Germination ();

  //============================================================================
  private: void   Sorting        ();
  private: double SeInDiSp       (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI      (double Min, double Max);
  private: double Scale          (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool Revers);

  private: double vec [];            //Vector
  private: int    ind [];
  private: double val [];
  private: S_WeedFitness wf [];      //Weed fitness
  private: bool   sowing;            //Sowing
  private: int    coordinates;       //Coordinates number
  private: int    numberSeeds;       //Number of seeds
  private: int    numberWeeds;       //Number of weeds
  private: int    totalNumWeeds;     //Total number of weeds
  private: int    maxNumberSeeds;    //Maximum number of seeds
  private: int    minNumberSeeds;    //Minimum number of seeds
  private: double maxDispersion;     //Maximum dispersion
  private: double minDispersion;     //Minimum dispersion
  private: int    maxIteration;      //Maximum iterations
};
//——————————————————————————————————————————————————————————————————————————————

В открытом методе функции инициализации назначим значение константным переменным, проверим входные параметры алгоритма на допустимые значения, так произведение родительских растений на минимально возможное значение семян не может превышать общее количество семян. Сумма родительских растений и семян понадобится для определения массива для выполнения сортировки.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Init (const int    coordinatesP,      //Number of coordinates
                     const int    numberSeedsP,      //Number of seeds
                     const int    numberWeedsP,      //Number of weeds
                     const int    maxNumberSeedsP,   //Maximum number of seeds per weed
                     const int    minNumberSeedsP,   //Minimum number of seeds per weed
                     const double maxDispersionP,    //Maximum dispersion
                     const double minDispersionP,    //Minimum dispersion
                     const int    maxIterationP)     //Maximum iterations
{
  MathSrand (GetTickCount ());
  sowing = false;
  fB     = -DBL_MAX;

  coordinates    = coordinatesP;
  numberSeeds    = numberSeedsP;
  numberWeeds    = numberWeedsP;
  maxNumberSeeds = maxNumberSeedsP;
  minNumberSeeds = minNumberSeedsP;
  maxDispersion  = maxDispersionP;
  minDispersion  = minDispersionP;
  maxIteration   = maxIterationP;


  if (minNumberSeeds < 1) minNumberSeeds = 1;
  if (numberWeeds * minNumberSeeds > numberSeeds) numberWeeds = numberSeeds / minNumberSeeds;
  else numberWeeds = numberWeedsP;

  totalNumWeeds  = numberWeeds + numberSeeds;

  ArrayResize (rangeMax,  coordinates);
  ArrayResize (rangeMin,  coordinates);
  ArrayResize (rangeStep, coordinates);
  ArrayResize (vec,       coordinates);
  ArrayResize (cB,        coordinates);

  ArrayResize (weeds,  totalNumWeeds);
  ArrayResize (weedsT, totalNumWeeds);
  ArrayResize (seeds,  numberSeeds);

  for (int i = 0; i < numberWeeds; i++)
  {
    ArrayResize (weeds  [i].c, coordinates);
    ArrayResize (weedsT [i].c, coordinates);
    weeds [i].f = -DBL_MAX;
    weeds [i].s = 0;
  }
  for (int i = 0; i < numberSeeds; i++)
  {
    ArrayResize (seeds [i].c, coordinates);
    seeds [i].s = 0;
  }

  ArrayResize (ind, totalNumWeeds);
  ArrayResize (val, totalNumWeeds);

  ArrayResize (wf, numberWeeds);
}
//——————————————————————————————————————————————————————————————————————————————

Первый открытый метод, вызываемый на каждой итерации Sowing (). В нём заложена основная логика алгоритма. Для простоты восприятия материала статьи разобьём метод на несколько частей для рассмотрения по отдельности.

Когда алгоритм находится на первой итерации необходимо посеять семена по всему пространству поиска. Обычно это делается случайно и равномерно. После генерации случайных чисел в диапазоне допустимых значений оптимизируемых параметров проверим полученные значения на выход за диапазон и зададим дискретность, установленную параметрами алгоритма. Здесь так же назначим вектор распределения, который нам понадобится при посеве семян далее в коде. Инициализируем значения приспособленности семян минимальным значение double и сбросим счетчик семян (семена станут растениями, у которых будет использоваться счетчик семян).

//the first sowing of seeds---------------------------------------------------
if (!sowing)
{
  fB = -DBL_MAX;

  for (int s = 0; s < numberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      seeds [s].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);

      vec [c] = rangeMax [c] - rangeMin [c];
    }

    seeds [s].f = -DBL_MAX;
    seeds [s].s = 0;
  }

  sowing = true;
  return;
}

В этом участке кода происходит вычисление дисперсии в зависимости от текущей итерации. Как раз в этом месте кода реализуется гарантированное минимальное количество семян для каждого родительского сорняка, о котором мы говорили ранее. Гарантированность минимального количества семян обеспечим двумя циклами, в первом из которых будем перебирать родительские растения, а во втором собственно генерировать новые семена, не забывая при этом увеличивать счетчик семян. Как видим, смысл создания нового потомка заключается в приращении к родительской координате случайного числа с распределением кубической функции с вычисленной ранее дисперсией. Полученное значение новой координаты проверяем на допустимые значения и назначаем дискретность.

//guaranteed sowing of seeds by each weed-------------------------------------
int    pos = 0;
double r   = 0.0;
double dispersion = ((maxIteration - iter) / (double)maxIteration) * (maxDispersion - minDispersion) + minDispersion;

for (int w = 0; w < numberWeeds; w++)
{
  weeds [w].s = 0;

  for (int s = 0; s < minNumberSeeds; s++)
  {
    for (int c = 0; c < coordinates; c++)
    {
      r = RNDfromCI (-1.0, 1.0);
      r = r * r * r;

      seeds [pos].c [c] = weeds [w].c [c] + r * vec [c] * dispersion;
      seeds [pos].c [c] = SeInDiSp (seeds [pos].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
    }

    pos++;
    weeds [w].s++;
  }
}

Этим кодом обеспечим поля вероятностей для каждого из родительских растений пропорционально приспособленности по принципу рулетки. Код выше обеспечивал гарантированное количество семян для каждого из растений в то время, когда здесь количество семян подчиняется случайному закону, поэтому чем более приспособлен сорняк, тем больше он способен оставить семян и наоборот, чем менее приспособлено растение, тем меньше будет давать семян.

//============================================================================
//sowing seeds in proportion to the fitness of weeds--------------------------

//the distribution of the probability field is proportional to the fitness of weeds
wf [0].start = weeds [0].f;
wf [0].end   = wf [0].start + (weeds [0].f - weeds [numberWeeds - 1].f);

for (int f = 1; f < numberWeeds; f++)
{
  if (f != numberWeeds - 1)
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f].f - weeds [numberWeeds - 1].f);
  }
  else
  {
    wf [f].start = wf [f - 1].end;
    wf [f].end   = wf [f].start + (weeds [f - 1].f - weeds [f].f) * 0.1;
  }
}

По полученным полям вероятностей выбираем родительское растение, которому выпадает право оставить потомка. Если счетчик семян достиг максимального разрешенного значения, то право переходит следующему по отсортированному списку. Если достигнут конец списка, тогда право не переходит следующему, а достается первому в списке. А далее формируется дочернее растение по правилу, описанному выше с вычисленной дисперсией.

bool seedingLimit = false;
int  weedsPos = 0;

for (int s = pos; s < numberSeeds; s++)
{
  r = RNDfromCI (wf [0].start, wf [numberWeeds - 1].end);

  for (int f = 0; f < numberWeeds; f++)
  {
    if (wf [f].start <= r && r < wf [f].end)
    {       
      weedsPos = f;
      break;
    }
  }

  if (weeds [weedsPos].s >= maxNumberSeeds)
  {
    seedingLimit = false;
    while (!seedingLimit)
    {
      weedsPos++;
      if (weedsPos >= numberWeeds)
      {
        weedsPos = 0;
        seedingLimit = true;
      }
      else
      {
        if (weeds [weedsPos].s < maxNumberSeeds)
        {
          seedingLimit = true;
        }
      }
    }
  }

  for (int c = 0; c < coordinates; c++)
  {
    r = RNDfromCI (-1.0, 1.0);
    r = r * r * r;

    seeds [s].c [c] = weeds [weedsPos].c [c] + r * vec [c] * dispersion;
    seeds [s].c [c] = SeInDiSp (seeds [s].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }

  seeds [s].s = 0;
  weeds [weedsPos].s++;
}

Второй открытый метод обязательный к исполнению на каждой итерации необходимый после расчета фитнесс функции для каждого дочернего сорняка. Перед применением сортировки поместим проросшие семена в общий массив с родительскими растениями в конец списка, заменив тем самым предыдущее поколение, в котором могли оказаться как потомки, так и родители с предыдущей итерации. Тем самым реализуется уничтожение слабоприспособленных сорняков, как это происходит в природе. После этого применяем сортировку, а первый в полученном списке сорняк будет достоен обновить глобально достигнутое лучшее решение, если конечно оно действительно лучше.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_IWO::Germination ()
{
  for (int s = 0; s < numberSeeds; s++)
  {
    weeds [numberWeeds + s] = seeds [s];
  }

  Sorting ();

  if (weeds [0].f > fB) fB = weeds [0].f;
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы тестового стенда:

2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    C_AO_IWO:50;12;5;2;0.2;0.01
2023.01.13 18:12:29.880    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    5 Rastrigin's; Func runs 10000 result: 79.71791976868334
2023.01.13 18:12:32.251    Test_AO_IWO (EURUSD,M1)    Score: 0.98775
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    25 Rastrigin's; Func runs 10000 result: 66.60305588198622
2023.01.13 18:12:36.564    Test_AO_IWO (EURUSD,M1)    Score: 0.82525
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    500 Rastrigin's; Func runs 10000 result: 45.4191288396659
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    Score: 0.56277
2023.01.13 18:13:14.024    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    5 Forest's; Func runs 10000 result: 1.302934874807614
2023.01.13 18:13:16.678    Test_AO_IWO (EURUSD,M1)    Score: 0.73701
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    25 Forest's; Func runs 10000 result: 0.5630336066477166
2023.01.13 18:13:22.113    Test_AO_IWO (EURUSD,M1)    Score: 0.31848
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    500 Forest's; Func runs 10000 result: 0.11082098547471195
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    Score: 0.06269
2023.01.13 18:14:05.092    Test_AO_IWO (EURUSD,M1)    =============================
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    5 Megacity's; Func runs 10000 result: 6.640000000000001
2023.01.13 18:14:09.102    Test_AO_IWO (EURUSD,M1)    Score: 0.55333
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    25 Megacity's; Func runs 10000 result: 2.6
2023.01.13 18:14:15.191    Test_AO_IWO (EURUSD,M1)    Score: 0.21667
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    500 Megacity's; Func runs 10000 result: 0.5668
2023.01.13 18:14:55.886    Test_AO_IWO (EURUSD,M1)    Score: 0.04723

Достаточно быстрого взгляда, чтобы заметить высокие результаты алгоритма на тестовых функциях. Заметно предпочтение работы на гладких функциях, хотя до сих пор ни один из рассмотренных алгоритмов не показал сходимость на дискретных функциях лучше, чем на гладких, что объясняется сложностью функций Forest и Megacity для всех без исключения алгоритмов. Возможно, хотя я очень сомневаюсь, что в будущем нам попадет на тесты какой-то алгоритм, который будет решать дискретные функции лучше, чем гладкие.

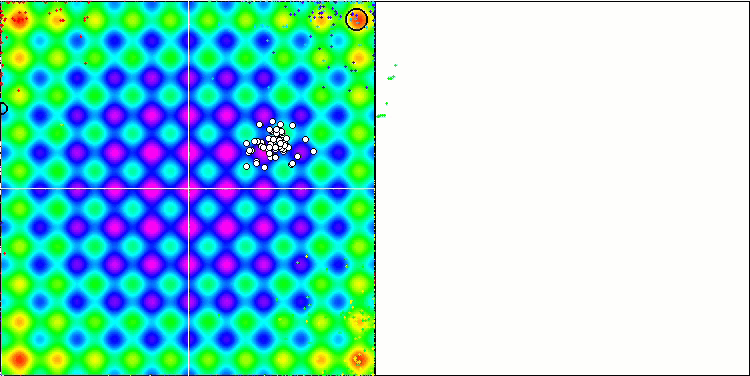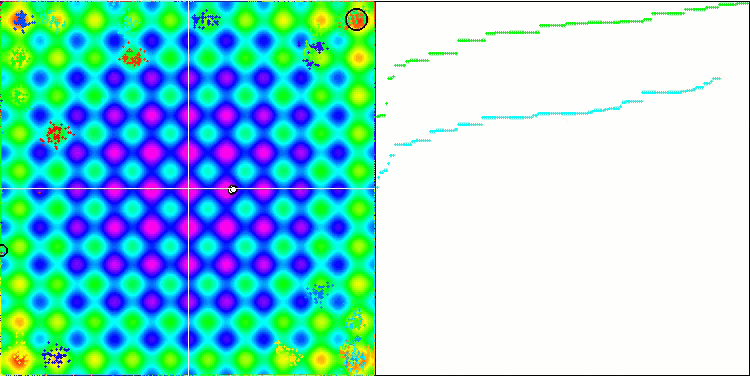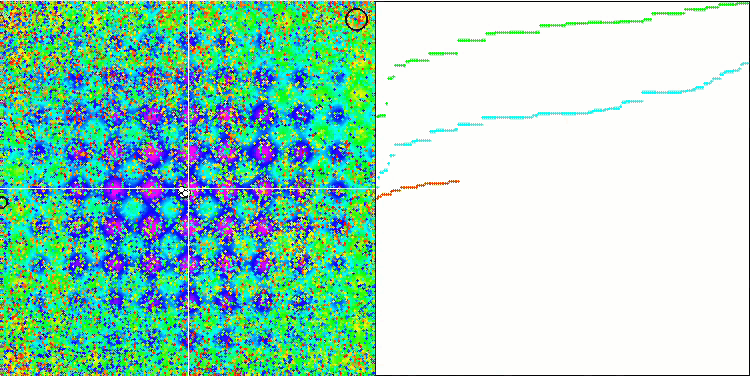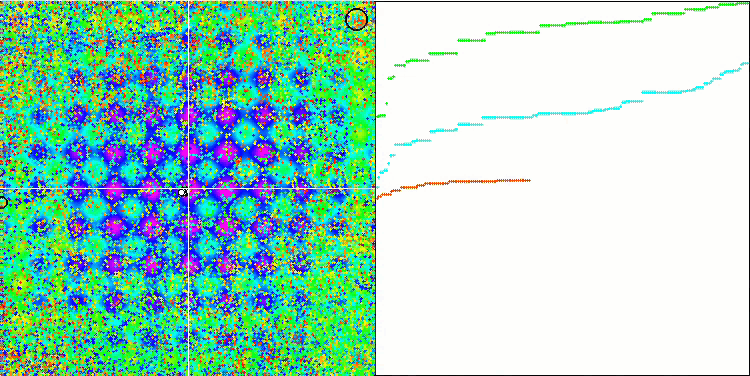
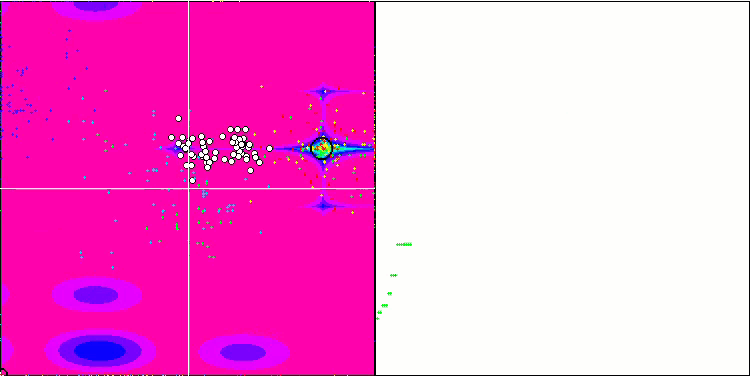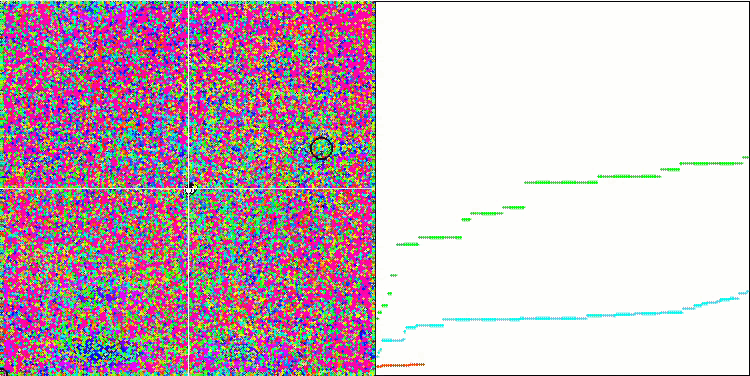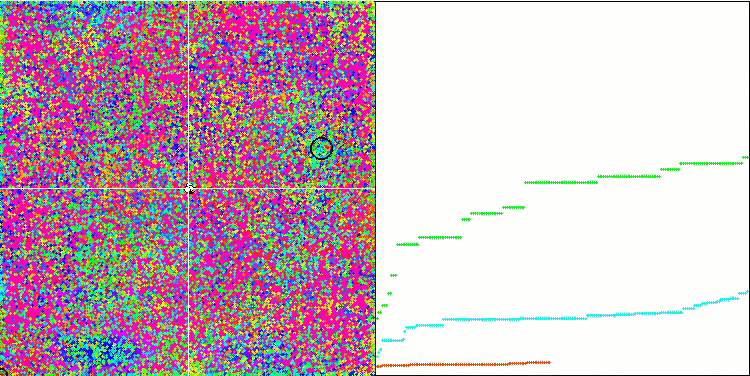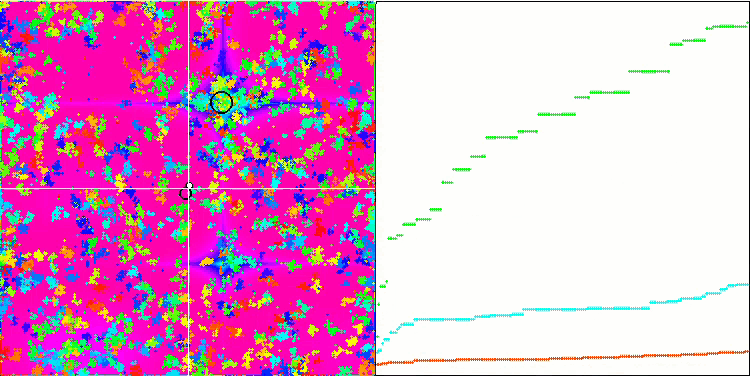
  IWO на тестовой функции Rastrigin.

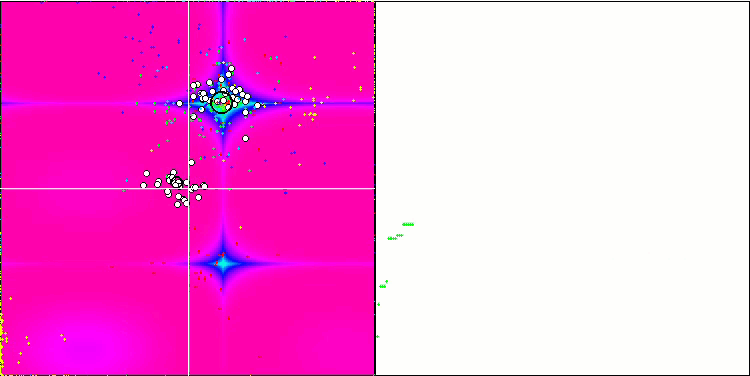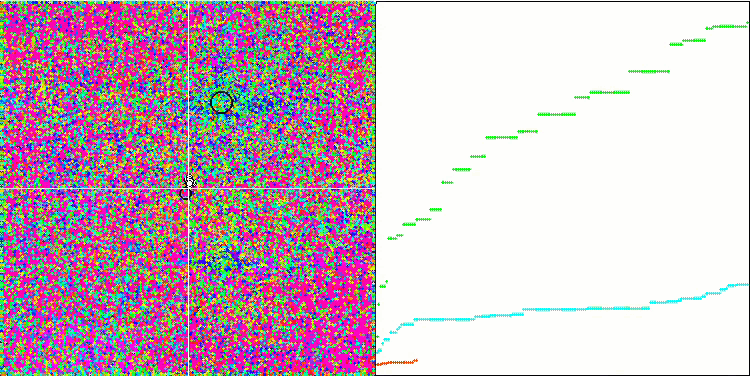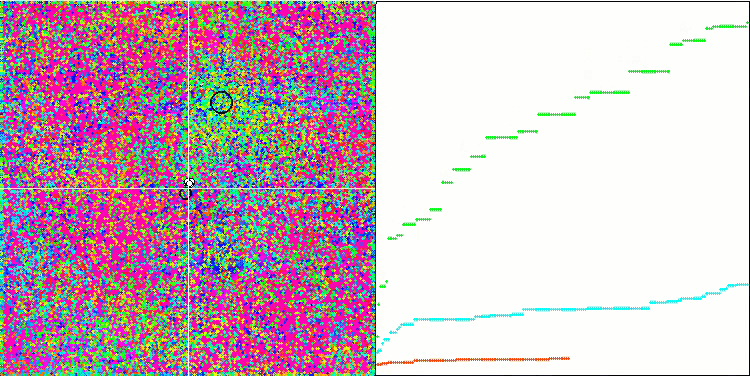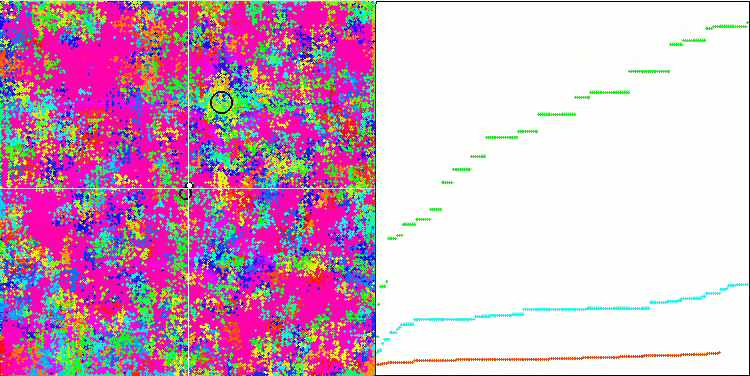
IWO на тестовой функции Forest.

IWO на тестовой функции Megacity.

Алгоритм инвазивных сорняков показал впечатляющие результаты на большинстве тестов, особенно проявил себя на гладкой функции Растригина с 10 и 50 параметров, на которой производительность несколько упала только на тесте с 1000 параметров, что в целом говорит о хорошей производительности на гладких функциях, что в принципе позволяет, рекомендовать алгоритм инвазивных сорняков для работы со сложными гладкими функциями, для работы с нейронными сетями. На функциях Forest алгоритм несколько отличился на первом тесте с 10 параметрами, но всё же показал средние результаты. На дискретной функции Megacity алгоритм инвазивных сорняков показал результаты выше средних, особенно проявив отличную масштабируемость на тесте с 1000 переменных, уступив первое место в тесте только светлячковому алгоритму но значительно опередив его на тестах с 10 и 50 параметров.

Хотя алгоритм инвазивных сорняков имеет достаточно большое количество параметров, это не хотелось бы отнести к недостаткам алгоритма, так как параметры очень интуитивно понятны и настройка параметров не представляет собой сложную задачу. К тому же в основном прецизионная настройка алгоритма влияет только на результаты тестов дискретной функции, при этом результаты на гладкой функции остаются хорошими.

На визуализации тестовых функций хорошо заметны способности алгоритма выделять и исследовать отдельные участки пространства поиска, так как это происходит в пчелином алгоритме и некоторых других, хотя в нескольких публикациях я встречал мнение, что алгоритм склонен к застреванию и слабых поисковых возможностях. При отсутствии у алгоритма ориентира на глобальный экстремум, а так же отсутствии у алгоритма механизмов "выпрыгивания" из локальных ловушек, IWO каким-то образом умудряется достойно работать на таких сложнейших функциях как Forest и Megacity. Причем при работе на дискретной функции чем больше оптимизируемых параметров, тем результаты стабильнее.

Поскольку дисперсия рассеивания семян уменьшается линейно с каждой итерацией, уточнение экстремумов усиливается все больше к завершению оптимизации. На мой взгляд это не совсем оптимально, потому что исследовательские способности алгоритма распределены по времени неравномерно, что мы можем заметить на визуализации тестовых функций как белый шум большую часть времени. Также о неравномерности поиска можно судить по графикам сходимости в правой части окна тестового стенда. Некоторое ускорение сходимости наблюдается в начале оптимизации, что характерно практически для всех алгоритмов, после резкого старта заметно замедление сходимости на большей части оптимизации. И только ближе к окончанию, мы видим опять существенное ускорение сходимости. Из выше сказанного делаю вывод, что динамическое изменение дисперсии — повод для дальнейших детальных исследований и экспериментов. Поскольку из этого видно, что сходимость могла бы и дальше происходить, будь количество итераций больше. Но при этом существуют ограничения проведения сравнительных тестов, которые необходимо выполнять, чтобы соблюсти объективность и практическую достоверность. 

Пора переходить к рассмотрению итоговой рейтинговой таблицы. Из таблицы видно, что абсолютным лидером на момент этой статьи становится IWO, алгоритм показал лучшие результаты в двух тестах из девяти, а в остальных отличные результаты гораздо лучше средних, поэтому итоговый результат у него 100 баллов. На второй строке рейтинга расположился ACOm, модифицированная версия алгоритма колонии муравьев, он остается лучшим в 5 тестах из 9.

AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)		10 params (5 F)	50 params (25 F)	1000 params (500 F)
IWO	invasive weed optimization	1,00000	1,00000	0,33519	2,33519	0,79937	0,46349	0,41071	1,67357	0,75912	0,44903	0,94088	2,14903	100,000
ACOm	ant colony optimization M	0,36118	0,26810	0,17991	0,80919	1,00000	1,00000	1,00000	3,00000	1,00000	1,00000	0,10959	2,10959	95,996
COAm	cuckoo optimization algorithm M	0,96423	0,69756	0,28892	1,95071	0,64504	0,34034	0,21362	1,19900	0,67153	0,34273	0,45422	1,46848	74,204
FAm	firefly algorithm M	0,62430	0,50653	0,18102	1,31185	0,55408	0,42299	0,64360	1,62067	0,21167	0,28416	1,00000	1,49583	71,024
BA	bat algorithm	0,42290	0,95047	1,00000	2,37337	0,17768	0,17477	0,33595	0,68840	0,15329	0,07158	0,46287	0,68774	59,650
ABC	artificial bee colony	0,81573	0,48767	0,22588	1,52928	0,58850	0,21455	0,17249	0,97554	0,47444	0,26681	0,35941	1,10066	57,237
FSS	fish school search	0,48850	0,37769	0,11006	0,97625	0,07806	0,05013	0,08423	0,21242	0,00000	0,01084	0,18998	0,20082	20,109
PSO	particle swarm optimisation	0,21339	0,12224	0,05966	0,39529	0,15345	0,10486	0,28099	0,53930	0,08028	0,02385	0,00000	0,10413	14,232
RND	random	0,17559	0,14524	0,07011	0,39094	0,08623	0,04810	0,06094	0,19527	0,00000	0,00000	0,08904	0,08904	8,142
GWO	grey wolf optimizer	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,00000	0,18977	0,04119	0,01802	0,24898	1,000

Алгоритм инвазивных сорняков отлично подходит для глобального поиска. Этот алгоритм имеет хорошую эксплуатационную способность, хотя лучший член популяции не используется и отсутствуют механизмы защищающие от потенциального застревания в локальных экстремумах. Баланс между исследованием и эксплуатацией алгоритма не предусмотрен, но это не сказалось отрицательно на точности и скорости алгоритма. У этого алгоритма есть и другие недостатки. Неравномерная работа поиска на протяжении оптимизации даёт основания полагать, что результативность IWO потенциально может быть выше, если решить проблемы, озвученные выше.

Гистограмма результатов тестирования алгоритмов на рисунке 4.

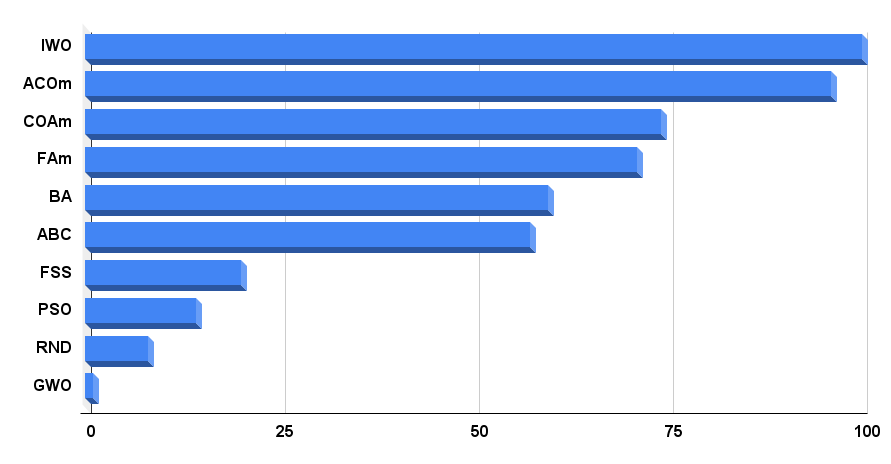
Рисунок 4. Гистограмма итоговых результатов тестирования алгоритмов.

Выводы по свойствам алгоритма оптимизации инвазивных сорняков (IWO):

Плюсы:
1. Быстрый.
2. Хорошо работает с различными видами функций, как гладкими так и дискретными.
3. Хорошая масштабируемость.

Минусы:
1. Очень много настроечных параметров (хотя параметры интуитивно понятны, большое количество параметров всё же минус).