Популяционные алгоритмы оптимизации: Метод Нелдера-Мида, или метод симплексного поиска (Nelder–Mead method, NM)

MetaTrader 5 — Примеры | 4 декабря 2023, 11:01

1 672

Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов

1. Введение

Метод Нелдера-Мида был разработан в 1965 году Джоном Нелдером и Роджером Мидом. Они искали метод оптимизации, который мог бы работать с функциями, не имеющими производных или не имеющими аналитических формул для производных. Они также хотели разработать метод, который был бы прост в реализации и эффективен для использования на вычислительных машинах того времени. Исследования привели их к идее использования симплекса - многогранника в пространстве параметров функции.

История создания метода началась с работы Джона Нелдера и его коллег в лаборатории компьютерных наук в Оксфорде. Они столкнулись с проблемой оптимизации функций, которые не имели аналитических производных или были слишком сложны для их вычисления. Традиционные методы оптимизации, такие как градиентные методы, не были применимы в таких случаях. Вместо этого, Нелдер и Мид предложили новый метод, который основывался на итеративном поиске оптимального решения в пространстве параметров функции.

Метод Нелдера-Мида получил название "симплекс-метод" и был опубликован в статье "A Simplex Method for Function Minimization" в журнале "The Computer Journal" в 1965 году. Этот метод был принят научным сообществом и стал широко использоваться в различных областях, требующих оптимизации функций.

Симплекс представляет собой набор точек, образующих многогранник, где каждая точка - это набор значений параметров оптимизируемой функции. Идея заключается в том, чтобы изменять и перемещать симплекс в пространстве параметров, чтобы найти оптимальное значение функции.

Метод Нелдера-Мида (метод симплекса Нелдера-Мида) относится к классу алгоритмов безусловной оптимизации. Это детерминированный алгоритм, который не требует использования производных функции и может работать с функциями, имеющими несколько локальных минимумов.

2. Описание алгоритма

Метод Нелдера-Мида не относится к популяционным, потому что используется только один агент оптимизации, представляющий симплекс, который в свою очередь состоит из набора точек в пространстве поиска, что само по себе можно считать популяцией. Однако мы будем использовать несколько агентов, каждый из которых имеет свой симплекс, поэтому данная реализация вполне может быть отнесена к популяционным алгоритмам.

Итак, для простоты понимания операции с симплексом примем, что необходимо оптимизировать две переменные функции, то есть размерность пространства z = 2, тогда симплекс будет состоять из z + 1 = 3 вершин. Изменение симплекса - это операция над худшей точкой из этих трех. Обозначим эти точки как Best, Good, Worst, причем Good является второй точкой после Worst (в случае, если размерность больше двух, то Good будет всегда вторым после Worst из сортированного списка вершин).

Далее с этими тремя вершинами нужно проводить вычисления и корректировку Worst относительно остальных вершин. Передвижение Worst осуществляем относительно геометрического центра вершин за исключением её самой, т.е. вычисляем центроид и передвигаем Worst относительно центроида.

На каждой итерации метода Недлера-Мида мы выполняем следующие шаги:

1. Сортировка вершин симплекса по значениям целевой функции, т.е.

f(P0) ⩾ f(P1) ⩾ ... ⩾ f(P(n-1))

где:

P0, P1 ... P(n-1) - точки симплекса
n - количество вершин симплекса

2. Вычисление центроида: вычислить среднее значение по соответствующим координатам всех вершин симплекса, кроме худшей вершины. Пусть вектор Xo будет центром тяжести всех вершин, кроме X(n-1), тогда:

Xo = (X0 + X1 + ... + X(n-2)) / (n-1)

где:

X0, X1 ... X(n-2) - соответствующие вектора координат всех вершин кроме худшей

3. Отражение (Reflection): операция отражения худшей вершины относительно центроида. Вектор Xr новой отражённой вершины вычисляется по следующей формуле:

Xr = Xo + α (Xo - Xw)

где:

Xw - вектор худшей вершины, соответсвует вершине P(n-1)
α - коэффициент отражения, обычно равный 1

4. Оценка новой вершины: вычисляется значение целевой функции в этой точке. Если новая вершина имеет значение целевой функции лучше, чем худшая вершина симплекса, то она может заменить её, т.е. отражение заменяет оригинал. Операция отражения позволяет исследовать новую область пространства параметров, отражаясь от центроида симплекса.

5. Расширение (Expansion): используется для дальнейшего исследования пространства параметров, когда операция отражения дала вершину лучше, чем самая лучшая, в предположении, что дальнейшее движение в направлении отражения позволит ещё больше улучшить её положение. Операция расширения позволяет исследовать еще бо'льшую область пространства параметров, чем операция отражения. Она увеличивает расстояние между центроидом и отраженной точкой, что может помочь найти новые локальные минимумы целевой функции. Вектор расширения Xe можем вычислить следующим образом:

Xe = Xo + γ(Xr - Xo)

где:

γ - коэффициент расширения, обычно больше 1, по умолчанию 2

5.1. В случае, если совершалась операция расширения: вычисляется фитнес функция для вершины Xe и если она лучше, чем вершина Xr, то она может заменить худшую вершину Xw симплекса. После выполнения расширения переходим к шагу 1.

Важно отметить, что коэффициент расширения γ должен быть выбран осторожно. Если он выбран слишком большим, это может привести к распространению симплекса на большую область пространства параметров, что может замедлить сходимость или привести к потере информации о локальных экстремумах. Если он выбран слишком маленьким, это может недостаточно исследовать новые области пространства параметров.

6. Сжатие (Contraction): используется для вычисления вершины Xc, когда операция отражения дала вершину хуже либо равной хорошей точке Xb (вторая после самой худшей), т.е. осуществляется в надежде найти положение лучше внутри симплекса. Она выполняется следующим образом:

Xc = Xo + β(Xw - Xo)

где:

β - коэффициент сжатия, обычно между 0 и 1, по умолчанию 0.5

6.1. В случае, если совершалась операция cжатия: вычисляется значение целевой функции для вершины Xc. Если новая вершина имеет значение целевой функции лучше, чем худшая вершина симплекса, то она может заменить худшую. После выполнения расширения переходим к шагу 1.

Операция сжатия позволяет смещать симплекс ближе к худшей точке, что может помочь в исследовании окрестности этой точки. Как и в случае с операцией расширения, важно выбирать коэффициент сжатия β осторожно. Если он выбран слишком большим, это может привести к слишком сильному сжатию симплекса, что приведёт к потере информации о локальных минимумах. Если он выбран слишком маленьким, сжатие может быть недостаточным для исследования окрестности худшей точки.

7. Усечение (Shrinkage): последняя операция в методе Нелдера-Мида выполняется, когда ни одна из предыдущих операций (отражение, растяжение, сжатие) не приводит к улучшению значения целевой функции. Операция усечение позволяет уменьшить размер симплекса, чтобы сужать область поиска и сосредоточиться вокруг наилучшей точки.

Как мы видим, у авторов есть четыре операции с симплексом. При работе с симплексами нужно иметь ввиду - для начала оптимизации необходимо рассчитать фитнес функцию для всех точек симплекса. Количество точек симплекса равно "z+1", где z - размерность пространства поиска. Например, если у нас есть размерность поиска 1000, то мы должны вычислить фитнес функцию 1001 раз, чтобы начать операции с симплексом. В то время как при обычном популяционном алгоритме с популяцией 50 агентов мы могли бы выполнить 20 эпох, то для этого алгоритма будет выполнена только одна эпоха и при этом будут истрачены большая часть ограниченного числа итераций.

Операция "Shrinkage" - это сдвиг всех точек к лучшей, после чего потребуется рассчитать фитнес функцию 1000 раз, т.е. это означает, что операция "Shrinkage" очень затратная. По идее авторов, эта операция должна вызываться при застревании алгоритма, когда перемещение худшей точки симплекса не приносит улучшения решения. Однако мои эксперименты показали, что эта операция очень затратная по отношению к вычислительным ресурсам и, более того, бессмысленна и самоубийственна для алгоритма оптимизации, поскольку схождение всех точек симплекса-агента к одному локальному экстремуму означало бы застревание и прекращение исследования пространства поиска. Поэтому я решил отказаться от операции "Shrinkage" для практической реализации алгоритма.

Итак, мы будем использовать первые 3 операции с симплексом, их можно для наглядности представить в виде рисунка 1:

NMrefl

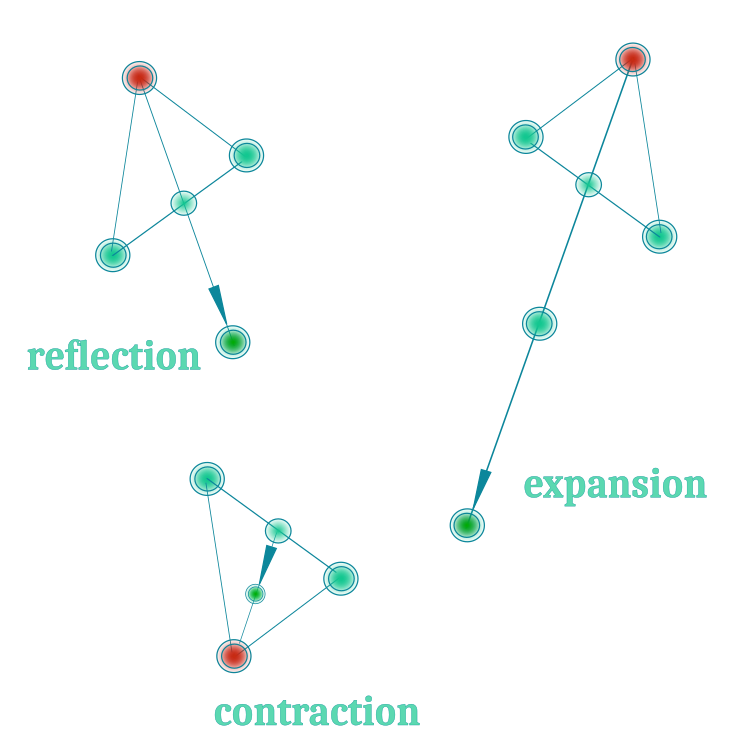
Рисунок 1. Три основные операции метода Нелдера - Мида.

Поскольку метод симплексного поиска может столкнуться с неудачным выбором начальных вершин, так как он детерминирован, результат его оптимизации может оказаться неудовлетворительным. Эксперименты с этим алгоритмом лишь подтвердили опасения: он работает приемлемо только в ограниченном пространстве координат.

Из-за проблем со сходимостью, вершины симплекса просто сдвигаются на фиксированное значение. Представьте себе, что вы стоите на ходулях и пытаетесь сесть на скамейку, но она находится слишком низко для этого. Точно такая же ситуация возникает с изменяющимся симплексом. Чтобы алгоритм сработал идеально, нужно иметь большую удачу, чтобы начальные вершины симплекса оказались в нужном месте. Это подобно ситуации с ходулями: чтобы безопасно сесть, нужна высокая скамейка. Алгоритм относительно хорошо сходится на гладких моноэкстремальных функциях, например, на параболе. Однако наши практические задачи намного сложнее и обычно полны локальных "ловушек", особенно в трейдерских задачах, которые по своей сути являются дискретными.

Тогда возникает вопрос: что делать, когда симплекс застревает "навсегда" в локальном экстремуме? Логика алгоритма Нелдера-Мида не предусматривает способов выбраться из этой "ловушки". После каждой операции, будь то сжатие или расширение, алгоритм возвращается к отражению, пытаясь преодолеть самую плохую точку. Визуально это выглядит как "мигание". Чтобы решить эту проблему, я попытался дать симплексу возможность покинуть локальную "ловушку" и продолжить поиск в новых областях пространства. Для этого я использовал Полеты Леви, которые в некоторых случаях помогали "оживить" популяцию, как описано в предыдущих статьях. Однако стоит отметить, что Полеты Леви не всегда полезны и их применение зависит от логики оптимизационного алгоритма. В нашем случае это был эксперимент, и результаты улучшения не были гарантированы.

Переходим к самому интересному - написанию кода.

После каждой итерации необходимо знать какая операция совершалась с худшей вершиной симплекса. Для этого удобно использовать энумератор. Помимо трёх основных операций с вершиной симплекса я добавил ещё один, "none", для случая, если придёт идея как-то дополнить алгоритм. Энумератор назовем E_SimplexOperation, поля которого:

none: не предусмотрено операций
reflection: операция "отражение"
expansion: операция "расширение"
contraction: операция "сжатие"

//——————————————————————————————————————————————————————————————————————————————
enum E_SimplexOperation
{
  none        = 0,
  reflection  = 1,
  expansion   = 2,
  contraction = 3
};
//——————————————————————————————————————————————————————————————————————————————

Для описания вершины симплекса понадобится структура S_Point, которая содержит следующие поля:

Init(int coords): инициализация точки, принимает аргумент "coords"
c []: массив координат точки в многомерном пространстве, размер массива определяется в методе "Init"
f: значение фитнес-функции вершины

//——————————————————————————————————————————————————————————————————————————————
struct S_Point
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;
  }
  double c [];
  double f;
};
//——————————————————————————————————————————————————————————————————————————————

Для симплекса будем использовать структуру S_Simplex, которая представляет собой простой симплекс для каждого агента и содержит следующие поля:

Init(int coords): инициализации симплекса, принимает аргумент "coords" - количество координат
S_Point p []: массив вершин симплекса, размер массива определяется в методе "Init"
c []: массив координат центроида симплекса, размер массива определяется в методе "Init".
S_Point Xr: точка отражения
S_Point Xe: точка расширения
S_Point Xc: точка сжатия
indG: индекс хорошей точки (Good) в симплексе
indW: индекс худшей точки в симплексе
E_SimplexOperation: тип операции симплекса

//——————————————————————————————————————————————————————————————————————————————
struct S_Simplex
{
  void Init (int coords)
  {
    ArrayResize (p, coords + 1);

    for (int i = 0; i <= coords; i++)
    {
      p [i].Init (coords);
    }

    ArrayResize (c, coords);

    Xr.Init (coords);
    Xe.Init (coords);
    Xc.Init (coords);

    operation = none;
  }

  S_Point p [];
  double c  []; //centroid

  S_Point Xr;  //reflection point
  S_Point Xe;  //expansion point
  S_Point Xc;  //expansion point

  int indG;    //index of good point
  int indW;    //index of worst point

  E_SimplexOperation operation; //type of simplex operation
};
//——————————————————————————————————————————————————————————————————————————————

Для агента оптимизации определим структуру S_Agent, которая содержит следующие поля:

Init (int coords): метод инициализации агента, принимает аргумент "coords", указывающий количество координат. Метод изменяет размер массива "c" на "coords" с помощью функции ArrayResize. Затем поле "f" устанавливается в значение -DBL_MAX, что является начальным значением для функции оценки агента. Далее вызывается метод "Init" для поля "s", которое представляет собой симплекс агента
c []: массив координат агента в многомерном пространстве для обмена с внешней программой. Размер массива определяется в методе "Init"
f: значение фитнес-функции агента
s: симплекс агента, представленный структурой S_Simplex. Симплекс инициализируется вызовом метода "Init" для поля "s"

//——————————————————————————————————————————————————————————————————————————————
struct S_Agent
{
  void Init (int coords)
  {
    ArrayResize (c, coords);
    f = -DBL_MAX;

    s.Init (coords);
  }

  double c  []; //coordinates
  double f;     //fitness
  S_Simplex s;  //agent simplex
};
//——————————————————————————————————————————————————————————————————————————————

Определим класс алгоритма метода симплексного поиска C_AO_NMm, который содержит следующие поля:

cB []: массив лучших координат
fB: значение фитнес-функции лучших координат
a []: массив агентов, представленных структурой S_Agent
rangeMax []: массив максимальных значений диапазона поиска для каждой координаты
rangeMin []: массив минимальных значений диапазона поиска для каждой координаты
rangeStep []: массив шагов поиска для каждой координаты
Init (const int coordsP, const int popSizeP, const double reflectionCoeffP, const double expansionCoeffP, const double contractionCoeffP): метод инициализации алгоритма, принимает аргументы, определяющие количество координат, размер популяции, коэффициенты для операций отражения, расширения, и сжатия, метод выполняет инициализацию всех полей класса
Moving (): метод выполняет движение агентов в алгоритме
Revision(): метод выполняет ревизию агентов в алгоритме
Sorting, CalcCentroid, Reflection, Expansion, Contraction, Flying: выполняют операции с симплексами. А методы
SeInDiSp, RNDfromCI, Scale: выполняются для генерации и преобразования значений в допустимые диапазоны с заданным шагом

//——————————————————————————————————————————————————————————————————————————————
class C_AO_NMm
{
  //----------------------------------------------------------------------------
  public: double cB [];  //best coordinates
  public: double fB;     //FF of the best coordinates
  public: S_Agent a [];  //agent

  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //manimum search range
  public: double rangeStep []; //step search

  public: void Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //Reflection coefficient
                     const double expansionCoeffP,    //Expansion coefficient
                     const double contractionCoeffP); //Contraction coefficient

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coords;        //coordinates number
  private: int    popSize;       //population size
  private: int    simplexPoints; //simplex points


  private: double reflectionCoeff;  //Reflection coefficient
  private: double expansionCoeff;   //Expansion coefficient
  private: double contractionCoeff; //Contraction coefficient

  private: bool   revision;

  private: S_Point pTemp [];
  private: int     ind   [];
  private: double  val   [];

  private: void   Sorting      (S_Point &p []);
  private: void   CalcCentroid (S_Simplex &s, int indW);
  private: void   Reflection   (S_Agent &agent, int indW);
  private: void   Expansion    (S_Agent &agent);
  private: void   Contraction  (S_Agent &agent, int indW);
  private: void   Flying       (S_Agent &agent, int indW);

  private: double SeInDiSp     (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI    (double min, double max);
  private: double Scale        (double In, double InMIN, double InMAX, double OutMIN, double OutMAX,  bool revers);
};
//——————————————————————————————————————————————————————————————————————————————

Для инициализации алгоритма будем использовать метод "Init" класса C_AO_NMm, выполняет инициализацию всех полей класса и создает необходимые массивы для работы алгоритма оптимизации.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Init (const int    coordsP,            //coordinates number
                     const int    popSizeP,           //population size
                     const double reflectionCoeffP,   //reflection coefficient
                     const double expansionCoeffP,    //expansion coefficient
                     const double contractionCoeffP)  //contraction coefficient
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coords        = coordsP;
  popSize       = popSizeP;
  simplexPoints = coords + 1;

  reflectionCoeff  = reflectionCoeffP;
  expansionCoeff   = expansionCoeffP;
  contractionCoeff = contractionCoeffP;

  ArrayResize (pTemp, simplexPoints);
  ArrayResize (ind,   simplexPoints);
  ArrayResize (val,   simplexPoints);

  ArrayResize (a, popSize);
  for (int i = 0; i < popSize; i++)
  {
    a [i].Init (coords);
  }

  ArrayResize (rangeMax,  coords);
  ArrayResize (rangeMin,  coords);
  ArrayResize (rangeStep, coords);
  ArrayResize (cB,        coords);
}
//——————————————————————————————————————————————————————————————————————————————

Обычно метод "Moving" мы используем для перемещения агентов в пространстве поиска, но для алгоритма NM оставим только функцию первоначального случайного размещения вершин симплексов агентов в пространстве поиска.
Для создания случайной вершины симплексов используем RNDfromCI и приведём в требуемый диапазон с нужным шагом методом SeInDiSp.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Moving ()
{
  if (!revision)
  {
    int cnt = 0;

    for (int i = 0; i < popSize; i++)
    {
      for (int p = 0; p < simplexPoints; p++)
      {
        cnt++;
        for (int c = 0; c < coords; c++)
        {
          a [i].s.p [p].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
          a [i].s.p [p].c [c] = SeInDiSp  (a [i].s.p [p].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
        }
      }
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Основная логика перемещения вершин симплексов агентов будем производить в методе "Revision".

Если ревизия ещё не выполнялась "if (!revision)", то необходимо отсортировать вершины в симплексе, построить центроид и выполнить операцию отражения для худших вершин симплексов агентов. Это самая первая операция с вершинами и она всегда "отражение". Тут же мы можем обновить глобальное решение, так как к этому моменту у нас есть знание о значении приспособленности для каждой вершины. Установка значения переменной "revision" в "true" и выход из метода.

Начиная со следующей итерации функцию приспособленности мы будем знать не для вершин симплексов, а для конкретных агентов оптимизации. И в соответствии с выполненными операциями над симплексами назначать известные решения агентов их соответствующим вершинам симплекса. Нужно обновить глобальное решение лучшими значениями приспособленности агентов.

Далее проверяем, какая операция была совершена над вершинами на предыдущей итерации. Имеем ввиду, что вершины симплексов - это векторы.

Если была выполнена операция "отражения":

назначить вектору Xr значение приспособленности агента
сравнить приспособленность вектора Xr с Xw, и если значение лучше, то обновить вектор Xw
сравнить приспособленность вектора Xr с Xb, и если значение лучше, то выполнить "расширение"
сравнить приспособленность вектора Xr с Xg (второй после самой худшей вершины), и если значение хуже, то выполнить "сжатие"
если было улучшение вершины, то выполнить "отражение", с предварительной сортировкой и постройкой центроида, в противном случае выполнить "Flying"

Если была выполнена операция "расширения":

назначить вектору Xe значение приспособленности агента
сравнить приспособленность вектора Xe с Xw, и если значение лучше, то обновить вектор Xw
выполнить "отражение", с предварительной сортировкой и постройкой центроида

Если была выполнена операция "сжатия":

назначить вектору Xс значение приспособленности агента
сравнить приспособленность вектора Xс с Xw, и если значение лучше, то обновить вектор Xw, в противном случае выполнить "Flying"
если было улучшение вершины, то выполнить "отражение", с предварительной сортировкой и постройкой центроида

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Revision ()
{
  //----------------------------------------------------------------------------
  if (!revision)
  {
    //отсортировать точки симплекса агентов по значению FF и назначить BGW
    for (int i = 0; i < popSize; i++)
    {
      Sorting (a [i].s.p);
    }

    //рассчитать центроид симлекса
    for (int i = 0; i < popSize; i++)
    {
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;

      CalcCentroid (a [i].s, a [i].s.indW);
    }

    //назначить следующий тип операции - reflection
    for (int i = 0; i < popSize; i++)
    {
      Reflection (a [i], a [i].s.indW);
      a [i].s.operation = reflection;
    }

    //запомним лучшую точку симплексов агентов как глобальное решение
    for (int i = 0; i < popSize; i++)
    {
      if (a [i].s.p [0].f > fB)
      {
        fB = a [i].s.p [0].f;
        ArrayCopy (cB, a [i].s.p [0].c, 0, 0, WHOLE_ARRAY);
      }
    }

    revision = true;
    return;
  }

  //----------------------------------------------------------------------------
  if (revision)
  {
    int pos = -1;

    for (int i = 0; i < popSize; i++)
    {
      if (a [i].f > fB) pos = i;
    }

    if (pos != -1)
    {
      fB = a [pos].f;
      ArrayCopy (cB, a [pos].c, 0, 0, WHOLE_ARRAY);
    }
  }

  //----------------------------------------------------------------------------
  for (int i = 0; i < popSize; i++)
  {
    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //если была операция reflection ++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == reflection)
    {
      a [i].s.Xr.f = a [i].f;
      bool needUpd = false;

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [a [i].s.indW].f)  //Xr > Xw                 |---w--Xr--g----------b---|
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xr;        //заменить Xw на Xr
        needUpd = true;
      }
      
      //------------------------------------------------------------------------
      if (a [i].s.Xr.f > a [i].s.p [0].f)             //если Xr > Xb            |---w----g----------b---Xr|
      {
        Expansion (a [i]);                            //выполнить expansion
        continue;
      }

      //------------------------------------------------------------------------
      if (a [i].s.Xr.f <= a [i].s.p [a [i].s.indG].f) //если Xr < Xg            |---w---Xr--g----------b--|
      {
        Contraction (a [i], a [i].s.indG);            //выполнить contraction
        continue;
      }
      
      if (needUpd)
      {
        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //если была операция expansion +++++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == expansion)
    {
      a [i].s.Xe.f = a [i].f;

      if (a [i].s.Xe.f > a [i].s.Xr.f) a [i].s.p [a [i].s.indW] = a [i].s.Xe;
      else                             a [i].s.p [a [i].s.indW] = a [i].s.Xr;

      Sorting (a [i].s.p);
      a [i].s.indG = simplexPoints - 2;
      a [i].s.indW = simplexPoints - 1;
      CalcCentroid (a [i].s, a [i].s.indW);
      Reflection   (a [i],   a [i].s.indW);

      continue;
    }

    //++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
    //если была операция contraction +++++++++++++++++++++++++++++++++++++++++++
    if (a [i].s.operation == contraction)
    {
      a [i].s.Xc.f = a [i].f;

      if (a [i].s.Xc.f > a [i].s.p [a [i].s.indW].f)
      {
        a [i].s.p [a [i].s.indW] = a [i].s.Xc;

        Sorting (a [i].s.p);
        a [i].s.indG = simplexPoints - 2;
        a [i].s.indW = simplexPoints - 1;
        CalcCentroid (a [i].s, a [i].s.indW);
        Reflection   (a [i],   a [i].s.indW);
      }
      else Flying (a [i], a [i].s.indW);

      continue;
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Для вычисления центроида напишем метод CalcCentroid, он вычисляет среднее значение координат в заданном симплексе "s" до указанного индекса indW.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::CalcCentroid (S_Simplex &s, int indW)
{
  double summ = 0.0;

  for (int c = 0; c < coords; c++)
  {
    summ = 0.0;

    for (int p = 0; p < simplexPoints; p++)
    {
      if (p != indW) summ += s.p [p].c [c];
    }

    s.c [c] = summ / coords;
  }
}
//——————————————————————————————————————————————————————————————————————————————

Операцию "отражения" будет выполнять метод "Reflection" для вершины индекса "indW" симплекса агента "agent".

Внутри цикла вычисление отраженного значения Xr по формуле Xr = Xo + reflectionCoeff * (Xo - Xw). Здесь reflectionCoeff - коэффициент отражения, определяющий степень отклонения отраженной вершины от начальной вершины.
Далее применение функции SeInDiSp к значению Xr, чтобы убедиться, что оно находится в пределах допустимого диапазона rangeMin[c] и rangeMax[c], с шагом rangeStep[c]. Результат сохраняется в agent.s.Xr.c[c].
Установка операции "reflection" для агента agent.s.operation, указывающей, что операция "отражения" была выполнена для данного агента.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Reflection (S_Agent &agent, int indW)
{
  double Xo;
  double Xr;
  double Xw;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c [c];
    Xw = agent.s.p [indW].c [c];

    //Xr = Xo + RNDfromCI (0.0, reflectionCoeff) * (Xo - Xw);
    Xr = Xo + reflectionCoeff * (Xo - Xw);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

Операцию "расширения" будет выполнять метод "Expansion" для агента "agent".

Внутри цикла вычисление расширенного значения Xe по формуле Xe = Xo + expansionCoeff * (Xr - Xo) . Здесь expansionCoeff - коэффициент расширения, определяющий степень увеличения отклонения расширенной вершины от начальной вершины.
Далее применение функции SeInDiSp к значению Xe, чтобы убедиться, что оно находится в пределах допустимого диапазона rangeMin[c] и rangeMax[c], с шагом rangeStep[c]. Результат сохраняется в agent.s.Xe.c[c].
Установка операции "expansion" для агента agent.s.operation, указывающей, что операция "расширения" была выполнена для данного агента.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Expansion (S_Agent &agent)
{
  double Xo;
  double Xr;
  double Xe;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xr = agent.s.Xr.c [c];

    //Xe = Xo + RNDfromCI (0.0, expansionCoeff) * (Xr - Xo);
    Xe = Xo + expansionCoeff * (Xr - Xo);

    agent.s.Xe.c [c] = SeInDiSp  (Xe, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xe.c [c];
  }

  agent.s.operation = expansion;
}
//——————————————————————————————————————————————————————————————————————————————

Операцию "сжатия" выполнит метод "Contraction" для вершины индекса "indW" симплекса агента "agent".

Внутри цикла вычисление сжатого значения Xc по формуле Xc = Xo + contractionCoeff * (Xw - Xo) . Здесь contractionCoeff - коэффициент сжатия, определяющий степень уменьшения отклонения сжатой вершины от начальной вершины.
Далее применение функции SeInDiSp к значению Xc, чтобы убедиться, что оно находится в пределах допустимого диапазона rangeMin[c] и rangeMax[c], с шагом rangeStep[c]. Результат сохраняется в agent.s.Xc.c[c].
Установка операции "contraction" для агента agent.s.operation, указывающей, что операция "сжатия" была выполнена для данного агента.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Contraction (S_Agent &agent, int indW)
{
  double Xo;
  double Xw;
  double Xc;

  for (int c = 0; c < coords; c++)
  {
    Xo = agent.s.c    [c];
    Xw = agent.s.p [indW].c [c];

    //Xc = Xo + RNDfromCI (0.0, contractionCoeff) * (Xw - Xo);
    Xc = Xo + contractionCoeff * (Xw - Xo);

    agent.s.Xc.c [c] = SeInDiSp  (Xc, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xc.c [c];
  }

  agent.s.operation = contraction;
}
//——————————————————————————————————————————————————————————————————————————————

Для Полётов Леви применим метод "Flying", выполняющий операцию "полета" для агента "agent" с целью вытолкнуть вершину симплекса в новые места пространства поиска со случайным распределением, которое сосредотачивает вероятность ближе к лучшему глобальному решению с уменьшением вероятности вплоть до 0 к границам исследуемого пространства.

После применения метода "Flying" установка операции "reflection" для агента agent.s.operation, что бы на последующих итерациях выполнять логику алгоритма так, как если бы была совершена операция отражения.
Применение функции SeInDiSp к значению Xr, чтобы убедиться, что оно находится в пределах допустимого диапазона rangeMin[c] и rangeMax[c], с шагом rangeStep[c]. Результат сохраняется в agent.s.Xr.c[c].

Таким образом, метод "Flying" выполняет операцию "полета" для агента, изменяя его координаты на основе текущих координат глобального лучшего решения и случайно сгенерированных значений. Это позволяет агенту исследовать новые области пространства решений и потенциально найти более оптимальные решения.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_NMm::Flying (S_Agent &agent, int indW)
{
  for (int c = 0; c < coords; c++)
  {
    double r1 = RNDfromCI (-1.0, 1.0);
    r1 = r1 > 0.5 ? 1.0 : -1.0;
    double r2 = RNDfromCI (1.0, 20.0);
    r2 = pow (r2, -2.0);

    if (r1 > 0.0) Xr = cB [c] + Scale (r2, 0.0, 1.0, 0.0, rangeMax [c] - cB [c], false);
    else          Xr = cB [c] - Scale (r2, 0.0, 1.0, 0.0, cB [c] - rangeMin [c], false);

    //Xr = RNDfromCI (rangeMin [c], rangeMax [c]);

    agent.s.Xr.c [c] = SeInDiSp  (Xr, rangeMin [c], rangeMax [c], rangeStep [c]);
    agent.c      [c] = agent.s.Xr.c [c];
  }

  agent.s.operation = reflection;
}
//——————————————————————————————————————————————————————————————————————————————

3. Результаты тестов

Распечатка работы алгоритма Нелдера - Мида на тестовом стенде:

C_AO_NMm:5;1.0;2.0;0.5
=============================
5 Rastrigin's; Func runs 10000 result: 77.96849465506082
Score: 0.96607
25 Rastrigin's; Func runs 10000 result: 61.68192953373487
Score: 0.76427
500 Rastrigin's; Func runs 10000 result: 50.62713783555849
Score: 0.62730
=============================
5 Forest's; Func runs 10000 result: 0.9552378700292385
Score: 0.54033
25 Forest's; Func runs 10000 result: 0.45877475613538293
Score: 0.25951
500 Forest's; Func runs 10000 result: 0.09902427974784639
Score: 0.05601
=============================
5 Megacity's; Func runs 10000 result: 5.6
Score: 0.46667
25 Megacity's; Func runs 10000 result: 2.304
Score: 0.19200
500 Megacity's; Func runs 10000 result: 0.40280000000000005
Score: 0.03357
=============================
All score: 3.90573

По результатам работы алгоритма можно заметить волне достойные результаты на гладкой функции Rastrigin.

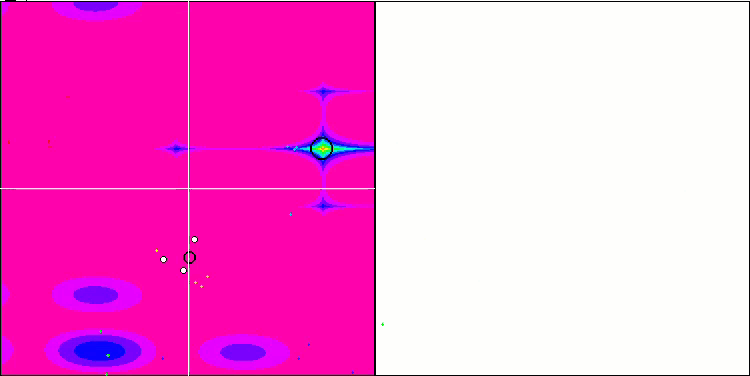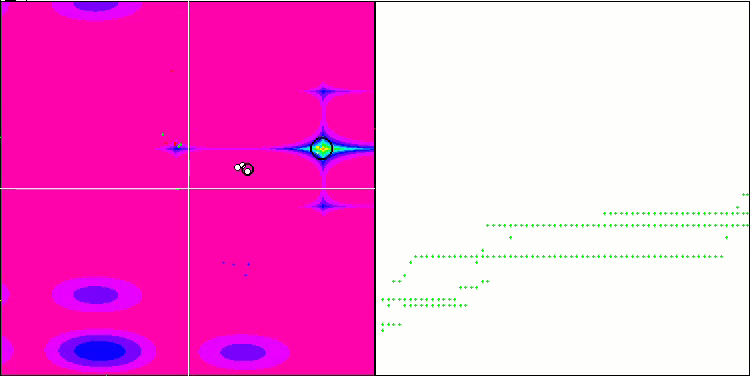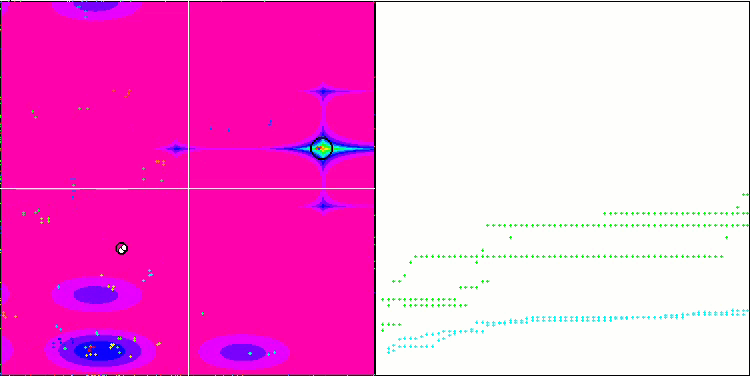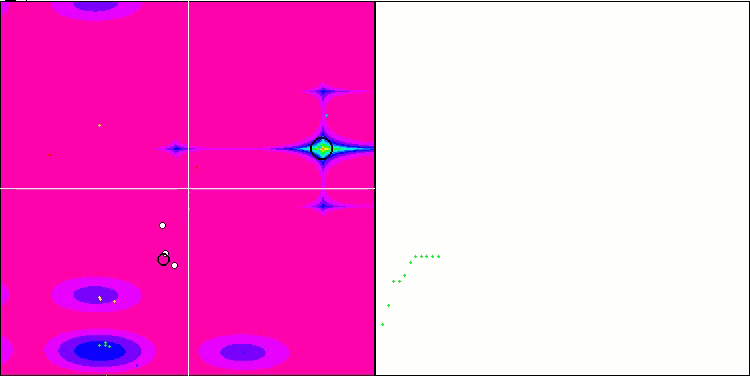
На визуализации можем заметить признаки вырождения популяции и сосредоточении агентов в одном месте. Ситуацию несколько спасает применение полетов Леви, это заметно по отдельным точкам соответствующих координат. Графики сходимости не очень стабильны, я привел визуализацию только двух первых тестов для каждой из функций, потому что выполнение третьего теста с 1000 переменных выполняется настолько долго, что не представляется возможности записи в GIF.

rastrigin

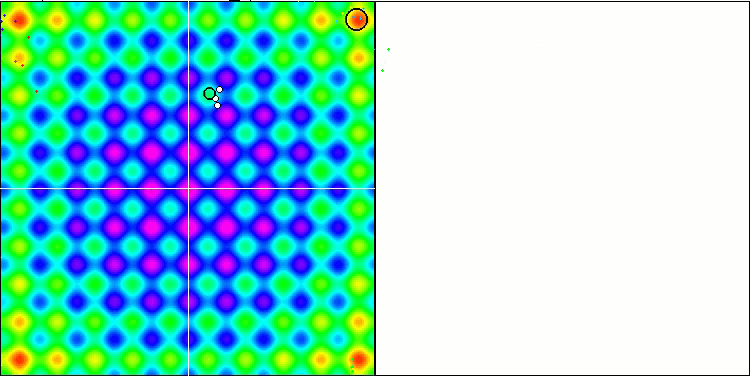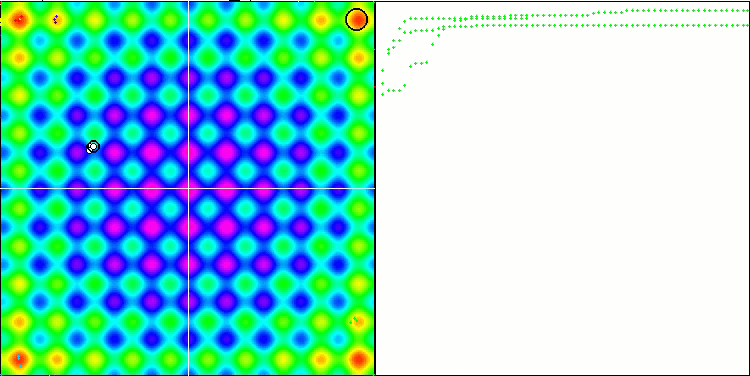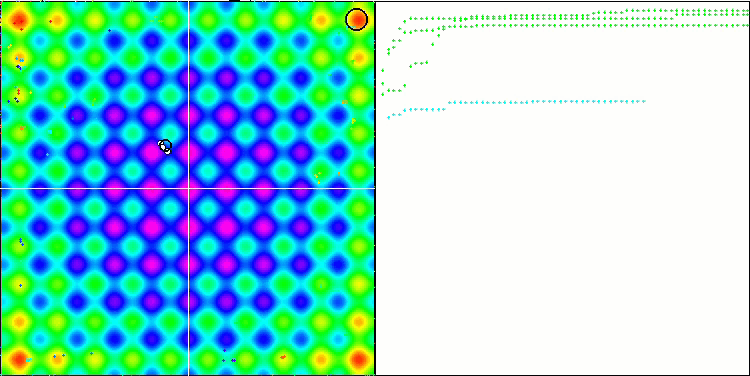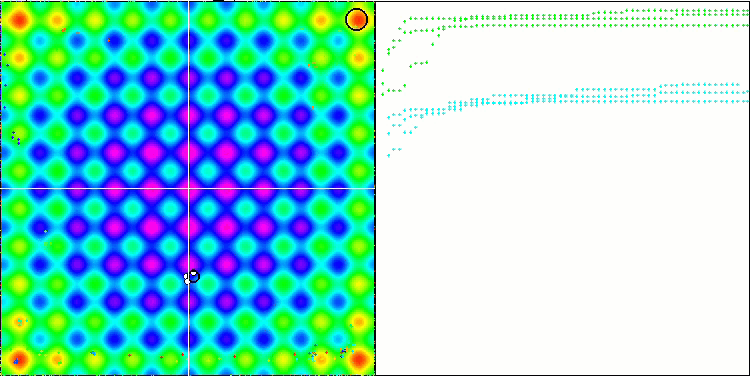
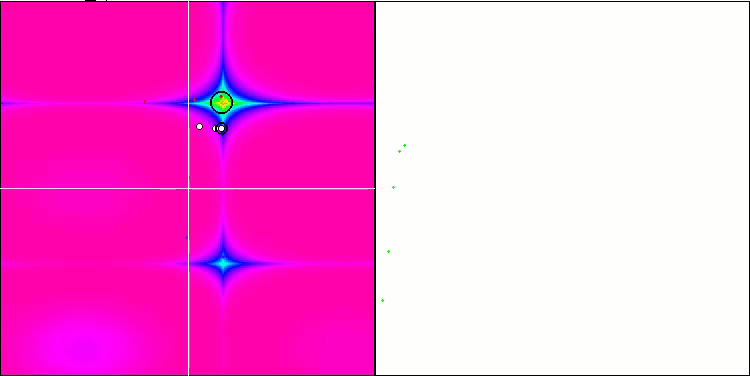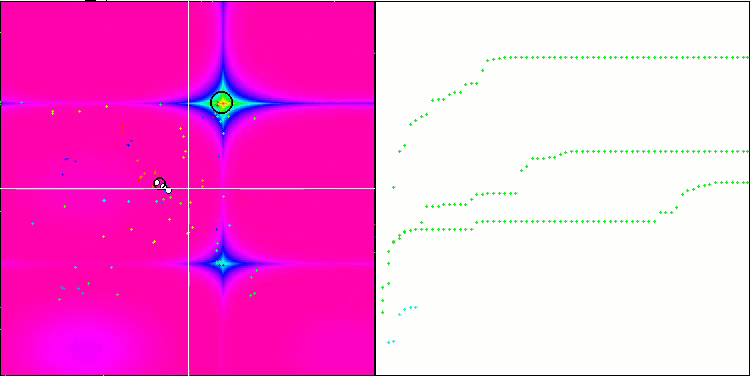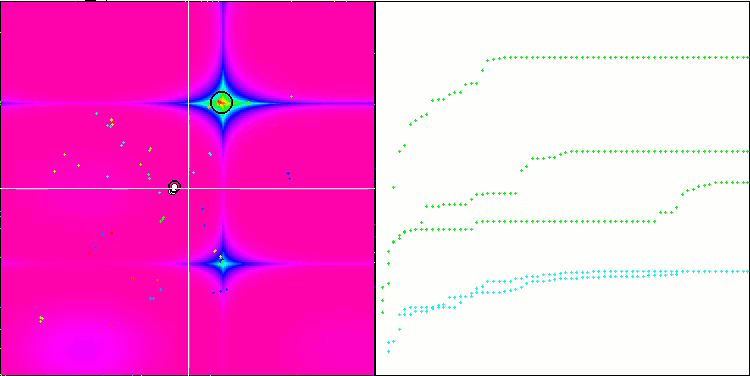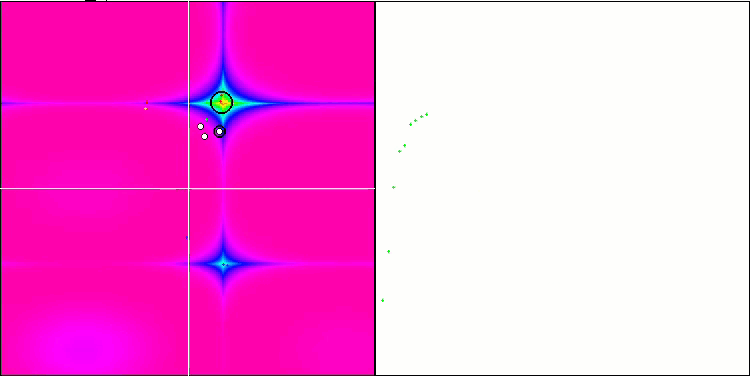
NMm на тестовой функции Rastrigin.

forest

NMm на тестовой функции Forest.

megacity

NMm на тестовой функции Megacity.

Алгоритм метода Нелдера - Мида, несмотря на его многочисленные недостатки, занял почетное 9-е место.

№	AO	Description	Rastrigin			Rastrigin final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result
№	AO	Description	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Rastrigin final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Forest final	10 p (5 F)	50 p (25 F)	1000 p (500 F)	Megacity final	Final result
1	SDSm	stochastic diffusion search M	0,99809	1,00000	0,69149	2,68958	0,99265	1,00000	1,00000	2,99265	1,00000	1,00000	1,00000	3,00000	100,000
2	SSG	saplings sowing and growing	1,00000	0,92761	0,51630	2,44391	0,72120	0,65201	0,83760	2,21081	0,54782	0,61841	0,99522	2,16146	77,683
3	DE	differential evolution	0,98295	0,89236	0,51375	2,38906	1,00000	0,84602	0,65510	2,50112	0,90000	0,52237	0,12031	1,54268	73,099
4	HS	harmony search	0,99676	0,88385	0,44686	2,32747	0,99148	0,68242	0,37529	2,04919	0,71739	0,71842	0,41338	1,84919	70,623
5	IWO	invasive weed optimization	0,95828	0,62227	0,27647	1,85703	0,70170	0,31972	0,26613	1,28755	0,57391	0,30527	0,33130	1,21048	48,250
6	ACOm	ant colony optimization M	0,34611	0,16683	0,15808	0,67103	0,86147	0,68980	0,64798	2,19925	0,71739	0,63947	0,05579	1,41265	47,387
7	MEC	mind evolutionary computation	0,99270	0,47345	0,21148	1,67763	0,60244	0,28046	0,21324	1,09615	0,66957	0,30000	0,26045	1,23002	44,049
8	SDOm	spiral dynamics optimization M	0,69840	0,52988	0,33168	1,55996	0,59818	0,38766	0,37600	1,36183	0,35653	0,15262	0,25842	0,76758	40,289
9	NMm	Nelder-Mead method M	0,88433	0,48306	0,45945	1,82685	0,46155	0,24379	0,21903	0,92437	0,46088	0,25658	0,16810	0,88555	39,660
10	COAm	cuckoo optimization algorithm M	0,92400	0,43407	0,24120	1,59927	0,57881	0,23477	0,13842	0,95200	0,52174	0,24079	0,17001	0,93254	37,830
11	FAm	firefly algorithm M	0,59825	0,31520	0,15893	1,07239	0,50637	0,29178	0,41704	1,21519	0,24783	0,20526	0,35090	0,80398	33,139
12	ABC	artificial bee colony	0,78170	0,30347	0,19313	1,27829	0,53379	0,14799	0,11177	0,79355	0,40435	0,19474	0,13859	0,73768	29,766
13	BA	bat algorithm	0,40526	0,59145	0,78330	1,78002	0,20664	0,12056	0,21769	0,54488	0,21305	0,07632	0,17288	0,46225	29,499
14	CSS	charged system search	0,56605	0,68683	1,00000	2,25289	0,13961	0,01853	0,13638	0,29452	0,07392	0,00000	0,03465	0,10856	27,930
15	GSA	gravitational search algorithm	0,70167	0,41944	0,00000	1,12111	0,31390	0,25120	0,27812	0,84322	0,42609	0,25525	0,00000	0,68134	27,807
16	BFO	bacterial foraging optimization	0,67203	0,28721	0,10957	1,06881	0,39364	0,18364	0,17298	0,75026	0,37392	0,24211	0,18841	0,80444	27,542
17	EM	electroMagnetism-like algorithm	0,12235	0,42928	0,92752	1,47915	0,00000	0,02413	0,29215	0,31628	0,00000	0,00527	0,10872	0,11399	19,002
18	SFL	shuffled frog-leaping	0,40072	0,22021	0,24624	0,86717	0,19981	0,02861	0,02221	0,25063	0,19565	0,04474	0,06607	0,30646	13,200
19	MA	monkey algorithm	0,33192	0,31029	0,13582	0,77804	0,09927	0,05443	0,07482	0,22852	0,15652	0,03553	0,10669	0,29874	11,777
20	FSS	fish school search	0,46812	0,23502	0,10483	0,80798	0,12730	0,03458	0,05458	0,21647	0,12175	0,03947	0,08244	0,24366	11,332
21	IWDm	intelligent water drops M	0,26459	0,13013	0,07500	0,46972	0,28358	0,05445	0,05112	0,38916	0,22609	0,05659	0,05054	0,33322	10,423
22	PSO	particle swarm optimisation	0,20449	0,07607	0,06641	0,34696	0,18734	0,07233	0,18207	0,44175	0,16956	0,04737	0,01947	0,23641	8,426
23	RND	random	0,16826	0,09038	0,07438	0,33302	0,13381	0,03318	0,03949	0,20648	0,12175	0,03290	0,04898	0,20363	5,054
24	GWO	grey wolf optimizer	0,00000	0,00000	0,02093	0,02093	0,06514	0,00000	0,00000	0,06514	0,23478	0,05789	0,02545	0,31812	1,000

Выводы

Алгоритм Нелдера-Мида мало применим в современных тяжелых задачах оптимизации, поскольку требует вычисления фитнес-функции для каждой вершины симплекса на начальном этапе, что сводит на нет его возможность применения для многомерных пространствах поиска, поэтому алгоритм не может быть рекомендован для применения, несмотря на его относительно неплохие результаты и место в рейтинговой таблице.

Алгоритм SDS был удален из таблицы и оставлена только его модифицированная версия.

rating table

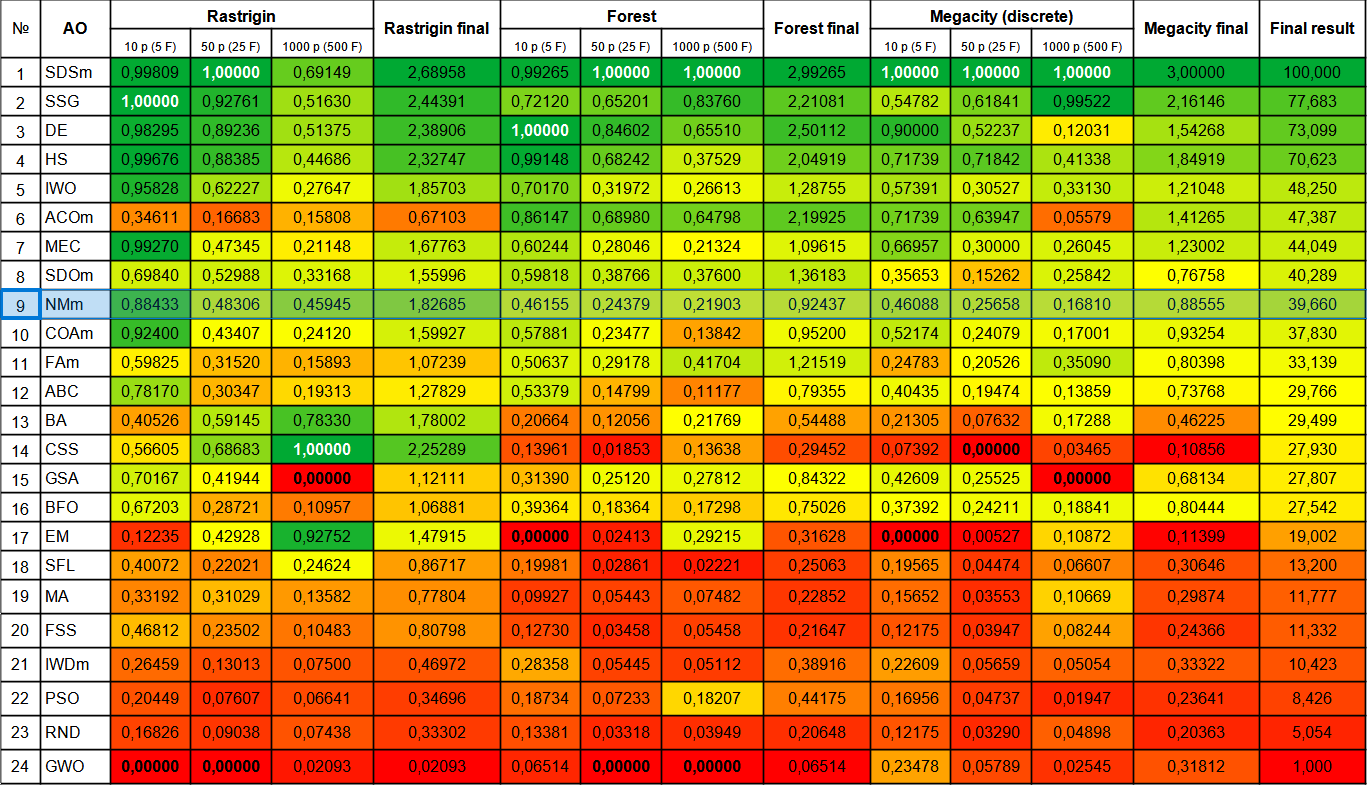
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам.

chart

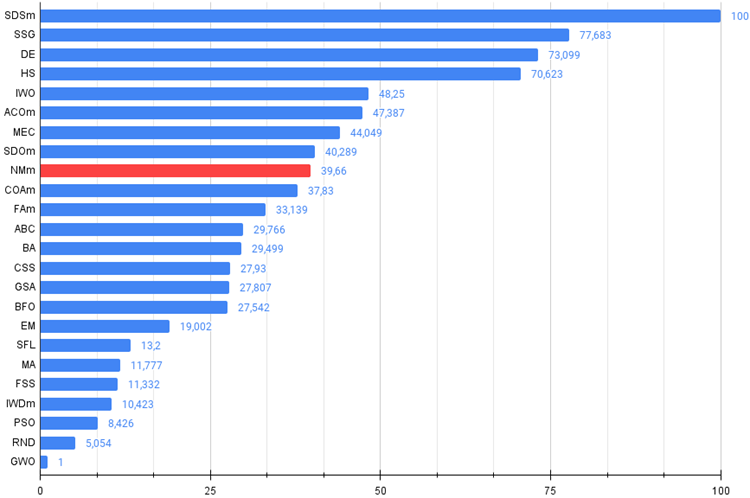
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,

в архиве скрипт для расчета рейтинговой таблицы по методике в этой статье).

Плюсы и минусы модифицированного алгоритма Нельдера-Мида (NMm):

Плюсы:

Небольшое количество внешних параметров.
Неплохие результаты на гладких функциях с малым количеством переменных.

Минусы:

Сложная реализация.
Сложность в использовании со сторонними приложениями из-за необходимости предварительного вычисления приспособленности для всех вершин симплекса.
Низкая скорость работы.
Очень плохая масштабируемость.
Высокий разброс результатов.
Склонность к застреванию в локальных экстремумах.

Обращаю внимание, что Плюсы и Минусы относятся именно к модифицированной версии симплексного поиска, а обычную версию NM даже нет смысла вносить в таблицу из-за очень слабых результатов.

К статье прикреплен архив с обновленными актуальными версиями кодов алгоритмов, описанных в предыдущих статьях. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.

Прикрепленные файлы |

Загрузить ZIP

24_The_world_of_AO_NM.ZIP (836.03 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Последние комментарии | Перейти к обсуждению на форуме трейдеров (1)

fxsaber | 4 дек. 2023 в 11:21

Спасибо, ждем ООП-обертку!

Создаем простой мультивалютный советник с использованием MQL5 (Часть 1): Сигналы на основе ADX в сочетании с Parabolic SAR

Под мультивалютным советником в этой статье понимается советник, или торговый робот, который может торговать (открывать/закрывать ордера, управлять ордерами и т. д.) более чем одной парой символов с одного графика.

Нейросети — это просто (Часть 66): Проблематика исследования в офлайн обучении

Обучение моделей в офлайн режиме осуществляется на данных ранее подготовленной обучающей выборки. Это дает нам ряд преимуществ, но при этом информация об окружающей среде сильно сжимается до размеров обучающей выборки. Что, в свою очередь, ограничивает возможности исследования. В данной статье хочу предложить познакомиться с методом, позволяющем наполнить обучающую выборку максимально разнообразными данными.

Теория категорий в MQL5 (Часть 16): Функторы с многослойными перцептронами

Мы продолжаем рассматривать функторы и то, как их можно реализовать с помощью искусственных нейронных сетей. Мы временно оставим подход, который включал в себя прогнозирование волатильности, и попытаемся реализовать собственный класс сигналов для установки сигналов входа и выхода из позиции.

Сделайте торговые графики лучше с интерактивным графическим интерфейсом на основе MQL5 (Часть III): Простой перемещаемый торговый интерфейс

В этой серии статей мы исследуем интеграцию интерактивных графических интерфейсов в перемещаемые торговые панели на MQL5. В третьей части мы используем наработки из предыдущих частей, чтобы превратить статические торговые панели в динамические.