
Собственные векторы и собственные значения: Разведочный анализ данных в MetaTrader 5
Введение
Метод главных компонент (Principal Component Analysis, PCA) широко известен благодаря его роли в уменьшении размерности при анализе данных. Однако его потенциал выходит далеко за рамки обычного сокращения больших наборов данных. В основе PCA лежать собственные значения и собственные векторы, имеющие огромное значение для выявления в данных скрытых взаимосвязей. В этой статье рассмотрим методы, использующие собственную структуру для выявления таких скрытых взаимосвязей.
Начнем с факторного анализа, чтобы показать, как собственная структура помогает выявить скрытые переменные, предлагая более комплексное понимание структуры, лежащей в основе данных. В поисках скрытых переменных можно выявить избыточность среди переменных, которые представляются независимыми. Это показывает, как несколько переменных могут просто отражать один и тот же базовый фактор. В дополнение к этому рассмотрим возможности использования собственных векторов и собственных значений для оценки взаимосвязей между переменными с течением времени. Анализируя собственную структуру данных, собранных через разные промежутки времени, можно получить ценную информацию о динамических связях между переменными. Это позволяет выявить переменные, которые демонстрируют взаимосвязь или изменение характеристик во времени на противоположные.
Скрытые переменные в данных: метод главных факторов
Факторный анализ — методология, направленная на выявление скрытых факторов, объясняющих взаимосвязи среди наблюдаемых переменных в данных. Она представляет измеряемые переменные в виде скрытых факторов, обозначающих структуры, которые, как известно, влияют на взаимосвязи, но при этом трудно поддаются измерениям или количественным оценкам. Например, рассмотрим индикаторы, используемые трейдером для оценки поведения рынка. Факторный анализ мог бы показать, что на эти индикаторы влияют такие базовые факторы, как настроения инвесторов или склонность к риску. Хотя расчет технических индикаторов может быть простым, количественная оценка рыночных настроений или готовности к риску может оказаться сложнее. Это как наблюдать за кругами на поверхности мутной водной глади. Круги — то, что мы видим, тогда как настоящая их причина остается скрытой. Цель факторного анализа — выявление таких скрытых причин.
Факторный анализ нередко ошибочно принимают за альтернативу методу главных компонент (PCA). Оба метода уменьшают размерность данных, но отличаются в том, как сокращенные переменные соотносятся с исходным набором данных. PCA сводит большой набор переменных к меньшему набору некоррелированных или ортогональных переменных, называемых главными компонентами. Эти компоненты фиксируют максимальное расхождение исходных данных. Представьте себе плотное множество данных с сотнями переменных. Проведение PCA может выявить, что только три переменные представляют более 99% содержащейся в данных информации. Эти три главных компоненты соответствуют важным свойствам, присущим наблюдаемым данным и объясняемым объединением битов исходных данных. На каждую главную компоненту влияет плотное множество переменных. Напротив, факторный анализ предполагает, что скрытые переменные влияют на наблюдаемые. В этой работе мы больше сконцентрируемся на вычислении таких скрытых измерений и уникальных перспективах, которые они раскрывают для наблюдаемых переменных, чем на уменьшении размерности.
Собственные значения и собственные векторы — фундаментальные математические понятия, имеющие решающее значение для понимания этой статьи. Если матрица A имеет размер p на p, x является вектором-столбцом длины p, а E — скаляр, то x — это собственный вектор матрицы A с собственным значением E при Ax=Ex. Значение имеет направление собственного вектора, а не его длина. Обычно его нормализуют до единичной длины. Геометрически умножение вектора на матрицу обычно поворачивает его, но собственные векторы не меняют направление при умножении на матрицу. Это направление — ключ к их релевантости. В нормализованном многомерном нормальном распределении ковариационной матрицей является матрица корреляции R. Пусть V будет матрицей размера p на m. У нового случайного вектора y=V'x есть ковариационная матрица C=V'RV.
У матрицы V есть желаемые свойства, которые транслируются в y. При m=1 V — отдельный столбец, а C — отклонение y. Нормализация матрицы V таким образом, чтобы ее компоненты в сумме давали единицу, приводит к получению собственного вектора R, соответствующего наибольшему собственному значению. Продолжением его до m=2, второго столбца матрицы V, ортогонального к первому, является собственный вектор R, соответствующий второму по величине собственному значению. Этот процесс продолжается для всех p столбцов, превращая собственные векторы R в матрицу преобразования для отображения переменных x в независимые переменные y, охватывающие максимальное отклонение.
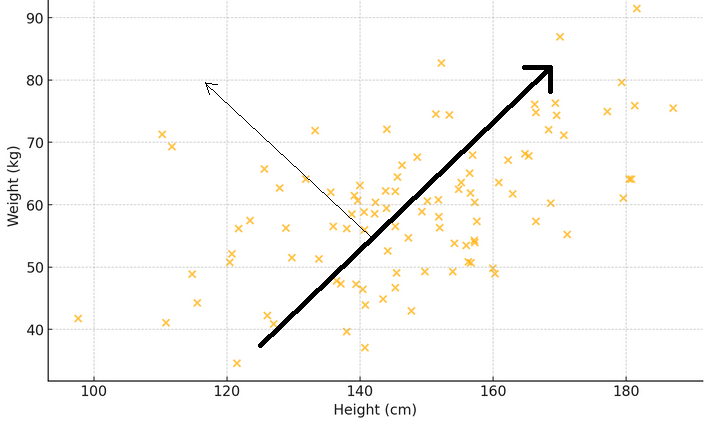
Для иллюстрации смысла двух предыдущих абзацев рассмотрим диаграмму рассеяния, где ось x измеряет вес, а ось y представляет рост выборки людей. Если провести линию через точки, наиболее соответствующие разбросу измерений, такая линия отобразит основную закономерность: более высокие люди, как правило, тяжелее. Теперь представьте собственный вектор в виде стрелки, указывающей в этом главном направлении, демонстрируя наиболее выраженную тенденцию или доминирующую модель. Соответствующее собственное значение показывает, насколько сильно это явление. Если нарисовать еще одну стрелку перпендикулярно первой, она покажет вторичную закономерность, например, что некоторые люди могут весить больше или меньше обычного для своего роста.
Цель — определить, как каждая наблюдаемая переменная соотносится с собственными значениями корреляционной матрицы. Это подразумевает расчет корреляций между собственными значениями и наблюдаемыми переменными. Такие корреляции образуют специальную матрицу, называемую матрицей факторных нагрузок и получаемую умножением каждого собственного вектора на кадратный корень из его соответствующего собственного значения. Исследуя варианты корреляции переменных с определенными собственными значениями, можно предположить наличие влияния на наблюдаемые переменные. Такой анализ помогает понять, какие переменные наиболее значимы для факторов, и подсказывает соответствующие количества факторов, влияющих на наблюдаемые переменные.
Пример: Метод главных факторов на финансовых индикаторах
В этом разделе продемонстрируем работу метода главных факторов (Principal Factor Analysis, PFA) на наборе данных финансовых индикаторов. Воспользуемся MQL5 для реализации всех этапов расчета матрицы факторных нагрузок. Начнем со сбора интересующих нас данных. В данном контексте он будет состоять из нескольких индикаторов, отобранных в указанном диапазоне длин окна. В целях демонстрации возьмем два часто используемых индикатора: предоставляющий информацию о тренде MA (Moving Average, скользящее среднее) и обеспечивающий базовую меру волатильности ATR (Average True Range, средний истинный диапазон). В течение определенного периода времени будут собраны данные по нескольким длинам окна.
Поскольку большая часть анализа предполагает изучение потенциально больших матриц, недостаточно просто напечатать их во вкладке экспертов терминала из-за их размера. Учитывая цель — выполнить все виды анализа в MetaTrader 5 без перехода на другие платформы, такие как Python или R, в приложение добавлен GUI, реализующий метод PFA. На графике ниже приведен набор данных, с которым мы будем работать в этом примере. Каждый столбец содержит значения индикатора для определенной длины окна, указанной в заголовке столбца. "ATR_2" — индикатор ATR с длиной окна 2. Нулевой индекс указывает на самое старое значение за период с 2019.12.31 по 2022.12.31 на основе дневных цен BitCoin (BTCUSD).
Прежде чем пытаться извлечь главные факторы, было бы целесообразно оценить, поддается ли набор данных факторному анализу. Есть два статистических теста, которые можно провести с набором данных для определения, можно ли объяснить переменные скрытыми факторами. Первый — тест Кайзера-Мейера-Олкина (KMO). Критерий KMO — статистический показатель, отражающий пригодность выборочных данных для факторного анализа. Он количественно определяет степень корреляции среди переменных и оценивает долю разброса между ними, которая может представлять собой обычную дисперсию, то есть относимую к базовым факторам. КМО сравнивает величину наблюдаемых коэффициентов корреляции с величиной частных коэффициентов корреляции. Диапазон значений — от 0 до 1, где:
- Значения, близкие к 1, указывают, что данные вполне подходят для факторного анализа.
- Значения ниже 0.6 обычно указывают, что данные не подходят для факторного анализа.
Математически статистические данные KMO определяются как:
Где:
- r(ij) — коэффициент корреляции между переменными i и j.
- p(ij) — коэффициент частичной корреляции между переменными i и j.
Ниже представлена реализация теста КМО на языке MQL5. Функции 'kmo()' требуется три входных параметра. Матрицу 'in' следует снабдить набором данных исследуемых переменных. Результаты теста будут выведены на второй и третий входные параметры соответственно. В векторе 'kmo_per_item' будут содержаться значения KMO для каждой переменной (соответствующие каждому столбцу матрицы 'in'), а 'kmo_total' — это общие статистические данные для составных переменных.
//+---------------------------------------------------------------------------+ //| Calculate the Kaiser-Meyer-Olkin criterion | //| In general, a KMO < 0.6 is considered inadequate. | //+---------------------------------------------------------------------------+ void kmo(matrix &in, vector &kmo_per_item, double &kmo_total) { matrix partial_corr = partial_correlations(in); matrix x_corr = (stdmat(in)).CorrCoef(false); np::fillDiagonal(x_corr,0.0); np::fillDiagonal(partial_corr,0.0); partial_corr = pow(partial_corr,2.0); x_corr = pow(x_corr,2.0); vector partial_corr_sum = partial_corr.Sum(0); vector corr_sum = x_corr.Sum(0); kmo_per_item = corr_sum/(corr_sum+partial_corr_sum); double corr_sum_total = x_corr.Sum(); double partial_corr_sum_total = partial_corr.Sum(); kmo_total = corr_sum_total/(corr_sum_total + partial_corr_sum_total); return; }
В качестве альтернативного или дополнительного теста, который можно провести для оценки набора данных, используют критерий сферичности Бартлетта (Bartlett’s Test of Sphericity, BTS). Это статистический текст для проверки, является ли корреляционная матрица также матрицей тождественности, что указывало бы: переменные не связаны между собой и не подходят для таких методов определения структуры, как факторный анализ. Фактически он проверяет, значительно ли отклоняется наблюдаемая корреляционная матрица от матрицы тождественности, где все диагональные элементы равны 1, что указывает на идеальную корреляцию переменных с самими собой, а недиагональные элементы равны 0, что указывает на отсутствие корреляции между различными переменными. Тест основан на критерии хи-квадрат, статистика которого рассчитывается по следующей формуле:
где:
– n — число наблюдений– p — число переменных.
-|R| — определитель корреляционной матрицы R.
Статистика теста следует за распределением хи-квадрата с (p(p-1))/2 степенями свободы. Если статистика теста Бартлетта велика, а связанное с ней значение p мало (обычно p < 0.05), мы отвергаем нулевую гипотезу. Это говорит о существенном отличии корреляционной матрицы от матрицы тождественности, что свидетельствует о взаимосвязи переменных и их пригодности для факторного анализа. В противном случае, если значение p велико, мы не можем отвергнуть нулевую гипотезу, предполагая, что корреляционная матрица близка к матрице тождественности, а переменные не имеют значительной корреляции.
Код ниже определяет функцию bartlet_sphericity(), реализующую BTS. Функция выводит полученные результаты в последние два входных параметра. Оба — скалярные величины. 'statistic' — это статистика хи-квадрата, а 'p_value' — вычисленное значение вероятности.
//+------------------------------------------------------------------+ //| Compute the Bartlett sphericity test. | //+------------------------------------------------------------------+ void bartlet_sphericity(matrix &in, double &statistic, double &p_value) { long n,p; n = long(in.Rows()); p = long(in.Cols()); matrix x_corr = (stdmat(in)).CorrCoef(false); double corr_det = x_corr.Det(); double neg = -log(corr_det); statistic = (corr_det>0.0)?neg*(double(n)-1.0-(2.0*double(p)+5.0)/6.0):DBL_MAX; double degrees_of_freedom = double(p)*(double(p)-1.0)/2.0; int error; p_value = 1.0 - MathCumulativeDistributionChiSquare(statistic,degrees_of_freedom,error); if(error) Print(__FUNCTION__, " MathCumulativeDistributionChiSquare() error ", error); return; }
Если один из тестов или оба дают обнадеживающие результаты, можем перейти к извлечению главного фактора. Используя набор данных индикаторов, можем видеть, что оба теста демонстрируют пригодность переменных для извлечения факторов.
Для следующего шага требуется немного предварительной обработки, в ходе которой нормализуется набор данных. Нормализация данных гарантирует равный вклад каждого индикатора в анализ, независимо от его масштаба.
//+------------------------------------------------------------------+ //| standardize a matrix | //+------------------------------------------------------------------+ matrix stdmat(matrix &in) { vector mean = in.Mean(0); vector std = in.Std(0); std+=1e-10; matrix out = in; for(ulong row =0; row<out.Rows(); row++) if(!out.Row((in.Row(row)-mean)/std,row)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(in.Rows(), in.Cols()); } return out; }
Корреляционная матрица рассчитывается на основе нормализованных данных.
m_data = stdmat(in);
m_corrmat = m_data.CorrCoef(false); Затем вычисляем собственные значения и собственные векторы корреляционной матрицы. Мы решили использовать реализацию разложения по собственным векторам, предоставленную библиотекой Aglib, из-за проблемы, возникшей при использовании метода Eig() для собственных матриц.
CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
Задачу лучше всего проиллюстрировать на примере. Приведенный ниже код определяет скрипт, который разлагает собственные векторы и значения симметричной матрицы.
//+------------------------------------------------------------------+ //| TestEigenDecompostion.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #include<Math\Alglib\linalg.mqh> //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- matrix dataset = { {1,0.5,-0.2}, {0.5,1,-0.8}, {-0.2,-0.8,1} }; matrix evectors; vector evalues; dataset.Eig(evectors,evalues); Print("Eigen decomposition of \n", dataset); Print(" EVD using built in Eig() \n", evectors); Print(evalues); CMatrixDouble data(dataset); CMatrixDouble vects; CRowDouble vals; CEigenVDetect::SMatrixEVD(data,data.Rows(),1,true,vals,vects); Print(" EVD using Alglib implementation \n", vects.ToMatrix()); Print(vals.ToVector()); } //+------------------------------------------------------------------+
Результат работы скрипта приведен ниже.
Он показывает разницу в представлении собственных векторов и значений. Реализация Alglib сортирует векторы и значения в порядке возрастания, что удобнее. Собственный метод MQL5 — Eig() — не обеспечивает упорядочивания, но не это главная причина пренебрежения им. Рассматривая последний собственный вектор (столбец), замечаем, что знаки отдельных значений противоположны знакам соответствующих значений, выведенных из кода Alglib. Неясно, почему так. Чтобы уточнить, была ли это аномалия, то же разложение было выполнено с помощью Numpy (библиотека в Python), и результаты Alglib были воспроизведены. Очевидно, что факторные нагрузки будут чувствительны к знаку значений функций собственного вектора. Поскольку нагрузки определяются как корреляции, знак значения играет важную роль.
Матрицу факторных нагрузок получают умножением каждого собственного вектора на квадратный корень из его соответствующего собственного значения. Чтобы предотвратить возможность получения неверных чисел, сначала заменим все собственные значения меньше нуля на 0. Это фактически отбрасывает связанное измерение (собственный вектор) в матрице факторных нагрузок.
m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; }
Увиденные нами до сих пор фрагменты кода были извлечены из класса Cpfa для проведения анализа методом главных факторов (PFA) в MetaTrader 5. Полный класс показан ниже, а за ним следует таблица, документирующая его открытые методы.
//+------------------------------------------------------------------+ //| Principal factor extraction | //+------------------------------------------------------------------+ class Cpfa { private: bool m_fitted; //flag showing if principal factors were extracted matrix m_corrmat, //correlation matrix m_data, //standardized data is here m_eigvectors, //matrix of eigen vectors of correlation matrix m_structmat; //factor loading matrix vector m_eigvalues, //vector of eigen values m_cumeigvalues; //eigen values sorted in descending order long m_indices[];//original order of column indices in input data matrix public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Cpfa(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~Cpfa(void) { } //+------------------------------------------------------------------+ //| fit() called with input matrix and extracts principal factors | //+------------------------------------------------------------------+ bool fit(matrix &in) { m_fitted = false; m_data = stdmat(in); m_corrmat = m_data.CorrCoef(false); CMatrixDouble cdata(m_corrmat); CMatrixDouble vects; CRowDouble vals; if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Cols(),1,true,vals,vects)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_eigvectors = vects.ToMatrix(); m_eigvalues = vals.ToVector(); double sum = 0.0; double total = m_eigvalues.Sum(); if(!np::reverseVector(m_eigvalues) || !np::reverseMatrixCols(m_eigvectors)) return m_fitted; m_cumeigvalues = m_eigvalues; for(ulong i=0 ; i<m_cumeigvalues.Size() ; i++) { sum += m_eigvalues[i] ; m_cumeigvalues[i] = 100.0 * sum/total; } m_structmat = m_eigvectors; vector copyevals = m_eigvalues; if(!copyevals.Clip(0.0,DBL_MAX)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } for(ulong i = 0; i<m_structmat.Cols(); i++) if(!m_structmat.Col(m_eigvectors.Col(i)*sqrt(copyevals[i]),i)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } if(!m_structmat.Clip(-1.0,1.0)) { Print(__FUNCTION__, "error ", GetLastError()); return m_fitted; } m_fitted = true; return m_fitted; } //+------------------------------------------------------------------+ //| returns factor loading matrix | //+------------------------------------------------------------------+ matrix get_factor_loadings(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_structmat; } //+------------------------------------------------------------------+ //| get the eigenvector and values of correlation matrix | //+------------------------------------------------------------------+ bool get_eigen_structure(matrix &out_eigvectors, vector &out_eigvalues) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return false; } out_eigvalues = m_eigvalues; out_eigvectors = m_eigvectors; return true; } //+------------------------------------------------------------------+ //| returns variance contributions for each factor as a percent | //+------------------------------------------------------------------+ vector get_cum_var_contributions(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return vector::Zeros(1); } return m_cumeigvalues; } //+------------------------------------------------------------------+ //| get the correlation matrix of the dataset | //+------------------------------------------------------------------+ matrix get_correlation_matrix(void) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } return m_corrmat; } //+------------------------------------------------------------------+ //| returns the rotated factor loadings | //+------------------------------------------------------------------+ matrix rotate_factorloadings(ENUM_FACTOR_ROTATION factor_rotation_type) { if(!m_fitted) { Print(__FUNCTION__, " invalid function call "); return matrix::Zeros(1,1); } CRotator rotator; if(!rotator.fit(m_structmat,factor_rotation_type,4,true)) return matrix::Zeros(1,1); else return rotator.get_transformed_loadings(); } };
| Метод | Описание | Тип возвращаемого значения |
|---|---|---|
| fit | Извлекает главные факторы из входной матрицы `in`. Эта функция стандартизирует входные данные, вычисляет матрицу корреляции и выполняет собственное разложение. Кроме того, она вычисляет матрицу факторных нагрузок и суммарные собственные значения. Именно этот метод следует вызывать первым после создания экземпляра объекта. | bool |
| get_factor_loadings | Возвращает матрицу факторных нагрузок, если извлечены главные факторы; иначе возвращает нулевую матрицу. Нагрузки будут отсортированы в убывающем порядке относительно наибольшего собственного значения. После успешного завершения 'fit()' этот и другие методы можно вызвать для получения свойств анализа. | матрица |
| get_eigen_structure | Возвращает собственные векторы и собственные значения матрицы корреляций. Опционально и сортирует их. | матрица, вектор |
| get_cum_var_contributions | Возвращает суммарные вклады дисперсии каждого фактора в процентах, если главные факторы извлечены; иначе возвращает нулевой вектор. | вектор |
| get_correlation_matrix | Возвращает матрицу корреляции набора данных, если извлечены главные факторы; иначе возвращает нулевую матрицу. | матрица |
| rotate_factorloadings | Возвращает повёрнутую матрицу факторных нагрузок, используя указанный тип поворота, если извлечены главные факторы; иначе возвращает нулевую матрицу. | матрица |
Теперь мы знаем, как получить факторные нагрузки. В следующем разделе увидим, что означают эти корреляции.
Интерпретация факторных нагрузок
Факторные нагрузки представляют собой корреляцию между наблюдаемыми переменными и лежащими в их основе скрытыми факторами. Они указывают на степень связи переменной с фактором. Для упрощения интерпретации собственные векторы расположены в убывающем порядке в соответствии с величиной соответствующих собственных значений. Это гарантирует соответствуие первого собственного вектора наибольшему собственному значению, которое относится к скрытому фактору с наибольшим влиянием на наблюдаемые переменные. Строки матрицы факторной нагрузки следуют тому же порядку, что и столбцы исходного набора данных, то есть каждая строка соответствует какой-то переменной. Столбцы отображают факторы, расположенные в порядке убывания объясняемой дисперсии. Корреляции выше 0.4 или ниже -0.4 считаются значимыми. Любая переменная с нагрузками в диапазоне от -0.4 до 0.4 указывает на незначительность влияния соответствующего фактора на эту переменную.
| Переменные | Фактор 1 | Фактор 2 | Фактор 3 |
|---|---|---|---|
| X1 | 0.8 | 0.3 | 0.1 |
| X2 | -0.3 | -0.93 | 0.00002 |
| X3 | 0.0 | 0.342 | -1 |
| X4 | 0.5 | 0.1 | -0.38 |
| X5 | 0.5 | -0.33 | 0.44 |
У наборов данных с простой факторной структурой есть переменные, сильно нагружающиеся на один фактор и слабо — на другие. Таблицы выше представляет факторные нагрузки гипотетического набора данных. Переменные X1—X4 показывают, что значительно нагружаются на отдельные факторы, а X5 дает смешанные сигналы, потому что умеренно нагружается на два фактора одновременно. Характеристики измеряемой переменной в сочетании с ее факторными нагрузками могут помочь понять характер базового фактора. Например, если на один фактор сильно нагружается несколько экономических показателей, такой фактор может представлять собой базовый экономический тренд или рыночные настроения. И наоборот, если переменная умеренно нагружается на несколько факторов, это может указывать на влияние на переменную нескольких базовых факторов, каждый из которых вносит вклад в различные аспекты поведения переменной.
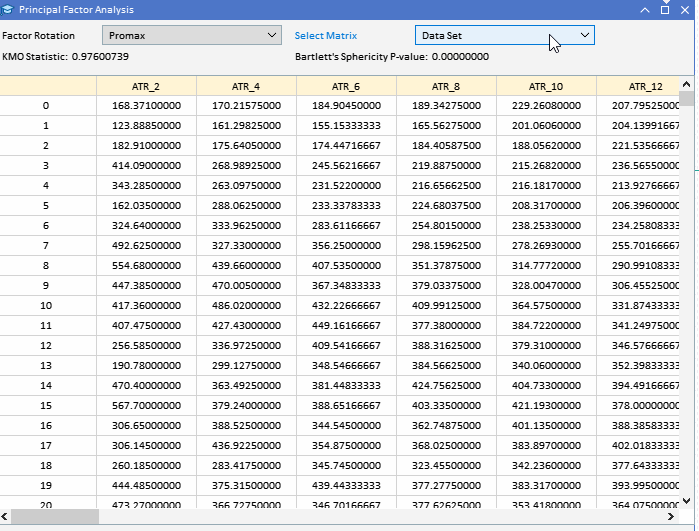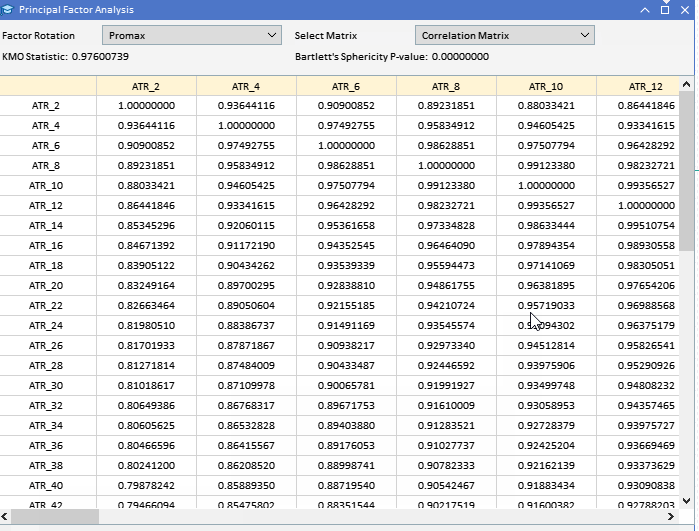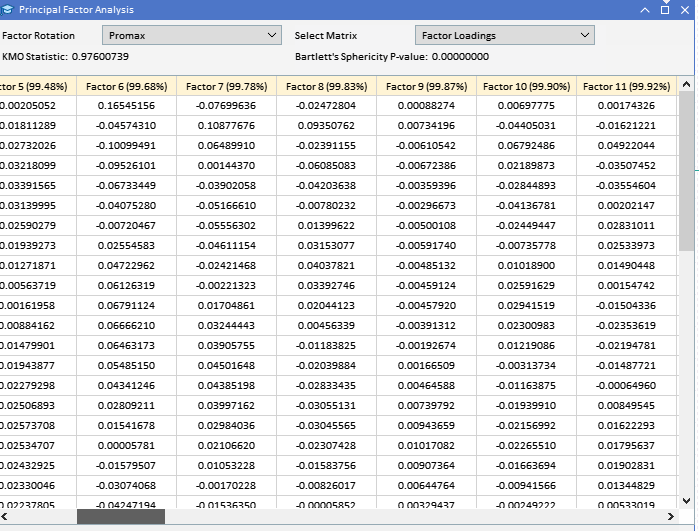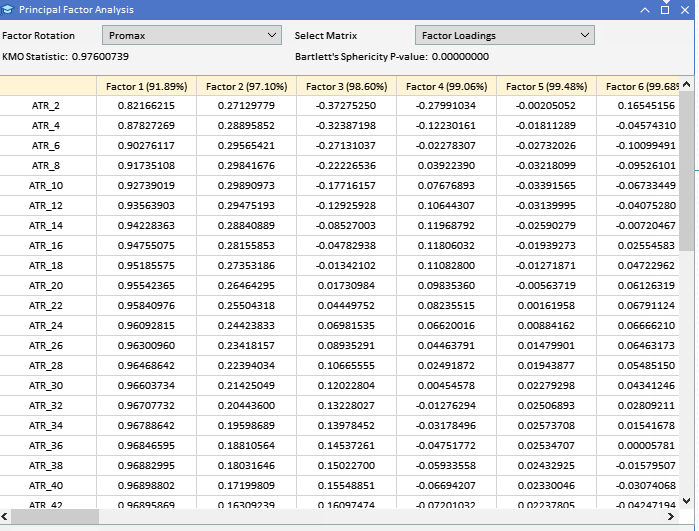
Рассматривая собранные ранее факторные нагрузки переменных ATR, понимаем, что у большинства переменных высокие нагрузки на Фактор 1. Это позволяет предположить, что именно этот фактор в первую очередь влияет на эти переменные. Фактор 1 объясняет значительную часть дисперсии этих переменных, при этом процент объясняемой дисперсии указан числом в скобках (91.89%). Хотя Фактор 1, по-видимому, доминирует, у некоторых переменных тоже есть заметные нагрузки на другие факторы. У ATR_4, ATR_6, ATR_10, ATR_14 и других есть умеренные нагрузки на Фактор 2, указывая на вторичное влияние. У ATR_2, ATR_4, ATR_6, ATR_8 — меньшие, но значимые нагрузки на Фактор 3. У Фактора 4 и последующих меньшие нагрузки по различным переменным. Это позволяет предположить, что они объясняют меньшую дисперсию в наборе данных, чем у первых трех факторов.
Если факторные нагрузки слишком трудно интерпретировать из-за сложности структуры факторов, можно упростить нагрузки, преобразовав их для повышения интерпретируемости. Такой вид преобразования называют вращением факторов. Есть два типа вращения, применимых к матрице факторных нагрузок. Ортогональные вращения сохраняют независимость факторов. Примерами служат методы вращения Varimax и Equamax. Если предполагается независимость факторов, следует применять ортогональные вращения. Косоугольные вращения допускают некоторую зависимость между факторами. Примерами служат вращения методами Promax и Oblimin. Целесообразно использовать косоугольные вращения, если предполагается, что факторы взаимосвязаны. Преобразование вращением приводит необработанные корреляции матрицы факторной структуры к экстремальным значениям (-1,0,1), чтобы упростить интерпретацию корреляций, усиливая влияние на наблюдаемые переменные.
Для упрощения вращений введем класс CRotator, реализующий методы Promax и Varimax.
//+------------------------------------------------------------------+ //| class implementing factor rotations | //| implements varimax and promax rotations | //+------------------------------------------------------------------+ class CRotator { private: bool m_normalize, //normalization flag m_done; //rotation flag int m_power, //exponent to which to raise the promax loadings m_maxIter; //maximum number of iterations. Used for 'varimax' double m_tol; //convergence threshold. Used for 'varimax' matrix m_loadings, //the rotated factor loadings m_rotation_mtx, //the rotation matrix m_phi; //factor correlations matrix. ENUM_FACTOR_ROTATION m_rotation_type; //rotation method employed //+------------------------------------------------------------------+ //| implements varimax rotation | //+------------------------------------------------------------------+ bool varimax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; vector norm_mat(X.Rows()); if(m_normalize) { for(ulong i = 0; i<X.Rows(); i++) norm_mat[i]=sqrt((pow(X.Row(i),2.0)).Sum()); X = X.Transpose()/np::repeat_vector_as_rows_cols(norm_mat,X.Rows()); X = X.Transpose(); } m_rotation_mtx = matrix::Eye(cols,cols); double d = 0,old_d; matrix diag,U,V,transformed,basis; vector S,ones; for(int i =0; i< m_maxIter; i++) { old_d = d; basis = X.MatMul(m_rotation_mtx); ones = vector::Ones(rows); diag.Diag(ones.MatMul(pow(basis,2.0))); transformed = X.Transpose().MatMul(pow(basis,3.0) - basis.MatMul(diag)/double(rows)); if(!transformed.SVD(U,V,S)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } m_rotation_mtx = U.Inner(V); d = S.Sum(); if(d<old_d*(1.0+m_tol)) break; } X = X.MatMul(m_rotation_mtx); if(m_normalize) { matrix xx = X.Transpose(); X = xx * np::repeat_vector_as_rows_cols(norm_mat,xx.Rows()); } else X = X.Transpose(); m_loadings = X.Transpose(); return true; } //+------------------------------------------------------------------+ //| implements promax rotation | //+------------------------------------------------------------------+ bool promax(matrix &in) { ulong rows,cols; rows = in.Rows(); cols = in.Cols(); matrix X = in; matrix weights,h2; h2.Init(1,1); if(m_normalize) { matrix array = X; matrix m = array.MatMul(array.Transpose()); vector dg = m.Diag(); h2.Resize(dg.Size(),1); h2.Col(dg,0); weights = array/np::repeat_vector_as_rows_cols(sqrt(dg),array.Cols(),false); } else weights = X; if(!varimax(weights)) return false; X = m_loadings; ResetLastError(); matrix Y = X * pow(MathAbs(X),double(m_power-1)); matrix coef = (((X.Transpose()).MatMul(X)).Inv()).MatMul(X.Transpose().MatMul(Y)); vector diag_inv = ((coef.Transpose()).MatMul(coef)).Inv().Diag(); if(GetLastError()) { diag_inv = ((coef.Transpose()).MatMul(coef)).PInv().Diag(); ResetLastError(); } matrix D; D.Diag(sqrt(diag_inv)); coef = coef.MatMul(D); matrix z = X.MatMul(coef); if(m_normalize) z = z * np::repeat_vector_as_rows_cols(sqrt(h2).Col(0),z.Cols(),false); m_rotation_mtx = m_rotation_mtx.MatMul(coef); matrix coef_inv = coef.Inv(); m_phi = coef_inv.MatMul(coef_inv.Transpose()); m_loadings = z; return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CRotator(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CRotator(void) { } //+------------------------------------------------------------------+ //| performs rotation on supplied factor loadings passed to /in/ | //+------------------------------------------------------------------+ bool fit(matrix &in, ENUM_FACTOR_ROTATION rot_type=MODE_VARIMX, int power = 4, bool normalize = true, int maxiter = 500, double tol = 1e-05) { m_rotation_type = rot_type; m_power = power; m_maxIter = maxiter; m_tol = tol; m_done=false; if(in.Cols()<2) { m_loadings = in; m_rotation_mtx = matrix::Zeros(in.Rows(), in.Cols()); m_phi = matrix::Zeros(in.Rows(),in.Cols()); m_done = true; return true; } switch(m_rotation_type) { case MODE_VARIMX: m_done = varimax(in); break; case MODE_PROMAX: m_done = promax(in); break; default: return m_done; } return m_done; } //+------------------------------------------------------------------+ //| get the rotated loadings | //+------------------------------------------------------------------+ matrix get_transformed_loadings(void) { if(m_done) return m_loadings; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the rotation matrix | //+------------------------------------------------------------------+ matrix get_rotation_matrix(void) { if(m_done) return m_rotation_mtx; else return matrix::Zeros(1,1); } //+------------------------------------------------------------------+ //| get the factor correlation matrix | //+------------------------------------------------------------------+ matrix get_phi(void) { if(m_done && m_rotation_type==MODE_PROMAX) return m_phi; else return matrix::Zeros(1,1); } };
Вот обзор его открытых методов:
| Метод | Описание | Параметры | Тип возвращаемого значения |
|---|---|---|---|
| fit | Выполняет заданное вращение (Varimax или Promax) на предоставленной матрице факторных нагрузок. | in: Матрица факторных нагрузок, подлежащая вращению | bool |
| get_transformed_loadings | Возвращает повернутую матрицу факторных нагрузок | Отсутствует | матрица |
| get_rotation_matrix | Возвращает матрицу вращения, использованную в преобразовании. | Отсутствует | матрица |
| get_phi | Возвращает матрицу корреляции факторов (только для вращения методом Promax). | Отсутствует | матрица |
Применение вращения к матрице факторных нагрузок.
CRotator rotator; if(!rotator.fit(m_structmat,MODE_PROMAX,4,false)) return; Print(" Rotated Loadings Matrix ", rotator.get_transformed_loadings());
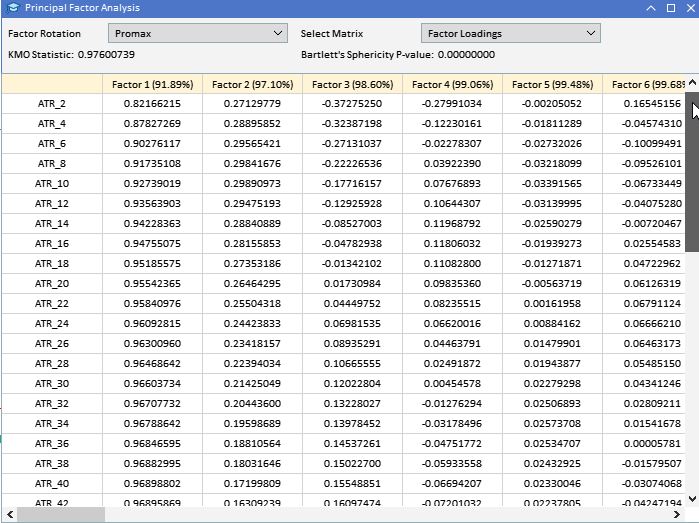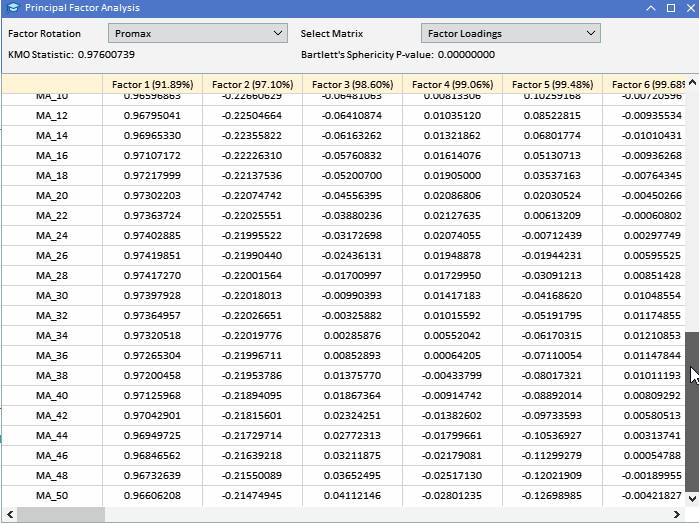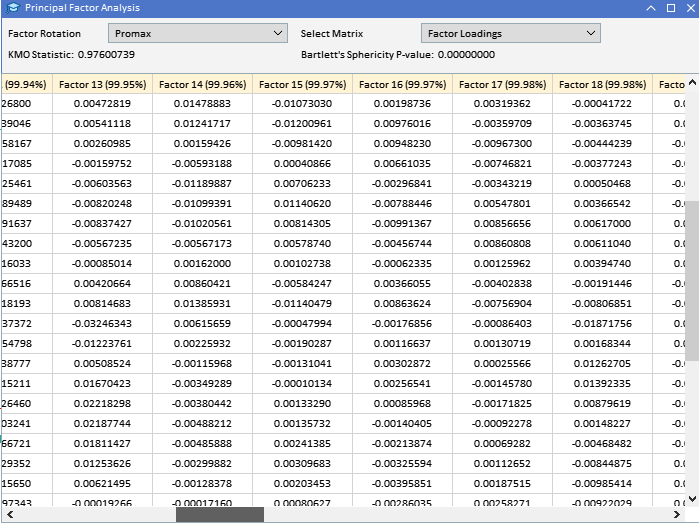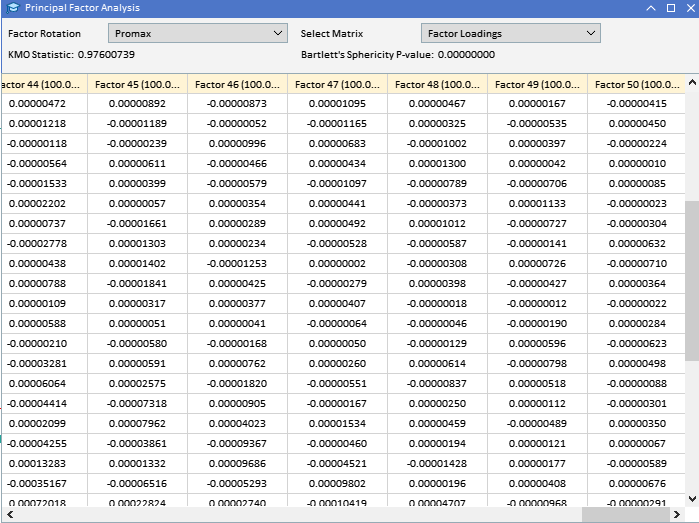
Факторные нагрузки, повернутые методом Promax, наглядно демонстрируют влияние Фактора 1 и Фактора 2 на два класса переменных. Фактор 1 оказывает доминирующее влияние на переменные MA.
Фактор 2 фиксирует дополнительное влияние на переменные ATR. Минимальное влияние прочих Факторов значительно усиливается выявлением менее значимых закономерностей в данных. Такое повернутое решение обеспечивает более четкое понимание базовой структуры набора данных, способствуя лучшей интерпретации. Хотя вращение факторов может значительно улучшить интерпретируемость факторных нагрузок, нужно учитывать некоторые недостатки и ограничения:
- Вращение может чрезмерно упростить базовую структуру, заставляя переменные сильно нагружаться на один фактор, потенциально маскируя более сложные взаимосвязи.
- Выбор между ортогональными и косоугольными вращениями основывается на теоретических предположениях о независимости факторов, которые не всегда могут быть четкими и обоснованными.
- В некоторых случаях вращение может привести к небольшой потере объясняемой дисперсии, поскольку целью вращения является улучшение интерпретируемости, а не максимальное увеличение объясняемой дисперсии.
- При большом количестве переменных и факторов интерпретация вращаемых нагрузок может по-прежнему вызывать затруднения, особенно если нет четкой простой структуры.
- Вращения, особенно итеративные, как в случае с методом Varimax, могут быть ресурсоемкими с точки зрения вычислений на больших наборах данных, что способно повлиять на производительность при работе в реальном времени.
На этом завершим обсуждение извлечения главных факторов. Далее рассмотрим избыточность переменных на основе скрытых факторов и изучим, как такие факторы могут выявлять скрытые взаимосвязи.
Избыточность переменных на основе скрытых факторов
При работе с большим количеством переменных полезно определить наборы в значительной степени избыточных переменных. Это означает, что некоторые переменные предоставляют схожую информацию и, возможно, нет необходимости учитывать их все. Обычно и сама избыточность составляет важную информацию, поскольку может указывать на общий эффект, влияющий на несколько переменных. При выявлении групп переменных с высокой избыточностью можно упростить анализ, сосредоточившись на нескольких репрезентативных переменных или одном факторе, хорошо коррелирующим с этой группой.
Одним из популярных методов выявления избыточных переменных является использование диаграмм рассеяния на главных или повернутых ортогональных осях. Переменные, которые группируются на графике, скорее всего, избыточны. Однако у этого метода есть свои ограничения. Во-первых, он субъективен, и обычно для проведения эффективного анализа целесообразно обрабатывать одновременно только два измерения. Интуитивный метод определения избыточности предполагает учет ненаблюдаемых базовых факторов. Например, если у нас есть три фактора (V1, V2, V3), порождающие наблюдаемые переменные (X1, X2, X3), и мы обнаружим, что один фактор (V3) — просто шум, тогда X1 и X2 могут оказаться избыточными, когда фактор V3 будет проигнорирован. Иными словами, если X2 — просто масштабированная версия переменной X1, они избыточны с точки зрения важных факторов (V1 и V2).
Для строгого измерения избыточности рассмотрим наблюдаемые переменные как векторы в пространстве, заданном базовыми факторами. Имея наблюдаемые переменные, можно представить их в виде векторов в многомерном пространстве, где каждое измерение соответствует базовому фактору. Эти векторы демонстрируют, как каждая переменная связана с факторами. Угол между этими векторами показывает, насколько схожи переменные с точки зрения содержащейся в них информации о базовых факторах. Меньший угол означает, что векторы направлены практически одинаково, и это указывает на высокую избыточность. Иными словами, переменные предоставляют схожую информацию.
Для количественной оценки такой избыточности можно использовать скалярное произведение нормализованных векторов (векторы длиной 1). Скалярное произведение находится в диапазоне от -1 до 1, при этом значение 1 указывает, что векторы идентичны. А это, в свою очередь, говорит о полной избыточности. При этому скалярное произведение, равное -1, означает, что векторы направлены противоположно друг другу, что также можно считать избыточность, поскольку знание одного дает противоположное значение другого. Скалярное произведение, равное 0, означает, что векторы ортогональны (независимы), что указывает на отсутствие избыточности.
Коэффициенты для вычисления наблюдаемых переменных из базовых факторов можно найти с помощью главных компонент. Как правило, доминирующие главные компоненты (с большими собственными значениями) содержат больше всего полезной информации, а компоненты с малыми собственными значениями часто являются шумом. Матрицу факторных нагрузок, показывающую корреляцию факторов с переменными, можно использовать для расчета стандартизированных наблюдаемых переменных из главных компонент. Практически мы часто принимаем абсолютное значение скалярного произведения для измерения избыточности, признавая, что противоположно направленные векторы также указывают на избыточность. Нормализация векторов гарантирует, что их длины равны 1, позволяя скалярному произведению стать непосредственной мерой косинуса угла между ними.
Для вычисления степени взаимосвязи двух переменных с точки зрения скрытого фактора, обычно нам сначала нужно определить количество главных компонент, которые мы считаем важными. Расчет кластеризации сфокусируется на данных в первом из этих столбцов матрицы факторных нагрузок. Каждая строка в этих столбцах будет перемасштабирована так, чтобы их общая сумма составила 1. Степень сходства между двум переменными становится абсолютным значением скалярного произведения двух соответствующих строк преобразованной матрицы факторных нагрузок.
Следующий шаг — группировка этих данных в наборы, представляющие собой переменные, очень похожие по своей связи со скрытым фактором. Одним из более эффективных алгоритмов кластеризации, известным своими хорошими результатами, является иерархическая кластеризация. При иерархической кластеризации, известной также как агломеративная иерархическая кластеризация (AHC), группировка начинается назначением каждой переменной группе с одним элементом. Тестируется каждая возможная комбинация двух групп, чтобы найти две наиболее близкие. Эти группы объединяют в одну. Процесс повторяется до тех пор, пока не останется одна группа или пока степень сходства не станет такой малой, что ее значением можно будет пренебречь.
Реализация AHC предусмотрена в порте MQL5 библиотеки Alglib. Она особенно подходит для наших целей, поскольку поддерживает возможность реализации пользовательской метрики расстояния. Такая функциональность предоставляется тремя классами Alglib. Для использования реализации иерархической агломеративной кластеризации Alglib необходим экземпляр структуры CAHCReport, чтобы хранить результаты операции.CAHCReport m_rep;
Класс CClusterizerState инкапсулирует компонент кластеризации. Без него нельзя выполнить кластеризацию.
CClusterizerState m_cs;
Процесс начинается с инициализации компонента кластеризации посредством вызова статического метода ClusterizerCreate() класса CClustering.
CClustering::ClusterizerCreate(m_cs);
После инициализации можно установить параметры процесса кластеризации с помощью других статических методов класса CClustering. Все они требуют инициализации компонента кластеризации.
CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage);
Наконец, метод ClusterizerRunAHC() запускает саму операцию.
CClustering::ClusterizerRunAHC(m_cs,m_rep);
Доступ к результатам можно получить через свойства экземпляра CAHCReport.
Как упоминалось выше, мы реализуем для операции пользовательскую метрику расстояния. Это достигается предоставлением матрицы с начальными расстояниями для каждой переменной (строка в факторных нагрузках). Приведенный ниже фрагмент кода показывает, как из предоставленных нагрузок рассчитываются начальные расстояния.
for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; }
Сначала нормализуем нагрузки с учетом рассматриваемых числовых измерений.
for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } }
И они используются для расчета расстояний. Кроме того, нормализованные нагрузки — это те, которые передаются в кластеризатор. Не те факторные нагрузки, которые не обработаны. Весь реализующий кластеризацию код приведен в классе CCluster.
//+------------------------------------------------------------------+ //| cluster a set of points | //+------------------------------------------------------------------+ class CCluster { private: CClusterizerState m_cs; CAHCReport m_rep; matrix m_pd[]; //+------------------------------------------------------------------+ //| Preprocesses input matrix before clusterization | //+------------------------------------------------------------------+ bool customDist(matrix &structure, ulong num_factors, matrix& out[], bool calculate_custom_distances = true) { int nvars; double dotprod, length; nvars = int(structure.Rows()); int ndim = (num_factors && num_factors<=structure.Cols())?int(num_factors):int(structure.Cols()); if(out.Size()<2) if(out.Size()<2 && (ArrayResize(out,2)!=2 || !out[0].Resize(nvars,ndim) || !out[1].Resize(nvars,nvars))) { Print(__FUNCTION__, " error ", GetLastError()); return false; } if(calculate_custom_distances) { for(int i=0 ; i<nvars ; i++) { length = 0.0 ; for(int j=0 ; j<ndim ; j++) length += structure[i][j] * structure[i][j] ; length = 1.0 / sqrt(length) ; for(int j=0 ; j<ndim ; j++) out[0][i][j] = length * structure[i][j] ; } out[1].Fill(0.0); for(int irow1=0 ; irow1<nvars-1 ; irow1++) { for(int irow2=irow1+1 ; irow2<nvars ; irow2++) { dotprod = 0.0 ; for(int i=0 ; i<ndim ; i++) dotprod += out[0][irow1][i] * out[0][irow2][i] ; out[1][irow1][irow2] = fabs(dotprod) ; } } } else { out[0] = np::sliceMatrixCols(structure,0,ndim); } return true; } public: //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CCluster(void) { CClustering::ClusterizerCreate(m_cs); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ ~CCluster(void) { } //+------------------------------------------------------------------+ //| cluster a set | //+------------------------------------------------------------------+ bool cluster(matrix &in_points, ulong factors=0, ENUM_LINK_METHOD linkage=MODE_COMPLETE, ENUM_DIST_CRIT dist = DIST_CUSTOM) { if(!customDist(in_points,factors,m_pd,dist==DIST_CUSTOM)) return false; CMatrixDouble pp(m_pd[0]); CMatrixDouble pd(m_pd[1]); CClustering::ClusterizerSetPoints(m_cs,pp,pp.Rows(),pp.Cols(),dist<22?dist:DIST_EUCLIDEAN); if(dist==DIST_CUSTOM) CClustering::ClusterizerSetDistances(m_cs,pd,pd.Cols(),true); CClustering::ClusterizerSetAHCAlgo(m_cs,linkage); CClustering::ClusterizerRunAHC(m_cs,m_rep); return m_rep.m_terminationtype==1; } //+------------------------------------------------------------------+ //| output clusters to vector array | //+------------------------------------------------------------------+ bool get_clusters(vector &out[]) { if(m_rep.m_terminationtype!=1) { Print(__FUNCTION__, " no cluster information available"); return false; } if(ArrayResize(out,m_rep.m_pz.Rows())!=m_rep.m_pz.Rows()) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int i = 0; i<m_rep.m_pm.Rows(); i++) { int zz = 0; for(int j = 0; j<m_rep.m_pm.Cols()-2; j+=2) { int from = m_rep.m_pm.Get(i,j); int to = m_rep.m_pm.Get(i,j+1); if(!out[i].Resize((to-from)+zz+1)) { Print(__FUNCTION__, " error ", GetLastError()); return false; } for(int k = from; k<=to; k++,zz++) out[i][zz] = m_rep.m_p[k]; } } return true; } };
Функция cluster() выполняет иерархическую кластеризацию по заданному набору входных точек. Для этого нужно четыре параметра: ссылка на матрицу входных точек, количество рассматриваемых факторов, используемый метод компоновки и критерий расстояния. Во-первых, она вычисляет пользовательскую матрицу расстояний, если указанный критерий расстояния является пользовательским. Если расчет расстояния не удается, функция возвращает false. Затем она инициализирует две матрицы, pp и pd, на основе рассчитанных данных о расстоянии. После этого функция задает точки для кластеризации с помощью критерия расстояния. По умолчанию — эвклидовыми значениями, если критерий не установлен в соответствии с пользовательской опцией. Если критерий расстояния — пользовательский, она соответствующим образом устанавливает расстояния для кластеризации. После настройки расстояния и точек функция конфигурирует алгоритм иерархической кластеризации указанным методом компоновки. Она запускает алгоритм агломеративной иерархической кластеризации и проверяет тип завершения процесса. Функция возвращает true, если тип завершения равен 1, что указывает на успешную кластеризацию. Иначе — возвращает false.
Функция get_clusters() извлекает и выводит кластеры из результатов иерархической кластеризации. Она принимает один параметр: массив векторов out[], который будет заполнен кластерами. Сначала функция проверяет, равен ли тип завершения кластеризации 1, что указывает на успешную кластеризацию. Если нет, печатает сообщение об ошибке и возвращает false. Затем функция выполняет итерацию по каждой строке матрицы m_rep.m_pm, содержащей информацию о кластеризации. Для каждой строки она инициализирует переменную zz для отслеживания индекса в выходном векторе. Затем она выполняет итерацию по столбцам текущей строки, обрабатывая пары столбцов (представляющих начальные и конечные индексы кластеров). Для каждой пары вычисляет диапазон индексов (от from до to) и изменяет размер текущего выходного вектора, чтобы он мог вместить элементы кластера. Если изменение размера не удается, она выводит сообщение об ошибке и возвращает false. Наконец, функция заполняет текущий выходной вектор элементами кластера, выполняя итерации от from до to и увеличивая zz для каждого элемента. В случае успешного завершения процесс функция возвращает true, указывая, что кластеры успешно извлечены и сохранены в массиве out.
Фрагмент кода ниже показывает, как использовать класс CCluster.
vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); }В MetaTrader 5 не хватает средств непосредственной визуализации результатов агломеративной иерархической кластеризации (AHC). Хотя консоль терминала может отображать некоторые выходные данные, она неудобна для просмотра сложных результатов, таких как результаты AHC. Результаты AHC лучше всего визуализировать с помощью дендрограмм, показывающих иерархическую структуру групп данных. Дендрограмма иллюстрирует, как кластеры формируются пошаговым слиянием точек данных или кластеров. Ниже представлена построенная вручную дендрограмма, которая показывает группировки из нашего набора индикаторов.
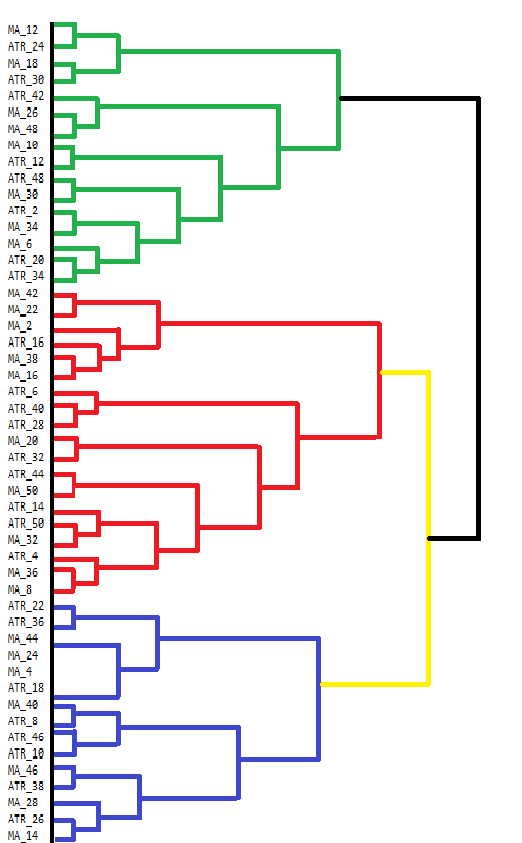
Дендрограмма иллюстрирует группировку переменных на основе их схожести. Переменные, объединенные на более низких уровнях (ближе к нижней части графика), больше похожи друг на друга, чем те, которые объединяются выше. Например, MA_12 и MA_24 больше похожи друг на друга по сравнению с ATR_18. Разные кластеры на дендрограмме обозначены разными цветами. Кластеры зеленого, красного, синего и желтого цветов выделяют группы тесно связанных между собой переменных. Каждый цвет представляет собой набор переменных, демонстрирующих высокое сходство или избыточность.
Высота, на которой объединяются два кластера, указывает на несходство между ними. Чем ниже уровень объединения, тем больше сходства между кластерами. Черная линия в верхней части обозначает финальное объединение кластеров с наиболее существенными различиями. Такой метод иерархической кластеризации может помочь в принятии решений при отборе переменных. Анализируя кластеры, можно сосредоточиться для дальнейшего анализа на определенных представителях переменных внутри каждого кластера, тем самым упростив набор данных без потери важной информации.
Код на MQL5, использованный для сбора и анализа набора данных индикаторов, содержится в скрипте EDA.mq5. Он использует все описанные в статье инструменты кодовой разработки, определенные в pfa.mqh.
//+------------------------------------------------------------------+ //| EDA.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\Slope.ex5" #resource "\\Indicators\\CMMA.ex5" #include<pfa.mqh> #include<ErrorDescription.mqh> #property script_show_inputs //+------------------------------------------------------------------+ //|indicator type | //+------------------------------------------------------------------+ enum SELECT_INDICATOR { CMMA=0,//CMMA SLOPE//SLOPE }; //--- input parameters input uint period_inc=2;//lookback increment input uint max_lookback=50; input ENUM_MA_METHOD AppliedMA = MODE_SMA; input datetime SampleStartDate=D'2019.12.31'; input datetime SampleStopDate=D'2022.12.31'; input string SetSymbol="BTCUSD"; input ENUM_TIMEFRAMES SetTF = PERIOD_D1; input ENUM_FACTOR_ROTATION AppliedFactorRotation = MODE_PROMAX; input ENUM_DIST_CRIT AppliedDistanceCriterion = DIST_CUSTOM; input ENUM_LINK_METHOD AppliedClusterAlgorithm = MODE_COMPLETE; input ulong Num_Dimensions = 10; //---- string csv_header=""; //csv file header int size_sample, //training set size size_observations, //size of of both training and testing sets combined maxperiod, //maximum lookback indicator_handle=INVALID_HANDLE; //long moving average indicator handle //--- vector indicator[]; //indicator indicator values; //--- matrix feature_matrix; //full matrix of features; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //---get relative shift of sample set int samplestart,samplestop,num_features; samplestart=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStartDate); samplestop=iBarShift(SetSymbol!=""?SetSymbol:NULL,SetTF,SampleStopDate); num_features = int((max_lookback/period_inc)*2); //---check for errors from ibarshift calls if(samplestart<0 || samplestop<0) { Print(ErrorDescription(GetLastError())); return; } //---set the size of the sample sets size_observations=(samplestart - samplestop) + 1 ; maxperiod=int(max_lookback); //---check for input errors if(size_observations<=0 || maxperiod<=0) { Print("Invalid inputs "); return; } //---allocate memory if(ArrayResize(indicator,num_features)<num_features) { Print(ErrorDescription(GetLastError())); return; } //----get the full collection of indicator values int period_len; int k=0; //--- for(SELECT_INDICATOR select_indicator = 0; select_indicator<2; select_indicator++) { for(int iperiod=0; iperiod<int(indicator.Size()/2); iperiod++) { period_len=int((iperiod+1) * period_inc); int try=10; while(try) { switch(select_indicator) { case CMMA: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\CMMA.ex5",AppliedMA,period_len); break; case SLOPE: indicator_handle=iCustom(SetSymbol!=""?SetSymbol:NULL,SetTF,"\\Indicators\\Slope.ex5",period_len); break; } if(indicator_handle==INVALID_HANDLE) try--; else break; } if(indicator_handle==INVALID_HANDLE) { Print("Invalid indicator handle ",EnumToString(select_indicator)," ", GetLastError()); return; } Comment("copying data to buffer for indicator ",period_len); try = 0; while(!indicator[k].CopyIndicatorBuffer(indicator_handle,0,samplestop,size_observations) && try<10) { try++; Sleep(5000); } if(try<10) ++k; else { Print("error copying to indicator buffers ",GetLastError()); Comment(""); return; } if(indicator_handle!=INVALID_HANDLE && IndicatorRelease(indicator_handle)) indicator_handle=INVALID_HANDLE; } } //---resize matrix if(!feature_matrix.Resize(size_observations,indicator.Size())) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //---copy collected data to matrix for(ulong i = 0; i<feature_matrix.Cols(); i++) if(!feature_matrix.Col(indicator[i],i)) { Print(ErrorDescription(GetLastError())); Comment(""); return; } //--- Comment(""); //---test dataset for principal factor analysis suitability //---kmo test vector kmo_vect; double kmo_stat; kmo(feature_matrix,kmo_vect,kmo_stat); Print("KMO test statistic ", kmo_stat); //---Bartlett sphericity test double bs_stat,bs_pvalue; bartlet_sphericity(feature_matrix,bs_stat,bs_pvalue); Print("Bartlett sphericity test p_value ", bs_pvalue); //---Extract the principal factors Cpfa fa; //--- if(!fa.fit(feature_matrix)) return; //--- matrix fld = fa.get_factor_loadings(); //--- matrix rotated_fld = fa.rotate_factorloadings(AppliedFactorRotation); //--- Print(" factor loading matrix ", fld); //--- Print("\n rotated factor loading matrix ", rotated_fld); //--- matrix egvcts; vector egvals; fa.get_eigen_structure(egvcts,egvals,false); Print("\n vects ", egvcts); Print("\n evals ", egvals); //--- vector clusters[]; CCluster fc; if(!fc.cluster(fld,Num_Dimensions,AppliedClusterAlgorithm,AppliedDistanceCriterion)) return; if(!fc.get_clusters(clusters)) return; for(uint i =0; i<clusters.Size(); i++) { Print("cluster at ", i, "\n variable indices ", clusters[i]); } } //+------------------------------------------------------------------+
Согласованность временных рядов
При анализе переменных во времени их взаимосвязи могут неожиданно изменяться. Обычно связанные переменные могут внезапно разойтись, что указывает на потенциальную проблему. Например, температурные колебания могут влиять на потребность в электроэнергии, что в свою очередь меняет цены на природный газ. При изменении их обычного характера это может свидетельствовать о том, что происходит нечто необычное. Аналогичным образом переменные, обычно ведущие себя независимо, могут внезапно начать меняться одинаково, например во время одновременного роста разных секторов фондового рынка в связи с появлением позитивных экономических новостей.
Измерение согласованности подразумевает количественную оценку взаимосвязанности набора переменных временного ряда в пределах подвижного временного окна. Одним из основных методов является проверка, насколько большую дисперсию фиксирует наибольшее собственное значение. Однако у этого метода могут быть ограничения, поскольку он учитывает только одно измерение. Более комплексный подход подразумевает суммирование наибольших собственных значений, особенно при наличии нескольких взаимосвязей между переменными. Такой подход представляет более точную картину общей согласованности в системе со сложными взаимосвязями, но для этого нужно заранее знать, какие факторы наиболее значимы. Что-то, вероятно, невозможное или просто слишком субъективное.
Более общий подход требуется для случаев, когда количество взаимосвязей неизвестно или колеблется во времени, особенно при большом количестве переменных. В сценариях с неизвестной размерностью можно визуализировать отсортированные собственные значения от наибольшего к наименьшему, как артистов оркестра. Ключ к прекрасному музыкальному исполнению — настройка разных инструментов в единой манере для согласованного звучания. Если отдельные музыканты в оркестре не смогут действовать согласованно, музыка получится отвратительная. Слаженность будет недостаточной. Представьте звуки, извлекаемые каждым музыкантом в оркестре, как взвешенную величину, составляющую той музыки, которую слышит публика. Дисбаланс этих значений отражает согласованность. Вычислим взвешенную сумма, где веса обозначают громкость, на которую способен каждый инструмент.
Если каждый инструмент (переменная) играет свою мелодию независимо, общее звучание становится неорганизованным и хаотичным, то есть имеет нулевую согласованность. Однако, если инструменты идеально синхронизированы и играют слаженно, они исполняют цельное и прекрасное музыкальное произведение, отражая полную согласованность. Согласованность в нашей аналогии похожа на гармонию в оркестре, которая показывает, насколько хорошо инструменты (переменные) играют совместно. Если гармония внезапно нарушается, это говорит о чем-то необычном, происходящем с инструментами или композицией.
Рассмотрим две крайности. Если переменные полностью независимы. Матрица корреляций этих переменных будет матрицей тождественности, и все собственные значения будут равны (1.0). Взвешенная сумма (благодаря симметричным весам) будет равна нулю, отражая нулевую согласованность. С другой стороны, при наличии идеальной корреляции между переменными существует только одно ненулевое собственное значение, равное количеству переменных. Взвешенная сумма становится числом переменных, которое после нормализации (деления на число переменных) приводит к согласованности, равной 1.0, отражая идеальную корреляцию. Этот метод предлагает меру согласованности 0-1 на основе дисбаланса в распределении собственных значений, не делая предположений о размерности.
Для иллюстрации согласованности создадим индикатор, измеряющий согласованность цен закрытия различных символов в течение одного временного окна. Назовем этот индикатор Coherence.mq5. Пользователи смогут измерять связность множества символов, добавляя их в виде списка названий инструментов через запятую. Индикатор применяет другой подход к расчету корреляций между несколькими переменными. На этот раз используем непараметрический коэффициент корреляции Спирмана.
covar[0][0] = 1.0 ; for(int i=1 ; i<npred ; i++) { for(int j=0 ; j<i ; j++) { for(int k=0 ; k<lookback ; k++) { nonpar1[k] = iClose(stringbuffer[i],PERIOD_CURRENT,ibar+k); nonpar2[k] = iClose(stringbuffer[j],PERIOD_CURRENT,ibar+k); } if(!MathCorrelationSpearman(nonpar1,nonpar2,covar[i][j])) Print(" MathCorrelationSpearman failed ", GetLastError(), " :", ibar); } covar[i][i] = 1.0 ; }
Поскольку мы используем реализацию EVD от Aglib, нам не нужно описывать полную матрицу корреляций, просто построим верхний или нижний треугольник. Нам нужны не собственные векторы, а только собственные значения.
CMatrixDouble cdata(covar); if(!CEigenVDetect::SMatrixEVD(cdata,cdata.Rows(),0,false,evals,evects)) { Print(" EVD failed ", GetLastError(), " :", ibar); coherenceBuffer[ibar]=0.0; continue; }
Чтобы получить правильную ориентацию распределения собственных значений, нужно развернуть вектор.
vector eval = evals.ToVector(); if(!np::reverseVector(eval)) Print(" failed vecter reversal operation : ", ibar);
Связность вычисляется с помощью собственных значений.
double center = 0.5 * (npred - 1) ; double sum = 0.0; for(ulong i=0 ; i<eval.Size() ; i++) { sum += (center - i) * eval[i] / center ; } coherenceBuffer[ibar] = sum / eval.Sum();
Полный код приложен в конце статьи. Посмотрим, как индикатор выглядит при других длинах окна, измеряя согласованность между криптовалютами BTCUSD, DOGUSD и XRPUSD.
Рассматривая 60-дневный график согласованности, можно сказать, что он развеял личные предубеждения о заметной связности движения этих символов. Удивительно, насколько сильно он колеблется. Причем величины изменяются по всему спектру возможных значений.
По мере продвижения к более длинным окнам мы увидим периоды стабильной согласованности, но природа этой согласованности снова окажется неожиданной. Существуют значительные промежутки времени, когда согласованность практически отсутствует.
Заключение
Использование в этих передовых методах собственных значений и собственных векторов подчеркивает их универсальность и фундаментальную значимость в исследованиях данных. Они обеспечивают надежную основу для снижения размерности, распознавания образов и обнаружения скрытых структур в сложных наборах данных. Выходя за пределы PCA, мы открываем для себя более широкий спектр инструментов, предлагающих детальную информацию. В этом тексте показано, что собственные векторы и собственные значения — нечто намного большее, чем математические абстракции; они представляют собой основу сложных аналитических методов, которые современные трейдеры могут использовать для получения конкурентного преимущества. Весь продемонстрированный в статье код приложен в виде сжатого архивного файла. В таблице ниже перечислены файлы, доступные для скачивания.| Файл | Описание |
|---|---|
| Mql5\Include\np.mqh | включаемый файл, содержащий различные утилиты матричных и векторных функций |
| Mql5\Include\pfa.mqh | pfa.mqh содержит определение классов Cpfa, CCluster и CRotator. А также определение функций для реализаций тестов KMO и BTS |
| Mql5\Scripts\EDA.mq5 | Скрипт демонстрирует использование всех описанных в статье средств разработки кода, собирая набор данных о пользовательских индикаторах для анализа методом главных факторов |
| Mql5\Scripts\TestEigenDecomposition.mq5 | Этот скрипт воспроизводит упомянутые проблемы с учетом встроенного матричного метода Eig() |
| Mql5\Indicators\Coherence.mq5 | Вот индикатор Coherence, примененный к 3 символам |
| Mql5\Experts\PrincipalFactors.mq5 | Это исходный код приложения, предназначенного для просмотра больших матриц. Код основан на многоуважаемой библиотеке Easy and Fast GUI, которую можно найти в базе MQL5 Codebase |
| Mql5\Experts\PrincipalFactors.ex5 | Скомпилированная версия вышеприведенного списка |
Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15229
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка системы репликации (Часть 61): Нажатие кнопки воспроизведения в сервисе (II)
Разработка системы репликации (Часть 61): Нажатие кнопки воспроизведения в сервисе (II)
 Алгоритм эволюционного путешествия во времени — Time Evolution Travel Algorithm (TETA)
Алгоритм эволюционного путешествия во времени — Time Evolution Travel Algorithm (TETA)
 Переосмысливаем классические стратегии (Часть III): Прогнозирование более высоких максимумов и более низких минимумов
Переосмысливаем классические стратегии (Часть III): Прогнозирование более высоких максимумов и более низких минимумов
 Создаем динамическую мультисимвольную мультипериодную панель индекса относительной силы (RSI) в MQL5
Создаем динамическую мультисимвольную мультипериодную панель индекса относительной силы (RSI) в MQL5
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования