
Популяционный ADAM (Adaptive Moment Estimation)
Содержание
Введение
В мире машинного обучения, где данные стремительно множатся, а алгоритмы становятся все более сложными, оптимизация играет ключевую роль в достижении высоких результатов. Среди множества методов, которые пытаются справиться с этой задачей, алгоритм ADAM (Adaptive Moment Estimation) выделяется своей элегантностью и эффективностью.
В 2014 году два выдающихся ума — Д. П. Кингма и Дж. Ба предложили алгоритм ADAM, который сочетает в себе лучшие черты своих предшественников, таких как AdaGrad и RMSProp. Алгоритм был специально разработан для оптимизации весов нейронных сетей с использованием градиентов активационных функций нейронов. Он основывается на адаптивных оценках первого и второго моментов, что делает его простым в реализации и высокоэффективным с точки зрения вычислений. Алгоритм требует минимальных ресурсов памяти и не зависит от диагонального изменения масштабов градиентов, что делает его особенно подходящим для задач с большими объемами данных и параметров.
ADAM также хорошо справляется с нестационарными целями и ситуациями, когда градиенты могут быть шумными или разреженными. Гиперпараметры алгоритма легко интерпретируются и обычно не требуют сложной настройки.
Однако, несмотря на свою эффективность в области нейронных сетей, ADAM ограничен использованием аналитических градиентов, что сужает спектр его применения. В данной статье мы предлагаем инновационный подход к модификации алгоритма ADAM, трансформируя его в популяционный алгоритм оптимизации, способный работать с численными градиентами. Эта модификация не только расширяет область применения ADAM за пределы нейронных сетей, но и открывает новые возможности для решения широкого спектра задач оптимизации в общем виде.
Наше исследование направлено на создание универсального оптимизатора, сохраняющего преимущества оригинального ADAM, но способного эффективно работать в условиях, где аналитические градиенты недоступны. Это позволит применять модифицированный ADAM в таких областях, как глобальная оптимизация и многокритериальная оптимизация, значительно расширяя его потенциал и практическую ценность.
Реализация алгоритма
Алгоритм ADAM часто классифицируют как стохастический градиентный метод оптимизации. Однако, важно отметить, что сам по себе ADAM не содержит внутренних стохастических элементов в своей основной логике. Стохастичность, ассоциируемая с ADAM, на самом деле проистекает из способа подготовки и подачи данных алгоритму, а не из его внутренней механики. Важно различать стохастичность в подготовке данных и детерминированность самого алгоритма оптимизации.
Сам алгоритм ADAM является полностью детерминированным. При одинаковых входных данных и начальных условиях он всегда будет производить идентичные результаты. Обновление параметров в ADAM происходит на основе четко определенных формул, не включающих элементы случайности.
Это разграничение между детерминированной природой алгоритма ADAM и стохастическим характером подготовки данных для него, важно для правильного понимания его работы и потенциала модификации. Признание этого факта открывает возможности для адаптации ADAM к задачам, где стохастическая подготовка данных может быть неприменима или нежелательна, сохраняя при этом его мощные оптимизационные свойства.
Давайте посмотрим на псевдокод с формулами:
1. Инициализация:
m₀ = 0 (инициализация первого момента)
v₀ = 0 (инициализация второго момента)
t = 0 (счетчик шагов)
2. На каждом шаге t:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (вычисление градиента)
3. Обновление скорректированных первого и второго моментов:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. Обновление параметров:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
Где:
θₜ - параметры модели на шаге t
f(θ) - целевая функция
α - скорость обучения (обычно α = 0.001)
β₁, β₂ - коэффициенты затухания для моментов (обычно β₁ = 0.9, β₂ = 0.999)
ε - малая константа для предотвращения деления на ноль (обычно 10⁻⁸)
mₜ, vₜ - оценки первого и второго моментов градиента
m̂ₜ, v̂ₜ - скорректированные оценки моментов
Эти формулы отражают суть алгоритма ADAM, показывая как он адаптивно корректирует скорость обучения для каждого параметра на основе оценок первого и второго моментов градиентов. Как видим, никакой стохастичности в алгоритме нет вообще. Как правило, алгоритм ADAM в своих многочисленных программных реализациях прочно вплетён в ткань архитектуры нейронных сетей. Однако в этой статье мы совершим маленькое волшебство: мы не только сделаем его самостоятельной и самодостаточной сущностью, но и превратим, внимание, в популяционный и поистине стохастический метод.
Для начала нам предстоит реализовать ADAM в популяционном формате, сохранив его исходные формулы, при этом добавив элемент случайности лишь на этапе первоначальной инициализации оптимизируемых параметров. Но это только начало! Затем мы внедрим случайность в динамику поведения этого градиентного метода и посмотрим, к каким результатам это может привести.
Определим структуру "S_Gradients", которая будет хранить градиенты и два вектора моментов (первого и второго). Метод "Init (int coords)" задает размер массивам и инициализирует их нулями.
//—————————————————————————————————————————————————————————————————————————————— // Структура для хранения градиентов и моментов struct S_Gradients { double g []; // Градиенты double m []; // Векторы первого момента double v []; // Векторы второго момента // Метод инициализации градиентов void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Инициализация градиентов нулями ArrayInitialize (m, 0.0); // Инициализация первого момента нулями ArrayInitialize (v, 0.0); // Инициализация второго момента нулями } }; //——————————————————————————————————————————————————————————————————————————————
Класс "C_AO_ADAM" реализует алгоритм оптимизации ADAM. Основные функции класса:
- Конструктор — инициализирует параметры алгоритма, такие как размер популяции, коэффициенты обучения и затухания.
- SetParams () — устанавливает значения параметров из массива "params", позволяя изменять их после инициализации.
- Init () — подготавливает алгоритм к работе, принимая диапазоны параметров и количество эпох.
- Moving () и Revision () — предназначены для выполнения шагов оптимизации, обновления параметров модели и проверки состояния алгоритма.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Деструктор класса ~C_AO_ADAM () { } // Конструктор класса C_AO_ADAM () { ao_name = "ADAM"; // Название алгоритма ao_desc = "Adaptive Moment Estimation"; // Описание алгоритма ao_link = "https://www.mql5.com/ru/articles/16443"; // Ссылка на статью popSize = 50; // Размер популяции alpha = 0.001; // Коэффициент обучения beta1 = 0.9; // Коэффициент экспоненциального затухания для первого момента beta2 = 0.999; // Коэффициент экспоненциального затухания для второго момента epsilon = 1e-8; // Маленькая константа для предотвращения деления на ноль // Инициализация массива параметров ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Метод для установки параметров void SetParams () { popSize = (int)params [0].val; // Установка размера популяции alpha = params [1].val; // Установка коэффициента обучения beta1 = params [2].val; // Установка beta1 beta2 = params [3].val; // Установка beta2 epsilon = params [4].val; // Установка epsilon } // Метод инициализации bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Метод для перемещения void Revision (); // Метод для ревизии //---------------------------------------------------------------------------- double alpha; // Коэффициент обучения double beta1; // Коэффициент экспоненциального затухания для первого момента double beta2; // Коэффициент экспоненциального затухания для второго момента double epsilon; // Маленькая константа S_Gradients grad []; // Массив градиентов private: //------------------------------------------------------------------- int step; // Шаг итерации int t; // Счетчик итераций }; //——————————————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_ADAM" выполняет инициализацию алгоритма:
- Вызывает "StandardInit ()" для стандартной настройки параметров; если неудачно, возвращает "false".
- Сбрасывает счетчики шагов "step" и итераций "t".
- Изменяет размер массива градиентов "grad" в соответствии с размером популяции "popSize".
- Инициализирует градиенты для каждого индивида в популяции, используя координаты "coords".
Если все операции успешны, метод возвращает "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Стандартная инициализация if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Сброс счетчика шагов t = 1; // Сброс счетчика итераций ArrayResize (grad, popSize); // Изменение размера массива градиентов for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Инициализация градиентов для каждого индивида return true; } //——————————————————————————————————————————————————————————————————————————————
Метод "Moving" класса "C_AO_ADAM" реализует шаг оптимизации в алгоритме ADAM:
1. Проверка шага, если шаг меньше 2:
- Для каждого индивида в популяции сохраняется предыдущее значение функции и координат.
- Генерируются новые случайные координаты в пределах заданного диапазона и корректируются до допустимых значений.
- Увеличивается счетчик шагов и метод завершает выполнение.
2. Вычисление градиентов: если шаг 2 или больше — для каждого индивида вычисляется изменение значения целевой функции и координат.
- Для предотвращения деления на ноль добавляется малое значение "epsilon" и, кроме этого, является внешним параметром алгоритма, влияющим на поисковые свойства.
- Вычисляется градиент для каждого параметра.
3. Обновление параметров для каждого индивида:
- Сохраняются предыдущие значения функции и координат.
- Обновляются смещенные оценки первого и второго моментов градиента.
- Вычисляются скорректированные оценки моментов и обновляются координаты с использованием формулы ADAM.
- Корректируются координаты, чтобы они оставались в допустимых границах.
4. Увеличивается счетчик итераций "t".
Таким образом, метод отвечает за обновление позиций индивидов в процессе оптимизации, используя адаптивные моменты градиента. Первые два шага алгоритма необходимы для вычисления градиента изменения значения фитнес-функции, поскольку градиент рассчитывается численно, без знания аналитической формулы решаемой задачи оптимизации. Для его вычисления требуется как минимум две точки, и на последующих шагах можно использовать решения, полученные на двух предыдущих этапах.
Логика алгоритма ADAM действительно не предполагает конкретного способа расчета градиента. Градиент может быть рассчитан как аналитически, так и численно, и его вычисление происходит вне самого алгоритма. Абстрагирование алгоритма от способов его применения действительно важно для понимания роли отдельных компонентов в общем проекте машинного обучения. Это позволяет лучше оценить влияние каждого элемента на итоговый результат и облегчает адаптацию алгоритма к различным задачам.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // Если шаг меньше 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Сохранение предыдущего значения функции for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Сохранение предыдущего значения координат // Генерация новых координат случайным образом a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение новых координат к допустимым значениям a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Увеличение счетчика шагов return; // Выход из метода } //---------------------------------------------------------------------------- double ΔF, ΔX; // Изменения функции и координат for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Вычисление изменения функции for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Вычисление изменения координат if (ΔX == 0.0) ΔX = epsilon; // Если изменение равно нулю, установить его на epsilon grad [i].g [c] = ΔF / ΔX; // Вычисление градиента } } // Обновление параметров с использованием алгоритма ADAM for (int i = 0; i < popSize; i++) { // Сохранение предыдущего значения функции a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Сохранение предыдущего значения координат a [i].cP [c] = a [i].c [c]; // Обновление смещенной оценки первого момента grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Обновление смещенной оценки второго момента grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Вычисление скорректированной оценки первого момента double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Вычисление скорректированной оценки второго момента double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Обновление координат a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Убедитесь, что координаты остаются в допустимых границах a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Увеличение счетчика итераций } //——————————————————————————————————————————————————————————————————————————————
Метод "Revision" класса "C_AO_ADAM" выполняет следующие действия:
- Инициализирует индекс лучшего индивида "ind" как -1.
- Проходит по всем индивидам в популяции и если значение функции текущего индивида больше лучшего найденного значения "fB", обновляет лучшее глобальное решение и сохраняет индекс лучшего индивида.
- Если был найден лучший индивид, копирует его координаты в массив "cB".
Таким образом, метод находит и сохраняет координаты лучшего индивида на основе значений фитнес-функции.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Индекс лучшего индивида for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // Если текущее значение функции больше лучшего { fB = a [i].f; // Обновление лучшего значения функции ind = i; // Сохранение индекса лучшего индивида } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшего индивида } //——————————————————————————————————————————————————————————————————————————————
Как видим, алгоритм ADAM теперь стал популяционным, а если установить внешний параметр размера популяции равным 1, то алгоритм будет вести себя полностью как обычный непопуляционный ADAM. Теперь можно провести и тестирование алгоритма на наших тестовых функциях. Посмотрим на результаты:
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs: 10000; result: 0.3857584301959297
25 Hilly's; Func runs: 10000; result: 0.29733109680042824
500 Hilly's; Func runs: 10000; result: 0.25390478702062613
=============================
5 Forest's; Func runs: 10000; result: 0.30772687797850234
25 Forest's; Func runs: 10000; result: 0.1982664040653052
500 Forest's; Func runs: 10000; result: 0.15554626746207786
=============================
5 Megacity's; Func runs: 10000; result: 0.18153846153846154
25 Megacity's; Func runs: 10000; result: 0.12430769230769231
500 Megacity's; Func runs: 10000; result: 0.09503076923077
=============================
All score: 1.99941 (22.22%)
Результаты, к сожалению, не самые лучшие, но это открывает возможности для потенциального роста и предоставляет нам пространство для реализации улучшений, в частности, внедрения настоящей стохастической составляющей в алгоритм.
В описанной выше реализации популяционного алгоритма ADAM каждый агент представляет собой отдельную "нитку" выполнения оригинальной логики авторов, подобно змейкам, ползущим по холмам пространства поиска, распределенным по полю благодаря начальной случайной инициализации. Эти змейки не взаимодействуют друг с другом и не обмениваются информацией о лучших решениях. Поскольку алгоритм является градиентным, ему важно учитывать изменения уровня поверхности в точках, расположенных как можно ближе друг к другу. Уменьшая шаг численного дифференцирования, мы можем столкнуться с медленной сходимостью, в то время как увеличение шага приводит к большим скачкам в пространстве, что затрудняет получение информации о поверхности между точками.
Чтобы решить эти проблемы, мы сделаем часть популяции гибридными особями, которые будут состоять из элементов решений других агентов. Идея заключается в следующем: мы сортируем популяцию по приспособленности особей, и в конце списка, где находятся самые слабые, мы создаем гибридов. Для таких особей решения будут генерироваться путем формирования новой точки в пространстве, основанной на элементах решений более приспособленных особей. Чем выше приспособленность особи, тем больше вероятность того, что она передаст гибридам информацию о своем положении.
Таким образом, часть особей в популяции будет представлять собой решения по оригинальной логике алгоритма, а другая часть — так называемые гибриды, которые являются комбинацией элементов решений из популяции. Полученный гибрид не просто копируется из частей других особей; каждая из этих частей изменяется в соответствии со степенным законом распределения вероятности. Степень этого закона мы назовем "устойчивостью гибрида": чем выше степень, тем меньше изменений претерпевает гибрид, и тем больше он похож на элементы лучших решений в популяции.
Теперь перейдем к обновленной версии алгоритма. В классе "C_AO_ADAMm" реализованы несколько изменений по сравнению с классом "C_AO_ADAM", которые, теоретически могут положительно повлиять на его функциональность и поведение. Вот основные изменения:
1. Новые параметры:
- hybridsPercentage - параметр определяет процент гибридов в популяции.
- hybridsResistance - параметр регулирует устойчивость гибридов к изменениям.
2. В конструкторе класса "C_AO_ADAMm" инициализируются новые параметры "hybridsPercentage" и "hybridsResistance", а также их значения добавляются в массив "params".
3. SetParams — в этом методе добавлены строки для установки новых параметров "hybridsPercentage" и "hybridsResistance", что позволяет динамически изменять их значения.
Если установить значение параметра процента гибридов на уровне "1", логика ADAM будет фактически отключена. В то время как установка этого значения на "0" приведет к отсутствию комбинаторных свойств алгоритма. В результате, опытным путем я подобрал оптимальное значение, равное "0.5", которое оказалось наилучшим.
Второй параметр отвечает за устойчивость гибридов к изменениям. При установке низких значений гибриды после наследования признаков значительно изменяются и могут охватывать весь диапазон допустимых значений оптимизируемых параметров. В то же время, если установить слишком высокие значения, например "20" и более, изменчивость гибридов стремится к "0", и они становятся только переносчиками лучших качеств родительских особей. Опытным путем было найдено оптимальное значение этого параметра - "10".
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Деструктор класса ~C_AO_ADAMm () { } // Конструктор класса C_AO_ADAMm () { ao_name = "ADAMm"; // Название алгоритма ao_desc = "Adaptive Moment Estimation M"; // Описание алгоритма ao_link = "https://www.mql5.com/ru/articles/16443"; // Ссылка на статью popSize = 100; // Размер популяции hybridsPercentage = 0.5; // Процент гибридов в популяции hybridsResistance = 10; // Устойчивость гибридов к изменениям alpha = 0.001; // Коэффициент обучения beta1 = 0.9; // Коэффициент экспоненциального затухания для первого момента beta2 = 0.999; // Коэффициент экспоненциального затухания для второго момента epsilon = 0.1; // Маленькая константа для предотвращения деления на ноль // Инициализация массива параметров ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Метод для установки параметров void SetParams () { popSize = (int)params [0].val; // Установка размера популяции hybridsPercentage = params [1].val; // Установка процента гибридов в популяции hybridsResistance = params [2].val; // Установка устойчивости гибридов к изменениям alpha = params [3].val; // Установка коэффициента обучения beta1 = params [4].val; // Установка beta1 beta2 = params [5].val; // Установка beta2 epsilon = params [6].val; // Установка epsilon } // Метод инициализации bool Init (const double &rangeMinP [], // минимальный диапазон поиска const double &rangeMaxP [], // максимальный диапазон поиска const double &rangeStepP [], // шаг поиска const int epochsP = 0); // количество эпох void Moving (); // Метод для перемещения void Revision (); // Метод для ревизии //---------------------------------------------------------------------------- double hybridsPercentage; // Процент гибридов в популяции double hybridsResistance; // Устойчивость гибридов к изменениям double alpha; // Коэффициент обучения double beta1; // Коэффициент экспоненциального затухания для первого момента double beta2; // Коэффициент экспоненциального затухания для второго момента double epsilon; // Маленькая константа S_Gradients grad []; // Массив градиентов private: //------------------------------------------------------------------- int step; // Шаг итерации int t; // Счетчик итераций int hybridsNumber; // Число гибридов в популяции }; //——————————————————————————————————————————————————————————————————————————————
В методе "Init" класса "C_AO_ADAMm" произошли следующие изменения по сравнению с аналогичным методом в предыдущем классе:
- Вычисляется количество гибридов в популяции на основе процента "hybridsPercentage". Это новое значение "hybridsNumber" используется для управления составом популяции.
- Добавлена проверка, чтобы убедиться, что количество гибридов не превышает размер популяции "popSize". Это предотвращает ошибки, связанные с выходом за пределы массива.
Эти изменения делают метод "Init" более адаптивным к особенностям алгоритма, связанным с гибридами, и обеспечивают корректное управление состоянием и инициализацией индивидов в популяции.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Стандартная инициализация if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Сброс счетчика шагов t = 1; // Сброс счетчика итераций hybridsNumber = int(popSize * hybridsPercentage); // Расчет числа гибридов в популяции if (hybridsNumber > popSize) hybridsNumber = popSize; // Корректировка ArrayResize (grad, popSize); // Изменение размера массива градиентов for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Инициализация градиентов для каждого индивида return true; } //——————————————————————————————————————————————————————————————————————————————
В методе "Moving" тоже несколько изменений по сравнению с предыдущей версией этого метода.
Обновление параметров с использованием алгоритма ADAM. В этом блоке добавлены условия для обработки гибридов. Если индекс индивида "i" больше или равен "popSize - hybridsNumber", генерируются новые координаты с использованием случайного распределения и параметра "hybridsResistance". Это позволяет гибридам иметь небольшие отклонения в наследуемых признаках от родительских особей (некий аналог мутации признаков). В противном случае, для индивидов, которые не являются гибридами, происходит обновление смещенной оценки первого и второго момента, а затем вычисляются скорректированные оценки.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // Если шаг меньше 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Сохранение предыдущего значения функции for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Сохранение предыдущего значения координат // Генерация новых координат случайным образом a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Приведение новых координат к допустимым значениям a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Увеличение счетчика шагов return; // Выход из метода } //---------------------------------------------------------------------------- double ΔF, ΔX; // Изменения функции и координат double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Вычисление изменения функции for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Вычисление изменения координат if (ΔX == 0.0) ΔX = epsilon; // Если изменение равно нулю, установить его на epsilon grad [i].g [c] = ΔF / ΔX; // Вычисление градиента } } // Обновление параметров с использованием алгоритма ADAM for (int i = 0; i < popSize; i++) { // Сохранение предыдущего значения функции a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Сохранение предыдущего значения координат a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Обновление смещенной оценки первого момента grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Обновление смещенной оценки второго момента grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Вычисление скорректированной оценки первого момента double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Вычисление скорректированной оценки второго момента double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Обновление координат //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Убедитесь, что координаты остаются в допустимых границах a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Увеличение счетчика итераций } //——————————————————————————————————————————————————————————————————————————————
В метод "Revision" внесены следующие изменения по сравнению с предыдущей версией этого метода.
Подготовка массива для сортировки: создается временный массив "aT" размером с популяцию и далее вызывается метод сортировки "u.Sorting ()". Отсортированный массив популяции позволяет реализовать наследование признаков гибридами с большей вероятностью от более приспособленных особей. Временный массив популяции можно было бы перенести в поля класса, но в данном случае так сделано для большей наглядности.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Индекс лучшего индивида for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // Если текущее значение функции больше лучшего { fB = a [i].f; // Обновление лучшего значения функции ind = i; // Сохранение индекса лучшего индивида } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Копирование координат лучшего индивида //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Результаты тестов
Посмотрим на результаты работы модифицированной версии действительно стохастического популяционного ADAMm:
ADAMm|Adaptive Moment Estimation M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8863499654810468
25 Hilly's; Func runs: 10000; result: 0.4476644542595641
500 Hilly's; Func runs: 10000; result: 0.2661291031673467
=============================
5 Forest's; Func runs: 10000; result: 0.8449728914068644
25 Forest's; Func runs: 10000; result: 0.3849320103361983
500 Forest's; Func runs: 10000; result: 0.16889385703816007
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.2704615384615384
500 Megacity's; Func runs: 10000; result: 0.10593846153846247
=============================
All score: 4.03688 (44.85%)
Полученные результаты значительно улучшились. Ниже представлена визуализация простого популяционного алгоритма ADAM, на которой видно своеобразное перемещение отдельных "змеек", расползающихся во все стороны в процессе исследования пространства поиска. Также представлены визуализации стохастического популяционного ADAMm, демонстрирующего более активное передвижение поисковых агентов к глобальному оптимуму, однако при этом характерный вид "змеек" утрачивается.
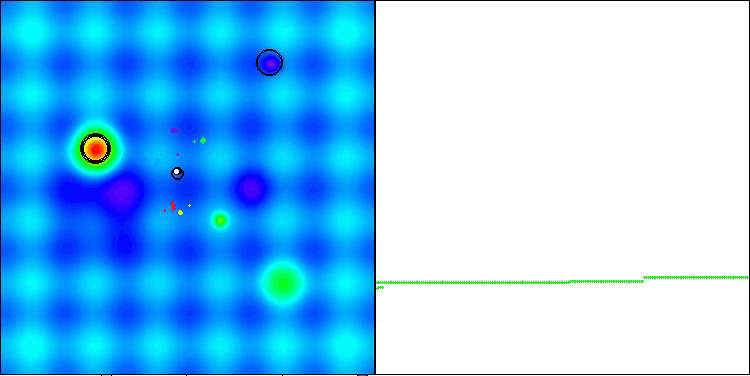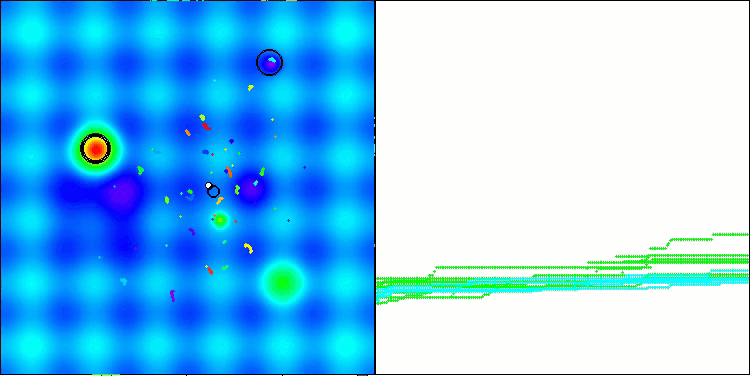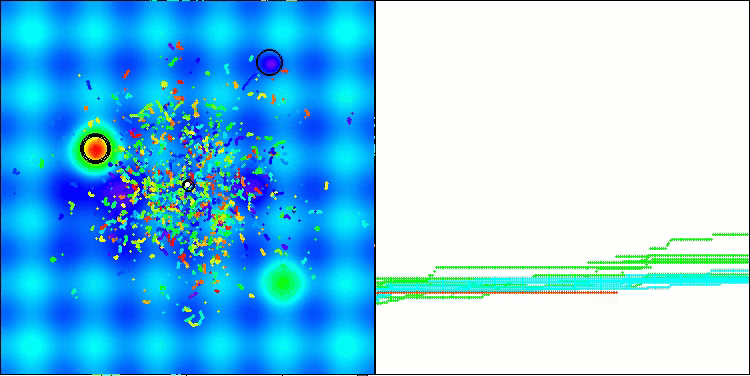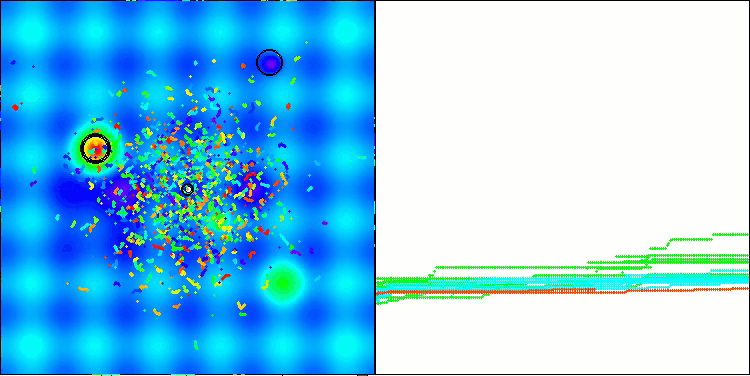
ADAM на тестовой функции Hilly

ADAMm на тестовой функции Hilly

ADAMm на тестовой функции Forest

ADAMm на тестовой функции Megacity
По итогам тестирования стохастическая популяционная версия ADAM занимает 32-е место в рейтинговой таблице, что является достаточно хорошим результатом. Оригинальная версия в таблицу попасть не смогла.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 14 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 15 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 16 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 17 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 18 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 20 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 21 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 22 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 23 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 24 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 25 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 27 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 29 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 30 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 31 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 32 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 33 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 34 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 35 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 36 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 37 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 38 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 39 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 40 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 41 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 42 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 43 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 44 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 45 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
Выводы
В статье представлена попытка адаптировать известный градиентный метод ADAM, традиционно используемый в нейросетях, для решения задач оптимизации в общем виде. Эта попытка оказалась успешной, поскольку полученный действительно стохастический популяционный ADAMm способен конкурировать с самыми мощными алгоритмами для задач глобальной оптимизации. Статья демонстрирует, что детерминированные подходы в задачах поиска оптимального решения часто не столь эффективны в многомерных пространствах поиска, как стохастические методы, и только дополнительные элементы случайности могут расширить поисковые способности каждого алгоритма оптимизации.
Однако следует отметить, что применение интегрированных в сеть градиентных методов, таких как классический ADAM, в обучении нейронных сетей по-прежнему остается практически вне конкуренции, так как они используют точное значение градиента при обратном распространении ошибки. Тем не менее, при обучении нейронных сетей с применением более сложных критериев оценки, чем функция минимизации ошибки, градиентные методы могут сталкиваться с трудностями и застреванием в локальных оптимумах, что отмечают многие авторы работ по машинному обучению.
Подход, представленный в этой статье, может быть полезен при классическом использовании интегрированных методов в нейронные сети, сохраняя великолепную точность и скорость сходимости, используя аналитический вид функции активации нейронов и многократно увеличивая способность противостоять застреванию при обучении нейронных сетей. Это позволит использовать классические методы и в задачах с очень сложными метриками и критериями при обучении. Надеюсь, что данная работа поможет исследователям и практикам взглянуть на проблемы оптимизации в целом и на методы машинного обучения в частности с новой перспективы.
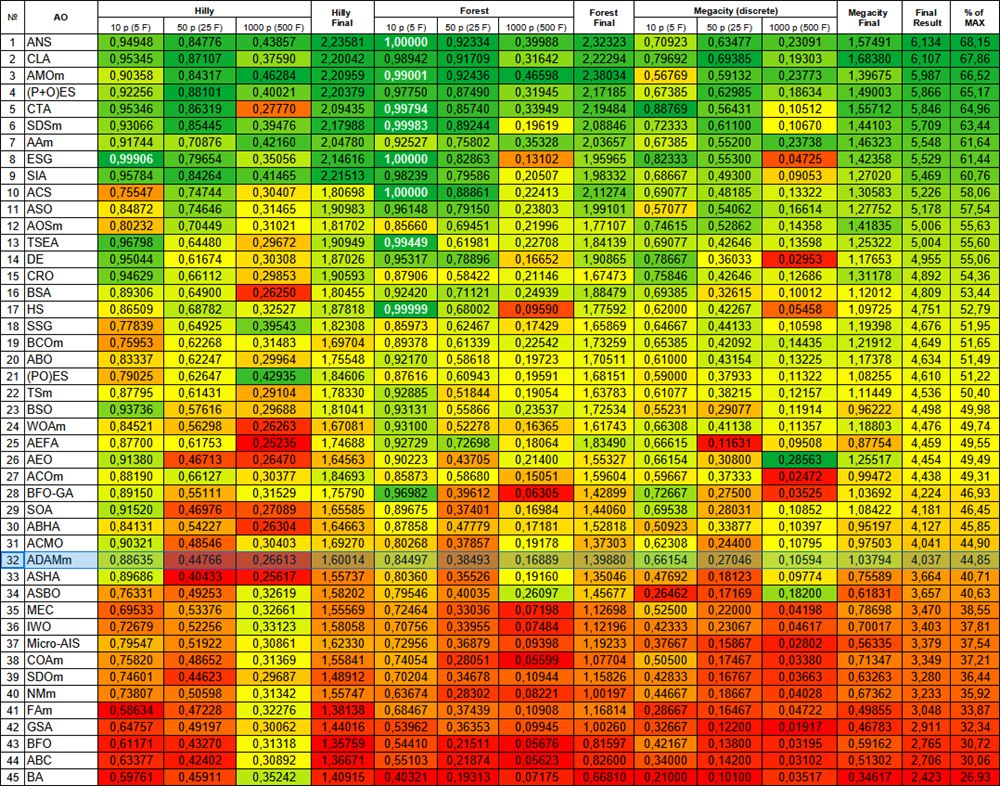
Рисунок 1. Цветовая градация алгоритмов по соответствующим тестам. Белым цветом подсвечены результаты больше или равные 0.99
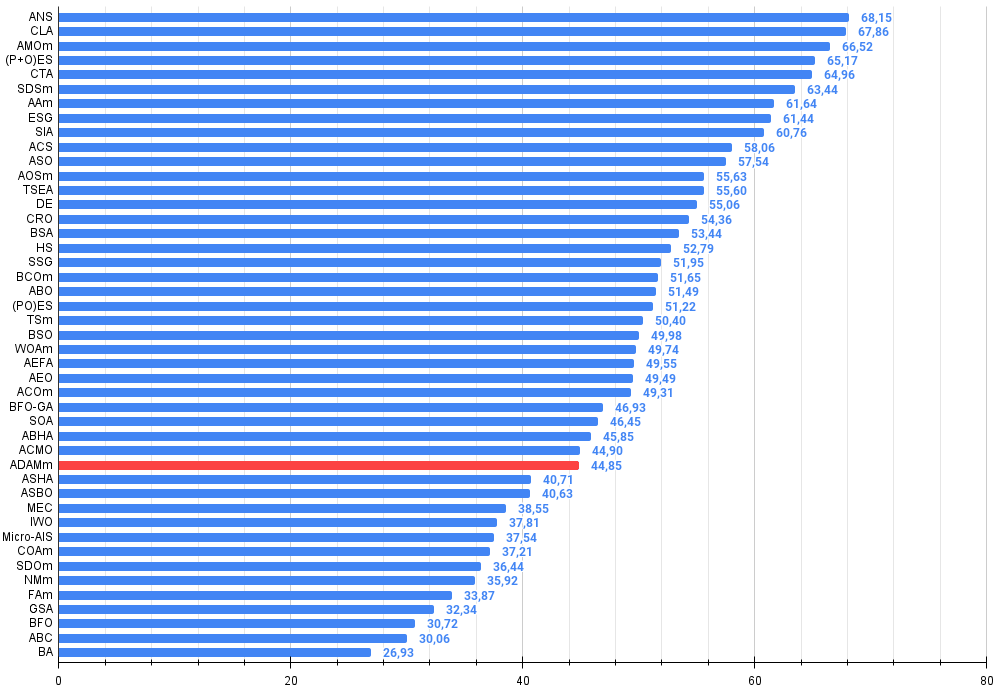
Рисунок 2. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше,
где 100 - максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма ADAMm:
Плюсы:
- Хорошие результаты на задачах малой размерности.
- Небольшой разброс результатов.
Минусы:
- Много внешних параметров.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_ADAM.mq5 | Скрипт | Испытательный стенд для ADAM и ADAMm |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Нейросети в трейдинге: Мультиагентная адаптивная модель (Окончание)
Нейросети в трейдинге: Мультиагентная адаптивная модель (Окончание)
 Возможности Мастера MQL5, которые вам нужно знать (Часть 23): CNN
Возможности Мастера MQL5, которые вам нужно знать (Часть 23): CNN
 Осваиваем рыночную динамику: Создание советника на основе стратегии поддержки и сопротивления
Осваиваем рыночную динамику: Создание советника на основе стратегии поддержки и сопротивления
 Создаем 3D-бары на основе времени, цены и объема
Создаем 3D-бары на основе времени, цены и объема
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования