MetaTrader 5 / Примеры
English 中文 Español Deutsch 日本語 Português
preview
Популяционные алгоритмы оптимизации: Электромагнитный алгоритм (ElectroMagnetism-like algorithm, ЕМ)

Популяционные алгоритмы оптимизации: Электромагнитный алгоритм (ElectroMagnetism-like algorithm, ЕМ)

MetaTrader 5 — Примеры | 29 марта 2023, 11:37
1 004 0
Andrey Dik
Andrey Dik

Содержание:

1. Введение
2. Описание алгоритма
3. Результаты тестов


1. Введение

За последние несколько десятилетий исследователи во всем мире придумали множество методов метаэвристического поиска для решения сложных задач глобальной оптимизации и способов их улучшения.

Алгоритм электромагнитно-подобного механизма (EM) — это относительно новый метаэвристический алгоритм поиска, основанный на имитации поведения электромагнитных частиц в физическом пространстве, впервые представленный Бирбилем  (I. Birbil) и Фэнгом  (S.С. Fang) в 2003 г. Он описывается как эволюционный алгоритм со случайными шумами и популяцией, основанной на электромагнитной силе взаимодействия между заряженными частицами.

Этот алгоритм вдохновлен механизмом притяжения и отталкивания зарядов в теории электромагнетизма для решения задач нелинейной оптимизации без ограничений в непрерывной области. Благодаря своим способностям решать сложные задачи глобальной оптимизации EM широко используется в качестве средства оптимизации во многих областях.

Интересные факты об электромагнетизме и электрических зарядах:

  • Существует два типа электрических зарядов: положительный и отрицательный. Все заряды соответствуют либо положительному, либо отрицательному знаку.
  • Электромагнитное поле может быть использовано для передачи информации в виде радиоволн. Мы используем это каждый день, когда слушаем радио или смотрим телевизор.
  • У нас есть магнитное поле Земли, которое защищает нас от солнечного ветра и космических лучей.
  • Существуют различные материалы, которые могут быть намагничены, и это позволяет создавать электромагниты. Электромагниты используются в различных приложениях, таких как генераторы электроэнергии.
  • Существует множество приложений, основанных на электромагнетизме. Например, компьютеры, мобильные телефоны и другие устройства используют электромагнитную технологию для своей работы.
  • Все светящиеся предметы (например, лампочки, огни на машинах) излучают электромагнитное излучение.
  • Электромагнетизм также играет важную роль в медицине. Медицинские устройства, такие как МРТ и КТ, используют электромагнитное поле для создания изображений внутри тела.
  • Некоторые животные, такие как акулы и электрические угри, могут использовать электромагнетизм для ориентации в пространстве.
  • Электромагнетизм является одним из четырех фундаментальных взаимодействий природы, наряду с гравитационным, слабым и сильным взаимодействием.


2. Описание алгоритма

Руководствуясь теорией электромагнетизма, EM имитирует механизм притяжения-отталкивания зарядов для достижения глобального оптимального решения с использованием ограниченных переменных. В алгоритме все решения рассматриваются как заряженные частицы в пространстве поиска, и заряд каждой частицы связан со значением целевой функции. Частицы с лучшим объективным выходом будут применять силы притяжения, в то время как частицы с худшими объективными значениями будут применять силы отталкивания к другим частицам. Чем лучше значение целевой функции, тем выше будет величина притяжения или отталкивания между частицами.

Принцип работы алгоритма заключается в том, что на начальном этапе формируется популяция случайных решений и каждое решение представлено вектором координат, соответствующих зарядам на электромагнитных частицах. Далее, на каждой итерации алгоритма происходит моделирование движения этих зарядов в пространстве под действием электромагнитных сил. В процессе движения, каждый заряд взаимодействует с другими зарядами, приводя к изменению направления движения и скорости. В результате, происходит постепенная сходимость решений к оптимальному значению целевой функции.

Основными компонентами EM-алгоритма являются:

  1. Формирование начальной популяции решений (зарядов), где каждый заряд представлен вектором координат и соответствует определенному решению оптимизационной задачи.
  2. Расчет электромагнитной силы взаимодействия между зарядами. Расчет производится на каждой итерации алгоритма и зависит от расстояния между зарядами (решениями).
  3. Движение зарядов в пространстве под действием электромагнитных сил взаимодействия.
  4. Обновление популяции решений на каждой итерации по целевой функции (целевой функцией может быть, например, функция потерь в задачах машинного обучения).
  5. Определение условия остановки алгоритма, например, достижение определенного значения целевой функции.

Частицы взаимодействуют друг с другом, притягиваясь или отталкиваясь в зависимости от заряда и расстояния между ними. Алгоритм выполняется в несколько итераций, на каждой из которых происходит обновление координат и зарядов частиц, а также вычисление новых значений функции приспособленности.

Логической единицей алгоритма оптимизации EM является частица, она может быть описана структурой S_Particle, которая представляет собой агента в пространстве поиска. Каждая частица имеет координаты c [], которые определяют ее положение в пространстве поиска, а также заряд C, который влияет на взаимодействие с другими частицами. Для каждой частицы вычисляется значение функции приспособленности f, которое оценивает качество решения, соответствующего данной координате. Кроме того, для каждой частицы вычисляются расстояния R до остальных частиц и векторы силы F, определяющие направление движения частицы в пространстве поиска. 

//——————————————————————————————————————————————————————————————————————————————
struct S_Particle
{
  double c  [];   //coordinates
  double C;       //charge
  double f;       //fitness
  double R  [];   //euclidean distance to other particles
  double F  [];   //force vector
};
//——————————————————————————————————————————————————————————————————————————————

Класс C_AO_EM представляет собой реализацию электромагнитного алгоритма оптимизации. Он используется для поиска оптимальных значений функции, заданной на некотором множестве вещественных чисел. Алгоритм основан на имитации процессов взаимодействия магнитных и электрических частиц в физической системе.

Класс содержит следующие поля:

  • S_Particle p[] — массив частиц, представляющих собой потенциальные решения задачи оптимизации.
  • double rangeMax[] — массив максимальных значений поискового диапазона для каждой координаты.
  • double rangeMin[] — массив минимальных значений поискового диапазона для каждой координаты.
  • double rangeStep[] — массив шагов поиска для каждой координаты.
  • double cB[] — массив координат лучшего решения.
  • double fB — значение функции наилучшего решения.

Класс содержит следующие методы:

  • void Init() — инициализирует алгоритм, задавая количество координат, количество частиц, константу окружения и шаг движения.
  • void Moving(int iter) — выполняет итерацию алгоритма, перемещая частицы в соответствии с правилами взаимодействия магнитных и электрических полей.
  • void Revision() — выполняет ревизию частиц, проверяя их на выход за пределы поискового диапазона и корректируя их положение при необходимости.

Класс также содержит приватные поля:

  • int coordinatesNumber — количество координат.
  • int particlesNumber — количество частиц.
  • double envConstant — константа окружения.
  • double movConstant — шаг движения.
  • double exponent — показатель степени расстояния.
  • double vect[] — массив векторов.
  • bool revision — флаг, указывающий на необходимость ревизии частиц.

Класс содержит приватные методы:

  • double SeInDiSp(double In, double InMin, double InMax, double Step) — распределяет точки на равномерной сетке.
  • double RNDfromCI(double min, double max) — генерирует случайное число в заданном диапазоне.
//——————————————————————————————————————————————————————————————————————————————
class C_AO_EM
{
  //----------------------------------------------------------------------------
  public: S_Particle p     []; //particles
  public: double rangeMax  []; //maximum search range
  public: double rangeMin  []; //minimum search range
  public: double rangeStep []; //step search
  public: double cB        []; //best coordinates
  public: double fB;           //FF of the best coordinates

  public: void Init (const int    coordinatesNumberP, //coordinates number
                     const int    particlesNumberP,   //particles number
                     const double envConstantP,       //environmental constant
                     const double movConstantP,       //movement step
                     const double exponentP);         //exponent

  public: void Moving   ();
  public: void Revision ();

  //----------------------------------------------------------------------------
  private: int    coordinatesNumber; //coordinates number
  private: int    particlesNumber;   //particles number
  private: double envConstant;       //environmental constant
  private: double movConstant;       //movement step
  private: double exponent;          //exponent
  private: double vect    [];        //vector
  private: bool   revision;

  private: double SeInDiSp  (double In, double InMin, double InMax, double Step);
  private: double RNDfromCI (double min, double max);
};
//——————————————————————————————————————————————————————————————————————————————

Метод инициализации алгоритма оптимизации "электромагнитный алгоритм" начинается со сброса генератора случайных чисел и установки начальных значений для некоторых переменных. Затем метод принимает на вход несколько параметров: количество координат, количество частиц, значение окружающей среды и шаг движения. Далее метод создает несколько массивов нужных размеров и заполняет их начальными значениями.

В массивах хранятся максимальные и минимальные значения диапазона для каждой координаты, шаг изменения координаты, вектор и текущее положение каждой частицы. Затем метод создает массив частиц и для каждой частицы создает массивы для хранения ее координат, матрицы расстояний до других частиц, вектора сил и текущего лучшего значения функции. В конце метод создает массив для хранения лучшей координаты из всех частиц. Таким образом, метод инициализирует все необходимые переменные и массивы для работы алгоритма оптимизации "электромагнитный алгоритм".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Init (const int    coordinatesNumberP, //coordinates number
                    const int    particlesNumberP,   //particles number
                    const double envConstantP,       //environmental constant
                    const double movConstantP,       //movement step
                    const double exponentP)          //exponent
{
  MathSrand ((int)GetMicrosecondCount ()); // reset of the generator
  fB       = -DBL_MAX;
  revision = false;

  coordinatesNumber = coordinatesNumberP;
  particlesNumber   = particlesNumberP;
  envConstant       = envConstantP;
  movConstant       = movConstantP;
  exponent          = exponentP;

  ArrayResize (rangeMax,  coordinatesNumber);
  ArrayResize (rangeMin,  coordinatesNumber);
  ArrayResize (rangeStep, coordinatesNumber);
  ArrayResize (vect,      coordinatesNumber);

  ArrayResize (p,  particlesNumber);

  for (int i = 0; i < particlesNumber; i++)
  {
    ArrayResize (p [i].c,  coordinatesNumber);
    ArrayResize (p [i].R,  particlesNumber);
    ArrayResize (p [i].F,  coordinatesNumber);
    p [i].f  = -DBL_MAX;
  }

  ArrayResize (cB, coordinatesNumber);
}
//——————————————————————————————————————————————————————————————————————————————

Метод Moving() является первым, обязательным к исполнению на каждой итерации. Он отвечает за перемещение частиц в пространстве поиска решений. Сначала метод проверяет, была ли уже проведена инициализация частиц. Если нет, то каждая частица получает случайные координаты в заданных пределах и обнуляет свою текущую оценку и заряд. Также вычисляется вектор разностей vect [] между максимальными и минимальными значениями в каждом измерении пространства поиска.

//----------------------------------------------------------------------------
if (!revision)
{
  fB = -DBL_MAX;

  for (int obj = 0; obj < particlesNumber; obj++)
  {
    for (int c = 0; c < coordinatesNumber; c++)
    {
      p [obj].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]);
      p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
      p [obj].C     = 0.0;
      p [obj].f     = -DBL_MAX;
    }
  }

  for (int c = 0; c < coordinatesNumber; c++)
  {
    vect [c] = rangeMax [c] - rangeMin [c];
  }

  revision = true;
}

Если инициализация уже была проведена, то метод вычисляет заряд каждой частицы на основе ее отклонения от глобального максимума, нормированного на сумму отклонений от глобального максимума всех частиц. Рассчитаем сумму разностей так:

//calculate the sum of the differences of the fitness of the particles with the global value
for (int obj = 0; obj < particlesNumber; obj++)
{
  sumDiff += fB - p [obj].f;
}

Заряд частицы рассчитаем по формуле:

p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
Как видим, значение заряда в формуле - положительное число, знак заряда будет учтён далее в алгоритме. Если сумма разниц отклонений от глобального максимума равна нулю, то заряд частицы принимаем равным нулю. Расчетный заряд частицы будет определять амплитуду силы, действующей со стороны частицы на другие соответствующие частицы на этапе расчета силы. Код расчета заряда частицы будет выглядеть так:

//calculating the charge of particles=======================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  if (sumDiff == 0.0)
  {
    p [obj].C = 0.0;
  }
  else
  {
    p [obj].C = exp (-particlesNumber * ((fB - p [obj].f) / sumDiff));
  }
}

Прежде, чем приступим к расчету расстояний между частицами, необходимо обнулить массив расстояний от частицы до остальных частиц, обнулим так же и вектор сил, действующих на частицу:

//calculation of Euclidean distances between all particles==================
for (int obj = 0; obj < particlesNumber; obj++)
{
  ArrayInitialize (p [obj].R, 0.0);
  ArrayInitialize (p [obj].F, 0.0);
}

Затем вычисляются расстояния между всеми парами частиц и силы, действующие между ними. Здесь используется формула, основанная на законе Кулона, который описывает взаимодействие между заряженными частицами. Силы, действующие на каждую частицу, вычисляются как векторная сумма всех сил, действующих на нее со стороны других частиц.

Согласно электромагнитной теории, сила воздействия одной частицы на другую обратно пропорциональна расстоянию между двумя частицами и прямо пропорциональна произведению их зарядов. Частица с более низким целевым значением прикладывает силу отталкивания к частице с относительно более высоким целевым значением. Аналогично, он отталкивает хорошую частицу от области с плохим целевым значением. С другой стороны, частица с более высоким целевым значением оказывает притяжение на частицы с относительно более низкими значениями.

Принимая во внимание все соответствующие силы, создаваемые всеми другими частицами, рассчитывается общий вектор силы для частицы. Этот комбинированный вектор силы определяет направление, в котором частица будет двигаться на этапе движения частицы. Авторы алгоритма рекомендуют нормализовать вектор сил частицы на вектор сил между всеми частицами, мои эксперименты показали, что без нормализации результаты лучше и код представлен без нормализации.

В зависимости от того, какая частица имеет больше значение целевой функции, зададим направление силы (имитация знака заряда). 

for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int obj2 = 0; obj2 < particlesNumber; obj2++)
  {
    if (obj != obj2)
    {
      if (p [obj].R [obj2] == 0.0)
      {
        for (int c = 0; c < coordinatesNumber; c++)
        {
          diffDist = p [obj].c [c] - p [obj2].c [c];
          p [obj].R [obj2] += diffDist * diffDist;
        }

        p [obj].R [obj2] = sqrt (p [obj].R [obj2]);
        p [obj2].R [obj] = p [obj].R [obj2];

        //calculation of the force------------------------------------------
        Fp = p [obj].C * p [obj2].C / (4.0 * M_PI * envConstant * pow (p [obj].R [obj2], exponent));

        for (int c = 0; c < coordinatesNumber; c++)
        {
          if (p [obj].f > p [obj2].f)
          {
            p [obj ].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;

          }
          else
          {
            p [obj ].F [c] -= (p [obj2].c [c] - p [obj].c [c]) * Fp;
            p [obj2].F [c] += (p [obj2].c [c] - p [obj].c [c]) * Fp;
          }
        }
      }
    }
  }
}

Наконец, для каждой частицы вычисляются новые координаты на основе ее текущей позиции и силы, действующей на нее. Необходимо отметить, что у частиц нет массы, а значит нет ускорения, частицы перемещаются, в отличии от алгоритма гравитационного поиска GSA, в новое местоположение мгновенно. Координаты перемещения ограничены диапазоном поиска и шагом изменения.

Закомментированный код возвращает частицу с противоположной стороны диапазона на расстоянии от соответствующей координаты в случае, если частица окажется вне допустимого диапазона.

//calculation of particle motions===========================================
for (int obj = 0; obj < particlesNumber; obj++)
{
  for (int c = 0; c < coordinatesNumber; c++)
  {
    r = RNDfromCI (0.0, 1.0);
    p [obj].c [c] = p [obj].c [c] + r * p [obj].F [c] * vect [c] * movConstant;

    //if (p [obj].c [c] > rangeMax [c]) p [obj].c [c] = rangeMin [c] + (p [obj].c [c] - rangeMax [c]);
    //if (p [obj].c [c] < rangeMin [c]) p [obj].c [c] = rangeMax [c] - (rangeMin [c] - p [obj].c [c]);

    p [obj].c [c] = SeInDiSp (p [obj].c [c], rangeMin [c], rangeMax [c], rangeStep [c]);
  }
}

Метод Revision(), второй, обязательный к исполнению на каждой итерации, в алгоритме оптимизации EM, отвечает за проверку лучшей позиции частицы на текущей итерации. Внутри метода проходит цикл по всем частицам и сравнивается значение их функции приспособленности с текущим лучшим значением fB. Если значение функции приспособленности текущей частицы больше, чем fB, то fB обновляется, а также копируется позиция частицы в массив cB.

Таким образом, метод Revision() позволяет отслеживать лучшую позицию частицы на каждой итерации алгоритма и сохранять ее в массиве cB. Это помогает оптимизировать процесс поиска оптимального решения и повышает эффективность работы алгоритма.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_EM::Revision ()
{
  for (int s = 0; s < particlesNumber; s++)
  {
    if (p [s].f > fB)
    {
      fB = p [s].f;
      ArrayCopy (cB, p [s].c, 0, 0, WHOLE_ARRAY);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

Метод SeInDiSp() в алгоритме оптимизации "электромагнитный алгоритм" используется для ограничения значений переменной In в заданном диапазоне [InMin, InMax] с шагом Step. Если значение In меньше или равно InMin, то метод возвращает InMin. Если значение In больше или равно InMax, то метод возвращает InMax. Если шаг равен нулю, то метод возвращает исходное значение In. В противном случае, метод вычисляет новое значение In, используя формулу: InMin + Step * (In - InMin) / Step, где MathRound() - метод округления числа до ближайшего целого.

Таким образом, метод SeInDiSp() позволяет контролировать изменение значения переменной In в заданных пределах и с заданным шагом, что помогает более эффективно и быстро оптимизировать функцию.

//——————————————————————————————————————————————————————————————————————————————
// Choice in discrete space
double C_AO_EM::SeInDiSp (double In, double InMin, double InMax, double Step)
{
  if (In <= InMin) return (InMin);
  if (In >= InMax) return (InMax);
  if (Step == 0.0) return (In);
  else return (InMin + Step * (double)MathRound ((In - InMin) / Step));
}
//——————————————————————————————————————————————————————————————————————————————


3. Результаты тестов

Распечатка работы электромагнитного алгоритма на тестовом стенде:

2023.03.26 18:27:39.259    C_AO_EM:50;0.1;0.8
2023.03.26 18:27:39.259    =============================
2023.03.26 18:27:43.215    5 Rastrigin's; Func runs 10000 result: 59.939529106561224
2023.03.26 18:27:43.215    Score: 0.74268
2023.03.26 18:27:52.960    25 Rastrigin's; Func runs 10000 result: 59.780143424645416
2023.03.26 18:27:52.960    Score: 0.74071
2023.03.26 18:29:22.856    500 Rastrigin's; Func runs 10000 result: 63.94951378068386
2023.03.26 18:29:22.856    Score: 0.79237
2023.03.26 18:29:22.856    =============================
2023.03.26 18:29:28.901    5 Forest's; Func runs 10000 result: 0.28698617113254693
2023.03.26 18:29:28.901    Score: 0.16233
2023.03.26 18:29:38.103    25 Forest's; Func runs 10000 result: 0.1571444033424823
2023.03.26 18:29:38.103    Score: 0.08889
2023.03.26 18:30:53.341    500 Forest's; Func runs 10000 result: 0.11734383105881332
2023.03.26 18:30:53.341    Score: 0.06638
2023.03.26 18:30:53.341    =============================
2023.03.26 18:30:58.108    5 Megacity's; Func runs 10000 result: 1.3599999999999999
2023.03.26 18:30:58.108    Score: 0.11333
2023.03.26 18:31:08.897    25 Megacity's; Func runs 10000 result: 0.776
2023.03.26 18:31:08.897    Score: 0.06467
2023.03.26 18:32:23.199    500 Megacity's; Func runs 10000 result: 0.34320000000000006
2023.03.26 18:32:23.199    Score: 0.02860
2023.03.26 18:32:23.199    =============================
2023.03.26 18:32:23.199    All score: 2.79996

Обращая внимание на анимации работы алгоритма ME на тестовых функциях, можно представить себе некое подобие "электризации" поля пространства поиска. Частицы образуют группы высоких зарядов следуя особенностям поверхности тестовой функции. Заметно сразу низкое, к сожалению, качество сходимости, однако красоты картинки алгоритму EM не занимать.

rastrigin

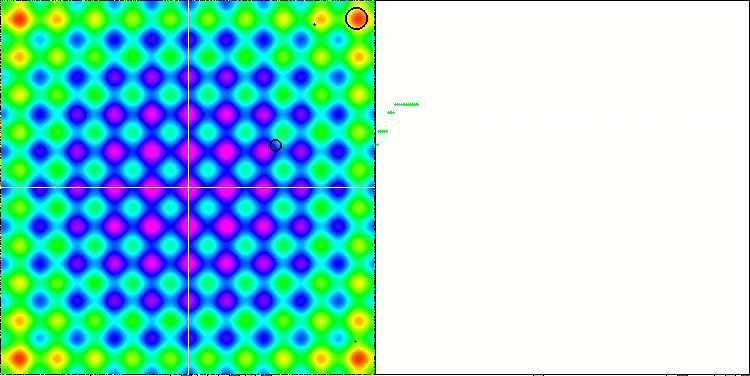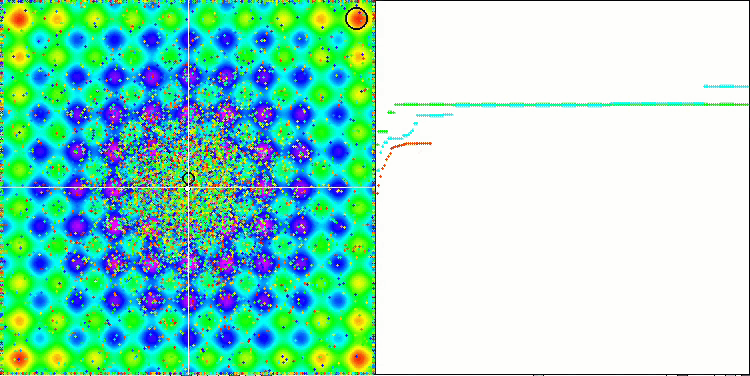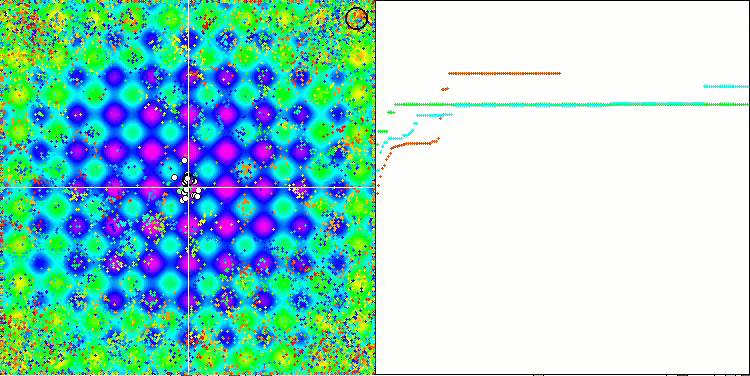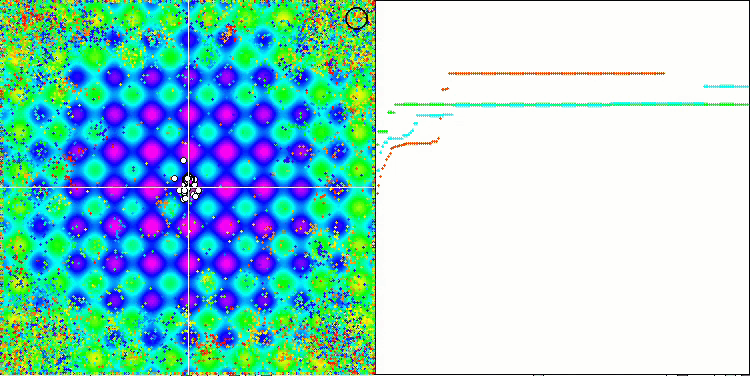
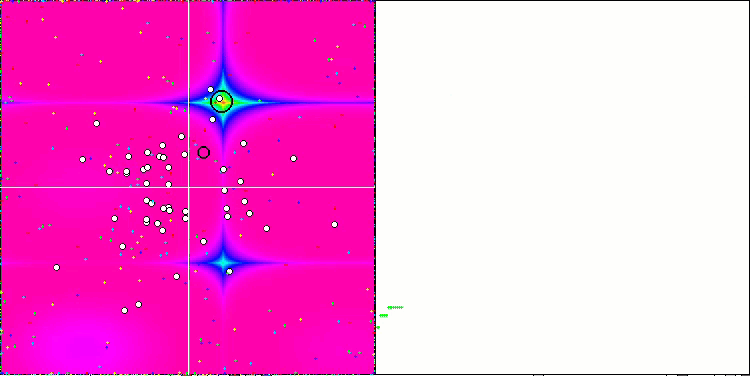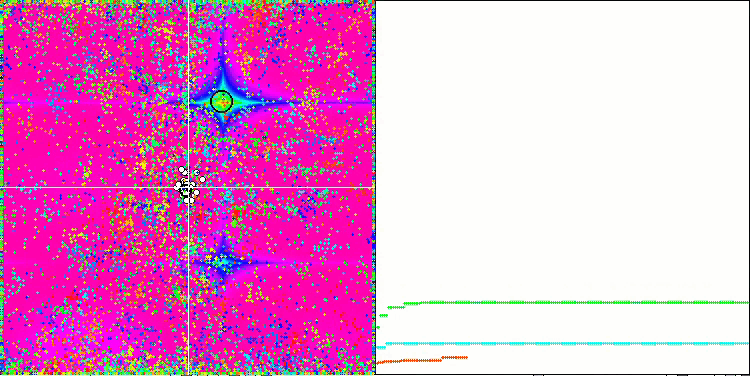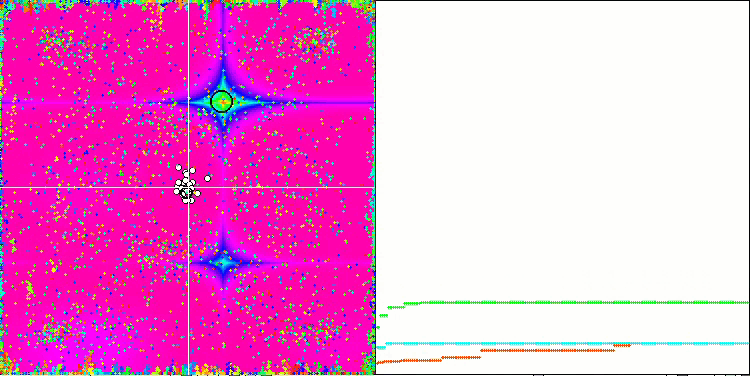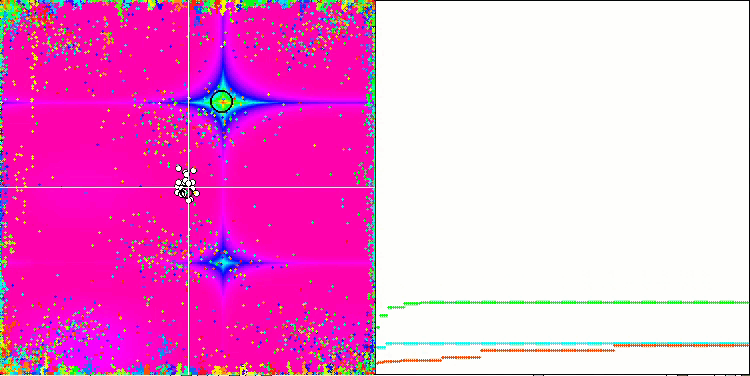
  EM на тестовой функции Rastrigin.

forest

  EM на тестовой функции Forest.

megacity

  EM на тестовой функции Megacity.

Переходим к результатам тестирования электромагнитного алгоритма оптимизации. EM продемонстрировал результаты ниже среднего по таблице с финальным значением 22. Практически во всех тестах из шести алгоритм показал низкие результаты. Исключением является тест на функции Rastrigin с 1000 параметрами, в котором EM оказался в этой дисциплине испытаний лучше таких мощнейших алгоритмов как SSG и BA, мало того, абсолютные значения функции на 1000 параметрах оказались выше, чем в тестах с 10 и 50 параметров!

Такого ещё не было на моей памяти, что бы с увеличением количества оптимизируемых параметров результаты поиска улучшались. Скорее всего данный феномен связан с особенностями самой поисковой стратегии EM. Необходимо отметить чувствительность EM к наличию градиента и дифференцируемости на всей области определения исследуемой функции.

AO

Description

Rastrigin

Rastrigin final

Forest

Forest final

Megacity (discrete)

Megacity final

Final result

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

10 params (5 F)

50 params (25 F)

1000 params (500 F)

SSG

saplings sowing and growing

1,00000

1,00000

0,55665

2,55665

0,72740

0,94522

1,00000

2,67262

0,76364

0,85977

1,00000

2,62340

100,000

HS

harmony search

0,99676

0,95282

0,48178

2,43136

1,00000

0,98931

0,44806

2,43736

1,00000

1,00000

0,41537

2,41537

92,329

ACOm

ant colony optimization M

0,34611

0,17985

0,17044

0,69640

0,86888

1,00000

0,77362

2,64249

1,00000

0,88930

0,05606

1,94536

65,347

IWO

invasive weed optimization

0,95828

0,67083

0,29807

1,92719

0,70773

0,46349

0,31773

1,48896

0,80000

0,42067

0,33289

1,55356

61,104

COAm

cuckoo optimization algorithm M

0,92400

0,46794

0,26004

1,65199

0,58378

0,34034

0,16526

1,08939

0,72727

0,33025

0,17083

1,22835

47,612

FAm

firefly algorithm M

0,59825

0,33980

0,17135

1,10941

0,51073

0,42299

0,49790

1,43161

0,34545

0,28044

0,35258

0,97847

41,537

ABC

artificial bee colony

0,78170

0,32715

0,20822

1,31707

0,53837

0,21455

0,13344

0,88636

0,56364

0,26569

0,13926

0,96858

36,849

GSA

gravitational search algorithm

0,70167

0,45217

0,00000

1,15384

0,31660

0,36416

0,33204

1,01280

0,59395

0,35054

0,00000

0,94448

36,028

BA

bat algorithm

0,40526

0,63761

0,84451

1,88738

0,20841

0,17477

0,25989

0,64308

0,29698

0,09963

0,17371

0,57032

35,888

BFO

bacterial foraging optimization

0,67203

0,30963

0,11813

1,09979

0,39702

0,26623

0,20652

0,86976

0,52122

0,33211

0,18932

1,04264

34,693

EM

electroMagnetism-like algorithm

0,12235

0,46278

1,00000

1,58513

0,00000

0,03498

0,34880

0,38377

0,00000

0,00000

0,10924

0,10924

22,091

MA

monkey algorithm

0,33192

0,33451

0,14644

0,81287

0,10012

0,07891

0,08932

0,26836

0,21818

0,04243

0,10720

0,36781

13,603

FSS

fish school search

0,46812

0,25337

0,11302

0,83451

0,12840

0,05013

0,06516

0,24369

0,16971

0,04796

0,08283

0,30050

12,655

PSO

particle swarm optimisation

0,20449

0,08200

0,07160

0,35809

0,18895

0,10486

0,21738

0,51119

0,23636

0,05903

0,01957

0,31496

10,031

RND

random

0,16826

0,09743

0,08019

0,34589

0,13496

0,04810

0,04715

0,23021

0,16971

0,03875

0,04922

0,25767

5,302

GWO

grey wolf optimizer

0,00000

0,00000

0,02256

0,02256

0,06570

0,00000

0,00000

0,06570

0,32727

0,07378

0,02557

0,42663

1,000


Выводы

  1. EM-алгоритм является эффективным методом оптимизации, способным решать различные задачи оптимизации, особенно связанных с обработкой большого количества данных и высокой размерности на гладких функциях.
  2. Алгоритм основан на имитации поведения электромагнитных частиц в физическом пространстве, что позволяет ему достигать высокой точности результата при работе со сложными многомерными функциями.
  3. EM-алгоритм не требует градиентных вычислений, что делает его более универсальным и легче применимым для различных задач, однако чувствителен к наличию градиента в оптимизируемой функции.
  4. Алгоритм может быть изменен и настроен в зависимости от конкретной задачи оптимизации, что делает его гибким инструментом для оптимизации различных функций.
  5. Существуют различные модификации EM-алгоритма, которые могут быть улучшены по сравнению с базовой версией и приспособлены к конкретным задачам оптимизации.
  6. EM-алгоритм может быть использован в различных областях, таких как машинное обучение, искусственный интеллект, оптимизация финансовых рынков и других.

Основным преимуществом электромагнитного алгоритма является возможность решения задач оптимизации в многомерных пространствах и большой размерности, при этом сохраняя высокую точность результата.

Таким образом, EM-алгоритм является эффективным инструментом для оптимизации различных функций и может использоваться в широком спектре задач оптимизации, особенно в случаях, когда требуется обработка большого количества данных и/или высокой размерности.

Этот рейтинг может быть полезен для выбора наиболее подходящего алгоритма для решения конкретной задачи оптимизации. Однако следует помнить, что эффективность алгоритма зависит от многих факторов, таких как размер задачи, тип функции, количество переменных и т.д. Поэтому выбор алгоритма должен быть основан на тщательном анализе конкретной задачи.


Гистограмма результатов тестирования алгоритмов на рисунке 1.

chart

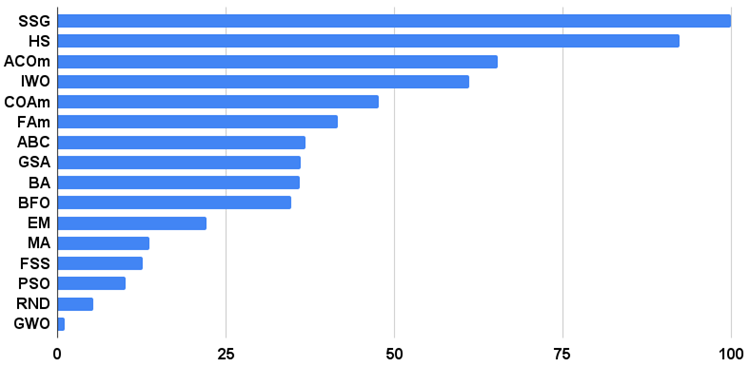
Рисунок 1. Гистограмма итоговых результатов тестирования алгоритмов.

Плюсы и минусы электромагнитного алгоритма (EM):

Плюсы:
1. Простота реализации.
2. Впечатляющая масштабируемость на гладких функциях.
3. Небольшое количество внешних параметров.

Минусы:
1. Высокая вычислительная трудоёмкость.
2. Невысокие результаты на дискретных функциях.
3. Застревание на функциях с ровными горизонтальными "площадками".

Каждой статье я прикрепляю архив, содержащий обновленные актуальные версии кодов алгоритмов, описанных в предыдущих статьях. Статьи созданы на основе накопленного опыта автора и его личного мнения, выводы и суждения основываются на результатах проведенных экспериментов.

Прикрепленные файлы |
Загрузить ZIP
16_The_world_of_AO_EM.ZIP (129.56 KB)
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров
Как выбрать торгового советника: Двадцать явных признаков плохого робота Как выбрать торгового советника: Двадцать явных признаков плохого робота
В этой статье мы попытаемся ответить на вопрос, как выбрать подходящего торгового советника. Какие из них лучше всего подходят для нашего портфеля и как мы можем отсеять большую часть торговых роботов, доступных на рынке? В статье представлены двадцать явных признаков некачественного советника. Статья поможет вам принимать более обоснованные решения и создать коллекцию прибыльных торговых советников.
Использование ONNX-моделей в MQL5 Использование ONNX-моделей в MQL5
ONNX (Open Neural Network Exchange) — открытый стандарт представления моделей нейронных сетей. В данной статье мы рассмотрим процесс создания модели СNN-LSTM для прогнозирования финансовых временных рядов и использование созданной ONNX-модели в MQL5-эксперте.
Машинное обучение и Data Science (Часть 10): Гребневая регрессия Машинное обучение и Data Science (Часть 10): Гребневая регрессия
Гребневая регрессия (ридж-регрессия) — это простой метод для уменьшения сложности модели и борьбы с подгонкой, которая может возникнуть в результате простой линейной регрессии.
Работа с матрицами, расширение функционала Стандартной библиотеки матриц и векторов Работа с матрицами, расширение функционала Стандартной библиотеки матриц и векторов
Матрица служит основой алгоритмов машинного обучения и компьютеров в целом из-за ее способности эффективно обрабатывать большие математические операции. В Стандартной библиотеке есть все, что нужно, но мы можем расширить ее, добавив несколько функций в файл utils.