
Алгоритм оптимизации одуванчика — Dandelion Optimizer (DO)
Содержание
Введение
В данной работе рассмотрим алгоритм оптимизации одуванчика (Dandelion Optimizer, DO) — это метаэвристический алгоритм, вдохновлённый жизненным циклом семян одуванчика. Авторы Shijie Zhao, Tianran Zhang, Shilin Ma и Miao Chen представили его в 2022 году в журнале Engineering Applications of Artificial Intelligence.
Одуванчик — одно из самых распространённых растений на планете. Секрет его эволюционного успеха кроется в уникальном механизме распространения семян. Каждое семя снабжено пушистым «парашютом» (паппусом), позволяющим ему преодолевать значительные расстояния по воздуху. Ветер поднимает семена, несёт их над землёй, а затем они опускаются в новых местах, где могут прорасти.
Реализация алгоритма
Каждый из нас видел, как ветер подхватывает пушистые семена одуванчика и разносит их по округе. Этот простой природный процесс оказался интересной стратегией поиска, которую исследователи превратили в алгоритм оптимизации.
Представьте себе поляну, где растёт одуванчик. Его задача — найти лучшие места для прорастания своих семян. Семена не могут выбирать направление сами, но ветер, турбулентность воздуха и особая форма пушистого парашюта (паппуса) создают сложные траектории полёта. В результате семена распределяются по большой территории, и некоторые из них находят идеальные условия для роста.
Алгоритм DO моделирует этот процесс. Каждое «семя» — это потенциальное решение задачи оптимизации. Координаты семени в пространстве — это значения оптимизируемых параметров. «Качество почвы» в точке приземления — это значение целевой функции.
Три фазы полёта семени. Полёт семени одуванчика разделён на три последовательные фазы, каждая из которых выполняет свою роль в поиске оптимального решения.
Фаза 1: Подъём (Rising). Когда ветер отрывает семя от головки одуванчика, оно начинает подниматься вверх. В зависимости от силы ветра возможны два сценария. Сильный ветер (80% случаев) создаёт вихревые потоки, и семя движется по спиральной траектории, непредсказуемо меняя направление. В алгоритме это реализовано через комбинацию тригонометрических функций и логнормального распределения:
новая позиция = текущая позиция + α × вихрь × случайное направление
Допустим, мы оптимизируем два параметра торговой стратегии: период скользящей средней (от 10 до 200) и множитель стоп-лосса (от 1.0 до 5.0). Семя находится в точке [50, 2.0]. Вихревой подъём может переместить его в точку [73, 2.8] — существенный скачок в новую область поиска.
Слабый ветер (20% случаев) поднимает семя более плавно. Оно движется линейно, слегка смещаясь относительно своей текущей позиции:
новая позиция = центр области + (текущая позиция - центр области) × k
Пример: то же семя [50, 2.0] при центре области [105, 3.0] и k = 0.9 переместится в [55.5, 2.1] — небольшое смещение к центру. Зачем нужна эта фаза? Подъём обеспечивает исследование пространства поиска. Семена разлетаются в разные стороны, покрывая большую территорию. Это помогает найти перспективные области, которые могут содержать глобальный оптимум.
Фаза 2: Снижение (Decline). После подъёма семя попадает в горизонтальные воздушные потоки и начинает дрейфовать. В этой фазе семена «общаются» друг с другом через среднюю позицию популяции. Сначала вычисляется центр масс всех семян:
среднее = сумма всех позиций / количество семян
Затем каждое семя корректирует свою траекторию с учётом этого среднего:
новая позиция = текущая позиция - β × α × (среднее - β × α × текущая позиция)
Пример: пусть в популяции 5 семян с позициями [30, 1.5], [80, 2.5], [120, 3.0], [60, 2.0], [90, 2.8]. Среднее положение: [76, 2.36]. Семя в позиции [30, 1.5] будет притягиваться к этому центру, смещаясь примерно в [45, 1.8]. Зачем это нужно? Снижение обеспечивает обмен информацией между семенами. Если большинство семян сконцентрировалось в какой-то области, значит, эта область перспективна. Отстающие семена подтягиваются к группе, не теряя при этом своей индивидуальности.
Фаза 3: Приземление (Landing). Вблизи земли воздушные потоки становятся турбулентными. Семя совершает финальный манёвр, стремясь приземлиться в наиболее благоприятном месте — рядом с лучшим найденным решением (элитой). Для моделирования турбулентности используется полёт Леви — особый тип случайного движения с редкими длинными прыжками:
шаг Леви = u / |v|^(2/3), где u и v - случайные числа
новая позиция = элита + шаг Леви × α × (элита - текущая позиция × ratio)
Пример: лучшее найденное решение (элита) находится в точке [85, 2.4]. Семя из позиции [60, 2.0] с шагом Леви 0.3 и ratio = 1.0 приземлится примерно в [77, 2.28] — ближе к элите, но не точно в ее координаты. Приземление обеспечивает эксплуатацию найденных решений. Семена концентрируются вокруг лучшей точки, тщательно исследуя её окрестности. Полёт Леви при этом сохраняет возможность случайного «выброса» — вдруг рядом есть решение ещё лучше.
Адаптивные параметры. Ключевая особенность алгоритма — параметры, которые автоматически изменяются в процессе оптимизации. Параметр "α" (интенсивность) убывает от 1 к 0:
α = случайное число × (t²/T² - 2t/T + 1)
В начале оптимизации (t мало) "α" близок к 1, шаги большие — семена активно исследуют пространство. К концу (t близко к T) "α" стремится к 0, шаги маленькие — идёт точная настройка решения.
Аналогия: поиск потерянных ключей. Сначала вы быстро обходите всю квартиру (большие шаги), а когда вспомнили, что ключи где-то на кухне, начинаете тщательно осматривать каждый угол (маленькие шаги).
Параметр ratio (прогресс) возрастает от 0 к 2: ratio = 2 × t / T. Чем больше "ratio", тем сильнее семена притягиваются к элите на фазе приземления. В начале поиска семена приземляются относительно свободно, к концу — практически все стремятся к лучшему решению.
Контроль границ. Что делать, если семя «улетело» за пределы допустимой области? Алгоритм использует механизм отражения, подобный тому, как мяч отскакивает от стены.
Если позиция < минимум: позиция = минимум + (минимум - позиция); если позиция > максимум: позиция = максимум - (позиция - максимум)
Пример: допустимый диапазон [10, 200]. Семя попыталось улететь в позицию 220. После отражения: 200 - (220 - 200) = 180. Семя «отскочило» от границы и оказалось внутри области.
Если после нескольких отражений семя всё ещё за границами (например, улетело очень далеко), тогда ему присваивается случайная позиция внутри области.
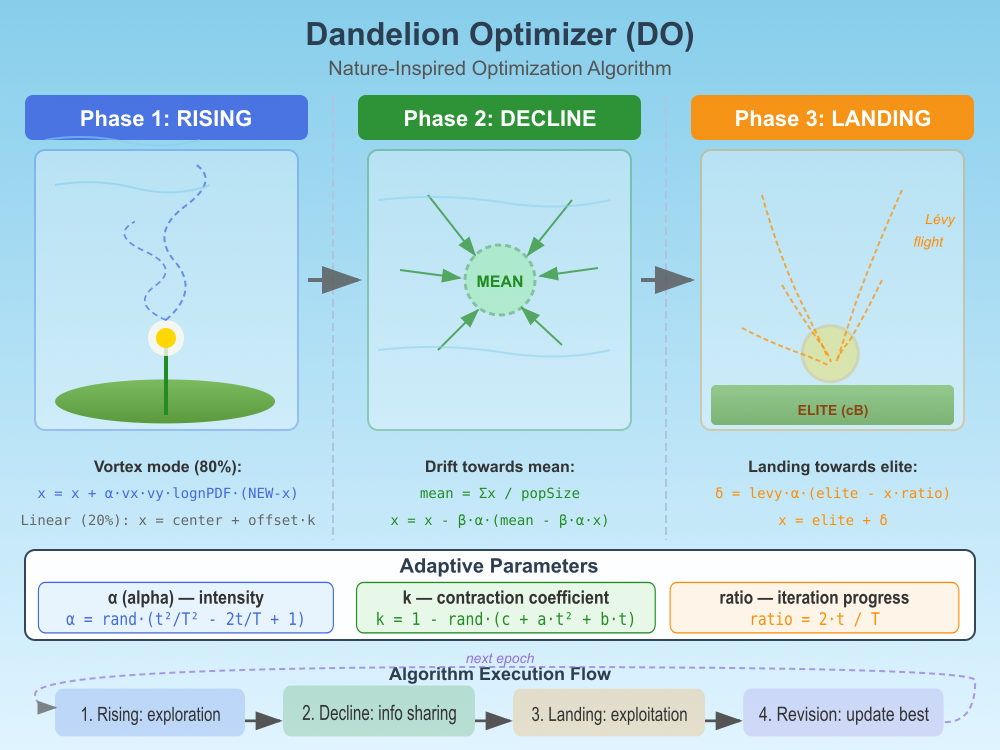
Рисунок 1. Иллюстрация работы алгоритма DO
На иллюстрации отображены три фазы работы алгоритма:
- Rising (синий) — семена поднимаются от одуванчика по спиральным траекториям, визуализирован вихревой подъём с формулами.
- Decline (зелёный) — семена дрейфуют к среднему положению популяции (MEAN), стрелки показывают направление движения.
- Landing (оранжевый) — семена приземляются к элитной позиции (ELITE/cB) по траекториям Lévy flight.
Дополнительные элементы: адаптивные параметры "α", "k" и "ratio" с формулами, порядок выполнения алгоритма с циклом возврата к следующей эпохе, семена одуванчика с паппусом (пушистым парашютом), элитное семя выделено золотым цветом. Можем приступить к написанию кода алгоритма DO.
ИНИЦИАЛИЗАЦИЯ
1. Для каждого семени i от 1 до popSize:
1.1. Для каждой координаты c:
— Присвоить случайное значение в пределах [rangeMin[c], rangeMax[c]]
1.2. Вычислить фитнес семени
2. Найти лучшее семя в популяции
3. Сохранить его координаты в cB[], фитнес в fB
ОСНОВНОЙ ЦИКЛ ОПТИМИЗАЦИИ
4. Для каждой эпохи t от 1 до epochs:
4.1. ВЫЧИСЛЕНИЕ АДАПТИВНЫХ ПАРАМЕТРОВ
— Вычислить параметр интенсивности alpha:
alpha уменьшается от 1 до 0 по мере роста t
(большие шаги в начале, малые в конце)
— Вычислить коэффициент сжатия k:
k определяет степень сжатия к центру области
4.2. ФАЗА ПОДЪЁМА (Rising Stage)
Сгенерировать случайное число rand
ЕСЛИ rand < 0.8 ТО
Вихревой подъём (сильный ветер)
Для каждого семени i:
— Вычислить случайный угол theta в диапазоне [-π, π]
— Рассчитать вихревые компоненты vx и vy
на основе логарифмической спирали
Для каждой координаты c:
— Сгенерировать случайную точку NEW в области поиска
— Сместить семя в направлении NEW с учётом
вихревого коэффициента и логнормального распределения
— Проверить и скорректировать границы
ИНАЧЕ
Линейный подъём (слабый ветер)
Для каждого семени i:
Для каждой координаты c:
— Вычислить смещение семени относительно центра области
— Умножить смещение на коэффициент k
— Новая позиция = центр + масштабированное смещение
— Проверить и скорректировать границы
4.3. ФАЗА СНИЖЕНИЯ (Decline Stage)
Вычисление среднего положения популяции
Для каждой координаты c:
mean[c] = сумма всех x[i][c] / popSize
Дрейф семян к среднему
Для каждого семени i:
Для каждой координаты c:
— Сгенерировать случайный коэффициент beta (нормальное распределение)
— Вычислить смещение на основе разницы между
текущей позицией и средним значением
— Ограничить смещение 30% от ширины диапазона
— Применить смещение к позиции семени
— Проверить и скорректировать границы
4.4. ФАЗА ПРИЗЕМЛЕНИЯ (Landing Stage)
Вычислить ratio = 2 * t / epochs
(ratio растёт от 0 до 2 по мере приближения к концу)
Для каждого семени i:
Генерация шага по распределению Леви
Для каждой координаты c:
— Сгенерировать два нормально распределённых числа u и v
— levy[c] = u / |v|^(2/3)
Приземление к элитному решению
Для каждой координаты c:
— Вычислить смещение delta на основе:
• шага Леви
• параметра alpha
• разницы между элитой и текущей позицией
— Ограничить delta 50% от ширины диапазона
— Новая позиция = elite[c] + delta
— Проверить и скорректировать границы
4.5. ВЫЧИСЛЕНИЕ ФИТНЕСА И ОБНОВЛЕНИЕ ЛУЧШЕГО РЕШЕНИЯ
Для каждого семени i:
— Вычислить фитнес новой позиции
Найти семя с лучшим фитнесом в текущей популяции
ЕСЛИ лучший фитнес популяции > fB ТО
— Обновить fB
— Скопировать координаты лучшего семени в cB[]
ЗАВЕРШЕНИЕ
5. Вернуть лучшее решение cB[] и его фитнес fB
КОНЕЦ АЛГОРИТМА
ВСПОМОГАТЕЛЬНАЯ ПРОЦЕДУРА: Проверка и коррекция границ
ПРОЦЕДУРА BoundaryControl(позиция семени):
Для каждой координаты c:
ПОКА позиция выходит за границы И попыток < 10:
ЕСЛИ позиция < минимум ТО
— Отразить от нижней границы:
позиция = минимум + (минимум - позиция)
ЕСЛИ позиция > максимум ТО
— Отразить от верхней границы:
позиция = максимум - (позиция - максимум)
ЕСЛИ позиция всё ещё за границами ТО
— Присвоить случайное значение в допустимом диапазоне
— Округлить позицию до ближайшего допустимого шага
КОНЕЦ ПРОЦЕДУРЫ
Теперь приступим к реализации в коде. Для хранения вспомогательных координатных данных используется простая структура:
//———————————————————————————————————————————————————————————————————— struct S_DO_Coord { double v; }; //————————————————————————————————————————————————————————————————————
Класс "C_AO_DO" наследуется от базового класса "C_AO" и представляет собой реализацию алгоритма DO.
Функционал, методы:
- SetParams — обновляет внутренние параметры алгоритма на основе значений, переданных через массив "params",
- Init — инициализирует алгоритм на основе заданных минимальных и максимальных диапазонов поиска для каждой размерности, шага и количества эпох,
- Moving — отвечает за шаг движения (эволюцию) популяции в процессе оптимизации,
- Revision — используется для пересмотра или корректировки позиций особей после определенного этапа,
- LevyFlight — приватный, отвечает за генерацию случайных шагов, следуя распределению Леви, как описано ранее,
- LognormalPDF — приватный метод для вычисления значения плотности вероятности логнормального распределения,
- BoundaryControl — приватный, применяется для обеспечения того, чтобы сгенерированные позиции оставались в пределах установленных границ поиска.
Внутренние переменные:
- epochs — максимальное количество итераций (эпох),
- currentEpoch — текущая итерация (эпоха),
- sigma_u — предварительно вычисленное значение стандартного отклонения для распределения Леви при β = 1.5 β=1.5,
- mean — массив средних позиций особей в пространстве поиска,
- levy — массив, хранящий сгенерированные шаги Леви для каждой координаты, используемые для перемещения особей,
- center — массив центральных точек диапазона поиска для каждой координаты,
- range — массив ширины диапазона поиска для каждой координаты.
Класс "C_AO_DO" инкапсулирует логику работы алгоритма Dandelion Optimizer, включая генерацию случайных перемещений по распределению Леви и управление параметрами поиска.
//———————————————————————————————————————————————————————————————————— class C_AO_DO : public C_AO { public: ~C_AO_DO () { } C_AO_DO () { ao_name = "DO"; ao_desc = "Dandelion Optimizer"; ao_link = "https://www.mql5.com/ru/articles/20540"; popSize = 50; ArrayResize (params, 1); params [0].name = "popSize"; params [0].val = popSize; } void SetParams () { popSize = (int)params [0].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP); void Moving (); void Revision (); private: //————————————————————————————————————————————————————————— int epochs; // maximum iterations int currentEpoch; // current iteration double sigma_u; // precomputed Levy sigma for beta=1.5 S_DO_Coord mean []; // mean position S_DO_Coord levy []; // levy flight steps S_DO_Coord center []; // center of search range S_DO_Coord range []; // range width void LevyFlight (); double LognormalPDF (double x, double mu, double sigma); void BoundaryControl (int idx); }; //————————————————————————————————————————————————————————————————————
Метод "Init" класса "C_AO_DO" отвечает за начальную настройку и подготовку алгоритма к работе. В первую очередь, он вызывает родительский метод "StandardInit", который выполняет общие для всех оптимизаторов инициализационные процедуры, такие как установка диапазонов поиска (минимальные, максимальные значения и шаги) и определение количества координат в целевой функции. Если эта стандартная инициализация не удалась, метод "Init" также вернет "false".
Установка параметров оптимизации:- epochs — задает максимальное количество итераций (эпох), которое будет выполнять алгоритм,
- currentEpoch — сбрасывает счетчик текущей эпохи на ноль, поскольку процесс оптимизации только начинается.
- mean — для хранения средних позиций,
- levy — для хранения шагов, рассчитанных по закону Леви,
- center — для хранения центров областей поиска,
- range — для хранения ширины областей поиска.
- center — координата центра области поиска, которая определяется как среднее между минимальным и максимальным допустимым значением для данной координаты,
- range — ширина области поиска, равная разнице между максимальным и минимальным допустимым значением.
Устанавливает предопределенное значение "sigma_u", которое является константой, используемой для расчета шагов Леви при заданном параметре бета, равном 1.5.
Значение σ u = 0.6966 (sigma_u = 0.6966) вычислено заранее по формуле: σ_u = (Γ(1+β) * sin(πβ/2) / (Γ((1+β)/2) * β * 2^((β-1)/2)))^(1/β); при β = 1.5 это даёт константу ≈ 0.6966. Это сделано для облегчения расчетов в алгоритме.
Если все этапы инициализации прошли успешно, метод возвращает "true". Таким образом, "Init" подготавливает все необходимые структуры данных, устанавливает глобальные параметры оптимизации и выполняет предварительные расчеты, необходимые для корректного выполнения последующих шагов алгоритма "Moving" и "Revision".
//———————————————————————————————————————————————————————————————————— bool C_AO_DO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //------------------------------------------------------------------ epochs = epochsP; currentEpoch = 0; ArrayResize (mean, coords); ArrayResize (levy, coords); ArrayResize (center, coords); ArrayResize (range, coords); // Предвычисление центра и ширины диапазона для каждой координаты for (int c = 0; c < coords; c++) { center [c].v = (rangeMax [c] + rangeMin [c]) * 0.5; range [c].v = rangeMax [c] - rangeMin [c]; } // Предвычисление sigma_u для Levy flight с beta=1.5 sigma_u = 0.6966; return true; } //————————————————————————————————————————————————————————————————————
Метод "Moving" является основным рабочим циклом алгоритма DO и отвечает за перемещение популяции решений в пространстве поиска в течение каждой эпохи оптимизации. Он разделен на три основные фазы: "Rising stage" (Подъем), "Decline stage" (Спад) и "Landing stage" (Приземление), каждая из которых использует свою специфическую стратегию обновления позиций.
Если флаг "revision" установлен в "false" (т.е. это первая итерация), метод случайным образом инициализирует позиции всех "popSize" особей в пределах заданных диапазонов "rangeMin" и "rangeMax" для каждой координаты. Применяется функция "SeInDiSp" для коррекции позиций с учетом шага "rangeStep". Флаг "revision" устанавливается в "true", и метод завершает выполнение для этой первой эпохи.
Расчет временных параметров. Счетчик текущей эпохи "currentEpoch" инкрементируется. Вычисляются относительные времена "t" (текущая эпоха) и "T" (максимальное количество эпох). Рассчитывается параметр "alpha", который является случайным числом, зависящим от текущей и максимальной эпохи, что управляет степенью изменений на этапе подъема. Рассчитываются параметры "aa", "bb", "cc" и "k", которые используются на этапе линейного подъема и управляют масштабированием смещения относительно центра диапазона.
Rising stage (Фаза подъема), имитирующая спиральное движение семени в восходящем потоке воздуха. С вероятностью 0.8 выполняется вихревой подъём: для каждой особи генерируются случайные значения "theta", "row", "vx", "vy" и "vxvy", имитирующие движение вихря. Для каждой координаты особи:
- рассчитывается случайная величина "lamb" из гауссовского распределения,
- вычисляется значение логнормального распределения,
- генерируется новое случайное значение в пределах абсолютных диапазонов,
- новая позиция особи вычисляется как текущая позиция плюс смещение, зависящее от "alpha", "vxvy", "lognPDF" и разницы между "NEW" и текущей позицией.
С вероятностью 0.2 выполняется линейный подъём: для каждой особи и каждой координаты вычисляется смещение текущей позиции относительно центра диапазона. Новая позиция рассчитывается путем масштабирования этого смещения с использованием параметра "k", а затем возвращается к центру диапазона. После обновления позиций в любой из подфаз подъема, применяется "BoundaryControl" для каждой особи, чтобы убедиться, что они остаются в пределах допустимых диапазонов.
Decline stage (Фаза снижения), на этой фазе семена дрейфуют в горизонтальном воздушном потоке. Рассчитывается средняя позиция всех особей по каждой координате. Для каждой особи и каждой координаты:
- генерируется случайный параметр "beta" из гауссовского распределения,
- вычисляется параметр "betaAlpha",
- рассчитывается смещение "delta", которое зависит от "betaAlpha", среднего положения и текущей позиции особи,
- для предотвращения слишком больших шагов, "delta" ограничивается 30% от ширины диапазона (range),
- новая позиция особи обновляется путем добавления "delta".
- получаются значения лучшей найденной позиции (elite, сохраняется в cB) и текущей позиции особи (current),
- вычисляется смещение "delta" по формуле, включающей шаг Леви, "alpha", "elite", "current" и "ratio",
- смещение "delta" ограничивается половиной ширины диапазона (range),
- новая позиция особи вычисляется как "elite" плюс "delta".
//———————————————————————————————————————————————————————————————————— void C_AO_DO::Moving () { //------------------------------------------------------------------ // Первая итерация: инициализация популяции if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //------------------------------------------------------------------ currentEpoch++; double t = (double)currentEpoch; double T = (double)epochs; // Параметр alpha (eq. 8): alpha = rand * (t?/T? - 2t/T + 1) double alpha = u.RNDfromCI (0.0, 1.0) * ((t * t) / (T * T) - 2.0 * t / T + 1.0); // Параметры для k (eq. 11) double denom = T * T - 2.0 * T + 1.0; if (MathAbs (denom) < 1e-10) denom = 1e-10; double aa = 1.0 / denom; double bb = -2.0 * aa; double cc = 1.0 - aa - bb; double k = 1.0 - u.RNDfromCI (0.0, 1.0) * (cc + aa * t * t + bb * t); //================================================================== // Rising stage (Фаза подъёма) //================================================================== if (u.RNDprobab () < 0.8) { // Вихревой подъём (eq. 5) for (int i = 0; i < popSize; i++) { double theta = (2.0 * u.RNDfromCI (0.0, 1.0) - 1.0) * M_PI; double row = 1.0 / MathExp (theta); double vx = row * MathCos (theta); double vy = row * MathSin (theta); double vxvy = vx * vy; for (int c = 0; c < coords; c++) { double lamb = MathAbs (u.GaussDistribution (0, 1, -3, 3)); double lognPDF = LognormalPDF (lamb, 0.0, 1.0); double NEW = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = a [i].c [c] + alpha * vxvy * lognPDF * (NEW - a [i].c [c]); } BoundaryControl (i); } } else { // Линейный подъём (eq. 10) - масштабирование относительно центра диапазона for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Смещение относительно центра, масштабирование, возврат double offset = a [i].c [c] - center [c].v; a [i].c [c] = center [c].v + offset * k; } BoundaryControl (i); } } //================================================================== // Decline stage (Фаза снижения) //================================================================== // Вычисление среднего положения (eq. 14) for (int c = 0; c < coords; c++) { mean [c].v = 0.0; } for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { mean [c].v += a [i].c [c]; } } for (int c = 0; c < coords; c++) { mean [c].v /= popSize; } // Обновление позиций (eq. 13) for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Ограничиваем beta типичным диапазоном нормального распределения double beta = u.GaussDistribution (0, 1, -3, 3); double betaAlpha = beta * alpha; double delta = -betaAlpha * (mean [c].v - betaAlpha * a [i].c [c]); // Ограничиваем смещение double maxDelta = range [c].v * 0.3; if (delta > maxDelta) delta = maxDelta; if (delta < -maxDelta) delta = -maxDelta; a [i].c [c] = a [i].c [c] + delta; } BoundaryControl (i); } //================================================================== // Landing stage (Фаза приземления) //================================================================== double ratio = 2.0 * t / T; if (ratio > 2.0) ratio = 2.0; // Ограничение ratio for (int i = 0; i < popSize; i++) { LevyFlight (); for (int c = 0; c < coords; c++) { double elite = cB [c]; double current = a [i].c [c]; // eq. 15: x = Elite + levy * alpha * (Elite - x * ratio) double delta = levy [c].v * alpha * (elite - current * ratio); // Ограничиваем итоговое смещение половиной диапазона double maxDelta = range [c].v * 0.5; if (delta > maxDelta) delta = maxDelta; if (delta < -maxDelta) delta = -maxDelta; a [i].c [c] = elite + delta; } BoundaryControl (i); } } //————————————————————————————————————————————————————————————————————
Метод "LevyFlight" предназначен для генерации случайных смещений, следующих распределению Леви. Это распределение с "тяжелыми хвостами" используется для улучшения глобального поиска и предотвращения застревания в локальных минимумах. В данной реализации используется параметр β = 1.5.
Метод обрабатывает каждую координату "c" в пространстве поиска. Генерация вспомогательных случайных величин:
- uu — случайная величина по нормальному распределению со средним 0 и стандартным отклонением "sigma_u". Диапазон значений "uu" ограничен интервалом от − 3.0 ⋅ σ до 3.0 ⋅ σ
- vv — случайная величина по стандартному нормальному распределению (среднее 0, стандартное отклонение 1). Значения vv ограничены интервалом от − 3 до 3.
//———————————————————————————————————————————————————————————————————— void C_AO_DO::LevyFlight () { // Levy flight с beta = 1.5 for (int c = 0; c < coords; c++) { double uu = u.GaussDistribution (0, sigma_u, -3.0 * sigma_u, 3.0 * sigma_u); double vv = u.GaussDistribution (0, 1, -3, 3); if (MathAbs (vv) < 1e-10) vv = 1e-10; levy [c].v = uu / MathPow (MathAbs (vv), 0.6667); } } //————————————————————————————————————————————————————————————————————
Метод "LognormalPDF" вычисляет значение функции плотности вероятности (PDF) логнормального распределения для заданного значения "x", с параметрами "mu" и "sigma". Если входное значение "x" меньше или равно нулю, функция сразу возвращает 0, что соответствует определению логнормального распределения (нельзя брать логарифм от нуля или отрицательного числа). Функция находит натуральный логарифм от "x" и сохраняет его в "logx". Высчитывает разницу между "logx" и параметром "mu", сохраняя результат в "diff". Частное, делённое на "x", sigma и корень из 2π. Это нормирующий множитель, обеспечивающий, чтобы сумма вероятностей по всей области равнялась 1. Экспоненциальная часть равна exp(-diff² / (2 * sigma²)), что соответствует гауссовой загруженности в логарифмическом пространстве. Итоговое значение функции плотности является произведением коэффициента и экспоненты.
Этот метод используется для оценки вероятности того, что переменная примет значение, приближающееся к "x", если она распределена по логнормальному закону с параметрами.
//———————————————————————————————————————————————————————————————————— double C_AO_DO::LognormalPDF (double x, double mu, double sigma) { if (x <= 0.0) return 0.0; double logx = MathLog (x); double diff = logx - mu; double coeff = 1.0 / (x * sigma * MathSqrt (2.0 * M_PI)); double expon = MathExp (-diff * diff / (2.0 * sigma * sigma)); return coeff * expon; } //————————————————————————————————————————————————————————————————————
Метод "BoundaryControl" класса "C_AO_DO" предназначен для приведения координат (c) особи (idx) в допустимые границы (rangeMin и rangeMax). Для каждой координаты "c" особи "idx" выполняется следующий цикл: извлекается текущее значение координаты "val". Получаются минимальное min = rangeMin[c] и максимальное max = rangeMax[c] значения для данной координаты. Далее происходит отражение от границ, чтобы вернуть значение в допустимый диапазон. Таким образом, метод гарантирует, что все координаты каждой особи алгоритма всегда находятся в пределах заданных ограничений, предотвращая тем самым выход за пределы исследуемой области. Если значение выходит за пределы допустимого диапазона, оно «отражается» от границы подобно мячу от стены. Такой подход предотвращает скопление частиц на границах области поиска.
//———————————————————————————————————————————————————————————————————— void C_AO_DO::BoundaryControl (int idx) { for (int c = 0; c < coords; c++) { double val = a [idx].c [c]; double min = rangeMin [c]; double max = rangeMax [c]; // Итеративное отражение от границ (максимум 10 итераций) int iter = 0; while ((val < min || val > max) && iter < 10) { if (val < min) val = min + (min - val); if (val > max) val = max - (val - max); iter++; } // Если отражение не помогло, случайная позиция if (val < min || val > max) { val = u.RNDfromCI (min, max); } a [idx].c [c] = u.SeInDiSp (val, min, max, rangeStep [c]); } } //————————————————————————————————————————————————————————————————————
Метод "Revision" предназначен для обновления лучшего решения (наиболее приспособленного образца) в популяции. Он находит образец с наилучшей приспособленностью в текущей популяции и если эта лучшая приспособленность превосходит ранее сохраненное глобальное лучшее значение, то глобальное лучшее значение и соответствующие ему координаты обновляются.
Этот метод является частью эволюционных алгоритмов и используется для поддержания "лучшего найденного решения" на протяжении всей работы алгоритма.
//———————————————————————————————————————————————————————————————————— void C_AO_DO::Revision () { int bestIdx = 0; double bestFit = a [0].f; for (int i = 1; i < popSize; i++) { if (a [i].f > bestFit) { bestFit = a [i].f; bestIdx = i; } } if (bestFit > fB) { fB = bestFit; ArrayCopy (cB, a [bestIdx].c, 0, 0, coords); } } //————————————————————————————————————————————————————————————————————
Результаты тестов
Можем познакомиться с результатами тестирования алгоритма DO на наших тестовых функциях, алгоритм набирает почти 46%, это хороший результат, однако недостаточный, чтобы оказаться в рейтинговой таблице.
DO|Dandelion Optimizer|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.8644615393164621
25 Hilly's; Func runs: 10000; result: 0.5314446096211787
500 Hilly's; Func runs: 10000; result: 0.30299240094063645
=============================
5 Forest's; Func runs: 10000; result: 0.7000244797507886
25 Forest's; Func runs: 10000; result: 0.35553834859463407
500 Forest's; Func runs: 10000; result: 0.18229100471466797
=============================
5 Megacity's; Func runs: 10000; result: 0.6784615384615384
25 Megacity's; Func runs: 10000; result: 0.3458461538461538
500 Megacity's; Func runs: 10000; result: 0.13560000000000136
=============================
All score: 4.09666 (45.52%)
На визуализации работы алгоритма DO заметен разброс значений на функциях малой размерности. На дискретной Megacity, этот разброс значений наиболее сильный.

DO на тестовой функции Hilly

DO на тестовой функции Forest

DO на тестовой функции Megacity
Как можно заметить, с некоторыми типами задач, алгоритм DO прекрасно справляется, показывая отличную сходимость.

DO на стандартной тестовой функции Ackley

DO на стандартной тестовой функции Shaffer
По результатам тестирования, в рейтинговой таблице лучших популяционных методов оптимизации, алгоритм DO представлен ознакомительно, ему совсем немного не хватило для получения места.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | DOAdingom | dingo_optimization_algorithm_M | 0,47968 | 0,45367 | 0,46369 | 1,39704 | 0,94145 | 0,87909 | 0,91454 | 2,73508 | 0,78615 | 0,86061 | 0,84805 | 2,49481 | 6,627 | 73,63 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 5 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 6 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 7 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 8 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 9 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 10 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 11 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 12 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 13 | EOm | extremal_optimization_M | 0,76166 | 0,77242 | 0,31747 | 1,85155 | 0,99999 | 0,76751 | 0,23527 | 2,00277 | 0,74769 | 0,53969 | 0,14249 | 1,42987 | 5,284 | 58,71 |
| 14 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 15 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 16 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 17 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 18 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 19 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 20 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 21 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 22 | BSA | backtracking_search_algorithm | 0,97309 | 0,54534 | 0,29098 | 1,80941 | 0,99999 | 0,58543 | 0,21747 | 1,80289 | 0,84769 | 0,36953 | 0,12978 | 1,34700 | 4,959 | 55,10 |
| 23 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 24 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 25 | BO | bonobo_optimizer | 0,77565 | 0,63805 | 0,32908 | 1,74278 | 0,88088 | 0,76344 | 0,25573 | 1,90005 | 0,61077 | 0,49846 | 0,14246 | 1,25169 | 4,895 | 54,38 |
| 26 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 27 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 28 | DOA | dream_optimization_algorithm | 0,85556 | 0,70085 | 0,37280 | 1,92921 | 0,73421 | 0,48905 | 0,24147 | 1,46473 | 0,77231 | 0,47354 | 0,18561 | 1,43146 | 4,825 | 53,62 |
| 29 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 30 | DEA | dolphin_echolocation_algorithm | 0,75995 | 0,67572 | 0,34171 | 1,77738 | 0,89582 | 0,64223 | 0,23941 | 1,77746 | 0,61538 | 0,44031 | 0,15115 | 1,20684 | 4,762 | 52,91 |
| 31 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 32 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 33 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 34 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 35 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 36 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 37 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 38 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 39 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 40 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 41 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 42 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 43 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 44 | CMAES | covariance_matrix_adaptation_evolution_strategy | 0,76258 | 0,72089 | 0,00000 | 1,48347 | 0,82056 | 0,79616 | 0,00000 | 1,61672 | 0,75846 | 0,49077 | 0,00000 | 1,24923 | 4,349 | 48,33 |
| 45 | DA_duelist | duelist_algorithm | 0,92782 | 0,53778 | 0,27792 | 1,74352 | 0,86957 | 0,47536 | 0,18193 | 1,52686 | 0,62153 | 0,33569 | 0,11715 | 1,07437 | 4,345 | 48,28 |
| DO | dandelion_optimizer | 0,86446 | 0,53144 | 0,30299 | 1,69889 | 0,70002 | 0,35553 | 0,18229 | 1,23784 | 0,67846 | 0,34584 | 0,13560 | 1,15990 | 4,097 | 45,52 | |
| RW | random walk | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Выводы
Алгоритм оптимизации одуванчика (Dandelion Optimizer, DO) представляет собой интересную метафору природного процесса распространения семян, переложенную на язык математической оптимизации. Трёхфазная структура алгоритма — подъём, снижение, приземление — создаёт логически обоснованный механизм поиска, где каждая фаза выполняет свою функцию в балансе между исследованием и эксплуатацией.
По результатам тестирования на нашем наборе тестовых функций алгоритм набрал 45.5%, что является приемлемым, но недостаточным результатом для включения в рейтинговую таблицу лучших популяционных методов оптимизации. Алгоритму буквально немного не хватило, чтобы преодолеть порог вхождения в группу лидеров.
Концептуальная ясность структуры. Три фазы полёта семени интуитивно понятны и легко визуализируются, что упрощает понимание логики работы алгоритма и его настройку. Адаптивные параметры "α" и "ratio" обеспечивают автоматический переход от глобального поиска к локальной оптимизации без необходимости ручной настройки момента переключения.
Использование полёта Леви на фазе приземления теоретически должно помогать выходу из локальных оптимумов благодаря редким длинным прыжкам. Механизм усреднения позиций на фазе снижения создаёт эффект коллективного разума, позволяя популяции обмениваться информацией о перспективных областях.
Наиболее существенной проблемой оказалась нестабильность на дискретных задачах, особенно при малой размерности пространства поиска. Алгоритм демонстрирует значительный разброс результатов от запуска к запуску, что снижает его надёжность в практических приложениях, где требуется предсказуемость. Вероятно, это связано с тем, что непрерывные операции алгоритма (логнормальное распределение, полёт Леви, вихревые траектории) плохо адаптируются к дискретной природе некоторых задач.
Вычислительная сложность алгоритма оказалась выше среднего. Несмотря на проведённые оптимизации кода — предвычисление константы "σ" для полёта Леви, кэширование центров и ширин диапазонов, вынесение инвариантов за циклы — алгоритм работает медленнее многих конкурентов. Причина кроется в самой архитектуре: три последовательные фазы на каждой итерации, вычисление среднего положения популяции, генерация множества случайных чисел из различных распределений (равномерного, нормального, логнормального, Леви). Каждое семя на каждой итерации проходит через все три фазы трансформации с многократными проверками границ.
Параметр "α", убывающий по параболическому закону, возможно, слишком быстро уменьшает интенсивность поиска. На поздних итерациях шаги становятся настолько малыми, что алгоритм фактически застывает вокруг текущего лучшего решения, теряя способность к выходу из локальных оптимумов даже с помощью полёта Леви.
Выбор между вихревым и линейным режимом подъёма с фиксированной вероятностью 80/20 выглядит несколько произвольным. Возможно, адаптивная настройка этого соотношения в зависимости от динамики улучшения фитнеса могла бы повысить эффективность.
Алгоритм может найти применение в задачах непрерывной оптимизации средней размерности, где критична не скорость работы, а качество конечного решения. Благодаря ясной структуре, DO хорошо подходит для образовательных целей как иллюстрация принципов популяционной оптимизации.
Для практического использования в задачах, требующих высокой производительности или работы с дискретными переменными, рекомендуется рассмотреть альтернативные алгоритмы из верхней части рейтинговой таблицы.
Потенциальными направлениями модификации алгоритма могут стать: адаптивная настройка вероятности выбора режима подъёма, более агрессивный механизм выхода из локальных оптимумов при стагнации, упрощение вычислительной схемы за счёт объединения фаз или сокращения числа генерируемых случайных величин. Отдельного исследования заслуживает разработка специализированной версии для дискретной оптимизации.
В целом, алгоритм оптимизации одуванчика представляет собой добротную, но невыдающуюся реализацию популяционного подхода. Он вносит вклад в разнообразие метаэвристических методов, однако не предлагает принципиально новых механизмов, способных существенно превзойти существующие решения.
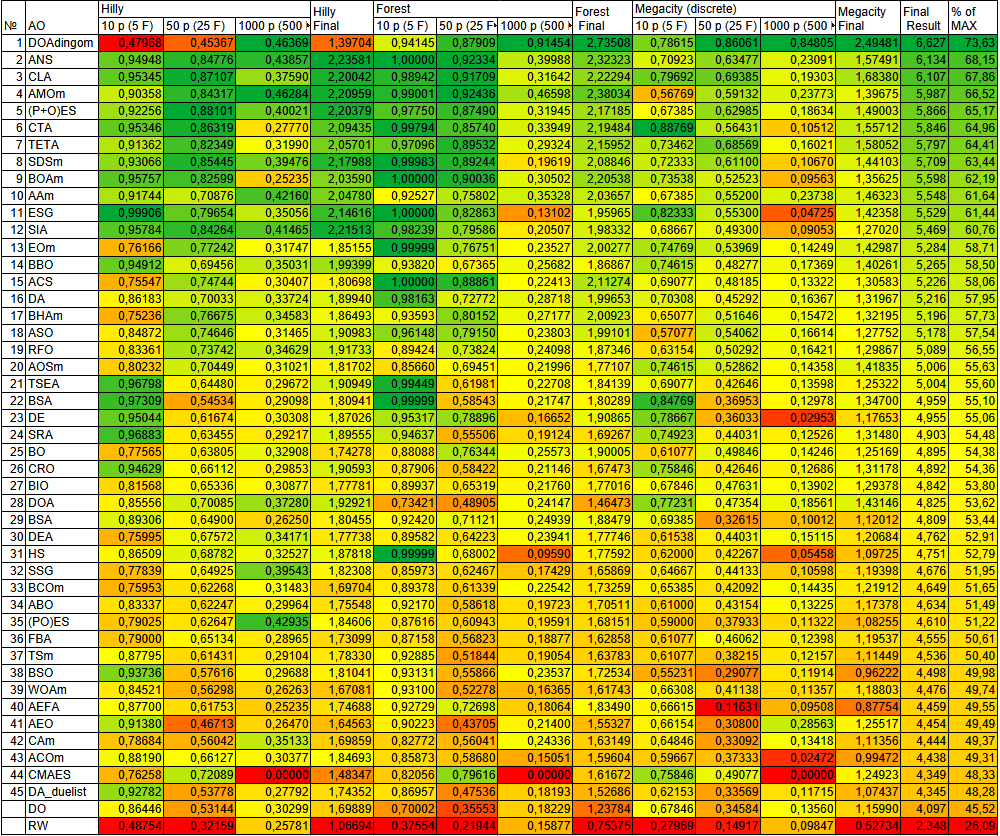
Рисунок 2. Цветовая градация алгоритмов по соответствующим тестам
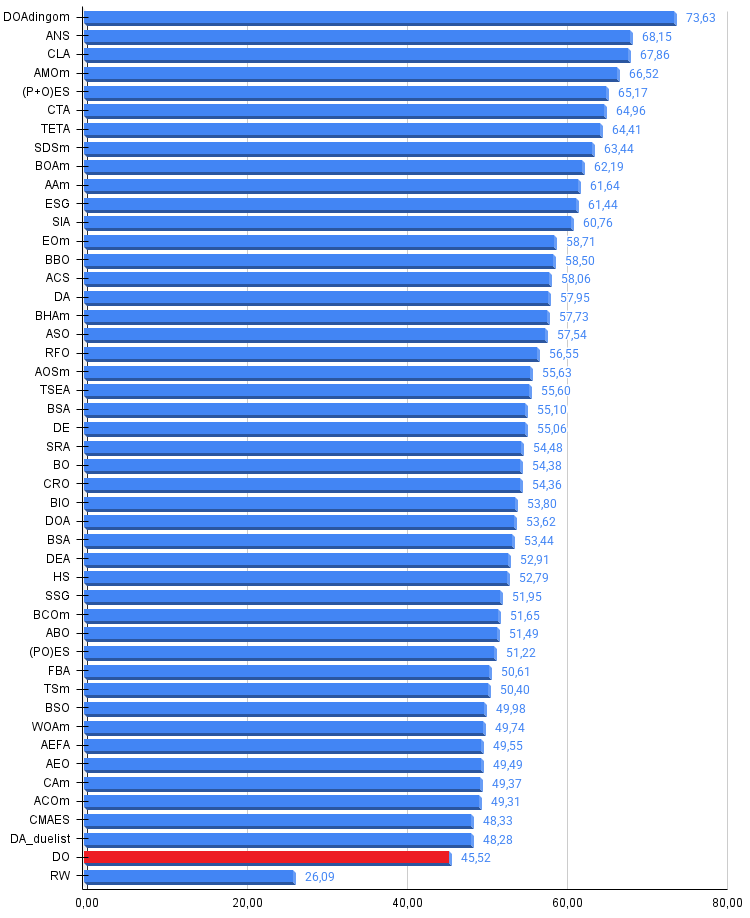
Рисунок 3. Гистограмма результатов тестирования алгоритмов (по шкале от 0 до 100, чем больше, тем лучше, где 100 — максимально возможный теоретический результат, в архиве скрипт для расчета рейтинговой таблицы)
Плюсы и минусы алгоритма DO:
Плюсы:
- Хорошо справляется с некоторым типом задач.
- Минимум внешних параметров, только размер популяции.
Минусы:
- Разброс значений на дискретных функциях.
- Медленный.
К статье прикреплён архив с актуальными версиями кодов алгоритмов. Автор статьи не несёт ответственности за абсолютную точность в описании канонических алгоритмов, во многие из них были внесены изменения для улучшения поисковых возможностей. Выводы и суждения, представленные в статьях, основываются на результатах проведённых экспериментов.
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | #C_AO.mqh | Включаемый файл | Родительский класс популяционных алгоритмов оптимизации |
| 2 | #C_AO_enum.mqh | Включаемый файл | Перечисление популяционных алгоритмов оптимизации |
| 3 | TestFunctions.mqh | Включаемый файл | Библиотека тестовых функций |
| 4 | TestStandFunctions.mqh | Включаемый файл | Библиотека функций тестового стенда |
| 5 | Utilities.mqh | Включаемый файл | Библиотека вспомогательных функций |
| 6 | CalculationTestResults.mqh | Включаемый файл | Скрипт для расчета результатов в сравнительную таблицу |
| 7 | Testing AOs.mq5 | Скрипт | Единый испытательный стенд для всех популяционных алгоритмов оптимизации |
| 8 | Simple use of population optimization algorithms.mq5 | Скрипт | Простой пример использования популяционных алгоритмов оптимизации без визуализации |
| 9 | Test_AO_DO.mq5 | Скрипт | Испытательный стенд для DO |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Реализация механизма безубыточности в MQL5 (Часть 1): Базовый класс и режим безубытка по фиксированным пунктам
Реализация механизма безубыточности в MQL5 (Часть 1): Базовый класс и режим безубытка по фиксированным пунктам
 Разработка инструментария для анализа движения цен (Часть 17): Советник TrendLoom
Разработка инструментария для анализа движения цен (Часть 17): Советник TrendLoom
 Объединяем LLM, CatBoost и квантовые вычисления в единую торговую систему
Объединяем LLM, CatBoost и квантовые вычисления в единую торговую систему
 Разработка инструментария для анализа движения цен (Часть 15): Введение в теорию четвертей (II) — советник Intrusion Detector
Разработка инструментария для анализа движения цен (Часть 15): Введение в теорию четвертей (II) — советник Intrusion Detector
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Здравствуйте, автор. Не могли бы вы написать простой пример советника (EA), использующий ваш алгоритм оптимизации?
Здравствуйте.
Конечно, вот:
Статьи
Советник на базе универсального аппроксиматора MLP
Andrey Dik, 2024.12.13 13:09
В статье представлен простой и доступный способ использования нейронной сети в торговом советнике, который не требует глубоких знаний в машинном обучении. Метод исключает нормализацию целевой функции и устраняет проблемы "взрыва весов" и "ступора сети", предлагая интуитивное обучение и наглядный контроль результатов.Статьи
Использование алгоритмов оптимизации для настройки параметров советника "на лету"
Andrey Dik, 2024.02.16 10:33
В статье рассматриваются практические аспекты использования алгоритмов оптимизации для поиска наилучших параметров советников "на лету", виртуализация торговых операций и логики советника. Данная статья может быть использована как своеобразная инструкция для внедрения алгоритмов оптимизации в торгового советника.