
Популяционные алгоритмы оптимизации: Алгоритм оптимизации с кукушкой (Cuckoo Optimization Algorithm — COA)
Содержание:
1. Введение2. Описание алгоритма, дерево решений и полёт Леви
3. Рассмотрение кода COA
4. Результаты тестов
1. Введение
Кукушка — очаровательная птица не только из-за сладкозвучного звука, который она может издавать, но и из-за своей агрессивной стратегии размножения, которая состоит в том, что при откладывании яиц птица использует гнезда других птиц, полностью перекладывая свои родительские обязанности для своего потомства на посторонние виды. Каждому виду присуща кладка яиц определённого цвета и размера, чтобы максимально соответствовать яйцам тех или иных приёмных родителей. Птенцы кукушек, подброшенные в чужие гнёзда, обычно больше и сильнее собственных птенцов хозяев гнезда, поэтому кукушатам требуется больше пищи. У птенцов кукушки Ходжсона при развитии на крыльях появляется особый узор в виде раскрытого клюва, что и позволяет получать им за счёт этой иллюзии больше еды от приёмных родителей. Но она далеко не единственная - гнездовой паразитизм обнаружен как минимум у 80 видов птиц. Также это явление широко распространено у некоторых видов социальных насекомых — шмелей, пчёл и муравьёв, самки которых проникают в чужую колонию, убивают матку и откладывают свои яйца. Гнездовой паразитизм существует и у рыб, например, у сомов из африканского озера Танганьика, которые подбрасывают икринки другим рыбам, инкубирующим икру у себя во рту.
Поиск с кукушкой — один из новейших эвристических алгоритмов, вдохновленных природой, разработанный Янгом и Деб 2009 г. Он основан на паразитизме некоторых видов кукушек. Этот алгоритм был дополнительно улучшен за счет так называемых полетов Леви, а не за счет простых методов изотропного случайного блуждания.
2. Описание алгоритма
Алгоритм оптимизации с кукушкой (COA) используется для непрерывной нелинейной оптимизации. COA вдохновлен образом жизни семейства этих птиц. Образ жизни этого вида, особенности яйцекладки и размножения лежат в основе разработки данного алгоритма оптимизации. Как и другие эволюционные подходы, COA начинается с начальной популяции. Основу алгоритма составляет попытка выжить. Соревнуясь за выживание, некоторые из них умирают. Выжившие кукушки переселяются в лучшие места и начинают размножаться и откладывать яйца. Наконец, выжившие кукушки сходятся таким образом, что получается общество кукушек с близкими значениями приспособленности.
Основным преимуществом этого метода является его простота: для поиска с кукушкой требуется всего четыре понятных параметра, поэтому настройка становится не сложной задачей.
В алгоритме поиска кукушки яйца в гнезде интерпретируются как возможные решения задачи оптимизации, а яйцо кукушки представляет собой новое решение. Конечной целью метода является использование этих новых (и потенциально лучших) решений, связанных с паразитическими яйцами кукушки, для замены текущего решения, связанного с яйцами в гнезде. Эта замена, осуществляемая итеративно и в конечном итоге приведет к решению задачи.
Профессора Янг и Деб предложили следующие три набора идеальных состояний для алгоритма:
1. Каждая кукушка откладывает по одному яйцу и сбрасывает его в случайно выбранное гнездо.
2. Лучшие гнезда с высоким качеством яиц будут переданы следующим поколениям.
3. Количество доступных гнезд фиксировано, и гнездо может обнаружить чужеродное яйцо с вероятностью pa. В этом случае птица - хозяин может либо выбросить яйцо, либо покинуть гнездо и яйцо погибнет.
Для простоты третье предположение можно аппроксимировать долей pa от n гнезд. Для задачи максимизации качество или соответствие решения может быть просто пропорционально целевой функции. Однако можно определить и другие (более сложные) выражения для фитнес функции.
Для каждой итерации g случайным образом выбирается яйцо кукушки i и генерируются новые решения xi (g+ 1) с использованием полета Леви, своего рода случайного блуждания, в котором шаги определяются в границах длин шагов, которые имеют определенное распределение вероятностей, причем направления шагов изотропны и случайны. По словам первоначальных создателей метода, стратегия использования полетов Леви предпочтительнее других простых случайных блужданий, поскольку она приводит к лучшей общей производительности. Общее уравнение полета Леви имеет вид
xi(g + 1) = xi(g) + α ⊕ levy(λ),
где g указывает номер текущего поколения, а α > 0 указывает размер шага, который должен быть связан с масштабом конкретной исследуемой проблемы. Символ ⊕ используется для обозначения поэлементного умножения. Обратите внимание, что это, по сути, представляет собой цепь Маркова, поскольку следующее местоположение в поколении g + 1 зависит только от текущего местоположения в поколении g и вероятности перехода, определяемой первым и вторым членами соответственно. Эта вероятность перехода модулируется распределением Леви как:
levy(λ) ∼ g−λ, (1 < λ ≤ 3),
который имеет бесконечную дисперсию с бесконечным средним значением. Практика показала, что наилучшие результаты достигаются с фиксированной степенью 2.0. Здесь шаги, по существу, образуют процесс случайного блуждания со степенным распределением длин шагов с тяжелым хвостом. С вычислительной точки зрения генерация случайных чисел с помощью полетов Леви состоит из двух этапов: во-первых, выбирается случайное направление в соответствии с равномерным распределением, затем выполняется генерация шагов в соответствии с выбранным распределением Леви. Затем алгоритм оценивает пригодность нового решения и сравнивает его с текущим. В случае, если новое решение обеспечивает лучшую пригодность, оно заменяет текущее. С другой стороны, часть гнезд забрасывается (хозяин гнезда выкинул яйцо кукушки либо покинул гнездо и яйцо погибло), чтобы увеличить исследование пространства поиска в поисках более перспективных решений. Скорость замещения определяется вероятностью pa, параметром модели, который необходимо настроить для повышения производительности. Алгоритм применяется итеративно до тех пор, пока не будет выполнен критерий остановки. Общие критерии завершения заключаются в том, что найдено решение, удовлетворяющее более низкому пороговому значению, достигнуто фиксированное количество поколений или что последовательные итерации больше не дают лучших результатов.
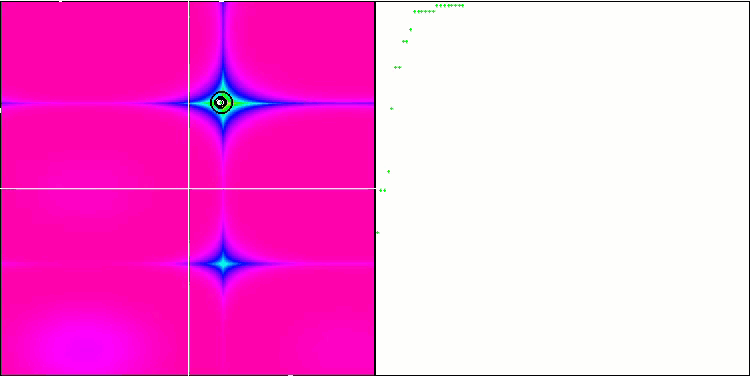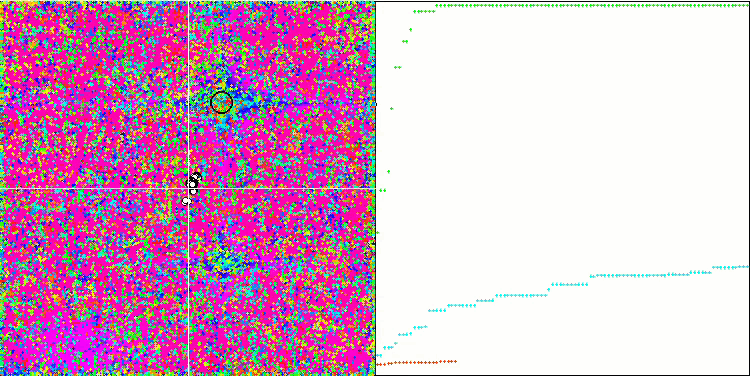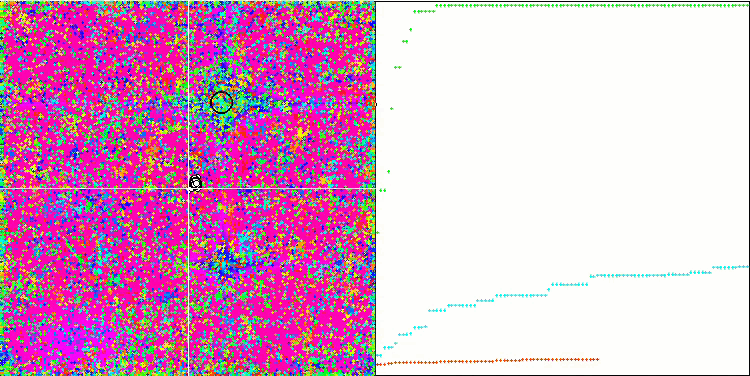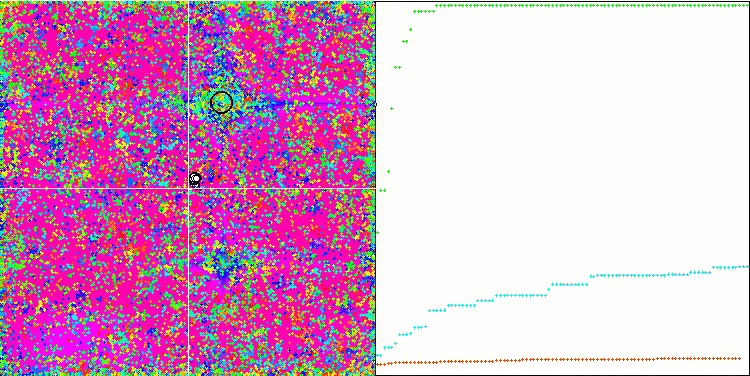
Остановимся более подробно на процессе подкладывания яиц кукушкой. Из всех гнезд будет выбрано случайным образом гнездо, куда предположительно будет отложено яйцо. Так как яйцо представляет собой решение, то оно может быть представлено качеством яйца, если яйцо кукушки более высокого качества, чем родительское, то оно будет заменено. В противном случае в гнезде останется родительское яйцо. По сути, последующая эволюция будет продолжатся от выжившего птенца. Это означает, что если выжил птенец родительского яйца, то эволюция продолжится с этого же места. Дальнейшее развитие возможно только, если яйцо кукушки окажется более жизнеспособно и поиск в решении задачи будет продолжен с нового места. Схематично дерево решений представлено на рисунке 1.
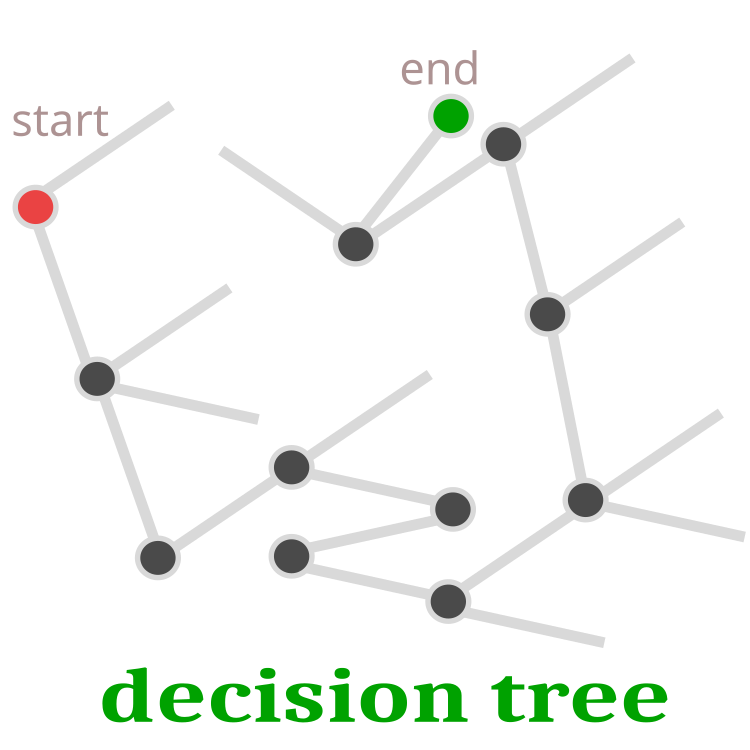
Рисунок 1. Дерево решений. Красная точка - начало, зелёная - окончательное решение.
Вторая компонента основы алгоритма после дерева решений - полет Леви. Полет Леви — это случайное блуждание (марковский статистический процесс), в котором длина скачка изменяется ступенчато, направление скачков изменяется случайным образом, а распределение вероятностей является частным случаем распределения Парето и характеризуется тяжёлыми хвостами. Определяется как скачок в пространстве, причем скачок осуществляется изотропно в случайных направлениях. Полёт Леви - инструмент описания аномальных стохастических процессов. Дисперсия бесконечна (возможны скачки большой длины), длины скачков само подобны на всех уровнях (короткие скачки перемежаются длинными полётами. Термин полёт Леви иногда распространяют и на случайное блуждание происходящее на дискретной сетке, а не в непрерывном пространстве.
Наглядное применение полета Леви в алгоритме кукушки можно представить, если рассмотреть задачу оптимизации с одним параметром. Возьмем гипотетическую функцию (линия черного цвета на рисунке 2), которая не изменяется на большей части своей области определения, т.е. горизонтальная линия (y=x). И только на небольшом участке функция изменяется и имеет один максимум. Если начать поиск максимума с оранжевой точки на рисунке 2, то получая случайное значение x с распределением Леви, будем удаляться от начальной точки, при этом не получая изменения функции. Однако, при сильном скачке, находящимся в хвосте распределения, получим зеленую точку, которая является лучшим решением, чем исходная оранжевая, и далее только с зеленой точки мы можем улучшать результат, приближаясь к максимуму функции. В данном примере полет Леви кардинальным образом улучшает поисковую способность алгоритма.
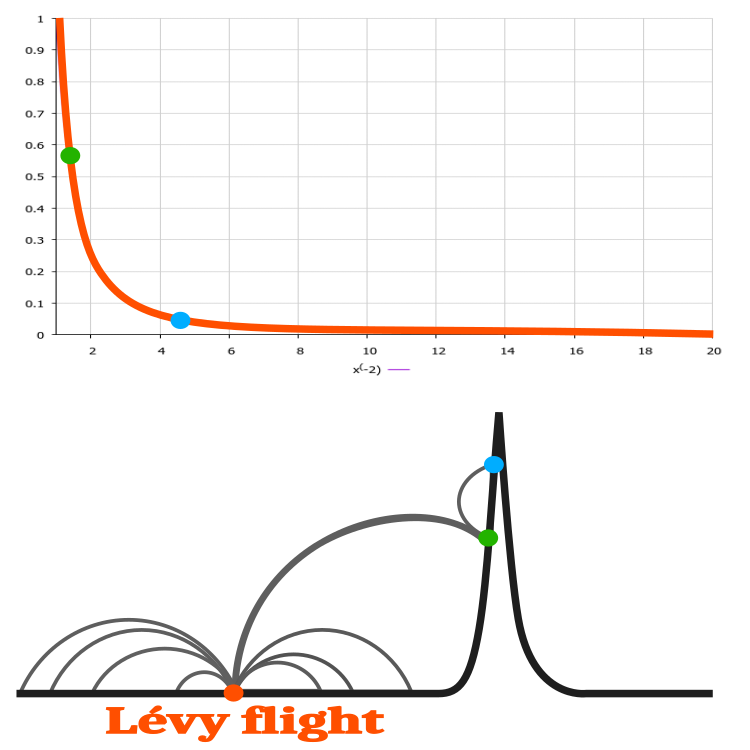
Рисунок 2. Пример поиска решения на гипотетической одномерной функции с помощью полёта Леви.
Понятие полетов Леви используют в теории хаоса, при моделировании случайных или псевдослучайных природных явлений (например, полёта альбатроса, сочетающего длинные и короткие траектории). Примеры включают в себя анализ данных о землетрясениях, финансовая математика, криптография, анализ сигналов, турбулентное движение, а также множество применений в астрономии, биологии и физике.
Псевдокод алгоритма COA (рисунок 3):
1. Инициализация кукушек случайными значениями.
2. Определение приспособленности.
3. Кладка яиц в случайные гнёзда.
4. Опустошить гнездо с заданной вероятностью
5. Отправить кукушек от текущего положения в случайную сторону на расстояние полёта Леви
6. Определение приспособленности.
7. Кладка яиц в случайные гнёзда.
8. Опустошить гнездо с заданной вероятностью.
9. Повторить п.5 до выполнения критерия останова.
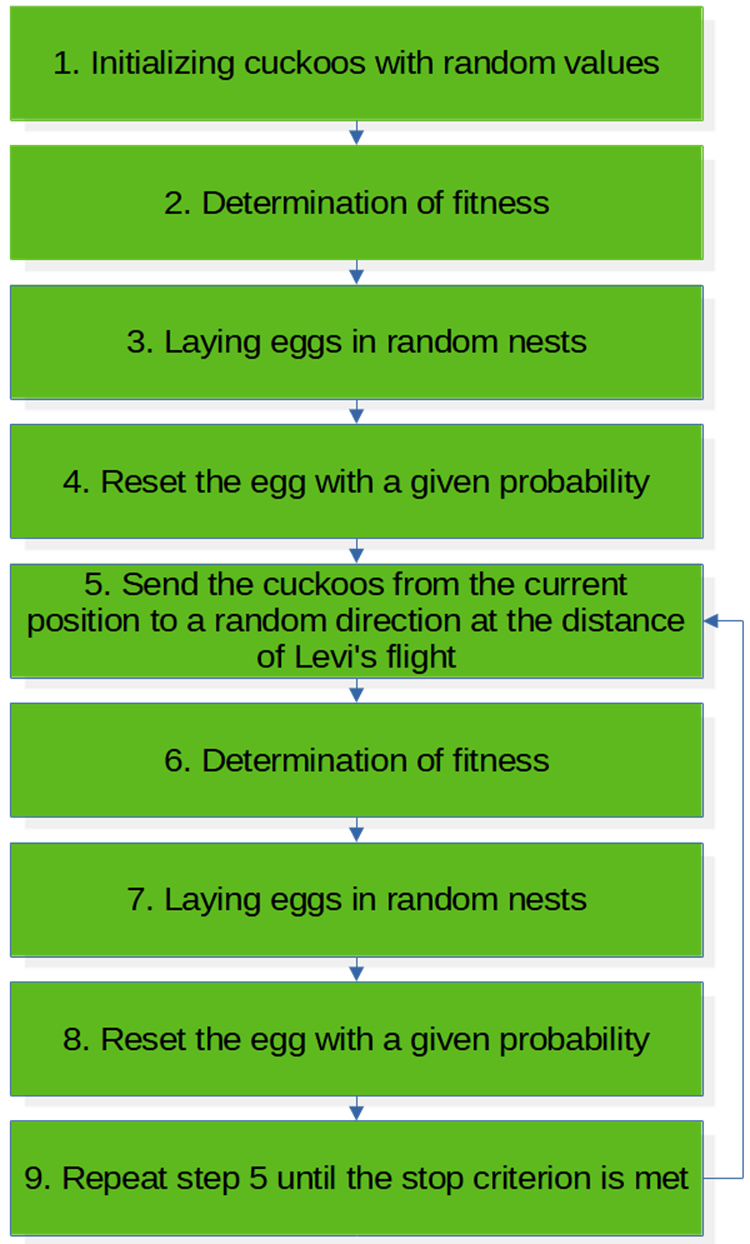
Рисунок 3. Блок-схема алгоритма COA.
3. Рассмотрение кода
Приступим к рассмотрению кода алгоритма. Решением задачи является кукушка, она же — яйцо. Это простая структура, которая включает в себя координаты в пространстве поиска и значение фитнес функции (качество яйца).
//—————————————————————————————————————————————————————————————————————————————— struct S_Cuckoo { double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Гнездо опишем в виде структуры. Здесь так же, как в структуре яйца, присутствуют координаты в пространстве и значение фитнесс функции. "Снести яйцо в гнездо", по сути, означает скопировать структуру яйца в структуру гнезда. При использовании вероятностного параметра pa выброс яйца из гнезда происходит при выпадении случайного числа от 0.0 до pa в диапазоне [0.0;1.0] и задание значения e равным -DBL_MAX.
//—————————————————————————————————————————————————————————————————————————————— struct S_Nest { void Init (int coordinates) { ArrayResize (c, coordinates); e = -DBL_MAX; } double c []; //coordinates (egg parameters) double e; //egg quality }; //——————————————————————————————————————————————————————————————————————————————
Класс алгоритма. Здесь объявлены публичные методы инициализации и основные два метода вызова в программе пользователя, диапазоны значений аргументов задачи оптимизации и дополнительные приватные методы, выполняющие сервисные функции.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_COA { //============================================================================ public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: S_Cuckoo cuckoos []; //all the cuckoos public: double cB []; //best coordinates (egg parameters) public: double eB; //best eggs quality public: void Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP); //step control value public: void CuckooFlight (); public: void LayEggs (); //============================================================================ private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double Min, double Max); private: double Scale (double In, double InMIN, double InMAX, double OutMIN, double OutMAX, bool Revers); private: S_Nest nests []; //nests private: int cuckoosNumber; //number of cuckoos private: int nestsNumber; //number of cuckoo nests private: double koef_pa; //probability of detection of cuckoo eggs private: double koef_alpha; //step control value private: double v []; private: int coordinates; //coordinates number private: bool clutchEggs; //clutch of eggs }; //——————————————————————————————————————————————————————————————————————————————
Публичный метод Init (). Здесь происходит сброс значений переменных и распределение памяти под массивы.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::Init (const int coordinatesP, //number of opt. parameters const int cuckoosP, //number of cuckoos const int nestsP, //number of cuckoo nests const double koef_paP, //probability of detection of cuckoo eggs const double koef_alphaP) //step control value { MathSrand (GetTickCount ()); clutchEggs = false; eB = -DBL_MAX; coordinates = coordinatesP; cuckoosNumber = cuckoosP; nestsNumber = nestsP; koef_pa = koef_paP; koef_alpha = koef_alphaP; ArrayResize (nests, nestsNumber); for (int i = 0; i < nestsNumber; i++) { nests [i].Init (coordinates); } ArrayResize (rangeMax, coordinates); ArrayResize (rangeMin, coordinates); ArrayResize (rangeStep, coordinates); ArrayResize (cB, coordinates); ArrayResize (v, coordinates); ArrayResize (cuckoos, cuckoosNumber); for (int i = 0; i < cuckoosNumber; i++) { ArrayResize (cuckoos [i].c, coordinates); } } //——————————————————————————————————————————————————————————————————————————————
Первый публичный метод, вызываемый на каждой итерации "полет кукушки". Если флаг clutchEggs сброшен, тогда отправляем кукушек в случайном направлении, генерируя случайные числа в диапазоне соответствующей координаты. Если же флаг взведен, тогда осуществляется собственно полет кукушки по распределению полета Леви в диапазоне вектора v. Вектор v предварительно рассчитывается в Init () для каждой координаты отдельно поскольку у каждой координаты диапазон значений может быть разный.
Выражение cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); означает, что к текущей координате кукушки прибавляем смещение r1 * v [c] * pow (r2, -2.0), где r1 - это число -1 либо 1, определяющее направление смещения от исходного положения, v - вектор перемещения, r2 - случайное число в диапазоне от 0.0 до 20.0, возведенное в степень -2.0. Возведение случайного числа в степень - это и есть функция полета Леви, график которой можно увидеть на рисунке 2.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::CuckooFlight () { //---------------------------------------------------------------------------- if (!clutchEggs) { for (int i = 0; i < coordinates; i++) v [i] = (rangeMax [i] - rangeMin [i]) * koef_alpha; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { cuckoos [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } clutchEggs = true; } else { double r1 = 0.0; double r2 = 0.0; for (int i = 0; i < cuckoosNumber; i++) { for (int c = 0; c < coordinates; c++) { r1 = RNDfromCI (0.0, 1.0); r1 = r1 > 0.5 ? 1.0 : -1.0; r2 = RNDfromCI (1.0, 20.0); cuckoos [i].c [c] = cuckoos [i].c [c] + r1 * v [c] * pow (r2, -2.0); cuckoos [i].c [c] = SeInDiSp (cuckoos [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } } //——————————————————————————————————————————————————————————————————————————————
Второй публичный метод, вызываемый на каждой итерации — "кладка яиц". В этом методе алгоритмически воспроизведена симуляция кладки яйца кукушки в гнездо. Это происходит путем выбора случайного гнезда из всех существующих. После этого идет сравнение качества яйца кукушки и того, которое уже лежит в гнезде. Если яйцо кукушки лучше, то происходит замена. Интересной особенностью алгоритма в этом методе является то, что вероятность того погибнет ли яйцо осуществляется после кладки, даже если яйцо кукушки было более приспособленное. Это означает, что существует вероятность koef_pa, что погибнет любое яйцо, какое бы там ни лежало, так же, как и в природе. Если яйцо погибло или было выкинуто из гнезда, что, по сути, одно и тоже, то гнездо будет свободно для новой кладки яйца любой приспособленности, даже более низкой, это алгоритмически означает исследование в новом месте.
Так кодом в несколько строк можно описать один из приемов природной эволюции, таких как гнездовой паразитизм. Многие авторы в своих публикациях рекомендуют инициализировать гнездо после удаления яйца новыми случайными значениями, что означает старт поиска с самого начала. В подавляющем большинстве случаев это не даст желаемого результата в плане повышения исследовательской способности алгоритма, мои собственные исследования показали, что целесообразнее просто оставить гнездо пустым и в него отложит яйцо одна из кукушек независимо от качества яйца, т.е. оно может быть любым. Это лучше, чем просто случайные значения, а вариабельность в исследовании обеспечивают случайные прыжки в случайных направлениях от текущих координат. В итоге количество итераций потребуется меньше в поиске наилучшего решения, тем самым увеличивая скорость сходимости алгоритма в целом.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_COA::LayEggs () { int ind = 0; //^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^ for (int i = 0; i < cuckoosNumber; i++) { ind = (int)round (RNDfromCI (0.0, nestsNumber - 1)); if (cuckoos [i].e > nests [ind].e) { nests [ind].e = cuckoos [i].e; ArrayCopy (nests [ind].c, cuckoos [i].c, 0, 0, WHOLE_ARRAY); if (cuckoos [i].e > eB) { eB = cuckoos [i].e; ArrayCopy (cB, cuckoos [i].c, 0, 0, WHOLE_ARRAY); } } else { ArrayCopy (cuckoos [i].c, nests [ind].c, 0, 0, WHOLE_ARRAY); } } //vvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvvv for (int n = 0; n < nestsNumber; n++) { if (RNDfromCI (0.0, 1.0) < koef_pa) { nests [ind].e = -DBL_MAX; } } } //——————————————————————————————————————————————————————————————————————————————
4. Результаты тестов
Распечатка результов тестирования:
2022.11.30 11:31:54.490 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.918379100238852
2022.11.30 11:31:54.507 Test_AO_COA_fast (EURUSD,M1) Score: 1.00000
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) 20 Skin's; Func runs 10000 result: 4.257477577760983
2022.11.30 11:31:54.854 Test_AO_COA_fast (EURUSD,M1) Score: 0.84220
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.3521208312080903
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) Score: 0.14849
2022.11.30 11:32:02.346 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.7600394018343262
2022.11.30 11:32:02.368 Test_AO_COA_fast (EURUSD,M1) Score: 0.99557
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.4968964923017033
2022.11.30 11:32:02.775 Test_AO_COA_fast (EURUSD,M1) Score: 0.28107
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.07638950254648778
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) Score: 0.04321
2022.11.30 11:32:13.125 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.11.30 11:32:13.148 Test_AO_COA_fast (EURUSD,M1) Score: 1.00000
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 2.69
2022.11.30 11:32:13.584 Test_AO_COA_fast (EURUSD,M1) Score: 0.22417
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.40800000000000003
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) Score: 0.03400
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) =============================
2022.11.30 11:32:24.379 Test_AO_COA_fast (EURUSD,M1) All score for C_AO_COA: 0.507633670637353
Алгоритм поиск кукушки с полетом Леви показал впечатляющие результаты, в большинстве тестов он опередил другие алгоритмы оптимизации. Так 100% сходимость алгоритм показал на гладкой функции Skin с двумя переменными и дискретной функцией Megacity с двумя переменными. Что еще более удивительно показал превосходную масштабируемость на дискретной функции. В остальных тестах он лишь немного уступает муравьиному алгоритму. На данный момент из рассмотренных алгоритмов оптимизации мы имеем несомненного лидера в рейтинговой таблице.
Хотелось бы уточнить, что все алгоритмы имеют настроечные параметры, которые в той или иной степени влияют на итоговые результаты, поэтому вполне возможно, что существуют еще более оптимальные параметры у какого-то из этих алгоритмов и рейтинговая таблица может выглядеть иначе. Я лишь показал результаты тестов с теми параметрами, которые смог найти для обеспечения наилучшего результата. Если кто-то из читателей подберет более оптимальные параметры и получит лучшие результаты, то рейтинговую таблицу я могу поправить исходя из этих результатов. Есть предположение, что с текущим лидером может успешно конкурировать муравьиный алгоритм, так как по некоторым показателям он опережает алгоритм поиска кукушки, и минимально от него отстает по итоговым показателям. А на функции Skin c 1000 переменных по-прежнему сильнейший — GWO. В любом случае тот, кто будет использовать алгоритмы в своих проектах при решении своих задач оптимизации, может ориентироваться по таблице и выбирать алгоритм под свою специфику.
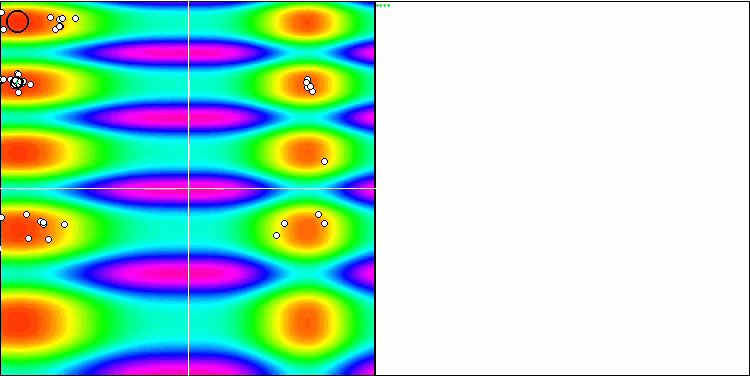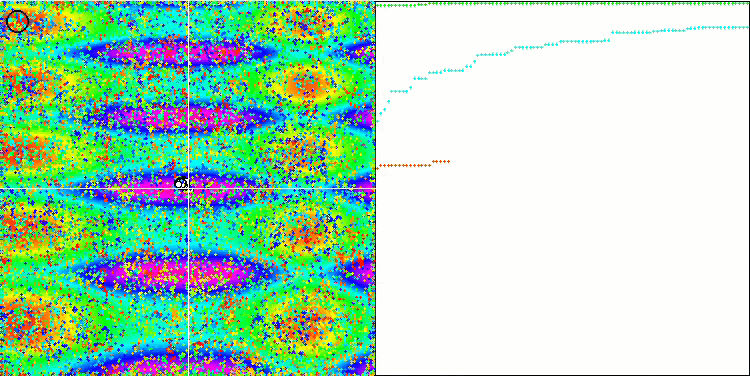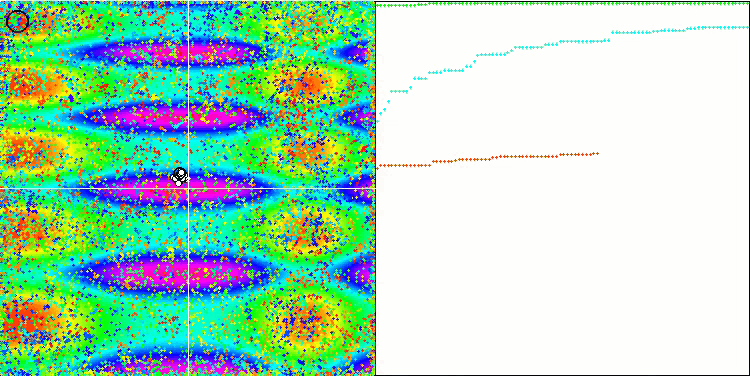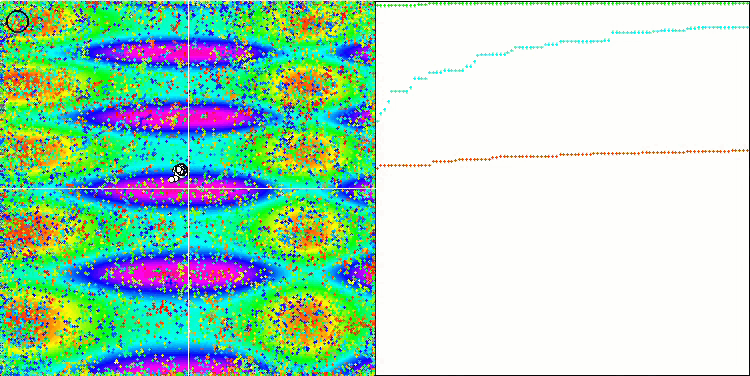
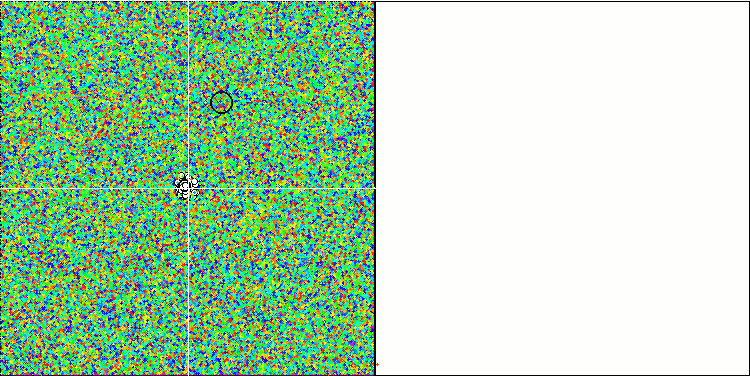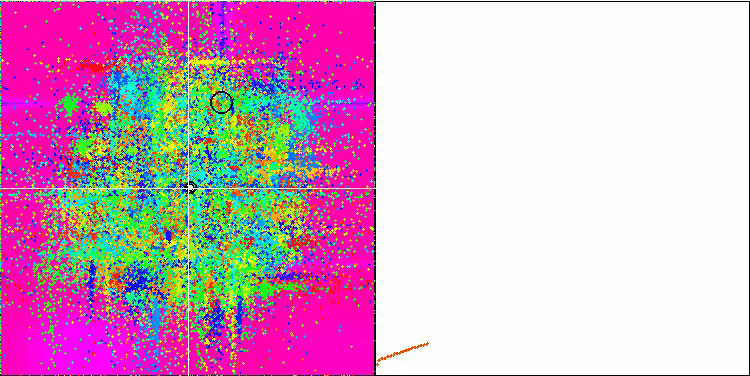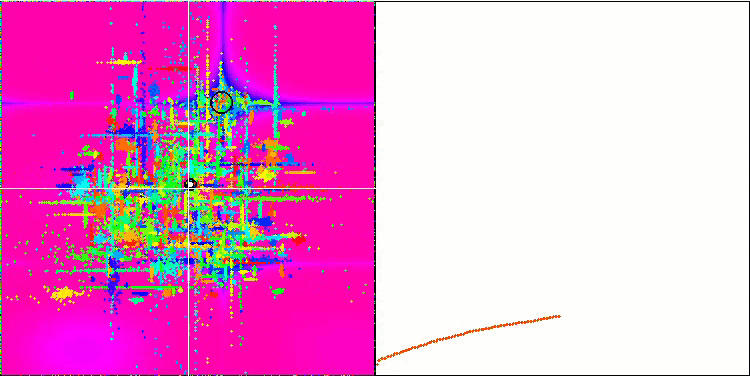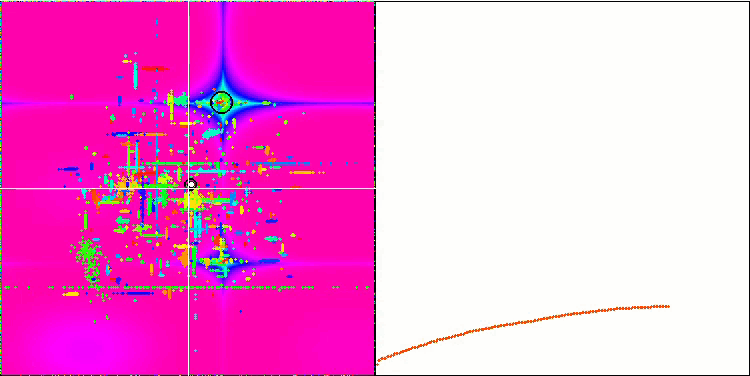
COA на тестовой функции Skin.
COA на тестовой функции Forest.
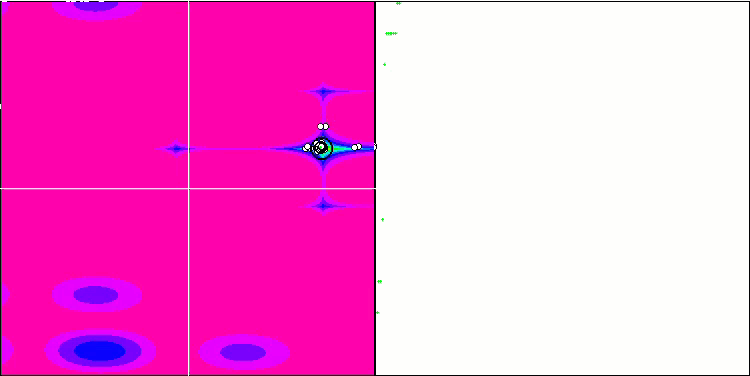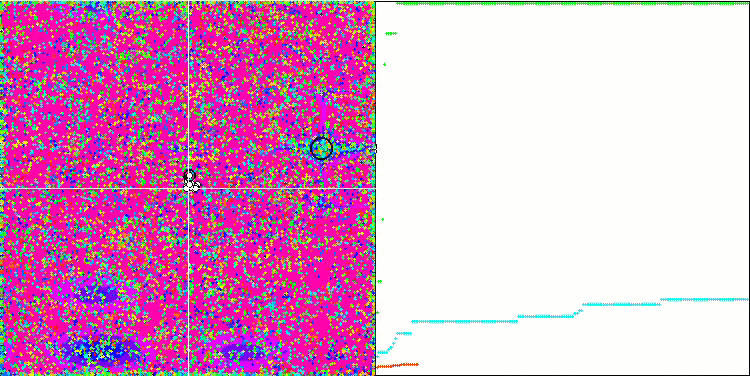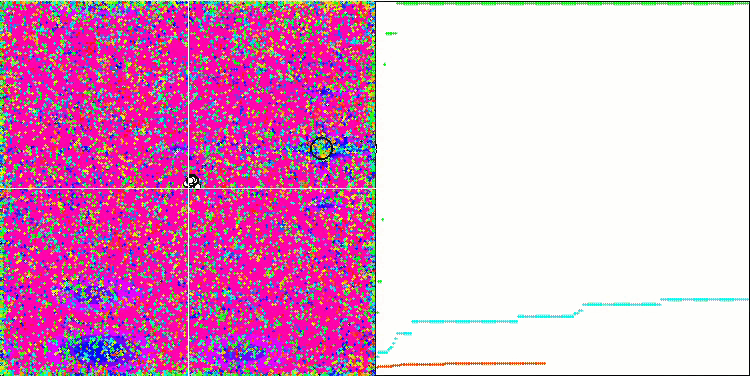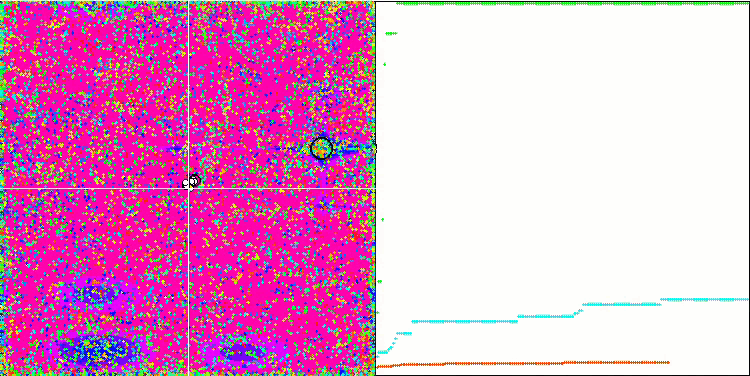
COA на тестовой функции Megacity.
На визуализации тестового стенда поведение алгоритма отличается от рассмотренных ранее, однако замечены некоторые особенности, характерные для алгоритмов, которые разбивают задачу на исследуемые области, такие как алгоритм пчелиной колонии. Это характеризует способность алгоритма не сосредотачиваться на каком-то одном экстремуме, а исследовать несколько потенциально перспективных областей, обеспечивая алгоритму устойчивость против застревания в локальных экстремумах. В связи с этим возникла мысль, что вероятно возможно улучшить алгоритм за счет сортировки гнезд и выбора кукушкой среди них пропорционально их качеству. Это означало бы то же самое, что кукушка выбирает гнезда, вместо того чтобы положить яйцо в случайно выбранное гнездо, как в каноническом варианте алгоритма. Однако это не улучшило результаты и показывает практически смысл именно случайного выбора гнезд. Возможно, это перекликается с тем, что происходит в природе, заменить яйцо у более умных хозяев сложнее, чем рандомно и статистически оправдано.
Другой особенностью алгоритма является поведение подобно случайному блужданию на функциях со многими переменными. Визуально это выглядит как белый шум или экран старого телевизора, и лишь к концу итераций заметно некоторое сосредоточение координат в местах локальных экстремумов. Хотелось бы обеспечить более четкую "кристаллизацию" параметров так, как это происходит у муравьиного алгоритма. Таким образом мы подошли к общей проблеме всех алгоритмов оптимизации, которая не имеет решения в общем виде. Многие авторы классических и достаточно новых алгоритмов пытались ее решить.
Суть проблемы заключается в следующем: заведомо неизвестно какой из оптимизируемых параметров исследуемой функции имеет приоритет или силу, неизвестно насколько и как влияет каждый из параметров на результат. Например: есть несколько параметров и алгоритм уже нашел нужный, но какой из них именно — неизвестно. Алгоритм будет продолжать пытаться изменять их все, хотя достаточно было изменить только некоторые, чтобы достичь глобального экстремума. Проблема усугубляется, когда речь заходит о функции со многими десятками и тысячами переменными, чем больше переменных, тем проблема проявляется острее. Визуально это и выглядит белым шумом на экране.
Мной предпринята попытка решить эту проблему, может быть не кардинально, по крайней мере частично. Если априори неизвестно какой из параметров исследуемой функции нужно изменить, а какой оставить прежним, можно попробовать решить это вероятностным способом. То есть мы делаем предположение, что нужно изменить только часть из всех параметров, а не все одновременно. Характерным образом ведет себя алгоритм PSO, который с увеличением количества параметров (аргументов) оптимизируемой функции ведет себя как облако, не имеющее способности сконцентрироваться. Для этого я ввел новый параметр для алгоритма, который задает вероятность того, что координата будет изменена, в противном случае координата будет оставлена прежней.
В итоге... Получилось!!! Результаты тестирования улучшились. На функциях со многими переменными проявилась та самая "кристаллизация", которой мы хотели добиться.
Распечатка работы тестового стенда:
2022.12.03 16:01:26.256 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) 1 Skin's; Func runs 10000 result: 4.918367945334852
2022.12.03 16:01:27.511 Test_AO_COAm (EURUSD,M1) Score: 1.00000
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) 20 Skin's; Func runs 10000 result: 4.328327964103814
2022.12.03 16:01:30.291 Test_AO_COAm (EURUSD,M1) Score: 0.85911
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) 500 Skin's; Func runs 10000 result: 1.3297901702583084
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) Score: 0.14316
2022.12.03 16:01:59.306 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) 1 Forest's; Func runs 10000 result: 1.755200932219688
2022.12.03 16:02:00.511 Test_AO_COAm (EURUSD,M1) Score: 0.99283
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) 20 Forest's; Func runs 10000 result: 0.5089243656052672
2022.12.03 16:02:03.566 Test_AO_COAm (EURUSD,M1) Score: 0.28787
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) 500 Forest's; Func runs 10000 result: 0.08044934398920801
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) Score: 0.04551
2022.12.03 16:02:35.468 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) 1 Megacity's; Func runs 10000 result: 12.0
2022.12.03 16:02:36.628 Test_AO_COAm (EURUSD,M1) Score: 1.00000
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) 20 Megacity's; Func runs 10000 result: 2.9899999999999998
2022.12.03 16:02:39.628 Test_AO_COAm (EURUSD,M1) Score: 0.24917
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) 500 Megacity's; Func runs 10000 result: 0.4244
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) Score: 0.03537
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) =============================
2022.12.03 16:03:11.892 Test_AO_COAm (EURUSD,M1) All score for C_AO_COAm: 0.5125572342985216
Прекрасно видно на визуализации "кристаллизация", экран, похожий вначале на белый шум, расчищается, координаты начинают концентрироваться, центры концентраций подвижны:

COAm на тестовой функции Megacity. Более выражен эффект "кристаллизации".
Обеспечена с одной стороны: вариабельность, т.е. способность динамично искать новые области, а с другой стороны: уточнять координаты уже достигнутых экстремумов. И для сравнения анимация работы алгоритма муравьиной колонии с ярко выраженной "кристаллизацией":
ACOm на тестовой функции Forest.
4. Результаты тестов
| AO | Description | Skin | Forest | Megacity (discrete) | Final result | ||||||
| 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | 2 params (1 F) | 40 params (20 F) | 1000 params (500 F) | |||
| cuckoo optimization algorithm | 1,00000 | 0,85911 | 0,14316 | 0,99283 | 0,28787 | 0,04551 | 1,00000 | 0,24917 | 0,03537 | 0,51255778 | |
| ant colony optimization | 0,98229 | 0,79108 | 0,12602 | 1,00000 | 0,62077 | 0,11521 | 0,38333 | 0,44000 | 0,02377 | 0,49805222 | |
| artificial bee colony M | 1,00000 | 0,63922 | 0,08076 | 0,99908 | 0,20112 | 0,03785 | 1,00000 | 0,16333 | 0,02823 | 0,46106556 | |
| artificial bee colony | 0,99339 | 0,73381 | 0,11118 | 0,99934 | 0,21437 | 0,04215 | 0,85000 | 0,16833 | 0,03130 | 0,46043000 | |
| grey wolf optimizer | 0,99900 | 0,48033 | 0,18924 | 0,83844 | 0,08755 | 0,02555 | 1,00000 | 0,10000 | 0,02187 | 0,41577556 | |
| particle swarm optimisation | 0,99627 | 0,38080 | 0,05089 | 0,93772 | 0,14540 | 0,04856 | 1,00000 | 0,09333 | 0,02233 | 0,40836667 | |
| random | 0,99932 | 0,44276 | 0,06827 | 0,83126 | 0,11524 | 0,03048 | 0,83333 | 0,09000 | 0,02403 | 0,38163222 | |
Одним из преимуществ алгоритма поиска с кукушкой является то, что его глобальный поиск использует полеты или процесс Леви, а не стандартные случайные блуждания. Поскольку полеты Леви имеют бесконечное среднее значение и дисперсию, COA может исследовать пространство поиска более эффективно, чем алгоритмы стандартного гауссовского процесса. Полет Леви: процесс, основанный на случайном блуждании, который характеризуется серией мгновенных скачков, выбранных из функции плотности вероятности, которая имеет хвост степенного закона.
В данный момент алгоритм является лидером таблицы, значительно опередив другие алгоритмы в отдельных тестах и ненамного отстаёт в других "дисциплинах". Достигнуты великолепные результаты на дискретной функции Megacity с 1000 аргументов, что делает поиск с кукушкой прекрасным инструментом для задач трейдеров (в большинстве случаев дискретные задачи). Отличные, но не лучшие, результаты по функции Skin c 1000 аргументов дают основания утверждать, что алгоритм подходит для обучения нейронных сетей в частности и машинного обучения в целом.
Плюсы:
1. Быстрый.
2. Универсальность. Может быть использован в самых различных задачах оптимизации.
3. Способность не сосредотачиваться только на локальных экстремумах.
4. Высокая сходимость как для гладких так и дискретных функций.
5. Масштабируем.
Минусы:
1. Много настроечных параметров.
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Разработка торговой системы на основе индикатора Alligator
Разработка торговой системы на основе индикатора Alligator
 Рецепты MQL5 — Сервисы
Рецепты MQL5 — Сервисы
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования
Эти статьи о метаэвристических методах оптимизации просто потрясающие! Вы делаете огромную работу, Андрей, это поразительно, как много опыта вы можете поделиться с нами, спасибо!
@METAQUOTES, пожалуйста, рассмотрите возможность внедрения этих целей метаэвристической оптимизации в оптимизатор! Это было бы здорово для программного обеспечения.
Что-то простое, что пользователь может установить внутри OnTester() как:
Привет из Бразилии