Redes neurais em trading: Dupla clusterização de séries temporais (Conclusão)

MetaTrader 5 — Sistemas de negociação | 7 outubro 2025, 14:43

165

Dmitriy Gizlyk

Introdução

Seguimos o desenvolvimento das abordagens apresentadas pelos autores do framework de dupla clusterização de séries temporais multivariadas DUET, que se mostra uma ferramenta poderosa para a previsão de mercados financeiros. DUET combina clusterização temporal e de canais, o que permite adaptação a padrões complexos e dinâmicos da movimentação do mercado, eliminando as deficiências dos métodos tradicionais, propensos a overfitting e com flexibilidade limitada.

DUET inclui vários módulos principais, cada um desempenhando um papel crucial. A primeira etapa do processamento dos dados é a normalização e a eliminação de valores atípicos, o que aumenta a robustez do modelo.

Em seguida vem a clusterização temporal, que divide a série temporal em grupos com dinâmica semelhante. Isso permite levar em conta deslocamentos de fase nos processos de mercado, sendo especialmente importante para a análise de ativos com alta volatilidade.

A clusterização de canais é utilizada para identificar as variáveis mais significativas entre os diversos fatores de mercado. Os dados financeiros contêm uma grande quantidade de ruído e informação redundante, o que dificulta a construção de previsões precisas. O DUET analisa as correlações entre os parâmetros e elimina os componentes irrelevantes, concentrando os recursos computacionais nas características mais importantes. A análise de frequência dos sinais e os mecanismos de extração de características latentes tornam o modelo menos sensível às flutuações aleatórias do mercado.

O módulo de unificação de dados sincroniza as informações obtidas pelos módulos de clusterização temporal e de canais, formando uma representação unificada do estado analisado do ambiente. Esse etapa se baseia em um mecanismo de atenção mascarada, que permite ao modelo focar nas características mais relevantes, minimizando a influência de dados não representativos. Graças a isso, DUET demonstra alta resistência a mudanças dinâmicas e melhora a qualidade das previsões de longo prazo.

O módulo final de previsão utiliza as características agregadas para calcular os valores futuros das séries temporais. A base dessa etapa são métodos avançados de redes neurais, capazes de identificar dependências não lineares entre os indicadores de mercado. A flexibilidade da arquitetura DUET permite adaptação dinâmica a diferentes condições, eliminando a necessidade de reconfiguração manual dos parâmetros do modelo.

A visualização autoral do framework DUET é apresentada abaixo.

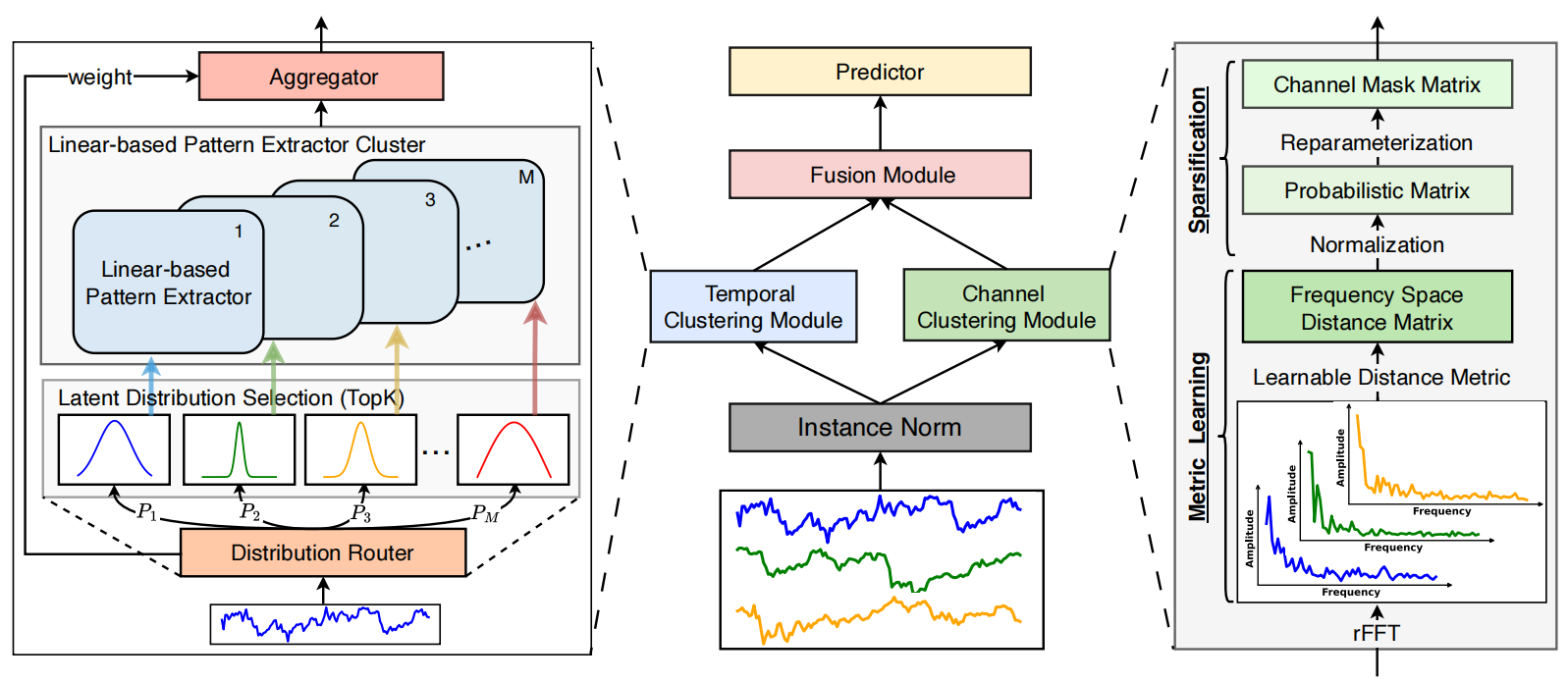
A visualização autoral do framework DUET

Na parte prática do artigo anterior foi mostrado um exemplo de implementação do módulo de clusterização temporal. Dando continuidade ao trabalho iniciado, passamos agora à construção do módulo de clusterização de canais.

Channel Clustering Module

O módulo de clusterização de canais resolve o problema do tratamento adequado das interconexões entre canais na previsão de séries temporais multivariadas. Aqui, os autores do framework DUET utilizam aprendizado métrico, voltado para a clusterização dos canais no espaço de frequências.

O aspecto central do funcionamento do CCM é a representação dos dados no domínio da frequência. Para isso, as séries temporais são decompostas em componentes de frequência utilizando a Transformada Rápida de Fourier (FFT). Como resultado, os sinais são analisados na região espectral, onde as correlações entre canais se tornam mais evidentes. Muitas dependências ocultas, imperceptíveis na análise tradicional, se manifestam apenas após a conversão para o domínio de frequência, o que torna esse método especialmente valioso para séries temporais complexas.

A avaliação das relações entre os canais é realizada com base em uma métrica de distância treinável. Como medida principal, é usada a representação em amplitude do espectro de frequência dos sinais, e a distância é calculada com base em uma métrica de Mahalanobis modificada proposta pelos autores do framework. Esse método leva em conta não apenas as distâncias par a par entre os canais, mas também suas correlações no espaço espectral.

Após o cálculo das distâncias entre os canais, é formada uma matriz de relações, na qual os coeficientes são normalizados no intervalo [0,1]. Essa normalização permite destacar as conexões mais significativas, eliminando flutuações aleatórias e vínculos pouco relevantes.

Para a filtragem final das informações, é criada uma matriz binária de mascaramento dos canais. Esse processo se baseia em uma amostragem probabilística, na qual a cada canal é atribuída uma probabilidade de utilidade na previsão. Esse mecanismo permite considerar a ambiguidade dos dados e evitar limiares rígidos. Assim, o modelo exclui automaticamente os canais irrelevantes, o que melhora consideravelmente a interpretabilidade dos resultados e reduz a redundância das informações.

No contexto deste trabalho, implementamos uma versão levemente simplificada do módulo de clusterização de canais. O algoritmo da Transformada Discreta de Fourier foi desenvolvido anteriormente, no âmbito da implementação do framework FITS e já está disponível em nossa biblioteca. Em vez da métrica de Mahalanobis, aplicamos um método mais simples, baseado nas distâncias vetoriais entre as amplitudes das componentes de frequência. Isso preserva as vantagens da análise no domínio da frequência, ao mesmo tempo em que reduz a complexidade computacional e simplifica o algoritmo.

Após converter as séries temporais para o domínio da frequência, são calculadas as normas dos espectros de amplitude de cada canal. Em seguida, é determinada a distância entre cada par deles, formando uma matriz de interconexões entre canais. Com o objetivo de eliminar dependências fracas da análise subsequente, aplica-se um processo de normalização que reduz o ruído e ajusta a escala das distâncias. Dessa forma, são preservadas apenas as correlações realmente significativas entre os canais. Com base nessa matriz, é construída uma representação probabilística das conexões. Cada canal recebe um peso de relevância que reflete sua influência sobre as demais séries.

O algoritmo descrito é implementado no kernel MaskByDistance no lado do programa OpenCL. Nos parâmetros do kernel são passados ponteiros para 3 buffers de dados. Os dois primeiros contêm os dados de entrada, representados pelas partes real e imaginária dos sinais analisados. O terceiro buffer é destinado ao armazenamento dos resultados do processamento. Neste caso será a matriz de mascaramento dos canais.

__kernel void MaskByDistance(__global const float *buf_real,
                             __global const float *buf_imag,
                             __global float *mask,
                             const int dimension
                            )
  {
   const size_t main = get_global_id(0);
   const size_t slave = get_local_id(1);
   const int total = (int)get_local_size(1);

No corpo do kernel, primeiramente identificamos o fluxo atual dentro do espaço bidimensional de tarefas. A primeira dimensão indica o canal que está sendo analisado, e a segunda representa o canal com o qual ele será comparado. Assim, são formados grupos de trabalho compostos pelos fluxos da segunda dimensão.

Em seguida, é criado um array de dados na memória local, utilizado para a troca de informações entre os fluxos pertencentes a um mesmo grupo de trabalho.

__local float Temp[LOCAL_ARRAY_SIZE];
int ls = min((int)total, (int)LOCAL_ARRAY_SIZE);

Depois, são definidos os deslocamentos dentro dos buffers globais de dados.

const int shift_main = main * dimension;
const int shift_slave = slave * dimension;
const int shift_mask = main * total + slave;

Concluída essa etapa de preparação, passamos diretamente aos cálculos e iniciamos o loop de determinação da distância entre dois vetores de amplitudes de frequência.

//--- calc distance
   float dist = 0;
   if(main != slave)
     {
#pragma unroll
      for(int d = 0; d < dimension; d++)
         dist += pow(ComplexAbs((float2)(buf_real[shift_main + d], buf_imag[shift_main + d])) -
                     ComplexAbs((float2)(buf_real[shift_slave + d], buf_imag[shift_slave + d])), 2.0f);
      dist = sqrt(dist);
     }

Vale observar que, na nossa matriz de fluxos, existem elementos posicionados na diagonal. Você provavelmente já percebeu que, nesses casos, o algoritmo calcula a distância entre duas cópias do mesmo vetor. Evidentemente, essa distância é igual a "0". Portanto, nessas situações, o loop de cálculo da distância não é executado, e o valor zero é simplesmente gravado na variável correspondente.

Em seguida, precisamos normalizar os valores obtidos. Para isso, é implementado um algoritmo de busca do valor máximo de distância dentro do grupo de trabalho. Inicialmente, é executado um loop que coleta os elementos máximos de subgrupos de fluxos e os armazena nos elementos do array local.

//--- Look Max
#pragma unroll
   for(int i = 0; i < total; i += ls)
     {
      if(i <= slave && (i + ls) > slave)
         Temp[slave % ls] = fmax((i == 0 ? 0 : Temp[slave % ls]), IsNaNOrInf(dist, 0));
      barrier(CLK_LOCAL_MEM_FENCE);
     }

Depois, o valor máximo entre os elementos do array local é encontrado.

int count = ls;
do
  {
   count = (count + 1) / 2;
   if(slave < count && (slave + count) < ls)
     {
      if(Temp[slave] < Temp[slave + count])
         Temp[slave] = Temp[slave + count];
      Temp[slave + count] = 0;
     }
   barrier(CLK_LOCAL_MEM_FENCE);
  }
while(count > 1);

Finalmente, a normalização das distâncias entre os vetores de amplitudes de frequência é realizada dentro do grupo de trabalho, dividindo cada valor pelo máximo identificado.

//--- Normalize
   if(Temp[0] > 0)
      dist /= Temp[0];

Acredito que agora esteja claro que todas as distâncias normalizadas estão no intervalo [0, 1]. Nesse caso, o valor "1" corresponde ao canal mais distante. No entanto, o nosso objetivo é justamente minimizar a influência desse canal. Por isso, no buffer de resultados, armazenamos o valor inverso da distância normalizada.

//--- result
   mask[shift_mask] = 1 - IsNaNOrInf(dist, 1);
  }

Assim concluímos o funcionamento do kernel.

Vale destacar uma característica importante da nossa implementação. No algoritmo apresentado, não existem parâmetros treináveis, pois a distância entre os vetores de amplitudes dos espectros de frequência é uma grandeza fixa, independente de outros fatores. Isso nos permite eliminar o processo de propagação reversa do erro, reduzindo os custos de otimização.

O próximo estágio do nosso trabalho consiste em configurar o funcional do módulo de clusterização de canais no lado do programa principal. Aqui, criamos uma nova classe chamada CNeuronChanelMask, cuja estrutura é apresentada a seguir.

class CNeuronChanelMask :  public CNeuronBaseOCL
  {
   //---
protected:
   uint              iUnits;
   uint              iFFTdimension;
   CBufferFloat      cbFFTReal;
   CBufferFloat      cbFFTImag;
   //---
   virtual bool      FFT(CBufferFloat *inp_re, CBufferFloat *inp_im,
                         CBufferFloat *out_re, CBufferFloat *out_im,
                         bool reverse = false);
   virtual bool      Mask(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) { return true; }
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) { return true; }

public:
                     CNeuronChanelMask(void) {};
                    ~CNeuronChanelMask(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint units_count,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronChanelMask; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
  };

Na estrutura apresentada, entre os poucos objetos internos, observamos apenas 2 buffers responsáveis por armazenar as partes real e imaginária das componentes de frequência do sinal analisado. Teremos um contato mais detalhado com o uso desses buffers durante a construção dos algoritmos dos métodos virtuais dessa nova classe.

Esses objetos são declarados de forma estática, a o que significa que podemos deixar o construtor e o destrutor da classe vazios. A inicialização dos objetos declarados e herdados é realizada no método Init.

bool CNeuronChanelMask::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                             uint window, uint units_count,
                             ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(window <= 0)
      return false;
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units_count * units_count, optimization_type, batch))
      return false;

Nos parâmetros desse método, como de costume, recebemos um conjunto de constantes que nos permitem interpretar de maneira inequívoca a arquitetura do objeto que está sendo criado:

window — o comprimento da sequência analisada;
units_count — o número de canais.

É importante observar que, na saída do objeto, esperamos obter uma matriz quadrada de mascaramento dos canais. As dimensões da matriz resultante de mascaramento correspondem ao número de canais e não dependem do comprimento da sequência analisada. No entanto, esse parâmetro ainda é necessário para o processamento adequado dos dados de entrada. Por isso, primeiro verificamos a validade do parâmetro recebido e, em seguida, chamamos o método homônimo da classe pai, onde já estão implementados os algoritmos de inicialização das interfaces herdadas.

Após a execução bem-sucedida das operações do método da classe pai, armazenamos as constantes obtidas.

//--- Save constants
   iUnits = units_count;
   activation = None;

Aqui vale lembrar que o algoritmo de Transformada Rápida de Fourier, que implementamos anteriormente, é aplicável apenas a sequências cujo tamanho seja uma potência de 2. De modo geral, isso não representa um problema, pois sempre podemos aumentar o tamanho da sequência adicionando a quantidade necessária de "0" ao final do vetor. No entanto, precisamos determinar o próximo valor superior mais próximo.

//--- Calculate FFT dimension
   int power = int(MathLog(window) / M_LN2);
   if(MathPow(2, power) != window)
      power++;
   iFFTdimension = uint(MathPow(2, power));

E só então inicializamos os buffers de armazenamento temporário das partes real e imaginária das componentes de frequência, com tamanho suficiente para comportar os dados processados.

   if(!cbFFTReal.BufferInit(iFFTdimension * iUnits, 0) ||
      !cbFFTReal.BufferCreate(OpenCL))
      return false;
   if(!cbFFTImag.BufferInit(iFFTdimension * iUnits, 0) ||
      !cbFFTImag.BufferCreate(OpenCL))
      return false;
//---
   return true;
  }

Com isso, concluímos o trabalho com os métodos de inicialização e passamos à construção do algoritmo de propagação para frente dentro do método CNeuronChanelMask::feedForward. E devo dizer que aqui tudo é bastante simples e direto.

bool CNeuronChanelMask::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!NeuronOCL)
      return false;
   if(!FFT(NeuronOCL.getOutput(), NULL, GetPointer(cbFFTReal), GetPointer(cbFFTImag), false))
      return false;
//---
   return Mask();
  }

Nos parâmetros do método, recebemos um ponteiro para o objeto de dados de entrada, cuja validade verificamos imediatamente. Em seguida, dividimos os dados originais em componentes de frequência e chamamos o método encapsulador do kernel apresentado anteriormente. O resultado lógico da execução dessas operações é então retornado ao programa chamador, encerrando o funcionamento do método.

Os métodos responsáveis pela organização do enfileiramento dos kernels para execução seguem o mesmo algoritmo que você já conhece, portanto, não nos deteremos em descrevê-los novamente aqui.

Como já foi mencionado anteriormente, neste caso não utilizamos o processo de propagação reversa. Os métodos correspondentes são sobrescritos por stubs (funções vazias) que retornam constantemente o valor true. Essa abordagem nos permite integrar o novo objeto à estrutura existente dos nossos modelos sem quaisquer conflitos ou restrições.

Com isso, encerramos o desenvolvimento dos algoritmos que compõem o módulo de clusterização de canais. O código completo desta classe e de todos os seus métodos pode ser consultado no anexo deste artigo.

Bloco DUET

Neste estágio, já construímos os módulos de clusterização temporal e de clusterização de canais. Esses dois módulos funcionam em paralelo, analisando séries temporais multivariadas sob duas representações distintas: temporal e espectral. Todos os resultados obtidos são combinados no módulo Fusion, que integra as informações sobre as interdependências entre os canais por meio de um mecanismo de atenção mascarada. Isso permite alinhar as previsões individuais de cada canal levando em conta as correlações identificadas. Fusion ajusta a influência de cada canal de acordo com o peso de sua dependência intercanal. Como resultado, a previsão final torna-se mais estável, e o modelo, menos suscetível a overfitting e a ruídos aleatórios.

Na prática, utilizamos um mecanismo de Self-Attention, no qual os coeficientes de dependência, obtidos com base nos resultados do módulo de clusterização temporal, são multiplicados pela máscara gerada pelo módulo de clusterização de canais. E somente após essa etapa os pesos são normalizados por meio da função SoftMax.

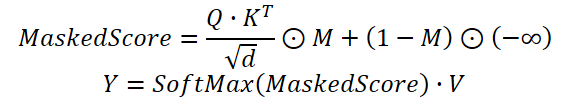
O algoritmo proposto é implementado dentro do objeto CNeuronDUET, que unifica em um único funcional os três módulos mencionados. A estrutura dessa nova classe é apresentada a seguir.

class CNeuronDUET :  public CNeuronTransposeOCL
  {
protected:
   uint                       iWindowKey;
   uint                       iHeads;
   //---
   CNeuronTransposeOCL        cTranspose;
   CNeuronMoE                 cExperts;
   CNeuronConvOCL             cQKV;
   CNeuronBaseOCL             cQ;
   CNeuronBaseOCL             cKV;
   CNeuronChanelMask          cMask;
   CBufferFloat               cbScores;
   CNeuronBaseOCL             cMHAttentionOut;
   CNeuronConvOCL             cPooling;
   CNeuronBaseOCL             cResidual;
   CNeuronMHFeedForward       cFeedForward;
   //---
   virtual bool      AttentionOut(void);
   virtual bool      AttentionInsideGradients(void);
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *prevLayer);

public:
                     CNeuronDUET(void) {};
                    ~CNeuronDUET(void) {};
   //---
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint window_key, uint units_count, uint heads,
                          uint units_out, uint experts, uint top_k,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override   const   {  return defNeuronDUET; }
   //---
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   //---
   virtual void      TrainMode(bool flag)
     {  bTrain = flag; cExperts.TrainMode(bTrain); }
  };

É importante observar que, neste caso, o uso de uma camada de transposição de dados como classe pai é justificado pela estrutura dos dados de entrada.

O modelo recebe como entrada uma série temporal multivariada apresentada em forma matricial, onde cada linha corresponde a um passo temporal distinto do sistema analisado. No entanto, todos os módulos descritos anteriormente operam com séries temporais unitárias. Isso também se aplica ao módulo de unificação de dados. Para garantir o processamento correto das informações, os dados de entrada são transpostos para um formato mais adequado à análise. Após a conclusão das operações, os resultados são reconvertidos para a forma original. Esse último processo planejamos executar por meio dos recursos da classe pai, o que assegura a consistência da estrutura dos dados e simplifica a integração do módulo.

Na estrutura do novo classe apresentada anteriormente, pode-se notar uma quantidade considerável de objetos internos, que desempenham um papel fundamental na construção do nosso algoritmo. O funcionamento detalhado desses objetos será abordado durante a implementação dos métodos virtuais da classe. Por ora, destacamos que todos eles são declarados de forma estática, o que nos permite manter o construtor e o destrutor da classe vazios. A inicialização de todos os objetos, inclusive dos herdados, é realizada dentro do método Init.

bool CNeuronDUET::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                       uint window, uint window_key, uint units_count,
                       uint heads, uint units_out, uint experts, uint top_k,
                       ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, window, units_out, optimization_type, batch))
      return false;

Nos parâmetros do método de inicialização, recebemos um conjunto de constantes que nos permite interpretar de maneira inequívoca a arquitetura do objeto que está sendo criado. A estrutura desses parâmetros já nos é familiar. Alguns foram utilizados na construção dos módulos de clusterização temporal e de clusterização de canais, enquanto outros aparecem nos blocos de atenção. Vale apenas chamar a atenção para o parâmetro units_out, que nos permite definir o comprimento desejado da sequência de saída do objeto.

No corpo do método, primeiramente chamamos o método homônimo da classe pai, no qual já estão implementados os processos de verificação de parte dos parâmetros recebidos e de inicialização das interfaces herdadas.

Em seguida, armazenamos os parâmetros necessários nas variáveis internas.

iWindowKey = MathMax(window_key, 1);
iHeads = MathMax(heads, 1);

Depois, passamos à inicialização dos objetos internos. Como mencionado anteriormente, antes do início da análise, os dados de entrada precisam ser transpostos. Essa função é executada por um objeto especializado.

int index = 0;
if(!cTranspose.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
   return false;

Logo após, inicializamos os módulos de clusterização temporal e de clusterização de canais.

index++;
if(!cExperts.Init(0, index, OpenCL, units_count, units_out, window, experts, top_k, optimization, iBatch))
   return false;
index++;
if(!cMask.Init(0, index, OpenCL, units_count, window, optimization, iBatch))
   return false;

Em seguida, vêm os objetos que compõem o módulo de unificação de dados. Essencialmente, trata-se de uma versão modificada do módulo de atenção. Aqui, primeiro inicializamos o objeto responsável pela geração das entidades Query, Key e Value. Nesse caso, utilizamos uma única camada convolucional capaz de gerar paralelamente as três entidades.

index++;
if(!cQKV.Init(0, index, OpenCL, units_out, units_out, iHeads * iWindowKey * 3, window, 1, optimization, iBatch))
   return false;

Neste mesmo bloco, adicionamos 2 objetos destinados à separação das entidades em tensores distintos.

index++;
if(!cQ.Init(0, index, OpenCL, cQKV.Neurons() / 3, optimization, iBatch))
   return false;
index++;
if(!cKV.Init(0, index, OpenCL, cQ.Neurons() * 2, optimization, iBatch))
   return false;

Os coeficientes de atenção serão armazenados em um buffer de dados.

if(!cbScores.BufferInit(cMask.Neurons()*iHeads, 0) ||
   !cbScores.BufferCreate(OpenCL))
   return false;

É importante observar que, em todos os casos, os tamanhos dos objetos são definidos levando em conta a transposição da matriz de dados de entrada.

Em seguida, inicializamos o objeto responsável pelos resultados do mecanismo de atenção multicanal.

index++;
if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch))
   return false;

Logo depois, criamos a camada convolucional de redução de dimensionalidade, cuja função é unificar os resultados provenientes das diferentes cabeças de atenção.

index++;
if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, units_out, window,
                                                                        1, optimization, iBatch))
   return false;
cPooling.SetActivationFunction(None);

Adicionamos também um objeto destinado ao armazenamento dos resultados das conexões residuais.

index++;
if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch))
   return false;
cResidual.SetActivationFunction(None);

A seguir, conforme a arquitetura proposta pelos autores, vem o tradicional bloco FeedForward. No entanto, aqui o substituímos por uma versão multicanal, adaptada do framework StockFormer.

   index++;
   if(!cFeedForward.Init(0, index, OpenCL, units_out, 4 * units_out, window, 1, heads, optimization, iBatch))
      return false;
//---
   return true;
  }

Concluímos, então, o método, retornando o resultado lógico da execução das operações para o programa chamador.

O próximo passo do nosso trabalho é a construção do algoritmo de propagação para frente dentro do método CNeuronDUET::feedForward.

bool CNeuronDUET::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   if(!cTranspose.FeedForward(NeuronOCL))
      return false;

Nos parâmetros do método, recebemos um ponteiro para o objeto de dados de entrada, que é imediatamente passado ao método homônimo do objeto interno responsável pela transposição dos dados. A partir daí, continuamos o processamento utilizando os resultados dessa transposição.

Primeiro, esses dados são enviados ao módulo de clusterização temporal, que gera os valores preditivos das sequências unitárias.

if(!cExperts.FeedForward(cTranspose.AsObject()))
   return false;

Em seguida, os resultados da transposição dos dados de entrada são passados ao módulo de clusterização de canais.

if(!cMask.FeedForward(cTranspose.AsObject()))
   return false;

Depois disso, passamos à organização da propagação para frente no módulo de unificação de dados. Inicialmente, com base nos resultados obtidos pelo módulo de clusterização temporal, geramos as entidades Query, Key e Value.

if(!cQKV.FeedForward(cExperts.AsObject()))
   return false;

Os resultados dessa operação são então divididos em dois tensores.

if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), iWindowKey, 2 * iWindowKey, cQKV.GetUnits()))
   return false;

Em seguida, chamamos o método encapsulador do mecanismo de Self-Attention multicanal com mascaramento.

if(!AttentionOut())
   return false;

Os resultados da atenção multicanal são então projetados para a mesma dimensionalidade dos resultados do módulo de clusterização temporal.

if(!cPooling.FeedForward(cMHAttentionOut.AsObject()))
   return false;

Aos valores obtidos, adicionamos as conexões residuais.

if(!SumAndNormilize(cExperts.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1))
   return false;

O bloco FeedForward multicanal é implementado como um módulo independente, que já inclui suas próprias conexões residuais. Por isso, basta chamarmos o método homônimo desse objeto, passando como dados de entrada os resultados das operações anteriores.

if(!cFeedForward.FeedForward(cResidual.AsObject()))
   return false;

Agora, resta apenas reconverter os resultados das operações para o formato original dos dados de entrada. Para isso, utilizamos o funcional da classe pai.

 return CNeuronTransposeOCL::feedForward(cFeedForward.AsObject());
}

O resultado lógico das operações é retornado ao programa chamador, encerrando o método.

Após finalizar a implementação dos processos de propagação para frente, passamos à construção do algoritmo de propagação reversa. Como você já sabe, aqui são utilizados dois métodos distintos:

distribuição do gradiente de erro entre os objetos internos e os dados de entrada, de acordo com sua influência no resultado final — calcInputGradients;
otimização dos parâmetros do modelo com o objetivo de minimizar o erro total — updateInputWeights.

Todos os parâmetros treináveis do nosso bloco DUET na implementação apresentada estão contidos nos objetos internos. Portanto, o processo de sua otimização se resume à chamada dos métodos homônimos desses objetos. Por esse motivo, a questão mais crítica passa a ser a correta distribuição do gradiente de erro entre os objetos internos e os dados de entrada.

Nos parâmetros do método calcInputGradients, recebemos um ponteiro para o objeto de dados de entrada. Trata-se do mesmo objeto utilizado durante o processo de propagação para frente. A diferença é que, desta vez, devemos transferir para ele os valores correspondentes ao gradiente de erro.

bool CNeuronDUET::calcInputGradients(CNeuronBaseOCL *prevLayer)
  {
   if(!prevLayer)
      return false;

É evidente que só podemos transferir os dados para um objeto válido. Por isso, logo no início, verificamos a integridade e a validade do ponteiro recebido. Caso contrário, todas as operações subsequentes perdem o sentido.

Como você sabe, a distribuição do gradiente de erro segue rigorosamente o fluxo de informações da propagação para frente, porém no sentido inverso. Encerramos o método de propagação para frente com a chamada do método da classe pai; consequentemente, as operações da propagação reversa começam também com a chamada do método da classe pai. A diferença é que, desta vez, chamamos o método responsável pela distribuição do gradiente de erro.

if(!CNeuronTransposeOCL::calcInputGradients(cFeedForward.AsObject()))
   return false;

Em seguida, conduzimos o gradiente de erro através do módulo FeedForward multicanal.

if(!cPooling.calcHiddenGradients(cFeedForward.AsObject()))
   return false;

Depois, distribuímos os valores do gradiente de erro entre as diferentes cabeças de atenção.

if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject()))
   return false;

O passo seguinte consiste em chamar o método encapsulador responsável pela distribuição do erro entre as entidades Query, Key e Value dentro do mecanismo de Self-Attention com mascaramento.

if(!AttentionInsideGradients())
   return false;

Os resultados dessas operações são então reunidos em um único tensor.

if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), iWindowKey, 2 * iWindowKey, iCount))
   return false;

Se necessário, ajustamos os valores obtidos levando em conta a derivada da função de ativação.

if(cQKV.Activation() != None)
   if(!DeActivation(cQKV.getOutput(), cQKV.getGradient(), cQKV.getGradient(), cQKV.Activation()))
      return false;

Após isso, encaminhamos o gradiente para o módulo de clusterização temporal.

if(!cExperts.calcHiddenGradients(cQKV.AsObject()) ||
   !DeActivation(cExperts.getOutput(), cExperts.getPrevOutput(), cPooling.getGradient(), cExperts.Activation()) ||
   !SumAndNormilize(cExperts.getGradient(), cExperts.getPrevOutput(), cExperts.getGradient(), iWindow, false,
                                                                                                   0, 0, 0, 1))
   return false;

Aqui é importante destacar que os resultados do módulo de clusterização temporal também foram utilizados para as conexões residuais; portanto, o gradiente de erro precisa ser transmitido também por esse fluxo de informação. Para isso, primeiro ajustamos o gradiente de erro na saída do bloco de atenção considerando a derivada da função de ativação do módulo de clusterização temporal e, em seguida, somamos os dados provenientes dos dois fluxos de informação.

Depois disso, o gradiente de erro é conduzido através do módulo de clusterização temporal.

   if(!cTranspose.calcHiddenGradients(cExperts.AsObject()))
      return false;

Por fim, o gradiente é transmitido até o nível dos dados de entrada.

   return prevLayer.calcHiddenGradients(cTranspose.AsObject());
  }

O resultado lógico das operações é retornado ao programa chamador, encerrando o método.

Note que, no processo de distribuição do gradiente de erro, o fluxo de informação do módulo de clusterização de canais está completamente ausente. Já mencionamos anteriormente a ausência de operações de propagação reversa nesse módulo e, neste estágio, simplesmente excluímos as operações que seriam desnecessárias por definição.

Com isso, encerramos a análise dos algoritmos que compõem nossa interpretação dos métodos propostos pelos autores do framework DUET. O código completo de todos os objetos apresentados e seus respectivos métodos pode ser consultado no anexo deste artigo.

Arquitetura do modelo

A próxima etapa do trabalho consiste na integração dos componentes desenvolvidos à arquitetura dos modelos treináveis. Para isso, passamos à descrição da solução arquitetural adotada.

Assim como em trabalhos anteriores, aplicaremos uma abordagem de aprendizado multitarefa, treinando simultaneamente 2 modelos: Ator e o modelo de previsão das probabilidades de direção do movimento futuro. A arquitetura deste último foi inteiramente herdada dos estudos anteriores, portanto, nesta etapa, focaremos na análise da arquitetura do Ator. A arquitetura de ambos os modelos é descrita no método CreateDescriptions.

bool CreateDescriptions(CArrayObj *&actor, CArrayObj *&probability)
  {
//---
   CLayerDescription *descr;
//---
   if(!actor)
     {
      actor = new CArrayObj();
      if(!actor)
         return false;
     }
   if(!probability)
     {
      probability = new CArrayObj();
      if(!probability)
         return false;
     }

Nos parâmetros do método, recebemos ponteiros para dois objetos dinâmicos destinados ao armazenamento da descrição arquitetural dos modelos. No corpo do método, verificamos imediatamente a validade dos ponteiros recebidos e, se necessário, criamos novas instâncias dos objetos.

A arquitetura do modelo Ator começa com uma camada totalmente conectada (fully connected layer), que desempenha o papel de interface de entrada dos dados. Essa camada deve ser suficientemente ampla para acomodar todo o volume de informações analisadas.

//--- Actor
   actor.Clear();
//--- Input layer
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   int prev_count = descr.count = (HistoryBars * BarDescr);
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Conforme proposto pelos autores do framework DUET, em seguida vem a camada de normalização em lote (batch normalization), cuja função é uniformizar os dados de entrada e minimizar a influência de valores atípicos.

//--- layer 1
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Logo depois, utilizamos 2 blocos DUET sequenciais, desenvolvidos anteriormente. No entanto, a abordagem de segmentação dos dados foi modificada. Em vez da segmentação tradicional, neste experimento adotamos uma representação dos dados em espaço de fases multidimensional. Esse método, inspirado nas abordagens do framework Attraos, permite capturar de forma mais precisa as dependências complexas nas séries temporais, aprimorando a interpretabilidade do modelo. No primeiro bloco, utilizamos um passo de 5 minutos.

No módulo de clusterização temporal, inicializamos o funcionamento de 16 codificadores paralelos. Para cada cluster, são selecionados os 4 mais adequados.

//--- layer 2
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDUET;
   descr.window = BarDescr * 5;  // 5 min
     {
      int temp[] = {HistoryBars / 5, HistoryBars / 5, 16, 4}; // {Units in (24), Units out (24), Experts, Top K}
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = 256;
   descr.step = 4;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

No segundo bloco DUET, aumentamos o passo da representação de fase para 15. Mas, mantemos os demais parâmetros inalterados.

//--- layer 3
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronDUET;
   descr.window = BarDescr * 15;  // 15 min
     {
      int temp[] = {HistoryBars / 15, HistoryBars / 15, 16, 4}; // {Units in (8), Units out (8), Experts, Top K}
      if(ArrayCopy(descr.units, temp) < (int)temp.Size())
         return false;
     }
   descr.window_out = 256;
   descr.step = 4;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

É importante observar que, durante o processamento dos dados, não alteramos o tamanho do tensor. Porém, na camada convolucional seguinte, reduzimos o comprimento da sequência em três vezes.

//--- layer 4
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   prev_count = descr.count = HistoryBars / 3;
   descr.window = BarDescr * 3;
   descr.step = descr.window;
   int prev_window = descr.window_out = BarDescr;
   descr.activation = SoftPlus;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Em seguida, vem o bloco de tomada de decisão composto por três camadas totalmente conectadas.

//--- layer 5
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.batch = 1e4;
   descr.activation = TANH;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 6
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   descr.count = LatentCount;
   descr.activation = TANH;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 7
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBaseOCL;
   prev_count = descr.count = NActions;
   descr.activation = SoftPlus;
   descr.batch = 1e4;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

Após o bloco de decisão, segue-se uma camada de normalização em lote.

//--- layer 8
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronBatchNormOCL;
   descr.count = prev_count;
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

E, na saída do modelo Ator, adicionamos o bloco de gerenciamento de risco.

//--- layer 9
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronMacroHFTvsRiskManager;
//--- Windows
     {
      int temp[] = {3, 15, NActions, AccountDescr}; //Window, Stack Size, N Actions, Account Description
      if(ArrayCopy(descr.windows, temp) < int(temp.Size()))
         return false;
     }
   descr.count = 10;
   descr.window_out = 64;
   descr.step = 4;                              // Heads
   descr.batch = 1e4;
   descr.activation = None;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }
//--- layer 10
   if(!(descr = new CLayerDescription()))
      return false;
   descr.type = defNeuronConvOCL;
   descr.count = NActions / 3;
   descr.window = 3;
   descr.step = 3;
   descr.window_out = 3;
   descr.activation = SIGMOID;
   descr.optimization = ADAM;
   if(!actor.Add(descr))
     {
      delete descr;
      return false;
     }

A arquitetura completa de ambos os modelos pode ser consultada no anexo. Nesse mesmo material estão incluídos os programas responsáveis pela interação com o ambiente e pelo treinamento dos modelos, que foram transferidos sem alterações em relação aos trabalhos anteriores.

Testes

Realizamos um trabalho extenso para desenvolver nossa própria interpretação dos métodos propostos no framework DUET, implementando-os em MQL5 e integrando-os em modelos treináveis. Agora chegamos à etapa crucial — testar a eficiência das soluções implementadas com base em dados históricos reais.

Para o treinamento dos modelos, foi criada uma amostra de dados históricos do par de moedas EURUSD, no timeframe M1, abrangendo todo o ano de 2024. Durante a coleta dos dados, foram utilizados os parâmetros padrão dos indicadores técnicos.

O treinamento do modelo foi dividido em duas etapas. Na primeira, definimos o tamanho do batch igual a 1, de modo que, a cada iteração, o modelo seleciona aleatoriamente um estado da amostra de treinamento. Essa estratégia ajuda a rede a se adaptar a novas condições. No entanto, isso não é suficiente para o funcionamento adequado do bloco de gerenciamento de risco. Por esse motivo, na segunda etapa do treinamento, aumentamos o tamanho do batch para 60, permitindo considerar uma sequência de 60 estados do ambiente e as respectivas ações do Ator. Essa abordagem torna o treinamento mais estável e eficiente.

O teste do modelo treinado foi realizado utilizando dados históricos de janeiro e fevereiro de 2025. Todas as configurações foram mantidas, o que garante uma avaliação objetiva da qualidade das previsões. Os resultados dos testes apresentados abaixo.

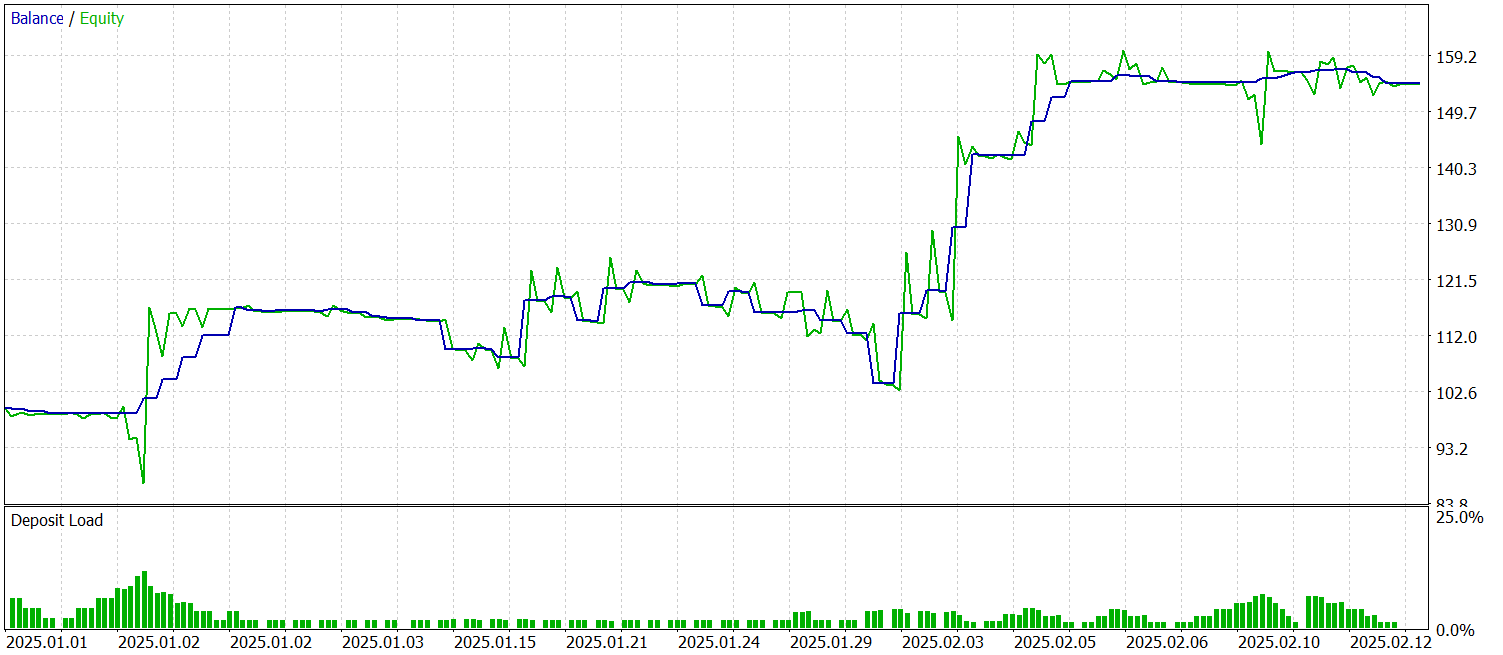
Os resultados dos testes

Durante o período de teste, o modelo realizou 53 operações de trading, sendo mais de 56% delas fechadas com lucro. É notável que a operação média lucrativa é quase duas vezes superior ao indicador correspondente das posições com prejuízo. Tudo isso permitiu fixar o fator de lucro em um nível de 2.44.

Considerações finais

Neste trabalho, conhecemos o framework DUET, cujos autores, para fins de análise de séries temporais multivariadas, combinaram análise de frequência, aprendizado métrico e filtragem probabilística. Tudo isso contribuiu para melhorar a qualidade das previsões e tornar o modelo mais resistente ao ruído.

Na parte prática, implementamos nossa interpretação dos métodos propostos utilizando MQL5 e integramos as soluções desenvolvidas em um modelo. Realizamos o treinamento do modelo com dados históricos reais e testamos o modelo treinado com dados fora da amostra de treinamento. Os resultados obtidos indicam o potencial existente do modelo. No entanto, antes de utilizá-lo em condições reais de trading, é necessário treinar o modelo com uma amostra mais representativa, seguida de testes abrangentes.

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	Expert Advisor	EA para coleta de exemplos
2	ResearchRealORL.mq5	Expert Advisor	EA para coleta de exemplos pelo método Real-ORL
3	Study.mq5	Expert Advisor	EA para treinamento de modelos
4	Test.mq5	Expert Advisor	EA para teste do modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura para descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
7	NeuroNet.cl	Biblioteca	Biblioteca de código da programa OpenCL

Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17487

Arquivos anexados |

Baixar como ZIP

MQL5.zip (2538.92 KB)

Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.

Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.

Outros artigos do autor

Ir para discussão

Visualização de estratégias em MQL5: distribuindo os resultados da otimização em gráficos de critérios

Neste artigo, escreveremos um exemplo de visualização do processo de otimização e exibiremos os três melhores passes para quatro critérios de otimização. Além disso, implementaremos a possibilidade de selecionar um dos três melhores passes para exibir seus dados em tabelas e no gráfico.

Simulação de mercado: Position View (XIII)

Neste artigo, mostrarei como você, pode sem muito esforço, conseguir implementar a indicação se uma posição, está lhe dando prejuízo ou mesmo lucro. Isto de maneira extremamente simples e eficaz. Usando este indicador que estou mostrando como desenvolver, você, mesmo sem muito conhecimento, conseguirá facilmente saber quando é hora de fechar uma posição. E ao fazê-lo, não virá a ter um resultado diferente do esperado. Isto por que, estamos efetuando o calculo de forma a termos a real situação de nossa posição.

Otimização por neuroboides — Neuroboids Optimization Algorithm (NOA)

Trata-se de uma nova metaheurística de otimização bioinspirada e autoral, denominada NOA (Neuroboids Optimization Algorithm), que combina princípios de inteligência coletiva e redes neurais. Ao contrário dos métodos clássicos, o algoritmo utiliza uma população de "neuroboides" autoaprendizes, cada um com sua própria rede neural, que adapta a estratégia de busca em tempo real. O artigo em questão apresenta a arquitetura do algoritmo, os mecanismos de autoaprendizado dos agentes e as perspectivas de aplicação dessa abordagem híbrida em tarefas complexas de otimização.

Do básico ao intermediário: Filas, Listas e Árvores (V)

Neste artigo começamos a trabalhar com a implementação do mecanismo de árvore. Como sei que este mecanismo pode ser extremamente complicado de ser compreendido e assimilado, no começo do aprendizado. Iremos implementar as coisas com calma e devagar. Assim todos irão conseguir entender como uma árvore funciona e qual o melhor momento para utiliza-la.