
Busca oscilatória determinística — Deterministic Oscillatory Search (DOS)
Conteúdo
Introdução
Na área moderna de otimização, ocorre uma evolução constante de algoritmos que buscam superar as limitações fundamentais dos métodos tradicionais. A maioria dos algoritmos meta-heurísticos de otimização depende fortemente de processos estocásticos e de números aleatórios. Essas abordagens demonstram uma capacidade impressionante de evitar ótimos locais, porém sua natureza não determinística pode criar problemas em áreas que exigem reprodutibilidade exata dos resultados.
Neste artigo será apresentada a busca oscilatória determinística (Deterministic Oscillatory Search, DOS), um novo algoritmo meta-heurístico que une as vantagens dos métodos tradicionais de gradiente com a eficiência dos algoritmos de enxame e, ao mesmo tempo, evita completamente o uso de números aleatórios.
Desenvolvido para resolver tarefas complexas de otimização global em 2017 pelo cientista Archana, o DOS é baseado no conceito de movimento oscilatório de partículas no espaço de busca, com distribuição determinística das posições iniciais. A característica fundamental do algoritmo reside em sua capacidade de trabalhar com tarefas multidimensionais, preservando ao mesmo tempo total reprodutibilidade: sob condições iniciais idênticas, o algoritmo sempre chega exatamente ao mesmo resultado.
Diferentemente da maioria dos algoritmos meta-heurísticos, o DOS introduz o conceito de "inclinação de fitness", um mecanismo que permite às partículas reconhecerem a qualidade de seu movimento e adaptar sua estratégia de busca. As partículas podem se encontrar em um de três estados de inclinação: positivo (o movimento melhora a solução), negativo (o movimento piora a solução) ou desconhecido.
Essas informações são usadas para controlar o comportamento oscilatório das partículas. Quando os métodos de gradiente convencionais alcançam um ponto em que todas as direções levam à piora da função objetivo, eles interrompem o processo. O DOS supera essa limitação graças ao mecanismo de enxame, que é ativado quando o movimento oscilatório não produz melhoria. Nesse caso, a partícula começa a se mover na direção da melhor solução global conhecida.
Neste artigo, analisaremos em detalhe as bases matemáticas do algoritmo DOS, examinaremos suas características e particularidades de implementação, além de observar sua eficácia em uma série de tarefas de teste.
Implementação do algoritmo
Agora vamos observar como o algoritmo DOS funciona. Em vez de uma caminhada aleatória, ele utiliza uma abordagem sistemática composta por várias regras simples; o DOS não depende da aleatoriedade. O algoritmo inicia seu funcionamento posicionando vários "exploradores" (partículas) em diferentes pontos da paisagem. O posicionamento não é aleatório; ele ocorre de acordo com uma fórmula específica, de modo a cobrir uniformemente toda a região. Cada explorador possui uma direção inicial e uma velocidade de movimento. À medida que avança, o explorador memoriza se o terreno se torna mais alto (melhor) ou mais baixo (pior). Isso é chamado de "inclinação", uma forma simples de acompanhar se você está se movendo na direção correta.
Agora começa a parte mais interessante. Quando o explorador detecta que deixou de subir e passou a descer (o fitness piorou), ele não simplesmente para nem retorna pelo mesmo caminho. Em vez disso, ele realiza um "rebote", isto é, muda de direção e continua se movendo no sentido oposto, porém com uma velocidade menor, equivalente à metade da anterior. Isso se assemelha a uma bola de tênis que rebate em uma parede, mas com menos energia.
Esse processo de rebote cria um movimento oscilatório; daí o nome do algoritmo. A cada rebote, o explorador localiza com maior precisão o ponto de extremo. Mas e se o explorador cair em uma armadilha, isto é, uma pequena elevação em torno da qual tudo é mais baixo, e esse extremo não for o ponto mais alto da região? Nesse caso, o DOS aplica outro recurso. Se o explorador tentou se mover em diferentes direções, mas em todas encontrou descida, ele alterna para outro modo, o "enxameamento". Nesse modo, ele começa a se mover na direção do melhor ponto encontrado por todos os exploradores até o momento.
Diferentemente da busca aleatória ou do método de tentativa e erro, o DOS explora sistematicamente o espaço de soluções, utilizando informações sobre a direção de melhoria e a experiência coletiva de todos os exploradores. Ao mesmo tempo, ele não exige cálculos complexos de derivadas nem o armazenamento de um grande histórico de busca. Assim, passo a passo, aplicando regras simples de movimento, reflexão e enxameamento, o DOS encontra soluções ótimas para problemas complexos.
Na imagem abaixo são apresentados os seguintes aspectos-chave do algoritmo: um espaço de busca bidimensional com um ótimo global e vários ótimos locais, representado por linhas de contorno, e o caminho desde o ponto inicial até o ótimo global, demonstrando o comportamento característico do algoritmo DOS:
- posição inicial determinística da partícula,
- movimento oscilatório (em zigue-zague) durante a exploração do espaço,
- movimento adaptativo em direção ao ótimo global.
Os componentes-chave do algoritmo são: inicialização determinística das partículas, uso do conceito de inclinação de fitness, movimento oscilatório e o mecanismo de enxameamento (movimento em direção à melhor solução conhecida).
O estado da inclinação pode ser:
- positivo (+1) – o movimento atual melhora o fitness,
- negativo (-1) – o movimento atual piora o fitness,
- desconhecido (0) – estado durante a inicialização ou após a mudança de estratégia.
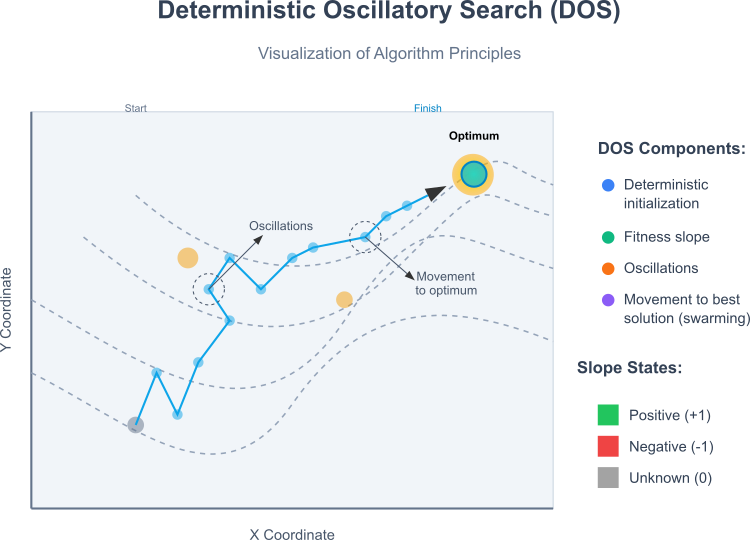
Figura 1. ilustração do funcionamento do
A ilustração mostra de forma clara como o DOS combina características dos métodos clássicos de gradiente (busca local por meio de oscilações) com as capacidades dos algoritmos de enxame, mantendo ao mesmo tempo um comportamento totalmente determinístico. Compreendidos os princípios de funcionamento do algoritmo, passaremos à escrita do pseudocódigo do algoritmo.
Passo 1: Preparação inicial
- Criar arrays para armazenar as posições, velocidades, valores anteriores de fitness e inclinações para cada partícula
- Inicializar a melhor solução encontrada com o menor valor de fitness possível
Passo 2: Inicialização determinística das partículas
- Para cada partícula:
- posicionar no espaço de busca por uma fórmula determinística que garanta cobertura uniforme
- definir a velocidade inicial como zero
- definir a inclinação inicial como "desconhecida" (0)
- definir o valor anterior de fitness como o menor valor possível
Passo 3: Ciclo principal de otimização
- Repetir até atingir o número máximo de iterações: Parte 1: Movimento das partículas
- Para cada partícula:
- salvar o valor atual de fitness como anterior
- atualizar a posição adicionando a velocidade atual
- se a nova posição ultrapassar os limites da busca, restringi-la aos limites permitidos
- Para cada partícula:
- calcular o novo valor de fitness
- se o fitness for melhor que a melhor solução encontrada, atualizar a melhor solução
- se a inclinação for "desconhecida" (0):
- se o novo fitness for melhor que o anterior, definir a inclinação como "positiva" (1)
- se o novo fitness for pior que o anterior, definir a inclinação como "negativa" (-1)
- se o fitness não se alterar, manter a inclinação como "desconhecida"
- se a inclinação for "positiva" (1):
- se o novo fitness for pior que o anterior:
- alterar a direção do movimento para a oposta
- reduzir a velocidade pela metade
- definir a inclinação como "negativa" (-1)
- se o novo fitness for pior que o anterior:
- se a inclinação for "negativa" (-1):
- se o novo fitness for pior que o anterior:
- aplicar o mecanismo de enxameamento: adicionar à velocidade atual um vetor direcionado à melhor solução, multiplicado pelo fator de movimento
- definir a inclinação como "desconhecida" (0)
- se o novo fitness for pior que o anterior:
- verificar se a velocidade é nula ou próxima de zero:
- se a velocidade for quase nula:
- definir a velocidade na direção da melhor solução encontrada, multiplicada pelo fator de movimento
- definir a inclinação como "desconhecida" (0)
- se a velocidade for quase nula:
- Para cada partícula:
Passo 4: Finalização
- Retornar a melhor solução encontrada e seu valor de fitness
Agora podemos prosseguir para a escrita do código do algoritmo DOS. Criaremos uma estrutura para armazenar o estado da partícula durante o processo de otimização. Essa estrutura conterá um campo para definir a inclinação da velocidade (positiva, negativa ou indefinida) e um array de componentes de velocidade por dimensão, o que permitirá armazenar e processar de forma conveniente os parâmetros de movimento da partícula.
Para a inicialização da estrutura, é previsto um método que define a inclinação com o valor padrão e cria um array de velocidade do tamanho especificado, preenchendo-o com zeros, garantindo assim um estado inicial correto antes do início do funcionamento.
Além disso, é implementada uma verificação de velocidade nula, um método que verifica todos os componentes da velocidade e retorna "true" se todos forem praticamente iguais a zero, considerando a precisão definida, ou "false" caso contrário. Isso ajuda a determinar se a partícula atingiu um estado estável ou se precisa continuar se movendo.
// Структура для хранения скорости частицы struct S_DOS_Velocity { int slope; // Наклон частицы (-1: отрицательный, 0: неизвестный, 1: положительный) double v []; // Компоненты скорости по каждому измерению void Init (int dims) { slope = 0; ArrayResize (v, dims); ArrayInitialize (v, 0.0); // Быстрая инициализация нулями всего массива } // Проверка на нулевую скорость bool IsZero (double epsilon = 1e-10) { for (int i = 0; i < ArraySize (v); i++) if (MathAbs (v [i]) > epsilon) return false; return true; } }; //——————————————————————————————————————————————————————————————————————————————
A classe "C_AO_DOS" representará a implementação do algoritmo. Ela herdará a funcionalidade da classe base "C_AO", adicionando a lógica específica do método DOS. As principais características da classe são: no construtor, são inicializados os parâmetros padrão, incluindo o tamanho da população e o fator de movimento em direção à melhor solução, além da criação de um array de parâmetros. O método "SetParams ()" fornece a possibilidade de definir e validar parâmetros, como o tamanho da população "popSize" e o coeficiente de movimento "movementFactor", levando em conta as restrições. O método "Init ()" é responsável pela preparação das condições iniciais, como os intervalos de busca, os passos de variação e o número de iterações.
Lógica de movimento das partículas, métodos:- Moving () – implementa o mecanismo principal de deslocamento das partículas no espaço de busca, com base nas velocidades atuais e nas avaliações.
- Revision () – destina-se à correção das posições ou velocidades após cada passo.
Dentro da classe, é definida a estrutura "S_DOS_Velocity velocities", que armazena os componentes de velocidade de cada partícula em todas as dimensões e contém métodos de inicialização e verificação de velocidade nula.
Métodos internos:- InitializeParticles () e ProcessParticleMovement () – funções auxiliares para inicializar e atualizar a posição das partículas, garantindo a lógica algorítmica.
De modo geral, a classe implementa uma abordagem estruturada do método DOS, na qual cada número e cada variável são direcionados a uma exploração controlada do espaço de soluções por meio de partículas, velocidades e direções.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_DOS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_DOS () { } C_AO_DOS () { ao_name = "DOS"; ao_desc = "Deterministic Oscillatory Search"; ao_link = "https://www.mql5.com/ru/articles/18154"; // Установка параметров по умолчанию popSize = 30; // размер популяции movementFactor = 0.95; // фактор движения к лучшему решению // Создание и инициализация массива параметров ArrayResize (params, 2); params [0].name = "Population Size"; params [0].val = popSize; params [1].name = "Movement Factor"; params [1].val = movementFactor; } void SetParams () { // Установка значений параметров с проверкой popSize = (int)MathMax (5, params [0].val); // Минимально 5 частиц для эффективности movementFactor = MathMax (0.1, MathMin (1.0, params [1].val)); // Ограничение от 0.1 до 1.0 } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double movementFactor; // фактор движения к лучшему решению S_DOS_Velocity velocities []; // Массив структур скоростей частиц private: //------------------------------------------------------------------- void InitializeParticles (); void ProcessParticleMovement (int particleIndex); }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" é responsável por preparar o algoritmo para a execução. Primeiramente, é chamado o método base de inicialização, que configura os intervalos iniciais de busca e os passos necessários para o funcionamento. Após a inicialização básica bem-sucedida, é alocada memória para os arrays nos quais será armazenada a informação sobre as velocidades das partículas "velocities".
Para cada elemento da população, são calculadas as velocidades iniciais em todas as dimensões, a fim de definir a dinâmica inicial do movimento das partículas. Ao final, é chamado o método que posiciona as partículas nas posições iniciais por meio de uma abordagem determinística específica, definindo seus pontos de partida no espaço de busca.
O resultado da execução desse método é uma população de partículas preparada para o funcionamento, com condições iniciais definidas, pronta para o início do processo iterativo de busca.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_DOS::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) // количество эпох { // Стандартная инициализация C_AO if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Выделение памяти под массивы ArrayResize (velocities, popSize); // Инициализация скоростей для каждого измерения for (int i = 0; i < popSize; i++) velocities [i].Init (coords); // Инициализация позиций частиц детерминистическим способом InitializeParticles (); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" implementa o deslocamento das partículas no espaço de busca do algoritmo DOS e processa sequencialmente cada partícula da população, percorrendo-as da primeira à última. Para cada partícula, é salvo o valor atual da função de fitness "f". Isso é necessário para a comparação posterior e para determinar se houve melhoria ou piora da posição da partícula.
Para cada coordenada (dimensão) da partícula, é calculado um novo valor adicionando o componente de velocidade correspondente à coordenada atual. As novas coordenadas são limitadas aos intervalos definidos "rangeMin [d]" e "rangeMax [d]" de acordo com o passo, de modo que as partículas não ultrapassem os limites da área de busca permitida.
Como resultado, o método "Moving" modifica as posições das partículas no espaço de busca, preservando informações sobre seu estado anterior e garantindo a correção das novas coordenadas, levando em conta as restrições e a discretização.
//+----------------------------------------------------------------------------+ //| Основной метод движения частиц | //+----------------------------------------------------------------------------+ void C_AO_DOS::Moving () { // Обработка всех частиц for (int i = 0; i < popSize; i++) { // Сохранение значения фитнеса a [i].fP = a [i].f; // Вычисление новых координат на основе скорости for (int d = 0; d < coords; d++) { // Обновление позиции a [i].c [d] += velocities [i].v [d]; // Округление до ближайшего допустимого шага a [i].c [d] = u.SeInDiSp (a [i].c [d], rangeMin [d], rangeMax [d], rangeStep [d]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável por atualizar as informações sobre as melhores soluções e por processar o movimento das partículas durante o processo de busca. O método processa sequencialmente todas as partículas da população. Para cada uma delas, é verificado se a solução atual da partícula melhora o valor do melhor fitness global "fB". Em caso afirmativo, o melhor resultado global é atualizado e as coordenadas correspondentes são armazenadas. Para cada partícula, é chamado um método separado, responsável pelo recálculo e ajuste de sua posição com base nas mudanças da função de fitness.
O resultado do funcionamento desse método é a atualização das melhores soluções e a preparação do sistema para a próxima etapa da busca, quando as partículas podem continuar o movimento levando em conta as atualizações mais recentes.
//+----------------------------------------------------------------------------+ //| Метод обновления фитнес-функций | //+----------------------------------------------------------------------------+ void C_AO_DOS::Revision () { // Обработка каждой частицы for (int i = 0; i < popSize; i++) { // Обновление лучшего решения, если текущее решение лучше if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } // Обработка движения частицы на основе изменения фитнеса ProcessParticleMovement (i); } } //——————————————————————————————————————————————————————————————————————————————
O método "ProcessParticleMovement" é responsável por regular o movimento de uma partícula individual no espaço de busca com base nas mudanças de sua função de fitness e nas direções atuais. Se o índice for inválido, o método encerra a execução. Para acelerar o acesso, são armazenados o fitness atual da partícula, o valor anterior de fitness e a inclinação atual do movimento. Com base na diferença entre o fitness atual e o anterior, bem como na inclinação atual, o algoritmo decide qual direção escolher para o movimento da partícula, se:
- a inclinação for desconhecida, seu sentido é determinado (positivo, negativo ou indefinido) com base na mudança do fitness;
- a inclinação for positiva e o fitness piorar, a inclinação é alternada para negativa e as velocidades em todos os eixos são reduzidas pela metade, o que favorece a mudança da direção do movimento;
- a inclinação for negativa e o fitness continuar piorando, ocorre o "enxameamento", isto é, o movimento em direção ao ótimo global, no qual as velocidades nos eixos aumentam na direção da melhor solução.
Se as velocidades em todas as direções forem iguais a zero, é iniciado o movimento em direção ao ótimo global, por meio da definição da velocidade com base na diferença entre as coordenadas atuais e as coordenadas da melhor solução global, levando em conta o fator de movimento. Como resultado, a direção e a magnitude da velocidade são ajustadas conforme a situação, o que permite à partícula reagir adequadamente às mudanças do fitness e "aprender" a se mover na direção ótima.
A tarefa final do método é garantir um movimento dinâmico e adaptativo das partículas, que leve em consideração as mudanças de suas soluções locais e globais para uma busca eficiente do ótimo.
//+----------------------------------------------------------------------------+ //| Обработка движения частицы после обновления фитнеса | //+----------------------------------------------------------------------------+ void C_AO_DOS::ProcessParticleMovement (int particleIndex) { // Локальные переменные для оптимизации доступа double currentFitness = a [particleIndex].f; double previousFitness = a [particleIndex].fP; int currentSlope = velocities [particleIndex].slope; // Сравнение фитнесов для определения направления движения double fitnessDiff = currentFitness - previousFitness; // Обработка наклона в соответствии с текущим состоянием if (currentSlope == 0) // Неизвестный наклон { // Определяем наклон на основе изменения фитнеса velocities [particleIndex].slope = (fitnessDiff > 0) ? 1 : (fitnessDiff < 0) ? -1 : 0; } else if (currentSlope == 1 && fitnessDiff < 0) // Положительный наклон и ухудшение фитнеса { // Меняем направление и уменьшаем скорость for (int d = 0; d < coords; d++) velocities [particleIndex].v [d] *= -0.5; // Оптимизированная форма деления на 2 velocities [particleIndex].slope = -1; // Меняем наклон на отрицательный } else if (currentSlope == -1 && fitnessDiff < 0) // Отрицательный наклон и ухудшение фитнеса { // Применяем механизм роения - движение к глобальному оптимуму for (int d = 0; d < coords; d++) velocities [particleIndex].v [d] += (cB [d] - a [particleIndex].c [d]) * movementFactor; velocities [particleIndex].slope = 0; // Сбрасываем наклон как неизвестный } // Проверка на нулевую скорость с использованием метода структуры if (velocities [particleIndex].IsZero ()) { // Инициализируем скорость движением к глобальному оптимуму for (int d = 0; d < coords; d++) velocities [particleIndex].v [d] = (cB [d] - a [particleIndex].c [d]) * movementFactor; // Сбрасываем наклон velocities [particleIndex].slope = 0; } } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Agora vamos observar os resultados. É possível notar que o algoritmo, que tem como base um método de gradiente com efeito de enxameamento incorporado, lida com as tarefas melhor do que os métodos de gradiente convencionais.
=============================
5 Hilly's; Func runs: 10000; result: 0.3422040822277234
25 Hilly's; Func runs: 10000; result: 0.3421751631202356
500 Hilly's; Func runs: 10000; result: 0.3421605659711745
=============================
5 Forest's; Func runs: 10000; result: 0.5708601371368296
25 Forest's; Func runs: 10000; result: 0.34628707444514434
500 Forest's; Func runs: 10000; result: 0.32879379664917996
=============================
5 Megacity's; Func runs: 10000; result: 0.19999999999999998
25 Megacity's; Func runs: 10000; result: 0.20923076923076928
500 Megacity's; Func runs: 10000; result: 0.23076923076922945
=============================
All score: 2.91248 (32.36%)
Na visualização, observa-se uma grande variação nos resultados em funções de baixa dimensionalidade.

DOS na função de teste Hilly
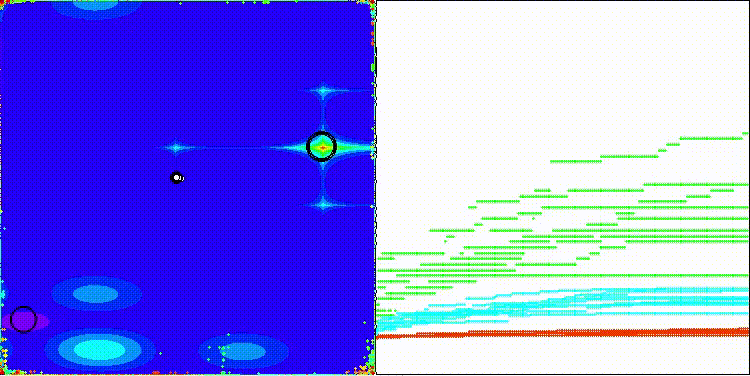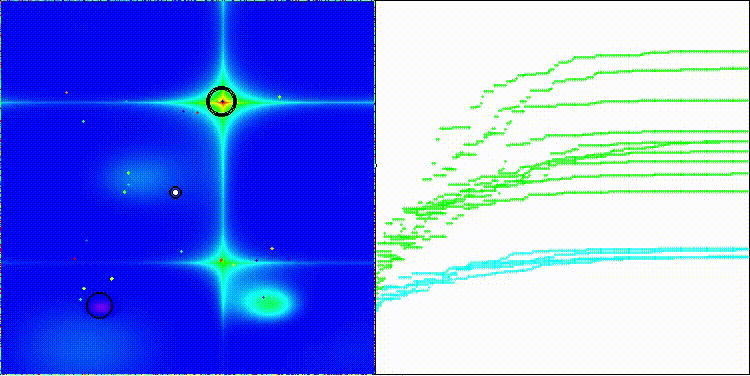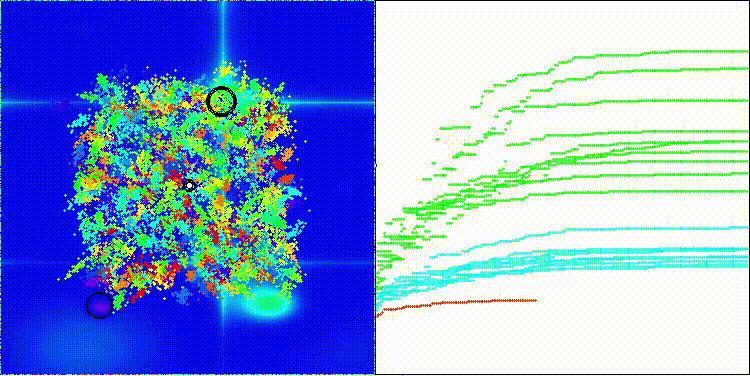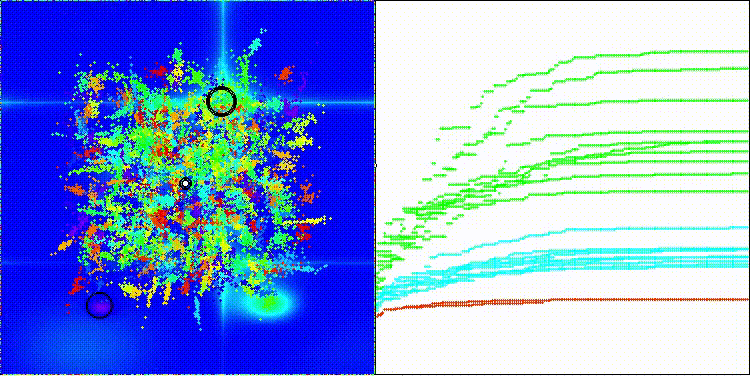
DOS na função de teste Forest
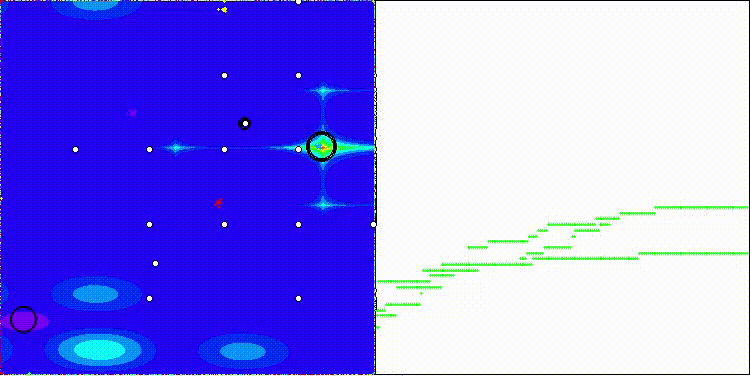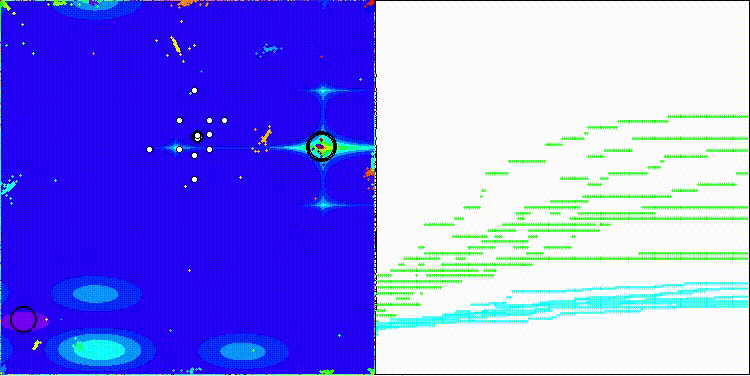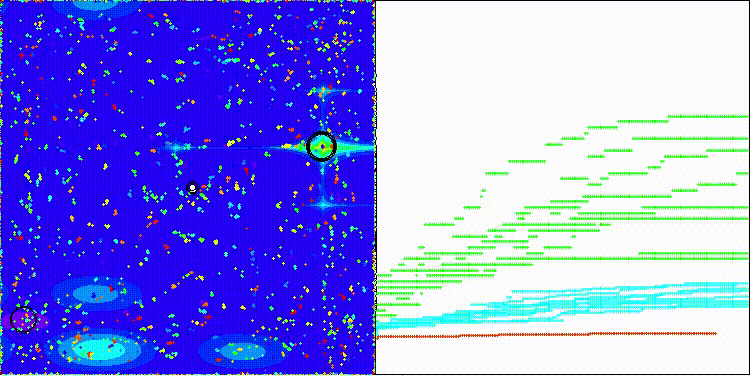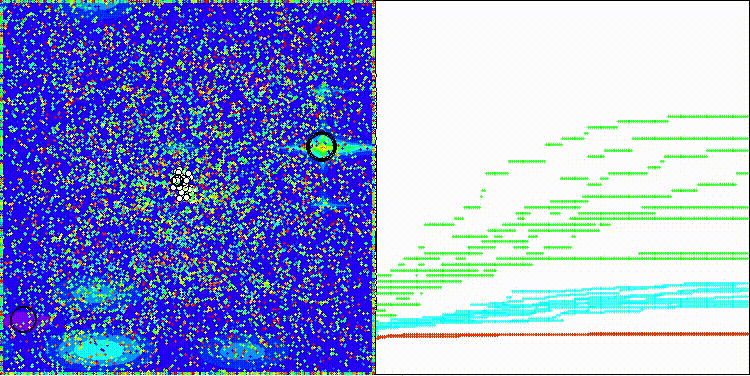
DOS na função de teste Megacity
Na tabela de classificação dos algoritmos populacionais de otimização, o DOS é apresentado de forma introdutória.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 13 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 14 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 15 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 16 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 17 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 18 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 19 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 20 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 21 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 22 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 23 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 24 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 25 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 26 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 27 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 28 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 29 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 30 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 31 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 32 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 33 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 34 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 35 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 36 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 37 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 38 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 39 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 40 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 41 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 42 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 43 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| 44 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 45 | CFO | central force optimization | 0,60961 | 0,54958 | 0,27831 | 1,43750 | 0,63418 | 0,46833 | 0,22541 | 1,32792 | 0,57231 | 0,23477 | 0,09586 | 0,90294 | 3,668 | 40,76 |
| DOS | deterministic oscillatory search | 0,34220 | 0,34218 | 0,34216 | 1,02654 | 0,57086 | 0,34629 | 0,32879 | 1,24594 | 0,20000 | 0,20923 | 0,23077 | 0,64000 | 2,912 | 32,36 | |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo possui um número mínimo de parâmetros para configuração (tamanho da população e fator de movimento), o que simplifica sua aplicação e reduz o risco de configuração incorreta.
O sistema de três estados de inclinação (positivo, negativo, desconhecido) garante um comportamento adaptativo das partículas de acordo com a qualidade da direção atual de busca; essa é a principal inovação presente no algoritmo. A ausência de operações matemáticas complexas o torna computacionalmente eficiente.
Sua principal força está na combinação da eficiência dos algoritmos de enxame com a confiabilidade e a reprodutibilidade dos métodos determinísticos. Embora, de modo geral, métodos determinísticos percam para os estocásticos, ainda assim, para a solução de determinadas tarefas, esses métodos se mostram justificados.
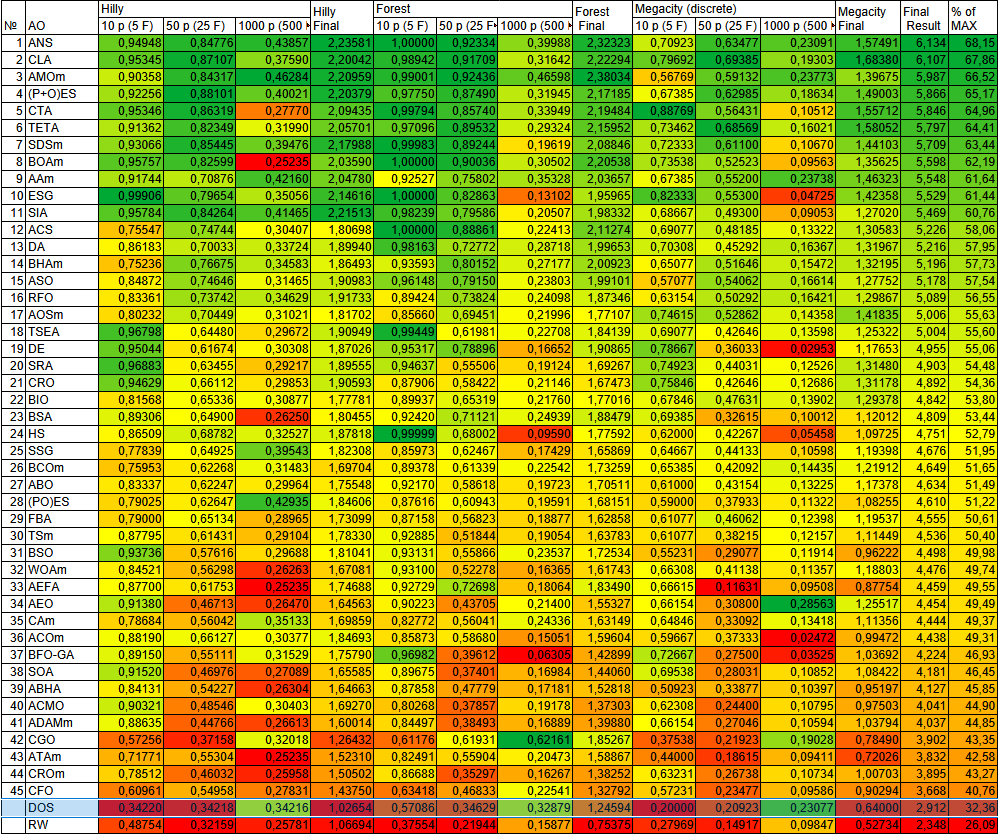
Figura 2. Graduação de cores dos algoritmos nos testes correspondentes
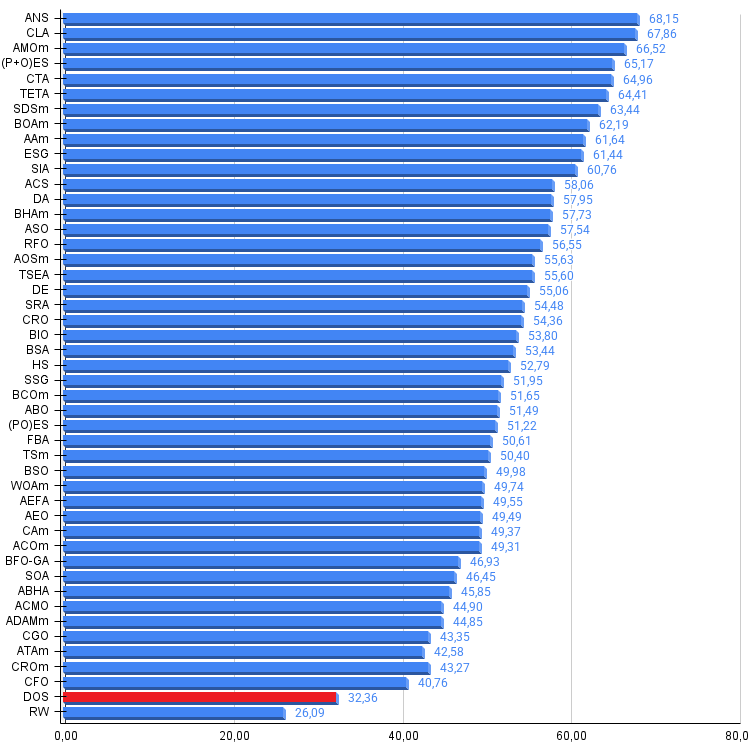
Figura 3. Histograma dos resultados de teste dos algoritmos (em escala de 0 a 100, quanto maior, melhor, onde 100 — resultado teórico máximo possível, no arquivo está o script para calcular a tabela de classificação)
Vantagens e desvantagens do algoritmo DOS:
Vantagens:
- Rápido.
- Implementação muito simples.
Desvantagens:
- Grande variação de resultados em funções de baixa dimensionalidade.
Um arquivo compactado com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo de inclusão | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo de inclusão | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo de inclusão | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo de inclusão | Biblioteca de funções do ambiente de testes |
| 5 | Utilities.mqh | Arquivo de inclusão | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo de inclusão | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de testes unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso de algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_DOS.mq5 | Script | Ambiente de testes para o DOS |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/18154
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Criando um Painel de Administração de Trading em MQL5 (Parte IX): Organização de Código (I)
Criando um Painel de Administração de Trading em MQL5 (Parte IX): Organização de Código (I)
 Engenharia de Recursos com Python e MQL5 (Parte III): Ângulo do Preço (2) Coordenadas Polares
Engenharia de Recursos com Python e MQL5 (Parte III): Ângulo do Preço (2) Coordenadas Polares
 Dominando Registros de Log (Parte 5): Otimizando o Handler com Cache e Rotação
Dominando Registros de Log (Parte 5): Otimizando o Handler com Cache e Rotação
 Desenvolvimento do Kit de Ferramentas de Análise de Price Action (Parte 11): EA de Sinal Heikin Ashi
Desenvolvimento do Kit de Ferramentas de Análise de Price Action (Parte 11): EA de Sinal Heikin Ashi
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso