Algoritmo de otimização baseado em brainstorming — Brain Storm Optimization (Parte I): Clusterização

Conteúdo:

1. Introdução
2. Descrição do algoritmo
3. K-Means

1. Introdução

O BSO (Brain Storm Optimization) é um dos algoritmos de otimização populacional, inovadores e empolgantes, inspirado na tempestade de ideias, ou "brainstorming". Este método oferece uma abordagem eficiente para resolver problemas complexos, usando princípios de inteligência e comportamento coletivos. O BSO imita o processo de geração de novas ideias e soluções, semelhante ao que ocorre em discussões em grupo, o que o torna uma ferramenta única e promissora para a busca de soluções ótimas em várias áreas. Neste artigo, examinamos os princípios básicos do BSO, suas vantagens e áreas de aplicação.

Os métodos baseados em populações são ferramentas importantes para resolver problemas complexos de otimização. No entanto, em problemas multimodais, que exigem encontrar várias soluções ótimas, as abordagens existentes enfrentam limitações. Neste artigo, apresentamos um novo método de otimização, o Brain Storm Optimization.

As abordagens existentes, como nichos e clusterização, dividem geralmente a população em subpopulações para buscar várias soluções. No entanto, essas abordagens sofrem com a necessidade de definir previamente o número de subpopulações, o que pode ser desafiador, especialmente quando o número de soluções ótimas é desconhecido. O BSO supera essa limitação ao transformar o espaço de busca em um espaço onde os indivíduos são agrupados e atualizados com base em suas coordenadas. Diferente de outros métodos que buscam um único ótimo global, o BSO direciona o processo de busca para várias soluções "significativas".

Vamos explorar em detalhes o BSO e sua aplicabilidade para problemas de otimização multimodal. O algoritmo BSO foi desenvolvido por Shi et al. em 2015 e é inspirado no processo natural de brainstorming, em que pessoas se reúnem para gerar e compartilhar ideias na solução de um problema.

Existem várias variações do algoritmo, como o Hypo Variance Brain Storm Optimization, onde a avaliação da função objetivo é baseada em uma variante hipotética, em vez da dispersão gaussiana. Há também outras variações, como o Global-best Brain Storm Optimization, onde o melhor global inclui um esquema de reinicialização ativado pelo estado atual da população, combinado com atualizações por variáveis e agrupamento baseado na aptidão.

É importante notar que cada indivíduo no algoritmo BSO não representa apenas uma solução para o problema a ser otimizado, mas também um ponto de dados que revela o panorama do problema. Técnicas de inteligência coletiva e análise de dados podem ser combinadas para obter vantagens que superam o que cada método poderia alcançar isoladamente.

2. Descrição do algoritmo

O algoritmo BSO opera modelando esse processo, onde a população de soluções candidatas (chamadas de "indivíduos" ou "ideias") é atualizada iterativamente para convergir para a solução ideal. O algoritmo consiste nas seguintes etapas principais:

1. Inicialização:

- O algoritmo começa gerando uma população inicial de indivíduos, onde cada um representa uma solução potencial para o problema de otimização.
- Cada indivíduo é representado por um conjunto de variáveis de solução que determinam as características da solução.

2. Brainstorming:

- Nesta etapa, o algoritmo modela o processo de brainstorming, onde os indivíduos geram novas ideias (ou seja, novas soluções candidatas)
combinando e modificando suas próprias ideias e as ideias de outros indivíduos. - O processo de brainstorming é guiado por um conjunto de regras inspiradas no processo humano de brainstorming, incluindo:

• Geração aleatória de novas ideias
• Combinação de ideias de diferentes indivíduos
• Modificação de ideias existentes

3. Avaliação:

- As ideias recém-criadas (novas soluções candidatas) são avaliadas usando a função objetivo do problema de otimização.
- A função objetivo mede a qualidade ou aptidão de cada solução candidata, e o algoritmo visa encontrar a solução que minimize (ou maximize) essa função.

4. Seleção:

- Após a avaliação, o algoritmo seleciona os melhores indivíduos da população para serem mantidos na próxima iteração.
- O processo de seleção é baseado nos valores de aptidão dos indivíduos, onde aqueles com maior aptidão têm maior probabilidade de serem escolhidos.

5. Finalização:

- O algoritmo continua iterando pelas etapas de brainstorming, avaliação e seleção até que um critério de término seja atingido, como o número máximo de iterações ou a obtenção de uma qualidade-alvo da solução.

As características únicas do BSO que o diferenciam de outros métodos de otimização populacional incluem:

1. Clusterização. Os indivíduos são agrupados em clusters com base na similaridade de sua posição no espaço de busca. Isso é implementado usando o algoritmo de clusterização K-means.
2. Convergência. Nesta fase, os indivíduos dentro de cada cluster se agrupam em torno do centroide do cluster, imitando a fase de brainstorming em que os participantes se reúnem para discutir ideias.
3. Divergência. Novos indivíduos são gerados com base em um ou dois indivíduos no cluster. Esse processo simula a fase de brainstorming em que os participantes pensam fora da caixa e propõem novas ideias.
4. Seleção. Após a geração de novos indivíduos, eles são inseridos no grupo principal, onde ocorre a ordenação para que a próxima iteração trabalhe com as ideias melhoradas.
5. Mutação. Após a combinação de ideias e criação de novas, todas as ideias recém-criadas passam por mutação, para adicionar diversidade extra à população e evitar a convergência prematura.

Vamos apresentar a lógica do algoritmo BSO em pseudocódigo:

1. Inicialização dos parâmetros e geração da população inicial
2. Cálculo da aptidão de cada indivíduo na população
3. Enquanto os critérios de parada não forem atingidos:
    4. Cálculo da aptidão de cada indivíduo na população
    5. Determinação do melhor indivíduo na população
    6. Divisão da população em clusters, estabelecendo o melhor indivíduo de cada cluster como centro
    7. Para cada novo indivíduo na população:
        |7.1. Se a probabilidade pReplace for atendida:
        |    |Gerar um novo centro deslocado de um cluster aleatório (o centro é deslocado aleatoriamente)
        |7.2. Se a probabilidade pOne for atendida:
        |    |Selecionar um cluster aleatório
        |    |Se a probabilidade pOne_center for atendida:
        |    |    |7.2.a Selecionar o centro do cluster
        |    |Caso contrário:
        |         |7.2.b Selecionar um indivíduo aleatório dentro do cluster
        |7.3 Caso contrário:
        |         |Selecionar dois clusters
        |         |Se a probabilidade pTwo_center for atendida:
        |             |7.3.a Criar um novo indivíduo combinando os centros dos dois clusters
        |         |Caso contrário:
        |             |7.3.b Criar um novo indivíduo combinando as posições de dois indivíduos selecionados, um de cada cluster (os clusters devem ser diferentes)
        |7.4 Mutação: Adicionar uma perturbação gaussiana à posição do novo indivíduo
        |7.5 Se o novo indivíduo ultrapassar os limites do espaço de busca, refletir sua posição de volta ao espaço válido
    8. Atualizar a população com os novos indivíduos
    9. Voltar ao passo 4 até que o critério de parada seja atendido
10. Retornar o melhor indivíduo como solução
11. Fim do BSO

Operações detalhadas do passo 7:

A operação 7.1, em essência, não cria um novo indivíduo diretamente, mas desloca o centro de um cluster. O deslocamento ocorre aleatoriamente para cada coordenada, seguindo uma distribuição normal com uma distância específica, configurada por parâmetros externos.

A operação 7.2 decide entre o uso do centro ou de um indivíduo dentro do cluster selecionado, com a mutação sendo aplicada no passo 7.4 para criar a nova solução.

A operação 7.3 tem o objetivo de criar um novo indivíduo combinando os centros de dois clusters, ou indivíduos de clusters diferentes. Caso só exista um cluster não vazio, a combinação é feita com dois indivíduos desse cluster, imitando a troca de ideias entre clusters.

A operação de fusão é a seguinte:

onde:
Xf - novo indivíduo após a fusão,
v - número aleatório de 0 a 1,
X1 e X2 - dois indivíduos (ou dois centros de clusters) que devem ser combinados.

O valor da fórmula de fusão é que uma ideia será criada em um ponto aleatório entre duas outras ideias.

A operação de mutação pode ser descrita pela seguinte fórmula:

onde:
Xm - novo indivíduo após a mutação,
Xs - indivíduo selecionado para mutação,
n(µ, σ) - número aleatório gaussiano com média µ e desvio σ,
ξ - coeficiente de mutação, expresso por uma equação matemática.

O coeficiente de mutação é calculado pela fórmula:

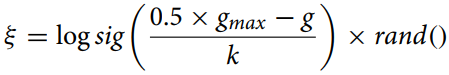
onde:
gmax - número máximo de iterações,
g - número da iteração atual,
k - coeficiente de ajuste.

Essa fórmula (coeficiente de mutação) é usada para calcular a distância reduzida entre indivíduos no algoritmo de otimização, permitindo uma mudança adaptativa no parâmetro de mutação. A função "logsig()" proporciona uma diminuição não linear suave do valor, enquanto a multiplicação por "rand" adiciona um elemento estocástico, útil para evitar convergência prematura e manter a diversidade da população.

O coeficiente de ajuste "k" no algoritmo Brain Storm Optimization (BSO) desempenha um papel importante no controle da velocidade de alteração do coeficiente "ξ" ao longo do tempo. O valor de "k" pode variar conforme a tarefa e os dados específicos, e é calculado empiricamente ou por métodos de ajuste de hiperparâmetros.

Em termos gerais, "k" deve ser escolhido para garantir o equilíbrio entre exploração e utilização prática no algoritmo. Se "k" for muito grande, "ξ" mudará muito lentamente, o que pode levar à convergência prematura do algoritmo. Se "k" for muito pequeno, "ξ" mudará muito rapidamente, resultando em uma exploração excessiva do espaço de busca e retardando a convergência.

A função sigmoide logística, também conhecida como função logística, é geralmente representada como σ(x) ou sig(x). Ela é calculada pela seguinte fórmula:

onde:
exp(-x) - representa a exponencial de -x.
1 / (1 + exp(-x)) garante um valor de saída no intervalo de 0 a 1.

Abaixo está o gráfico da função sigmoide. A diminuição não linear da função garante uma exploração nas iterações iniciais e um refinamento nas posteriores.

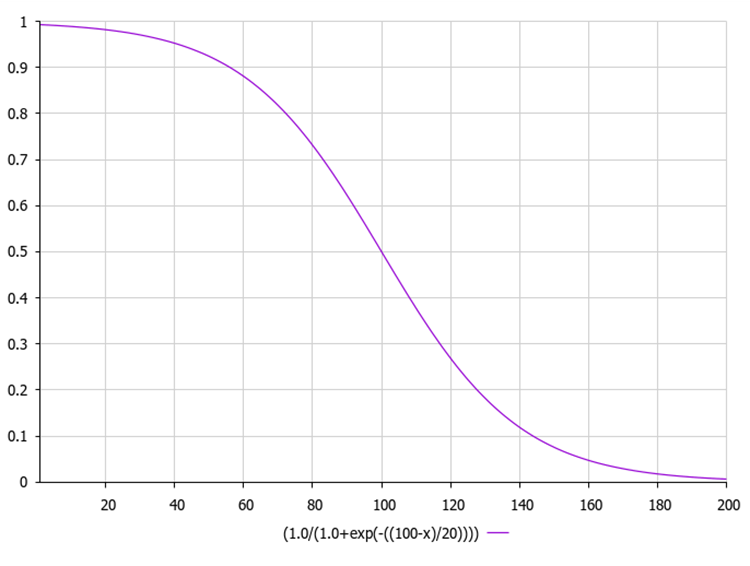
Abaixo está um exemplo de código para calcular o coeficiente de mutação juntamente com a função sigmoide, calculada por meio da exponencial.

Neste código, a função "sigmoid" calcula o valor sigmoide de um número de entrada "x", e a função "xi" calcula o valor de "ξ" segundo a fórmula acima. Aqui, "gmax" é o número máximo de iterações, "g" é o número da iteração atual, e "k" é o coeficiente de ajuste. A função "MathRand" gera um número aleatório de 0 a 32767, portanto, dividimos por 32767.0 para obter um número aleatório entre 0 e 1. Em seguida, calculamos o valor sigmoide desse número aleatório. Esse valor é retornado pela função "xi".

double sigmoid(double x) 
{
    return 1.0 / (1.0 + MathExp(-x));
}

double xi(int gmax, int g, double k) 
{
    double randNum = MathRand() / 32767.0; // Generate a random number from 0 to 1
    return sigmoid (0.5 * (gmax - g) / k) * randNum;
}

3. Método de Clusterização K-Means

No algoritmo BSO, para dividir ideias em grupos separados, é utilizado o método de análise de cluster com o uso de K-Médias (K-Means). O conjunto atual de "n" soluções para entrada na iteração é dividido em "m" categorias, com o objetivo de imitar o comportamento dos participantes de uma discussão em grupo e aumentar a eficiência da busca.

Um cluster separado é descrito pela estrutura "S_Cluster", que implementa o algoritmo K-Médias, sendo um método de clusterização popular.

Vamos analisar a estrutura:

• centroid[] - matriz representando o centroide do cluster.
• f - valor da aptidão do centroide.
• count - número de pontos no cluster.
• ideasList[] - lista de ideias.

A função "Init" inicializa a estrutura, ajustando o tamanho das matrizes "centroid" e "ideasList", além de definir o valor inicial de "f".

//——————————————————————————————————————————————————————————————————————————————
struct S_Cluster
{
    double centroid [];  //cluster centroid
    double f;            //centroid fitness
    int    count;        //number of points in the cluster
    int    ideasList []; //list of ideas

    void Init (int coords)
    {
      ArrayResize (centroid, coords);
      f = -DBL_MAX;
      ArrayResize (ideasList, 0, 100);
    }
};
//——————————————————————————————————————————————————————————————————————————————

A classe C_BSO_KMeans é uma implementação do algoritmo K-Médias para a clusterização de agentes no algoritmo de otimização BSO. Aqui está o que cada método faz:

1. KMeansInit - o método inicializa os centroides dos clusters, selecionando agentes aleatórios a partir dos dados. Para cada cluster, é escolhido um agente aleatório, e suas coordenadas são copiadas para o centroide do cluster.
2. VectorDistance - o método calcula a distância euclidiana entre dois vetores. Ele aceita dois vetores como argumentos e retorna a distância euclidiana entre eles.
3. KMeans - o método executa a lógica principal do algoritmo K-Médias para a clusterização de dados. Ele aceita um array de dados e um array de clusters como argumentos.

O método KMeans, durante sua execução, realiza os seguintes passos:

• Atribuição de pontos de dados ao centroide mais próximo.
• Atualização dos centroides com base na média dos pontos atribuídos a cada cluster.
• Repetição desses dois passos até que os centroides parem de mudar ou até que o número máximo de iterações seja atingido.

Центроид no método de clusterização K-Médias é o ponto central do cluster. No contexto do método K-Médias, o centroide representa a média aritmética de todos os pontos de dados pertencentes a esse cluster.
Em cada iteração do algoritmo K-Médias, os centroides são recalculados, e os pontos de dados são novamente agrupados em clusters de acordo com o centroide mais próximo com base na métrica escolhida.
Assim, os centroides desempenham um papel fundamental no método K-Médias, determinando a forma e a posição dos clusters.

Essa classe é uma parte essencial do algoritmo de otimização BSO, proporcionando a clusterização dos agentes para melhorar o processo de busca. O algoritmo K-Médias realiza a atribuição iterativa de pontos aos clusters e recalcula os centroides até que as mudanças cessem ou o número máximo de iterações seja atingido.

//——————————————————————————————————————————————————————————————————————————————
class C_BSO_KMeans
{
  public: //--------------------------------------------------------------------

  void KMeansInit (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    for (int i = 0; i < ArraySize (clust); i++)
    {
      int ind = MathRand () % dataSizeClust;
      ArrayCopy (clust [i].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);
    }
  }

  double VectorDistance (double &v1 [], double &v2 [])
  {
    double distance = 0.0;
    for (int i = 0; i < ArraySize (v1); i++)
    {
      distance += (v1 [i] - v2 [i]) * (v1 [i] - v2 [i]);
    }
    return MathSqrt (distance);
  }

  void KMeans (S_BSO_Agent &data [], int dataSizeClust, S_Clusters &clust [])
  {
    bool changed   = true;
    int  nClusters = ArraySize (clust);
    int  cnt       = 0;

    while (changed && cnt < 100)
    {
      cnt++;
      changed = false;

      //Assigning data points to the nearest centroid
      for (int d = 0; d < dataSizeClust; d++)
      {
        int    closest_centroid = -1;
        double closest_distance = DBL_MAX;

        if (data [d].f != -DBL_MAX)
        {
          for (int cl = 0; cl < nClusters; cl++)
          {
            double distance = VectorDistance (data [d].c, clust [cl].centroid);

            if (distance < closest_distance)
            {
              closest_distance = distance;
              closest_centroid = cl;
            }
          }

          if (data [d].label != closest_centroid)
          {
            data [d].label = closest_centroid;
            changed = true;
          }
        }
        else
        {
          data [d].label = -1;
        }
      }


      //Updating centroids
      double sum_c [];
      ArrayResize (sum_c, ArraySize (data [0].c));

      for (int cl = 0; cl < nClusters; cl++)
      {
        ArrayInitialize (sum_c, 0.0);

        clust [cl].count = 0;
        ArrayResize (clust [cl].ideasList, 0);

        for (int d = 0; d < dataSizeClust; d++)
        {
          if (data [d].label == cl)
          {
            for (int k = 0; k < ArraySize (data [d].c); k++)
            {
              sum_c [k] += data [d].c [k];
            }

            clust [cl].count++;
            ArrayResize (clust [cl].ideasList, clust [cl].count);
            clust [cl].ideasList [clust [cl].count - 1] = d;
          }
        }

        if (clust [cl].count > 0)
        {
          for (int k = 0; k < ArraySize (sum_c); k++)
          {
            clust [cl].centroid [k] = sum_c [k] / clust [cl].count;
          }
        }
      }
    }
  }
};
//——————————————————————————————————————————————————————————————————————————————

No algoritmo Brain Storm Optimization (BSO), a aptidão de um indivíduo é determinada pela qualidade da solução que ele representa, e na tarefa de otimização, a aptidão pode ser igual ao valor da função a ser otimizada.

O método específico de clusterização pode variar. Um dos enfoques comuns é o uso do método K-Médias, onde os centroides dos clusters são inicializados aleatoriamente e, em seguida, atualizados de forma iterativa para minimizar a soma dos quadrados das distâncias de cada ponto ao centroide do seu cluster.

É importante notar que, embora a aptidão desempenhe um papel fundamental no processo de clusterização, ela não é o único fator que influencia a formação dos clusters. Outros aspectos, como a distância entre os indivíduos no espaço de soluções, também podem desempenhar um papel importante. Isso ajuda o algoritmo a manter a diversidade na população e evitar a convergência prematura para soluções inadequadas.

O número de iterações necessárias para a convergência do algoritmo K-Médias depende de vários fatores, como o estado inicial dos centroides, a distribuição dos dados e o número de clusters. No entanto, em geral, o K-Médias costuma convergir em algumas dezenas até algumas centenas de iterações.

Também vale considerar que o K-Médias minimiza a soma dos quadrados das distâncias dos pontos até seus centroides mais próximos, o que pode não ser sempre o ideal dependendo da tarefa específica e da forma dos clusters nos dados. Em alguns casos, outros algoritmos de clusterização podem ser mais adequados.

O K-Means++ é uma versão aprimorada do algoritmo K-Médias, proposta em 2007 por David Arthur e Sergei Vassilvitskii. A principal diferença do K-Means++ em relação ao K-Médias padrão está na forma de inicializar os centroides. Em vez de escolher centroides iniciais de forma aleatória, o K-Means++ os seleciona de maneira a maximizar a distância entre eles. Isso ajuda a melhorar a qualidade da clusterização e acelera a convergência do algoritmo.

Aqui estão os principais passos da inicialização no K-Means++:

1. Escolher aleatoriamente o primeiro centroide dos pontos de dados.
2. Para cada ponto de dados, calcular sua distância até o centroide mais próximo, selecionado anteriormente.
3. Escolher o próximo centroide entre os pontos de dados de tal forma que a probabilidade de uma escolha seja diretamente proporcional à sua distância até o centroide mais próximo (ou seja, o ponto que tem a maior distância até o centroide mais próximo tem a maior probabilidade de ser selecionado como o próximo centroide).
4. Repetir os passos 2 e 3 até que k centroides tenham sido selecionados.

Após a inicialização dos centroides, o K-Means++ continua funcionando da mesma forma que o algoritmo K-Médias padrão. Esse método de inicialização ajuda a melhorar a qualidade da clusterização e acelera a convergência do algoritmo. No entanto, esse método é mais custoso em termos computacionais.

Se houver 1000 coordenadas para cada ponto, isso pode aumentar o custo computacional do algoritmo K-Means++, pois ele precisará calcular distâncias em um espaço de alta dimensionalidade. Contudo, o K-Means++ ainda pode ser eficiente (experimentos são necessários para confirmar essa hipótese), pois geralmente resulta em uma convergência mais rápida e uma melhor qualidade dos clusters.

Vale notar que, ao lidar com dados de alta dimensionalidade (como 1000 coordenadas), podem surgir problemas adicionais relacionados à "maldição da dimensionalidade". Isso pode tornar as distâncias entre os pontos menos significativas e dificultar a clusterização. Nesses casos, pode ser útil usar métodos de redução de dimensionalidade, como a PCA (Análise de Componentes Principais), antes de aplicar K-means ou K-means++. Isso pode ajudar a reduzir a dimensionalidade dos dados e tornar a clusterização mais eficiente.

A redução da dimensionalidade dos dados é uma etapa importante no processamento, especialmente ao lidar com inúmeras coordenadas ou atributos. Isso ajuda a simplificar os dados, reduzir os custos computacionais e melhorar o desempenho dos algoritmos de clusterização. A seguir, alguns métodos de redução de dimensionalidade frequentemente usados na clusterização:

1. Análise de Componentes Principais (PCA). Este método transforma um conjunto de dados com muitas variáveis em um conjunto com um número menor, preservando o máximo de informação possível.
2. Escalonamento Multidimensional (MDS). O método busca encontrar uma estrutura de baixa dimensionalidade que mantenha as distâncias entre os pontos, como no espaço original de alta dimensionalidade.
3. t-Distributed Stochastic Neighbor Embedding (t-SNE). Este é um método não linear de redução de dimensionalidade, especialmente eficaz para a visualização de dados de alta dimensionalidade.
4. Autoencoders. São redes neurais usadas para reduzir a dimensionalidade dos dados. Eles funcionam aprendendo a codificar os dados de entrada em uma representação compacta e, em seguida, decodificá-la de volta para os dados originais.
5. Análise de Componentes Independentes (ICA). Este método estatístico transforma o conjunto de dados em componentes independentes, que podem ser mais informativos (refletindo melhor a estrutura ou os aspectos importantes dos dados, como fatores ocultos ou separação de classes) do que os dados originais.
6. Análise Discriminante Linear (LDA). Esse método é usado para encontrar combinações lineares de características que separam bem duas ou mais classes.

Portanto, embora o K-Means++ possa ser mais custoso computacionalmente na fase de inicialização, especialmente para dados de alta dimensionalidade, ele ainda pode ser justificado em alguns casos. No entanto, é sempre importante realizar experimentos e comparar diferentes abordagens para determinar qual funciona melhor para sua tarefa e conjunto de dados específicos.

Para quem deseja experimentar mais com o método K-means++, segue o método de inicialização para esse algoritmo (o restante do código não difere do código do K-means simples).

O código abaixo apresenta uma implementação da inicialização do algoritmo K-means++. A função recebe um array de pontos de dados, representados pela estrutura S_BSO_Agent, o tamanho dos dados (dataSizeClust), e um array de clusters, representados pela estrutura S_Cluster. O método inicializa o primeiro centroide aleatoriamente a partir dos pontos de dados. Em seguida, para cada centroide subsequente, o algoritmo calcula a distância de cada ponto de dados até o centroide mais próximo e escolhe o próximo centroide com uma probabilidade proporcional à distância. Isso é feito gerando um número aleatório "r" no intervalo da soma de todas as distâncias e, em seguida, percorrendo todos os pontos de dados, subtraindo "r" pela distância de cada ponto, até que "r" seja menor ou igual à distância do ponto atual. Nesse caso, o ponto atual é selecionado como o próximo centroide. Esse processo é repetido até a inicialização de todos os centroides.

No geral, a inicialização do K-Means++ foi implementada, sendo uma versão aprimorada da inicialização no algoritmo K-Means padrão. Os centroides são escolhidos de maneira a minimizar a soma potencial dos quadrados das distâncias entre os centroides e os pontos de dados, o que resulta em uma clusterização mais eficiente e estável.

void KMeansPlusPlusInit (S_BSO_Agent &data [], int dataSizeClust, S_Cluster &clust [])
{
  // Choose the first centroid randomly
  int ind = MathRand () % dataSizeClust;
  ArrayCopy (clust [0].centroid, data [ind].c, 0, 0, WHOLE_ARRAY);

  for (int i = 1; i < ArraySize (clust); i++)
  {
    double sum = 0;
      
    // Compute the distance from each data point to the nearest centroid
    for (int j = 0; j < dataSizeClust; j++)
    {
      double minDist = DBL_MAX;
       
      for (int k = 0; k < i; k++)
      {
        double dist = VectorDistance (data [j].c, clust [k].centroid);
          
        if (dist < minDist)
        {
            minDist = dist;
        }
      }
        
      data [j].minDist = minDist;
      sum += minDist;
    }

    // Choose the next centroid with a probability proportional to the distance
    double r = MathRand () * sum;
      
    for (int j = 0; j < dataSizeClust; j++)
    {
      if (r <= data [j].minDist)
      {
        ArrayCopy (clust [i].centroid, data [j].c, 0, 0, WHOLE_ARRAY);
        break;
      }
      r -= data [j].minDist;
    }
  }
}

Continua...

Neste artigo, examinamos a estrutura lógica do algoritmo BSO, bem como os métodos de clusterização e formas de redução da dimensionalidade na tarefa de otimização. No próximo artigo, concluiremos o estudo do algoritmo BSO e faremos uma análise de seu desempenho.