Algoritmo de Busca Cooperativa Artificial (Artificial Cooperative Search, ACS)

Conteúdo:

1.Introdução
2.Implementação do algoritmo
3.Resultados dos testes

1. Introdução

A natureza é uma fonte inesgotável de inspiração para cientistas e engenheiros que buscam criar soluções inovadoras. Um dos fenômenos notáveis é o mutualismo. Ele se trata de uma interação biológica benéfica entre diferentes espécies vivas. Os organismos vivos que participam de relações mutualísticas buscam obter benefícios mútuos dessa interação, voltados para o desenvolvimento e a diversidade da população. Para entender isso, darei alguns exemplos de relações mutualísticas (simbióticas) entre organismos vivos, nas quais ambos obtêm benefícios:

1. Plantas com flores e polinizadores:

• As plantas produzem néctar e outras recompensas para atrair polinizadores, como insetos, pássaros e morcegos.
• Os polinizadores, por sua vez, transportam o pólen de uma flor para outra, o que favorece a reprodução das plantas.

2. Fungos e raízes de plantas (micorriza):

• Os fungos penetram nas raízes das plantas e recebem delas compostos orgânicos, produtos da fotossíntese. 
• Os fungos, por sua vez, aumentam a superfície de absorção das raízes, melhorando a disponibilidade de água e minerais para as plantas.

3. Cupins e bactérias simbióticas:

• Os cupins abrigam em seu intestino bactérias simbióticas, que os ajudam a digerir a celulose, principal componente da madeira.
• As bactérias recebem nutrientes dos cupins, enquanto os cupins obtêm a capacidade de digerir fibras.

Esses exemplos demonstram como os organismos vivos interagem para obter benefícios mútuos e aumentar suas chances de sobrevivência.

O algoritmo ACS também se inspira no comportamento migratório de superorganismos eusociais que habitam o mesmo ambiente. Alguns exemplos desse comportamento migratório de superorganismos eusociais:

1. Colônias de formigas:

• Durante a migração, as colônias de formigas transportam larvas, pupas e outros elementos importantes do ninho consigo.

2. Famílias de abelhas:

• Durante a enxameação, as famílias de abelhas podem migrar temporariamente de sua colmeia para fundar uma nova colônia em outro local.
• Durante a migração do enxame, as abelhas transportam rainhas, larvas e os suprimentos necessários de mel para fundar o novo ninho.

Uma característica comum desses exemplos é que os superorganismos eusociais, como formigas, cupins, abelhas e vespas, são capazes de deslocar coletivamente suas colônias em resposta a mudanças no ambiente ou ao esgotamento de recursos. Essa capacidade migratória permite que se adaptem a condições mutáveis e assegura a sobrevivência de todo o superorganismo. A interação biológica mutualística e cooperativa entre dois superorganismos eusociais, que habitam o mesmo ambiente, inspirou a criação do algoritmo ACS. Neste algoritmo, o conceito de habitat corresponde à noção de espaço de busca, relacionado à tarefa de otimização correspondente.

Conceitualmente, o algoritmo ACS considera soluções aleatórias do problema como superorganismos artificiais, que migram para áreas de forrageamento mais produtivas. Dois superorganismos principais, designados como α e β, contêm sub-superorganismos artificiais, cujo tamanho corresponde ao tamanho da população. A dimensionalidade da população é equivalente ao número de indivíduos nesses sub-superorganismos. No processo de evolução conjunta, os superorganismos α e β interagem de forma semelhante a predadores e presas, utilizando duas populações dinâmicas para explorar eficientemente o espaço de busca e encontrar o ótimo global para problemas de otimização numérica.

O algoritmo ACS foi proposto por Pinar Civicioglu em 2013. Ele começa a funcionar usando duas populações básicas, que contêm soluções candidatas dentro da região de confiança. Em seguida, o algoritmo cria duas novas populações — predadores e presas, mapeando os valores das populações iniciais α e β usando passos aleatórios e uma matriz binária. Além disso, uma quinta população é calculada com base nos valores nas populações de predadores e presas. O processo envolve a atualização das populações iniciais ao longo de um número especificado de iterações, sendo a melhor solução extraída dessas duas populações.

A migração e a evolução de dois superorganismos artificiais, que interagem biologicamente entre si para alcançar o valor extremo global da função objetivo, em um processo semelhante ao comportamento cooperativo na natureza, são a chave para a alta eficiência do ACS em problemas de otimização numérica. Essa abordagem única de interação biologicamente motivada entre populações permite que o algoritmo ACS alcance uma impressionante velocidade de convergência e alta precisão nas soluções. Graças à sua capacidade de encontrar soluções ótimas de forma rápida e precisa, o ACS se mostrou uma poderosa ferramenta para resolver uma ampla gama de problemas de otimização numérica.

Neste artigo, descreverei em detalhes o conceito por trás do algoritmo ACS e demonstrarei suas notáveis capacidades. Os leitores obterão uma compreensão profunda de como a inspiração biológica pode ser implementada com sucesso em algoritmos de otimização avançados, capazes de resolver problemas complexos com alta eficiência. Então, vamos lá...

2. Implementação do algoritmo

O algoritmo de Busca Cooperativa Artificial (ACS) funciona da seguinte maneira:

1. Inicialização. Define-se o tamanho da população "popSize", o número de variáveis "N", os limites inferiores "XLow" e superiores "XHi" para as variáveis, bem como a probabilidade de interação biológica no ACS "Probab". Em seguida, são geradas as posições iniciais das populações "A" e "B", e seus valores de adaptabilidade "YA" e "YB" são calculados.

2. Ciclo por iterações. Em cada iteração, os seguintes passos são executados:

• Seleção. Determina-se qual conjunto de agentes das populações "A" ou "B" será usado como "predador" na iteração atual.
• Embaralhamento das "presas". As posições dos agentes no conjunto selecionado são embaralhadas.
• Mutação. As posições dos agentes são atualizadas usando um coeficiente de escala "R" gerado aleatoriamente. Os "predadores" sofrem mutação utilizando as informações dos vetores de solução das "presas".
  
• Preenchimento da matriz binária "M". É criada uma matriz binária "M", que determina quais variáveis serão atualizadas na iteração atual.
• Atualização das posições dos agentes. As posições dos agentes são atualizadas com base nos valores da matriz "M". Se o valor na "M" for 1, a variável correspondente do agente é atualizada.
• Controle de limites. Se a posição atualizada do agente ultrapassar os limites estabelecidos, ela é ajustada.
• Atualização da seleção. Neste estágio, as melhores soluções são preservadas para a próxima iteração do algoritmo.
• Atualização da melhor solução global. Se uma solução melhor for encontrada, ela é armazenada.

3. Retorno do resultado. Ao final da execução do algoritmo, retornam-se a melhor solução global e seu valor de adaptabilidade.

É importante destacar que este algoritmo utiliza alguns operadores exclusivos, como o operador de embaralhamento das "presas" e o operador de mutação, que envolvem o uso da matriz binária "M".

A matriz "M" é um array bidimensional com "popSize" linhas (número de candidatos na população) e "N" colunas (número de variáveis em cada candidato). Cada elemento da matriz pode ser 0 ou 1. A matriz "M" é usada para determinar quais candidatos serão selecionados para atualização na população. Os valores 0 e 1 na matriz indicam se o candidato correspondente será selecionado para atualização com base em valores aleatórios "Rand" e na probabilidade de interação "Probab".
A matriz "M" ajuda a regular o processo de seleção de candidatos para atualização na população. Assim, a matriz "M" desempenha um papel fundamental no processo de evolução da população e na busca da solução ótima no ACS.

Vamos analisar cada passo do algoritmo ACS em forma de pseudocódigo:

1. Inicialização:
   - Definir os parâmetros:
       - popSize - tamanho da população
       - N - número de variáveis
       - MaxIter - número máximo de iterações
       - XLow - limites inferiores para as variáveis
       - XHi - limites superiores para as variáveis
       - Probab - probabilidade de interação biológica
   - Rand - função que retorna números uniformemente distribuídos no intervalo (0, 1)
   - GlobMax inicializado com o valor negativo de DBL_MAX

2. Ciclo principal:
   - Para cada elemento da população (I = 1 até popSize):
      - Para cada variável (J = 1 até N):
        - Calcular os valores iniciais A(I,J) e B(I,J) no intervalo [XLow(J), XHi(J)]
     - Calcular os valores iniciais da função objetivo YA(I) = Fx(A(I,:)) e YB(I) = Fx(B(I,:))
   - Iniciar o ciclo principal de iterações (Iter = 1 até MaxIter)

3. Seleção:
   - Selecionar aleatoriamente se A ou B será usado como predador (Predator):
     - Se Rand < 0,5, então Predator = A, Ypred = YA, Key = 1
     - Caso contrário, Predator = B, Ypred = YB, Key = 2
   - Seleciona-se aleatoriamente se A ou B será usado como presa (Prey):
      - Se Rand < 0,5, então Prey = A
      - Caso contrário, Prey = B
   - Prey é embaralhado aleatoriamente
   - Calcula-se o parâmetro R:
      - Se Rand < 0,5, então R = 4 * Rand * (Rand - Rand)
      - Caso contrário, R = 1/exp(4 * Rand)
   - Cria-se uma matriz binária M de tamanho popSize x N, preenchida com 1
   - Alguns elementos da matriz M são definidos como 0 aleatoriamente com probabilidade Probab
   - Se Rand < Probab, alguns elementos da matriz M são definidos aleatoriamente como 0 ou 1
   - Para cada linha da matriz M, se a soma dos elementos for igual a N, um elemento é selecionado aleatoriamente e definido como 0

4. Mutação:
   - Calcula-se um novo valor X = Predator + R * (Prey - Predator)
   - Para cada elemento da população (I = 1 até popSize) e cada variável (J = 1 até N):
     - Se o elemento correspondente na matriz M for maior que 0, então X(I,J) = Predator(I,J)
     - Se X(I,J) ultrapassar os limites [XLow(J), XHi(J)], então X(I,J) é ajustado para um valor aleatório dentro desse intervalo

5. Atualização da seleção:
   - Para cada elemento da população (I = 1 até popSize):
     - Se Fx(X(I,:)) < Ypred(i), então Predator(I,:) = X(I,:) e Ypred(I) = Fx(X(I,:))
   - Se Key = 1, então A = Predator e YA = Ypred, caso contrário, B = Predator e YB = Ypred
   - Ybest = min(Ypred)
   - Ibest = índice da linha do Predator correspondente a Ybest
   - Se Ybest > GlobMax, então GlobMax = Ybest e GlobMax = Predator(Ibest,:)

6. Retorno do resultado:
   - Retornam-se GlobMax e o vetor GlobMaxX

Passamos para a descrição da implementação do algoritmo ACS. Para descrever as populações (cinco no algoritmo), usaremos uma estrutura simples "S_D":

• c [] - é um array para armazenar coordenadas (parâmetros a serem otimizados na tarefa)
  
• Init (int coords) - o método ajusta o tamanho do array "c" para o valor especificado em "coords" (número de coordenadas), utilizando a função "ArrayResize"

De modo geral, essa estrutura é usada para criar um objeto que contém um array de números reais. O método "Init" é utilizado para ajustar o tamanho desse array.

//——————————————————————————————————————————————————————————————————————————————
struct S_D
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    double c [];
};
//——————————————————————————————————————————————————————————————————————————————

Para descrever a matriz "M" vamos criar a estrutura "S_C", que se diferencia da estrutura "S_D" pelo tipo de campo:

• c[] - array que armazena os caracteres da matriz "0" e "1"
  
• Init (int coords) - o método ajusta o tamanho do array "c" para o valor especificado em "coords", utilizando a função "ArrayResize"

//——————————————————————————————————————————————————————————————————————————————
struct S_C
{
    void Init (int coords)
    {
      ArrayResize (c, coords);
    }
    char c [];
};
//——————————————————————————————————————————————————————————————————————————————

O algoritmo será descrito na forma da classe "C_AO_ACS", que é derivada da classe base "C_AO" e contém os seguintes campos:

•  ~C_AO_ACS () { } - destrutor da classe, chamado quando o objeto da classe é excluído. Neste caso, o destrutor é vazio.
• C_AO_ACS () - construtor da classe, que inicializa os membros de dados da classe e ajusta o tamanho do array "params" e define os valores padrão dos parâmetros do algoritmo.
• SetParams () - método que define os valores de "popSize" e "bioProbab" com base nos valores no array "params".
• Init () - método recebe vários argumentos e retorna um valor booleano. 
  
• Moving () e Revision () - são métodos que contêm a lógica principal do algoritmo.
• bioProbab - membro de dados que armazena a probabilidade de interação biológica.
• S_D A [], S_D B [], S_D Predator [], S_D Prey [], S_C M [], double YA [], double YB [], double Ypred [], int Key, int phase - membros de dados privados da classe.
• ArrayShuffle () - método privado, embaralha os elementos do array.
  

//——————————————————————————————————————————————————————————————————————————————
class C_AO_ACS : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ACS () { }
  C_AO_ACS ()
  {
    ao_name = "ACS";
    ao_desc = "Artificial Cooperative Search";
    ao_link = "https://www.mql5.com/ru/articles/15004";

    popSize   = 1;   //population size
    bioProbab = 0.9; //biological interaction probability

    ArrayResize (params, 2);

    params [0].name = "popSize";   params [0].val = popSize;
    params [1].name = "bioProbab"; params [1].val = bioProbab;
  }

  void SetParams ()
  {
    popSize   = (int)params [0].val;
    bioProbab = params      [1].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  double bioProbab; //biological interaction probability

  private: //-------------------------------------------------------------------
  S_D A              [];
  S_D B              [];
  S_D Predator       [];
  S_D Prey           [];

  S_C M              [];

  double YA          [];
  double YB          [];
  double Ypred       [];

  int Key;
  int phase;

  void ArrayShuffle (double &arr []);
};
//——————————————————————————————————————————————————————————————————————————————

A seguir, apresentamos o método "Init" da classe "C_AO_ACS". O método realiza a inicialização do objeto da classe:

• Init () - declaração do método. Ele recebe quatro argumentos: intervalo mínimo de busca "rangeMinP", intervalo máximo de busca "rangeMaxP", passo de busca "rangeStepP" e número de épocas "epochsP", que por padrão é 0.
• if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; - chamada da função "StandardInit", que realiza a inicialização padrão da classe base. Se "StandardInit" retornar "false", o método "Init" é imediatamente finalizado e retorna "false".
• No laço for (int i = 0; i < popSize; i++), cada elemento dos arrays "A", "B", "Predator", "Prey" e "M" é inicializado utilizando o método "Init".
• ArrayResize (YA, popSize) e linhas semelhantes ajustam o tamanho dos arrays "YA", "YB" e "Ypred" para o tamanho "popSize".
• ArrayInitialize (YA, -DBL_MAX) e linhas semelhantes inicializam todos os elementos dos arrays "YA", "YB" e "Ypred" com o valor "-DBL_MAX".
• No laço aninhado "for", cada elemento "c" de cada objeto nos arrays "A" e "B" é inicializado com um valor aleatório dentro do intervalo especificado.
• phase = 0 define o valor de phase como 0.
  

O algoritmo original, descrito pelos autores, não divide a lógica em fases. Para implementar o algoritmo de acordo com o estilo adotado por nós para todos os algoritmos populacionais, tive que adicionar fases. Isso foi necessário porque o ACS utiliza o cálculo prévio da adaptabilidade dos agentes para as duas populações "A" e "B". Para realizar essas operações de forma sequencial nos métodos, foi adicionada a divisão em fases.

//——————————————————————————————————————————————————————————————————————————————
bool C_AO_ACS::Init (const double &rangeMinP  [], //minimum search range
                     const double &rangeMaxP  [], //maximum search range
                     const double &rangeStepP [], //step search
                     const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  ArrayResize (A,         popSize);
  ArrayResize (B,         popSize);
  ArrayResize (Predator,  popSize);
  ArrayResize (Prey,      popSize);

  ArrayResize (M,         popSize);

  for (int i = 0; i < popSize; i++)
  {
    A         [i].Init (coords);
    B         [i].Init (coords);
    Predator  [i].Init (coords);
    Prey      [i].Init (coords);

    M         [i].Init (coords);
  }

  ArrayResize (YA,    popSize);
  ArrayResize (YB,    popSize);
  ArrayResize (Ypred, popSize);

  ArrayInitialize (YA,    -DBL_MAX);
  ArrayInitialize (YB,    -DBL_MAX);
  ArrayInitialize (Ypred, -DBL_MAX);

  // Initialization
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      A [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
      B [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab();
    }
  }

  phase = 0;
 
  return true;
}
//——————————————————————————————————————————————————————————————————————————————

O método "Moving" da classe "C_AO_ACS" implementa a lógica principal de movimentação dos indivíduos no algoritmo. Este método realiza várias operações, incluindo a cópia de arrays, seleção, permutação, mutação e cruzamento.

• if (phase == 0) - nesta fase, os indivíduos da população "A" são copiados.
  
• if (phase == 1) - nesta fase, a adaptabilidade dos indivíduos da população "A" é retornada, e os indivíduos da população "B" são copiados.
• if (phase == 2) - nesta fase, a adaptabilidade dos indivíduos da população "B" é retornada, e toda a lógica subsequente do algoritmo é executada. 
  
• Selection - o bloco executa a operação de seleção. Dependendo de um número aleatório, os arrays "A" ou "B" são copiados para o array "Predator", e os valores correspondentes são copiados para o array "Ypred".
• Permutation of Prey - neste bloco, ocorre a operação de permutação dos elementos do array "Prey".
• R - a variável é declarada e, em seguida, inicializada com um dos dois valores possíveis, dependendo de um número aleatório.
• Fill binary matrix M with 1s - neste bloco, a matriz binária "M" é preenchida com valores 1.
• Additional operations with matrix M - o bloco realiza operações adicionais com a matriz "M", incluindo a alteração de alguns de seus elementos para 0 ou 1, dependendo de um número aleatório e da probabilidade de interação biológica "bioProbab".
• Mutation - o bloco realiza a operação de mutação, na qual os elementos do array "a" são modificados com base nos elementos dos arrays "Predator" e "Prey", além do valor de "R".
• Crossover - o bloco realiza a operação de cruzamento, onde alguns elementos do array "a" são substituídos por elementos do array "Predator".
• Boundary control - neste bloco, é feito o controle de limites, em que os elementos do array "a" que ultrapassam os limites do intervalo dos parâmetros otimizados são substituídos por valores aleatórios dentro desse intervalo.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Moving ()
{
  //----------------------------------------------------------------------------
  if (phase == 0)
  {
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, A [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 1)
  {
    for (int i = 0; i < popSize; i++) YA [i] = a [i].f;
    for (int i = 0; i < popSize; i++) ArrayCopy (a [i].c, B [i].c);

    phase++;
    return;
  }

  //----------------------------------------------------------------------------
  if (phase == 2)
  {
    for (int i = 0; i < popSize; i++) YB [i] = a [i].f;

    phase++;
  }

  //----------------------------------------------------------------------------
  // Selection
  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, A [i].c);
    }

    ArrayCopy (Ypred, YA);
    Key = 1;
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Predator [i].c, B [i].c);
    }

    ArrayCopy (Ypred, YB);
    Key = 2;
  }

  if (u.RNDprobab () < 0.5)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, A [i].c);
    }
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (Prey [i].c, B [i].c);
    }
  }

  // Permutation of Prey
  for (int i = 0; i < popSize; i++)
  {
    ArrayShuffle (Prey [i].c);
  }

  double R;

  if (u.RNDprobab () < 0.5)
  {
    R = 4 * u.RNDprobab () * u.RNDfromCI (-1.0, 1.0);
  }
  else R = 1 / MathExp (4 * MathRand () / 32767.0);

  // Fill binary matrix M with 1s
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      M [i].c [j] = 1;
    }
  }

  // Additional operations with matrix M
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      if (u.RNDprobab () < bioProbab)
      {
        M [i].c [j] = 1;
      }
      else
      {
        M [i].c [j] = 0;
      }
    }
  }

  for (int i = 0; i < popSize; i++)
  {
    int sum = 0;

    for (int c = 0; c < coords; c++) sum += M [i].c [c];

    if (sum == coords)
    {
      int j = MathRand () % coords;
      M [i].c [j] = 0;
    }
  }

  // Mutation
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = Predator [i].c [j] + R * (Prey [i].c [j] - Predator [i].c [j]);

      // Crossover
      if (M [i].c [j] > 0)
      {
        a [i].c [j] = Predator [i].c [j];
      }

      // Boundary control
      if (a [i].c [j] < rangeMin [j] || a [i].c [j] > rangeMax [j])
      {
        a [i].c [j] = rangeMin [j] + (rangeMax [j] - rangeMin [j]) * u.RNDprobab ();
      }
    }
  }
 
  for (int i = 0; i < popSize; i++)
  {
    for (int j = 0; j < coords; j++)
    {
      a [i].c [j] = u.SeInDiSp (a [i].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
    }
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "Revision" da classe "C_AO_ACS". Este método realiza várias operações, como a ordenação e cópia inversa dos arrays, além da atualização do melhor valor da solução global.

• if (phase < 3) return - a lógica principal do método não é executada até que as três fases de preparação das populações sejam concluídas, permitindo sua interação posterior.
• Selection update - o bloco realiza a atualização da seleção de indivíduos. Para cada indivíduo no array "a", verifica-se se seu valor de adaptabilidade "f" supera o valor correspondente no array "Ypred".
• if (Key == 1) e else - nesses blocos, dependendo do valor de "Key", os elementos do array "Predator" são copiados do array "A" ou "B", e os valores correspondentes são copiados do array "Ypred" de "YA" ou "YB".
• ArraySort (Ypred); ArrayReverse (Ypred, 0, WHOLE_ARRAY) - o array "Ypred", que contém os valores de adaptabilidade, é ordenado e depois invertido para que os valores fiquem em ordem decrescente.
• Ybest = Ypred [0]; int Ibest = ArrayMaximum (Ypred) - aqui, "Ybest" é definido como o valor máximo em "Ypred", e "Ibest" é o índice desse valor máximo.
• if (Ybest > fB) - se "Ybest" exceder o melhor valor atual "fB", então "fB" é atualizado, e os elementos correspondentes dos arrays "a" e "cB" são copiados do array "Predator".

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::Revision ()
{
  if (phase < 3) return;

  // Selection update
  for (int i = 0; i < popSize; i++)
  {
    double d = a [i].f;

    if (d > Ypred [i])
    {
      ArrayCopy (Predator [i].c, a [i].c);
      Ypred [i] = d;
    }
  }

  if (Key == 1)
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (A [i].c, Predator [i].c);
    }

    ArrayCopy (YA, Ypred);
  }
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      ArrayCopy (B [i].c, Predator [i].c);
    }

    ArrayCopy (YB, Ypred);
  }

  ArraySort (Ypred);
  ArrayReverse (Ypred, 0, WHOLE_ARRAY);
  double Ybest = Ypred [0];
  int Ibest = ArrayMaximum (Ypred);

  if (Ybest > fB)
  {
    fB = Ybest;
    ArrayCopy (a [Ibest].c, Predator [Ibest].c);
    ArrayCopy (cB, Predator [Ibest].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

O método "ArrayShuffle" da classe "C_AO_ACS" realiza a operação de embaralhamento aleatório dos elementos do array.

• for (int i = n - 1; i > 0; i--) - o laço percorre o array "arr" de trás para frente, começando do último elemento.
• j = MathRand () % (i + 1) - a variável "j" é definida como um número aleatório entre "0" e "i".
• tmp = arr [i]; arr [i] = arr [j]; arr [j] = tmp - essas linhas trocam os elementos "arr[i]" e "arr[j]" de posição.

Como resultado deste método, os elementos do array "arr" são embaralhados em ordem aleatória.

//——————————————————————————————————————————————————————————————————————————————
void C_AO_ACS::ArrayShuffle (double &arr [])
{
  int n = ArraySize (arr);
  for (int i = n - 1; i > 0; i--)
  {
    int j = MathRand () % (i + 1);
    double tmp = arr [i];
    arr [i] = arr [j];
    arr [j] = tmp;
  }
}
//——————————————————————————————————————————————————————————————————————————————

3. Resultados dos testes

A originalidade do algoritmo é confirmada pelos testes realizados. Este algoritmo se destaca por sua capacidade de alcançar resultados excepcionais mesmo com a redução do tamanho da população. Uma característica interessante é que, ao aumentar o número de iterações, o algoritmo pode atingir 100% de convergência em determinadas funções de teste, o que o diferencia de outros algoritmos, que não conseguem convergir mesmo com o aumento do número de execuções da função de adaptabilidade (fitness). Essa característica é notável, pois o algoritmo mostra resistência a ficar preso em "armadilhas" locais.

Vamos observar como os resultados do algoritmo mudam em função do tamanho da população. Normalmente, utilizamos uma média de 50 indivíduos na população; no entanto, durante os testes, o algoritmo começou a apresentar bons resultados com valores mais baixos de tamanho de população.

Nos resultados impressos do algoritmo no ambiente de testes, com o parâmetro de 10 indivíduos na população e o número constante de execuções da função de adaptabilidade em 10.000, o algoritmo atingiu um resultado de 49,97%.

ACS|Artificial Cooperative Search|10.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8213829114300768
25 Hilly's; Func runs: 10000; result: 0.5418951009344799
500 Hilly's; Func runs: 10000; result: 0.2811381329747021
=============================
5 Forest's; Func runs: 10000; result: 0.9750514085798038
25 Forest's; Func runs: 10000; result: 0.5078176955906151
500 Forest's; Func runs: 10000; result: 0.20112458337102135
=============================
5 Megacity's; Func runs: 10000; result: 0.736923076923077
25 Megacity's; Func runs: 10000; result: 0.31446153846153846
500 Megacity's; Func runs: 10000; result: 0.11721538461538572
=============================
All score: 4.49701 (49.97%)

Nos resultados impressos do algoritmo no ambiente de testes, com o parâmetro de 3 indivíduos na população e o número constante de execuções da função de adaptabilidade em 10.000, o algoritmo atingiu um resultado de 55,23%.

ACS|Artificial Cooperative Search|3.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.8275253778390631
25 Hilly's; Func runs: 10000; result: 0.6349216357701294
500 Hilly's; Func runs: 10000; result: 0.29382093872076825
=============================
5 Forest's; Func runs: 10000; result: 0.9998874875962974
25 Forest's; Func runs: 10000; result: 0.6985911632646721
500 Forest's; Func runs: 10000; result: 0.2132502183011688
=============================
5 Megacity's; Func runs: 10000; result: 0.7507692307692307
25 Megacity's; Func runs: 10000; result: 0.4270769230769231
500 Megacity's; Func runs: 10000; result: 0.1252615384615397
=============================
All score: 4.97110 (55.23%)

Nos resultados impressos do algoritmo no ambiente de testes, com o parâmetro de 1 indivíduo na população e o número constante de execuções da função de adaptabilidade em 10.000, o algoritmo atingiu um resultado de 58,06%.

ACS|Artificial Cooperative Search|1.0|0.9|
=============================
5 Hilly's; Func runs: 10000; result: 0.7554725186591347
25 Hilly's; Func runs: 10000; result: 0.7474431551529281
500 Hilly's; Func runs: 10000; result: 0.3040669213089683
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999993218
25 Forest's; Func runs: 10000; result: 0.888607840003743
500 Forest's; Func runs: 10000; result: 0.2241289484506152
=============================
5 Megacity's; Func runs: 10000; result: 0.6907692307692308
25 Megacity's; Func runs: 10000; result: 0.4818461538461539
500 Megacity's; Func runs: 10000; result: 0.1332153846153859
=============================
All score: 5.22555 (58.06%)

Pode surgir a dúvida de como ocorre a interação na população quando há apenas um indivíduo. Lembre-se de que o algoritmo utiliza 5 populações, e a interação acontece entre os indivíduos dessas populações. Apesar do número muito pequeno de indivíduos, o algoritmo mantém a diversidade nas populações e evita o efeito de "gargalo".

Na visualização do comportamento do algoritmo em funções de teste, vale destacar a ausência de qualquer efeito de clusterização e o comportamento aparentemente caótico dos agentes. Os agentes exploram áreas do espaço de busca, inclusive em regiões onde não há direções promissoras. Essa característica é bem visível nas funções Forest e Megacity, que possuem amplas áreas planas com pouca variação no relevo.

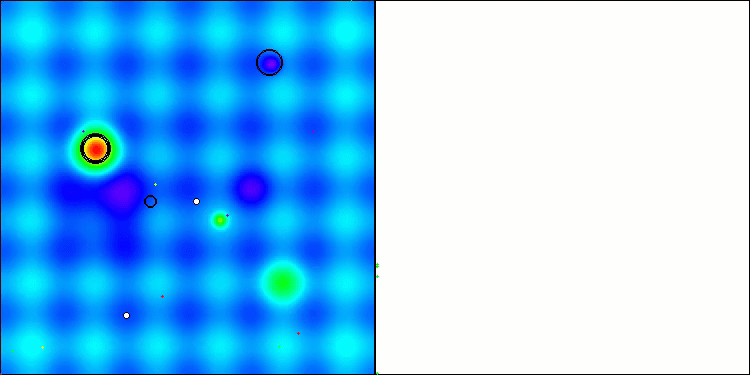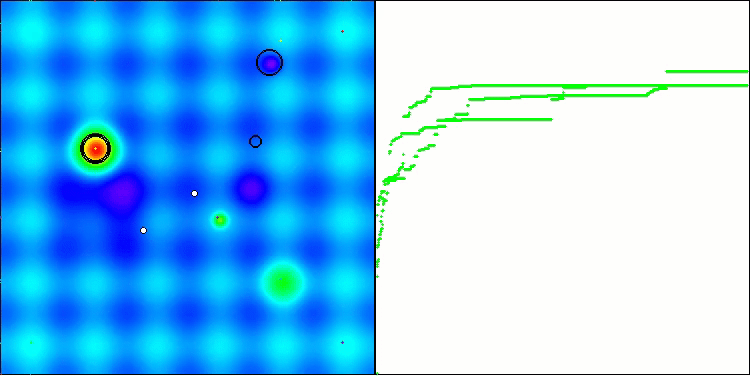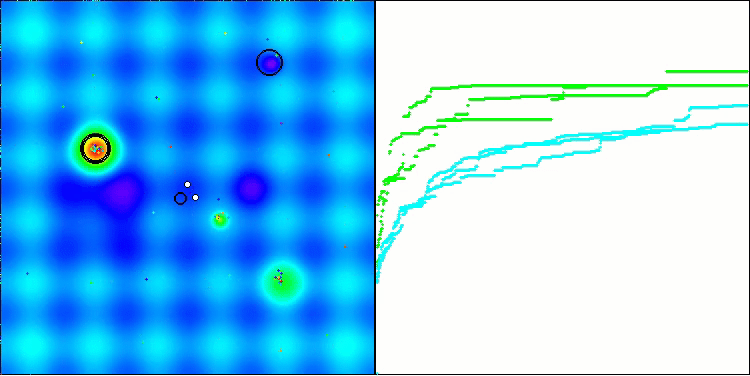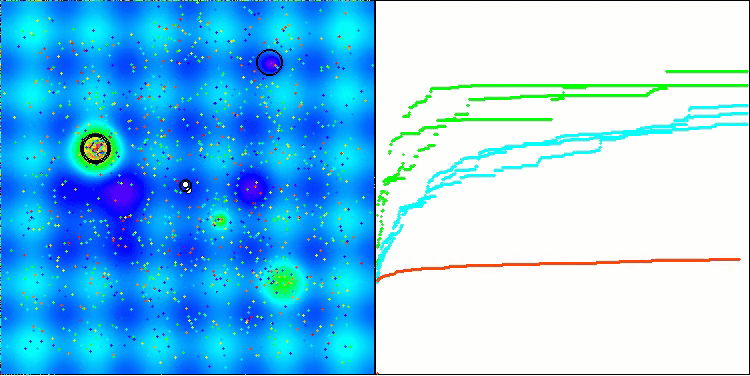
  ACS na função de teste Hilly.

  ACS na função de teste Forest.

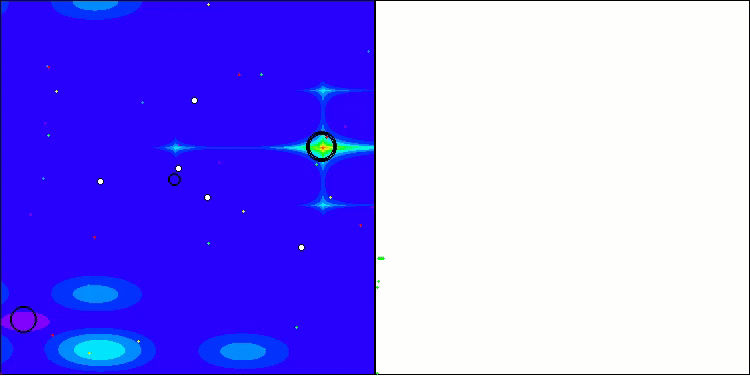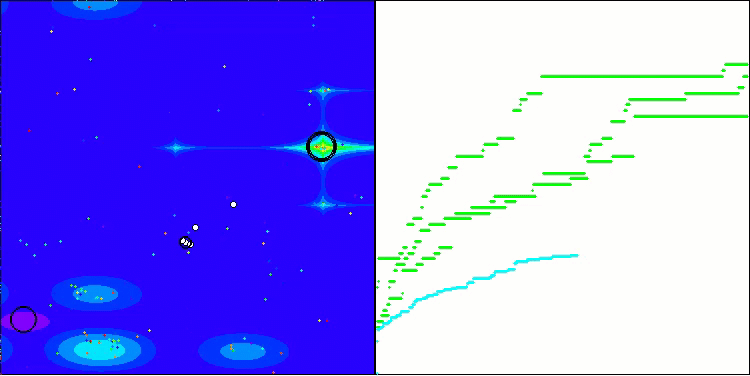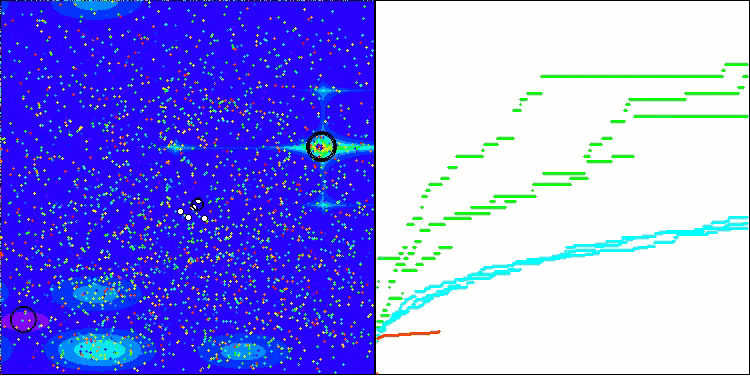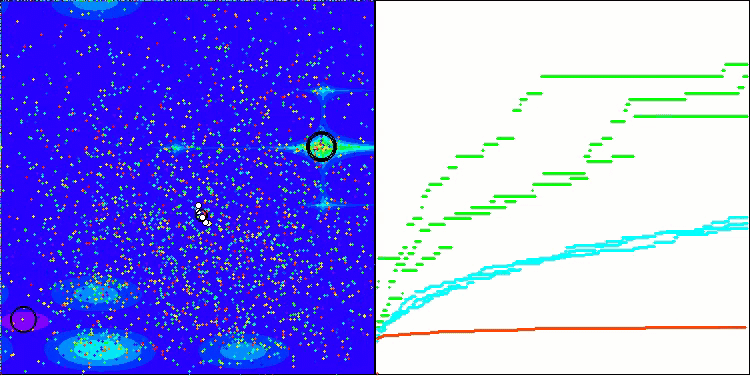
  ACS na função de teste Megacity.

Nos resultados dos testes, o algoritmo ficou em 8º lugar. O ACS se destacou especialmente nas funções Forest e Megacity.

№	AO	Description	Hilly			Hilly final	Forest			Forest final	Megacity (discrete)			Megacity final	Final result	% of MAX
			10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)		10 p (5 F)	50 p (25 F)	1000 p (500 F)
1	BGA	binary genetic algorithm	0,99989	0,99518	0,42835	2,42341	0,96153	0,96181	0,32027	2,24360	0,91385	0,95908	0,24220	2,11512	6,782	75,36
2	CLA	code lock algorithm	0,95345	0,87107	0,37590	2,20042	0,98942	0,91709	0,31642	2,22294	0,79692	0,69385	0,19303	1,68380	6,107	67,86
3	(P+O)ES	(P+O) evolution strategies	0,92256	0,88101	0,40021	2,20379	0,97750	0,87490	0,31945	2,17185	0,67385	0,62985	0,18634	1,49003	5,866	65,17
4	CTA	comet tail algorithm	0,95346	0,86319	0,27770	2,09435	0,99794	0,85740	0,33949	2,19484	0,88769	0,56431	0,10512	1,55712	5,846	64,96
5	SDSm	stochastic diffusion search M	0,93066	0,85445	0,39476	2,17988	0,99983	0,89244	0,19619	2,08846	0,72333	0,61100	0,10670	1,44103	5,709	63,44
6	ESG	evolution of social groups	0,99906	0,79654	0,35056	2,14616	1,00000	0,82863	0,13102	1,95965	0,82333	0,55300	0,04725	1,42358	5,529	61,44
7	SIA	simulated isotropic annealing	0,95784	0,84264	0,41465	2,21513	0,98239	0,79586	0,20507	1,98332	0,68667	0,49300	0,09053	1,27020	5,469	60,76
8	ACS	artificial cooperative search	0,75547	0,74744	0,30407	1,80698	1,00000	0,88861	0,22413	2,11274	0,69077	0,48185	0,13322	1,30583	5,226	58,06
9	TSEA	turtle shell evolution algorithm	0,96798	0,64480	0,29672	1,90949	0,99449	0,61981	0,22708	1,84139	0,69077	0,42646	0,13598	1,25322	5,004	55,60
10	DE	differential evolution	0,95044	0,61674	0,30308	1,87026	0,95317	0,78896	0,16652	1,90865	0,78667	0,36033	0,02953	1,17653	4,955	55,06
11	BSA	bird swarm algorithm	0,89306	0,64900	0,26250	1,80455	0,92420	0,71121	0,24939	1,88479	0,69385	0,32615	0,10012	1,12012	4,809	53,44
12	HS	harmony search	0,86509	0,68782	0,32527	1,87818	0,99999	0,68002	0,09590	1,77592	0,62000	0,42267	0,05458	1,09725	4,751	52,79
13	SSG	saplings sowing and growing	0,77839	0,64925	0,39543	1,82308	0,85973	0,62467	0,17429	1,65869	0,64667	0,44133	0,10598	1,19398	4,676	51,95
14	(PO)ES	(PO) evolution strategies	0,79025	0,62647	0,42935	1,84606	0,87616	0,60943	0,19591	1,68151	0,59000	0,37933	0,11322	1,08255	4,610	51,22
15	BSO	brain storm optimization	0,93736	0,57616	0,29688	1,81041	0,93131	0,55866	0,23537	1,72534	0,55231	0,29077	0,11914	0,96222	4,498	49,98
16	WOAm	wale optimization algorithm M	0,84521	0,56298	0,26263	1,67081	0,93100	0,52278	0,16365	1,61743	0,66308	0,41138	0,11357	1,18803	4,476	49,74
17	ACOm	ant colony optimization M	0,88190	0,66127	0,30377	1,84693	0,85873	0,58680	0,15051	1,59604	0,59667	0,37333	0,02472	0,99472	4,438	49,31
18	BFO-GA	bacterial foraging optimization - ga	0,89150	0,55111	0,31529	1,75790	0,96982	0,39612	0,06305	1,42899	0,72667	0,27500	0,03525	1,03692	4,224	46,93
19	MEC	mind evolutionary computation	0,69533	0,53376	0,32661	1,55569	0,72464	0,33036	0,07198	1,12698	0,52500	0,22000	0,04198	0,78698	3,470	38,55
20	IWO	invasive weed optimization	0,72679	0,52256	0,33123	1,58058	0,70756	0,33955	0,07484	1,12196	0,42333	0,23067	0,04617	0,70017	3,403	37,81
21	Micro-AIS	micro artificial immune system	0,79547	0,51922	0,30861	1,62330	0,72956	0,36879	0,09398	1,19233	0,37667	0,15867	0,02802	0,56335	3,379	37,54
22	COAm	cuckoo optimization algorithm M	0,75820	0,48652	0,31369	1,55841	0,74054	0,28051	0,05599	1,07704	0,50500	0,17467	0,03380	0,71347	3,349	37,21
23	SDOm	spiral dynamics optimization M	0,74601	0,44623	0,29687	1,48912	0,70204	0,34678	0,10944	1,15826	0,42833	0,16767	0,03663	0,63263	3,280	36,44
24	NMm	Nelder-Mead method M	0,73807	0,50598	0,31342	1,55747	0,63674	0,28302	0,08221	1,00197	0,44667	0,18667	0,04028	0,67362	3,233	35,92
25	FAm	firefly algorithm M	0,58634	0,47228	0,32276	1,38138	0,68467	0,37439	0,10908	1,16814	0,28667	0,16467	0,04722	0,49855	3,048	33,87
26	GSA	gravitational search algorithm	0,64757	0,49197	0,30062	1,44016	0,53962	0,36353	0,09945	1,00260	0,32667	0,12200	0,01917	0,46783	2,911	32,34
27	BFO	bacterial foraging optimization	0,61171	0,43270	0,31318	1,35759	0,54410	0,21511	0,05676	0,81597	0,42167	0,13800	0,03195	0,59162	2,765	30,72
28	ABC	artificial bee colony	0,63377	0,42402	0,30892	1,36671	0,55103	0,21874	0,05623	0,82600	0,34000	0,14200	0,03102	0,51302	2,706	30,06
29	BA	bat algorithm	0,59761	0,45911	0,35242	1,40915	0,40321	0,19313	0,07175	0,66810	0,21000	0,10100	0,03517	0,34617	2,423	26,93
30	SA	simulated annealing	0,55787	0,42177	0,31549	1,29513	0,34998	0,15259	0,05023	0,55280	0,31167	0,10033	0,02883	0,44083	2,289	25,43
31	IWDm	intelligent water drops M	0,54501	0,37897	0,30124	1,22522	0,46104	0,14704	0,04369	0,65177	0,25833	0,09700	0,02308	0,37842	2,255	25,06
32	PSO	particle swarm optimisation	0,59726	0,36923	0,29928	1,26577	0,37237	0,16324	0,07010	0,60572	0,25667	0,08000	0,02157	0,35823	2,230	24,77
33	Boids	boids algorithm	0,43340	0,30581	0,25425	0,99346	0,35718	0,20160	0,15708	0,71586	0,27846	0,14277	0,09834	0,51957	2,229	24,77
34	MA	monkey algorithm	0,59107	0,42681	0,31816	1,33604	0,31138	0,14069	0,06612	0,51819	0,22833	0,08567	0,02790	0,34190	2,196	24,40
35	SFL	shuffled frog-leaping	0,53925	0,35816	0,29809	1,19551	0,37141	0,11427	0,04051	0,52618	0,27167	0,08667	0,02402	0,38235	2,104	23,38
36	FSS	fish school search	0,55669	0,39992	0,31172	1,26833	0,31009	0,11889	0,04569	0,47467	0,21167	0,07633	0,02488	0,31288	2,056	22,84
37	RND	random	0,52033	0,36068	0,30133	1,18234	0,31335	0,11787	0,04354	0,47476	0,25333	0,07933	0,02382	0,35648	2,014	22,37
38	GWO	grey wolf optimizer	0,59169	0,36561	0,29595	1,25326	0,24499	0,09047	0,03612	0,37158	0,27667	0,08567	0,02170	0,38403	2,009	22,32
39	CSS	charged system search	0,44252	0,35454	0,35201	1,14907	0,24140	0,11345	0,06814	0,42299	0,18333	0,06300	0,02322	0,26955	1,842	20,46
40	EM	electroMagnetism-like algorithm	0,46250	0,34594	0,32285	1,13129	0,21245	0,09783	0,10057	0,41085	0,15667	0,06033	0,02712	0,24412	1,786	19,85

Considerações finais

O Algoritmo de Busca Cooperativa Artificial (ACS) demonstrou ser uma abordagem interessante para otimização, destacando-se pelo uso de várias populações de agentes que interagem entre si, garantindo diversidade e resistência a armadilhas de ótimos locais. O uso de operadores especiais, como o embaralhamento das "presas" e a mutação com o auxílio de uma matriz binária, trouxe originalidade ao algoritmo. Sua capacidade de alcançar excelentes resultados com um tamanho de população muito reduzido (até 1 indivíduo em cada uma das cinco populações) é uma característica única. A originalidade da abordagem e a capacidade de trabalhar com populações pequenas (o que ressalta sua resistência à degeneração da colônia) tornam o ACS um algoritmo de otimização realmente promissor.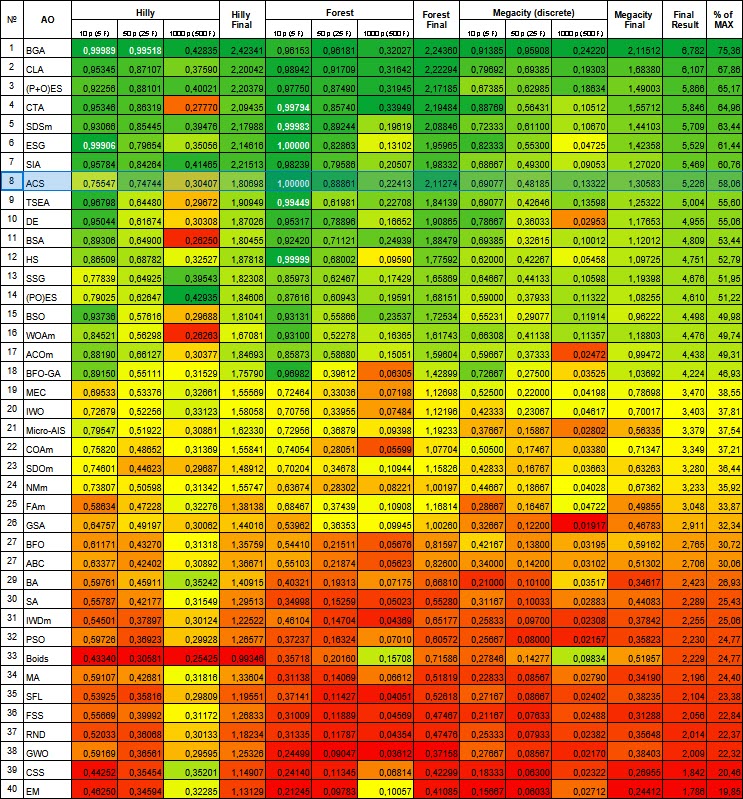

Figura 1. Graduação de cores dos algoritmos nos testes correspondentes. Os resultados iguais ou superiores a 0.99 estão destacados em branco.

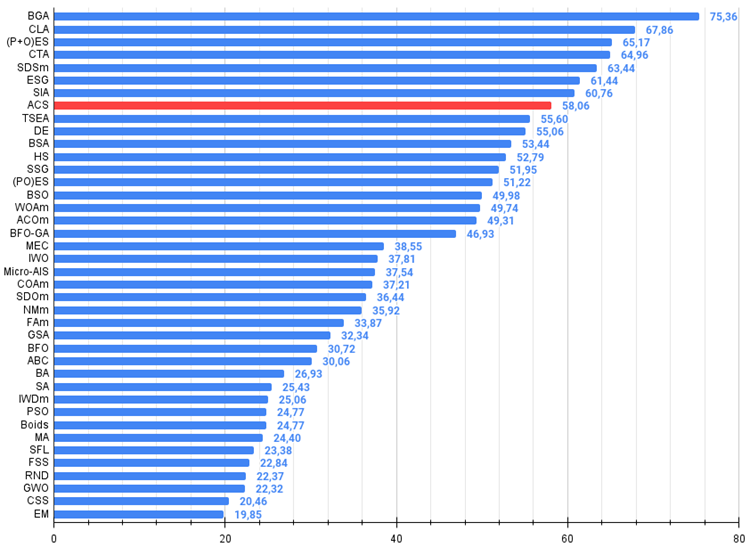
Figura 2. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, sendo que quanto maior, melhor,

onde 100 é o resultado teórico máximo possível; no arquivo está o script para cálculo da tabela de classificação)

Prós e contras do Algoritmo de Busca Cooperativa Artificial (ACS):

Prós:

1. Poucos parâmetros externos (apenas 1).
   
2. Boa convergência em diferentes tipos de funções.

Contras:

1. Variabilidade nos resultados em funções com baixa dimensionalidade.
   

Um arquivo com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois várias modificações foram feitas para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos são baseados nos resultados dos experimentos realizados.

• github: https://github.com/JQSakaJoo/Population-optimization-algorithms-MQL5
• CodeBase: https://www.mql5.com/pt/code/49355