
Algoritmo de busca através de vizinhança — Across Neighborhood Search (ANS)
1. Introdução
No mundo moderno, o desenvolvimento de métodos eficazes de otimização é fundamental para resolver uma diversidade de problemas, desde aplicações de engenharia até pesquisas científicas em aprendizado de máquina e inteligência artificial. Nesse contexto, os algoritmos evolutivos meta-heurísticos são ferramentas poderosas para solucionar tarefas complexas de otimização. No entanto, para melhorar ainda mais seu desempenho e eficácia, é necessário o contínuo desenvolvimento e modificação de métodos existentes, bem como a criação de novos algoritmos.
Neste artigo, apresentamos um algoritmo de otimização conhecido como Across Neighborhood Search (ANS), proposto por Guohua Wu em 2014, baseado na busca por populações para otimização numérica. O algoritmo ANS desenvolvido é um avanço significativo na área de otimização, prometendo resolver uma ampla gama de problemas do mundo real com alta eficiência e precisão; se isso é verdade ou não, confirmaremos ou desmentiremos adiante. A ideia central do ANS é modelar o comportamento de um sistema multiagente, onde cada agente se movimenta no espaço de soluções, interagindo com vizinhos e trocando informações. Essa abordagem permite uma exploração eficaz do espaço de busca, combinando otimização local e global.
Apresentaremos a estrutura detalhada do algoritmo ANS e os princípios de seu funcionamento, além de realizar uma análise comparativa com métodos de otimização já existentes. O algoritmo ANS desenvolvido abre novas possibilidades no campo da otimização, possibilitando resolver uma variedade de problemas com alto desempenho. Além disso, no contexto do desenvolvimento da inteligência artificial, é importante notar que o ANS representa um passo significativo em direção à criação de métodos de otimização mais flexíveis e inteligentes, que considerem a especificidade da tarefa e a dinâmica do ambiente.
2. Implementação do algoritmo
O algoritmo Across Neighborhood Search, ANS (busca através de vizinhança), é um método de otimização que usa ideias da área de algoritmos evolutivos e meta-heurísticas, projetado para encontrar soluções ideais no espaço de parâmetros do problema.
Principais características do ANS:
- Busca através de vizinhança: agentes exploram as vizinhanças das soluções atuais, permitindo encontrar ótimos locais de maneira mais eficaz.
- Uso de distribuição normal: ANS utiliza a distribuição normal para gerar novos valores de parâmetros.
- Coleções de soluções: no ANS, são usadas coleções das melhores soluções, que ajudam a orientar o algoritmo em várias direções promissoras simultaneamente.
No ANS, um grupo de indivíduos realiza conjuntamente uma busca no espaço de soluções para otimizar a tarefa em questão. A ideia principal do algoritmo é manter e atualizar dinamicamente uma coleção de soluções superiores descobertas pelos indivíduos até o momento. Em cada geração, o indivíduo busca diretamente em sua vizinhança por várias soluções boas, seguindo a distribuição normal de probabilidades. Isso explora a ideia de que podem existir múltiplas soluções potencialmente boas, já que não se sabe antecipadamente qual será a melhor.
A seguir, descrevemos completamente o algoritmo ANS com fórmulas e etapas, conforme a concepção original do autor. O ANS realiza os seguintes passos:
1. Inicialização de parâmetros:
- Tamanho da população m
- Coleção de um conjunto das melhores soluções c
- Desvio padrão da distribuição gaussiana sigma
- Dimensionalidade do espaço de busca D
- Número máximo de gerações MaxG
2. Inicialização da população. Inicializa-se aleatoriamente a posição de cada indivíduo da população no espaço de busca.
3. Atualização das melhores soluções. Cada indivíduo na população atualiza sua posição, explorando as vizinhanças das melhores soluções da coleção, usando a distribuição normal.
4. Escolha da coordenada para busca. Seleciona-se um número aleatório n (grau de busca em vizinhança) para definir a coordenada atual da posição do indivíduo no espaço de soluções.
5. Atualização da posição do indivíduo. Atualiza-se a posição do indivíduo i conforme o passo anterior.
Fórmulas e operações:
1. Atualização da posição pos_i do indivíduo i (exploração da vizinhança de uma solução da coleção):
- A posição do indivíduo i é atualizada pela distribuição Gaussiana: pos_i = r_g + G (r_g - pos_i), onde:
- G - valor aleatório da distribuição gaussiana
- r_g - posição da melhor solução da coleção
2. Atualização da posição pos_i do indivíduo i (exploração da vizinhança de sua própria melhor solução):
- A posição do indivíduo i é atualizada pela distribuição Gaussiana: pos_i = r_i + G (r_i - pos_i), onde:
- G - valor aleatório da distribuição gaussiana
- r_i - posição da melhor solução do indivíduo
3. Atualização do conjunto das melhores soluções:
- A coleção das melhores soluções é atualizada com base nas novas posições dos indivíduos.
Dessa forma, as fórmulas refletem o mecanismo de busca do indivíduo i nas vizinhanças de sua melhor solução r_i, bem como nas vizinhanças de outras melhores soluções r_g da coleção R. Esses passos constituem a lógica principal do método ANS (Across Neighborhood Search) para resolver problemas de otimização. O algoritmo inclui a inicialização de parâmetros, a inicialização aleatória das posições dos indivíduos, a atualização dessas posições considerando as vizinhanças das melhores soluções, e a atualização da coleção das melhores soluções. O processo continua até que a condição de parada seja atendida.
A busca por melhores soluções ou indivíduos é uma técnica comum em algoritmos que empregam estratégias populacionais, embora os processos que implementam esse mecanismo possam variar entre diferentes algoritmos de otimização. Nesse caso, além da população principal de agentes, é introduzida uma população adicional: uma coleção de melhores soluções (direções de busca potenciais). O tamanho da coleção é determinado por parâmetros externos do algoritmo e pode ser configurado como menor ou maior que o tamanho da população principal.
A estratégia de busca no algoritmo ANS começa com o preenchimento da coleção das melhores soluções e prossegue com a exploração da vizinhança dessas melhores soluções na coleção, além das melhores soluções individuais de cada agente. O tamanho do desvio padrão sigma desempenha um papel muito importante no algoritmo. Valores pequenos de sigma promovem uma exploração mais ampla do espaço de busca, enquanto valores maiores permitem o refinamento de soluções, concentrando a busca em suas vizinhanças. Esse parâmetro é importante para o equilíbrio entre intensificação e diversificação da busca. Em alguns algoritmos, esse equilíbrio está vinculado ao número da época atual, garantindo um ajuste dinâmico entre exploração e refinamento. Porém, neste caso, os autores configuraram a regulação desse equilíbrio como um parâmetro externo do ANS.
Assim, o algoritmo ANS combina a exploração das melhores soluções encontradas (por meio da busca em suas vizinhanças) e a exploração do espaço de soluções (através da busca nas vizinhanças das melhores soluções individuais dos agentes). Isso, teoricamente, deve garantir um bom equilíbrio entre a intensificação e a diversificação da busca.
Agora, vamos à implementação e análise do código do algoritmo ANS. Definiremos a estrutura "S_ANS_Agent", que será usada para representar os agentes no algoritmo ANS. Campos da estrutura:
- c: array para armazenar as coordenadas do agente.
- cBest: array para armazenar as melhores coordenadas do agente.
- f: valor de aptidão (fitness) do agente.
- fBest: melhor valor de aptidão do agente.
- Init(int coords): método de inicialização que define os tamanhos dos arrays "c" e "cBest" e configura os valores iniciais de "f" e "fBest".
Essa parte do código define a estrutura básica do agente, cujo conjunto (array) de agentes formará a população principal no algoritmo ANS.
//—————————————————————————————————————————————————————————————————————————————— struct S_ANS_Agent { double c []; //coordinates double cBest []; //best coordinates double f; //fitness double fBest; //best fitness void Init (int coords) { ArrayResize (c, coords); ArrayResize (cBest, coords); f = -DBL_MAX; fBest = -DBL_MAX; } }; //—————————————————————————————————————————————————————————————————————————————
Para descrever a coleção de melhores soluções, implementaremos a estrutura "S_Collection", que será usada para armazenar informações sobre as melhores coordenadas no espaço de busca e o respectivo valor de aptidão. A estrutura contém os seguintes campos:
- c: array para armazenar as coordenadas.
- f: valor de aptidão (fitness) para a solução na coleção.
- Init(int coords): método de inicialização que define o tamanho do array "c" e configura o valor inicial de "f" para o menor valor possível do tipo "double".
//—————————————————————————————————————————————————————————————————————————————— struct S_Collection { double c []; //coordinates double f; //fitness void Init (int coords) { ArrayResize (c, coords); f = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Declararemos a classe "C_AO_ANS", que é derivada da classe base "C_AO" e representa a implementação do algoritmo Across Neighborhood Search (ANS). Aqui estão alguns pontos importantes:
- ao_name, ao_desc, ao_link: propriedades que descrevem o algoritmo ANS.
- popSize: tamanho da população.
- collectionSize, sigma, range, collChoiceProbab: parâmetros do algoritmo ANS.
- SetParams(): método para definir os parâmetros.
- Init(), Moving(), Revision(): métodos para inicializar, mover os agentes e atualizar a população e a coleção de soluções.
- S_ANS_Agent, S_Collection: estruturas para armazenamento de dados dos agentes e da coleção.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ANS : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ANS () { } C_AO_ANS () { ao_name = "ANS"; ao_desc = "Across Neighbourhood Search"; ao_link = "https://www.mql5.com/ru/articles/15049"; popSize = 50; //population size collectionSize = 20; //Best solutions collection sigma = 3.0; //Form of normal distribution range = 0.5; //Range of values dispersed collChoiceProbab = 0.8; //Collection choice probab ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "collectionSize"; params [1].val = collectionSize; params [2].name = "sigma"; params [2].val = sigma; params [3].name = "range"; params [3].val = range; params [4].name = "collChoiceProbab"; params [4].val = collChoiceProbab; } void SetParams () { popSize = (int)params [0].val; collectionSize = (int)params [1].val; sigma = params [2].val; range = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- int collectionSize; //Best solutions collection double sigma; //Form of normal distribution double range; //Range of values dispersed double collChoiceProbab; //Collection choice probab S_ANS_Agent agent []; private: //------------------------------------------------------------------- S_Collection coll []; S_Collection collTemp []; }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" inicializa os parâmetros do algoritmo ANS (Across Neighborhood Search).
- rangeMinP, rangeMaxP, rangeStepP: arrays que representam os valores mínimos, máximos e o passo do intervalo de busca.
- epochsP: número de épocas (gerações).
Dentro do método:
- Verifica-se a inicialização bem-sucedida dos parâmetros padrão com "StandardInit".
- São criados arrays de agentes "agent" e das coleções "coll" (segunda população para armazenamento das melhores soluções) e "collTemp" (array temporário para ordenação da coleção).
- Para cada agente e elemento da coleção, o método "Init" é chamado para definir os valores iniciais.
Esse método é essencial para preparar o algoritmo ANS para a execução da otimização. É importante destacar que os arrays "coll" e "collTemp" são inicializados com o dobro do tamanho especificado pelo parâmetro "collectionSize". Isso é feito para que os novos agentes adicionados à coleção sejam inseridos na segunda metade do array. Em seguida, a coleção é ordenada como um todo, mas somente a primeira metade, que contém os melhores agentes, é usada para as operações subsequentes.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ANS::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords); ArrayResize (coll, collectionSize * 2); ArrayResize (collTemp, collectionSize * 2); for (int i = 0; i < collectionSize * 2; i++) { coll [i].Init (coords); collTemp [i].Init (coords); } return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" realiza o movimento (deslocamento) dos agentes no algoritmo ANS. Vamos detalhar o funcionamento deste código:
1. Inicialização (se "revision" for "false"):
- Se for o primeiro passo (primeira geração), para cada agente:
- Gera-se um valor aleatório "val" no intervalo de "rangeMin[c]" a "rangeMax[c]".
- Aplica-se o operador "SeInDiSp" para considerar o passo "rangeStep[c]".
- O valor "val" é atribuído às coordenadas do agente "agent[i].c[c]".
- O valor "val" também é atribuído às melhores coordenadas do agente "agent[i].cBest[c]" (nesta fase, os valores de aptidão dos agentes ainda não são conhecidos, então as melhores coordenadas são iguais às coordenadas iniciais).
- O valor "val" é atribuído ao array de agentes "a[i].c[c]".
2. Movimento dos agentes (se "revision" for "true"):
- Para cada agente e cada coordenada:
- Se um número aleatório for menor que "collChoiceProbab", escolhe-se uma solução aleatória da coleção:
- Seleciona-se um índice aleatório "ind" da coleção (até que uma solução não nula seja encontrada).
- O valor "p" é extraído das coordenadas atuais do agente.
- O valor "r" é retirado da solução selecionada da coleção.
- Caso contrário, usam-se as melhores coordenadas do agente:
- O valor "p" é extraído das coordenadas atuais do agente.
- O valor "r" é retirado das melhores coordenadas do agente.
- Calcula-se a distância "dist" e o intervalo ("min" e "max") para o movimento.
- Os valores "min" e "max" são limitados pelos intervalos "rangeMin[c]" e "rangeMax[c]".
- Aplica-se a distribuição normal com os parâmetros "r", "min", "max" e "sigma".
- O valor "val" é atribuído às coordenadas do agente "agent[i].c[c]".
- O valor "val" também é atribuído ao array de agentes "a[i].c[c]".
Este trecho de código atualiza as coordenadas dos agentes no algoritmo ANS, levando em conta as melhores coordenadas próprias dos agentes e as soluções armazenadas na coleção.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Moving () { double val = 0.0; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { val = u.RNDfromCI (rangeMin [c], rangeMax [c]); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; agent [i].cBest [c] = val; a [i].c [c] = val; } } revision = true; return; } //---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); agent [i].c [c] = val; a [i].c [c] = val; } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" realiza uma revisão (ou atualização) dos agentes e da coleção no algoritmo ANS. Aqui estão os principais pontos:
- Primeira parte do método: busca o agente cuja aptidão (fitness) é melhor que a do melhor resultado global, identificado por "fB", e salva suas coordenadas no array "cB".
- Segunda parte do método: atualiza as melhores coordenadas dos agentes "agent[i].cBest" com base na aptidão atual "a[i].f".
- Terceira parte do método: atualiza a coleção "coll" usando as melhores coordenadas dos agentes.
- A coleção é, então, ordenada.
Este método desempenha um papel crucial na atualização contínua dos agentes e da coleção de soluções durante a execução do algoritmo. Os agentes da população são inseridos na segunda metade da coleção. Em seguida, a coleção é ordenada, e apenas a primeira metade, contendo as melhores soluções, é usada nas etapas seguintes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ANS::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (a [i].f > agent [i].fBest) { agent [i].fBest = a [i].f; ArrayCopy (agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY); } } //---------------------------------------------------------------------------- int cnt = 0; for (int i = collectionSize; i < collectionSize * 2; i++) { if (cnt < popSize) { coll [i].f = agent [cnt].fBest; ArrayCopy (coll [i].c, agent [cnt].cBest, 0, 0, WHOLE_ARRAY); cnt++; } else break; } u.Sorting (coll, collTemp, collectionSize * 2); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados dos testes
Resultados impressos da execução do algoritmo ANS em um conjunto de funções de teste:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9494753644543816
25 Hilly's; Func runs: 10000; result: 0.8477633752716718
500 Hilly's; Func runs: 10000; result: 0.43857039929159747
=============================
5 Forest's; Func runs: 10000; result: 0.9999999999988883
25 Forest's; Func runs: 10000; result: 0.9233446583489741
500 Forest's; Func runs: 10000; result: 0.3998822848099108
=============================
5 Megacity's; Func runs: 10000; result: 0.709230769230769
25 Megacity's; Func runs: 10000; result: 0.6347692307692309
500 Megacity's; Func runs: 10000; result: 0.2309076923076936
=============================
All score: 6.13394 (68.15%)
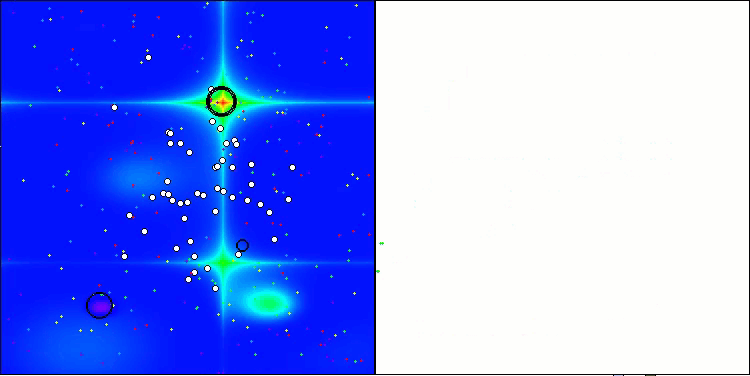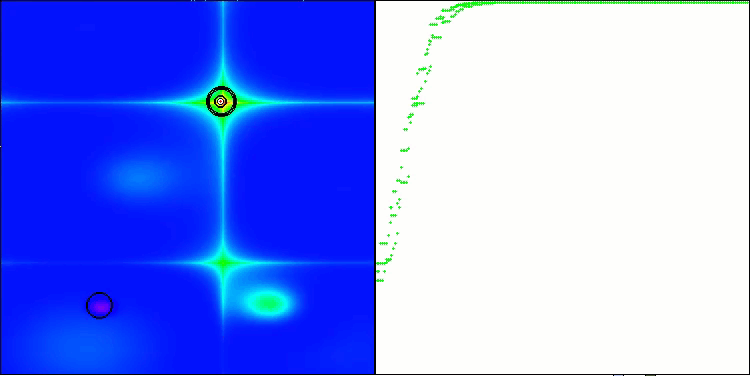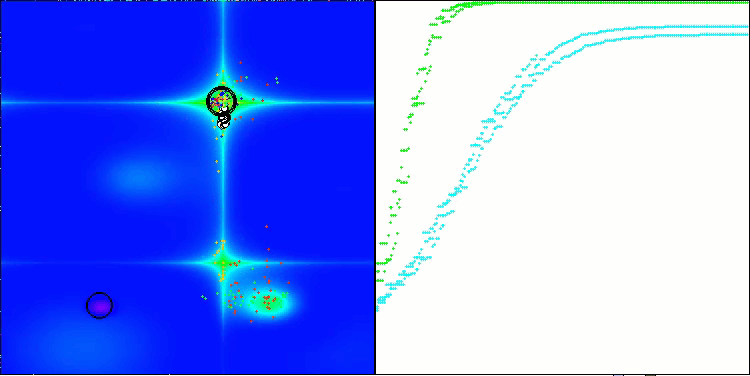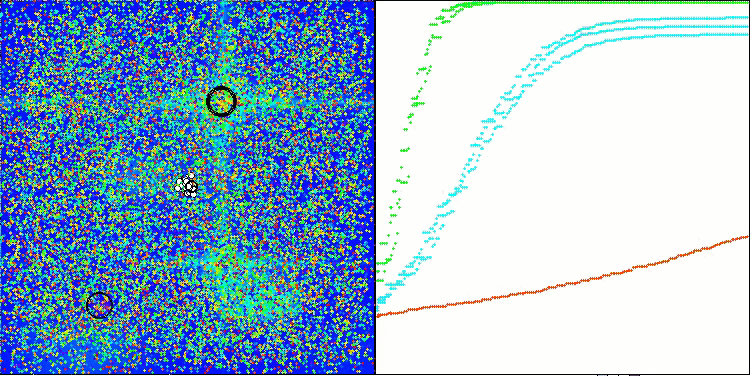
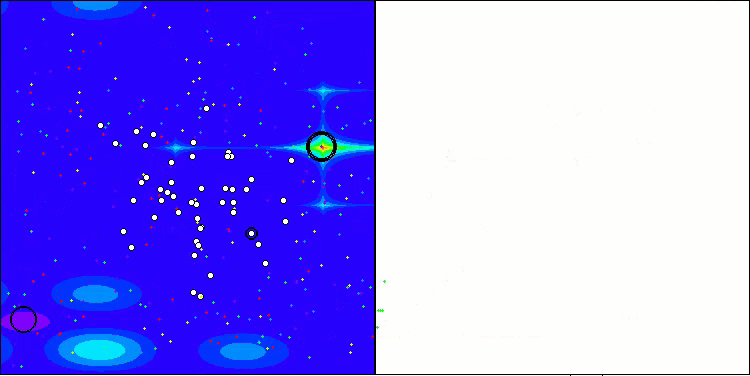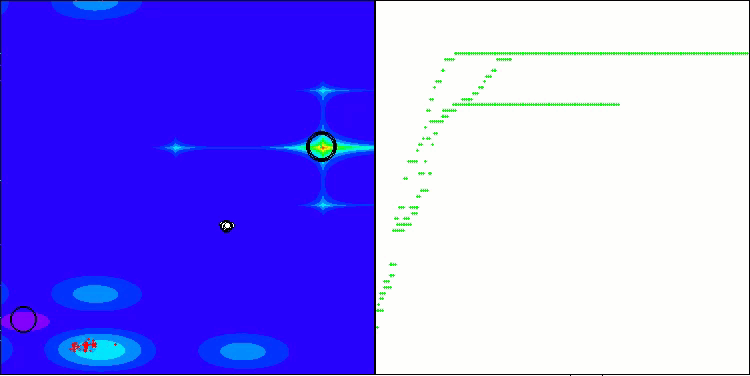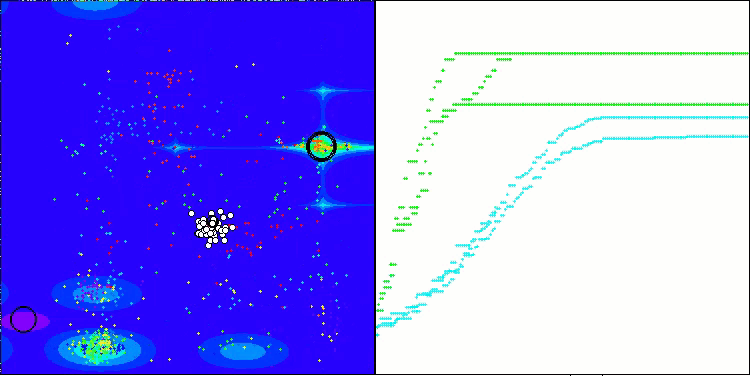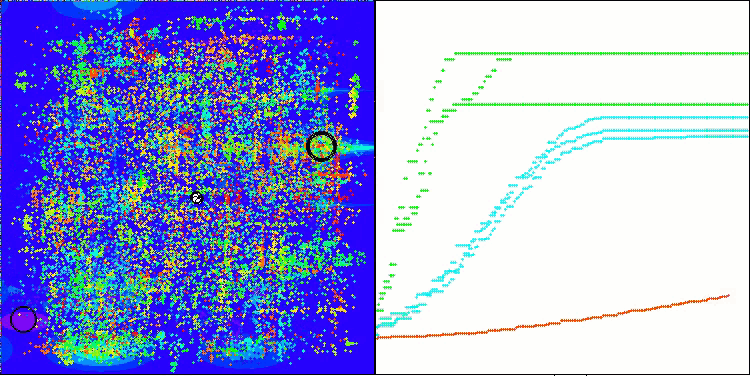
O ANS apresenta resultados impressionantes em todas as funções de teste. Agora, veremos a visualização do funcionamento desse algoritmo no ambiente de testes. Embora os resultados do ANS sejam realmente extraordinários, a visualização levanta algumas questões. Em particular, observa-se o comportamento da população, que parece desaparecer do campo de visão. Percebe-se que o espaço de soluções é esvaziado, e o terreno da função permanece sem agentes. Isso pode indicar apenas uma coisa: apesar dos resultados notáveis do algoritmo, a população tende à degeneração. A coleção de soluções superiores acaba sendo preenchida por soluções muito semelhantes, o que impede a criação de novas soluções, já que todas são derivadas das que já existem.
Essa dinâmica populacional sugere a necessidade de aperfeiçoar os mecanismos de manutenção da diversidade dentro da população. Talvez seja interessante considerar a adição de um operador de mutação ou a introdução de outros mecanismos que contribuam para preservar uma maior variedade de soluções durante o processo de otimização. Isso ajudaria a evitar a degeneração da população e garantiria um desempenho mais estável do algoritmo.
Execução do ANS na função de teste Hilly.
Execução do ANS na função de teste Forest.
Execução do ANS na função de teste Megacity.
O algoritmo analisado neste artigo conquistou com segurança a segunda posição no ranking. Dispensa comentários adicionais, mas alguns pontos principais merecem destaque: o algoritmo demonstra uma escalabilidade impressionante, mantendo a capacidade de busca mesmo em problemas de alta dimensionalidade.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 3 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 8 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 9 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 10 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 11 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 12 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 13 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 14 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 15 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 16 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 17 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 18 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 19 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 20 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 21 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 22 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 23 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 24 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 25 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 26 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 27 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 28 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 29 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 30 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 31 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 32 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 33 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 34 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 35 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 36 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 37 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 38 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 39 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 40 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 41 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 42 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
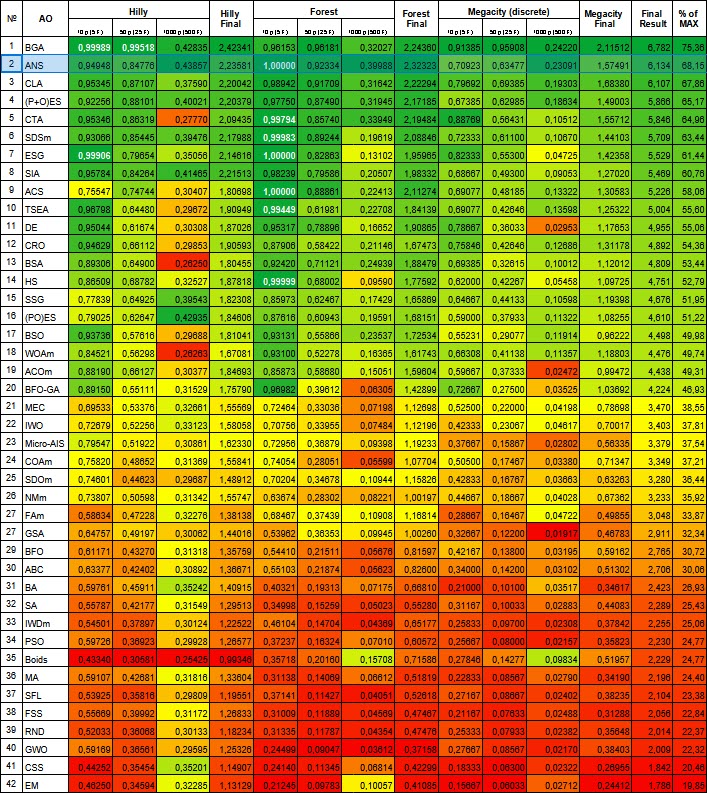
Figura 1. Graduação de cores dos algoritmos para os respectivos testes. Os resultados iguais ou superiores a 0,99 são destacados em branco.
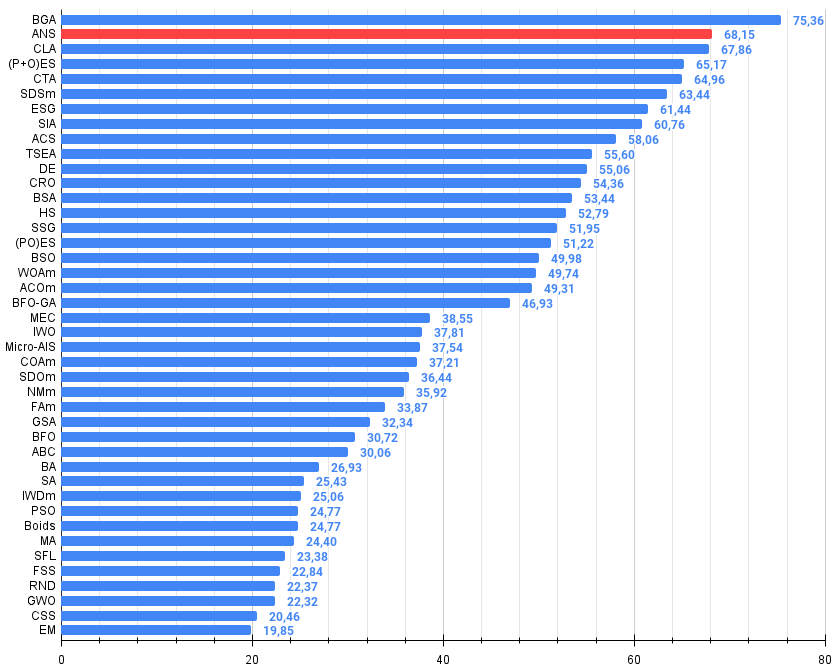
Figura 2. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível; o script para cálculo da tabela de classificação está incluído no arquivo).
Como mencionado anteriormente, a população do algoritmo ANS tende a se degenerar. Para mitigar esse problema crítico, decidi modificar o algoritmo, adicionando um operador de mutação. Neste caso, a mutação consiste em uma probabilidade gaussiana de gerar uma nova coordenada nas proximidades da melhor solução do agente, mas dentro do intervalo permitido para essa coordenada, variando de um valor mínimo a um máximo. Para isso, é necessário fazer algumas alterações no método "Moving".
Aqui está um resumo das mudanças e da lógica aplicada no método:
- Se um número aleatório for menor que 0,005, ocorre uma mutação usando a distribuição normal.
- Caso contrário, um solução aleatória é escolhida da coleção, ou as melhores coordenadas do agente são usadas.
- Calcula-se a distância e o intervalo para a distribuição normal.
- A distribuição normal é então aplicada para gerar novos valores de coordenadas.
//---------------------------------------------------------------------------- double min = 0.0; double max = 0.0; double dist = 0.0; int ind = 0; double r = 0.0; double p = 0.0; for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < 0.005) { val = u.GaussDistribution (agent [i].cBest [c], rangeMin [c], rangeMax [c], sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } else { if (u.RNDprobab () < collChoiceProbab) { do ind = u.RNDminusOne (collectionSize); while (coll [ind].f == -DBL_MAX); p = agent [i].c [c]; r = coll [ind].c [c]; } else { p = agent [i].c [c]; r = agent [i].cBest [c]; } dist = fabs (p - r) * range; min = r - dist; max = r + dist; if (min < rangeMin [c]) min = rangeMin [c]; if (max > rangeMax [c]) max = rangeMax [c]; val = u.GaussDistribution (r, min, max, sigma); val = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } agent [i].c [c] = val; a [i].c [c] = val; } }
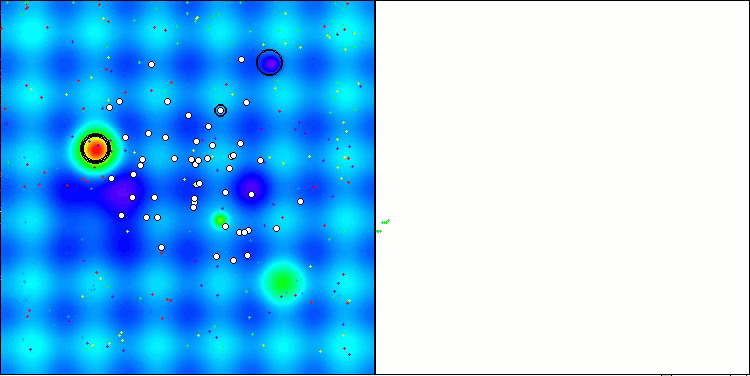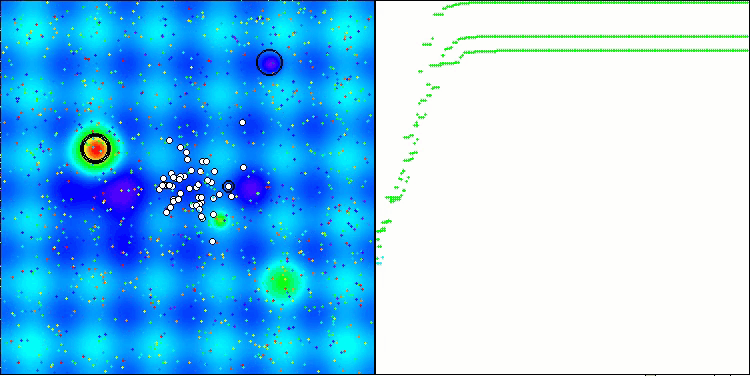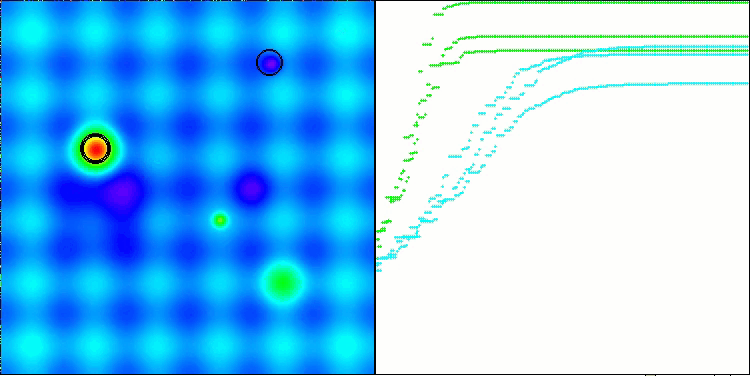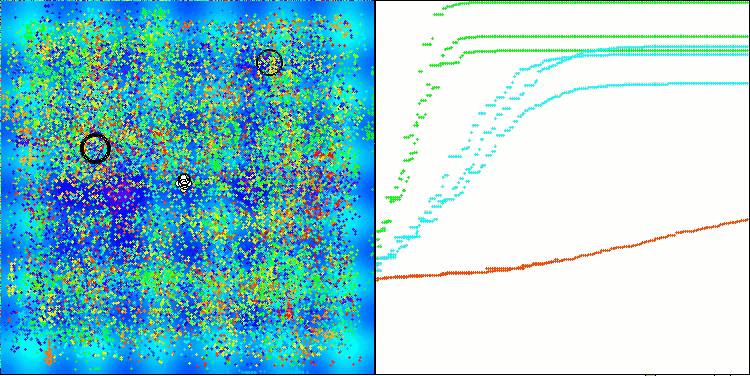
Após a introdução do operador de mutação, o algoritmo continua explorando o espaço de busca, independentemente do número de épocas, como ilustrado na Figura 3 (captura de tela da visualização do funcionamento do algoritmo).
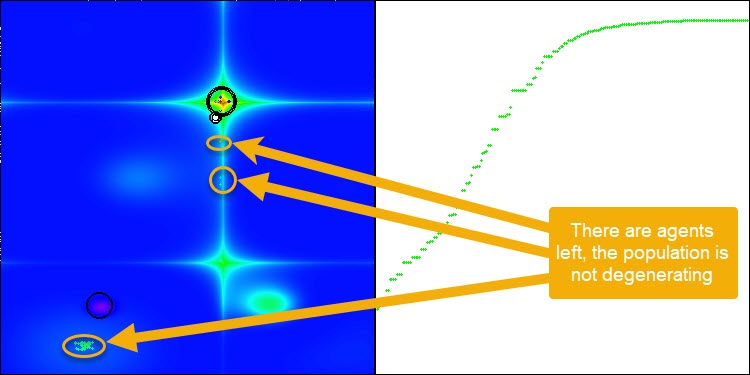
Figura 3. Os agentes permanecem, a população não se degenera (parâmetro mut = 0,005).
- O operador de mutação com o parâmetro "mut = 0,1" teve um impacto negativo no resultado geral. Com um coeficiente de mutação tão alto (10% do total de operações em cada coordenada), observou-se uma piora no desempenho do algoritmo. Por isso, foi decidido reduzir gradualmente esse parâmetro. À medida que o valor foi diminuído, os resultados melhoraram, e finalmente, estabeleci o valor de 0,005. Esse coeficiente mostrou-se suficiente para evitar a degeneração da população, ao mesmo tempo garantindo uma melhoria no desempenho do algoritmo, conforme ilustrado nas impressões abaixo.
Resultados do algoritmo com a probabilidade de mutação mut = 0,1:
=============================
All score: 6.05103 (67.23%)
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534829314854332
25 Hilly's; Func runs: 10000; result: 0.8136803288623282
500 Hilly's; Func runs: 10000; result: 0.31144979106165716
=============================
5 Forest's; Func runs: 10000; result: 0.9996561274415626
25 Forest's; Func runs: 10000; result: 0.81670393859872
500 Forest's; Func runs: 10000; result: 0.25620559379918284
=============================
5 Megacity's; Func runs: 10000; result: 0.8753846153846153
25 Megacity's; Func runs: 10000; result: 0.5778461538461539
500 Megacity's; Func runs: 10000; result: 0.13375384615384744
=============================
All score: 5.73816 (63.76%)
Resultados do algoritmo com a probabilidade de mutação mut = 0.01:
=============================
5 Hilly's; Func runs: 10000; result: 0.9073657389037575
25 Hilly's; Func runs: 10000; result: 0.871278233418226
500 Hilly's; Func runs: 10000; result: 0.3960769225373809
=============================
5 Forest's; Func runs: 10000; result: 0.989394440004635
25 Forest's; Func runs: 10000; result: 0.9513150500729907
500 Forest's; Func runs: 10000; result: 0.35407610928209116
=============================
5 Megacity's; Func runs: 10000; result: 0.7492307692307691
25 Megacity's; Func runs: 10000; result: 0.6387692307692309
500 Megacity's; Func runs: 10000; result: 0.19352307692307838
=============================
All score: 6.05103 (67.23%)
Resultados do algoritmo com a probabilidade de mutação mut = 0.005:
ANS|Across Neighbourhood Search|50.0|100.0|8.0|1.0|0.6|
=============================
5 Hilly's; Func runs: 10000; result: 0.949632264944664
25 Hilly's; Func runs: 10000; result: 0.871206955779846
500 Hilly's; Func runs: 10000; result: 0.40738389742274217
=============================
5 Forest's; Func runs: 10000; result: 0.9924803131691761
25 Forest's; Func runs: 10000; result: 0.9493489251290264
500 Forest's; Func runs: 10000; result: 0.3666276564633121
=============================
5 Megacity's; Func runs: 10000; result: 0.8061538461538461
25 Megacity's; Func runs: 10000; result: 0.6732307692307691
500 Megacity's; Func runs: 10000; result: 0.20844615384615534
=============================
All score: 6.22451 (69.16%)
Considerações finais
Agora que analisamos os resultados obtidos com a introdução do operador de mutação, podemos tirar as seguintes conclusões:
1. Simplicidade e facilidade de implementação.
2. Equilíbrio entre exploração e exploração intensiva.
3. Eficiência na resolução de diferentes tipos de problemas.
4. Adaptabilidade a várias tarefas.
5. Potencial para futuras melhorias.
Portanto, o ANS é um algoritmo de otimização simples, mas eficaz, que apresenta resultados competitivos em uma ampla variedade de problemas e possui um grande potencial para desenvolvimento futuro.
Vantagens e desvantagens gerais do algoritmo de busca através de vizinhança (ANS):
Vantagens:
- Boa convergência em diferentes tipos de funções.
- Alta velocidade de execução.
- Implementação simples.
- Excelente escalabilidade.
Desvantagens:
- Ocasionalmente, fica preso em extremos locais.
O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois foram realizadas diversas modificações para aprimorar as capacidades de busca. As conclusões e observações apresentadas são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15049
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Redes neurais de maneira fácil (Parte 97): Treinamento do modelo usando o MSFformer
Redes neurais de maneira fácil (Parte 97): Treinamento do modelo usando o MSFformer
 Redes neurais de maneira fácil (Parte 96): Extração multinível de características (MSFformer)
Redes neurais de maneira fácil (Parte 96): Extração multinível de características (MSFformer)
 Redes neurais em trading: Representação linear por partes de séries temporais
Redes neurais em trading: Representação linear por partes de séries temporais
 Do básico ao intermediário: União (II)
Do básico ao intermediário: União (II)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso