
ADAM Populacional (estimativa adaptativa de momentos)
Conteúdo
Introdução
No mundo do aprendizado de máquina, onde os dados crescem rapidamente e os algoritmos se tornam cada vez mais complexos, a otimização desempenha um papel fundamental na obtenção de resultados de alto desempenho. Entre os diversos métodos que buscam lidar com esse desafio, o algoritmo ADAM (Estimativa Adaptativa de Momentos) se destaca por sua elegância e eficiência.
Em 2014, dois grandes nomes — D. P. Kingma e J. Ba — propuseram o algoritmo ADAM, que combina as melhores características de seus antecessores, como o AdaGrad e o RMSProp. O algoritmo foi projetado especificamente para otimizar os pesos de redes neurais utilizando gradientes das funções de ativação dos neurônios. Ele se baseia em estimativas adaptativas do primeiro e segundo momentos, o que o torna simples de implementar e altamente eficiente do ponto de vista computacional. O algoritmo exige poucos recursos de memória e não depende de mudanças diagonais nas escalas dos gradientes, o que o torna especialmente adequado para tarefas com grandes volumes de dados e parâmetros.
O ADAM também se sai bem em objetivos não estacionários e em situações onde os gradientes podem ser ruidosos ou esparsos. Seus hiperparâmetros são fáceis de interpretar e normalmente não exigem configurações complexas.
No entanto, apesar de sua eficácia no campo das redes neurais, o ADAM é limitado ao uso de gradientes analíticos, o que restringe seu campo de aplicação. Neste artigo, propomos uma abordagem inovadora para modificar o algoritmo ADAM, transformando-o em um algoritmo populacional de otimização capaz de trabalhar com gradientes numéricos. Essa modificação não apenas amplia o uso do ADAM para além das redes neurais, mas também abre novas possibilidades para resolver uma ampla gama de problemas de otimização em geral.
Nossa proposta de pesquisa tem como foco a criação de um otimizador universal, que mantenha as vantagens do ADAM original, mas que seja capaz de funcionar de forma eficaz em contextos onde os gradientes analíticos não estão disponíveis. Isso permitirá aplicar o ADAM modificado em áreas como otimização global e otimização multicritério, expandindo significativamente seu potencial e valor prático.
Implementação do algoritmo
O algoritmo ADAM é frequentemente classificado como um método de otimização por gradiente estocástico. No entanto, é importante observar que o ADAM, em si, não contém elementos estocásticos internos em sua lógica principal. A estocasticidade associada ao ADAM, na verdade, deriva da forma como os dados são preparados e alimentados ao algoritmo, e não de sua mecânica interna. É essencial distinguir entre a estocasticidade na preparação dos dados e a natureza determinística do próprio algoritmo de otimização.
O próprio algoritmo ADAM é completamente determinístico. Dadas as mesmas entradas e condições iniciais, ele sempre produzirá os mesmos resultados. A atualização dos parâmetros no ADAM é feita com base em fórmulas bem definidas, que não incluem elementos aleatórios.
Essa distinção entre a natureza determinística do ADAM e o caráter estocástico da preparação dos dados para ele é fundamental para uma compreensão correta de seu funcionamento e de seu potencial de modificação. Reconhecer esse fato abre possibilidades para adaptar o ADAM a problemas onde a preparação estocástica dos dados possa ser impraticável ou indesejada, mantendo ao mesmo tempo suas poderosas capacidades de otimização.
Vamos analisar o pseudocódigo com as fórmulas:
1. Inicialização:
m₀ = 0 (inicialização do primeiro momento)
v₀ = 0 (inicialização do segundo momento)
t = 0 (contador de passos)
2. A cada passo t:
t = t + 1
gₜ = ∇ₜf(θₜ₋₁) (cálculo do gradiente)
3. Atualização dos momentos ajustados do primeiro e segundo ordem:
mₜ = β₁ · mₜ₋₁ + (1 - β₁) · gₜ
vₜ = β₂ · vₜ₋₁ + (1 - β₂) · gₜ²
m̂ₜ = mₜ / (1 - β₁ᵗ)
v̂ₜ = vₜ / (1 - β₂ᵗ)
4. Atualização dos parâmetros:
θₜ = θₜ₋₁ - α · m̂ₜ / (√v̂ₜ + ε)
Onde:
θₜ - parâmetros do modelo no passo t
f(θ) - função objetivo
α - taxa de aprendizado (geralmente α = 0.001)
β₁, β₂ - coeficientes de decaimento dos momentos (geralmente β₁ = 0.9, β₂ = 0.999)
ε - pequena constante para evitar divisão por zero (geralmente 10⁻⁸)
mₜ, vₜ - estimativas dos primeiros e segundos momentos do gradiente
m̂ₜ, v̂ₜ - estimativas corrigidas dos momentos
Essas fórmulas capturam a essência do algoritmo ADAM, mostrando como ele ajusta de forma adaptativa a taxa de aprendizado de cada parâmetro com base nas estimativas dos momentos do gradiente. Como podemos ver, não há estocasticidade no algoritmo em si. Normalmente, o ADAM, em suas muitas implementações em software, está firmemente entrelaçado com a arquitetura de redes neurais. No entanto, neste artigo faremos uma pequena mágica: não apenas o transformaremos em uma entidade autônoma e independente, mas também o converteremos, atenção, em um método populacional e verdadeiramente estocástico.
Para começar, precisamos implementar o ADAM em formato populacional, mantendo suas fórmulas originais, mas adicionando um elemento de aleatoriedade apenas na fase de inicialização dos parâmetros a serem otimizados. Mas isso é só o começo! Em seguida, vamos inserir aleatoriedade na dinâmica de comportamento desse método de gradiente e observar os resultados que isso pode gerar.
Definimos a estrutura "S_Gradients", que armazenará os gradientes e dois vetores de momentos (primeiro e segundo). O método "Init (int coords)" define o tamanho dos arrays e os inicializa com zeros.
//—————————————————————————————————————————————————————————————————————————————— // Structure for storing gradients and moments struct S_Gradients { double g []; // Gradients double m []; // Vectors of the first moment double v []; // Vectors of the second moment // Method for initializing gradients void Init (int coords) { ArrayResize (g, coords); ArrayResize (m, coords); ArrayResize (v, coords); ArrayInitialize (g, 0.0); // Initialize gradients to zeros ArrayInitialize (m, 0.0); // Initialize the first moment with zeros ArrayInitialize (v, 0.0); // Initialize the second moment with zeros } }; //——————————————————————————————————————————————————————————————————————————————
A classe "C_AO_ADAM" implementa o algoritmo de otimização ADAM. As funções principais da classe são:
- Construtor — inicializa os parâmetros do algoritmo, como tamanho da população, coeficientes de aprendizado e de decaimento.
- SetParams () — define os valores dos parâmetros a partir do array "params", permitindo modificá-los após a inicialização.
- Init () — prepara o algoritmo para operação, recebendo os intervalos de parâmetros e o número de épocas.
- Moving () e Revision () — são destinadas a executar os passos da otimização, atualizar os parâmetros do modelo e verificar o estado do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAM : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAM () { } // Class constructor C_AO_ADAM () { ao_name = "ADAM"; // Algorithm name ao_desc = "Adaptive Moment Estimation"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 50; // Population size alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 1e-8; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "alpha"; params [1].val = alpha; params [2].name = "beta1"; params [2].val = beta1; params [3].name = "beta2"; params [3].val = beta2; params [4].name = "epsilon"; params [4].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size alpha = params [1].val; // Set the learning ratio beta1 = params [2].val; // Set beta1 beta2 = params [3].val; // Set beta2 epsilon = params [4].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" da classe "C_AO_ADAM" executa a inicialização do algoritmo:
- Chama "StandardInit ()" para a configuração padrão dos parâmetros; se falhar, retorna "false".
- Zera os contadores de passos "step" e de iterações "t".
- Redimensiona o array de gradientes "grad" de acordo com o tamanho da população "popSize".
- Inicializa os gradientes para cada indivíduo da população usando as coordenadas "coords".
Se todas as operações forem bem-sucedidas, o método retorna "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAM::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" da classe "C_AO_ADAM" implementa um passo de otimização no algoritmo ADAM:
1. Verifica o passo atual; se o passo for menor que 2:
- Para cada indivíduo na população, o valor anterior da função e das coordenadas é salvo.
- São geradas novas coordenadas aleatórias dentro do intervalo definido e ajustadas para valores permitidos.
- O contador de passos é incrementado e o método finaliza a execução.
2. Cálculo dos gradientes: se o passo for 2 ou maior — para cada indivíduo é calculada a variação do valor da função objetivo e das coordenadas.
- Para evitar divisão por zero, adiciona-se um pequeno valor "epsilon", que além disso é um parâmetro externo do algoritmo, influenciando suas propriedades de busca.
- O gradiente é calculado para cada parâmetro.
3. Atualização dos parâmetros para cada indivíduo:
- São mantidos os valores anteriores da função e das coordenadas.
- São atualizadas as estimativas deslocadas do primeiro e do segundo momentos do gradiente.
- Calculam-se as estimativas corrigidas dos momentos e atualizam-se as coordenadas usando a fórmula do ADAM.
- As coordenadas são ajustadas para permanecerem dentro dos limites permitidos.
4. O contador de iterações "t" é incrementado.
Dessa forma, o método é responsável por atualizar as posições dos indivíduos durante o processo de otimização, utilizando os momentos adaptativos do gradiente. Os dois primeiros passos do algoritmo são necessários para calcular o gradiente da variação do valor da função de fitness, já que o gradiente é calculado numericamente, sem o conhecimento da fórmula analítica do problema de otimização. Para isso, são necessárias no mínimo duas amostragens, e nos passos seguintes é possível usar as soluções obtidas nas duas etapas anteriores.
A lógica do algoritmo ADAM de fato não exige um método específico de cálculo do gradiente. O gradiente pode ser calculado tanto de forma analítica quanto numérica, e seu cálculo ocorre fora do próprio algoritmo. Abstrair o algoritmo dos métodos de aplicação é realmente importante para entender o papel de cada componente dentro de um projeto de aprendizado de máquina. Isso permite avaliar melhor o impacto de cada elemento no resultado final e facilita a adaptação do algoritmo a diferentes tipos de problema.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" da classe "C_AO_ADAM" executa as seguintes ações:
- Inicializa o índice do melhor indivíduo "ind" como -1.
- Percorre todos os indivíduos na população e, se o valor da função do indivíduo atual for maior que o melhor valor encontrado "fB", atualiza a melhor solução global e salva o índice do melhor indivíduo.
- Se um melhor indivíduo for encontrado, suas coordenadas são copiadas para o array "cB".
Dessa forma, o método identifica e armazena as coordenadas do melhor indivíduo com base nos valores da função de fitness.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAM::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual } //——————————————————————————————————————————————————————————————————————————————
Como podemos ver, o algoritmo ADAM agora se tornou populacional, e se o parâmetro externo do tamanho da população for definido como 1, o algoritmo se comportará exatamente como o ADAM convencional, não populacional. Agora já podemos testar o algoritmo com nossas funções de teste. Vamos conferir os resultados:
ADAM|Adaptive Moment Estimation|50.0|0.001|0.9|0.999|0.00000001|
=============================
5 Hilly's; Func runs: 10000; result: 0.3857584301959297
25 Hilly's; Func runs: 10000; result: 0.29733109680042824
500 Hilly's; Func runs: 10000; result: 0.25390478702062613
=============================
5 Forest's; Func runs: 10000; result: 0.30772687797850234
25 Forest's; Func runs: 10000; result: 0.1982664040653052
500 Forest's; Func runs: 10000; result: 0.15554626746207786
=============================
5 Megacity's; Func runs: 10000; result: 0.18153846153846154
25 Megacity's; Func runs: 10000; result: 0.12430769230769231
500 Megacity's; Func runs: 10000; result: 0.09503076923077
=============================
All score: 1.99941 (22.22%)
Os resultados, infelizmente, não são os melhores, mas isso abre espaço para crescimento potencial e nos dá margem para implementar melhorias, especialmente pela introdução de um verdadeiro componente estocástico no algoritmo.
Na implementação descrita acima do algoritmo populacional ADAM, cada agente representa uma "trilha" independente da lógica original dos autores, semelhante a pequenas cobras deslizando sobre colinas do espaço de busca, distribuídas pelo campo devido à inicialização aleatória. Essas cobras não interagem entre si nem compartilham informações sobre as melhores soluções. Pois o algoritmo é baseado em gradiente, é essencial considerar as variações do relevo nas proximidades das coordenadas. Reduzir o passo da diferenciação numérica pode levar a uma convergência lenta, enquanto aumentá-lo resulta em saltos grandes no espaço, dificultando a coleta de informações sobre a superfície entre os pontos.
Para resolver esses problemas, tornaremos parte da população composta por indivíduos híbridos, que serão formados a partir de elementos das soluções de outros agentes. A ideia é a seguinte: classificamos a população de acordo com a adaptabilidade dos indivíduos e, no fim da lista, onde estão os mais fracos, criaremos híbridos. Para esses indivíduos, as soluções serão geradas por meio da criação de um novo ponto no espaço, com base em elementos das soluções dos indivíduos mais adaptáveis. Quanto maior a adaptabilidade de um indivíduo, maior a probabilidade de ele contribuir com informações sobre sua posição para os híbridos.
Assim, uma parte dos indivíduos da população representará soluções conforme a lógica original do algoritmo, e outra parte será composta pelos chamados híbridos, que são combinações de elementos das soluções da população. O híbrido gerado não é simplesmente uma cópia de partes de outros indivíduos; cada parte é modificada de acordo com uma lei de distribuição de probabilidade baseada em potência. Chamaremos o grau dessa lei de "resistência do híbrido": quanto maior o grau, menores as alterações sofridas pelo híbrido, e mais ele se assemelha aos elementos das melhores soluções na população.
Agora passamos para a versão atualizada do algoritmo. Na classe "C_AO_ADAMm" foram implementadas várias mudanças em relação à classe "C_AO_ADAM", que teoricamente podem influenciar positivamente sua funcionalidade e comportamento. Aqui estão as principais alterações:
1. Novos parâmetros:
- hybridsPercentage — parâmetro que define a porcentagem de híbridos na população.
- hybridsResistance — parâmetro que regula a resistência dos híbridos às modificações.
2. No construtor da classe "C_AO_ADAMm", os novos parâmetros "hybridsPercentage" e "hybridsResistance" são inicializados, e seus valores são adicionados ao array "params".
3. SetParams — neste método, foram adicionadas linhas para configurar os novos parâmetros "hybridsPercentage" e "hybridsResistance", permitindo que seus valores sejam alterados dinamicamente.
Se o valor do parâmetro de porcentagem de híbridos for definido como "1", a lógica do ADAM será efetivamente desativada. Por outro lado, definir esse valor como "0" resultará na ausência de propriedades combinatórias no algoritmo. Como resultado, por meio de testes empíricos, encontrei o valor ideal em "0.5", que se mostrou o mais eficaz.
O segundo parâmetro é responsável pela resistência dos híbridos às alterações. Quando se atribuem valores baixos, os híbridos, após herdarem características, sofrem modificações significativas e podem abranger todo o intervalo permitido dos parâmetros otimizados. Ao mesmo tempo, se valores muito altos forem definidos, como "20" ou mais, a variabilidade dos híbridos tende a "0", tornando-os apenas transmissores das melhores qualidades das criaturas parentais. Por meio de testes empíricos, foi identificado que o valor ideal para esse parâmetro é "10".
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ADAMm : public C_AO { public: //-------------------------------------------------------------------- // Class destructor ~C_AO_ADAMm () { } // Class constructor C_AO_ADAMm () { ao_name = "ADAMm"; // Algorithm name ao_desc = "Adaptive Moment Estimation M"; // Algorithm description ao_link = "https://www.mql5.com/en/articles/16443"; // Link to the article popSize = 100; // Population size hybridsPercentage = 0.5; // Percentage of hybrids in the population hybridsResistance = 10; // Resistance of hybrids to changes alpha = 0.001; // Learning ratio beta1 = 0.9; // Exponential decay ratio for the first moment beta2 = 0.999; // Exponential decay ratio for the second moment epsilon = 0.1; // Small constant to prevent division by zero // Initialize the parameter array ArrayResize (params, 7); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "hybridsPercentage"; params [1].val = hybridsPercentage; params [2].name = "hybridsResistance"; params [2].val = hybridsResistance; params [3].name = "alpha"; params [3].val = alpha; params [4].name = "beta1"; params [4].val = beta1; params [5].name = "beta2"; params [5].val = beta2; params [6].name = "epsilon"; params [6].val = epsilon; } // Method for setting parameters void SetParams () { popSize = (int)params [0].val; // Set population size hybridsPercentage = params [1].val; // Set the percentage of hybrids in the population hybridsResistance = params [2].val; // Set hybrids' resistance to change alpha = params [3].val; // Set the learning ratio beta1 = params [4].val; // Set beta1 beta2 = params [5].val; // Set beta2 epsilon = params [6].val; // Set epsilon } // Initialization method bool Init (const double &rangeMinP [], // minimum search range const double &rangeMaxP [], // maximum search range const double &rangeStepP [], // search step const int epochsP = 0); // number of epochs void Moving (); // Moving method void Revision (); // Revision method //---------------------------------------------------------------------------- double hybridsPercentage; // Percentage of hybrids in the population double hybridsResistance; // Resistance of hybrids to changes double alpha; // Learning ratio double beta1; // Exponential decay ratio for the first moment double beta2; // Exponential decay ratio for the second moment double epsilon; // Small constant S_Gradients grad []; // Array of gradients private: //------------------------------------------------------------------- int step; // Iteration step int t; // Iteration counter int hybridsNumber; // Number of hybrids in the population }; //——————————————————————————————————————————————————————————————————————————————
No método "Init" da classe "C_AO_ADAMm", foram realizadas as seguintes alterações em comparação com o método equivalente da classe anterior:
- É calculada a quantidade de híbridos na população com base na porcentagem "hybridsPercentage". Esse novo valor "hybridsNumber" é utilizado para controlar a composição da população.
- Foi adicionada uma verificação para garantir que o número de híbridos não ultrapasse o tamanho da população "popSize". Isso evita erros relacionados a ultrapassagem dos limites do array.
Essas modificações tornam o método "Init" mais adaptável às particularidades do algoritmo relacionadas aos híbridos, garantindo o controle correto do estado e da inicialização dos indivíduos na população.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ADAMm::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { // Standard initialization if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- step = 0; // Reset step counter t = 1; // Reset iteration counter hybridsNumber = int(popSize * hybridsPercentage); // Calculation of the number of hybrids in the population if (hybridsNumber > popSize) hybridsNumber = popSize; // Correction ArrayResize (grad, popSize); // Resize the gradient array for (int i = 0; i < popSize; i++) grad [i].Init (coords); // Initialize gradients for each individual return true; } //——————————————————————————————————————————————————————————————————————————————
No método "Moving", também há algumas alterações em relação à versão anterior desse método.
Atualização dos parâmetros usando o algoritmo ADAM. Neste bloco foram adicionadas condições para o tratamento dos híbridos. Se o índice do indivíduo "i" for maior ou igual a "popSize - hybridsNumber", novas coordenadas são geradas usando uma distribuição aleatória e o parâmetro "hybridsResistance". Isso permite que os híbridos apresentem pequenas variações nas características herdadas dos indivíduos parentais (uma espécie de análogo à mutação de características). Caso contrário, para os indivíduos que não são híbridos, ocorre a atualização das estimativas deslocadas do primeiro e segundo momentos e, em seguida, o cálculo das estimativas corrigidas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Moving () { //---------------------------------------------------------------------------- if (step < 2) // If step is less than 2 { for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; // Save the previous value of the function for (int c = 0; c < coords; c++) { a [i].cP [c] = a [i].c [c]; // Save the previous coordinate value // Generate new coordinates randomly a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Bringing new coordinates to acceptable values a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } step++; // Increase the step counter return; // Exit the method } //---------------------------------------------------------------------------- double ΔF, ΔX; // Changes in function and coordinates double cNew; for (int i = 0; i < popSize; i++) { ΔF = a [i].f - a [i].fP; // Calculate the change of the function for (int c = 0; c < coords; c++) { ΔX = a [i].c [c] - a [i].cP [c]; // Calculate the change in coordinates if (ΔX == 0.0) ΔX = epsilon; // If change is zero, set it to epsilon grad [i].g [c] = ΔF / ΔX; // Calculate the gradient } } // Update parameters using ADAM algorithm for (int i = 0; i < popSize; i++) { // Save the previous value of the function a [i].fP = a [i].f; for (int c = 0; c < coords; c++) { // Save the previous coordinate value a [i].cP [c] = a [i].c [c]; if (i >= popSize - hybridsNumber) { double pr = u.RNDprobab (); pr *= pr; int ind = (int)u.Scale (pr, 0, 1, 0, popSize - 1); cNew = u.PowerDistribution (a [ind].c [c], rangeMin [c], rangeMax [c], hybridsResistance); } else { // Update the biased first moment estimate grad [i].m [c] = beta1 * grad [i].m [c] + (1.0 - beta1) * grad [i].g [c]; // Update the biased second moment estimate grad [i].v [c] = beta2 * grad [i].v [c] + (1.0 - beta2) * grad [i].g [c] * grad [i].g [c]; // Calculate the adjusted first moment estimate double m_hat = grad [i].m [c] / (1.0 - MathPow (beta1, t)); // Calculate the adjusted estimate of the second moment double v_hat = grad [i].v [c] / (1.0 - MathPow (beta2, t)); // Update coordinates //a [i].c [c] = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); cNew = a [i].c [c] + (alpha * m_hat / (MathSqrt (v_hat) + epsilon)); } // Make sure the coordinates stay within the allowed range a [i].c [c] = u.SeInDiSp (cNew, rangeMin [c], rangeMax [c], rangeStep [c]); } } t++; // Increase the iteration counter } //——————————————————————————————————————————————————————————————————————————————
No método "Revision", as seguintes alterações foram feitas em comparação com a versão anterior:
Preparação do array para ordenação: é criado um array temporário "aT" com o tamanho da população e, em seguida, é chamado o método de ordenação "u.Sorting ()". O array ordenado da população permite implementar a herança de características pelos híbridos com maior probabilidade a partir dos indivíduos mais adaptáveis. O array temporário da população poderia ser transferido para os campos da classe, mas neste caso foi feito assim para fins de maior clareza.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ADAMm::Revision () { int ind = -1; // Best individual index for (int i = 0; i < popSize; i++) { if (a [i].f > fB) // If the current value of the function is greater than the best one { fB = a [i].f; // Update the best value of the function ind = i; // Store the index of the best individual } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); // Copy the coordinates of the best individual //---------------------------------------------------------------------------- S_AO_Agent aT []; ArrayResize (aT, popSize); u.Sorting (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Vamos analisar os resultados obtidos com a versão modificada e verdadeiramente estocástica do algoritmo populacional ADAMm:
ADAMm|Adaptive Moment Estimation M|100.0|0.5|10.0|0.001|0.9|0.999|0.1|
=============================
5 Hilly's; Func runs: 10000; result: 0.8863499654810468
25 Hilly's; Func runs: 10000; result: 0.4476644542595641
500 Hilly's; Func runs: 10000; result: 0.2661291031673467
=============================
5 Forest's; Func runs: 10000; result: 0.8449728914068644
25 Forest's; Func runs: 10000; result: 0.3849320103361983
500 Forest's; Func runs: 10000; result: 0.16889385703816007
=============================
5 Megacity's; Func runs: 10000; result: 0.6615384615384616
25 Megacity's; Func runs: 10000; result: 0.2704615384615384
500 Megacity's; Func runs: 10000; result: 0.10593846153846247
=============================
All score: 4.03688 (44.85%)
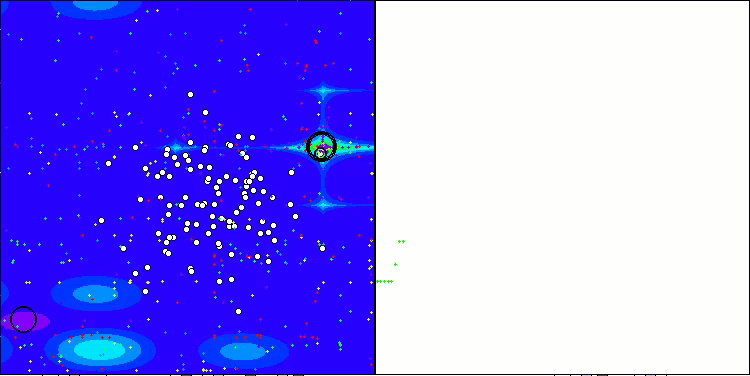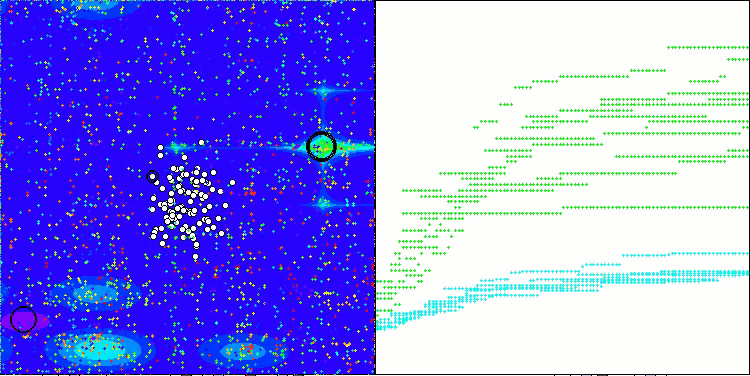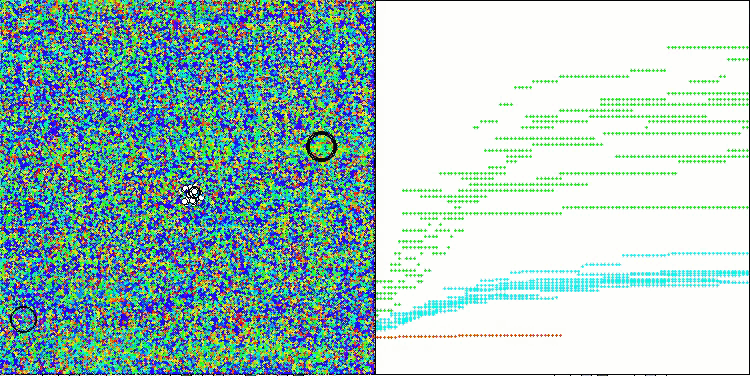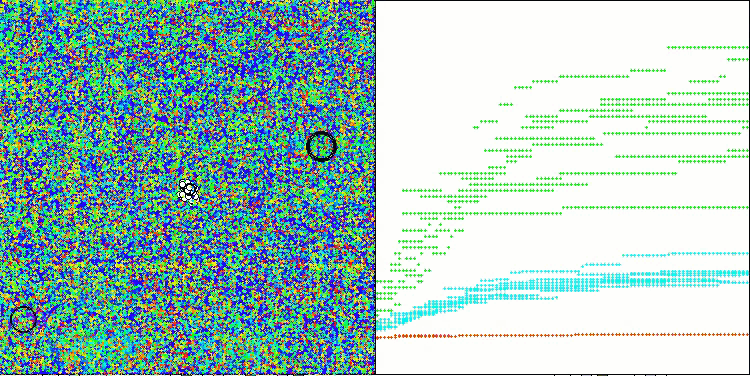
Os resultados obtidos melhoraram consideravelmente. Abaixo, é apresentada uma visualização do algoritmo ADAM populacional simples, onde é possível observar o deslocamento característico das pequenas "cobras", que se espalham em todas as direções durante a exploração do espaço de busca. Também são apresentadas visualizações do ADAMm populacional estocástico, que mostram um movimento mais ativo dos agentes de busca em direção ao ótimo global, embora com a perda do formato típico das "cobras".
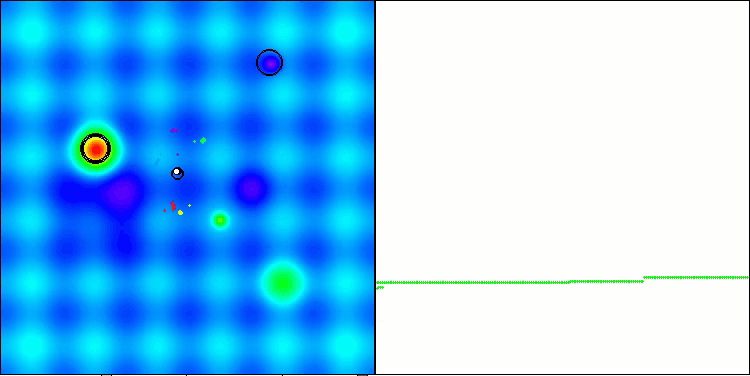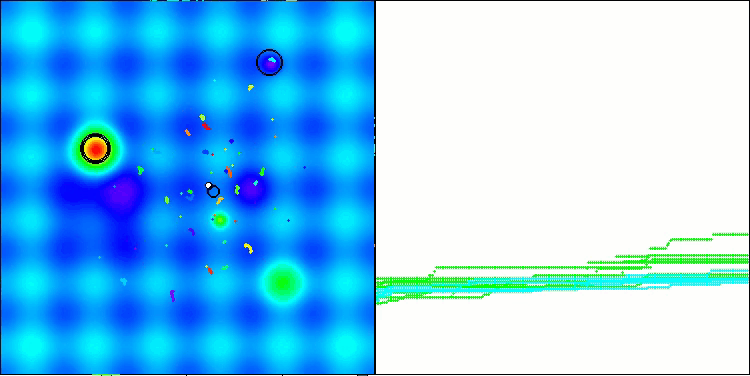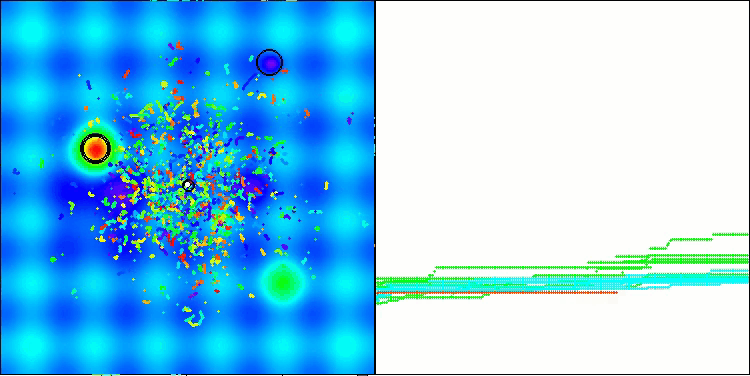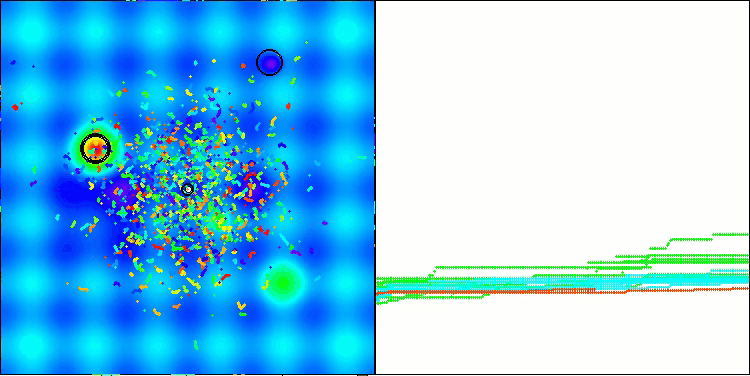
ADAM na função de teste Hilly
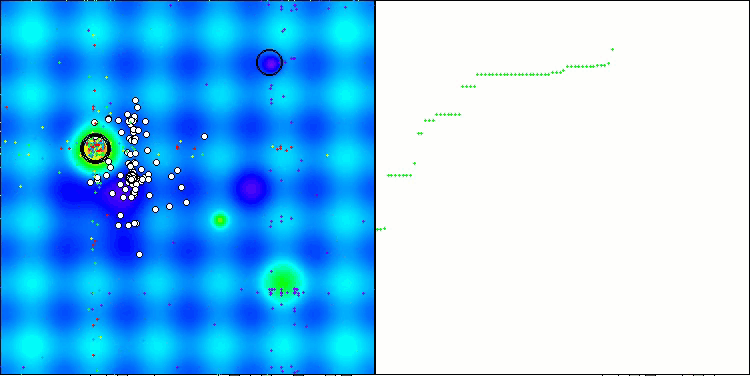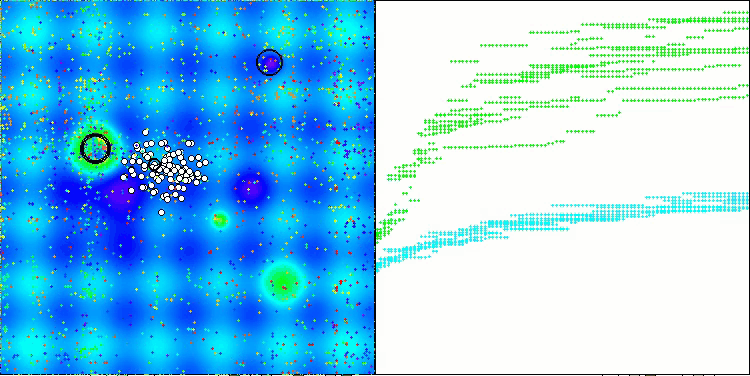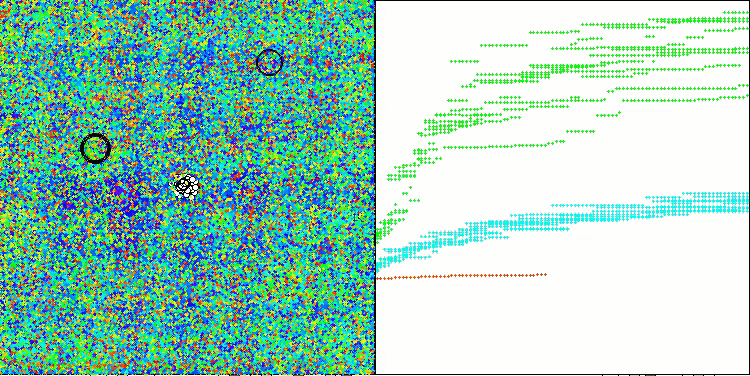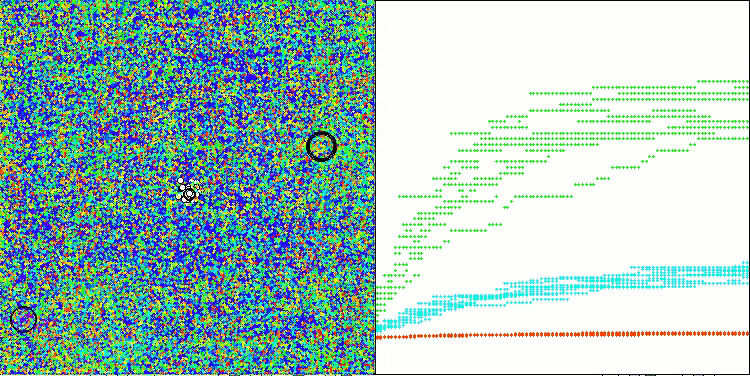
ADAMm na função de teste Hilly
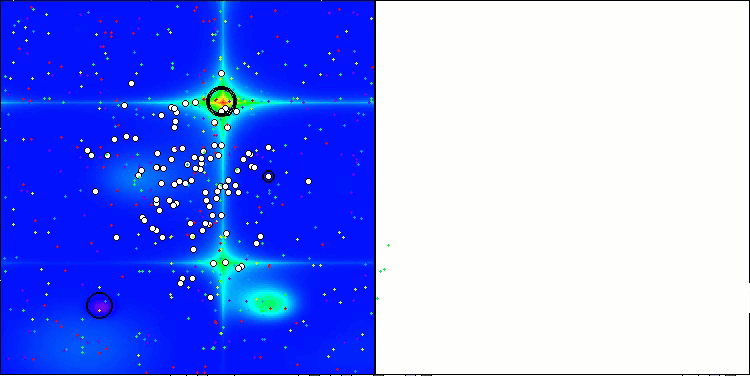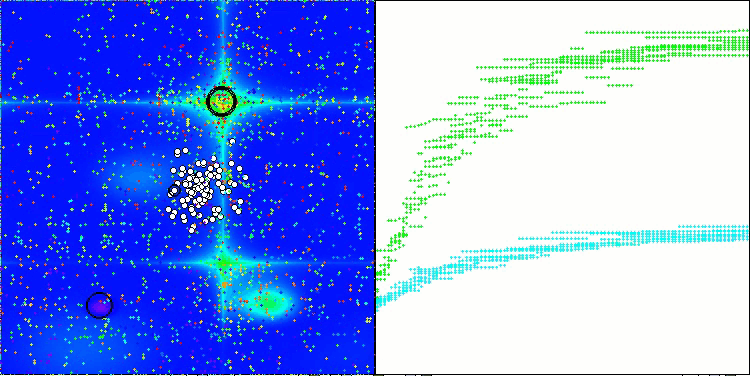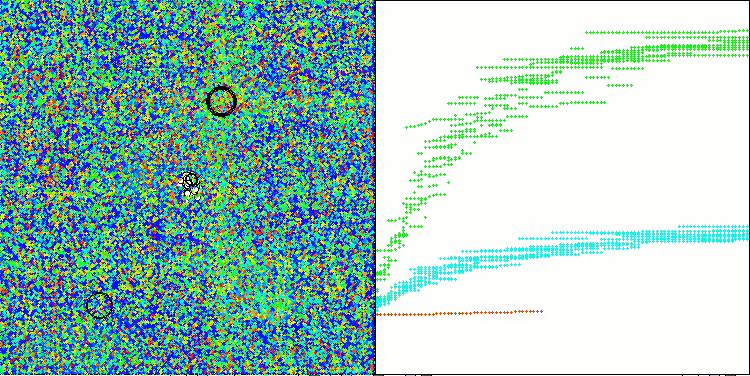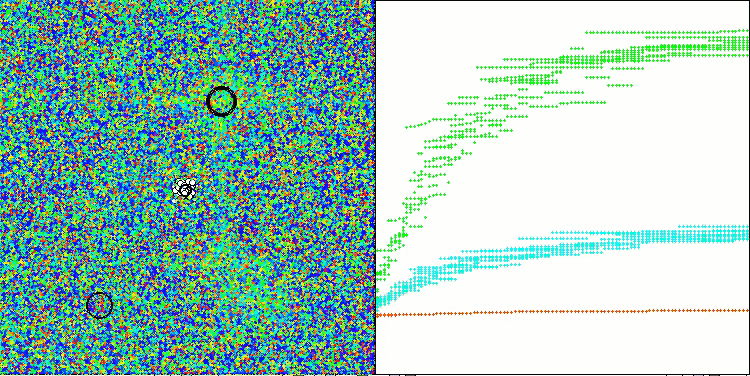
ADAMm na função de teste Forest
ADAMm na função de teste Megacity
Ao final dos testes, a versão estocástica e populacional do ADAM ocupa a 32ª posição na tabela de classificação, o que representa um resultado bastante satisfatório. A versão original não conseguiu entrar na tabela.
| # | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0.94948 | 0.84776 | 0.43857 | 2.23581 | 1.00000 | 0.92334 | 0.39988 | 2.32323 | 0.70923 | 0.63477 | 0.23091 | 1.57491 | 6.134 | 68.15 |
| 2 | CLA | code lock algorithm (joo) | 0.95345 | 0.87107 | 0.37590 | 2.20042 | 0.98942 | 0.91709 | 0.31642 | 2.22294 | 0.79692 | 0.69385 | 0.19303 | 1.68380 | 6.107 | 67.86 |
| 3 | AMOm | animal migration ptimization M | 0.90358 | 0.84317 | 0.46284 | 2.20959 | 0.99001 | 0.92436 | 0.46598 | 2.38034 | 0.56769 | 0.59132 | 0.23773 | 1.39675 | 5.987 | 66.52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0.92256 | 0.88101 | 0.40021 | 2.20379 | 0.97750 | 0.87490 | 0.31945 | 2.17185 | 0.67385 | 0.62985 | 0.18634 | 1.49003 | 5.866 | 65.17 |
| 5 | CTA | comet tail algorithm (joo) | 0.95346 | 0.86319 | 0.27770 | 2.09435 | 0.99794 | 0.85740 | 0.33949 | 2.19484 | 0.88769 | 0.56431 | 0.10512 | 1.55712 | 5.846 | 64.96 |
| 6 | SDSm | stochastic diffusion search M | 0.93066 | 0.85445 | 0.39476 | 2.17988 | 0.99983 | 0.89244 | 0.19619 | 2.08846 | 0.72333 | 0.61100 | 0.10670 | 1.44103 | 5.709 | 63.44 |
| 7 | AAm | archery algorithm M | 0.91744 | 0.70876 | 0.42160 | 2.04780 | 0.92527 | 0.75802 | 0.35328 | 2.03657 | 0.67385 | 0.55200 | 0.23738 | 1.46323 | 5.548 | 61.64 |
| 8 | ESG | evolution of social groups (joo) | 0.99906 | 0.79654 | 0.35056 | 2.14616 | 1.00000 | 0.82863 | 0.13102 | 1.95965 | 0.82333 | 0.55300 | 0.04725 | 1.42358 | 5.529 | 61.44 |
| 9 | SIA | simulated isotropic annealing (joo) | 0.95784 | 0.84264 | 0.41465 | 2.21513 | 0.98239 | 0.79586 | 0.20507 | 1.98332 | 0.68667 | 0.49300 | 0.09053 | 1.27020 | 5.469 | 60.76 |
| 10 | ACS | artificial cooperative search | 0.75547 | 0.74744 | 0.30407 | 1.80698 | 1.00000 | 0.88861 | 0.22413 | 2.11274 | 0.69077 | 0.48185 | 0.13322 | 1.30583 | 5.226 | 58.06 |
| 11 | ASO | anarchy society optimization | 0.84872 | 0.74646 | 0.31465 | 1.90983 | 0.96148 | 0.79150 | 0.23803 | 1.99101 | 0.57077 | 0.54062 | 0.16614 | 1.27752 | 5.178 | 57.54 |
| 12 | AOSm | atomic orbital search M | 0.80232 | 0.70449 | 0.31021 | 1.81702 | 0.85660 | 0.69451 | 0.21996 | 1.77107 | 0.74615 | 0.52862 | 0.14358 | 1.41835 | 5.006 | 55.63 |
| 13 | TSEA | turtle shell evolution algorithm (joo) | 0.96798 | 0.64480 | 0.29672 | 1.90949 | 0.99449 | 0.61981 | 0.22708 | 1.84139 | 0.69077 | 0.42646 | 0.13598 | 1.25322 | 5.004 | 55.60 |
| 14 | DE | differential evolution | 0.95044 | 0.61674 | 0.30308 | 1.87026 | 0.95317 | 0.78896 | 0.16652 | 1.90865 | 0.78667 | 0.36033 | 0.02953 | 1.17653 | 4.955 | 55.06 |
| 15 | CRO | chemical reaction optimization | 0.94629 | 0.66112 | 0.29853 | 1.90593 | 0.87906 | 0.58422 | 0.21146 | 1.67473 | 0.75846 | 0.42646 | 0.12686 | 1.31178 | 4.892 | 54.36 |
| 16 | BSA | bird swarm algorithm | 0.89306 | 0.64900 | 0.26250 | 1.80455 | 0.92420 | 0.71121 | 0.24939 | 1.88479 | 0.69385 | 0.32615 | 0.10012 | 1.12012 | 4.809 | 53.44 |
| 17 | HS | harmony search | 0.86509 | 0.68782 | 0.32527 | 1.87818 | 0.99999 | 0.68002 | 0.09590 | 1.77592 | 0.62000 | 0.42267 | 0.05458 | 1.09725 | 4.751 | 52.79 |
| 18 | SSG | saplings sowing and growing | 0.77839 | 0.64925 | 0.39543 | 1.82308 | 0.85973 | 0.62467 | 0.17429 | 1.65869 | 0.64667 | 0.44133 | 0.10598 | 1.19398 | 4.676 | 51.95 |
| 19 | BCOm | bacterial chemotaxis optimization M | 0.75953 | 0.62268 | 0.31483 | 1.69704 | 0.89378 | 0.61339 | 0.22542 | 1.73259 | 0.65385 | 0.42092 | 0.14435 | 1.21912 | 4.649 | 51.65 |
| 20 | ABO | african buffalo optimization | 0.83337 | 0.62247 | 0.29964 | 1.75548 | 0.92170 | 0.58618 | 0.19723 | 1.70511 | 0.61000 | 0.43154 | 0.13225 | 1.17378 | 4.634 | 51.49 |
| 21 | (PO)ES | (PO) evolution strategies | 0.79025 | 0.62647 | 0.42935 | 1.84606 | 0.87616 | 0.60943 | 0.19591 | 1.68151 | 0.59000 | 0.37933 | 0.11322 | 1.08255 | 4.610 | 51.22 |
| 22 | TSm | tabu search M | 0.87795 | 0.61431 | 0.29104 | 1.78330 | 0.92885 | 0.51844 | 0.19054 | 1.63783 | 0.61077 | 0.38215 | 0.12157 | 1.11449 | 4.536 | 50.40 |
| 23 | BSO | brain storm optimization | 0.93736 | 0.57616 | 0.29688 | 1.81041 | 0.93131 | 0.55866 | 0.23537 | 1.72534 | 0.55231 | 0.29077 | 0.11914 | 0.96222 | 4.498 | 49.98 |
| 24 | WOAm | wale optimization algorithm M | 0.84521 | 0.56298 | 0.26263 | 1.67081 | 0.93100 | 0.52278 | 0.16365 | 1.61743 | 0.66308 | 0.41138 | 0.11357 | 1.18803 | 4.476 | 49.74 |
| 25 | AEFA | artificial electric field algorithm | 0.87700 | 0.61753 | 0.25235 | 1.74688 | 0.92729 | 0.72698 | 0.18064 | 1.83490 | 0.66615 | 0.11631 | 0.09508 | 0.87754 | 4.459 | 49.55 |
| 26 | AEO | artificial ecosystem-based optimization algorithm | 0.91380 | 0.46713 | 0.26470 | 1.64563 | 0.90223 | 0.43705 | 0.21400 | 1.55327 | 0.66154 | 0.30800 | 0.28563 | 1.25517 | 4.454 | 49.49 |
| 27 | ACOm | ant colony optimization M | 0.88190 | 0.66127 | 0.30377 | 1.84693 | 0.85873 | 0.58680 | 0.15051 | 1.59604 | 0.59667 | 0.37333 | 0.02472 | 0.99472 | 4.438 | 49.31 |
| 28 | BFO-GA | bacterial foraging optimization - ga | 0.89150 | 0.55111 | 0.31529 | 1.75790 | 0.96982 | 0.39612 | 0.06305 | 1.42899 | 0.72667 | 0.27500 | 0.03525 | 1.03692 | 4.224 | 46.93 |
| 29 | SOA | simple optimization algorithm | 0.91520 | 0.46976 | 0.27089 | 1.65585 | 0.89675 | 0.37401 | 0.16984 | 1.44060 | 0.69538 | 0.28031 | 0.10852 | 1.08422 | 4.181 | 46.45 |
| 30 | ABHA | artificial bee hive algorithm | 0.84131 | 0.54227 | 0.26304 | 1.64663 | 0.87858 | 0.47779 | 0.17181 | 1.52818 | 0.50923 | 0.33877 | 0.10397 | 0.95197 | 4.127 | 45.85 |
| 31 | ACMO | atmospheric cloud model optimization | 0.90321 | 0.48546 | 0.30403 | 1.69270 | 0.80268 | 0.37857 | 0.19178 | 1.37303 | 0.62308 | 0.24400 | 0.10795 | 0.97503 | 4.041 | 44.90 |
| 32 | ADAMm | adaptive moment estimation M | 0.88635 | 0.44766 | 0.26613 | 1.60014 | 0.84497 | 0.38493 | 0.16889 | 1.39880 | 0.66154 | 0.27046 | 0.10594 | 1.03794 | 4.037 | 44.85 |
| 33 | ASHA | artificial showering algorithm | 0.89686 | 0.40433 | 0.25617 | 1.55737 | 0.80360 | 0.35526 | 0.19160 | 1.35046 | 0.47692 | 0.18123 | 0.09774 | 0.75589 | 3.664 | 40.71 |
| 34 | ASBO | adaptive social behavior optimization | 0.76331 | 0.49253 | 0.32619 | 1.58202 | 0.79546 | 0.40035 | 0.26097 | 1.45677 | 0.26462 | 0.17169 | 0.18200 | 0.61831 | 3.657 | 40.63 |
| 35 | MEC | mind evolutionary computation | 0.69533 | 0.53376 | 0.32661 | 1.55569 | 0.72464 | 0.33036 | 0.07198 | 1.12698 | 0.52500 | 0.22000 | 0.04198 | 0.78698 | 3.470 | 38.55 |
| 36 | IWO | invasive weed optimization | 0.72679 | 0.52256 | 0.33123 | 1.58058 | 0.70756 | 0.33955 | 0.07484 | 1.12196 | 0.42333 | 0.23067 | 0.04617 | 0.70017 | 3.403 | 37.81 |
| 37 | Micro-AIS | micro artificial immune system | 0.79547 | 0.51922 | 0.30861 | 1.62330 | 0.72956 | 0.36879 | 0.09398 | 1.19233 | 0.37667 | 0.15867 | 0.02802 | 0.56335 | 3.379 | 37.54 |
| 38 | COAm | cuckoo optimization algorithm M | 0.75820 | 0.48652 | 0.31369 | 1.55841 | 0.74054 | 0.28051 | 0.05599 | 1.07704 | 0.50500 | 0.17467 | 0.03380 | 0.71347 | 3.349 | 37.21 |
| 39 | SDOm | spiral dynamics optimization M | 0.74601 | 0.44623 | 0.29687 | 1.48912 | 0.70204 | 0.34678 | 0.10944 | 1.15826 | 0.42833 | 0.16767 | 0.03663 | 0.63263 | 3.280 | 36.44 |
| 40 | NMm | Nelder-Mead method M | 0.73807 | 0.50598 | 0.31342 | 1.55747 | 0.63674 | 0.28302 | 0.08221 | 1.00197 | 0.44667 | 0.18667 | 0.04028 | 0.67362 | 3.233 | 35.92 |
| 41 | FAm | firefly algorithm M | 0.58634 | 0.47228 | 0.32276 | 1.38138 | 0.68467 | 0.37439 | 0.10908 | 1.16814 | 0.28667 | 0.16467 | 0.04722 | 0.49855 | 3.048 | 33.87 |
| 42 | GSA | gravitational search algorithm | 0.64757 | 0.49197 | 0.30062 | 1.44016 | 0.53962 | 0.36353 | 0.09945 | 1.00260 | 0.32667 | 0.12200 | 0.01917 | 0.46783 | 2.911 | 32.34 |
| 43 | BFO | bacterial foraging optimization | 0.61171 | 0.43270 | 0.31318 | 1.35759 | 0.54410 | 0.21511 | 0.05676 | 0.81597 | 0.42167 | 0.13800 | 0.03195 | 0.59162 | 2.765 | 30.72 |
| 44 | ABC | artificial bee colony | 0.63377 | 0.42402 | 0.30892 | 1.36671 | 0.55103 | 0.21874 | 0.05623 | 0.82600 | 0.34000 | 0.14200 | 0.03102 | 0.51302 | 2.706 | 30.06 |
| 45 | BA | bat algorithm | 0.59761 | 0.45911 | 0.35242 | 1.40915 | 0.40321 | 0.19313 | 0.07175 | 0.66810 | 0.21000 | 0.10100 | 0.03517 | 0.34617 | 2.423 | 26.93 |
Considerações finais
Este artigo apresentou uma tentativa de adaptar o conhecido método de gradiente ADAM, tradicionalmente utilizado em redes neurais, para a resolução de problemas de otimização em geral. Essa tentativa mostrou-se bem-sucedida, uma vez que o ADAMm populacional verdadeiramente estocástico se revelou capaz de competir com os algoritmos mais poderosos voltados para problemas de otimização global. O artigo demonstra que abordagens determinísticas para a busca de soluções ótimas frequentemente não são tão eficazes em espaços de busca multidimensionais quanto os métodos estocásticos, sendo que apenas a introdução de elementos adicionais de aleatoriedade pode ampliar a capacidade de exploração de qualquer algoritmo de otimização.
No entanto, vale destacar que o uso de métodos de gradiente integrados à rede, como o ADAM clássico, ainda é praticamente imbatível no treinamento de redes neurais, já que se baseia no valor exato do gradiente durante a propagação reversa do erro. Ainda assim, quando o treinamento de redes neurais envolve critérios de avaliação mais complexos do que a simples minimização do erro, os métodos de gradiente podem enfrentar dificuldades, como ficar presos em ótimos locais — problema amplamente citado por diversos autores na área de aprendizado de máquina.
A abordagem apresentada neste artigo pode ser útil mesmo no uso clássico dos métodos integrados em redes neurais, mantendo excelente precisão e velocidade de convergência, ao utilizar a forma analítica da função de ativação dos neurônios e, ao mesmo tempo, ampliando significativamente a resistência ao travamento durante o treinamento das redes. Isso permitirá aplicar os métodos clássicos até mesmo em problemas com métricas e critérios extremamente complexos durante o treinamento. Espero que este trabalho ajude pesquisadores e profissionais a reconsiderarem os desafios da otimização em geral e dos métodos de aprendizado de máquina em particular sob uma nova perspectiva.
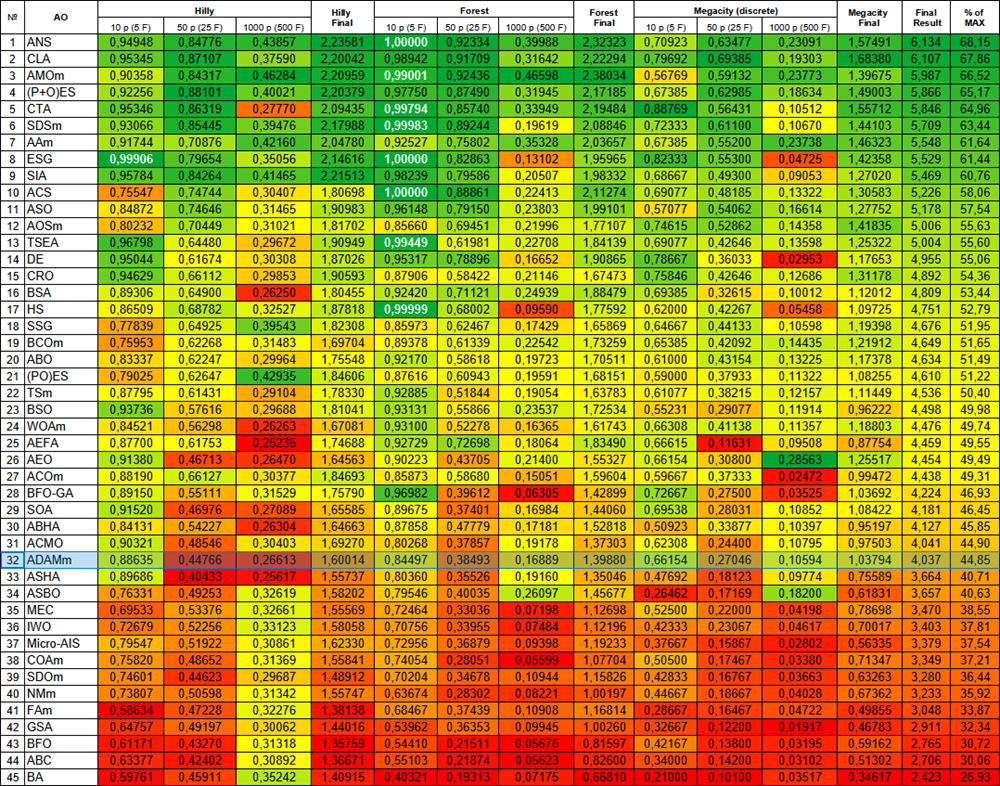
Figura 1. Gradação de cores dos algoritmos conforme os respectivos testes. A cor branca destaca resultados maiores ou iguais a 0.99
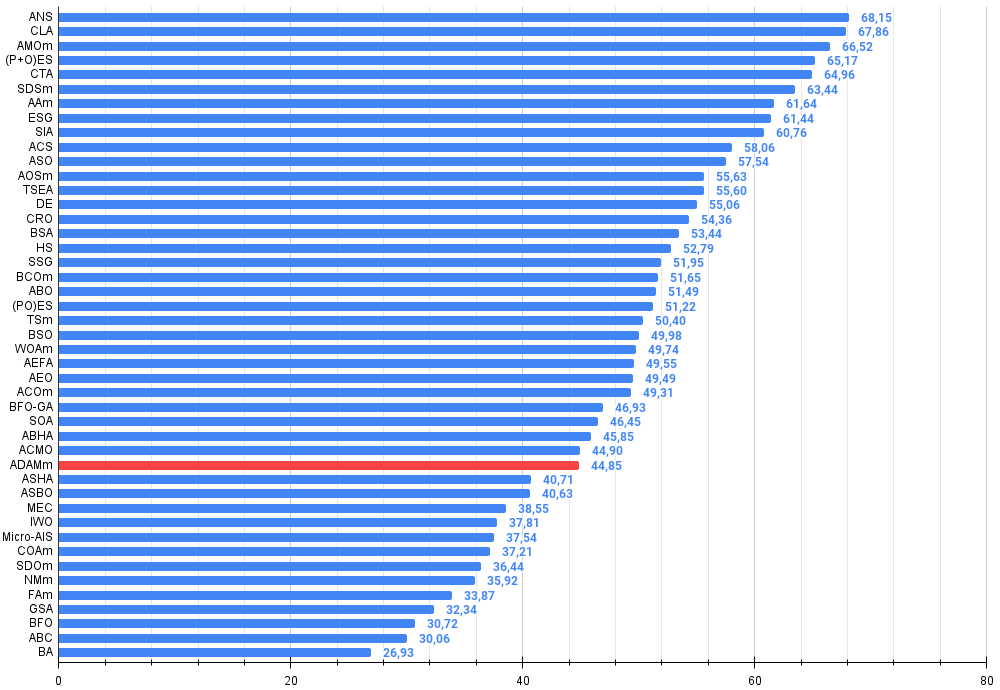
Figura 2. Histograma dos resultados de testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo compactado há um script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo ADAMm:
Vantagens:
- Bons resultados em problemas de baixa dimensionalidade.
- Pequena dispersão nos resultados.
Desvantagens:
- Muitos parâmetros externos.
Está anexado ao artigo um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, já que muitos deles foram modificados para melhorar a capacidade de busca. As conclusões e interpretações apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | C_AO.mqh | Arquivo incluível | Classe pai dos algoritmos populacionais de otimização |
| 2 | C_AO_enum.mqh | Arquivo incluível | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo incluível | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo incluível | Biblioteca de funções da bancada de testes |
| 5 | Utilities.mqh | Arquivo incluível | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo incluível | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Bancada de testes unificada para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso de algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_ADAM.mq5 | Script | Bancada de testes para o ADAM e o ADAMm |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/16443
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Técnicas do MQL5 Wizard que você deve conhecer (Parte 37): Regressão por Processo Gaussiano com Núcleos Lineares e de Matérn
Técnicas do MQL5 Wizard que você deve conhecer (Parte 37): Regressão por Processo Gaussiano com Núcleos Lineares e de Matérn
 Redes neurais em trading: Conjunto de agentes com uso de mecanismos de atenção (MASAAT)
Redes neurais em trading: Conjunto de agentes com uso de mecanismos de atenção (MASAAT)
 Negociação algorítmica baseada em padrões de reversão 3D
Negociação algorítmica baseada em padrões de reversão 3D
 Indicador de perfil de mercado — Market Profile (Parte 2): Otimização e desenho em canvas
Indicador de perfil de mercado — Market Profile (Parte 2): Otimização e desenho em canvas
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso