Algoritmo de otimização da sociedade anárquica — Anarchic society optimization (ASO)
78
0
Conteúdo
1. Introdução
Sempre me interessei pelo tema das relações sociais e pela possibilidade de construir um algoritmo para modelar conexões sociais, pois isso representa um dos fenômenos mais interessantes no desenvolvimento da sociedade e oferece um vasto campo de atuação para descrever algoritmicamente a estrutura do sistema de relações e implementar um algoritmo de otimização baseado nisso.
Em artigos anteriores, já analisamos algoritmos de comportamento social, como evolution of social groups, artificial cooperative search. Neste artigo, tentaremos compreender a concepção da sociedade anárquica, um sistema de interação social no qual não há autoridade centralizada nem estruturas hierárquicas, e no qual se presume que as pessoas possam organizar suas vidas e interagir com base em acordos voluntários.
A sociedade anárquica é baseada nos princípios de autonomia e liberdade, nos quais cada indivíduo pode tomar decisões de forma independente e autônoma sobre sua vida, sem interferência externa. Ela também é baseada nos princípios de cooperação voluntária, nos quais as pessoas interagem com base no consentimento de todos os participantes, sem coerção, e nos princípios de igualdade de direitos e oportunidades. Além disso, a sociedade anárquica é baseada nos princípios de solidariedade, ajuda mútua e colaboração. Essa ideia é muito interessante para a implementação de um algoritmo, e já existem tentativas de traduzir essa estrutura social para o algoritmo de otimização Anarchic Society Optimization (ASO). O algoritmo foi proposto por Ahmadi Javid e publicado em 2011.
A principal ideia transmitida pelo criador do ASO foi a de desenvolver um método de otimização inspirado no comportamento dos indivíduos em sociedades anárquicas. Diferentemente dos métodos existentes de inteligência de enxame, desenvolvidos com base em colônias de insetos ou bandos de animais, PSO e ACO, a construção de um algoritmo baseado no estudo da formação de uma sociedade humana padrão pode ter apenas sucesso limitado, pois uma sociedade bem organizada não pode alcançar seus desejos por meio de decisões individuais. Além disso, nenhum membro da sociedade é realmente independente e autônomo, nem pode melhorar radicalmente sua situação em um período de tempo determinado. A compreensão desse fato levou o criador do algoritmo a adotar a concepção principal para o desenvolvimento de uma sociedade baseada em uma estrutura anômala.
A base do ASO é um grupo de indivíduos instáveis, aventureiros, que não gostam de estabilidade e frequentemente se comportam de maneira irracional, movendo-se para posições piores que já ocuparam na fase de exploração. À medida que as diferenças em suas situações se intensificam, o nível de comportamento anárquico entre os membros aumenta. Utilizando esses participantes, o ASO explora o espaço de soluções e tenta evitar cair em armadilhas de ótimos locais. Dessa forma, o criador do ASO tenta transmitir a ideia de que o estudo e a aplicação de princípios baseados no comportamento anômalo da comunidade podem levar à criação de algoritmos eficazes para resolver problemas complexos de otimização. Analisaremos uma estrutura unificada para o ASO, que pode ser utilizada tanto para problemas contínuos quanto discretos.
2. Implementação do algoritmo
Antes de escrever o código do algoritmo, é preciso entender sua estrutura e quais são os principais mecanismos incorporados pelo autor. O algoritmo ASO é um método de otimização que combina as vantagens do algoritmo particle swarm optimisation (PSO) com novos mecanismos característicos do comportamento social anárquico. A natureza adaptativa e a capacidade de equilibrar entre diferentes estratégias de movimento são o principal destaque do algoritmo.
Vamos começar com uma descrição detalhada do algoritmo ASO:
1. Inicialização:
- Cria-se uma população (popSize) de membros da sociedade.
- Cada membro é inicializado com uma posição aleatória no espaço de busca.
- Para cada membro, são armazenadas suas melhores posições pessoais e anteriores.
2. Ciclo principal de otimização:
A cada iteração, o algoritmo executa os seguintes passos para cada membro da sociedade:
a) Cálculo dos índices:
- Fickleness Index (FI) — índice de instabilidade que reflete a volatilidade do membro da sociedade e mede seu descontentamento em comparação com outros indivíduos.
- External Irregularity Index (EI) — índice externo de irregularidade que avalia a diversidade de posições na sociedade e indica o desvio da melhor solução global.
- Internal Irregularity Index (II) — índice interno de irregularidade que avalia as mudanças de posição do indivíduo a cada iteração e reflete o desvio da sua melhor solução pessoal.
b) Escolha da política de movimento:
Com base na comparação dos índices FI, EI e II, é escolhida uma das três políticas de movimento:
- Current Movement Policy (CurrentMP) — usa a fórmula do PSO com inércia e coeficientes de aceleração.
- Society Movement Policy (SocietyMP) — aplica crossover com um membro aleatório da sociedade.
- Past Movement Policy (PastMP) — utiliza informações sobre a posição anterior do indivíduo.
c) Comportamento anárquico: com uma probabilidade "anarchyProb", a posição do indivíduo pode ser completamente aleatorizada.
d) Atualização da posição: a nova posição é verificada para garantir que esteja dentro das restrições do espaço de busca.
e) Atualização das melhores posições:
- A melhor posição pessoal "pBest" é atualizada se a posição atual for melhor.
- A melhor posição global "gBest" é atualizada se for encontrada uma nova melhor solução.
3. Adaptação de parâmetros:
- A probabilidade de comportamento anárquico "anarchyProb" diminui gradualmente.
- O parâmetro "alpha" para o cálculo de "FI" aumenta gradualmente.
- O peso inercial "omega" diminui gradualmente.
4. Parâmetros do algoritmo:
- popSize — tamanho da população.
- omega, lambda1, lambda2 — parâmetros para o cálculo da velocidade em "CurrentMP" (como no PSO).
- anarchyProb — probabilidade de comportamento anárquico.
- alpha, theta, delta — parâmetros para o cálculo dos índices "FI", "EI" e "II", respectivamente.
O algoritmo é bastante complexo, e eu tentarei explicar seu mecanismo de funcionamento de forma clara e estruturada para facilitar a compreensão. No próximo passo, analisaremos as fórmulas utilizadas no algoritmo.
A principal fórmula no algoritmo ASO é herdada do algoritmo PSO e representa o cálculo da atualização da velocidade: V_i (k+1) = ω * V_i (k) + λ1 * r1 * (P_i (k) - X_i (k)) + λ2 * r2 * (G (k) - X_i (k)), onde:
- V_i (k) — velocidade da partícula "i" na iteração "k".
- X_i (k) — posição da partícula "i" na iteração "k".
- P_i (k) — melhor posição encontrada pela partícula "i" até a iteração "k".
- G (k) — melhor posição global encontrada por todas as partículas até a iteração "k".
- ω — coeficiente de inércia.
- λ1, λ2 — coeficientes de aceleração.
- r1, r2 — números aleatórios do intervalo (0, 1).
O autor menciona que a fórmula do PSO é um caso particular da estrutura geral do ASO quando há políticas de movimento apropriadas e uma regra de combinação definida. Na versão original, a velocidade do agente era considerada nos cálculos. Eu modifiquei essa abordagem, mantendo apenas o valor atual da velocidade, o que resultou em uma melhora significativa na eficiência do algoritmo.
As fórmulas (1) e (2) determinam o índice de instabilidade "fickleness index", "FI" para o membro da sociedade "i" na iteração "k" no algoritmo ASO. Essas fórmulas ajudam a avaliar o grau de insatisfação do indivíduo com sua posição atual em comparação com outras posições. Vamos analisá-las em detalhes:
1. Fórmula (1) para o cálculo do índice de instabilidade: (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (Xi (k*)) - f (Xi (k))).
Essa fórmula mostra o quanto a posição atual do indivíduo "i" difere de sua melhor posição pessoal e da melhor posição global, ponderada pelo parâmetro "α" (alpha).
2. Fórmula (2) para o cálculo do índice de instabilidade do indivíduo "i" na iteração "k": (kFI)i = α - α (f (Xi (k)) - f (Pi (k))) / (f (G (k)) - f (Xi (k))).
Essa fórmula é semelhante à primeira, mas é usada para fins diferentes, onde a posição atual, a melhor posição pessoal e a melhor posição global são comparadas.
Ambas as fórmulas servem para avaliar o nível de insatisfação dos membros da sociedade, permitindo que eles tomem decisões mais embasadas sobre como modificar suas posições na busca pela solução ótima.
As fórmulas (3) e (4) descrevem os índices de irregularidade externa e interna "external irregularity index" e "internal irregularity index" para os membros da sociedade no algoritmo.
3. Fórmula (3) — índice externo de irregularidade do indivíduo "i" na iteração "k": (kEI)i = exp (-(θi) (f (G) - f (Xi (k)))).
4. Fórmula (4) — índice interno de irregularidade do indivíduo "i" na iteração "k": (kEI)i = 1 - exp (-δi (kD)).
Onde:
- (kFI)i — índice de instabilidade do indivíduo "i" na iteração "k".
- α — número não negativo "alpha" no intervalo [0,1].
- f (Xi (k)) — valor da função objetivo para a posição do indivíduo "i" na iteração "k".
- f (Pi (k)) — valor da função objetivo para a melhor posição previamente visitada pelo indivíduo "i".
- f (Xi (k)) — valor da função objetivo para a posição do melhor indivíduo na iteração "k".
- f (G (k)) — valor da função objetivo para a melhor posição global visitada pela sociedade até a iteração "k".
- (kEI)i — índice externo de irregularidade do indivíduo "i" na iteração "k".
- θi — número positivo "theta".
- kD — medida apropriada da diversidade na sociedade, por exemplo, coeficiente de variação dos valores da função objetivo dos indivíduos.
- δi — número positivo "delta".
Essas fórmulas mostram que, se a diversidade na sociedade aumentar (ou seja, os indivíduos tiverem valores da função objetivo mais distintos), os indivíduos tenderão a se comportar de maneira mais irregular. As fórmulas servem para avaliar a variabilidade do comportamento dos membros da sociedade no algoritmo ASO, permitindo que tomem decisões mais diversificadas e adaptativas durante o processo de busca pela solução ótima.
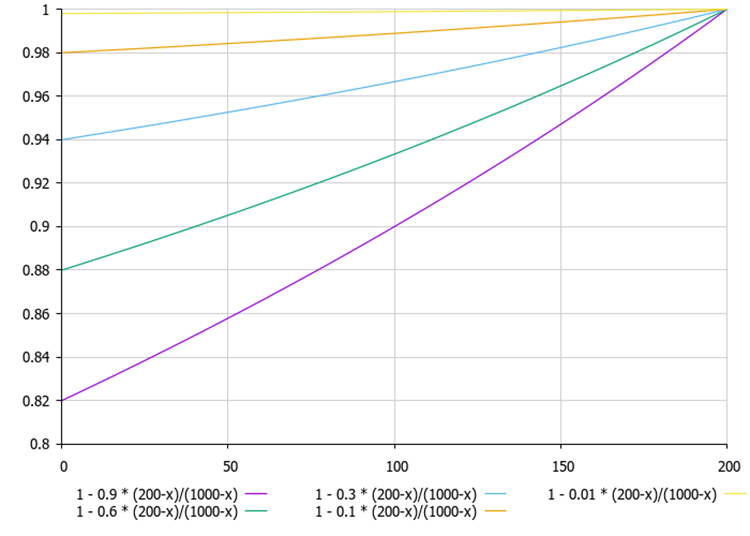
Figura 1. Se a melhor solução atual do agente (200) for significativamente menor do que a melhor solução da população de agentes (1000), a linha no gráfico se altera quase linearmente.
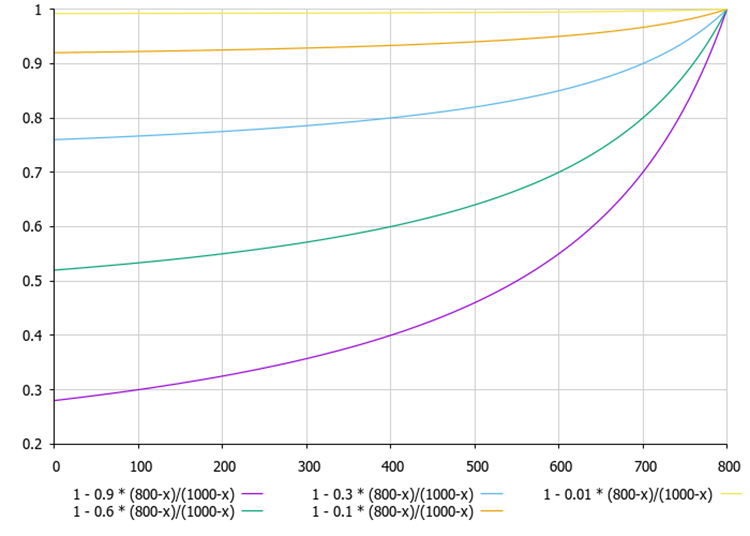
Figura 2. Quanto menor a diferença entre a melhor solução atual do agente (800) e a melhor solução da população de agentes (1000), mais não linear se torna a linha no gráfico.
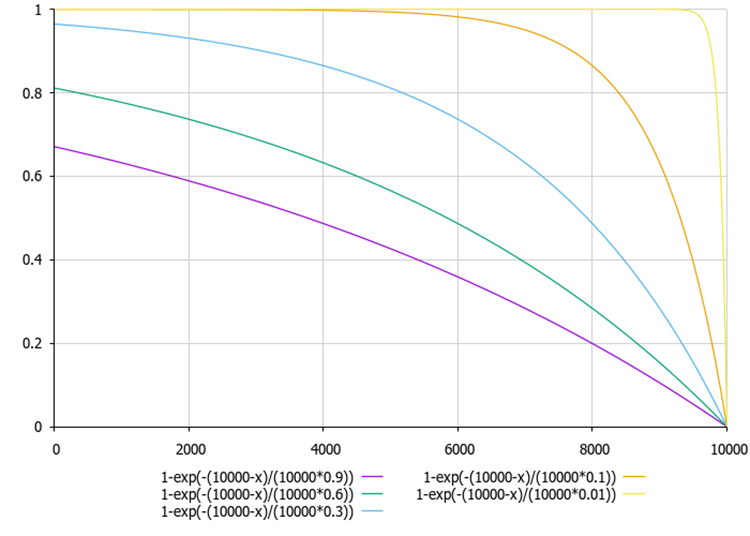
Figura 3. Gráfico da dependência dos índices de irregularidade externa e interna em relação aos coeficientes "theta" e "delta" (com valores de exemplo variando de 0.01 a 0.9).
Dessa forma, os membros da sociedade podem utilizar informações sobre outros membros para tomar decisões sobre seus movimentos e entender como seu comportamento pode variar de acordo com o nível de diversidade na sociedade.
Agora já sabemos um pouco mais sobre o algoritmo ASO e, com base na teoria adquirida, podemos avançar para a parte prática, ou seja, elaborar o pseudocódigo do algoritmo para sua implementação em código. Algoritmo ASO — pseudocódigo:
Inicialização:
1. Definir os parâmetros: popSize, omega, lambda1, lambda2, anarchyProb, alpha, theta, delta, rangeMin [], rangeMax [], rangeStep []
2. Criar uma população de popSize membros: para cada membro i de 0 a popSize-1: para cada coordenada c de 0 a coords-1:
position [i].[c] = número aleatório entre rangeMin [c] e rangeMax [c]
pBest [i].[c] = position [i].[c]
prevPosition [i].[c] = position [i].[c]
pBestFitness [i] = -infinito
3. Definir gBest = melhor posição da população inicial
4. Definir gBestFitness = fitness de gBest
Ciclo principal:
5. Enquanto o critério de parada não for atingido: para cada membro i de 0 a popSize-1:
5.1 Calcular os índices
FI = CalculateFI (i)
EI = CalculateEI (i)
II = CalculateII (i)
5.2 Escolher a política de movimento
Se FI > EI e FI > II: newPosition = CurrentMP (i)
Senão, se EI > FI e EI > II: newPosition = SocietyMP (i)
Caso contrário: newPosition = PastMP (i)
5.3 Aplicar comportamento anárquico
Se um número aleatório < anarchyProb: para cada coordenada c de 0 a coords-1:
newPosition [c] = número aleatório entre rangeMin [c] e rangeMax [c]
5.4 Atualizar a posição para cada coordenada c de 0 a coords-1:
prevPosition [i].[c] = position [i].[c]
position [i].[c] = limitar (newPosition [c], rangeMin [c], rangeMax [c], rangeStep [c])
5.5 Avaliar a nova posição fitness = avaliar_fitness (position [i])
5.6 Atualizar o best pessoal se fitness > pBestFitness [i]:
pBestFitness [i] = fitness
pBest [i] = position [i]
5.7 Atualizar o best global se fitness > gBestFitness:
gBestFitness = fitness
gBest = position [i]
5.8 Adaptar o parâmetro AdaptParameters ()
5.9 Função CalculateFI (i): return 1 - alpha * (fitness [i] - pBestFitness [i]) / (gBestFitness - fitness [i])
5.10 Função CalculateEI (i): return 1 - exp(-(gBestFitness - fitness [i]) / theta)
5.11 Função CalculateII (i): return 1 - exp(-(pBestFitness [i] - fitness [i]) / delta)
5.12 Função CurrentMP (i): para cada coordenada c de 0 a coords-1:
r1 = número aleatório entre 0 e 1
r2 = número aleatório entre 0 e 1
velocity = omega * (position [i].[c] - pBest [i].[c]) + lambda1 * r1 * (pBest [i].[c] - position [i].[c]) + lambda2 * r2 * (gBest [c] - position [i].[c])
newPosition [c] = position [i].[c] + velocity
return newPosition
5.13 Função SocietyMP (i): j = membro aleatório da população, diferente de i, para cada coordenada c de 0 a coords - 1:
Se um número aleatório < 0.5:
newPosition [c] = position [i].[c]
Senão: newPosition [c] = position [j].[c]
return newPosition
5.14 Função PastMP (i): para cada coordenada c de 0 a coords - 1:
Se um número aleatório < 0.5:
newPosition [c] = position [i].[c]
Senão: newPosition [c] = prevPosition [i].[c]
return newPosition
Agora que temos o pseudocódigo pronto, podemos começar a escrever o código do algoritmo. Descreveremos a estrutura "S_ASO_Member", que é usada para representar um participante (agente) no algoritmo.
1. Campos da estrutura:
- pPrev [] — array das posições anteriores dos participantes.
- pBest [] — array das melhores posições conhecidas dos participantes (bests pessoais).
- pBestFitness — variável que armazena o valor do fitness (qualidade) da melhor posição conhecida.
2. O método "Init" inicializa os arrays "pPrev" e "pBest", definindo seus tamanhos de acordo com o número de coordenadas (ou a dimensão do espaço de busca), passado como parâmetro "coords". "ArrayResize(pBest, coords)" e "ArrayResize(pPrev, coords)" — essas chamadas ajustam o tamanho dos arrays para o valor "coords". "pBestFitness = -DBL_MAX" — define o valor inicial para o fitness da melhor posição, garantindo que qualquer valor encontrado será melhor que esse.
A estrutura "S_ASO_Member" é destinada ao armazenamento de informações sobre cada participante no algoritmo de otimização. Ela permite rastrear tanto as posições atuais quanto as melhores posições do participante, bem como sua adaptabilidade.
//—————————————————————————————————————————————————————————————————————————————— struct S_ASO_Member { double pPrev []; // Previous position double pBest []; // Personal best position double pBestFitness; // Personal best fitness void Init (int coords) { ArrayResize (pBest, coords); ArrayResize (pPrev, coords); pBestFitness = -DBL_MAX; } }; //——————————————————————————————————————————————————————————————————————————————
Definimos a classe "C_AO_ASO", que herda da classe base "C_AO". Vamos analisá-la em mais detalhes:
1. Parâmetros:
- popSize — tamanho da população (quantidade de membros da sociedade).
- anarchyProb — probabilidade de comportamento anárquico, permitindo que alguns participantes ajam independentemente dos outros.
- omega, lambda1, lambda2 — parâmetros relacionados à inércia e aceleração, usados para controlar o comportamento dos participantes.
- alpha, theta, delta — parâmetros usados para calcular os indicadores (FI, EI, II).
2. params — array de parâmetros, onde cada elemento contém um nome e um valor.
3. SetParams () — método que atualiza os valores dos parâmetros a partir do array "params", permitindo modificar os parâmetros do algoritmo após sua inicialização.
4. Init () — método que inicializa o algoritmo com os intervalos e passos definidos. Ele recebe os arrays "rangeMinP", "rangeMaxP" e "rangeStepP", além do número de épocas "epochsP".
5. Moving() e Revision () — métodos que implementam a lógica principal do movimento dos participantes e sua revisão (atualização) durante o processo de otimização.
6. Campos da classe:
S_ASO_Member member [] — array de membros da sociedade que armazena informações sobre cada participante do algoritmo.
7. Métodos privados:
- CalculateFI — método para calcular o valor do FI (Fitness Indicator) para um participante específico.
- CalculateEI — método para calcular o valor do EI (Exploration Indicator).
- CalculateII — método para calcular o valor do II (Inertia Indicator).
- CurrentMP, SocietyMP, PastMP — métodos que implementam a lógica de interação dos participantes com suas posições atuais, sociais e passadas.
A classe "C_AO_ASO" representa a implementação do conceito de "sociedade anárquica", onde os participantes podem agir tanto coletivamente quanto de forma independente. Ela inclui parâmetros que controlam o comportamento dos participantes e métodos para sua inicialização e atualização.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASO () { } C_AO_ASO () { ao_name = "ASO"; ao_desc = "Anarchy Society Optimization"; ao_link = "https://www.mql5.com/en/articles/15511"; popSize = 50; // Population size anarchyProb = 0.1; // Probability of anarchic behavior omega = 0.7; // Inertia weight lambda1 = 1.5; // Acceleration coefficient for P-best lambda2 = 1.5; // Acceleration coefficient for G-best alpha = 0.5; // Parameter for FI calculation theta = 1.0; // Parameter for EI calculation delta = 1.0; // Parameter for II calculation ArrayResize (params, 8); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "anarchyProb"; params [1].val = anarchyProb; params [2].name = "omega"; params [2].val = omega; params [3].name = "lambda1"; params [3].val = lambda1; params [4].name = "lambda2"; params [4].val = lambda2; params [5].name = "alpha"; params [5].val = alpha; params [6].name = "theta"; params [6].val = theta; params [7].name = "delta"; params [7].val = delta; } void SetParams () { popSize = (int)params [0].val; anarchyProb = params [1].val; omega = params [2].val; lambda1 = params [3].val; lambda2 = params [4].val; alpha = params [5].val; theta = params [6].val; delta = params [7].val; } bool Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0); void Moving (); void Revision (); //---------------------------------------------------------------------------- double anarchyProb; // Probability of anarchic behavior double omega; // Inertia weight double lambda1; // Acceleration coefficient for P-best double lambda2; // Acceleration coefficient for G-best double alpha; // Parameter for FI calculation double theta; // Parameter for EI calculation double delta; // Parameter for II calculation S_ASO_Member member []; // Vector of society members private: //------------------------------------------------------------------- double CalculateFI (int memberIndex); double CalculateEI (int memberIndex); double CalculateII (int memberIndex); void CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); void SocietyMP (S_AO_Agent &agent, int coordInd); void PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd); }; //——————————————————————————————————————————————————————————————————————————————
Agora, vamos analisar o próximo método "Init" da classe "C_AO_ASO". Lógica do método:
- StandardInit — método chamado para executar a inicialização padrão usando os intervalos fornecidos. Se este método retornar "false" — significa que ocorreu um erro.
- ArrayResize — método que altera o tamanho do array "member" para o valor "popSize", que define o número de participantes (membros da sociedade) no algoritmo.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASO::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (member, popSize); for (int i = 0; i < popSize; i++) member [i].Init (coords); return true; } //——————————————————————————————————————————————————————————————————————————————
Agora, analisaremos o código do método "Moving" da classe "C_AO_ASO". Estrutura e lógica do método:
1. Verificação da primeira chamada:
- Se "revision" for igual a "false", o método inicializa o array "a" com valores aleatórios dentro dos intervalos definidos "rangeMin" e "rangeMax".
- Para cada coordenada "c" de cada membro da população "i", o método "u.RNDfromCI" é chamado para gerar um valor aleatório, que é então normalizado usando "u.SeInDiSp".
- Os valores são armazenados em "member [i].pPrev [c]" para uso futuro.
- Após isso, "revision" é definido como "true", e o método encerra sua execução.
2. Lógica principal de movimentação:
- Para cada membro da população "i", são calculados três índices: "fi", "ei" e "ii", que representam métricas caracterizando o estado do membro da população.
- Para cada coordenada "c", as seguintes etapas são executadas:
- O valor atual é salvo em "member [i].pPrev [c]".
- Um número aleatório "rnd" é gerado usando "u.RNDprobab ()".
- Se o número aleatório for menor que "anarchyProb" (indicando a probabilidade de comportamento anárquico), a coordenada "c" do membro "i" será inicializada aleatoriamente dentro do intervalo.
- Caso contrário, dependendo dos valores de "fi", "ei" e "ii", são chamados os métodos "CurrentMP", "SocietyMP" ou "PastMP".
- Após todas as modificações, para cada coordenada "c", o valor é ajustado usando "u.SeInDiSp".
O método "Moving" implementa a lógica de movimentação dos membros da população dentro do espaço de soluções, com base em seus estados atuais e métricas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); member [i].pPrev [c] = a [i].c [c]; } } revision = true; return; } //---------------------------------------------------------------------------- double fi = 0.0; //fickleness index double ei = 0.0; //external irregularity index double ii = 0.0; //internal irregularity index double rnd = 0.0; for (int i = 0; i < popSize; i++) { fi = CalculateFI (i); ei = CalculateEI (i); ii = CalculateII (i); for (int c = 0; c < coords; c++) { member [i].pPrev [c] = a [i].c [c]; rnd = u.RNDprobab (); if (u.RNDprobab () < anarchyProb) a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); else { if (rnd > fi) CurrentMP (a [i], member [i], c); else { if (rnd < ei) SocietyMP (a [i], c); else { if (rnd < ii) PastMP (a [i], member [i], c); } } } } for (int c = 0; c < coords; c++) { a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
Do método "Moving", passamos para o método "Revision". Estrutura geral e lógica:
1. A variável "ind" é inicializada com o valor "-1". Ela será usada para armazenar o índice do membro da população que possui o melhor valor da função "f".
2. O método percorre todos os membros da população, de "0" a "popSize - 1".
3. Busca do melhor valor da função: para cada membro da população "a [i]", verifica-se se o valor da sua função "f" é maior que o melhor valor atual "fB". Se for, "fB" é atualizado com o valor "a [i].f", e o índice "ind" é definido como "i".
4. Atualização do melhor valor pessoal: o método também verifica se o valor da função "a [i].f" é maior que o melhor valor pessoal atual desse membro da população "member [i].pBestFitness". Se for, o valor é atualizado, e as coordenadas atuais ""a[i].c" são copiadas para "member[i].pBest" usando a função "ArrayCopy".
5. Cópia da melhor solução: após a conclusão do loop, se um índice "ind" foi encontrado (ou seja, pelo menos um membro da população obteve um valor da função maior que "fB"), as coordenadas desse membro da população são copiadas para "cB" usando "ArrayCopy".
O método "Revision" é responsável por atualizar a melhor solução encontrada na população, bem como atualizar os melhores valores pessoais para cada membro da população. Ele utiliza uma lógica simples de comparação de valores da função para determinar quais soluções são as melhores e as armazena para uso futuro.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::Revision () { int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > member [i].pBestFitness) { member [i].pBestFitness = a [i].f; ArrayCopy (member [i].pBest, a [i].c, 0, 0, WHOLE_ARRAY); } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); } //——————————————————————————————————————————————————————————————————————————————
A seguir, o método "CalculateFI" da classe "C_AO_ASO". Descrição do método:
1. O método recebe o índice do membro da população "memberIndex", para o qual o fitness será calculado.
2. Obtenção dos valores de fitness:
- currentFitness — obtém o valor atual do fitness do membro da população a partir do array "a" pelo índice "memberIndex".
- personalBestFitness — obtém o melhor valor pessoal de fitness desse membro a partir do array "member".
- globalBestFitness — obtém o melhor valor global de fitness armazenado na variável "fB".
3. Cálculo do índice de fitness (FI) — o método retorna um valor calculado pela fórmula.
A fórmula normaliza a diferença entre o melhor fitness pessoal e o fitness atual, dividindo-a pela diferença entre o melhor fitness global e o fitness atual. O método "CalculateFI" calcula o índice de fitness para um membro da população, que é usado para avaliar sua qualidade em comparação com seus melhores valores pessoal e global.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateFI (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; double globalBestFitness = fB; //1 - 0.9 * (800-x)/(1000-x) return 1 - alpha * (personalBestFitness - currentFitness) / (globalBestFitness - currentFitness); } //——————————————————————————————————————————————————————————————————————————————
Em seguida, temos o método "CalculateEI" da classe "C_AO_ASO". O método executa quase as mesmas ações que o método anterior, mas usa para o cálculo o melhor fitness global e o próprio fitness atual.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateEI (int memberIndex) { double currentFitness = a [memberIndex].f; double globalBestFitness = fB; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(globalBestFitness - currentFitness) / (globalBestFitness * theta)); } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateII" da classe "C_AO_ASO" é completamente análogo ao anterior, mas usa o melhor fitness pessoal e o fitness atual.
A função exponencial ajuda a suavizar as mudanças e garante uma transição gradual entre os valores. O método "CalculateII" calcula o índice de melhoria para um membro da população, levando em conta como o estado atual do fitness se relaciona com suas conquistas pessoais.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_ASO::CalculateII (int memberIndex) { double currentFitness = a [memberIndex].f; double personalBestFitness = member [memberIndex].pBestFitness; //1-exp(-(10000-x)/(10000*0.9)) return 1 - MathExp (-(personalBestFitness - currentFitness) / (personalBestFitness * delta)); } //——————————————————————————————————————————————————————————————————————————————
Passamos agora para o método "CurrentMP" da classe "C_AO_ASO". Descrição:
1. Geração de números aleatórios:
- r1 = u.RNDprobab () — gera um número aleatório "r1" no intervalo [0, 1].
- r2 = u.RNDprobab () — gera um número aleatório "r2" no intervalo [0, 1].
2. Cálculo da velocidade "velocity" — a fórmula inclui três componentes:
- omega * (agent.c [coordInd] - memb.pBest [coordInd]) — componente inercial, movimento do agente considerando sua posição anterior.
- lambda1 * r1 * (memb.pBest[coordInd] - agent.c[coordInd]) — direciona o agente considerando sua melhor posição pessoal.
- lambda2 * r2 * (cB[coordInd] - agent.c[coordInd]) — direciona o agente considerando a melhor posição da população.
3. Atualização da posição do agente, adicionando a velocidade ao valor atual da coordenada.
O método "CurrentMP" implementa a atualização da posição do agente no espaço com base em sua posição atual, na sua melhor posição pessoal e na melhor posição da população.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::CurrentMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { double r1 = u.RNDprobab (); double r2 = u.RNDprobab (); double velocity = omega * (agent.c [coordInd] - memb.pBest [coordInd]) + lambda1 * r1 * (memb.pBest [coordInd] - agent.c [coordInd]) + lambda2 * r2 * (cB [coordInd] - agent.c [coordInd]); agent.c [coordInd] += velocity; } //——————————————————————————————————————————————————————————————————————————————
O método "SocietyMP" da classe "C_AO_ASO" atualiza a coordenada do agente com base em uma escolha aleatória entre a informação do grupo e a informação pessoal. Isso permite que o agente se adapte ao estado tanto da população quanto do indivíduo isolado.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::SocietyMP (S_AO_Agent &agent, int coordInd) { int otherMember = u.RNDminusOne (popSize); agent.c [coordInd] = u.RNDprobab () < 0.5 ? cB [coordInd] : member [otherMember].pBest [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
O método "PastMP" da classe "C_AO_ASO" atualiza a coordenada do agente com base em uma escolha aleatória entre o melhor estado atual do membro da população e seu estado anterior. Isso permite que o agente leve em consideração tanto as conquistas atuais do membro da população quanto seus resultados passados. Essa abordagem melhora as propriedades combinatórias do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASO::PastMP (S_AO_Agent &agent, S_ASO_Member &memb, int coordInd) { agent.c [coordInd] = u.RNDprobab () < 0.5 ? memb.pBest [coordInd] : memb.pPrev [coordInd]; } //——————————————————————————————————————————————————————————————————————————————
3. Resultados dos testes
Impressão dos resultados da execução do algoritmo ASO em um ambiente de teste com funções de avaliação:
ASO | Anarchy Society Optimization | 50.0 | 0.01 | 0.7 | 1.5 | 1.5 | 0.5 | 0.1 | 0.1 |
=============================
5 Hilly's; Func runs: 10000; result: 0.8487202680440514
25 Hilly's; Func runs: 10000; result: 0.746458607174428
500 Hilly's; Func runs: 10000; result: 0.31465494017509904
=============================
5 Forest's; Func runs: 10000; result: 0.9614752193694915
25 Forest's; Func runs: 10000; result: 0.7915027321897546
500 Forest's; Func runs: 10000; result: 0.23802894131144553
=============================
5 Megacity's; Func runs: 10000; result: 0.5707692307692309
25 Megacity's; Func runs: 10000; result: 0.5406153846153848
500 Megacity's; Func runs: 10000; result: 0.16613846153846298
=============================
All score: 5.17836 (57.54%)
Ao analisar a visualização do funcionamento do algoritmo, podem-se tirar algumas conclusões: há uma dispersão nos resultados. No entanto, o algoritmo demonstra boas capacidades de busca ao trabalhar com funções de alta dimensionalidade, o que também é confirmado pelos resultados impressos de sua execução.
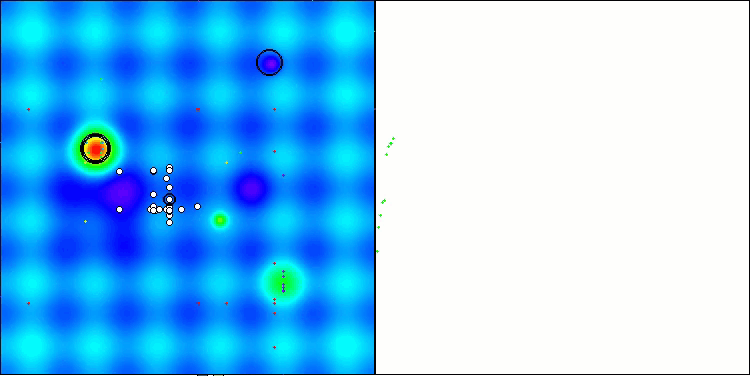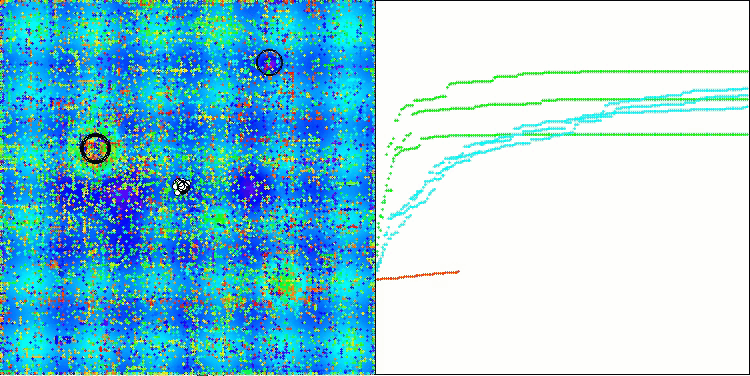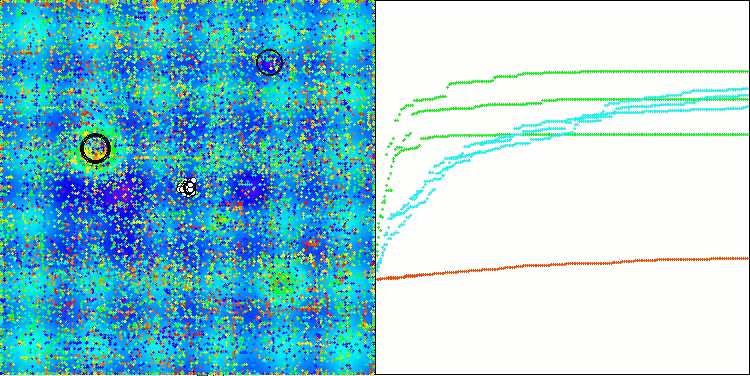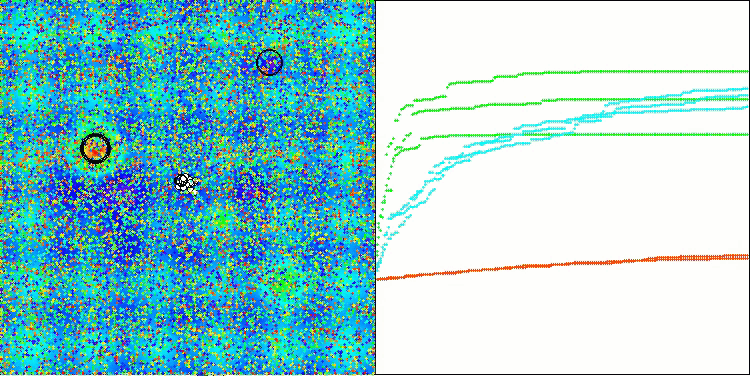
ASO na função de teste Hilly
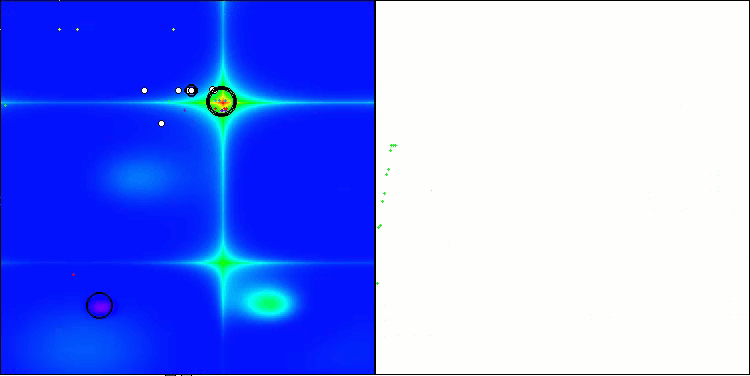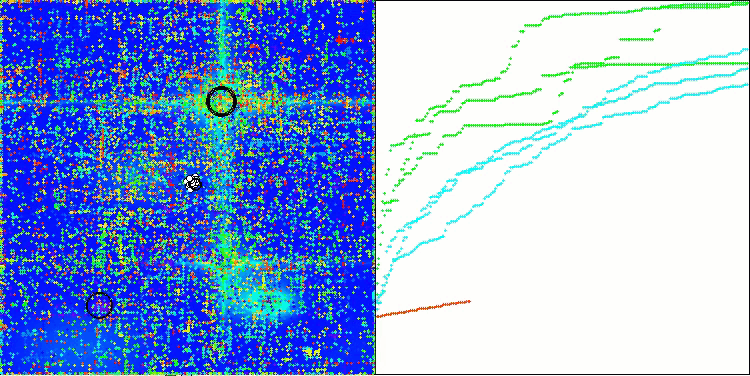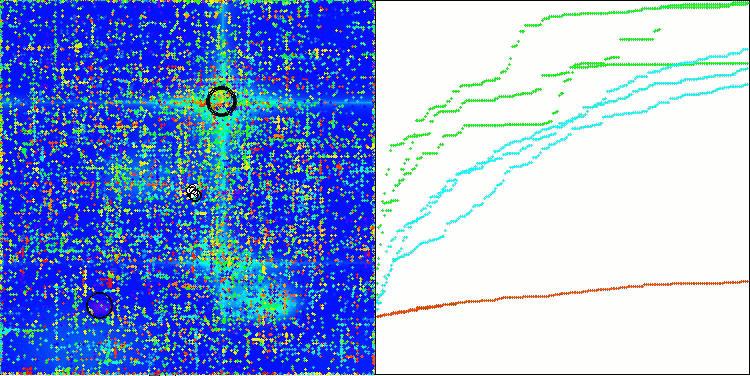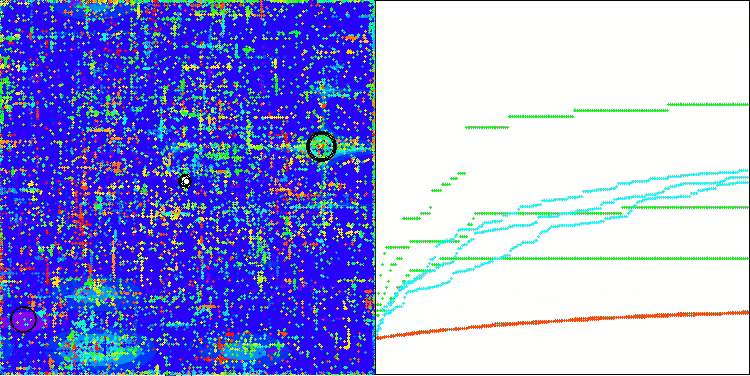
ASO na função de teste Forest
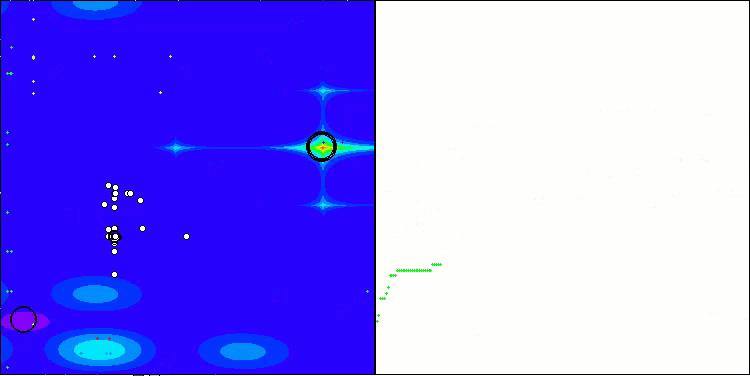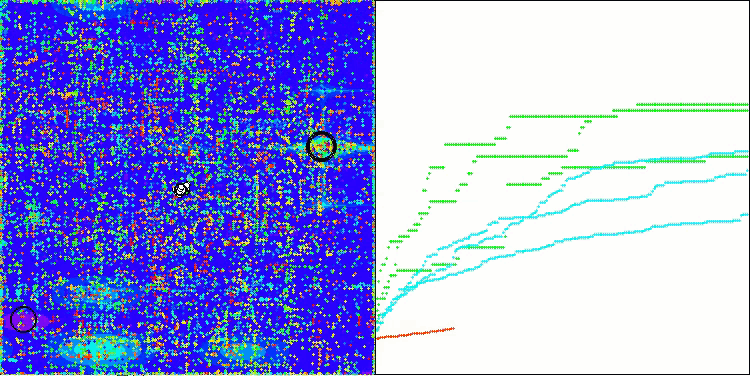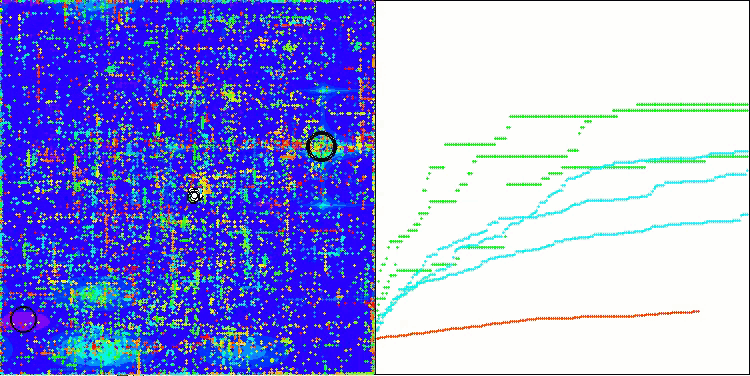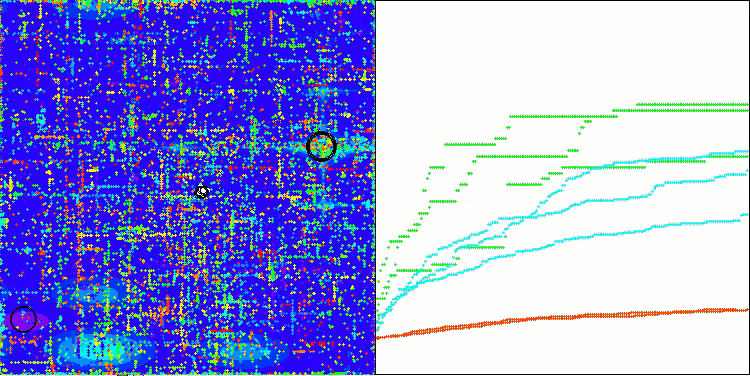
ASO na função de teste Megacity
Tabela de classificação dos algoritmos populacionais de otimização: O algoritmo ASO, após os testes, ficou entre os dez melhores e ocupou a 9ª posição na tabela de classificação.
| № | AO | Descrição | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 4 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 5 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 6 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 7 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 8 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 9 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 10 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 11 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 12 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 13 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 14 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 15 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 16 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 17 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 18 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 19 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 20 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 21 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 22 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 23 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 24 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 25 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 26 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 27 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 28 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 29 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 30 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 31 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 32 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 33 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 34 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 35 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 36 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 37 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 38 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 39 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 40 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 41 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 42 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 43 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 44 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 45 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Considerações finais
Com base nos resultados da execução do algoritmo em funções de teste de diferentes dimensões, podem-se tirar as seguintes conclusões: ASO apresenta resultados medianos na função suave Hilly em comparação com seus vizinhos mais próximos na tabela, mas resultados muito sólidos na função "afiada" Forest e, especialmente, na função discreta Megacity. A pontuação total foi de 5.17836 (57.54%). O algoritmo demonstra boas capacidades de busca, especialmente ao lidar com funções de alta dimensionalidade, o que significa que se escala bem. O algoritmo pode ser recomendado para a resolução de problemas de otimização discretos, o que é uma prioridade para os traders.
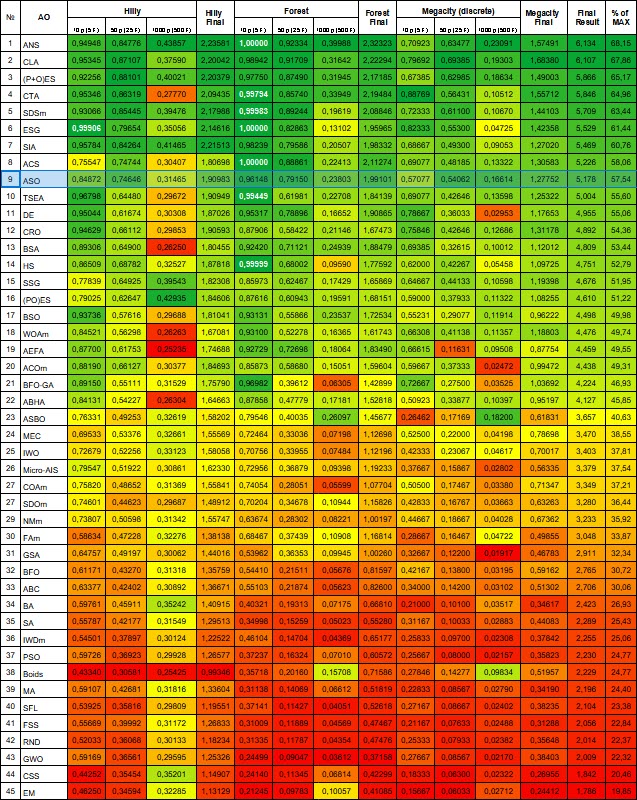
Figura 4. Graduação de cores dos algoritmos para os respectivos testes. Os resultados destacados em branco são maiores ou iguais a 0.99
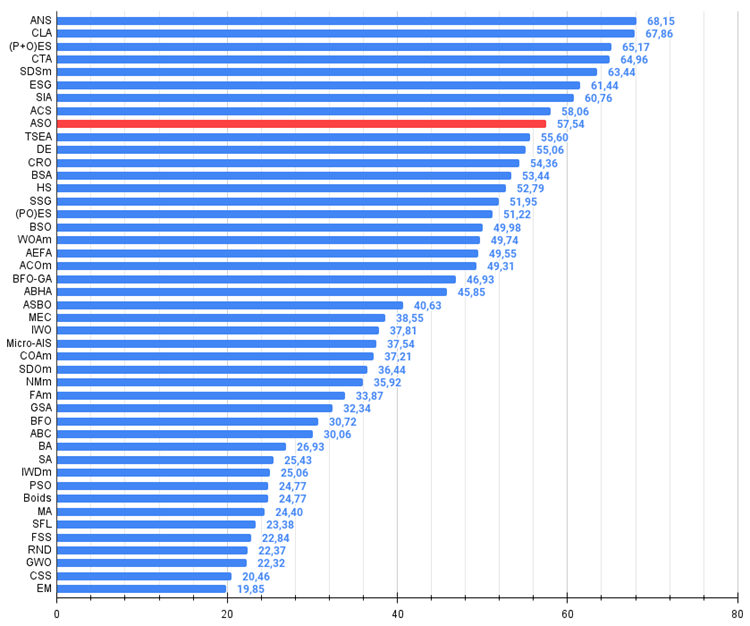
Figura 5. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, e o arquivo contém um script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo ASO:
Prós:
- Boa convergência em diversas funções.
- Excelentes resultados em funções discretas.
Contras:
- Grande número de parâmetros (muito difícil configurar o algoritmo).
- Variação nos resultados em funções de baixa dimensionalidade.
- Implementação complexa.
O artigo inclui um arquivo com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15511
Métodos de William Gann (Parte II): Criando um Indicador do Quadrado de Gann
Métodos de William Gann (Parte I): Criando um indicador de ângulos de Gann
Introdução ao MQL5 (Parte 8): Guia do Iniciante para Construção de Expert Advisors (II)
Algoritmo de otimização de migração animal (AMO)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso