
Algoritmo de Irrigação Artificial — Artificial Showering Algorithm (ASHA)
Conteúdo
Introdução
Os volumes de dados no mundo moderno estão crescendo rapidamente, e os problemas se tornam cada vez mais complexos e exigentes em termos de energia, tornando a necessidade de métodos eficientes de otimização mais relevante do que nunca. Os algoritmos metaheurísticos, com sua alta taxa de convergência e velocidade de processamento, abrem novos horizontes para a resolução de diversos tipos de problemas em diferentes áreas, desde os mercados financeiros até as pesquisas científicas.
A velocidade de processamento dos dados e a qualidade das soluções obtidas são fundamentais para o sucesso dos projetos. Em situações com restrições de tempo rigorosas, onde cada momento pode ter um impacto crítico, os algoritmos metaheurísticos permitem alcançar resultados que antes pareciam inatingíveis. Eles não apenas processam grandes volumes de informação rapidamente, como também ajudam a encontrar soluções de melhor qualidade quando comparados com métodos numéricos tradicionais.
A economia de recursos é outro aspecto importante a se considerar na otimização. Em cenários com capacidade computacional limitada, tais algoritmos exigem menos tempo e memória, o que é especialmente valioso em ambientes de computação em nuvem. A adaptabilidade dos algoritmos às condições em mudança e sua capacidade de reagir rapidamente a novos dados os tornam praticamente ideais para sistemas dinâmicos. Isso permite manter a relevância das soluções e aumentar a eficiência na resolução de problemas em condições reais.
A comparação entre diferentes algoritmos com base em suas características, como velocidade de convergência, qualidade das soluções e resistência a ficar preso em extremos locais, permite escolher os mais eficazes. Isso, por sua vez, impulsiona a inovação e o desenvolvimento de métodos completamente novos, muitas vezes inspirados pela natureza, sendo um passo importante no campo da otimização.
O Algoritmo de Irrigação Artificial (ASHA), ou Artificial Showering Algorithm, é um novo método metaheurístico desenvolvido para resolver problemas gerais de otimização. Esse algoritmo é baseado na simulação dos processos de fluxo e acúmulo de água, distribuída por equipamentos controlados manualmente em um campo ideal. O ASHA simula o processo de distribuição de água (irrigação) em um campo, onde a água representa unidades de recurso e o campo é o espaço de busca. O algoritmo utiliza os princípios de fluxo e acúmulo para encontrar soluções ótimas em problemas sem restrições. O Algoritmo de Irrigação Artificial (ASHA) foi desenvolvido por um grupo de autores: Ali J., M. Said, N. A. Chaudhry, M. Luqman e M. F. Tabassum, e publicado em 2015.
Implementação do algoritmo
O método se baseia nos seguintes postulados:
- Campo ideal. O espaço de busca é considerado um campo ideal, onde a água flui sem resistência, e a infiltração ocorre apenas no ponto mais baixo.
- Ausência de fatores externos. Não ocorre evaporação, nem chuva, nem fluxo adicional de água.
- Disponibilidade dos aspersores. Cada parte do espaço de busca está ao alcance dos aspersores localizados acima do campo.
- Quantidade constante de água. Há água em abundância, e sua quantidade em um sistema fechado permanece constante ao longo de todas as iterações.
- Movimento da água. Cada unidade de água tem uma tendência probabilística de se mover para baixo na encosta.
Descrição do algoritmo ASHA (Artificial Showering Algorithm) passo a passo.
Parâmetros do algoritmo:
- f - função objetivo a ser minimizada
- Rⁿ - espaço de busca n-dimensional
- K - posição atual no contador de iterações
- m - quantidade de unidades de água (agentes de busca)
- F - velocidade do fluxo de água
- δ - nível de resistência (limiar de infiltração)
- ρ₀ - probabilidade inicial
- β - parâmetro que controla a taxa de variação da probabilidade
- M - número máximo de iterações
Passos do algoritmo:
1. Inicialização:
Definimos o valor inicial ρ = ρ₀
Criamos m unidades de água e as posicionamos aleatoriamente no espaço de busca Rⁿ
2. Avaliação do relevo: para cada unidade de água, calculamos o valor da função objetivo f em sua posição atual
3. Laço principal (repetimos M vezes): para cada unidade de água i (1 ≤ i ≤ m):
a) Escolhemos um número aleatório r_i ∈ (0, 1)
b) Se r_i < ρ:
Escolhemos uma posição aleatória x_lower abaixo da atual
Geramos um vetor aleatório s ∈ (0, 1)*n
Calculamos a nova posição:
x_new = x_old + F × (s ∘ (x_lower − x_old))
onde ∘ representa multiplicação elemento a elemento
Se x_new estiver em um nível mais baixo que x_old:
Aceitamos a nova posição
Caso contrário:
Geramos um número aleatório r ∈ (0, 1)
Encontramos a posição mais baixa x_lowest entre todas as unidades de água
Calculamos a nova posição:
x_new = x_old + F × r × (x_lowest − x_old)
c) Verificação de infiltração:
Se a unidade de água ultrapassar o nível de resistência δ:
Criamos uma nova unidade de água em uma posição aleatória
d) Comparação com a posição mais baixa:
Encontramos a unidade de água com o menor valor da função objetivo
Se a unidade atual tiver valor menor, trocamos suas posições
e) Atualização da probabilidade ρ = max((M − K) / (β × M), ρ₀)
4. Encerramento:
Encontramos a unidade de água com o menor valor da função objetivo
Retornamos sua posição como a melhor solução encontrada
Esclarecimentos sobre o algoritmo:
1. O algoritmo simula o processo de irrigação de um campo, onde cada unidade de água representa um agente de busca.
2. O espaço de busca é interpretado como um relevo, onde valores mais baixos da função objetivo correspondem a pontos mais baixos do terreno.
3. As unidades de água tendem a "escorrer" para pontos mais baixos do relevo, o que corresponde à busca pelo mínimo da função objetivo.
4. O parâmetro ρ controla o equilíbrio entre exploração do espaço (valores altos de ρ) e exploração das soluções encontradas (valores baixos de ρ).
5. O mecanismo de infiltração ajuda a evitar que o algoritmo fique preso em mínimos locais, ao criar novas unidades de água em posições aleatórias.
6. A comparação e troca com a posição mais baixa garante a preservação da melhor solução encontrada.
7. A atualização dinâmica de ρ permite ao algoritmo fazer uma transição gradual da exploração para a exploração intensiva conforme aumentam as iterações.
O algoritmo usa a analogia do fluxo de água para realizar a otimização, em que a água (agentes de busca) tenta encontrar os pontos mais baixos do relevo (mínimos da função objetivo).
Segundo os autores, as principais vantagens deste algoritmo são:
- Capacidade de explorar amplamente o espaço de soluções graças ao movimento aleatório da água.
- Capacidade de evitar mínimos locais por meio do mecanismo de infiltração.
- Comportamento adaptativo possibilitado pela variação dinâmica da probabilidade ρ.
Analisemos detalhadamente todas as fórmulas utilizadas pelo algoritmo.
1. Fórmula de atualização da posição no caso de cumprimento da probabilidade "ρ": x_new = x_old + F × (s ∘ (x_lower − x_old)), onde:
- x_new - nova posição da unidade de água
- x_old - posição atual da unidade de água
- F - velocidade do fluxo de água (parâmetro do algoritmo)
- s - vetor aleatório no intervalo (0, 1)
- x_lower - posição escolhida aleatoriamente abaixo da atual
- ∘ - operador de multiplicação elemento a elemento
A fórmula modela o movimento da água descendo a encosta. O vetor aleatório "s" adiciona um elemento de aleatoriedade ao movimento, enquanto "F" controla o tamanho do passo.
2. Fórmula alternativa, no caso de não cumprimento da probabilidade "ρ", atualização da posição: x_new = x_old + F × r × (x_lowest − x_old), onde:
- r - número aleatório no intervalo (0, 1)
- x_lowest - posição com o menor valor da função objetivo
A fórmula é usada quando a fórmula principal não leva a uma melhoria. Ela direciona a unidade de água na direção do mínimo global.
Como se vê nestas fórmulas, a água sempre tende a se mover em direção a posições mais baixas do que sua posição atual. Se o algoritmo for implementado apenas até essa etapa, ele certamente ficará preso em extremos locais.
3. Fórmula de atualização da probabilidade, ρ = max((M − K) / (β × M), ρ₀), onde:
- ρ - probabilidade atual de movimento da água
- M - número máximo de iterações
- K - número da iteração atual
- β - parâmetro que controla a taxa de variação da probabilidade
- ρ₀ - probabilidade inicial
Esta fórmula reduz gradualmente a probabilidade de a água se mover para posições mais baixas escolhidas aleatoriamente e aumenta a probabilidade de se mover em direção ao mínimo global. Isso permite que o algoritmo passe da exploração do espaço para o refinamento das soluções encontradas.
4. Condição de infiltração, se f(x_current) < δ, então uma nova unidade de água é criada, onde:
- f(x_current) - valor da função objetivo na posição atual
- δ - nível de resistência (limiar de infiltração)
Essa condição permite criar novas unidades de água em posições aleatórias quando a unidade de água atual encontra um ponto suficientemente baixo. Isso foi projetado para evitar que o algoritmo fique preso em mínimos locais.
5. Comparação de posições: se f(x_i) < f(x_lowest), então trocamos x_i e x_lowest, onde:
- f(x_i) - valor da função objetivo para a i-ésima unidade de água
- f(x_lowest) - menor valor da função objetivo encontrado
As fórmulas acima formam a base do algoritmo ASHA.
- A fórmula de atualização da posição imita o movimento da água descendo a encosta. O elemento aleatório (s ou r) adiciona diversidade à busca, permitindo explorar diferentes áreas do espaço de soluções.
- A fórmula alternativa de atualização da posição é usada com aumento da probabilidade a cada nova iteração para garantir um refinamento progressivo da solução global ao longo do tempo.
- A fórmula de atualização da probabilidade ρ garante o equilíbrio entre exploração e exploração intensiva. No início do algoritmo, a probabilidade de se mover para posições mais baixas aleatórias no relevo é alta, favorecendo a exploração ampla do espaço. À medida que as iterações avançam, a probabilidade diminui, levando a uma investigação mais precisa de regiões promissoras.
- A condição de infiltração permite ao algoritmo “reiniciar” a busca a partir de novas posições aleatórias, quando uma boa solução é encontrada. Isso ajuda a evitar que o algoritmo fique preso em mínimos locais.
- A comparação de posições assegura que o algoritmo sempre “lembre” da melhor solução encontrada e a utilize para guiar a busca futura.
Assim, a essência é que o algoritmo inicialmente tenta encontrar a melhor posição movendo-se em direção a um ponto mais baixo escolhido aleatoriamente. Se isso não for possível, ele tenta se mover na direção da melhor posição global encontrada. Isso garante um equilíbrio entre a busca local e a exploração global do espaço de soluções.
O princípio de infiltração no algoritmo ASHA pode não ser evidente à primeira vista. Vamos analisá-lo juntos em mais detalhes:
- Temos o parâmetro δ (delta), que é chamado de nível de resistência ou limiar de infiltração.
- A cada iteração, para cada unidade de água, verificamos se ela não ficou “boa demais”, ou seja, se não desceu abaixo do nível δ.
- Se o valor da função objetivo para essa unidade de água ficar abaixo de δ, considera-se que a água “se infiltrou” ou “penetrou” no solo.
- Nesse caso, nós “criamos” uma nova unidade de água, colocando-a em uma posição aleatória no espaço de busca.
Formalmente, isso pode ser descrito assim: se f(x_i) < δ, então x_i = posição_aleatória(), onde f(x_i) — valor da função objetivo para a i-ésima unidade de água, x_i — posição da i-ésima unidade de água.
O sentido desse mecanismo é evitar que todas as unidades de água fiquem presas em um mesmo mínimo local; continuar explorando o espaço de busca mesmo após encontrar uma boa solução; e, potencialmente, encontrar soluções ainda melhores em regiões não exploradas.
É importante escolher corretamente o valor de δ. Se δ for muito pequeno, a infiltração pode não ocorrer; se δ for muito grande, o algoritmo pode acabar se “reiniciando” o tempo todo, sem tempo suficiente para encontrar uma solução ótima. Além disso, determinar um valor apropriado para δ pode ser uma tarefa não trivial, especialmente quando não conhecemos previamente o intervalo de valores da função objetivo e não conseguimos definir esse parâmetro externamente. Por isso, introduzi um contador de tentativas de “infiltração” para cada gota, e um parâmetro externo deve definir seu valor máximo. A cada nova tentativa, a probabilidade de “se infiltrar” aumenta segundo uma lei quadrática, ou seja, com aceleração. Dessa forma, nenhuma gota permanecerá tempo demais no mesmo lugar, o que ajuda a evitar que fiquem presas em extremos locais.
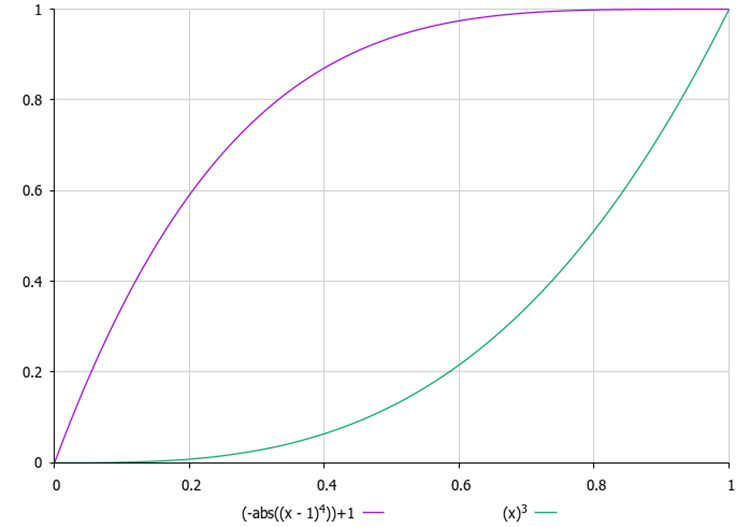
Figura 1. Exemplos de alteração da probabilidade de infiltração em função do número de tentativas
Quanto ao uso das coordenadas do ponto mais baixo, normalmente aplica-se a seguinte abordagem:
- Identifica-se a unidade de água com o menor valor da função objetivo (chamemo-la de x_lowest).
- Ao atualizar a posição, são utilizadas todas as coordenadas desse ponto mais baixo: x_new = x_old + F × r × (x_lowest − x_old). Aqui, x_new, x_old e x_lowest são vetores que contêm todas as coordenadas.
- Essa equação vetorial é aplicada a todas as coordenadas ao mesmo tempo. Ou seja, a nova posição é “atraída” ao ponto mais baixo em todas as dimensões do espaço de busca.
Essa abordagem permite direcionar a busca para a região mais promissora do espaço de soluções, levando em conta todas as dimensões simultaneamente.
Parece que tudo o que queríamos destacar já foi dito, então agora vamos partir para a codificação do algoritmo. Ah, mais um ponto: para este algoritmo e, possivelmente, para os próximos, foi necessário estender a estrutura padrão para armazenar informações adicionais sobre o agente de otimização, os campos adicionados estão marcados em verde.
Vamos relembrar como é a estrutura padrão do agente de otimização à qual o programa do usuário se refere, "S_AO_Agent", e como ela fica com as extensões:
1. Campos da estrutura:
- c [] - array das coordenadas atuais do agente no espaço de busca.
- cP [] - array das coordenadas anteriores do agente.
- cB [] - array das melhores coordenadas já encontradas pelo agente.
- f - valor da função de adaptabilidade (fitness) para as coordenadas atuais, usado para avaliar quão bem o agente está executando a tarefa.
- fP - valor da função de adaptabilidade para as coordenadas anteriores, permitindo acompanhar a mudança de desempenho do agente.
- fB - valor da função de adaptabilidade para as melhores coordenadas, guarda o melhor resultado alcançado pelo agente.
- cnt - contador para acompanhar o número de iterações.
2. Init() - o método de inicialização recebe a quantidade de coordenadas necessárias para o agente e executa as seguintes ações:
- ajusta o tamanho do array "c" para "coords", alocando memória para armazenar as coordenadas atuais.
- de forma semelhante, ajusta o tamanho do array "cP" para armazenar as coordenadas anteriores e o tamanho do array "cB" para armazenar as melhores coordenadas.
- inicializa o valor atual da função de adaptabilidade com o menor valor possível, permitindo que o agente o atualize na primeira avaliação.
- inicializa o valor anterior e o melhor valor da função de adaptabilidade da mesma forma.
- inicializa o valor do contador em zero.
Assim, a estrutura "S_AO_Agent" permite armazenar informações sobre o estado atual do agente, seu desempenho e o histórico de mudanças. As alterações feitas na estrutura não afetam os algoritmos de otimização já escritos com base nela, mas facilitam o desenvolvimento de novos algoritmos no futuro.
//—————————————————————————————————————————————————————————————————————————————— struct S_AO_Agent { double c []; //coordinates double cP []; //previous coordinates double cB []; //best coordinates double f; //fitness double fP; //previous fitness double fB; //best fitness int cnt; //counter void Init (int coords) { ArrayResize (c, coords); ArrayResize (cP, coords); ArrayResize (cB, coords); f = -DBL_MAX; fP = -DBL_MAX; fB = -DBL_MAX; cnt = 0; } }; //——————————————————————————————————————————————————————————————————————————————
A classe "C_AO_ASHA" herda da classe base "C_AO" e representa a implementação do algoritmo de otimização ASHA. Vamos analisar sua estrutura e funcionalidades:
- F, δ, β, ρ0 – parâmetros específicos do algoritmo, já descritos anteriormente, que definem seu comportamento.
- params - array de estruturas que armazena os parâmetros do algoritmo. Cada elemento do array contém o nome do parâmetro e seu respectivo valor.
O método "SetParams()" é utilizado para definir os valores dos parâmetros do algoritmo a partir do array "params".
O método "Init()" inicializa o algoritmo, recebendo como entrada os limites mínimos e máximos da busca, o passo de busca e a quantidade de épocas.
Os métodos "Moving()" e "Revision()" são responsáveis por movimentar os agentes no espaço de busca, revisar e atualizar o estado dos agentes e suas posições com base nos critérios de otimização.
Campos privados:
- S_AO_Agent aT[] – array para a população temporária, utilizado para ordenação da população.
- epochs - quantidade total de épocas usadas no processo de otimização.
- epochNow - época atual em que o algoritmo se encontra.
A classe "C_AO_ASHA" inclui os parâmetros, métodos e estruturas necessárias para gerenciar o processo de otimização e a interação entre os agentes.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_ASHA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_ASHA () { } C_AO_ASHA () { ao_name = "ASHA"; ao_desc = "Artificial Showering Algorithm"; ao_link = "https://www.mql5.com/en/articles/15980"; popSize = 100; //population size F = 0.3; //water flow velocity δ = 2; //resistance level(infiltration threshold) β = 0.8; //parameter that controls the rate of change in probability ρ0 = 0.1; //initial probability ArrayResize (params, 5); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "F"; params [1].val = F; params [2].name = "δ"; params [2].val = δ; params [3].name = "β"; params [3].val = β; params [4].name = "ρ0"; params [4].val = ρ0; } void SetParams () { popSize = (int)params [0].val; F = params [1].val; δ = (int)params [2].val; β = params [3].val; ρ0 = params [4].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); //---------------------------------------------------------------------------- double F; //water flow velocity int δ; //resistance level(infiltration threshold) double β; //parameter that controls the rate of change in probability double ρ0; //initial probability private: //------------------------------------------------------------------- S_AO_Agent aT []; int epochs; int epochNow; }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" é responsável pela inicialização do algoritmo de otimização. Lógica do método:
1. Verificação da inicialização padrão: o método chama "StandardInit", que executa verificações básicas e inicializa os parâmetros.
2. Definição dos contadores:
- epochs – recebe o valor passado em "epochsP" (quantidade total de iterações que o algoritmo deve executar).
- epochNow - inicializado com zero, já que o algoritmo está apenas começando e ainda não completou nenhuma época.
3. Reserva de memória para a população temporária de agentes.
4. Se todas as etapas de inicialização forem concluídas com sucesso, o método retorna "true", indicando que a inicialização do algoritmo foi bem-sucedida.
O método "Init" é essencial para preparar o algoritmo para execução. Ele verifica a validade dos parâmetros de entrada, define os valores necessários para controlar o processo de otimização e aloca memória para os agentes. A inicialização bem-sucedida permite que o algoritmo continue com as operações seguintes, como movimentação e revisão dos agentes.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_ASHA::Init (const double &rangeMinP [], const double &rangeMaxP [], const double &rangeStepP [], const int epochsP = 0) { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- epochs = epochsP; epochNow = 0; ArrayResize (aT, popSize); return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" implementa a lógica de movimentação dos agentes no espaço de busca dentro do algoritmo ASHA, vamos analisá-lo passo a passo:
1. O método incrementa o contador da época atual, o que permite acompanhar o número de iterações realizadas.
2. Inicialização inicial (se a revisão não for necessária): para cada agente "i" e para cada coordenada "c"
- o método gera posições iniciais para todos os agentes dentro dos intervalos definidos usando "u.RNDfromCI" e aplica a discretização.
- depois disso, "revision" é definido como "true", e o método encerra a execução.
3. Laço principal de movimentação dos agentes: para cada agente "i", são executadas as seguintes ações:
- inf - uma probabilidade, calculada usando "u.Scale" para obter um valor baseado no contador "cnt" do agente. Esse valor é então elevado à quarta potência para amplificar seu impacto.
- um número aleatório "rnd" é gerado para tomada de decisões.
4. Laço sobre as coordenadas: para cada coordenada "c", são realizadas as seguintes ações:
- um índice "ind" é gerado para selecionar outro agente com uma posição inferior no espaço de busca, que será usado para atualizar as coordenadas.
- se "i < 1", então: se "rnd < inf", as coordenadas do agente atual são atualizadas usando uma distribuição normal em torno das melhores coordenadas "cB" via "u.GaussDistribution".
- se "i >= 1", então: se "rnd < inf", as coordenadas do agente atual são atualizadas da mesma forma em relação às coordenadas de outro agente "a[ind].cB".
- caso contrário: mantém-se o valor antigo "xOld". Se o número aleatório gerado for menor que "ρ", então:
- " xNew" é atualizado com base no melhor valor de outro agente "xLower".
- caso contrário: "xNew" é atualizado com base no melhor valor global "xLowest".
- em seguida, o novo valor "xNew" é atribuído ao agente atual.
5. Correção das coordenadas: por fim, cada novo valor de coordenada é ajustado com "u.SeInDiSp" para que fique dentro dos limites definidos e respeite os passos estabelecidos.
O método "Moving" garante tanto a inicialização das posições dos agentes quanto sua atualização, durante o processo de otimização, com base em seu estado atual e interação com os demais agentes.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Moving () { epochNow++; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double xOld = 0.0; double xNew = 0.0; double xLower = 0.0; double xLowest = 0.0; double ρ = MathMax (β * (epochs - epochNow) / epochs, ρ0); double inf = 0.0; int ind = 0; double rnd = 0.0; for (int i = 0; i < popSize; i++) { inf = u.Scale (a [i].cnt, 0, δ, 0, 1); inf = inf * inf * inf * inf; rnd = u.RNDprobab (); for (int c = 0; c < coords; c++) { ind = (int)u.RNDintInRange (0, i - 1); if (i < 1) { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (cB [c], rangeMin [c], rangeMax [c], 8); } } else { if (rnd < inf) { a [i].c [c] = u.GaussDistribution (a [ind].cB [c], rangeMin [c], rangeMax [c], 8); } else { xOld = a [i].c [c]; if (u.RNDprobab () < ρ) { xLower = a [ind].cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLower - xOld)); } else { xLowest = cB [c]; xNew = xOld + F * (u.RNDprobab () * (xLowest - xOld)); } a [i].c [c] = xNew; } } a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é responsável por atualizar as informações sobre as melhores soluções (agentes) da população, assim como acompanhar sua adaptabilidade. Vamos ver isso passo a passo:
1. A variável "ind" é inicializada com o valor "-1" e será usada para armazenar o índice do agente com o melhor valor da função de adaptabilidade "f".
2. Laço sobre os agentes: o método percorre todos os agentes na população "popSize":
- se o valor da função de adaptabilidade "f" do agente atual for maior que seu valor ótimo atual "fB", então "fB" é atualizado e o índice desse agente é armazenado na variável "ind".
- se o valor da função de adaptabilidade "f" do agente atual for maior que seu melhor valor local "fB", esse valor também é atualizado.
- as coordenadas "c" do agente são copiadas para "cB", representando suas melhores coordenadas conhecidas.
- o contador "cnt" é zerado; caso contrário, se o valor da função de adaptabilidade não tiver melhorado, o contador "cnt" é incrementado.
3. Cópia das melhores coordenadas: se foi encontrado um agente com o melhor valor da função (índice "ind" diferente de "-1"), então suas coordenadas são copiadas para a variável global "cB".
4. Ordenação dos agentes: ao final, o método "u.Sorting_fB" é chamado, ordenando os agentes com base em seus melhores valores locais "fB".
O método "Revision" desempenha um papel fundamental no algoritmo, monitorando o desempenho dos agentes e atualizando suas melhores soluções conhecidas.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_ASHA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } if (a [i].f > a [i].fB) { a [i].fB = a [i].f; ArrayCopy (a [i].cB, a [i].c, 0, 0, WHOLE_ARRAY); a [i].cnt = 0; } else { a [i].cnt++; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- u.Sorting_fB (a, aT, popSize); } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Os resultados dos testes do algoritmo ASHA mostraram um desempenho médio: =============================
5 Hilly's; Func runs: 10000; result: 0.8968571984324711
25 Hilly's; Func runs: 10000; result: 0.40433437407600525
500 Hilly's; Func runs: 10000; result: 0.25617375427148387
=============================
5 Forest's; Func runs: 10000; result: 0.8036024134603961
25 Forest's; Func runs: 10000; result: 0.35525531625936474
500 Forest's; Func runs: 10000; result: 0.1916000538491299
=============================
5 Megacity's; Func runs: 10000; result: 0.4769230769230769
25 Megacity's; Func runs: 10000; result: 0.1812307692307692
500 Megacity's; Func runs: 10000; result: 0.09773846153846236
=============================
All score: 3.66372 (40.71%)
Observando o funcionamento do ASHA em um ambiente de teste, é difícil identificar características marcantes desse algoritmo; não se observam estudos isolados de áreas promissoras do espaço de busca.

ASHA na função de teste Hilly

ASHA na função de teste Forest
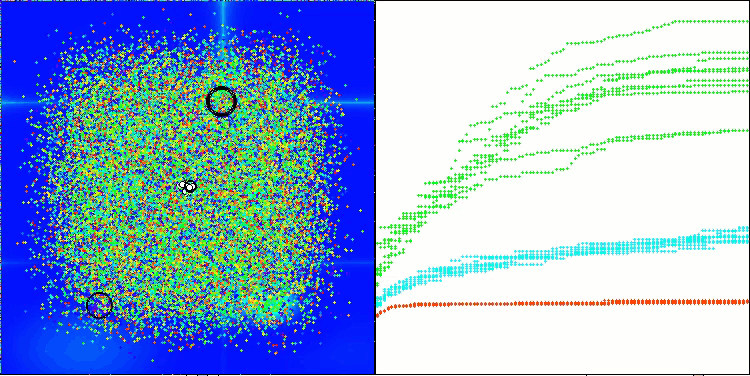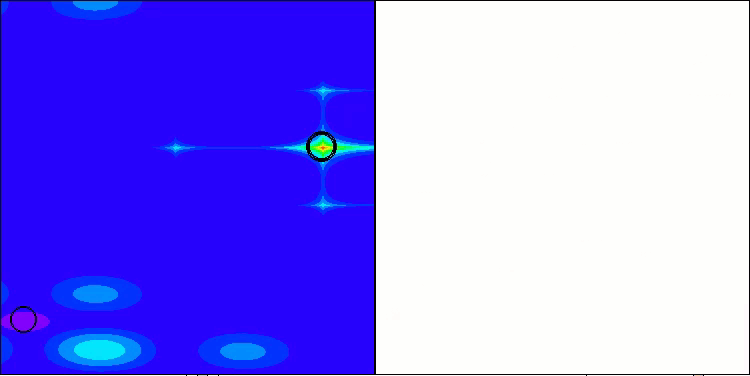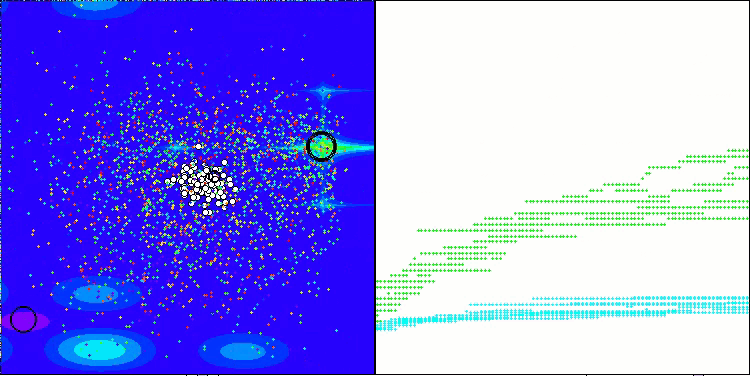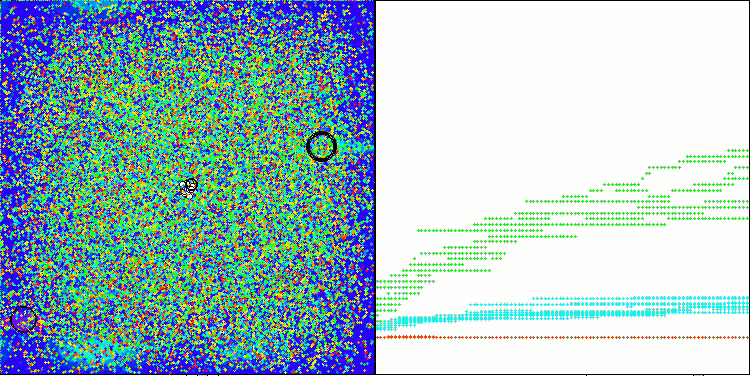
ASHA na função de teste Megacity
Com base nos resultados dos testes realizados, o algoritmo ASHA ficou em 28º lugar na tabela de classificação.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 7 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 8 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 9 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 10 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 11 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 12 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 13 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 14 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 15 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 16 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 17 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 18 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 19 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 20 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 21 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 22 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 23 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 24 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 25 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 26 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 27 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 28 | ASHA | artificial showering algorithm | 0,89686 | 0,40433 | 0,25617 | 1,55737 | 0,80360 | 0,35526 | 0,19160 | 1,35046 | 0,47692 | 0,18123 | 0,09774 | 0,75589 | 3,664 | 40,71 |
| 29 | ASBO | adaptive social behavior optimization | 0,76331 | 0,49253 | 0,32619 | 1,58202 | 0,79546 | 0,40035 | 0,26097 | 1,45677 | 0,26462 | 0,17169 | 0,18200 | 0,61831 | 3,657 | 40,63 |
| 30 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 31 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 32 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 33 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 34 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 35 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 36 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 37 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 38 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 39 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 40 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 41 | AAA | algae adaptive algorithm | 0,50007 | 0,32040 | 0,25525 | 1,07572 | 0,37021 | 0,22284 | 0,16785 | 0,76089 | 0,27846 | 0,14800 | 0,09755 | 0,52402 | 2,361 | 26,23 |
| 42 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 43 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 44 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 45 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
Considerações finais
Gostei da ideia do algoritmo, porém, durante a implementação e os testes, ficou a impressão de que falta algo. Não se pode dizer que seus resultados são os mais fracos, mas também estão longe dos melhores. Isso abre uma oportunidade para pesquisadores continuarem trabalhando com ele, especialmente graças à sua simplicidade, já que a ideia em si, na minha opinião, é muito promissora. Além disso, os autores não forneceram uma explicação mais detalhada sobre o coeficiente de infiltração, o que permite múltiplas interpretações, limitadas apenas pela criatividade do pesquisador.
A principal conclusão que pode ser extraída deste artigo é a seguinte: nem toda ideia simples é tão eficaz quanto ideias mais complexas. A eficácia de um algoritmo de otimização é uma questão complexa e envolve escolhas com base em compensações. Espero que este algoritmo se torne mais uma página no grande livro do conhecimento sobre as sutilezas e os truques da arte de encontrar as melhores soluções.
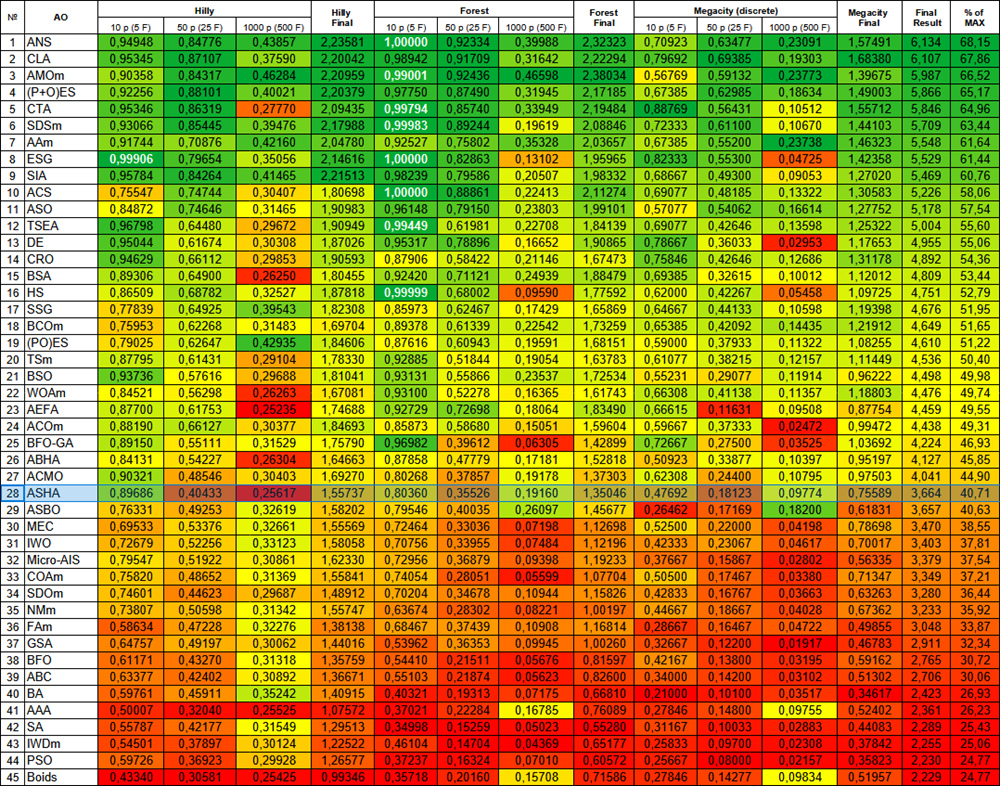
Figura 2. Gradação de cores dos algoritmos conforme os testes correspondentes. Resultados iguais ou superiores a 0.99 são destacados em branco.
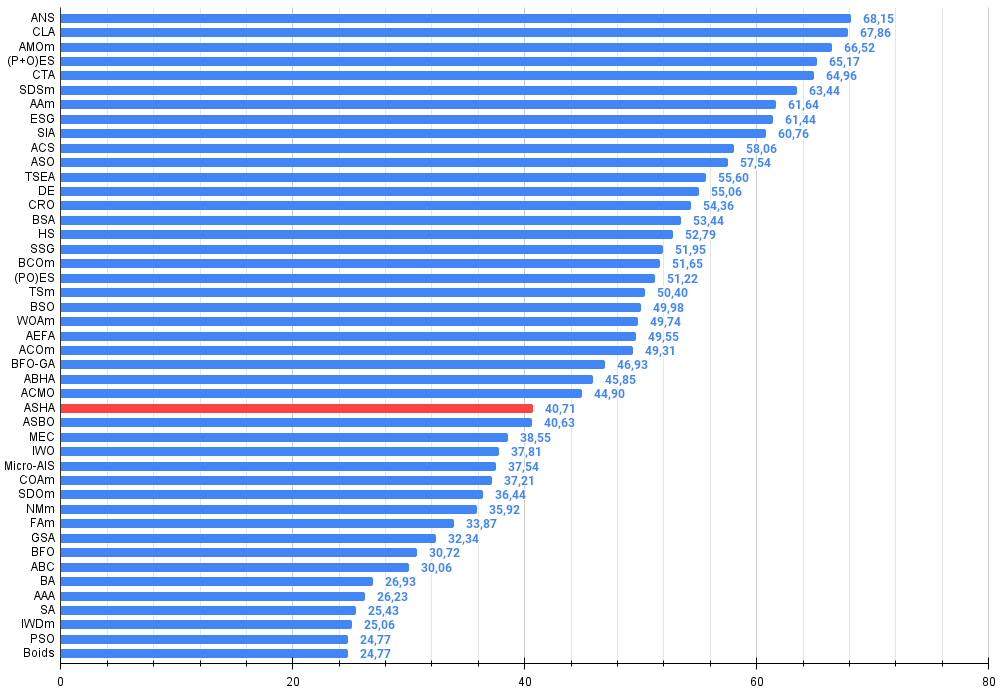
Figura 3. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
onde 100 é o resultado teórico máximo possível, no arquivo compactado há um script para cálculo da tabela de classificação)
Vantagens e desvantagens do algoritmo ASHA:
Vantagens:
- Rápido.
- Implementação simples.
Desvantagens:
- Baixa precisão de convergência.
Está anexado ao artigo um arquivo compactado com as versões atualizadas dos códigos dos algoritmos. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e opiniões apresentadas nos artigos baseiam-se nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/15980
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Construção de previsões econômicas: potencialidades do Python
Construção de previsões econômicas: potencialidades do Python
 Redes neurais em trading: Segmentação de dados com base em expressões de referência
Redes neurais em trading: Segmentação de dados com base em expressões de referência
 Busca de padrões arbitrários em pares de moedas no Python com o uso do MetaTrader 5
Busca de padrões arbitrários em pares de moedas no Python com o uso do MetaTrader 5
 Simulação de mercado (Parte 13): Sockets (VII)
Simulação de mercado (Parte 13): Sockets (VII)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso