
Algoritmos populacionais de otimização: Evolução diferencial (Differential Evolution, DE)
Conteúdo:
1. Introdução
2. Descrição do algoritmo
3. Resultados dos testes
1. Introdução
Os métodos metaheurísticos de otimização compõem uma classe de algoritmos que se valem de abordagens heurísticas para abordar problemas complexos de otimização. Distintos dos métodos numéricos tradicionais, que se apoiam em análise matemática e frequentemente necessitam de conhecimento sobre gradientes ou derivadas da função alvo, os métodos metaheurísticos se destacam por sua habilidade em explorar vastos espaços de busca e alcançar ótimos globais, mesmo quando a função alvo apresenta múltiplos ótimos locais ou é descontínua e não diferenciável. Uma vantagem notável dos métodos metaheurísticos é sua capacidade de operar com funções tipo "caixa preta", para as quais não existe solução analítica. Esses métodos, que se baseiam em conceitos estocásticos e probabilísticos, tendem a oferecer soluções de alta qualidade.
Entre as várias classes de métodos metaheurísticos, os Algoritmos Evolutivos (EA) modelam o processo de evolução natural para resolver problemas de otimização complexos, inspirando-se em mecanismos de hereditariedade, mutação, cruzamento e seleção natural. Nesse contexto, a evolução modelada nesses algoritmos espelha a seleção natural, em que soluções mais adaptadas têm maiores chances de persistir e transmitir suas características para gerações futuras, conduzindo gradualmente a população à solução ótima. Algoritmos genéticos, programação evolutiva, estratégias de evolução e programação genética são alguns dos mais conhecidos algoritmos evolutivos, cada qual com suas peculiaridades e áreas de aplicação.
No geral, os algoritmos evolutivos são uma ferramenta poderosa para resolver problemas de otimização complexos, especialmente em casos onde não há acesso a uma expressão analítica da função ou ao gradiente. Eles permitem explorar o espaço de busca e encontrar soluções ótimas combinando informações de diferentes soluções individuais.
A Evolução Diferencial (DE), um dos métodos metaheurísticos para otimização, em particular, é reconhecida por sua simplicidade e eficácia. Ela emprega uma população de vetores, que mutam e se cruzam para gerar novas soluções, operando sem a necessidade do conhecimento do gradiente e capaz de atingir ótimos globais.
Desenvolvida nos anos 90 por Storn e Price (publicada como "Differential Evolution - A Simple and Efficient Heuristic for global Optimization over Continuous Spaces"), a DE utiliza uma abordagem onde vetores de parâmetros são continuamente ajustados em busca da solução ideal.
2. Descrição do algoritmo
A estratégia da Evolução Diferencial se baseia em sua combinação de simplicidade e eficácia. Utilizando uma população de vetores que representam soluções potenciais, cada vetor é formado por componentes que correspondem aos valores das variáveis do problema em questão.
Na DE, a função do agente de busca é desempenhada pelo vetor. O processo inicia com uma população aleatória de vetores, seguido de um ciclo iterativo de mutação e cruzamento com outros vetores da população. A mutação envolve a adição da diferença entre dois vetores aleatórios a um terceiro vetor, gerando uma nova solução candidata.
Após a mutação, ocorre o cruzamento desse vetor mutado com o vetor original, possibilitando a combinação de informações e a criação de novas variantes de soluções. O resultado obtido é comparado com a melhor solução atual na população. Se o novo vetor for melhor, ele substitui o vetor antigo e passa a fazer parte da população. A mutação permite explorar o espaço de busca, enquanto o cruzamento permite combinar informações de diferentes vetores e criar novas variantes de soluções.
Esse processo é repetido diversas vezes, até que se atinja um critério de parada pré-estabelecido, como um número específico de iterações ou a obtenção de uma solução com a precisão desejada, neste caso, alcançar 10000 execuções da função de adaptação.
Graças a essas características, a DE se destaca como uma ferramenta valiosa no campo da otimização, especialmente em situações onde não se dispõe de expressão analítica para a função alvo ou seu gradiente. Aqui estão as fórmulas principais usadas no algoritmo diferencial:
1. Fórmula para criação de um novo candidato (diferenciação):
r = r1 + F * (r2 - r3)
onde:
- v - representa o componente do novo vetor
- r1, r2 e r3 - componentes de vetores aleatoriamente selecionados (soluções individuais da população)
- F - coeficiente de diferenciação, que controla o grau de variabilidade da solução (dispersão dos valores obtidos), geralmente adotado no intervalo (0.0;1.0]
2. Fórmula para cruzamento (crossover):
u = crossover (x, v)
Esta fórmula descreve o processo de cruzamento entre a solução atual x e o novo candidato v. O operador de cruzamento determina quais componentes da solução serão retirados do novo candidato. Essa é a probabilidade de usar um novo componente do vetor, caso contrário, o componente permanece inalterado, usando valores (0.0;1.0].
Vamos agora criar o pseudocódigo para o algoritmo DE, que se destaca pela sua simplicidade (o código real é quase tão direto quanto o próprio pseudocódigo):
- Criar uma população aleatória de vetores
- Calcular a função de adaptação
- Atualizar a melhor solução
- Atualizar a população (substituir vetores pelos melhores mutantes)
- Criar componente mutante do vetor ou manter o anterior, dependendo de qual é melhor
- Repetir a partir do passo 2.
Para descrever um vetor no algoritmo DE, escreveremos uma estrutura, chamada S_Vector, que representa um vetor em espaço n-dimensional. A estrutura possui os seguintes campos:
- Init (int coords): função que inicializa um vetor do comprimento especificado coords. Ela cria dois arrays: "c" e "cPrev", que representam as coordenadas do vetor e suas coordenadas anteriores, respectivamente. Também define os valores iniciais para f e fPrev como -DBL_MAX.
- c []: array que contém as coordenadas do vetor
- cPrev []: array que contém as coordenadas do vetor na iteração anterior
- f: valor da função de adaptação para o vetor atual
- fPrev: valor da função de adaptação para o vetor na iteração anterior
//—————————————————————————————————————————————————————————————————————————————— struct S_Vector { void Init (int coords) { ArrayResize (c, coords); ArrayResize (cPrev, coords); f = -DBL_MAX; fPrev = -DBL_MAX; } double c []; //coordinates double cPrev []; //previous coordinates double f; //fitness double fPrev; //previous fitness }; //——————————————————————————————————————————————————————————————————————————————
Para um algoritmo tão simples quanto o DE, a descrição da classe é muito simples, chamemos a classe de C_AO_DE. Os campos da classe C_AO_DE contêm informações sobre o estado atual do algoritmo e seus parâmetros, e os métodos realizam várias operações relacionadas à otimização da função.
A classe possui os seguintes campos e métodos:
- cB []: array contém as melhores coordenadas encontradas pelo algoritmo
- fB: valor da função de adaptação para as melhores coordenadas
- v []: array de estruturas S_Vector, que representa a população de vetores
- rangeMax[]: array contém os valores máximos para cada coordenada do vetor
- rangeMin[]: array contém os valores mínimos para cada coordenada do vetor
- rangeStep[]: array contém os valores de passo para cada coordenada do vetor
- Init (int coordsP, int popSizeP, double diffWeightP, double crossProbabP): função que inicializa os parâmetros do algoritmo. Ela aceita o número de coordenadas "coordsP", o tamanho da população "popSizeP", o peso diferencial "diffWeightP" e a probabilidade de cruzamento "crossProbabP".
- Moving (): função executa uma etapa do algoritmo de evolução diferencial
- Revision (): função realiza uma revisão da população de vetores
- SeInDiSp (double In, double InMin, double InMax, double Step): método calcula um novo valor de coordenada dentro do intervalo especificado com o passo dado
- RNDfromCI (double min, double max): função gera um número aleatório no intervalo [min, max]
//—————————————————————————————————————————————————————————————————————————————— class C_AO_DE { //---------------------------------------------------------------------------- public: double cB []; //best coordinates public: double fB; //FF of the best coordinates public: S_Vector v []; //vector public: double rangeMax []; //maximum search range public: double rangeMin []; //manimum search range public: double rangeStep []; //step search public: void Init (const int coordsP, //coordinates number const int popSizeP, //population size const double diffWeightP, //differential weight const double crossProbabP); //crossover robability public: void Moving (); public: void Revision (); //---------------------------------------------------------------------------- private: int coords; //coordinates number private: int popSize; //population size private: double diffWeight; //differential weight private: double crossProbab; //crossover robability private: bool revision; private: double SeInDiSp (double In, double InMin, double InMax, double Step); private: double RNDfromCI (double min, double max); }; //——————————————————————————————————————————————————————————————————————————————
O método Init da classe C_AO_DE inicializa os parâmetros do algoritmo de evolução diferencial. O método aceita quatro parâmetros:
- "coordsP" - número de coordenadas,
- "popSizeP" - tamanho da população,
- "diffWeightP" - peso diferencial
- "crossProbabP" - probabilidade de cruzamento.
No início, o método usa a função MathSrand para redefinir o gerador de números aleatórios. Isso garante que cada vez que o algoritmo é iniciado, ele utiliza uma nova sequência de números aleatórios.
Em seguida, o método inicializa as variáveis "fB" e "revision". A variável "fB" contém o melhor valor da função de adaptação encontrado pelo algoritmo. Inicialmente, é definido como "-DBL_MAX", ou seja, um número muito baixo. A variável "revision" é definida como "false", o que significa que a população de vetores ainda não foi revisada.
Em seguida, o método inicializa as variáveis "coords", "popSize", "diffWeight" e "crossProbab" com os valores fornecidos como parâmetros.
Depois, o método cria um array "v" do tamanho "popSize", que contém a população de vetores.
Em seguida, o método cria três arrays: "rangeMax", "rangeMin" e "rangeStep", cada um do tamanho de coords (número de coordenadas).
Por fim, o método cria o array "cB" do tamanho de coords, que contém as melhores coordenadas encontradas pelo algoritmo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_DE::Init (const int coordsP, //coordinates number const int popSizeP, //population size const double diffWeightP, //differential weight const double crossProbabP) //crossover robability { MathSrand ((int)GetMicrosecondCount ()); // reset of the generator fB = -DBL_MAX; revision = false; coords = coordsP; popSize = popSizeP; diffWeight = diffWeightP; crossProbab = crossProbabP; ArrayResize (v, popSize); for (int i = 0; i < popSize; i++) v [i].Init (coords); ArrayResize (rangeMax, coords); ArrayResize (rangeMin, coords); ArrayResize (rangeStep, coords); ArrayResize (cB, coords); } //——————————————————————————————————————————————————————————————————————————————
Para modificar os vetores-solução no espaço de busca, escreveremos o método "Moving" da classe C_AO_DE. Este método aplica operadores de mutação e cruzamento para gerar novos vetores-candidatos e seleciona a melhor solução baseada na função de adaptação.
O primeiro bloco de código, que começa com a condição "if (!revision)", é executado apenas na primeira execução do método "Moving" ou após a chamada do método "Init". Ele inicializa a população inicial de vetores com valores aleatórios dentro dos limites definidos e com o passo especificado no array "rangeStep".
Em seguida, o método utiliza um laço "for" para atualizar cada vetor na população. Para cada vetor, o método seleciona três vetores aleatórios diferentes da população (r1, r2, r3), que não sejam o vetor atual (i), e aplica os operadores de mutação e cruzamento para obter um novo vetor-candidato. O operador de mutação calcula a diferença entre os vetores "r2" e "r3", multiplicada pelo peso diferencial "diffWeight", e adiciona o resultado ao vetor "r1". O operador de cruzamento escolhe uma coordenada do vetor e substitui-a pela coordenada correspondente do novo vetor-candidato com uma probabilidade "crossProbab". Se a probabilidade de cruzamento não é atingida, a coordenada atual do vetor permanece inalterada.
Um leitor atento ao analisar o código abaixo descobrirá que o método de modificação de vetores "Moving" não prevê a criação de coordenadas no espaço, além das que podem ser obtidas a partir das existentes. Assim, a estocasticidade do algoritmo consiste apenas na escolha de vetores para cruzamento, mas não na criação de novos e originais. Esta característica tem implicações de longo alcance, as quais discutiremos abaixo.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_DE::Moving () { //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { v [i].c [c] = RNDfromCI (rangeMin [c], rangeMax [c]); v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } } revision = true; return; } //---------------------------------------------------------------------------- double rnd = 0.0; int r = 0; int r1 = 0; int r2 = 0; int r3 = 0; for (int i = 0; i < popSize; i++) { do { r = (int)RNDfromCI (0, popSize); if (r >= popSize) r = popSize - 1; r1 = r; } while (r1 == i); do { r = (int)RNDfromCI (0, popSize); if (r >= popSize) r = popSize - 1; r2 = r; } while (r2 == i || r2 == r1); do { r = (int)RNDfromCI (0, popSize); if (r >= popSize) r = popSize - 1; r3 = r; } while (r3 == i || r3 == r1 || r3 == r2); for (int c = 0; c < coords; c++) { rnd = RNDfromCI (0, 1.0); if (rnd < crossProbab) { v [i].c [c] = v [r1].cPrev [c] + diffWeight * (v [r2].cPrev [c] - v [r3].cPrev [c]); v [i].c [c] = SeInDiSp (v [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } else { v [i].c [c] = v [i].cPrev [c]; } } } } //——————————————————————————————————————————————————————————————————————————————
E finalmente, precisaremos do método "Revision" da classe C_AO_DE, que atualiza a melhor solução na população e salva os valores anteriores da função de adaptação e as coordenadas dos vetores.
Primeiramente, o método inicializa a variável "ind" com o valor "-1". Então, ele usa um laço "for" para percorrer todos os vetores na população e verifica se a função de adaptação do vetor atual é maior do que "fB" (a melhor função de adaptação encontrada até agora), então salva o índice desse vetor na variável "ind".
Se "ind" não for "-1", o método atualiza o valor de "fB" para o valor da função de adaptação do vetor no índice "ind" e salva suas coordenadas no array "cB".
Depois, o método usa outro laço "for" para percorrer todos os vetores na população e verifica se a função de adaptação do vetor atual é maior do que seu valor anterior, então o método salva o valor atual da função de adaptação e as coordenadas do vetor nos campos correspondentes v[i].fPrev e v[i].cPrev.
Este método permite que a classe C_AO_DE mantenha a melhor solução na população e os valores anteriores da função de adaptação e coordenadas dos vetores para uso futuro na otimização da função de adaptação.
Pode-se notar que a população não avançará mais no espaço de busca até que um vetor melhor do que sua versão original (parental) seja encontrado. Esse ponto é um acréscimo ao anterior.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_DE::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (v [i].f > fB) ind = i; } if (ind != -1) { fB = v [ind].f; ArrayCopy (cB, v [ind].c, 0, 0, WHOLE_ARRAY); } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { if (v [i].f > v [i].fPrev) { v [i].fPrev = v [i].f; ArrayCopy (v [i].cPrev, v [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
3. Resultados dos testes
Impressão do desempenho do algoritmo de evolução diferencial em um banco de testes:
C_AO_DE:50;0.2;0.8
=============================
5 Rastrigin's; Func runs 10000 result: 80.30183306326985
Score: 0.99498
25 Rastrigin's; Func runs 10000 result: 76.15178282331799
Score: 0.94356
500 Rastrigin's; Func runs 10000 result: 52.17316317703311
Score: 0.64645
=============================
5 Forest's; Func runs 10000 result: 1.7348423083855402
Score: 0.98131
25 Forest's; Func runs 10000 result: 1.28572746338484
Score: 0.72727
500 Forest's; Func runs 10000 result: 0.20833645141168078
Score: 0.11785
=============================
5 Megacity's; Func runs 10000 result: 9.640000000000002
Score: 0.80333
25 Megacity's; Func runs 10000 result: 3.9199999999999995
Score: 0.32667
500 Megacity's; Func runs 10000 result: 0.3548
Score: 0.02957
=============================
All score: 5.57100
A partir dos valores de saída do algoritmo, vemos excelentes resultados de teste.
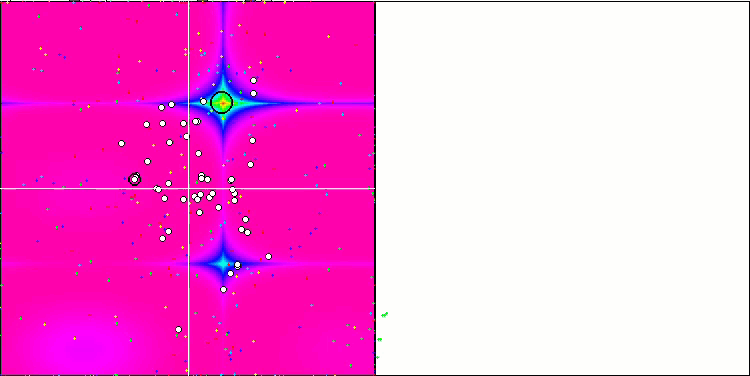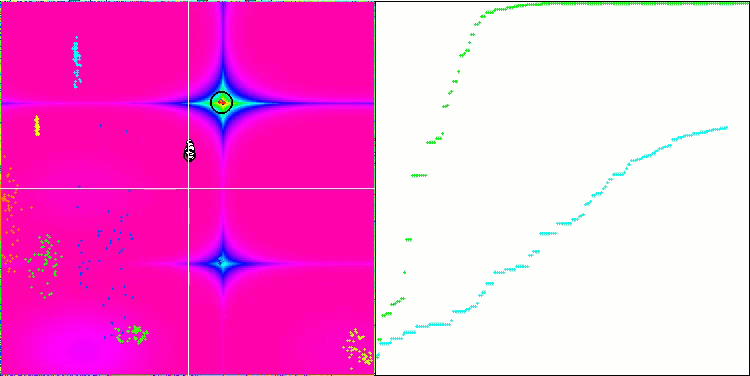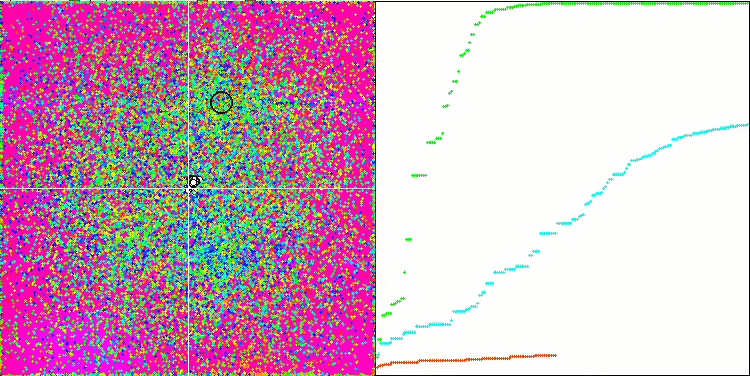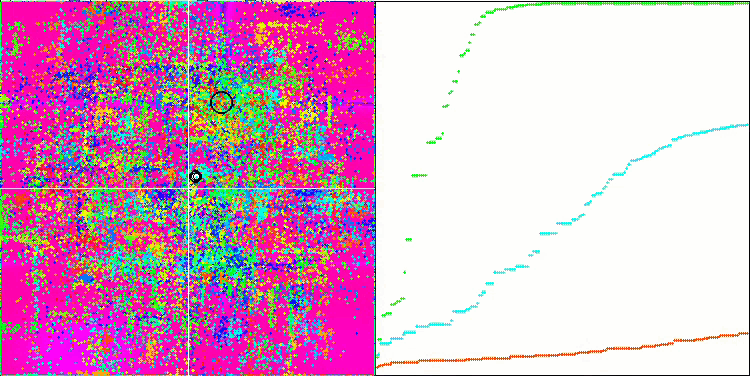
Na representação abaixo, observamos a impressionante convergência do algoritmo, que denota a eficiência do mesmo. Contudo, a peculiaridade discutida anteriormente nas descrições dos métodos "Moving" e "Revision" também se torna evidente. Nessa representação, observamos a impressionante convergência do algoritmo, que denota a eficiência do mesmo. Esta inconsistência é atribuída à degeneração da população, onde cada vetor converge singularmente para um extremo específico, que pode não representar a solução ótima global. Conforme abordado previamente, o algoritmo carece de mecanismos que permitam a continuação da exploração do espaço de pesquisa através da geração de novos vetores distintos. O método DE não introduz novos vetores, limitando-se a recombinar os já existentes. Tal processo resulta na completa degeneração da população, visto que não há introdução de "sangue novo" para enriquecer o "pool genético" da mesma.
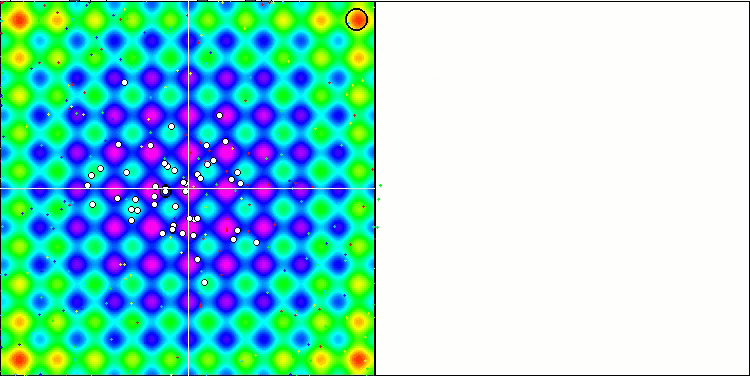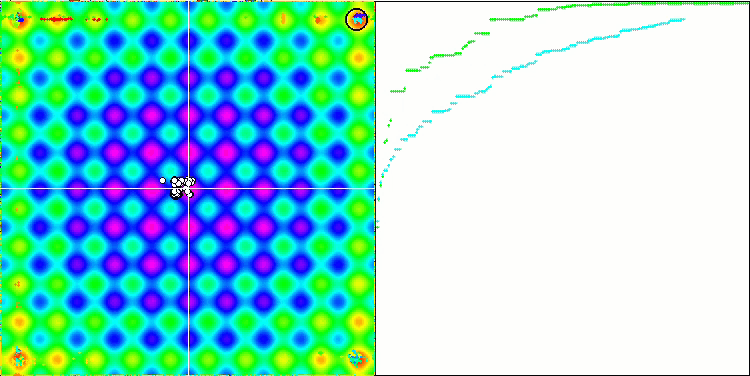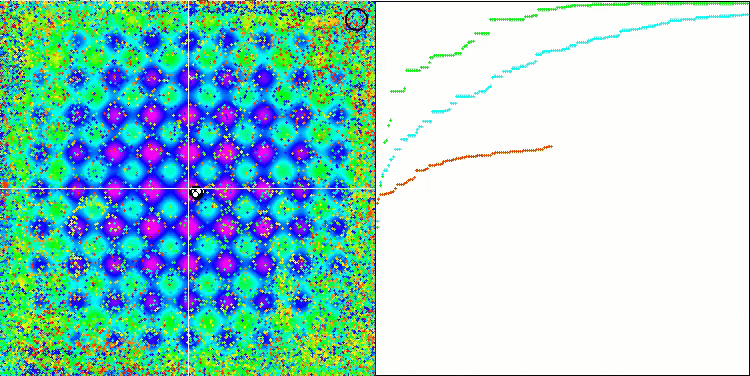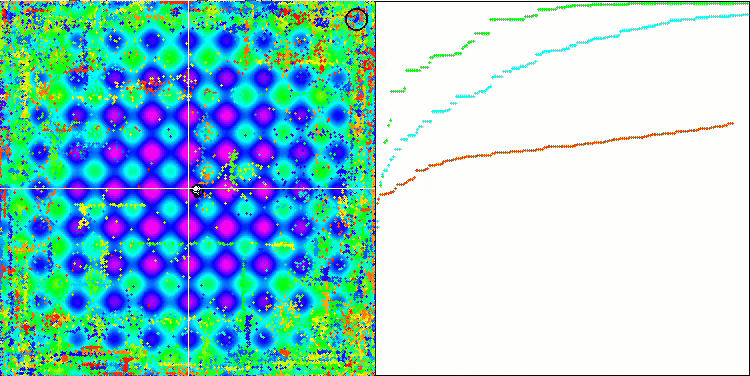
DE na função de teste de Rastrigin.
DE na função de teste Forest.
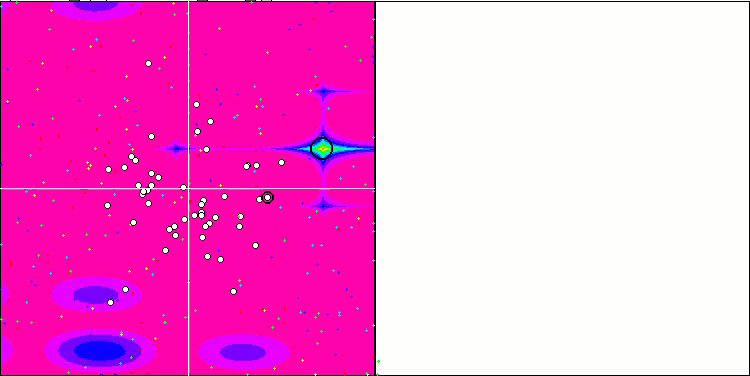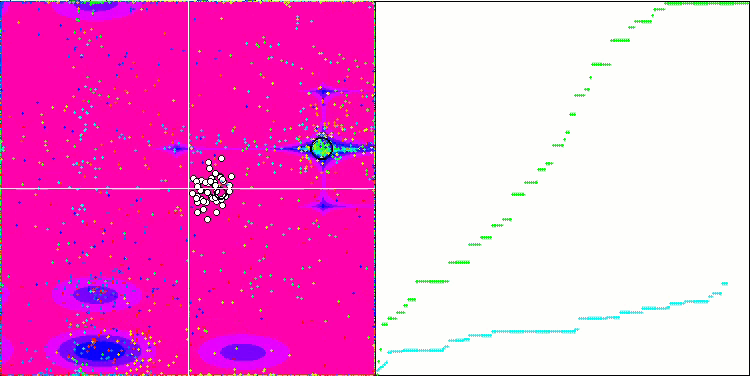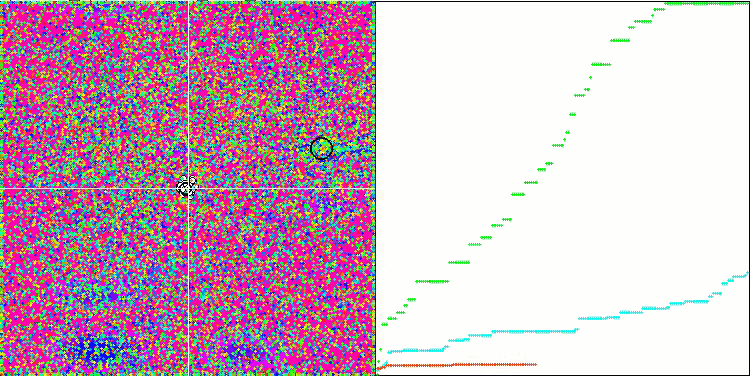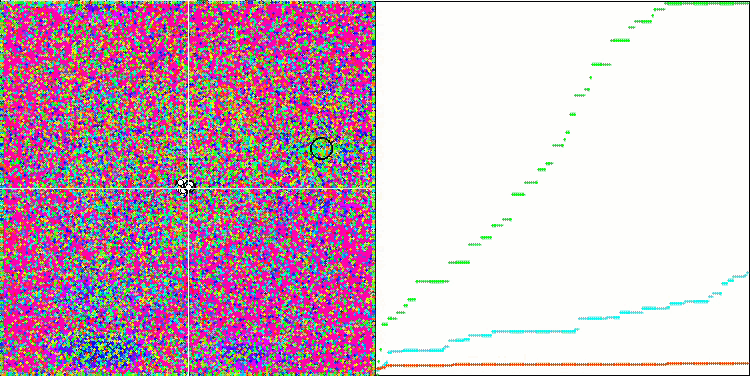
DE na função de teste Megacity.
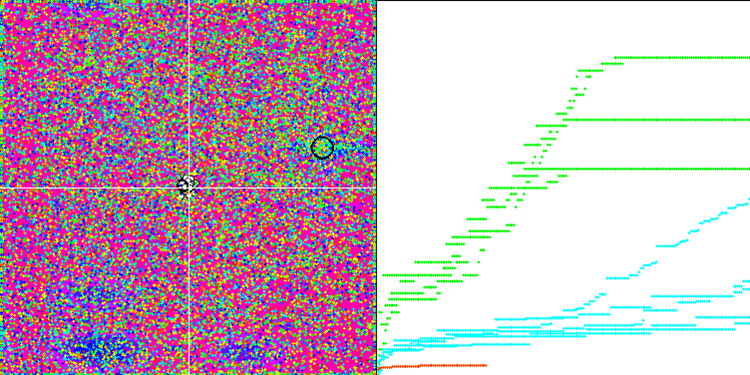
Um exemplo de uma enorme disseminação da convergência. Especialmente visível nas funções Forest e Megacity.
Avançamos agora para a tabela de classificação final, que acolhe um novo concorrente: o algoritmo DE. Este conseguiu superar o líder atual, SDSm, no teste Forest envolvendo 10 variáveis, conquistando assim o primeiro lugar. As performances nos outros testes também foram destacadas, com o DE posicionando-se em quarto lugar, logo após o SSG. Importa mencionar que, ao contrário da prática habitual de realizar cinco execuções para cada função de teste, foi necessário efetuar dez iterações nos testes das funções Forest e Megacity, devido à grande variação observada nos resultados. Na função Rastrigin suave, a dispersão dos resultados é menos acentuada.
| № | AO | Description | Rastrigin | Rastrigin final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | |||||||
| 1 | SDSm | stochastic diffusion search M | 0,99809 | 1,00000 | 0,69149 | 2,68958 | 0,99265 | 1,00000 | 1,00000 | 2,99265 | 1,00000 | 1,00000 | 1,00000 | 3,00000 | 100,000 |
| 2 | SDS | stochastic Diffusion Search | 0,99737 | 0,97322 | 0,58904 | 2,55963 | 0,96067 | 0,93572 | 0,79649 | 2,69288 | 0,78696 | 0,93815 | 0,71804 | 2,44315 | 88,201 |
| 3 | SSG | saplings sowing and growing | 1,00000 | 0,92761 | 0,51630 | 2,44391 | 0,72120 | 0,65201 | 0,83760 | 2,21081 | 0,54782 | 0,61841 | 0,99522 | 2,16146 | 77,683 |
| 4 | DE | differential evolution | 0,98295 | 0,89236 | 0,51375 | 2,38906 | 1,00000 | 0,84602 | 0,65510 | 2,50112 | 0,90000 | 0,52237 | 0,12031 | 1,54268 | 73,099 |
| 5 | HS | harmony search | 0,99676 | 0,88385 | 0,44686 | 2,32747 | 0,99148 | 0,68242 | 0,37529 | 2,04919 | 0,71739 | 0,71842 | 0,41338 | 1,84919 | 70,623 |
| 6 | IWO | invasive weed optimization | 0,95828 | 0,62227 | 0,27647 | 1,85703 | 0,70170 | 0,31972 | 0,26613 | 1,28755 | 0,57391 | 0,30527 | 0,33130 | 1,21048 | 48,250 |
| 7 | ACOm | ant colony optimization M | 0,34611 | 0,16683 | 0,15808 | 0,67103 | 0,86147 | 0,68980 | 0,64798 | 2,19925 | 0,71739 | 0,63947 | 0,05579 | 1,41265 | 47,387 |
| 8 | MEC | mind evolutionary computation | 0,99270 | 0,47345 | 0,21148 | 1,67763 | 0,60244 | 0,28046 | 0,21324 | 1,09615 | 0,66957 | 0,30000 | 0,26045 | 1,23002 | 44,049 |
| 9 | SDOm | spiral dynamics optimization M | 0,69840 | 0,52988 | 0,33168 | 1,55996 | 0,59818 | 0,38766 | 0,37600 | 1,36183 | 0,35653 | 0,15262 | 0,25842 | 0,76758 | 40,289 |
| 10 | COAm | cuckoo optimization algorithm M | 0,92400 | 0,43407 | 0,24120 | 1,59927 | 0,57881 | 0,23477 | 0,13842 | 0,95200 | 0,52174 | 0,24079 | 0,17001 | 0,93254 | 37,830 |
| 11 | FAm | firefly algorithm M | 0,59825 | 0,31520 | 0,15893 | 1,07239 | 0,50637 | 0,29178 | 0,41704 | 1,21519 | 0,24783 | 0,20526 | 0,35090 | 0,80398 | 33,139 |
| 12 | ABC | artificial bee colony | 0,78170 | 0,30347 | 0,19313 | 1,27829 | 0,53379 | 0,14799 | 0,11177 | 0,79355 | 0,40435 | 0,19474 | 0,13859 | 0,73768 | 29,766 |
| 13 | BA | bat algorithm | 0,40526 | 0,59145 | 0,78330 | 1,78002 | 0,20664 | 0,12056 | 0,21769 | 0,54488 | 0,21305 | 0,07632 | 0,17288 | 0,46225 | 29,499 |
| 14 | CSS | charged system search | 0,56605 | 0,68683 | 1,00000 | 2,25289 | 0,13961 | 0,01853 | 0,13638 | 0,29452 | 0,07392 | 0,00000 | 0,03465 | 0,10856 | 27,930 |
| 15 | GSA | gravitational search algorithm | 0,70167 | 0,41944 | 0,00000 | 1,12111 | 0,31390 | 0,25120 | 0,27812 | 0,84322 | 0,42609 | 0,25525 | 0,00000 | 0,68134 | 27,807 |
| 16 | BFO | bacterial foraging optimization | 0,67203 | 0,28721 | 0,10957 | 1,06881 | 0,39364 | 0,18364 | 0,17298 | 0,75026 | 0,37392 | 0,24211 | 0,18841 | 0,80444 | 27,542 |
| 17 | EM | electroMagnetism-like algorithm | 0,12235 | 0,42928 | 0,92752 | 1,47915 | 0,00000 | 0,02413 | 0,29215 | 0,31628 | 0,00000 | 0,00527 | 0,10872 | 0,11399 | 19,002 |
| 18 | SFL | shuffled frog-leaping | 0,40072 | 0,22021 | 0,24624 | 0,86717 | 0,19981 | 0,02861 | 0,02221 | 0,25063 | 0,19565 | 0,04474 | 0,06607 | 0,30646 | 13,200 |
| 19 | MA | monkey algorithm | 0,33192 | 0,31029 | 0,13582 | 0,77804 | 0,09927 | 0,05443 | 0,07482 | 0,22852 | 0,15652 | 0,03553 | 0,10669 | 0,29874 | 11,777 |
| 20 | FSS | fish school search | 0,46812 | 0,23502 | 0,10483 | 0,80798 | 0,12730 | 0,03458 | 0,05458 | 0,21647 | 0,12175 | 0,03947 | 0,08244 | 0,24366 | 11,332 |
| 21 | IWDm | intelligent water drops M | 0,26459 | 0,13013 | 0,07500 | 0,46972 | 0,28358 | 0,05445 | 0,05112 | 0,38916 | 0,22609 | 0,05659 | 0,05054 | 0,33322 | 10,423 |
| 22 | PSO | particle swarm optimisation | 0,20449 | 0,07607 | 0,06641 | 0,34696 | 0,18734 | 0,07233 | 0,18207 | 0,44175 | 0,16956 | 0,04737 | 0,01947 | 0,23641 | 8,426 |
| 23 | RND | random | 0,16826 | 0,09038 | 0,07438 | 0,33302 | 0,13381 | 0,03318 | 0,03949 | 0,20648 | 0,12175 | 0,03290 | 0,04898 | 0,20363 | 5,054 |
| 24 | GWO | grey wolf optimizer | 0,00000 | 0,00000 | 0,02093 | 0,02093 | 0,06514 | 0,00000 | 0,00000 | 0,06514 | 0,23478 | 0,05789 | 0,02545 | 0,31812 | 1,000 |
Considerações finais
O algoritmo de evolução diferencial se destaca por sua rapidez e habilidade em identificar ótimos globais, apesar de resultados apenas medianos em testes isolados. Este método é vastamente aplicado para otimização em diversas áreas, incluindo ajuste de modelos e otimização econômica. Sugiro múltiplas rodadas de otimização com o DE, já que a qualidade dos resultados pode variar significativamente com a escolha da população inicial. Pode ser útil aumentar o tamanho da população enquanto se aumenta o número de iterações.
Embora simples e rápido, o DE não está isento de falhas, como a possível degeneração da população, que pode levar ao aprisionamento em mínimos locais. Tais desvantagens devem ser consideradas ao optar por esse método.
O algoritmo DE discutido neste documento é uma espécie de modelo, que serviu de base para a criação de algumas modificações. Minhas sugestões para melhorar o algoritmo de evolução diferencial (DE) são as seguintes:
1. Uso de métodos adaptativos para controle de parâmetros: O DE tem alguns parâmetros que precisam ser ajustados porque influenciam significativamente os resultados.O parâmetro de peso diferencial recomendado pelos autores é "0,2", e esse é o valor padrão que adotei no script para o teste. Esse parâmetro afeta significativamente a diversidade da população. Se escolhermos um valor menor que "0,2", poderemos obter uma convergência ainda melhor do algoritmo, mas teremos ainda mais dispersão nos resultados. Por outro lado, se aumentarmos o valor desse parâmetro, o algoritmo se resiste à degeneração da população e a ficar preso em extremos locais, mas, ao mesmo tempo, a qualidade da convergência diminui rapidamente para um número limitado de iterações e o tempo de busca aumenta inevitavelmente.
O parâmetro de probabilidade de cruzamento também afeta a qualidade da otimização. Os autores recomendam o valor "0.9", mas meus experimentos mostraram que um valor mais adequado, na minha opinião, é "0.8".
Dado o exposto, parece apropriado usar métodos adaptativos para controlar e mudar dinamicamente os parâmetros, permitindo que o algoritmo se ajuste automaticamente de acordo com a tarefa em questão.
2. Utilização de diferentes estratégias de mutação e cruzamento.
3. Uso de métodos híbridos: é possível combinar o DE com outros métodos de otimização, como algoritmos genéticos, métodos de otimização baseados em gradiente, métodos de otimização baseados em enxame de partículas, etc. Isso pode melhorar o desempenho do algoritmo e ajudar a melhorar a eficiência do algoritmo como um todo.
4. Melhorar a convergência: aplicar a criação de vetores aleatórios adicionais para aumentar a diversidade na população.
5. Uso de estratégias diferentes para selecionar indivíduos para mutação: esse algoritmo considera um método completamente aleatório de seleção de indivíduos para cruzamento, mas também é possível complementar ou substituí-lo completamente pelo uso de outras estratégias de seleção de indivíduos para cruzamento/mutação, como a estratégia de seleção de indivíduos com base na adaptação. Isso pode ajudar a aumentar a diversidade da população e melhorar significativamente a robustez do algoritmo contra interferências.
Em suma, o DE impressiona pela eficácia e simplicidade. Para tarefas de alta complexidade e dimensionalidade, este algoritmo é uma escolha robusta, dado que problemas de diversidade populacional são minimizados com o aumento dos parâmetros a otimizar. A DE demonstrou com segurança que os algoritmos podem ser muito eficientes e, ainda assim, incrivelmente simples e rápidos. O algoritmo de evolução diferencial pode ser recomendado para resolver problemas complexos de otimização com alta dimensionalidade, pois o efeito da queda da diversidade durante a evolução é menos pronunciado quando o número de parâmetros otimizados é grande.
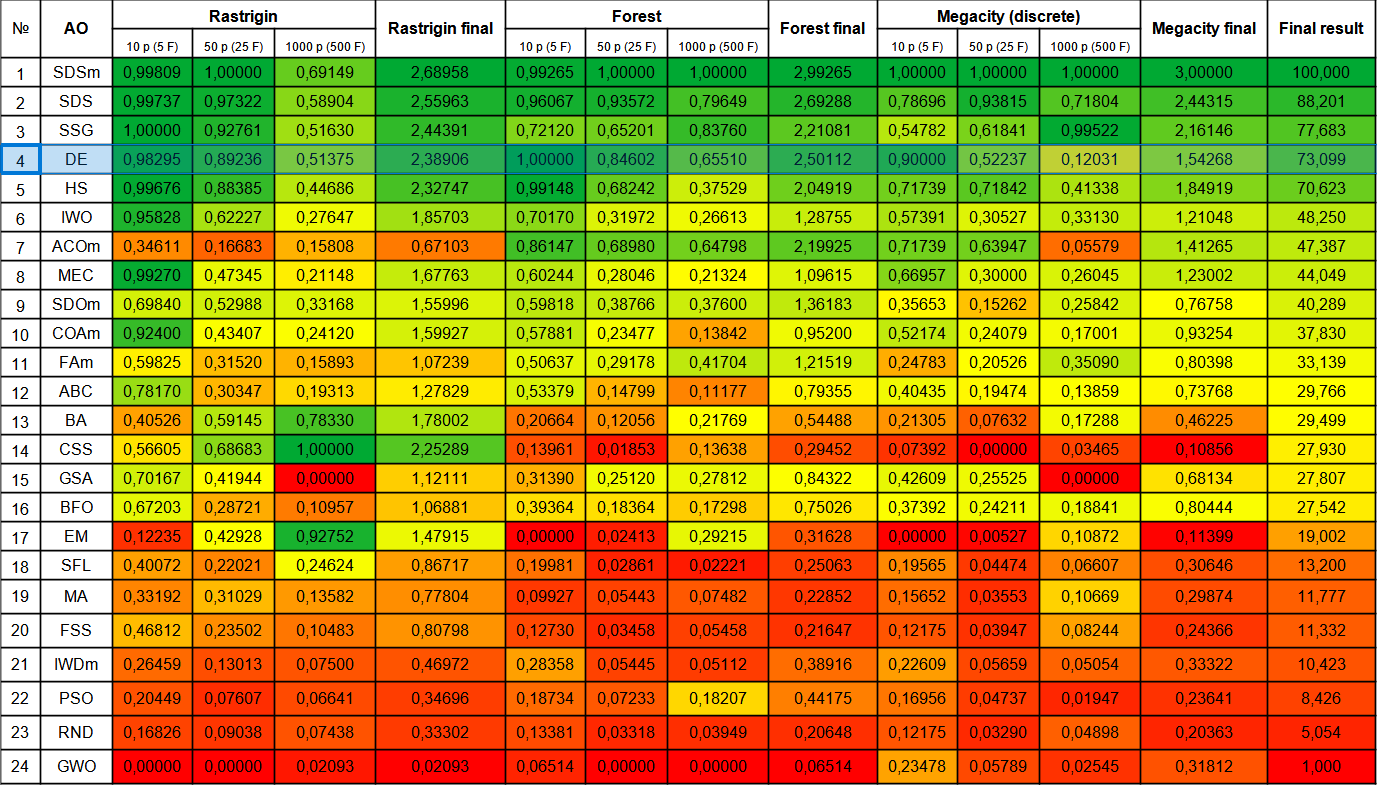
Figura 1. Graduação de cores dos algoritmos de acordo com os testes correspondentes.
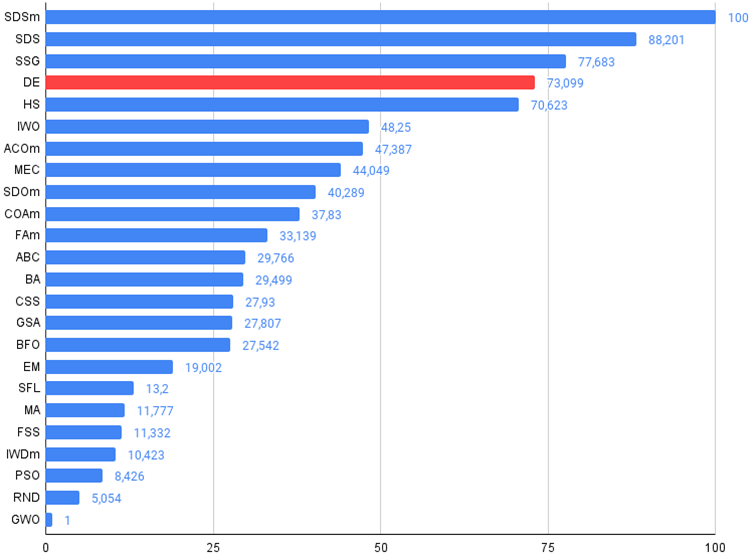
Figura 2. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, quanto maior, melhor,
no anexo, há um script para calcular a tabela de classificação de acordo com a metodologia deste artigo).
Prós e contras do algoritmo de evolução diferencial (DE)
Prós:
- Poucos parâmetros externos.
- Implementação simples.
- Rapidez de execução.
- Boa escalabilidade.
- Desempenho muito bom em diferentes tipos de funções (considerando os pontos negativos).
Contras:
- Variação muito alta nos resultados.
- Tendência a ficar preso em extremos locais.
O artigo inclui um arquivo com versões atualizadas dos códigos dos algoritmos descritos nos artigos anteriores. O autor do artigo não assume responsabilidade pela precisão absoluta na descrição dos algoritmos canônicos, muitos deles foram modificados para melhorar os recursos de pesquisa. As conclusões e opiniões apresentadas nos artigos são baseados nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/13781
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Desenvolvendo um sistema de Replay (Parte 48): Entendendo e compreendendo alguns conceitos
Desenvolvendo um sistema de Replay (Parte 48): Entendendo e compreendendo alguns conceitos
 Redes neurais de maneira fácil (Parte 65): aprendizado supervisionado ponderado por distância (DWSL)
Redes neurais de maneira fácil (Parte 65): aprendizado supervisionado ponderado por distância (DWSL)
 Python, ONNX e MetaTrader 5: Montando um modelo RandomForest com pré-processamento de dados via RobustScaler e PolynomialFeatures
Python, ONNX e MetaTrader 5: Montando um modelo RandomForest com pré-processamento de dados via RobustScaler e PolynomialFeatures
 Algoritmos de otimização populacionais: otimização de dinâmica espiral (Spiral Dynamics Optimization, SDO)
Algoritmos de otimização populacionais: otimização de dinâmica espiral (Spiral Dynamics Optimization, SDO)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Por favor, adicione links para a descrição de cada algoritmo na ordem do diagrama.
Mais uma vez, obrigado por compartilhar.
Adicione links para a descrição de cada algoritmo na ordem do diagrama.
Mais uma vez, obrigado por compartilhar.
Cometi um erro, a imagem da mesa colorida do artigo anterior foi substituída pela atual.
Após verificar a versão mais recente do artigo, a nova imagem estará disponível. No entanto, há uma tabela colorida real no arquivo e você pode dar uma olhada nela.
Aqui está ela: