Algoritmo de Fechadura Codificada (Code Lock Algorithm, CLA)
161
0
Conteúdo:
1.Introdução
2.Implementação do algoritmo
3.Resultados dos testes
1. Introdução
As fechaduras codificadas, também conhecidas como fechaduras digitais ou fechaduras de combinação, são mecanismos de segurança usados para controlar o acesso a locais, cofres, armários e outros objetos. Elas diferem das fechaduras comuns porque, em vez de usar uma chave, é necessário inserir uma combinação numérica específica para abri-las.
As fechaduras codificadas geralmente são equipadas com um teclado, cilindros especiais ou outros mecanismos rotativos, onde é necessário inserir uma sequência numérica correta para destravar a fechadura. Após a inserção da combinação correta, a fechadura codificada ativa o mecanismo que a destrava, permitindo abrir a porta ou acessar o conteúdo do cofre. O usuário pode definir seu próprio código ou usar o código fornecido para abrir a fechadura.
Vantagens das fechaduras codificadas:
- Segurança: as fechaduras codificadas podem proporcionar um alto nível de segurança, especialmente se os códigos forem trocados regularmente.
- Conveniência: não é necessário carregar chaves, o que torna as fechaduras codificadas convenientes de usar.
- Possibilidade de definir vários códigos: alguns modelos permitem a definição de diversos códigos para diferentes usuários ou para intervalos de tempo distintos.
As fechaduras codificadas são usadas em várias áreas, como segurança residencial, edifícios comerciais, hotéis, escolas, escritórios e outras instituições onde o controle de acesso é necessário. O uso de fechaduras codificadas no contexto de algoritmos de otimização pode representar uma ideia interessante. Uma das possíveis aplicações das fechaduras codificadas em algoritmos de otimização pode ser a criação de um sistema que utilize os princípios de funcionamento dessas fechaduras para resolver problemas de otimização, como a busca pelos valores ideais de parâmetros em problemas de aprendizado de máquina ou para resolver outras tarefas de otimização.
O princípio de funcionamento das fechaduras codificadas, baseado na inserção da combinação numérica correta para destravá-las, pode ser análogo aos mecanismos dos algoritmos de otimização, que tentam encontrar a solução ideal por meio da alteração iterativa de parâmetros e da avaliação de sua eficácia.
Por exemplo, podemos imaginar um algoritmo de otimização que usa a analogia com uma fechadura codificada da seguinte forma:
- Combinação como parâmetros: os parâmetros que precisam ser otimizados podem ser representados como uma "combinação" de valores de entrada.
- Verificação da combinação correta: o algoritmo pode alterar os valores dos parâmetros e avaliar sua eficácia, de forma semelhante ao usuário que insere várias combinações na fechadura para verificar sua correção.
- Solução ótima como desbloqueio: quando o algoritmo encontra os valores ótimos dos parâmetros, isso pode ser visto como o "desbloqueio" da solução ideal.
Dessa forma, as fechaduras codificadas me inspiraram a desenvolver um algoritmo de otimização que utiliza os princípios de seu funcionamento, que pode ser usado para encontrar soluções ótimas em várias tarefas, incluindo aprendizado de máquina e desenvolvimento de sistemas de trading.
2. Implementação do algoritmo
Vamos imaginar uma população de agentes como uma população de fechaduras, onde cada fechadura representa uma solução para o problema. A seguir, apresento um exemplo de pseudocódigo para o algoritmo da fechadura codificada:
1. Inicialização:
Criar um array de fechaduras de tamanho "popSize", onde cada fechadura possui conjuntos de discos "coords", e cada conjunto tem "lockDiscs" discos.
2. Ajuste das combinações das fechaduras:
Se for o primeiro passo, inicializar cada disco de cada conjunto de cada fechadura com um número aleatório entre 0 e 9.
Caso contrário, para cada fechadura:
- Se o número aleatório for menor que "copyProb", copiar o conjunto de discos de uma fechadura escolhida aleatoriamente.
- Caso contrário, para cada conjunto de discos:
- Se o número aleatório for menor que "rotateProb", definir o disco com um número aleatório entre 0 e 9.
- Caso contrário, copiar o disco de uma fechadura escolhida aleatoriamente.
3. Avaliação da qualidade das combinações das fechaduras:
Atualizar a qualidade da combinação de cada fechadura.
Encontrar a fechadura com a melhor combinação e atualizar a solução global, se necessário.
Copiar todas as fechaduras para um pool comum de fechaduras.
Ordenar o pool de fechaduras pela adaptabilidade.
4. Repetir os passos 2 e 3 pelo número especificado de épocas ou até que o critério de parada seja atingido.
O conceito é bastante empolgante, porém alguns aspectos ainda levantam questões. Em particular, não está totalmente claro como a combinação de códigos em uma fechadura pode representar uma solução para o problema. Para uma compreensão mais profunda, seria útil ter uma ilustração.
Assim, imagine que a solução de um problema, onde é necessário otimizar um ou mais parâmetros, é representada como uma fechadura codificada. Nesse caso, cada parâmetro pode ser representado como uma combinação de dígitos, onde cada dígito está localizado em um disco separado. O número de discos pode ser qualquer e é definido como um parâmetro externo do algoritmo. Assim, cada parâmetro é representado por um conjunto de discos com marcações numéricas.
Se, por exemplo, o parâmetro do problema tiver um conjunto de 9 discos, em cada um dos quais há números de 0 a 9, a combinação pode variar de 000000000 a 999999999. O número obtido na combinação é escalado para o intervalo de "min" a "max" do respectivo parâmetro. Assim, se tivermos, por exemplo, três parâmetros a serem otimizados, nossa fechadura terá 3 x 9 = 27 discos numéricos. A Figura 1 ilustra o mecanismo de codificação para um parâmetro.
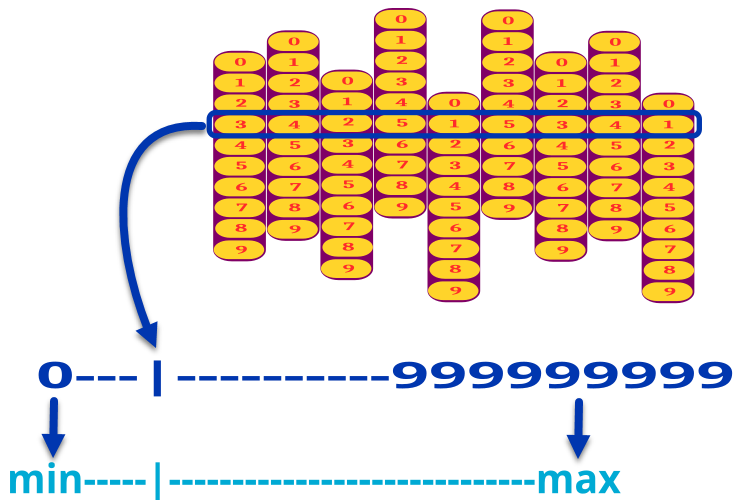
Figura 1. Decodificação do parâmetro do problema de um código numérico para um valor real
Os operadores em algoritmos de otimização, como crossover e mutação, podem ser integrados ao algoritmo de otimização CLA (Code Lock Algorithm), utilizando a ideia de uma fechadura codificada.
1. Crossover (Cruzamento). O crossover em algoritmos genéticos é utilizado para combinar o material genético de dois "pais" para gerar descendentes.
- No contexto das fechaduras codificadas, podemos imaginar o crossover como a combinação dos valores dos discos de diferentes fechaduras para criar uma nova combinação de parâmetros codificados do problema.
- Esse processo fornece ao algoritmo a capacidade de explorar novas combinações de parâmetros, de forma similar à maneira como o usuário pode experimentar diferentes combinações em uma fechadura e, ao mesmo tempo, reutilizar as combinações mais bem-sucedidas de dígitos em diferentes fechaduras.
2. Mutação (Mutation). A mutação em algoritmos genéticos refere-se à alteração aleatória do material genético para introduzir diversidade na população.
- No contexto das fechaduras codificadas, a mutação pode ser interpretada como uma rotação aleatória dos discos para qualquer número, alterando assim a combinação da fechadura.
- Esse processo ajuda o algoritmo a explorar novas combinações de parâmetros em todo o espaço de soluções, evitando ficar preso em ótimos locais.
De modo geral, a integração do crossover e da mutação no algoritmo de otimização pode aumentar a diversidade das soluções, acelerar a convergência para a solução ótima e ajudar a evitar uma convergência prematura. Tal abordagem pode ser útil em problemas de otimização com grandes espaços de busca e funções-objetivo complexas. Aliás, não temos outra escolha senão girar os discos, utilizando a analogia com os operadores genéticos.
Para resolver o problema, é necessário encontrar a combinação correta de números na fechadura codificada. Precisamos girar os discos até encontrar a combinação certa que abrirá a fechadura. Ao contrário dos algoritmos genéticos, onde ao "girar" o valor de um código binário nos genes a probabilidade é de 50/50 (ou 0 ou 1), no algoritmo da fechadura codificada podemos usar distribuições de probabilidade na estratégia de rotação dos discos. Vamos considerar algumas opções.
Podemos utilizar uma distribuição Gaussiana, onde os parâmetros da combinação são submetidos a mutações, com cada parâmetro alterado por um valor aleatório retirado de uma distribuição normal (Gaussiana). Isso permitirá introduzir algumas mudanças aleatórias nos parâmetros, mantendo, ao mesmo tempo, o valor atual em certa medida.
A aplicação da distribuição Gaussiana para mutação pode ser útil porque permite controlar o grau de alteração dos parâmetros. Os parâmetros podem ser modificados por valores pequenos, próximos dos atuais, o que ajuda a preservar as boas propriedades da solução atual, enquanto o caráter aleatório da mutação permite que o algoritmo explore novas áreas no espaço de busca.
Dessa forma, o uso da distribuição Gaussiana para mutação pode ajudar a equilibrar a exploração de novas soluções com a preservação das boas propriedades das soluções atuais, promovendo uma busca eficiente pela solução ótima em espaços de parâmetros complexos.
Também podemos utilizar a distribuição de potência no processo de mutação. Ao contrário da distribuição Gaussiana, a distribuição de potência possui caudas mais pesadas, o que significa que grandes mudanças nos parâmetros podem ocorrer com maior probabilidade, o que pode ser útil em casos onde uma exploração mais radical do espaço de parâmetros é necessária. A distribuição de potência pode ajudar o algoritmo a "escapar" de armadilhas locais.
Podemos também tentar usar uma terceira opção – a distribuição uniforme, na qual há uma probabilidade igual de escolher qualquer número no disco da fechadura.
Agora podemos passar da parte teórica para a escrita de código e investigações práticas.
No algoritmo CLA, o agente que representa a solução do problema será descrito pela estrutura "S_CLA_Agent". Aqui estão seus componentes principais:
- f – Esta variável armazena o valor de adaptabilidade do agente. Ela é inicializada como -DBL_MAX, o que significa o menor valor possível para o tipo double.
- struct S_Lock – Esta é uma estrutura aninhada, que contém o array "lock". Este array é utilizado para armazenar a combinação codificada de um parâmetro otimizado específico do problema.
- S_Lock code [] – Este é o array de estruturas "S_Lock". Todo esse array representa a "fechadura".
- void Init (int coords, int lockDiscs) – Esta é uma função de inicialização. Ela recebe dois parâmetros: "coords" – que define o número de conjuntos de parâmetros, e "lockDiscs" – que define o número de discos em cada conjunto. Dentro desta função, ocorre a inicialização do array "code".
No geral, essa estrutura representa o agente do algoritmo de otimização CLA. Cada agente tem sua própria adaptabilidade e descrição da combinação da "fechadura", que serão otimizadas durante a execução do algoritmo.
//—————————————————————————————————————————————————————————————————————————————— struct S_CLA_Agent { double f; //fitness struct S_Lock { int lock []; }; S_Lock code []; void Init (int coords, int lockDiscs) { f = -DBL_MAX; ArrayResize (code, coords); for (int i = 0; i < coords; i++) { ArrayResize (code [i].lock, lockDiscs); } } }; //——————————————————————————————————————————————————————————————————————————————
Agora, vamos descrever a classe "C_AO_CLA", que deriva da classe "C_AO". Seus componentes principais são:
- C_AO_CLA () – O construtor da classe, que inicializa o objeto da classe. Dentro deste construtor, são inicializados parâmetros como "popSize", "lockDiscs", "copyProb", "rotateProb" e "params"".
- SetParams () – Função que define os parâmetros do algoritmo com base nos valores do array "params".
- Init () – Função de inicialização, que recebe os intervalos de busca e o número de épocas como parâmetros.
- Moving (), Revision () – São funções utilizadas para executar a lógica principal do algoritmo.
- lockDiscs, copyProb, rotateProb – Variáveis que armazenam os parâmetros do algoritmo.
- S_CLA_Agent agent [] – Um array de agentes, cada um dos quais representa um objeto da estrutura "S_CLA_Agent".
- maxLockNumber, S_CLA_Agent parents [], S_CLA_Agent parTemp [] – Variáveis e arrays privados que são utilizados dentro da classe.
- ArrayToNumber (), LockToDouble () – Métodos privados usados para converter o array da combinação codificada em um número e a fechadura em um número com ponto flutuante, respectivamente.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_CLA : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_CLA () { } C_AO_CLA () { ao_name = "CLA"; ao_desc = "Code Lock Algorithm"; ao_link = "https://www.mql5.com/ru/articles/14878"; popSize = 100; //population size lockDiscs = 8; //lock discs copyProb = 0.8; //copying probability rotateProb = 0.03; //rotate disc probability ArrayResize (params, 4); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "lockDiscs"; params [1].val = lockDiscs; params [2].name = "copyProb"; params [2].val = copyProb; params [3].name = "rotateProb"; params [3].val = rotateProb; } void SetParams () { popSize = (int)params [0].val; lockDiscs = (int)params [1].val; copyProb = params [2].val; rotateProb = params [3].val; } bool Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0); //number of epochs void Moving (); void Revision (); void Injection (const int popPos, const int coordPos, const double value); //---------------------------------------------------------------------------- int lockDiscs; //lock discs double copyProb; //copying probability double rotateProb; //rotate disc probability S_CLA_Agent agent []; private: //------------------------------------------------------------------- int maxLockNumber; //max lock number S_CLA_Agent parents []; S_CLA_Agent parTemp []; int ArrayToNumber (int &arr []); double LockToDouble (int lockNum, int coordPos); }; //——————————————————————————————————————————————————————————————————————————————
Definimos o método "Init" na classe "C_AO_CLA". Esse método inicializa o algoritmo com os intervalos de busca e o número de épocas especificados. Descrição de cada etapa:
1. if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; – chama a função StandardInit com os intervalos de busca definidos. Se a inicialização falhar, a função retorna false.
2. ArrayResize (agent, popSize); – esta linha altera o tamanho do array agent para o tamanho da população "popSize".
3. for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs); – o laço inicializa cada agente da população com o número de coordenadas "coords" e discos de fechadura "lockDiscs" definidos.
4. ArrayResize (parents, popSize * 2); ArrayResize<2>} (parTemp, popSize * 2); – estas linhas redimensionam os arrays "parents" e "parTemp" para o dobro do tamanho da população.
5. for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs); parTemp<2>} [i].Init<3>} (coords, lockDiscs); } – o laço inicializa cada pai e pai temporário nos arrays "parents" e "parTemp".
6. maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); } – o laço calcula o número máximo de combinações da fechadura "maxLockNumber<2>}", utilizando o número de discos da fechadura "lockDiscs<3>}".
7. return true; – se todas as operações anteriores forem bem-sucedidas, a função retorna true.
Essa função inicializa os agentes e pais no algoritmo de otimização, usando fechaduras codificadas CLA, e define o número máximo de combinações da fechadura com base na quantidade de discos.
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_CLA::Init (const double &rangeMinP [], //minimum search range const double &rangeMaxP [], //maximum search range const double &rangeStepP [], //step search const int epochsP = 0) //number of epochs { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- ArrayResize (agent, popSize); for (int i = 0; i < popSize; i++) agent [i].Init (coords, lockDiscs); ArrayResize (parents, popSize * 2); ArrayResize (parTemp, popSize * 2); for (int i = 0; i < popSize * 2; i++) { parents [i].Init (coords, lockDiscs); parTemp [i].Init (coords, lockDiscs); } maxLockNumber = 0; for (int i = 0; i < lockDiscs; i++) { maxLockNumber += 9 * (int)pow (10, i); } return true; } //——————————————————————————————————————————————————————————————————————————————
O processo de ajuste das combinações numéricas nas fechaduras será descrito no método "Moving" na classe "C_AO_CLA". O processo é o seguinte:
- val = 0.0; code<2>} = 0; pos <3>} = 0; – inicializa as variáveis que serão usadas no método.
- if (!revision) {...} – o bloco de código é executado se "revision" for false. Dentro desse bloco, os agentes e os pais são inicializados com valores aleatórios.
- Em seguida, para cada agente e pai, são calculados os valores "code" e "val<3>}", usados para atualizar as coordenadas do agente. Depois disso, "revision" é definido como true, e a função é finalizada.
- for (int i = 0; i < popSize; i++) {...} – o bloco de código é executado se "revision" for true. Dentro desse bloco, os agentes são atualizados. Se o número aleatório for menor que "copyProb", o código da fechadura de um dos pais é copiado para o agente. Caso contrário, o código da fechadura do agente é atualizado com um valor aleatório ou com o código de um dos pais.
- Em seguida, para cada agente, são calculados os valores "code" e "val<2>}", usados para atualizar as coordenadas do agente.
Essa função é usada para atualizar os agentes no algoritmo de otimização CLA.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CLA::Moving () { double val = 0.0; int code = 0; int pos = 0; //---------------------------------------------------------------------------- if (!revision) { for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { for (int l = 0; l < lockDiscs; l++) { agent [i].code [c].lock [l] = u.RNDminusOne (10); } code = ArrayToNumber (agent [i].code [c].lock); val = LockToDouble (code, c); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } } for (int i = 0; i < popSize * 2; i++) { for (int c = 0; c < coords; c++) { for (int l = 0; l < lockDiscs; l++) { parents [i].code [c].lock [l] = u.RNDminusOne (10); } } } revision = true; return; } //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { if (u.RNDprobab () < copyProb) { int pos = u.RNDminusOne (popSize); ArrayCopy (agent [i].code [c].lock, parents [pos].code [c].lock, 0, 0, WHOLE_ARRAY); } else { for (int l = 0; l < lockDiscs; l++) { if (u.RNDprobab () < rotateProb) { //pos = u.RNDminusOne (popSize); //agent [i].code [c].lock [l] = (int)round (u.GaussDistribution (agent [i].codePrev [c].lock [l], 0, 9, 8)); //agent [i].code [c].lock [l] = (int)round (u.PowerDistribution (agent [i].codePrev [c].lock [l], 0, 9, 20)); agent [i].code [c].lock [l] = u.RNDminusOne (10); } else { pos = u.RNDminusOne (popSize); agent [i].code [c].lock [l] = parents [pos].code [c].lock [l]; } } } code = ArrayToNumber (agent [i].code [c].lock); val = LockToDouble (code, c); a [i].c [c] = u.SeInDiSp (val, rangeMin [c], rangeMax [c], rangeStep [c]); } } } //——————————————————————————————————————————————————————————————————————————————O método "Revision" na classe "C_AO_CLA" é projetado para atualizar a solução global. Ele realiza as seguintes ações:
- ind = -1; – inicializa a variável "ind", que será usada para rastrear o índice do agente com a melhor aptidão.
- for (int i = 0; i < popSize; i++) {...} – o loop percorre cada agente na população e verifica se a aptidão do agente é maior que o valor atual da melhor aptidão "fB". Se for, "fB" é atualizado e "ind" é definido para o índice atual.
- if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); – se for encontrado um agente com melhor aptidão, suas coordenadas são copiadas para "cB".
- for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; } – o loop atualiza a aptidão de cada agente com base nos valores atuais do array "a".
- for (int i = 0; i < popSize; i++) { parents [i + popSize] = agent [i]; } – o loop copia cada agente para o array "parents", começando da posição "popSize", ou seja, na segunda metade da população de pais.
- u.Sorting (parents, parTemp, popSize * 2); – essa linha classifica o array "parents" usando o array "parTemp" como armazenamento temporário.
//—————————————————————————————————————————————————————————————————————————————— void C_AO_CLA::Revision () { //---------------------------------------------------------------------------- int ind = -1; for (int i = 0; i < popSize; i++) { if (a [i].f > fB) { fB = a [i].f; ind = i; } } if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY); //---------------------------------------------------------------------------- for (int i = 0; i < popSize; i++) { agent [i].f = a [i].f; } for (int i = 0; i < popSize; i++) { parents [i + popSize] = agent [i]; } u.Sorting (parents, parTemp, popSize * 2); } //——————————————————————————————————————————————————————————————————————————————
O método "ArrayToNumber" é usado para converter combinações de código de fechaduras em um número. As ações do método são:
- result = 0; – inicializa a variável que será usada para armazenar o resultado.
- for (int i = 0; i < ArraySize (arr); i++) {...} – o loop percorre cada elemento do array "arr". Para cada elemento "arr"[i]", o valor atual de "result" é multiplicado por 10 e o valor de "arr"[i] é adicionado.
- return result; – a linha retorna o valor final de "result".
Em suma, esse método converte um array de números inteiros em um único número, interpretando cada elemento do array como um dígito na representação decimal.
Por exemplo, se o array de entrada "arr" (combinação de código) for: |0|3|1|5|7|0|. Precisamos descartar todos os zeros à esquerda da combinação e começar a formar o número a partir do 3. O resultado seria o número 31570. Se todas as células do array na combinação contiverem zeros, o resultado será 0.
//—————————————————————————————————————————————————————————————————————————————— int C_AO_CLA::ArrayToNumber (int &arr []) { int result = 0; for (int i = 0; i < ArraySize (arr); i++) { result = result * 10 + arr [i]; } return result; } //——————————————————————————————————————————————————————————————————————————————
O método "LockToDouble" na classe "C_AO_CLA" é usado para converter um número de código de fechadura para a escala de um parâmetro otimizado. Veja o que ele faz:
- LockToDouble (int lockNum, int coordPos) – o método recebe dois parâmetros: "lockNum", que representa o número da fechadura, e "coordPos", que representa a posição da coordenada no array de coordenadas (parâmetro a ser otimizado).
- return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); – a linha retorna o valor que resulta ao escalar "lockNum" do intervalo [0, maxLockNumber] para o intervalo [rangeMin [coordPos], rangeMax<6>} [coordPos]].
Em resumo, este método é utilizado para converter o número da fechadura em um valor de ponto flutuante com base no intervalo especificado, ou seja, os números da fechadura são transformados em valores dos parâmetros otimizáveis do problema.
//—————————————————————————————————————————————————————————————————————————————— double C_AO_CLA::LockToDouble (int lockNum, int coordPos) { return u.Scale (lockNum, 0, maxLockNumber, rangeMin [coordPos], rangeMax [coordPos]); } //——————————————————————————————————————————————————————————————————————————————
3. Resultados dos testes
Os resultados da execução do algoritmo de otimização CLA em funções de teste são excelentes. Alcançar 67,86% do valor máximo possível é um resultado impressionante. Isso demonstra o alto desempenho do algoritmo CLA na otimização de funções complexas.
Esses resultados mostram que o CLA é bastante eficaz e pode ser aplicado com sucesso em várias tarefas que exigem a otimização de funções multidimensionais. Sua escalabilidade e capacidade de lidar com problemas complexos o tornam uma ferramenta promissora para resolver uma ampla gama de problemas de otimização.
CLA|Code Lock Algorithm|100.0|8.0|0.8|0.03|
=============================
5 Hilly's; Func runs: 10000; result: 0.9534490932631814
25 Hilly's; Func runs: 10000; result: 0.8710742215971827
500 Hilly's; Func runs: 10000; result: 0.375900385878165
=============================
5 Forest's; Func runs: 10000; result: 0.9894215656296362
25 Forest's; Func runs: 10000; result: 0.917091907561472
500 Forest's; Func runs: 10000; result: 0.3164221021938828
=============================
5 Megacity's; Func runs: 10000; result: 0.7969230769230768
25 Megacity's; Func runs: 10000; result: 0.693846153846154
500 Megacity's; Func runs: 10000; result: 0.19303076923077062
=============================
All score: 6.10716 (67.86%)
Nas visualizações do desempenho do algoritmo em funções de teste, observa-se uma dispersão dos resultados em funções de baixa dimensionalidade, no entanto, com o aumento do número de parâmetros do problema, a dispersão diminui. Além disso, o potencial do algoritmo em problemas de alta dimensionalidade (1000 parâmetros) é evidente na forma da curva de convergência (linha vermelha), que cresce de forma acelerada. Se o limite de execuções da função de fitness fosse removido (conforme as regras de nossos testes), o algoritmo continuaria a se aproximar do ótimo global.
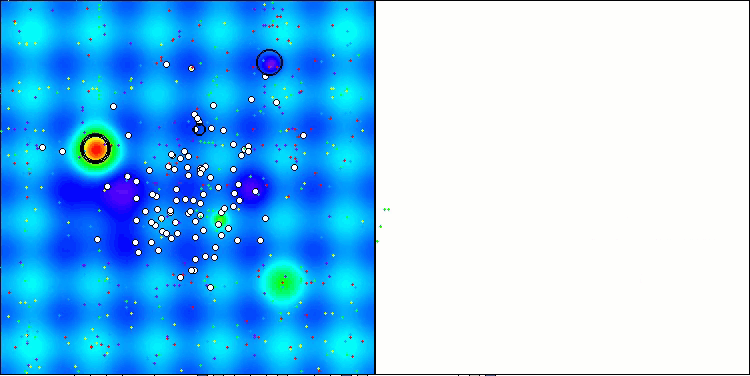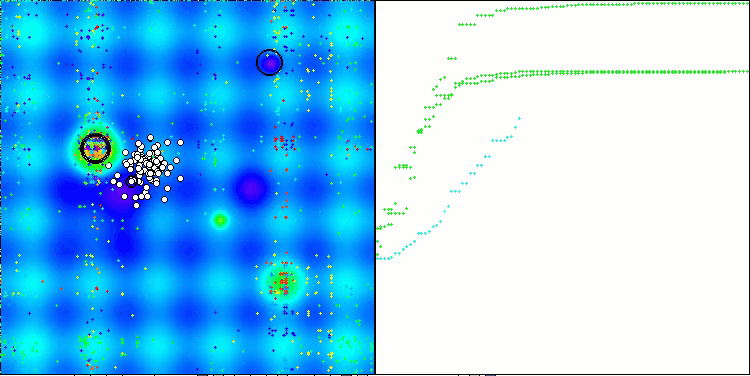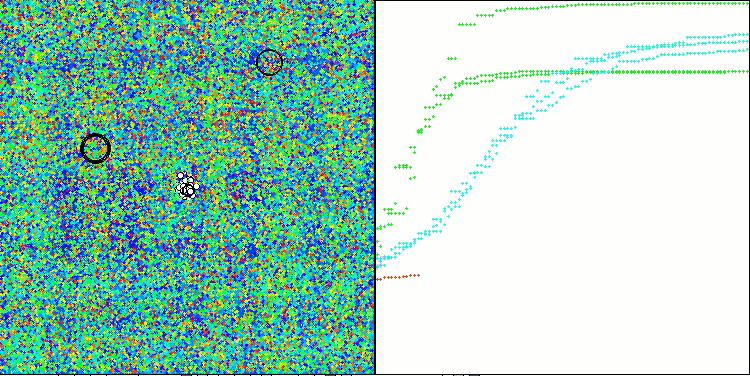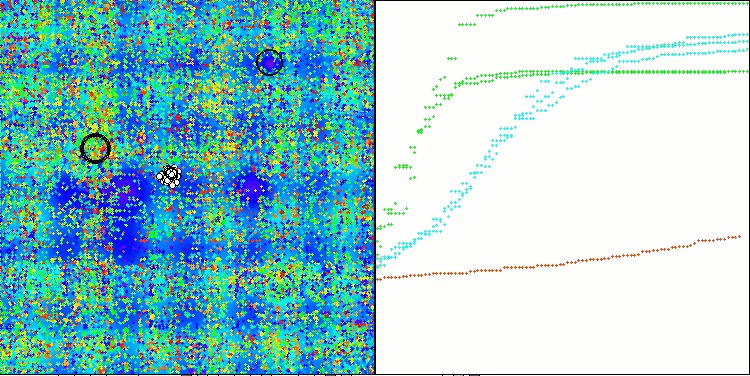
CLA na função de teste Hilly.
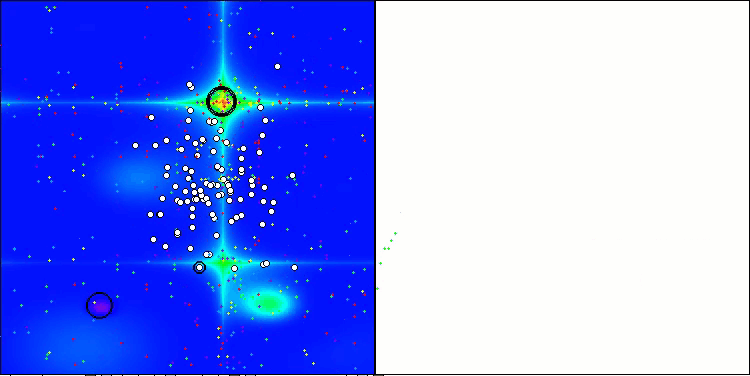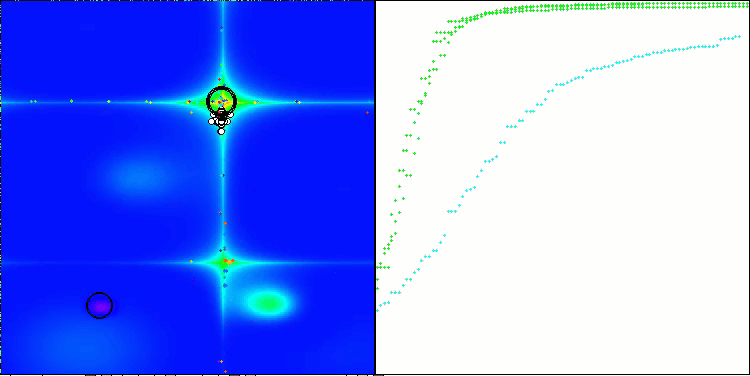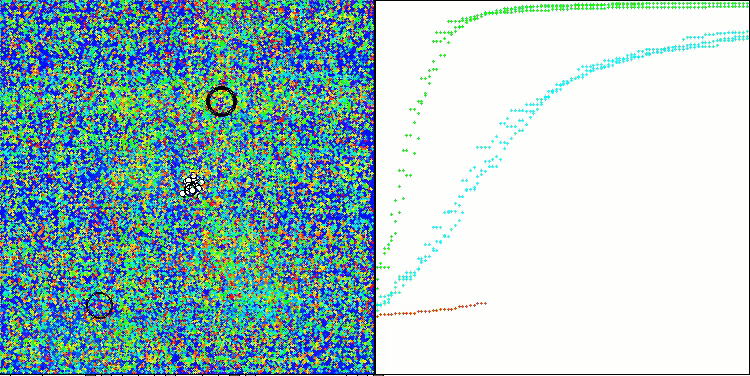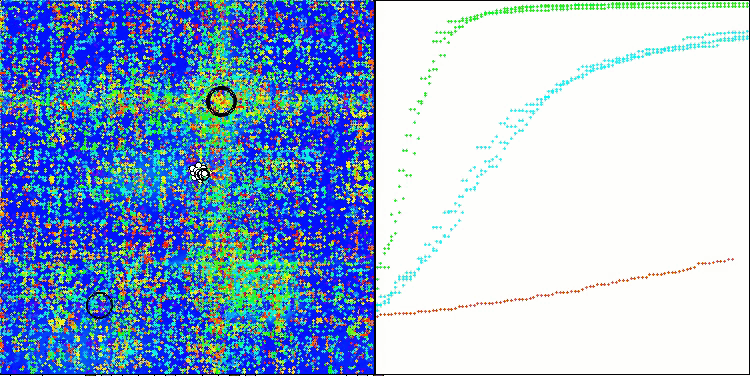
CLA na função de teste Forest.
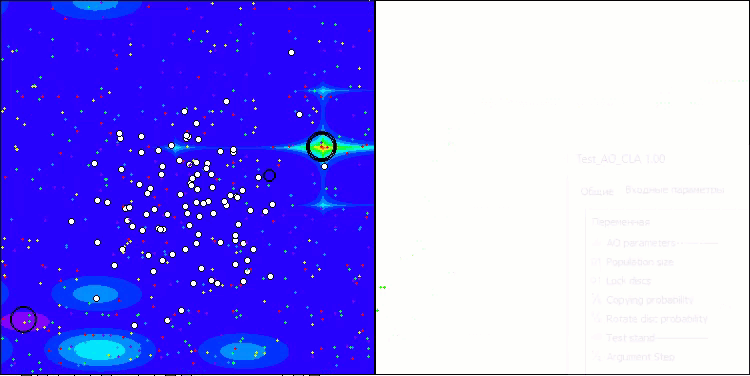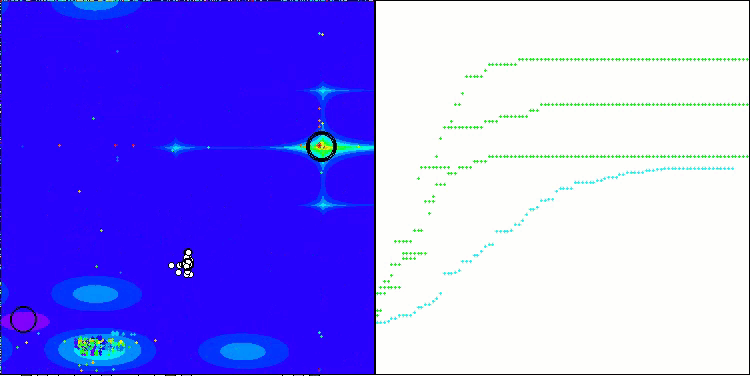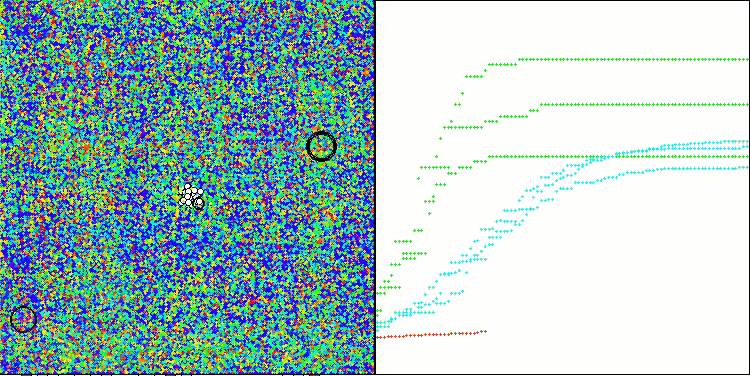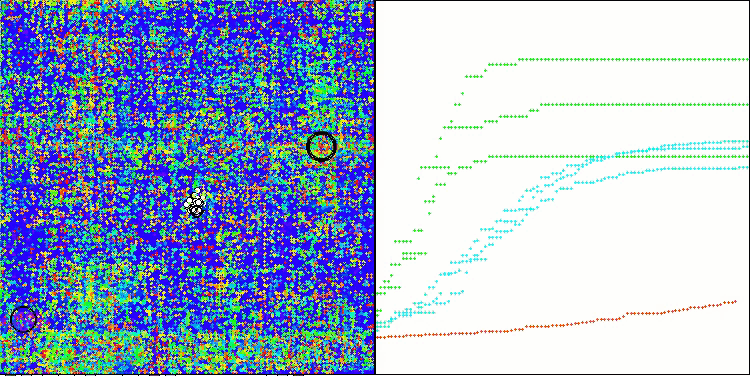
CLA na função de teste Megacity.
O algoritmo de fechadura codificada ficou em segundo lugar no ranking. Na função aguda Forest com 10 parâmetros, o CLA conseguiu até mesmo superar o líder do ranking, o BGA. A coloração verde das células de resultados em todas as funções de teste (em comparação com os demais algoritmos no ranking) indica uma performance muito consistente em diferentes tipos de problemas, sem falhas notáveis em testes individuais.
| № | AO | Description | Hilly | Hilly final | Forest | Forest final | Megacity (discrete) | Megacity final | Final result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | BGA | binary genetic algorithm | 0,99989 | 0,99518 | 0,42835 | 2,42341 | 0,96153 | 0,96181 | 0,32027 | 2,24360 | 0,91385 | 0,95908 | 0,24220 | 2,11512 | 6,782 | 75,36 |
| 2 | CLA | code lock algorithm | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 4 | CTA | comet tail algorithm | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 5 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 6 | ESG | evolution of social groups | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 7 | SIA | simulated isotropic annealing | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 8 | TSEA | turtle shell evolution algorithm | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 9 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 10 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 11 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 12 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 13 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 14 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 15 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 16 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 17 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 18 | MEC | mind evolutionary computation | 0,69533 | 0,53376 | 0,32661 | 1,55569 | 0,72464 | 0,33036 | 0,07198 | 1,12698 | 0,52500 | 0,22000 | 0,04198 | 0,78698 | 3,470 | 38,55 |
| 19 | IWO | invasive weed optimization | 0,72679 | 0,52256 | 0,33123 | 1,58058 | 0,70756 | 0,33955 | 0,07484 | 1,12196 | 0,42333 | 0,23067 | 0,04617 | 0,70017 | 3,403 | 37,81 |
| 20 | Micro-AIS | micro artificial immune system | 0,79547 | 0,51922 | 0,30861 | 1,62330 | 0,72956 | 0,36879 | 0,09398 | 1,19233 | 0,37667 | 0,15867 | 0,02802 | 0,56335 | 3,379 | 37,54 |
| 21 | COAm | cuckoo optimization algorithm M | 0,75820 | 0,48652 | 0,31369 | 1,55841 | 0,74054 | 0,28051 | 0,05599 | 1,07704 | 0,50500 | 0,17467 | 0,03380 | 0,71347 | 3,349 | 37,21 |
| 22 | SDOm | spiral dynamics optimization M | 0,74601 | 0,44623 | 0,29687 | 1,48912 | 0,70204 | 0,34678 | 0,10944 | 1,15826 | 0,42833 | 0,16767 | 0,03663 | 0,63263 | 3,280 | 36,44 |
| 23 | NMm | Nelder-Mead method M | 0,73807 | 0,50598 | 0,31342 | 1,55747 | 0,63674 | 0,28302 | 0,08221 | 1,00197 | 0,44667 | 0,18667 | 0,04028 | 0,67362 | 3,233 | 35,92 |
| 24 | FAm | firefly algorithm M | 0,58634 | 0,47228 | 0,32276 | 1,38138 | 0,68467 | 0,37439 | 0,10908 | 1,16814 | 0,28667 | 0,16467 | 0,04722 | 0,49855 | 3,048 | 33,87 |
| 25 | GSA | gravitational search algorithm | 0,64757 | 0,49197 | 0,30062 | 1,44016 | 0,53962 | 0,36353 | 0,09945 | 1,00260 | 0,32667 | 0,12200 | 0,01917 | 0,46783 | 2,911 | 32,34 |
| 26 | BFO | bacterial foraging optimization | 0,61171 | 0,43270 | 0,31318 | 1,35759 | 0,54410 | 0,21511 | 0,05676 | 0,81597 | 0,42167 | 0,13800 | 0,03195 | 0,59162 | 2,765 | 30,72 |
| 27 | ABC | artificial bee colony | 0,63377 | 0,42402 | 0,30892 | 1,36671 | 0,55103 | 0,21874 | 0,05623 | 0,82600 | 0,34000 | 0,14200 | 0,03102 | 0,51302 | 2,706 | 30,06 |
| 28 | BA | bat algorithm | 0,59761 | 0,45911 | 0,35242 | 1,40915 | 0,40321 | 0,19313 | 0,07175 | 0,66810 | 0,21000 | 0,10100 | 0,03517 | 0,34617 | 2,423 | 26,93 |
| 29 | SA | simulated annealing | 0,55787 | 0,42177 | 0,31549 | 1,29513 | 0,34998 | 0,15259 | 0,05023 | 0,55280 | 0,31167 | 0,10033 | 0,02883 | 0,44083 | 2,289 | 25,43 |
| 30 | IWDm | intelligent water drops M | 0,54501 | 0,37897 | 0,30124 | 1,22522 | 0,46104 | 0,14704 | 0,04369 | 0,65177 | 0,25833 | 0,09700 | 0,02308 | 0,37842 | 2,255 | 25,06 |
| 31 | PSO | particle swarm optimisation | 0,59726 | 0,36923 | 0,29928 | 1,26577 | 0,37237 | 0,16324 | 0,07010 | 0,60572 | 0,25667 | 0,08000 | 0,02157 | 0,35823 | 2,230 | 24,77 |
| 32 | Boids | boids algorithm | 0,43340 | 0,30581 | 0,25425 | 0,99346 | 0,35718 | 0,20160 | 0,15708 | 0,71586 | 0,27846 | 0,14277 | 0,09834 | 0,51957 | 2,229 | 24,77 |
| 33 | MA | monkey algorithm | 0,59107 | 0,42681 | 0,31816 | 1,33604 | 0,31138 | 0,14069 | 0,06612 | 0,51819 | 0,22833 | 0,08567 | 0,02790 | 0,34190 | 2,196 | 24,40 |
| 34 | SFL | shuffled frog-leaping | 0,53925 | 0,35816 | 0,29809 | 1,19551 | 0,37141 | 0,11427 | 0,04051 | 0,52618 | 0,27167 | 0,08667 | 0,02402 | 0,38235 | 2,104 | 23,38 |
| 35 | FSS | fish school search | 0,55669 | 0,39992 | 0,31172 | 1,26833 | 0,31009 | 0,11889 | 0,04569 | 0,47467 | 0,21167 | 0,07633 | 0,02488 | 0,31288 | 2,056 | 22,84 |
| 36 | RND | random | 0,52033 | 0,36068 | 0,30133 | 1,18234 | 0,31335 | 0,11787 | 0,04354 | 0,47476 | 0,25333 | 0,07933 | 0,02382 | 0,35648 | 2,014 | 22,37 |
| 37 | GWO | grey wolf optimizer | 0,59169 | 0,36561 | 0,29595 | 1,25326 | 0,24499 | 0,09047 | 0,03612 | 0,37158 | 0,27667 | 0,08567 | 0,02170 | 0,38403 | 2,009 | 22,32 |
| 38 | CSS | charged system search | 0,44252 | 0,35454 | 0,35201 | 1,14907 | 0,24140 | 0,11345 | 0,06814 | 0,42299 | 0,18333 | 0,06300 | 0,02322 | 0,26955 | 1,842 | 20,46 |
| 39 | EM | electroMagnetism-like algorithm | 0,46250 | 0,34594 | 0,32285 | 1,13129 | 0,21245 | 0,09783 | 0,10057 | 0,41085 | 0,15667 | 0,06033 | 0,02712 | 0,24412 | 1,786 | 19,85 |
Considerações finais
O algoritmo genético binário (BGA) desempenhou um papel importante na concepção do algoritmo CLA. Meu objetivo era desenvolver um algoritmo mais rápido. Foi então que tive a ideia de substituir a codificação binária pela decimal, e o mecanismo das fechaduras codificadas serviu como protótipo para a criação do algoritmo, o que se mostrou uma decisão bem-sucedida. O CLA opera de maneira mais rápida que o BGA, competindo com ele em termos de eficiência. Além disso, a codificação decimal permite o uso de vários tipos de distribuições ao gerar combinações numéricas, o que pode ser útil para certas tarefas (no código, as distribuições normal e de potência estão comentadas e podem ser utilizadas se necessário). Os experimentos demonstraram que o uso de uma distribuição uniforme simples foi mais eficaz neste caso.
Podemos resumir o que foi dito: o algoritmo de fechadura codificada (CLA) mostrou excelentes resultados, estabilidade e eficiência em todas as funções de teste. Isso evidencia a grande escalabilidade do algoritmo, sua capacidade de lidar com problemas complexos, e destaca a flexibilidade e o potencial do CLA em diferentes cenários de otimização.
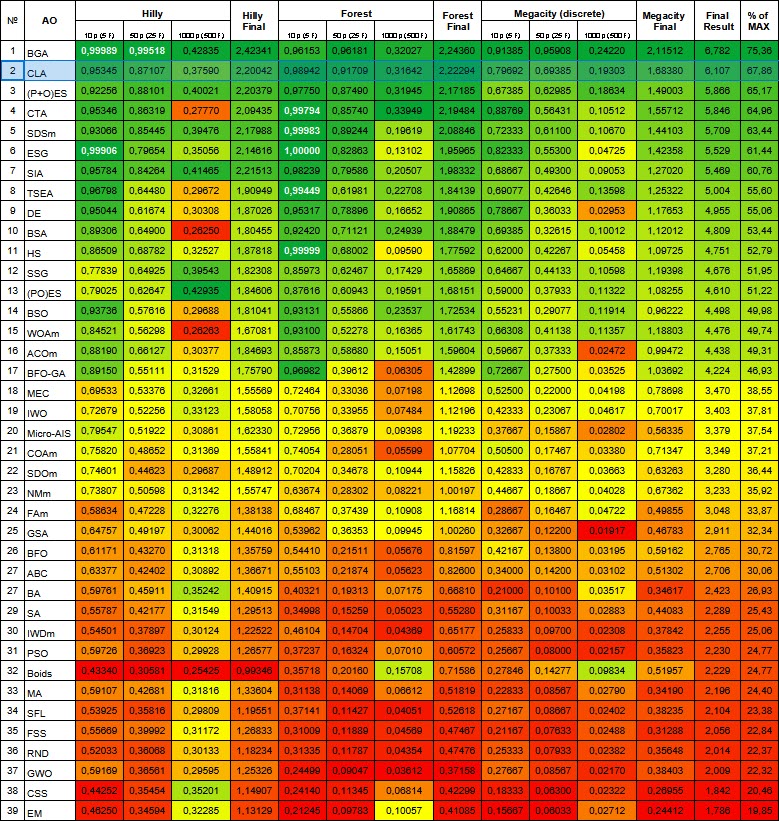
Figura 2. Graduação de cores dos algoritmos em testes correspondentes. Resultados maiores ou iguais a 0,99 estão destacados em branco.
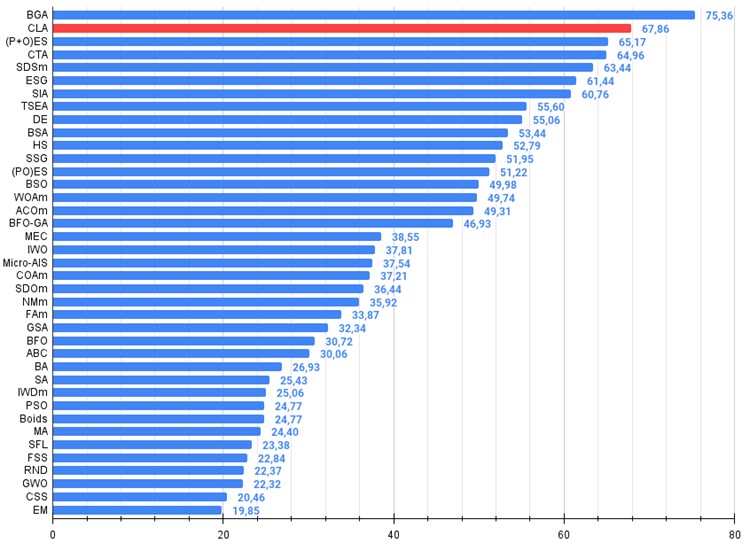
Figura 3. Histograma dos resultados dos testes dos algoritmos (em uma escala de 0 a 100, onde quanto maior, melhor,
e 100 é o resultado máximo teoricamente possível, o script para cálculo do ranking está no arquivo)
Pontos positivos e negativos do algoritmo de fechadura codificada (CLA):
Pontos positivos:
- 1. Excelente convergência em diferentes tipos de funções.
- 2. Implementação simples.
Pontos negativos:
- 1. Dispersão dos resultados em funções de baixa dimensionalidade.
Um arquivo com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela exatidão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar suas capacidades de busca. As conclusões e julgamentos apresentados no artigo são baseadas nos resultados dos experimentos realizados.
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/14878
Desenvolvendo um EA multimoeda (Parte 12): Gerenciamento de Risco como em empresas de prop trading
Redes neurais de maneira fácil (Parte 91): previsão na área de frequência (FreDF)
Desenvolvimento de robô em Python e MQL5 (Parte 2): Escolha do modelo, criação e treinamento, testador customizado Python
Desenvolvendo um EA multimoeda (Parte 11): Início da automação do processo de otimização
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso