
Otimização baseada em biogeografia — Biogeography-Based Optimization (BBO)
Conteúdo
Introdução
Ao revisar alguns algoritmos de otimização, chamou-me a atenção o algoritmo de otimização biogeográfica (BBO), desenvolvido pelo professor Dan Simon em 2008. O BBO se inspira na biogeografia, ciência que estuda a distribuição geográfica dos organismos biológicos. Modelos matemáticos que descrevem a distribuição de espécies foram desenvolvidos pela primeira vez na década de 1960. Assim como os algoritmos genéticos se inspiraram na genética biológica e as redes neurais, nos neurônios biológicos, o BBO utiliza princípios matemáticos da biogeografia para resolver problemas de otimização.
Na natureza, ilhas de arquipélagos com condições favoráveis, ou seja, com alto índice de adequação do habitat (HSI), possuem grande quantidade de espécies e alta emigração, ao passo que ilhas com condições ruins possuem poucas espécies e alta imigração. Essa dinâmica natural de migração de espécies entre ilhas serviu de base para o mecanismo de otimização do BBO. O algoritmo utiliza o conceito de migração de espécies para trocar características entre soluções. A probabilidade de mutação é baseada em um modelo teórico de distribuição de espécies. Além disso, as boas soluções compartilham ativamente suas características, mas permanecem resistentes a mudanças. Esse diferencial é a principal característica do algoritmo.
Neste artigo, analisaremos a elegante concepção do algoritmo BBO, um método simples e eficiente para resolver tarefas de otimização. Realizaremos sua implementação em código e observaremos e avaliaremos os resultados de seu funcionamento.
Implementação do algoritmo
Imagine arquipélagos de ilhas, onde em cada ilha vivem diferentes espécies de animais.
1. Habitat (Habitat) = Ilha = Solução do problema. Cada ilha em nosso algoritmo representa uma possível solução. Se você tem 50 ilhas, então você tem 50 soluções diferentes.
2. HSI (Habitat Suitability Index) = Adequação da ilha para a vida = Qualidade da solução. Uma ilha rica, com água doce, frutas e bom clima = Boa solução (HSI alto). Uma ilha desértica sem água = Solução ruim (HSI baixo).
3. Espécies (Species) = Características da solução. Em uma ilha rica vivem muitas espécies de animais. Em uma ilha pobre há poucas espécies, pois ela não é diversa.
Como funciona a migração? Exemplo da vida real: Havaí (ilha rica), muitas espécies → animais frequentemente nadam/voam para outras ilhas (alta emigração), mas poucos chegam (baixa imigração, pois a ilha já está lotada). Ilha desabitada: poucas espécies → animais raramente vão embora (baixa emigração), mas novos chegam com frequência (alta imigração, há muito espaço livre).
No algoritmo: Solução ruim (poucas espécies) → Alta imigração → recebe características de boas soluções. Boa solução (muitas espécies) → Alta emigração → compartilha características com outras.
Outro exemplo da vida real: digamos que estamos buscando a melhor localização de uma loja na cidade. Cada "ilha" é uma opção de localização. Criamos 50 localizações aleatórias (ilhas), das quais:
Ilha 1: local ruim, periferia
Ilha 2: local excelente, centro
Ilha 50: local medianamente bom
Avaliamos cada localização (HSI): Ilha 2 (centro): HSI = 95 (muitos clientes, boa acessibilidade), Ilha 1 (periferia): HSI = 20 (poucos clientes); então a Ilha 1 (ruim) tem alta imigração e ela "recebe" algumas características da Ilha 2 (boa). Por exemplo, se a Ilha 2 fica "perto do metrô", então a Ilha 1 também tentará encontrar um local perto do metrô. Às vezes podem ocorrer "catástrofes" (terremotos, tsunamis), quando a solução muda aleatoriamente, isto é, a loja "salta" para um lugar totalmente novo, e esse deslocamento ajuda a encontrar soluções inesperadamente boas.
Por que as soluções médias sofrem mutação com menos frequência? Na natureza, ilhas muito ricas (como as Galápagos) são raras e instáveis; ao mesmo tempo, ilhas muito pobres também são raras e instáveis; já as ilhas médias são as mais comuns e estáveis. No algoritmo, isso significa:
Soluções muito boas (HSI = 95): alta probabilidade de mutação
Soluções muito ruins (HSI = 5): alta probabilidade de mutação
Soluções médias (HSI = 50): baixa probabilidade de mutação
As 2 melhores ilhas (soluções) são protegidas de mudanças, esses são nossos "reservas". Não queremos perder as melhores soluções encontradas! Então, o processo final de otimização: criamos 50 soluções aleatórias (ilhas), ordenamos por qualidade (das melhores para as piores); em seguida, soluções ruins aprendem com as boas, e algumas soluções mudam aleatoriamente. Assim, o BBO imita o processo natural de distribuição de espécies entre ilhas para buscar a solução ótima. Abaixo está apresentada uma ilustração do funcionamento do algoritmo.
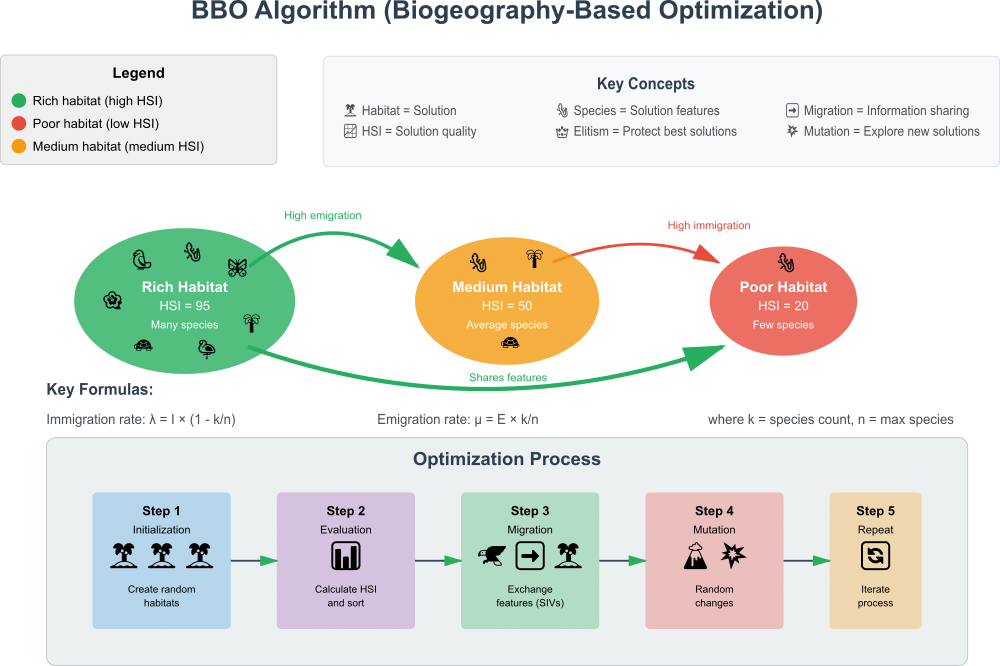
Figura 1. Ilustração do funcionamento do algoritmo BBO
De acordo com o esquema da figura 1, que mostra visualmente:
- Três tipos de ilhas— (rica, média, pobre) com diferentes quantidades de espécies
- Processo de migração — setas mostram como as espécies se movem entre as ilhas
- Processo de otimização passo a passo — da inicialização até a repetição
- Conceitos-chave — legenda e princípios principais do algoritmo
A ilustração demonstra claramente como ilhas ricas (boas soluções) têm alta emigração, ilhas pobres (soluções ruins) têm alta imigração; ocorre a troca de características entre as soluções, e todo o ciclo de otimização funciona. Depois de destrinchar o algoritmo em detalhes, passamos à escrita do pseudocódigo.
1. INICIALIZAÇÃO:
- Definir os parâmetros:
* tamanho da população (quantidade de habitats) = 50
* velocidade máxima de imigração I = 1.0
* velocidade máxima de emigração E = 1.0
* probabilidade de mutação = 0.01
* quantidade de soluções elitistas = 2
* quantidade máxima de espécies = 50
* número de iterações
* Criar uma população de N habitats aleatórios (soluções)
* Calcular o HSI (adequação) para cada habitat
* Calcular as probabilidades de existência para diferentes quantidades de espécies
2. CICLO PRINCIPAL (repetir o número definido de iterações):
2.1. AVALIAÇÃO E ORDENAÇÃO:
- Calcular o HSI para cada habitat
- Ordenar os habitats por HSI em ordem decrescente
- Salvar a melhor solução
2.2. CÁLCULO DOS PARÂMETROS DE MIGRAÇÃO:
Para cada habitat i:
- Determinar a quantidade de espécies: Si = Smax × (N - rank_i) / N
- Calcular a taxa de imigração: λi = I × (1 - Si/Smax)
- Calcular a taxa de emigração: μi = E × (Si/Smax)
- Determinar a probabilidade de existência com base em Si
2.3. MIGRAÇÃO (troca de características):
Para cada habitat Hi (exceto os elitistas):
SE número_aleatório < λi (taxa de imigração) ENTÃO:
Para cada variável da solução (SIV) j:
SE número_aleatório < λi ENTÃO:
- Selecionar um habitat doador:
* calcular a soma de todas as taxas de emigração (exceto Hi)
* utilizar seleção por roleta com base em μ
* escolher o habitat Hk com probabilidade μk/Σμ
- Copiar a variável j de Hk para Hi
FIM SE
FIM do ciclo pelas variáveis
FIM SE
FIM do ciclo pelos habitats
2.4. MUTAÇÃO (diversificação de novas soluções):
Para cada habitat Hi (exceto os elitistas):
- Calcular a taxa de mutação: m_rate = m × (1 - probabilidade_de_existência_i)
SE número_aleatório < m_rate ENTÃO:
- Selecionar uma variável aleatória j
- Substituí-la por um valor aleatório dentro do intervalo permitido
FIM SE
FIM do ciclo pelos habitats
2.5. SUBSTITUIÇÃO E ATUALIZAÇÃO:
- Calcular novos valores de HSI
- Atualizar a melhor solução encontrada
- Salvar os valores atuais de fitness para a próxima iteração
3. RETORNO da melhor solução encontrada
Agora resta muito pouco, vamos escrever a classe "C_AO_BBO", que será herdeira da classe "C_AO" e será destinada à implementação do algoritmo BBO. A herança pressupõe que "C_AO_BBO" utilize a funcionalidade base de otimização fornecida pela classe pai.
A classe contém um conjunto de parâmetros, o tamanho da população e parâmetros específicos do BBO, tais como: velocidade máxima de imigração/emigração (immigrationMax, emigrationMax), probabilidade de mutação (mutationProb), quantidade de soluções elitistas preservadas sem alterações (elitismCount) e quantidade máxima de espécies (speciesMax). O construtor da classe inicializa os parâmetros do BBO com valores padrão, atribui o nome, a descrição e o link para o artigo sobre o algoritmo. O método "SetParams ()" permite alterar os valores dos parâmetros utilizando dados do array "params".
Métodos principais:- Init () inicializa o algoritmo, incluindo a criação e inicialização da população, os intervalos de valores definidos, o passo e o número de épocas, além de inicializar os arrays para armazenamento dos dados dos habitats.
- Moving () implementa a lógica principal de movimentação, ou seja, migração das soluções entre os habitats de acordo com os princípios do BBO.
- Revision () inclui a lógica para a revisão e o ajuste das soluções (habitats).
- S_HabitatData é uma estrutura interna que contém informações sobre cada habitat (solução), incluindo a quantidade de espécies (speciesCount), as taxas de imigração/emigração (immigration, emigration) e a probabilidade de existência (probability).
- habitatData é um array de estruturas "S_HabitatData" que armazena os dados de cada habitat da população.
- probabilities é um array de probabilidades utilizado no processo de mutação.
Métodos privados contêm a implementação das etapas principais do algoritmo BBO, tais como a inicialização da população, o cálculo das taxas de migração e a mutação.
//—————————————————————————————————————————————————————————————————————————————— class C_AO_BBO : public C_AO { public: //-------------------------------------------------------------------- ~C_AO_BBO () { } C_AO_BBO () { ao_name = "BBO"; ao_desc = "Biogeography-Based Optimization"; ao_link = "https://www.mql5.com/ru/articles/18354"; popSize = 50; // размер популяции (количество хабитатов) immigrationMax = 1.0; // максимальная скорость иммиграции emigrationMax = 1.0; // максимальная скорость эмиграции mutationProb = 0.5; // вероятность мутации elitismCount = 2; // количество элитных решений speciesMax = 50; // максимальное количество видов ArrayResize (params, 6); params [0].name = "popSize"; params [0].val = popSize; params [1].name = "immigrationMax"; params [1].val = immigrationMax; params [2].name = "emigrationMax"; params [2].val = emigrationMax; params [3].name = "mutationProb"; params [3].val = mutationProb; params [4].name = "elitismCount"; params [4].val = elitismCount; params [5].name = "speciesMax"; params [5].val = speciesMax; } void SetParams () { popSize = (int)params [0].val; immigrationMax = params [1].val; emigrationMax = params [2].val; mutationProb = params [3].val; elitismCount = (int)params [4].val; speciesMax = (int)params [5].val; } bool Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0); // количество эпох void Moving (); void Revision (); //---------------------------------------------------------------------------- double immigrationMax; // максимальная скорость иммиграции double emigrationMax; // максимальная скорость эмиграции double mutationProb; // вероятность мутации int elitismCount; // количество элитных решений int speciesMax; // максимальное количество видов private: //------------------------------------------------------------------- struct S_HabitatData { int speciesCount; // количество видов в хабитате double immigration; // скорость иммиграции double emigration; // скорость эмиграции double probability; // вероятность существования }; S_HabitatData habitatData []; // данные для каждого хабитата double probabilities []; // вероятности для подсчета мутаций // Вспомогательные методы void InitializePopulation (); void CalculateRates (); void Migration (); void Mutation (); double CalculateProbability (int speciesCount); }; //——————————————————————————————————————————————————————————————————————————————
O método "Init" configura o algoritmo BBO antes do início da execução. Ele realiza a inicialização básica (verificações e configurações), aloca memória para armazenar os dados dos "habitats" e das probabilidades de migração. Em seguida, calcula e normaliza as probabilidades de migração com base na quantidade de espécies em cada habitat. Em caso de conclusão bem-sucedida, retorna "true".
//—————————————————————————————————————————————————————————————————————————————— bool C_AO_BBO::Init (const double &rangeMinP [], // минимальные значения const double &rangeMaxP [], // максимальные значения const double &rangeStepP [], // шаг изменения const int epochsP = 0) // количество эпох { if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false; //---------------------------------------------------------------------------- // Инициализация массивов для каждого хабитата ArrayResize (habitatData, popSize); ArrayResize (probabilities, speciesMax + 1); // Расчет вероятностей для различного количества видов double sum = 0.0; for (int i = 0; i <= speciesMax; i++) { probabilities [i] = CalculateProbability (i); sum += probabilities [i]; } // Нормализация вероятностей if (sum > 0) { for (int i = 0; i <= speciesMax; i++) { probabilities [i] /= sum; } } return true; } //——————————————————————————————————————————————————————————————————————————————
O método "Moving" implementa o ciclo principal de otimização do algoritmo BBO. Na primeira chamada do método, é verificado o flag "revision". Se ele estiver definido com o valor que indica que a população ainda não foi criada, ocorre a sua inicialização. Isso inclui a criação de soluções aleatórias, a avaliação da sua adequação e a definição dos parâmetros iniciais. Após isso, o flag é redefinido.
Depois que a inicialização é concluída, é executada uma série de etapas características do ciclo algorítmico: a população de soluções é ordenada pelo valor da sua adequação, de modo a identificar os melhores e os piores agentes. Isso auxilia no controle das migrações e mutações. Nesta etapa, são calculadas as probabilidades e as taxas de troca de espécies entre os habitats, com base no estado atual e na qualidade das soluções. Esses parâmetros determinam como as espécies "migram" de um habitat para outro. Nesse passo ocorre a troca de "SIV" entre os habitats.
Como resultado, locais com diversidade insuficiente recebem novas espécies de variantes mais ricas, o que favorece a diversificação do espaço de soluções. Após a migração, ocorre a introdução aleatória de alterações nas soluções, isto é, a mutação, para manter a diversidade genética. As probabilidades de mutação podem depender do estado atual da solução e dos parâmetros do algoritmo. Ao final do ciclo, os valores atuais da função de adequação das soluções são salvos para serem utilizados na ordenação e na análise na próxima iteração do algoritmo.
//+----------------------------------------------------------------------------+ //| Основной метод оптимизации | //+----------------------------------------------------------------------------+ void C_AO_BBO::Moving () { // Первая итерация - инициализация начальной популяции if (!revision) { InitializePopulation (); revision = true; return; } // Основной процесс оптимизации // 1. Сортировка популяции по HSI (fitness) static S_AO_Agent aTemp []; ArrayResize (aTemp, popSize); u.Sorting (a, aTemp, popSize); // 2. Расчет скоростей иммиграции и эмиграции CalculateRates (); // 3. Миграция (обмен SIV между хабитатами) Migration (); // 4. Мутация на основе вероятностей Mutation (); // 5. Сохранение состояния для следующей итерации for (int i = 0; i < popSize; i++) { a [i].fP = a [i].f; } } //——————————————————————————————————————————————————————————————————————————————
O método "Revision" é destinado à atualização da melhor solução atual da população. Ele percorre todos os agentes (soluções) da população corrente e compara o valor da função de adequação de cada um com o valor armazenado na variável "fB", que guarda o melhor resultado obtido até o momento.
Se o valor da função de fitness de algum agente for melhor do que o melhor atual, então ele o substitui, e os parâmetros correspondentes da solução são copiados para a variável que armazena a melhor solução. Como resultado, após a execução do método, essa variável sempre contém a melhor solução encontrada.
//+----------------------------------------------------------------------------+ //| Обновление лучшего решения | //+----------------------------------------------------------------------------+ void C_AO_BBO::Revision () { // Поиск лучшего решения в текущей популяции for (int i = 0; i < popSize; i++) { // Обновление лучшего решения if (a [i].f > fB) { fB = a [i].f; ArrayCopy (cB, a [i].c, 0, 0, WHOLE_ARRAY); } } } //——————————————————————————————————————————————————————————————————————————————
O método "InitializePopulation" é responsável pela criação da população inicial de soluções para o algoritmo BBO. Ele cria "popSize" (tamanho da população) indivíduos (habitats), distribuídos uniformemente no espaço de busca.
Para cada indivíduo, o método gera coordenadas aleatórias (valores dos parâmetros da solução) dentro dos limites definidos pelos arrays "rangeMin" (limites mínimos) e "rangeMax" (limites máximos) para cada coordenada "coords". É utilizada a função "u.RNDfromCI" para gerar um número aleatório dentro do intervalo especificado.
Em seguida, o método arredonda as coordenadas geradas para o passo válido mais próximo, definido pelo array "rangeStep". Isso garante que as soluções estejam dentro de um espaço de busca discreto permitido. Para isso, é utilizada a função "SeInDiSp". Após a inicialização das coordenadas, o método inicializa a estrutura de dados "habitatData" para cada indivíduo, zerando os valores de "speciesCount", "immigration", "emigration" e "probability". Esses valores serão utilizados no processo de otimização para o cálculo das taxas de imigração, emigração e das probabilidades de mutação.
//+----------------------------------------------------------------------------+ //| Инициализация начальной популяции | //+----------------------------------------------------------------------------+ void C_AO_BBO::InitializePopulation () { // Инициализация начальной популяции равномерно по всему пространству for (int i = 0; i < popSize; i++) { for (int c = 0; c < coords; c++) { // Генерация случайных координат в допустимых пределах a [i].c [c] = u.RNDfromCI (rangeMin [c], rangeMax [c]); // Округление до ближайшего допустимого шага a [i].c [c] = u.SeInDiSp (a [i].c [c], rangeMin [c], rangeMax [c], rangeStep [c]); } // Инициализация данных хабитата habitatData [i].speciesCount = 0; habitatData [i].immigration = 0.0; habitatData [i].emigration = 0.0; habitatData [i].probability = 0.0; } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateRates" é destinado ao cálculo das taxas de migração, isto é, imigração e emigração, e da probabilidade de existência de cada habitat na população.
É utilizado um modelo linear, no qual a quantidade de espécies associada a cada solução é determinada proporcionalmente ao seu posto, sendo que as melhores soluções possuem mais espécies. A taxa de imigração diminui à medida que a quantidade de espécies aumenta, ou seja, quanto mais espécies uma solução possui, menor é a sua probabilidade de aceitar novos indivíduos. A taxa de emigração cresce com o aumento da quantidade de espécies, isto é, quanto mais espécies uma solução possui, maior é a probabilidade de deixá-la.
A probabilidade de existência do habitat é definida com base nas probabilidades previamente estabelecidas para cada quantidade de espécies. Se a quantidade de espécies exceder o máximo permitido, a probabilidade é definida como zero.
//+----------------------------------------------------------------------------+ //| Расчет скоростей иммиграции и эмиграции | //+----------------------------------------------------------------------------+ void C_AO_BBO::CalculateRates () { // Для линейной модели миграции for (int i = 0; i < popSize; i++) { // Количество видов обратно пропорционально рангу (лучшие решения имеют больше видов) habitatData [i].speciesCount = speciesMax - (i * speciesMax / popSize); // Скорость иммиграции уменьшается с увеличением количества видов habitatData [i].immigration = immigrationMax * (1.0 - (double)habitatData [i].speciesCount / speciesMax); // Скорость эмиграции увеличивается с увеличением количества видов habitatData [i].emigration = emigrationMax * (double)habitatData [i].speciesCount / speciesMax; // Вероятность существования хабитата if (habitatData [i].speciesCount <= speciesMax) { habitatData [i].probability = probabilities [habitatData [i].speciesCount]; } else { habitatData [i].probability = 0.0; } } } //——————————————————————————————————————————————————————————————————————————————
O método "Migration" implementa o processo de migração, ou seja, a troca de SIV, Habitat Suitability Index Variables, isto é, valores das coordenadas, entre os habitats da população. A essência do método é que habitats com altas taxas de imigração, isto é, aqueles com poucas espécies, podem "receber" SIV de outros habitats que possuem altas taxas de emigração, onde há muitas espécies.
O ciclo percorre todos os habitats da população, mas ignora os primeiros "elitismCount" habitats, que são considerados "elitistas" e não participam da migração. Para cada habitat, exceto os elitistas, é determinado aleatoriamente se ele será modificado na iteração atual. A probabilidade de modificação é determinada pelo valor "habitatData[i].immigration", a taxa de imigração do habitat atual. Se o habitat for selecionado para migração, inicia-se a iteração por todas as suas coordenadas (SIV). Para cada coordenada, novamente é determinado aleatoriamente se ela será modificada. A probabilidade de modificação também é definida pelo valor "habitatData[i].immigration".
Se uma coordenada for selecionada para modificação, é determinado o habitat do qual o valor dessa coordenada será "emprestado". Essa escolha é baseada na seleção por roleta (roulette wheel selection), proporcionalmente aos valores de "habitatData[j].emigration", ou seja, às taxas de emigração dos outros habitats. Isso significa que habitats com taxas de emigração mais altas têm maiores chances de se tornarem a fonte da migração. No cálculo das probabilidades, é considerado que o habitat atual não pode ser selecionado como fonte para si mesmo. Se a fonte de migração for escolhida, o valor da coordenada correspondente (SIV) é copiado do habitat de origem para o habitat atual.
Como resultado, o método executa um processo controlado de troca de informações (SIV) entre os habitats, no qual habitats com baixo número de espécies (alta imigração) recebem informações de habitats com alto número de espécies (alta emigração). Isso permite disseminar bons SIV por toda a população, ao mesmo tempo em que mantém as melhores soluções inalteradas.
//+----------------------------------------------------------------------------+ //| Миграция (обмен SIV между хабитатами) | //+----------------------------------------------------------------------------+ void C_AO_BBO::Migration () { for (int i = 0; i < popSize; i++) { // Пропускаем элитные решения if (i < elitismCount) continue; // Определяем, будет ли хабитат модифицирован if (u.RNDprobab () < habitatData [i].immigration) { // Для каждой координаты (SIV) for (int c = 0; c < coords; c++) { // Определяем, будет ли эта координата модифицирована if (u.RNDprobab () < habitatData [i].immigration) { // Выбор источника миграции на основе скоростей эмиграции double sumEmigration = 0.0; for (int j = 0; j < popSize; j++) { if (j != i) sumEmigration += habitatData [j].emigration; } if (sumEmigration > 0) { // Рулеточная селекция источника double roulette = u.RNDprobab () * sumEmigration; double cumSum = 0.0; for (int j = 0; j < popSize; j++) { if (j != i) { cumSum += habitatData [j].emigration; if (roulette <= cumSum) { // Копирование SIV из хабитата j в хабитат i a [i].c [c] = a [j].c [c]; break; } } } } } } } } } //——————————————————————————————————————————————————————————————————————————————
O método "Mutation" realiza a mutação dos habitats na população. O objetivo da mutação é introduzir alterações aleatórias nas soluções para evitar o aprisionamento em ótimos locais e explorar novas regiões do espaço de busca.
Assim como no método de migração, as soluções elitistas, isto é, os primeiros "elitismCount" habitats, são ignoradas e não sofrem mutação. Isso é necessário para preservar as melhores soluções encontradas. Para cada habitat restante, é calculada a probabilidade de mutação. É importante notar que a probabilidade de mutação é inversamente proporcional à probabilidade de existência do habitat (habitatData[i].probability). Isso significa que habitats com baixa probabilidade de existência, ou seja, soluções menos bem-sucedidas, irão sofrer mutação com mais frequência, favorecendo a exploração de novas áreas.
Se o número aleatório gerado for menor do que a "mutationRate" calculada, ocorre a mutação. Uma coordenada "mutateCoord" (SIV) é selecionada aleatoriamente dentre todas as coordenadas "coords". Para a coordenada selecionada, é gerado um novo valor aleatório dentro do intervalo definido. Em seguida, a função "SeInDiSp" é aplicada ao novo valor, restringindo-o aos limites estabelecidos.
Dessa forma, o método "Mutation" introduz um elemento de aleatoriedade no processo de busca, permitindo que o algoritmo encontre novas soluções potencialmente melhores, especialmente em regiões que ainda não foram suficientemente exploradas. A frequência de mutação é regulada pela probabilidade de existência do habitat, de modo a equilibrar a diversificação e a intensificação (exploration vs. exploitation).
//+----------------------------------------------------------------------------+ //| Мутация на основе вероятностей | //+----------------------------------------------------------------------------+ void C_AO_BBO::Mutation () { for (int i = 0; i < popSize; i++) { // Пропускаем элитные решения if (i < elitismCount) continue; // Скорость мутации обратно пропорциональна вероятности существования double mutationRate = mutationProb * (1.0 - habitatData [i].probability); if (u.RNDprobab () < mutationRate) { // Выбираем случайную координату для мутации int mutateCoord = MathRand () % coords; // Генерируем новое значение для выбранной координаты a [i].c [mutateCoord] = u.RNDfromCI (rangeMin [mutateCoord], rangeMax [mutateCoord]); a [i].c [mutateCoord] = u.SeInDiSp (a [i].c [mutateCoord], rangeMin [mutateCoord], rangeMax [mutateCoord], rangeStep [mutateCoord]); } } } //——————————————————————————————————————————————————————————————————————————————
O método "CalculateProbability" calcula a probabilidade de existência de um habitat para uma determinada quantidade de espécies. O método utiliza um modelo simplificado: a probabilidade máxima é alcançada próximo ao valor de equilíbrio das espécies, isto é, no meio do intervalo, e à medida que se afasta desse ponto, a probabilidade diminui rapidamente seguindo uma curva gaussiana. Quanto mais distante "speciesCount" estiver de "speciesMax/2", menor será a probabilidade.
De modo geral, o método cria um modelo no qual habitats com uma quantidade de espécies próxima ao valor de equilíbrio possuem uma probabilidade de existência maior do que habitats cuja quantidade de espécies se desvia fortemente desse valor. Isso representa um modelo simplificado, porém eficaz, de "adequação" do habitat com base na sua diversidade biológica.
//+----------------------------------------------------------------------------+ //| Расчет вероятности для заданного количества видов | //+----------------------------------------------------------------------------+ double C_AO_BBO::CalculateProbability (int speciesCount) { // Упрощенная модель вероятности // Максимальная вероятность в середине диапазона (равновесие) int equilibrium = speciesMax / 2; double distance = MathAbs (speciesCount - equilibrium); double probability = MathExp (-distance * distance / (2.0 * equilibrium * equilibrium)); return probability; } //——————————————————————————————————————————————————————————————————————————————
Resultados dos testes
Após experimentar um pouco com os parâmetros, revelaram-se excelentes resultados do funcionamento do algoritmo BBO.
BBO|Biogeography-Based Optimization|50.0|1.0|1.0|0.5|2.0|50.0|
=============================
5 Hilly's; Func runs: 10000; result: 0.9491244808033844
25 Hilly's; Func runs: 10000; result: 0.6945610309062928
500 Hilly's; Func runs: 10000; result: 0.35031241665471596
=============================
5 Forest's; Func runs: 10000; result: 0.9381951766964413
25 Forest's; Func runs: 10000; result: 0.6736501622157315
500 Forest's; Func runs: 10000; result: 0.2568167323109364
=============================
5 Megacity's; Func runs: 10000; result: 0.7461538461538464
25 Megacity's; Func runs: 10000; result: 0.4827692307692309
500 Megacity's; Func runs: 10000; result: 0.17369230769230892
=============================
All score: 5.26528 (58.50%)
Na visualização é possível ver como o algoritmo BBO funciona de forma notável. Na dificílima função discreta Megacity, o algoritmo apresenta um resultado excelente.
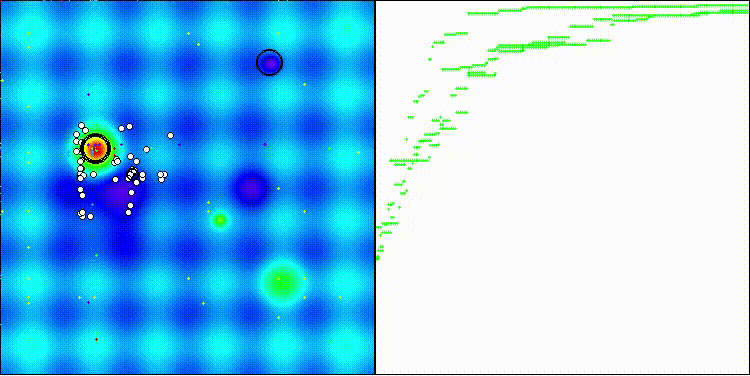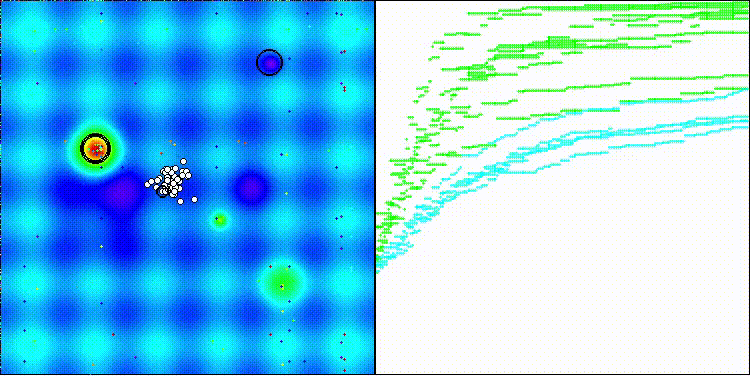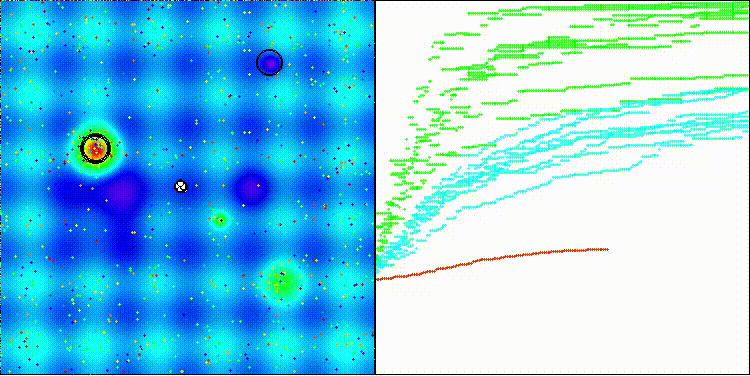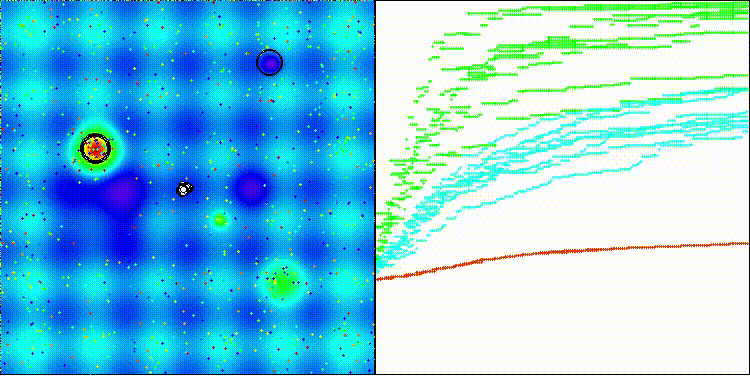
BBO na função de teste Hilly
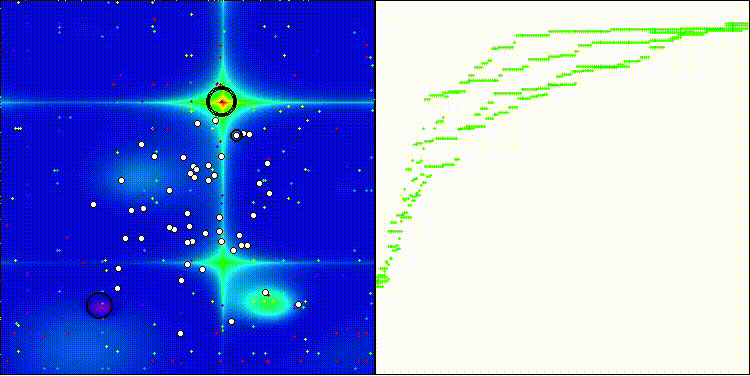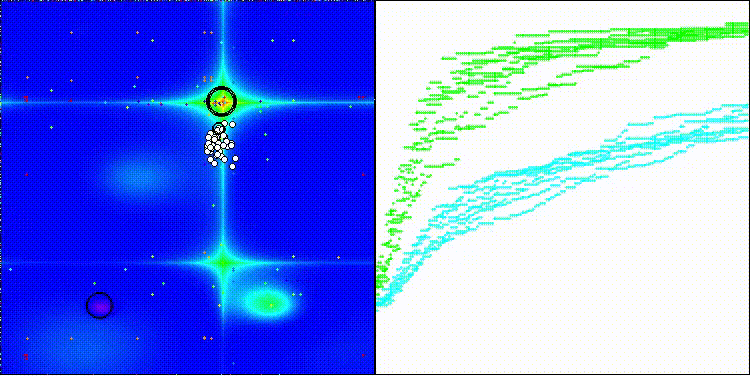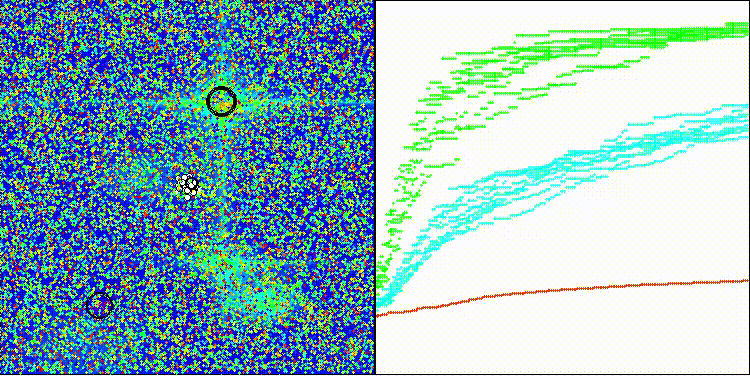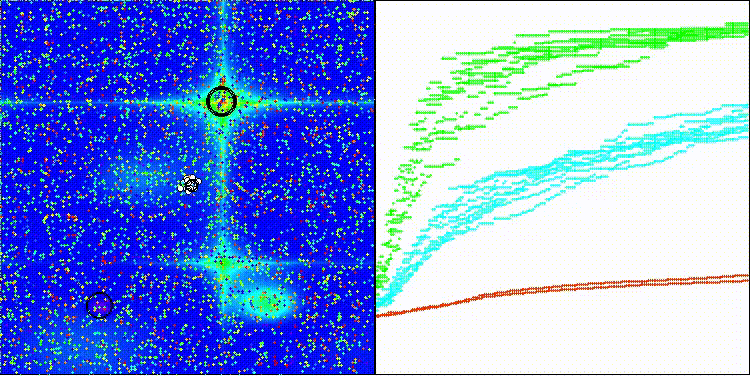
BBO na função de teste Forest

BBO na função de teste Megacity
Ao final dos testes, o elegante algoritmo BBO ocupa uma elevada 12ª posição na parte superior da tabela classificatória.
| № | AO | Description | Hilly | Hilly Final | Forest | Forest Final | Megacity (discrete) | Megacity Final | Final Result | % of MAX | ||||||
| 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | 10 p (5 F) | 50 p (25 F) | 1000 p (500 F) | ||||||||
| 1 | ANS | across neighbourhood search | 0,94948 | 0,84776 | 0,43857 | 2,23581 | 1,00000 | 0,92334 | 0,39988 | 2,32323 | 0,70923 | 0,63477 | 0,23091 | 1,57491 | 6,134 | 68,15 |
| 2 | CLA | code lock algorithm (joo) | 0,95345 | 0,87107 | 0,37590 | 2,20042 | 0,98942 | 0,91709 | 0,31642 | 2,22294 | 0,79692 | 0,69385 | 0,19303 | 1,68380 | 6,107 | 67,86 |
| 3 | AMOm | animal migration ptimization M | 0,90358 | 0,84317 | 0,46284 | 2,20959 | 0,99001 | 0,92436 | 0,46598 | 2,38034 | 0,56769 | 0,59132 | 0,23773 | 1,39675 | 5,987 | 66,52 |
| 4 | (P+O)ES | (P+O) evolution strategies | 0,92256 | 0,88101 | 0,40021 | 2,20379 | 0,97750 | 0,87490 | 0,31945 | 2,17185 | 0,67385 | 0,62985 | 0,18634 | 1,49003 | 5,866 | 65,17 |
| 5 | CTA | comet tail algorithm (joo) | 0,95346 | 0,86319 | 0,27770 | 2,09435 | 0,99794 | 0,85740 | 0,33949 | 2,19484 | 0,88769 | 0,56431 | 0,10512 | 1,55712 | 5,846 | 64,96 |
| 6 | TETA | time evolution travel algorithm (joo) | 0,91362 | 0,82349 | 0,31990 | 2,05701 | 0,97096 | 0,89532 | 0,29324 | 2,15952 | 0,73462 | 0,68569 | 0,16021 | 1,58052 | 5,797 | 64,41 |
| 7 | SDSm | stochastic diffusion search M | 0,93066 | 0,85445 | 0,39476 | 2,17988 | 0,99983 | 0,89244 | 0,19619 | 2,08846 | 0,72333 | 0,61100 | 0,10670 | 1,44103 | 5,709 | 63,44 |
| 8 | BOAm | billiards optimization algorithm M | 0,95757 | 0,82599 | 0,25235 | 2,03590 | 1,00000 | 0,90036 | 0,30502 | 2,20538 | 0,73538 | 0,52523 | 0,09563 | 1,35625 | 5,598 | 62,19 |
| 9 | AAm | archery algorithm M | 0,91744 | 0,70876 | 0,42160 | 2,04780 | 0,92527 | 0,75802 | 0,35328 | 2,03657 | 0,67385 | 0,55200 | 0,23738 | 1,46323 | 5,548 | 61,64 |
| 10 | ESG | evolution of social groups (joo) | 0,99906 | 0,79654 | 0,35056 | 2,14616 | 1,00000 | 0,82863 | 0,13102 | 1,95965 | 0,82333 | 0,55300 | 0,04725 | 1,42358 | 5,529 | 61,44 |
| 11 | SIA | simulated isotropic annealing (joo) | 0,95784 | 0,84264 | 0,41465 | 2,21513 | 0,98239 | 0,79586 | 0,20507 | 1,98332 | 0,68667 | 0,49300 | 0,09053 | 1,27020 | 5,469 | 60,76 |
| 12 | BBO | biogeography based optimization | 0,94912 | 0,69456 | 0,35031 | 1,99399 | 0,93820 | 0,67365 | 0,25682 | 1,86867 | 0,74615 | 0,48277 | 0,17369 | 1,40261 | 5,265 | 58,50 |
| 13 | ACS | artificial cooperative search | 0,75547 | 0,74744 | 0,30407 | 1,80698 | 1,00000 | 0,88861 | 0,22413 | 2,11274 | 0,69077 | 0,48185 | 0,13322 | 1,30583 | 5,226 | 58,06 |
| 14 | DA | dialectical algorithm | 0,86183 | 0,70033 | 0,33724 | 1,89940 | 0,98163 | 0,72772 | 0,28718 | 1,99653 | 0,70308 | 0,45292 | 0,16367 | 1,31967 | 5,216 | 57,95 |
| 15 | BHAm | black hole algorithm M | 0,75236 | 0,76675 | 0,34583 | 1,86493 | 0,93593 | 0,80152 | 0,27177 | 2,00923 | 0,65077 | 0,51646 | 0,15472 | 1,32195 | 5,196 | 57,73 |
| 16 | ASO | anarchy society optimization | 0,84872 | 0,74646 | 0,31465 | 1,90983 | 0,96148 | 0,79150 | 0,23803 | 1,99101 | 0,57077 | 0,54062 | 0,16614 | 1,27752 | 5,178 | 57,54 |
| 17 | RFO | royal flush optimization (joo) | 0,83361 | 0,73742 | 0,34629 | 1,91733 | 0,89424 | 0,73824 | 0,24098 | 1,87346 | 0,63154 | 0,50292 | 0,16421 | 1,29867 | 5,089 | 56,55 |
| 18 | AOSm | atomic orbital search M | 0,80232 | 0,70449 | 0,31021 | 1,81702 | 0,85660 | 0,69451 | 0,21996 | 1,77107 | 0,74615 | 0,52862 | 0,14358 | 1,41835 | 5,006 | 55,63 |
| 19 | TSEA | turtle shell evolution algorithm (joo) | 0,96798 | 0,64480 | 0,29672 | 1,90949 | 0,99449 | 0,61981 | 0,22708 | 1,84139 | 0,69077 | 0,42646 | 0,13598 | 1,25322 | 5,004 | 55,60 |
| 20 | DE | differential evolution | 0,95044 | 0,61674 | 0,30308 | 1,87026 | 0,95317 | 0,78896 | 0,16652 | 1,90865 | 0,78667 | 0,36033 | 0,02953 | 1,17653 | 4,955 | 55,06 |
| 21 | SRA | successful restaurateur algorithm (joo) | 0,96883 | 0,63455 | 0,29217 | 1,89555 | 0,94637 | 0,55506 | 0,19124 | 1,69267 | 0,74923 | 0,44031 | 0,12526 | 1,31480 | 4,903 | 54,48 |
| 22 | CRO | chemical reaction optimisation | 0,94629 | 0,66112 | 0,29853 | 1,90593 | 0,87906 | 0,58422 | 0,21146 | 1,67473 | 0,75846 | 0,42646 | 0,12686 | 1,31178 | 4,892 | 54,36 |
| 23 | BIO | blood inheritance optimization (joo) | 0,81568 | 0,65336 | 0,30877 | 1,77781 | 0,89937 | 0,65319 | 0,21760 | 1,77016 | 0,67846 | 0,47631 | 0,13902 | 1,29378 | 4,842 | 53,80 |
| 24 | BSA | bird swarm algorithm | 0,89306 | 0,64900 | 0,26250 | 1,80455 | 0,92420 | 0,71121 | 0,24939 | 1,88479 | 0,69385 | 0,32615 | 0,10012 | 1,12012 | 4,809 | 53,44 |
| 25 | HS | harmony search | 0,86509 | 0,68782 | 0,32527 | 1,87818 | 0,99999 | 0,68002 | 0,09590 | 1,77592 | 0,62000 | 0,42267 | 0,05458 | 1,09725 | 4,751 | 52,79 |
| 26 | SSG | saplings sowing and growing | 0,77839 | 0,64925 | 0,39543 | 1,82308 | 0,85973 | 0,62467 | 0,17429 | 1,65869 | 0,64667 | 0,44133 | 0,10598 | 1,19398 | 4,676 | 51,95 |
| 27 | BCOm | bacterial chemotaxis optimization M | 0,75953 | 0,62268 | 0,31483 | 1,69704 | 0,89378 | 0,61339 | 0,22542 | 1,73259 | 0,65385 | 0,42092 | 0,14435 | 1,21912 | 4,649 | 51,65 |
| 28 | ABO | african buffalo optimization | 0,83337 | 0,62247 | 0,29964 | 1,75548 | 0,92170 | 0,58618 | 0,19723 | 1,70511 | 0,61000 | 0,43154 | 0,13225 | 1,17378 | 4,634 | 51,49 |
| 29 | (PO)ES | (PO) evolution strategies | 0,79025 | 0,62647 | 0,42935 | 1,84606 | 0,87616 | 0,60943 | 0,19591 | 1,68151 | 0,59000 | 0,37933 | 0,11322 | 1,08255 | 4,610 | 51,22 |
| 30 | FBA | fractal-based Algorithm | 0,79000 | 0,65134 | 0,28965 | 1,73099 | 0,87158 | 0,56823 | 0,18877 | 1,62858 | 0,61077 | 0,46062 | 0,12398 | 1,19537 | 4,555 | 50,61 |
| 31 | TSm | tabu search M | 0,87795 | 0,61431 | 0,29104 | 1,78330 | 0,92885 | 0,51844 | 0,19054 | 1,63783 | 0,61077 | 0,38215 | 0,12157 | 1,11449 | 4,536 | 50,40 |
| 32 | BSO | brain storm optimization | 0,93736 | 0,57616 | 0,29688 | 1,81041 | 0,93131 | 0,55866 | 0,23537 | 1,72534 | 0,55231 | 0,29077 | 0,11914 | 0,96222 | 4,498 | 49,98 |
| 33 | WOAm | wale optimization algorithm M | 0,84521 | 0,56298 | 0,26263 | 1,67081 | 0,93100 | 0,52278 | 0,16365 | 1,61743 | 0,66308 | 0,41138 | 0,11357 | 1,18803 | 4,476 | 49,74 |
| 34 | AEFA | artificial electric field algorithm | 0,87700 | 0,61753 | 0,25235 | 1,74688 | 0,92729 | 0,72698 | 0,18064 | 1,83490 | 0,66615 | 0,11631 | 0,09508 | 0,87754 | 4,459 | 49,55 |
| 35 | AEO | artificial ecosystem-based optimization algorithm | 0,91380 | 0,46713 | 0,26470 | 1,64563 | 0,90223 | 0,43705 | 0,21400 | 1,55327 | 0,66154 | 0,30800 | 0,28563 | 1,25517 | 4,454 | 49,49 |
| 36 | CAm | camel algorithm M | 0,78684 | 0,56042 | 0,35133 | 1,69859 | 0,82772 | 0,56041 | 0,24336 | 1,63149 | 0,64846 | 0,33092 | 0,13418 | 1,11356 | 4,444 | 49,37 |
| 37 | ACOm | ant colony optimization M | 0,88190 | 0,66127 | 0,30377 | 1,84693 | 0,85873 | 0,58680 | 0,15051 | 1,59604 | 0,59667 | 0,37333 | 0,02472 | 0,99472 | 4,438 | 49,31 |
| 38 | BFO-GA | bacterial foraging optimization - ga | 0,89150 | 0,55111 | 0,31529 | 1,75790 | 0,96982 | 0,39612 | 0,06305 | 1,42899 | 0,72667 | 0,27500 | 0,03525 | 1,03692 | 4,224 | 46,93 |
| 39 | SOA | simple optimization algorithm | 0,91520 | 0,46976 | 0,27089 | 1,65585 | 0,89675 | 0,37401 | 0,16984 | 1,44060 | 0,69538 | 0,28031 | 0,10852 | 1,08422 | 4,181 | 46,45 |
| 40 | ABHA | artificial bee hive algorithm | 0,84131 | 0,54227 | 0,26304 | 1,64663 | 0,87858 | 0,47779 | 0,17181 | 1,52818 | 0,50923 | 0,33877 | 0,10397 | 0,95197 | 4,127 | 45,85 |
| 41 | ACMO | atmospheric cloud model optimization | 0,90321 | 0,48546 | 0,30403 | 1,69270 | 0,80268 | 0,37857 | 0,19178 | 1,37303 | 0,62308 | 0,24400 | 0,10795 | 0,97503 | 4,041 | 44,90 |
| 42 | ADAMm | adaptive moment estimation M | 0,88635 | 0,44766 | 0,26613 | 1,60014 | 0,84497 | 0,38493 | 0,16889 | 1,39880 | 0,66154 | 0,27046 | 0,10594 | 1,03794 | 4,037 | 44,85 |
| 43 | CGO | chaos game optimization | 0,57256 | 0,37158 | 0,32018 | 1,26432 | 0,61176 | 0,61931 | 0,62161 | 1,85267 | 0,37538 | 0,21923 | 0,19028 | 0,78490 | 3,902 | 43,35 |
| 44 | CROm | coral reefs optimization M | 0,78512 | 0,46032 | 0,25958 | 1,50502 | 0,86688 | 0,35297 | 0,16267 | 1,38252 | 0,63231 | 0,26738 | 0,10734 | 1,00703 | 3,895 | 43,27 |
| 45 | ATAm | artificial tribe algorithm M | 0,71771 | 0,55304 | 0,25235 | 1,52310 | 0,82491 | 0,55904 | 0,20473 | 1,58867 | 0,44000 | 0,18615 | 0,09411 | 0,72026 | 3,832 | 42,58 |
| RW | neuroboids optimization algorithm 2(joo) | 0,48754 | 0,32159 | 0,25781 | 1,06694 | 0,37554 | 0,21944 | 0,15877 | 0,75375 | 0,27969 | 0,14917 | 0,09847 | 0,52734 | 2,348 | 26,09 | |
Considerações finais
O algoritmo de otimização baseada em biogeografia (BBO) demonstrou resultados impressionantes nos testes realizados, ocupando a 12ª posição entre os 45 melhores algoritmos populacionais de otimização, com um índice geral de eficiência de 58.5 %. Trata-se de um resultado excepcional para um algoritmo baseado em uma metáfora natural tão elegante e intuitiva.
É especialmente notável a capacidade do BBO de trabalhar de forma eficiente com tarefas de média e alta dimensionalidade, o que evidencia sua escalabilidade e resistência ao "mal da dimensionalidade", um problema enfrentado por muitos algoritmos de otimização.
A base conceitual do BBO, a migração de espécies entre ilhas, mostrou-se não apenas uma metáfora bonita, mas também um mecanismo altamente eficaz de balanceamento entre a diversificação do espaço de busca e a intensificação do uso das soluções encontradas. O modelo linear de migração, no qual habitats ricos compartilham ativamente suas características e habitats pobres as recebem ativamente, cria um gradiente natural de fluxo de informação das melhores soluções para as piores.
Merece atenção especial o operador de mutação do BBO, que difere radicalmente das abordagens clássicas. Em vez de uma probabilidade de mutação fixa ou aleatória, o BBO utiliza um modelo teoricamente fundamentado, no qual a probabilidade de mutação é inversamente proporcional à probabilidade de existência do habitat. Isso significa que as soluções mais "naturais" e estáveis, com quantidade média de espécies, sofrem mutação raramente, enquanto soluções extremas, tanto muito boas quanto muito ruins, são submetidas a mudanças mais frequentes. Essa abordagem cria um mecanismo adaptativo que regula automaticamente o equilíbrio entre estabilidade e variabilidade da população.
O algoritmo demonstra excelente estabilidade em diferentes tipos de paisagens: nas cores, ele se mantém uniformemente verde em todos os testes e em nenhum deles apresenta queda de desempenho em comparação com outros algoritmos de otimização.
Uma vantagem importante do BBO é sua simplicidade conceitual aliada à alta eficiência. Diferentemente de algumas meta-heurísticas modernas, que exigem inúmeros parâmetros e operadores complexos, o BBO opera com conceitos intuitivos: migração, quantidade de espécies e adequação do habitat.
Os resultados dos testes confirmam que o BBO não é apenas "mais um" algoritmo bioinspirado, mas um método de otimização completo e competitivo, capaz de enfrentar dignamente os líderes consagrados da área. A combinação de fundamentação teórica, eficiência computacional e aplicabilidade prática faz do BBO uma valiosa adição ao arsenal dos métodos modernos de otimização global.
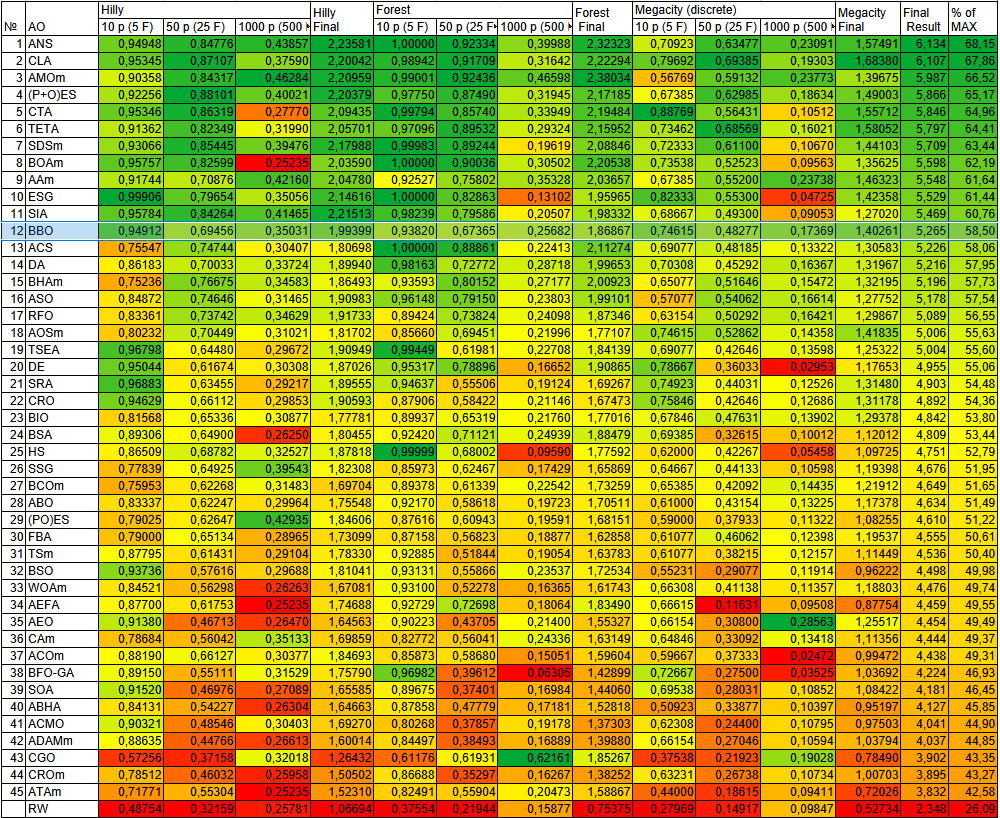
Figura 2. Graduação de cores dos algoritmos pelos testes correspondentes
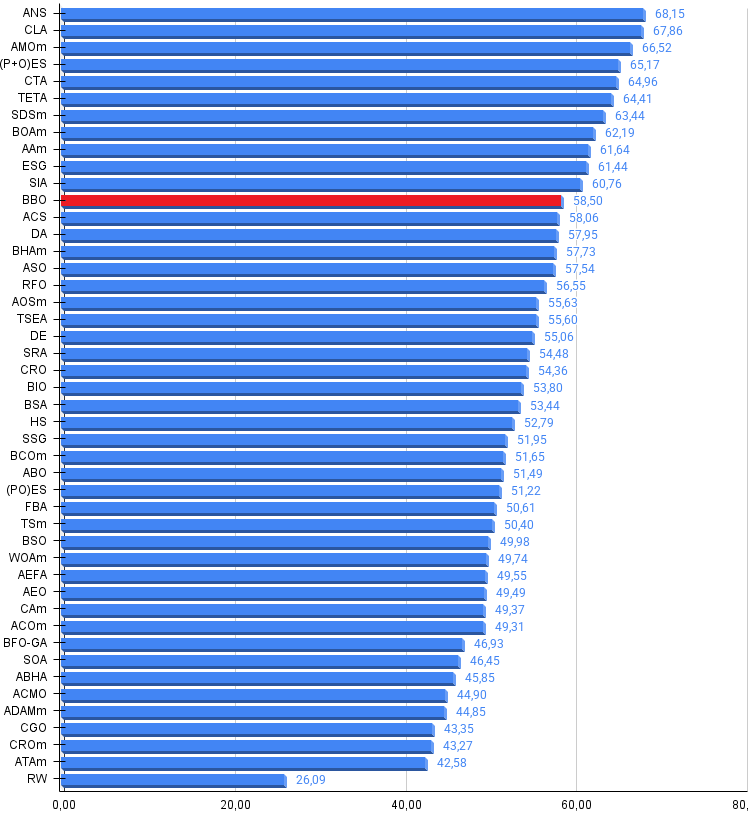
Figura 3. Histograma dos resultados dos testes dos algoritmos (na escala de 0 a 100, quanto maior, melhor, onde 100 — resultado teórico máximo possível, no arquivo compactado há um script para cálculo da tabela classificatória)
Vantagens e desvantagens do algoritmo BBO:
Vantagens:
- Rápido.
- Implementação simples.
- Bons resultados em uma ampla faixa de dimensionalidades dos problemas.
Desvantagens:
- Grande quantidade de parâmetros.
Um arquivo compactado com as versões atualizadas dos códigos dos algoritmos está anexado ao artigo. O autor do artigo não se responsabiliza pela precisão absoluta na descrição dos algoritmos canônicos, pois muitos deles foram modificados para melhorar as capacidades de busca. As conclusões e julgamentos apresentados nos artigos baseiam-se nos resultados dos experimentos realizados.
Programas utilizados no artigo
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | #C_AO.mqh | Arquivo de inclusão | Classe base dos algoritmos populacionais de otimização |
| 2 | #C_AO_enum.mqh | Arquivo de inclusão | Enumeração dos algoritmos populacionais de otimização |
| 3 | TestFunctions.mqh | Arquivo de inclusão | Biblioteca de funções de teste |
| 4 | TestStandFunctions.mqh | Arquivo de inclusão | Biblioteca de funções do ambiente de testes |
| 5 | Utilities.mqh | Arquivo de inclusão | Biblioteca de funções auxiliares |
| 6 | CalculationTestResults.mqh | Arquivo de inclusão | Script para cálculo dos resultados na tabela comparativa |
| 7 | Testing AOs.mq5 | Script | Ambiente de testes unificado para todos os algoritmos populacionais de otimização |
| 8 | Simple use of population optimization algorithms.mq5 | Script | Exemplo simples de uso de algoritmos populacionais de otimização sem visualização |
| 9 | Test_AO_BBO.mq5 | Script | Ambiente de testes para BBO |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/18354
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Caminhe em novos trilhos: Personalize indicadores no MQL5
Caminhe em novos trilhos: Personalize indicadores no MQL5
 Processos gaussianos em aprendizado de máquina: modelo de regressão em MQL5
Processos gaussianos em aprendizado de máquina: modelo de regressão em MQL5
 Está chegando o novo MetaTrader 5 e MQL5
Está chegando o novo MetaTrader 5 e MQL5
 Redes neurais em trading: Framework de previsão cruzada de domínio de séries temporais (TimeFound)
Redes neurais em trading: Framework de previsão cruzada de domínio de séries temporais (TimeFound)
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso