外国為替におけるポートフォリオ最適化：VaRとマーコウィッツ理論の統合

はじめに：FXにおけるポートフォリオ最適化の課題

私はこの3年間、FX用の自動売買ロボットを開発してきました。正直に言うと、リスク管理は本当に厄介です。最初の頃は固定のストップを置くだけでしたが、数回の口座破綻を経験しました。そこでさらに深く調べて、マーコウィッツのポートフォリオ最適化理論に出会いました。

相関を計算し、重みを最適化するなど、一見すると素晴らしい理論に見えました。しかし実際のFXではうまく機能しません。なぜでしょうか。FXの通貨ペアはすべて相互に関連しているからです。たとえばEURUSDとEURGBPを同時に取引してみてください。ユーロが急変動すれば、両方のポジションが同時に動きます。美しい理論は、厳しい現実の前にあっけなく崩れ去りました。

そこで私は別のアプローチを探し始めました。そして最終的にたどり着いたのがVaR (Value at Risk)手法でした。複雑な数式ばかりで、最初は何のことか分かりませんでした。しかしある時、これこそが必要なものだと気づきました。VaRは、ある確率での最大損失を示してくれます。つまり、1日、1週間、1か月でどれくらい失う可能性があるかを直接見積もることができるのです。

結局、私はマーコウィッツとVaRを組み合わせることにしました。おかしいと思われるかもしれませんが、他に選択肢は見えませんでした。マーコウィッツは資金の最適な配分を与え、VaRは証拠金維持率を守ってくれる。理論上は完璧に見えました。

そこから研究プログラマーとしての過酷な日常が始まりました。Python、MetaTrader 5端末、大量の履歴データ…簡単ではないことは分かっていましたが、現実は想像を超えていました。これからお話しするのは、「バックテストではきれいに見えるだけでなく、実際に機能するシステム」を作ろうとした私の試みです。

FXの自動売買を試したことがある方なら、私の苦労を理解していただけるでしょう。そうでないなら、私の経験が少なくともいくつかの落とし穴を避ける手助けになるかもしれません。

VaRとマーコウィッツ理論の理論的および数学的基盤

では、理論から始めましょう。最初の1か月は、とにかく数学を理解しようと必死でした。マーコウィッツの理論は複雑そうに見えます。方程式の山、行列、二次最適化…。しかし実際はシンプルです。資産リターンを取り、相関を計算し、所与のリターンに対してリスクが最小になるように重みを決定するだけです。

最初は喜びました。ところが実際のFXデータでテストを始めてから、事態は変わりました。たとえばEURUSDの1年分の履歴データを使うと、リターン分布は全く正規分布になっていません。GBPUSDでも同じです。これはマーコウィッツ理論の根本的な前提です。つまり、計算はすべて水泡に帰すということです。

私は1週間ほど解決策を探しました。学術論文を漁り、Googleで検索し、フォーラムを読み漁りました。そこで再び出会ったのがVaR (Value at Risk)に関する記事でした。難しそうに聞こえますが、要は「95%（あるいは任意の確率）でどれくらい損失する可能性があるか」を計算するだけです。まずは最もシンプルな方法であるパラメトリックVaRを試しました。式は単純で、平均値からシグマを分位数分引くだけ。しかしパフォーマンスは正直イマイチでした。

次に試したのはヒストリカルVaRです。発想はシンプルで、実際の履歴を取り、ワースト5%のケースでどれだけ損失が出たかを見る方法です。これは現実にかなり近いですが、大量のデータが必要です。そして最後に残ったのはモンテカルロ法です。通貨ペア間の相関を考慮しつつ大量のランダムシナリオを生成し、ここでようやく現実的な結果が得られるようになりました。

最も難しかったのは、VaRとマーコウィッツ最適化をどう組み合わせるかという点でした。その結果生まれたのが、標準的な最適化をおこないつつ、VaR制約を追加するアプローチです。つまり「所与のリターンに対してリスクを最小化するが、VaRが一定レベルを超えないようにする」という方法です。

紙の上ではすべて完璧です。しかし問題は、それを実際にプログラムに落とし込むことです。次のセクションでは、これらの方程式をどのようにして実際のPythonコードに変換したかをお見せします。

PythonからMetaTrader 5への接続

私のシステムの実装は、まず取引端末との安定した接続を確立するところから始まりました。いくつかの方法を試した結果、最も信頼性が高く高速だったのは、Python用MetaTrader 5ライブラリを用いた直接接続でした。

import MetaTrader5 as mt5
import time

def initialize_mt5(account=12345, server="MetaQuotes-Demo", password="abc123"):
    if not mt5.initialize():
        print(f"initialize() failed, error code = {mt5.last_error()}")
        return False
        
    authorized = mt5.login(account, password=password, server=server)
    if not authorized:
        print(f"login failed, error code = {mt5.last_error()}")
        mt5.shutdown()
        return False
        
    return True

別の頭痛の種は、ブローカーのサーバーとローカルシステムとの時間同期でした。わずか数秒のズレでも、VaRの計算に深刻な問題を引き起こしかねません。そのため、特別な補正メカニズムを実装する必要がありました。

def get_time_correction():
    server_time = mt5.symbol_info_tick("EURUSD").time
    local_time = int(time.time())
    return server_time - local_time

def get_corrected_time():
    correction = get_time_correction()
    return int(time.time()) + correction

多くの時間を割いたのがデータ取得の最適化です。最初は各通貨ペアごとに個別にリクエストを送っていましたが、バッチ処理を導入したところ、処理速度は数倍に向上しました。

def fetch_data_batch(symbols, timeframe, start_pos, count):
    data = {}
    for symbol in symbols:
        rates = mt5.copy_rates_from_pos(symbol, timeframe, start_pos, count)
        if rates is not None and len(rates) > 0:
            data[symbol] = rates
        else:
            print(f"Failed to get data for {symbol}")
            return None
    return data

意外なことに、プログラムを正しく終了させるのは驚くほど難しい作業でした。そのため、特別な「グレースフルシャットダウン」手順を開発する必要がありました。

def safe_shutdown():
    try:
        positions = mt5.positions_get()
        if positions:
            for position in positions:
                close_position(position.ticket)
        
        orders = mt5.orders_get()
        if orders:
            for order in orders:
                mt5.order_send(request={"action": mt5.TRADE_ACTION_REMOVE,
                                      "order": order.ticket})
    finally:
        mt5.shutdown()

その結果、24時間稼働しても停止しない堅牢な基盤が完成しました。この基盤の上に、さらに複雑なポートフォリオ最適化ロジックを構築できるようになりました。しかし、それについては次のセクションでお話しすることにしましょう。

履歴データの取得とその前処理

マーケットデータを扱ってきた年月の中で、私はひとつの単純な真理を学びました。履歴データの品質は、あらゆる取引システムの成否を左右するということです。特にポートフォリオ最適化においては、データの誤りが連鎖的に影響を及ぼしかねません。

そこで、まずは信頼できる履歴取得システムを構築しました。最初のバージョンはかなり単純なものでしたが、実際の運用ですぐに欠点が露呈しました。クオートにはギャップやスパイクが含まれることがあり、時には明らかに誤った値さえ存在するのです。以下は、基本的な検証を組み込んだ最終的なデータ取得コードの例です。

def load_historical_data(symbols, timeframe, start_date, end_date):
    data_frames = {}
    for symbol in symbols:
        # Load with a reserve to compensate for gaps
        rates = mt5.copy_rates_range(symbol, timeframe, 
                                   start_date - timedelta(days=30), 
                                   end_date)
        if rates is None:
            print(f"Failed to load data for {symbol}")
            continue
            
        df = pd.DataFrame(rates)
        df['time'] = pd.to_datetime(df['time'], unit='s')
        df.set_index('time', inplace=True)
        
        # Basic anomaly check
        df = detect_and_remove_spikes(df)
        df = fill_gaps(df)
        data_frames[symbol] = df
    
    return data_frames

別の問題は週末のギャップ処理でした。最初は単純にこれらの日を削除していましたが、それではボラティリティ計算が歪んでしまいました。長い試行錯誤の末、各通貨ペアの特性を考慮した補間手法を導入するに至りました。

def fill_gaps(df, method='time'):
    if df.empty:
        return df
        
    # Check the intervals between points
    time_delta = df.index.to_series().diff()
    gaps = time_delta[time_delta > pd.Timedelta(hours=2)].index
    
    for gap_start in gaps:
        gap_end = df.index[df.index.get_loc(gap_start) + 1]
        # Create new points with interpolated values
        new_points = pd.date_range(gap_start, gap_end, freq='1H')[1:-1]
        
        for point in new_points:
            df.loc[point] = df.asof(point)
    
    return df.sort_index()

リターンを計算するためにいくつかの方法を試しました。単純なパーセンテージ変化ではノイズが多すぎることが分かりました。最終的に、対数リターンがVaRの推定に最も適しているという結論に至りました。

def calculate_returns(df):
    df['returns'] = np.log(df['close'] / df['close'].shift(1))
    df['rolling_std'] = df['returns'].rolling(window=20).std()
    df['rolling_mean'] = df['returns'].rolling(window=20).mean()
    
    # Clean out emissions using the 3-sigma rule
    mean = df['returns'].mean()
    std = df['returns'].std()
    df = df[abs(df['returns'] - mean) <= 3 * std]
    
    return df

データ検証システムの開発は重要なマイルストーンとなりました。各データセットは計算に使用される前に、複数段階のチェックを受けます。

def verify_data_quality(df, symbol):
    checks = {
        'missing_values': df.isnull().sum().sum() == 0,
        'price_continuity': (df['close'] > 0).all(),
        'timestamp_uniqueness': df.index.is_unique,
        'reasonable_returns': abs(df['returns']).max() < 0.1
    }
    
    if not all(checks.values()):
        failed_checks = [k for k, v in checks.items() if not v]
        print(f"Data quality issues for {symbol}: {failed_checks}")
        return False
        
    return True

市場の異常の取り扱いには特に注意を払いました。ニュースによる急激な値動きやフラッシュクラッシュなど、さまざまな事象がリスク評価を大きく歪める可能性があります。それらを正確に識別し処理するための特別なアルゴリズムを開発しました。

def detect_market_anomalies(df, window=20, threshold=3):
    volatility = df['returns'].rolling(window=window).std()
    typical_range = volatility.mean() + threshold * volatility.std()
    
    anomalies = df[abs(df['returns']) > typical_range].index
    if len(anomalies) > 0:
        print(f"Detected {len(anomalies)} market anomalies")
        
    return anomalies

その結果、信頼性の高いデータ処理パイプラインが構築され、すべての後続計算の基盤となりました。高品質な過去データは基盤であり、これがなければ効率的なポートフォリオ管理システムを構築することは不可能です。次のセクションでは、このデータがどのようにしてVaRの計算に使用されるかを考察します。

通貨ペアのVaR計算の実装

長期間にわたって過去データを扱った後、VaR計算の実装に取り組みました。最初は、既存の式をそのままコードに落とし込めば十分だと思われました。しかし実際には、FXの特殊性により標準的な手法の大幅な修正が必要であることがわかりました。

まず、3つの古典的なVaR計算手法の実装から始めました。パラメトリックアプローチは次のようになります。

def parametric_var(returns, confidence_level=0.95, holding_period=1):
    mu = returns.mean()
    sigma = returns.std()
    z_score = norm.ppf(1 - confidence_level)
    
    daily_var = -(mu + z_score * sigma)
    return daily_var * np.sqrt(holding_period)

しかし、FXにおいてリターンが正規分布に従うという仮定はしばしば成立しないことがすぐに明らかになりました。歴史的シミュレーションアプローチの方が、より信頼性が高いことがわかりました。

def historical_var(returns, confidence_level=0.95, holding_period=1):
    sorted_returns = np.sort(returns)
    index = int((1 - confidence_level) * len(sorted_returns))
    daily_var = -sorted_returns[index]
    return daily_var * np.sqrt(holding_period)

しかし、最も興味深い結果をもたらしたのはモンテカルロ法でした。私はこれを、外国為替市場の特性を考慮するように修正しました。

def monte_carlo_var(returns, confidence_level=0.95, holding_period=1, simulations=10000):
    mu = returns.mean()
    sigma = returns.std()
    
    # Consider auto correlation of returns
    corr = returns.autocorr()
    
    simulated_returns = []
    for _ in range(simulations):
        daily_returns = []
        last_return = returns.iloc[-1]
        
        for _ in range(holding_period):
            # Generate the next value taking auto correlation into account
            innovation = np.random.normal(0, 1)
            next_return = mu + corr * (last_return - mu) + sigma * np.sqrt(1 - corr**2) * innovation
            daily_returns.append(next_return)
            last_return = next_return
            
        total_return = sum(daily_returns)
        simulated_returns.append(total_return)
    
    return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

結果の検証には特に注意を払い、VaRの精度を確認するためのバックテストシステムも開発しました。

def backtest_var(returns, var, confidence_level=0.95):
    violations = (returns < -var).sum()
    expected_violations = len(returns) * (1 - confidence_level)
    
    z_score = (violations - expected_violations) / np.sqrt(expected_violations)
    p_value = 1 - norm.cdf(abs(z_score))
    
    return {
        'violations': violations,
        'expected': expected_violations,
        'z_score': z_score,
        'p_value': p_value
    }

通貨ペア間の相関関係を考慮するために、ポートフォリオVaRの計算を実装する必要がありました。

def portfolio_var(returns_df, weights, confidence_level=0.95, method='historical'):
    if method == 'parametric':
        portfolio_returns = returns_df.dot(weights)
        return parametric_var(portfolio_returns, confidence_level)
    
    elif method == 'historical':
        portfolio_returns = returns_df.dot(weights)
        return historical_var(portfolio_returns, confidence_level)
    
    elif method == 'monte_carlo':
        # Use the covariance matrix to generate
        # correlated random variables
        cov_matrix = returns_df.cov()
        L = np.linalg.cholesky(cov_matrix)
        
        means = returns_df.mean().values
        simulated_returns = []
        
        for _ in range(10000):
            Z = np.random.standard_normal(len(weights))
            R = means + L @ Z
            portfolio_return = weights @ R
            simulated_returns.append(portfolio_return)
            
        return -np.percentile(simulated_returns, (1 - confidence_level) * 100)

その結果、FXの特性に適応した柔軟なVaR計算システムが完成しました。次のセクションでは、これらの計算がポートフォリオ最適化のためのマーコウィッツ理論とどのように統合されるかを説明します。

マーコウィッツ法によるポートフォリオ最適化

信頼性の高いVaR計算を実装した後、ポートフォリオ最適化に注力し始めました。マーコウィッツの古典的理論は、FXの現実に合わせて大幅な調整が必要でした。数か月にわたる実験とテストを通じて、いくつかの重要な発見に至りました。

まず最初に気づいたのは、標準的なリスクとリターンの指標は、株式市場とは異なる動きをするということです。通貨ペア同士には、時間とともに変化する複雑な関係があります。多くの実験を重ねた結果、改良された期待リターン計算関数を開発しました。

def calculate_expected_returns(returns_df, method='ewma', halflife=30):
    if method == 'ewma':
        # Exponentially weighted average gives more weight to recent data
        return returns_df.ewm(halflife=halflife).mean().iloc[-1]
    elif method == 'capm':
        # Modified CAPM for Forex
        risk_free_rate = 0.02  # annual risk-free rate
        market_returns = returns_df.mean(axis=1)  # market returns proxy
        betas = calculate_currency_betas(returns_df, market_returns)
        return risk_free_rate + betas * (market_returns.mean() - risk_free_rate)

共分散行列の計算も見直しが必要でした。単純な過去データに基づく方法では、結果が不安定になりすぎることがありました。そこで、収縮推定を導入し、最適化のロバスト性を大幅に向上させました。

def shrinkage_covariance(returns_df, shrinkage_factor=None):
    sample_cov = returns_df.cov()
    n_assets = len(returns_df.columns)
    
    # The target matrix is diagonal with average variance
    target = np.diag(np.repeat(sample_cov.values.trace() / n_assets, n_assets))
    
    if shrinkage_factor is None:
        # Estimation of the optimal 'shrinkage' ratio
        shrinkage_factor = estimate_optimal_shrinkage(returns_df, sample_cov, target)
    
    shrunk_cov = (1 - shrinkage_factor) * sample_cov + shrinkage_factor * target
    return pd.DataFrame(shrunk_cov, index=sample_cov.index, columns=sample_cov.columns)

最も難しかったのは、ポートフォリオの重み最適化です。多くのテストを重ねた結果、改良版の二次計画法アルゴリズムを採用することにしました。

def optimize_portfolio(returns_df, expected_returns, covariance, target_return=None, constraints=None):
    n_assets = len(returns_df.columns)
    
    # Risk minimization function
    def portfolio_volatility(weights):
        return np.sqrt(weights.T @ covariance @ weights)
    
    # Limitations
    constraints = []
    # The sum of the weights is 1
    constraints.append({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
    
    if target_return is not None:
        # Target income limit
        constraints.append({
            'type': 'eq',
            'fun': lambda x: x @ expected_returns - target_return
        })
    
    # Add leverage restrictions for Forex
    constraints.append({
        'type': 'ineq',
        'fun': lambda x: 20 - np.sum(np.abs(x))  # max leverage 20
    })
    
    # Initial approximation - equal weights
    initial_weights = np.repeat(1/n_assets, n_assets)
    
    # Optimization
    result = minimize(
        portfolio_volatility,
        initial_weights,
        method='SLSQP',
        constraints=constraints,
        bounds=tuple((0, 1) for _ in range(n_assets))
    )
    
    if not result.success:
        raise OptimizationError("Failed to optimize portfolio: " + result.message)
        
    return result.x

解の安定性の問題には特に注意を払いました。入力データのわずかな変化でポートフォリオが大きく変わってしまうことがあってはなりません。このため、正則化の手法を開発しました。

def regularized_optimization(returns_df, current_weights, lambda_reg=0.1):
    # Add a penalty for deviation from the current weights
    def objective(weights):
        volatility = portfolio_volatility(weights)
        turnover_penalty = lambda_reg * np.sum(np.abs(weights - current_weights))
        return volatility + turnover_penalty

その結果、FXの特性を考慮し、頻繁なリバランスを必要としない信頼性の高いポートフォリオ最適化ツールが完成しました。しかし、最も重要なステップはまだ残っていました。それは、このアプローチをVaRベースのリスク管理システムと統合することです。

VaRとマーコウィッツの統合

この二つの手法を組み合わせることが、最も難しい課題であることがわかりました。両方の方法の利点を活かしつつ、互いに矛盾を生じさせない形で統合する必要がありました。数か月にわたる実験の結果、洗練された解決策を見出しました。

鍵となるアイデアは、VaRをマーコウィッツ最適化問題の追加制約として用いることです。コード上では次のようになります。

def integrated_portfolio_optimization(returns_df, target_return, max_var_limit, current_weights=None):
    n_assets = len(returns_df.columns)
    
    # Calculation of basic metrics
    exp_returns = calculate_expected_returns(returns_df)
    covariance = shrinkage_covariance(returns_df)
    
    def objective_function(weights):
        # Portfolio standard deviation (Markowitz)
        portfolio_std = np.sqrt(weights.T @ covariance @ weights)
        
        # component VaR
        portfolio_var = calculate_portfolio_var(returns_df, weights)
        var_penalty = max(0, portfolio_var - max_var_limit)
        
        return portfolio_std + 100 * var_penalty  # Penalty for exceeding VaR

市場の動的な性質を考慮するために、パラメータを再計算するための適応型システムを開発しました。

def adaptive_risk_limits(returns_df, base_var_limit, window=60):
    # Adapting VaR limits to current volatility
    recent_vol = returns_df.tail(window).std()
    long_term_vol = returns_df.std()
    vol_ratio = recent_vol / long_term_vol
    
    adjusted_var_limit = base_var_limit * np.sqrt(vol_ratio)
    return min(adjusted_var_limit, base_var_limit * 1.5)  # Limit growth

解の安定性の問題には特に注意を払う必要がありました。そのため、ポートフォリオの状態間を滑らかに移行させる仕組みを実装しました。

def smooth_rebalancing(old_weights, new_weights, max_change=0.1):
    weight_diff = new_weights - old_weights
    excess_change = np.abs(weight_diff) - max_change
    
    where_excess = excess_change > 0
    if where_excess.any():
        # Limit changes in weights
        adjustment = np.sign(weight_diff) * np.minimum(
            np.abs(weight_diff),
            np.where(where_excess, max_change, np.abs(weight_diff))
        )
        return old_weights + adjustment
    return new_weights

統合アプローチの効率を評価するための特別な指標を開発しました。

def evaluate_integrated_model(returns_df, weights, var_limit):
    # Calculation of performance metrics
    portfolio_returns = returns_df.dot(weights)
    realized_var = historical_var(portfolio_returns)
    sharpe = calculate_sharpe_ratio(portfolio_returns)
    var_efficiency = abs(realized_var - var_limit) / var_limit
    
    return {
        'sharpe_ratio': sharpe,
        'var_efficiency': var_efficiency,
        'max_drawdown': calculate_max_drawdown(portfolio_returns),
        'turnover': calculate_turnover(weights)
    }

テストの結果、このモデルは特にボラティリティが高い時期に優れた性能を発揮することがわかりました。VaRの要素がリスクを効果的に制限する一方で、マーコウィッツ最適化は引き続き収益の機会を追求します。

システムの最終バージョンには、自動パラメータ調整の仕組みも組み込まれています。

def auto_tune_parameters(returns_df, initial_params, optimization_window=252):
    best_params = initial_params
    best_score = float('-inf')
    
    for var_limit in np.arange(0.01, 0.05, 0.005):
        for shrinkage in np.arange(0.2, 0.8, 0.1):
            params = {'var_limit': var_limit, 'shrinkage': shrinkage}
            score = backtest_model(returns_df, params, optimization_window)
            
            if score > best_score:
                best_score = score
                best_params = params
                
    return best_params

次のセクションでは、この統合モデルが実際の取引における動的なポジション管理にどのように応用されるかを説明します。

動的ポジションサイズ管理

理論モデルを実際の取引システムに落とし込むには、多くの技術的課題を解決する必要がありました。主な課題は、現在の市場状況と計算された最適ポートフォリオの重みを考慮した、ポジションサイズの動的管理です。

システムの基盤となるのは、ポジション管理用のクラスでした。

class PositionManager:
    def __init__(self, account_balance, risk_limit=0.02):
        self.balance = account_balance
        self.risk_limit = risk_limit
        self.positions = {}
        
    def calculate_position_size(self, symbol, weight, var_estimate):
        symbol_info = mt5.symbol_info(symbol)
        pip_value = symbol_info.trade_tick_value * 10
        
        # Calculate the position size taking into account VaR
        max_risk_amount = self.balance * self.risk_limit * abs(weight)
        position_size = max_risk_amount / (abs(var_estimate) * pip_value)
        
        # Round to minimum lot
        return round(position_size / symbol_info.volume_step) * symbol_info.volume_step

ポジションを滑らかに変更するために、部分的注文の仕組みを開発しました。

def adjust_positions(self, target_positions):
    for symbol, target_size in target_positions.items():
        current_size = self.get_current_position(symbol)
        if abs(target_size - current_size) > self.min_adjustment:
            # Break big changes into pieces
            steps = min(5, int(abs(target_size - current_size) / self.min_adjustment))
            step_size = (target_size - current_size) / steps
            
            for i in range(steps):
                next_size = current_size + step_size
                self.execute_order(symbol, next_size - current_size)
                current_size = next_size
                time.sleep(1)  # Prevent order flooding

ポジションを変更する際には、リスク管理に特に注意しました。

def execute_order(self, symbol, size_delta, max_slippage=10):
    if size_delta > 0:
        order_type = mt5.ORDER_TYPE_BUY
    else:
        order_type = mt5.ORDER_TYPE_SELL
    
    # Get current prices
    tick = mt5.symbol_info_tick(symbol)
    
    # Set VaR-based stop loss
    if order_type == mt5.ORDER_TYPE_BUY:
        stop_loss = tick.bid - (self.var_estimates[symbol] * tick.bid)
        take_profit = tick.bid + (self.var_estimates[symbol] * 2 * tick.bid)
    else:
        stop_loss = tick.ask + (self.var_estimates[symbol] * tick.ask)
        take_profit = tick.ask - (self.var_estimates[symbol] * 2 * tick.ask)
    
    request = {
        "action": mt5.TRADE_ACTION_DEAL,
        "symbol": symbol,
        "volume": abs(size_delta),
        "type": order_type,
        "price": tick.ask if order_type == mt5.ORDER_TYPE_BUY else tick.bid,
        "sl": stop_loss,
        "tp": take_profit,
        "deviation": max_slippage,
        "magic": 234000,
        "comment": "var_based_adjustment",
        "type_time": mt5.ORDER_TIME_GTC,
        "type_filling": mt5.ORDER_FILLING_IOC,
    }
    
    result = mt5.order_send(request)
    return self.handle_order_result(result)

急激な市場変動から守るために、ボラティリティ監視システムを追加しました。

def monitor_volatility(self, returns_df, threshold=2.0):
    # Current volatility calculation
    current_vol = returns_df.tail(20).std() * np.sqrt(252)
    historical_vol = returns_df.std() * np.sqrt(252)
    
    if current_vol > historical_vol * threshold:
        # Reduce positions in case of increased volatility
        self.reduce_exposure(current_vol / historical_vol)
        return False
        
    return True

システムには、リスクが臨界レベルに達した際に自動でポジションをクローズする仕組みも組み込まれています。

def emergency_close(self, max_loss_percent=5.0):
    total_loss = sum(pos.profit for pos in mt5.positions_get())
    if total_loss < -self.balance * max_loss_percent / 100:
        print("Emergency closure triggered!")
        for position in mt5.positions_get():
            self.close_position(position.ticket)

その結果、多様な市場環境において効果的に運用できる堅牢なポジション管理システムが実現します。次のセクションでは、VaRベースのリスク管理システムに焦点を当てます。

ポートフォリオリスク管理システム

動的なポジション管理を導入した後、ポートフォリオ全体の包括的なリスク管理システムを構築する必要に直面しました。経験上、個別ポジションごとの局所的なリスク管理だけでは不十分であり、全体的なアプローチが求められることが分かっています。

まず最初に、ポートフォリオリスクを監視するためのクラスを作成しました。

class PortfolioRiskManager:
    def __init__(self, max_portfolio_var=0.03, max_correlation=0.7, max_drawdown=0.1):
        self.max_portfolio_var = max_portfolio_var
        self.max_correlation = max_correlation
        self.max_drawdown = max_drawdown
        self.current_drawdown = 0
        self.peak_balance = 0
        
    def update_portfolio_metrics(self, positions, returns_df):
        # Calculation of current portfolio weights
        total_exposure = sum(abs(pos.volume) for pos in positions)
        weights = {pos.symbol: pos.volume/total_exposure for pos in positions}
        
        # Update portfolio VaR
        self.current_var = self.calculate_portfolio_var(returns_df, weights)
        
        # Check correlations
        self.check_correlations(returns_df, weights)

特に、銘柄間の相関関係の監視に注力しました。

def check_correlations(self, returns_df, weights):
    corr_matrix = returns_df.corr()
    high_corr_pairs = []
    
    for i in returns_df.columns:
        for j in returns_df.columns:
            if i < j and abs(corr_matrix.loc[i,j]) > self.max_correlation:
                if weights.get(i, 0) > 0 and weights.get(j, 0) > 0:
                    high_corr_pairs.append((i, j, corr_matrix.loc[i,j]))
                    
    if high_corr_pairs:
        self.handle_high_correlations(high_corr_pairs, weights)

市場の状況に応じて動的なリスク管理を実施しました。

def adjust_risk_limits(self, market_state):
    volatility_factor = market_state.get('volatility_ratio', 1.0)
    trend_strength = market_state.get('trend_strength', 0.5)
    
    # Adapt limits to market conditions
    self.max_portfolio_var *= np.sqrt(volatility_factor)
    if trend_strength > 0.7:  # Strong trend
        self.max_drawdown *= 1.2  # Allow a big drawdown
    elif trend_strength < 0.3:  # Weak trend
        self.max_drawdown *= 0.8  # Reduce the acceptable drawdown

ドローダウン監視システムは特に興味深いものであることがわかりました。

def monitor_drawdown(self, current_balance):
    if current_balance > self.peak_balance:
        self.peak_balance = current_balance
    
    self.current_drawdown = (self.peak_balance - current_balance) / self.peak_balance
    
    if self.current_drawdown > self.max_drawdown:
        return self.handle_excessive_drawdown()
    elif self.current_drawdown > self.max_drawdown * 0.8:
        return self.reduce_risk_exposure(0.8)
    
    return True

極端な事態に備えてストレステストシステムを追加しました。

def stress_test_portfolio(self, returns_df, weights, scenarios=1000):
    results = []
    
    for _ in range(scenarios):
        # Simulate extreme conditions
        stress_returns = returns_df.copy()
        
        # Increase volatility
        vol_multiplier = np.random.uniform(1.5, 3.0)
        stress_returns *= vol_multiplier
        
        # Add random shocks
        shock_magnitude = np.random.uniform(-0.05, 0.05)
        stress_returns += shock_magnitude
        
        # Calculate losses in a stress scenario
        portfolio_return = (stress_returns * weights).sum(axis=1)
        results.append(portfolio_return.min())
    
    return np.percentile(results, 1)  # 99% VaR in case of a stress

その結果、過度なリスクを効果的に防ぎ、高ボラティリティ期を乗り切るための多層的な資本保護システムが構築されました。次のセクションでは、これらすべてのコンポーネントが実際の取引においてどのように連携して機能するのかを説明します。

分析結果の可視化

可視化は、私の研究において重要な段階となりました。すべての計算モジュールを実装した後、その結果を視覚的に表現する必要がありました。そこで、システムのパフォーマンスをリアルタイムで監視するのに役立つ、いくつかの主要なグラフィカルコンポーネントを開発しました。

まずは、ポートフォリオの構造とその推移を可視化することから始めました。

def plot_portfolio_composition(weights_history):
    plt.figure(figsize=(15, 8))
    ax = plt.gca()
    
    # Create a graph of weight changes over time
    dates = weights_history.index
    bottom = np.zeros(len(dates))
    
    for symbol in weights_history.columns:
        plt.fill_between(dates, bottom, bottom + weights_history[symbol], 
                        label=symbol, alpha=0.6)
        bottom += weights_history[symbol]
    
    plt.title('Evolution of portfolio structure')
    plt.legend(bbox_to_anchor=(1.05, 1), loc='upper left')
    plt.grid(True, alpha=0.3)

リスクの可視化には特に注意が払われました。また、さまざまな通貨ペアのVaRヒートマップも作成しました。

def plot_var_heatmap(var_matrix):
    plt.figure(figsize=(12, 8))
    sns.heatmap(var_matrix, annot=True, cmap='RdYlBu_r', 
                fmt='.2%', center=0)
    plt.title('Portfolio risk map (VaR)')
    
    # Add a timestamp
    plt.annotate(f'Last update: {datetime.now().strftime("%Y-%m-%d %H:%M")}',
                xy=(0.01, -0.1), xycoords='axes fraction')

収益性を分析するために、重要なイベントを強調表示したインタラクティブなチャートを作成しました。

def plot_performance_analytics(returns_df, var_values, significant_events):
    fig = plt.figure(figsize=(15, 10))
    gs = GridSpec(2, 1, height_ratios=[3, 1])
    
    # Returns graph
    ax1 = plt.subplot(gs[0])
    cumulative_returns = (1 + returns_df).cumprod()
    ax1.plot(cumulative_returns.index, cumulative_returns, 
             label='Portfolio returns')
    
    # Mark important events
    for date, event in significant_events.items():
        ax1.axvline(x=date, color='r', linestyle='--', alpha=0.3)
        ax1.annotate(event, xy=(date, ax1.get_ylim()[1]),
                    xytext=(10, 10), textcoords='offset points',
                    rotation=45)
    
    # VaR graph
    ax2 = plt.subplot(gs[1])
    ax2.fill_between(var_values.index, -var_values, 
                     color='lightblue', alpha=0.5,
                     label='Value at Risk')

ポートフォリオのステータスを監視するためのインタラクティブなダッシュボードを追加しました。

class PortfolioDashboard:
    def __init__(self):
        self.fig = plt.figure(figsize=(15, 10))
        self.setup_subplots()
        
    def setup_subplots(self):
        gs = self.fig.add_gridspec(3, 2)
        self.ax_returns = self.fig.add_subplot(gs[0, :])
        self.ax_weights = self.fig.add_subplot(gs[1, 0])
        self.ax_risk = self.fig.add_subplot(gs[1, 1])
        self.ax_metrics = self.fig.add_subplot(gs[2, :])
        
    def update(self, portfolio_data):
        self._plot_returns(portfolio_data['returns'])
        self._plot_weights(portfolio_data['weights'])
        self._plot_risk_metrics(portfolio_data['risk'])
        self._update_metrics_table(portfolio_data['metrics'])
        
        plt.tight_layout()
        plt.show()

相関関係を分析するために動的な視覚化を開発しました。

def plot_correlation_dynamics(returns_df, window=60):
    # Calculation of dynamic correlations
    correlations = returns_df.rolling(window=window).corr()
    
    # Create an animated graph
    fig, ax = plt.subplots(figsize=(10, 10))
    
    def update(frame):
        ax.clear()
        sns.heatmap(correlations.loc[frame], 
                    vmin=-1, vmax=1, center=0,
                    cmap='RdBu', ax=ax)
        ax.set_title(f'Correlations on {frame.strftime("%Y-%m-%d")}')

これらすべての可視化、ポートフォリオの状態を迅速に評価し、取引の決定を下すのに役立ちます。次のセクションでは、システムをテストします。

戦略バックテスト

システムの全コンポーネントの開発を終えた後、徹底的なテストをおこなう必要に直面しました。そのプロセスは、単に過去データを流すだけよりもはるかに複雑でした。スリッページ、手数料、そしてブローカーごとの注文執行の特徴といった多くの要因を考慮する必要があったのです。

最初のバックテストの試みでは、固定スプレッドを用いた従来の手法では結果が過度に楽観的になることが分かりました。ボラティリティや時間帯によってスプレッドが変動する点を考慮した、より現実的なモデルを構築する必要がありました。

また、データの欠損や流動性の問題をモデル化することにも特に注意を払いました。実際の取引では、注文が想定価格で約定できない状況がしばしば発生します。こうしたシナリオをテスト段階で正しく処理することが不可欠です。

以下に、バックテストシステムの完全な実装を示します。

class PortfolioBacktester:
    def __init__(self, initial_capital=100000, commission=0.0001):
        self.initial_capital = initial_capital
        self.commission = commission
        self.positions = {}
        self.trades_history = []
        self.balance_history = []
        self.var_history = []
        self.metrics = {}
        
    def run_backtest(self, returns_df, optimization_params):
        self.current_capital = self.initial_capital
        portfolio_returns = []
        
        # Preparing sliding windows for calculations
        window = 252  # Trading yesr
        for i in range(window, len(returns_df)):
            # Receive historical data for calculation
            historical_returns = returns_df.iloc[i-window:i]
            
            # Optimize the portfolio
            weights = self.optimize_portfolio(
                historical_returns, 
                optimization_params['target_return'],
                optimization_params['max_var']
            )
            
            # Calculate VaR for the current distribution
            current_var = self.calculate_portfolio_var(
                historical_returns, 
                weights,
                optimization_params['confidence_level']
            )
            
            # Check the need for rebalancing
            if self.should_rebalance(weights, current_var):
                self.execute_rebalancing(weights, returns_df.iloc[i])
            
            # Update positions and calculate profitability
            portfolio_return = self.update_positions(returns_df.iloc[i])
            portfolio_returns.append(portfolio_return)
            
            # Update metrics
            self.update_metrics(portfolio_return, current_var)
            
            # Check stop losses triggering
            self.check_stop_losses(returns_df.iloc[i])
        
        # Calculate the final metrics
        self.calculate_final_metrics(portfolio_returns)
        
    def optimize_portfolio(self, returns, target_return, max_var):
        # Using our hybrid optimization model
        opt = HybridOptimizer(returns, target_return, max_var)
        weights = opt.optimize()
        return self.apply_position_limits(weights)
        
    def execute_rebalancing(self, target_weights, current_prices):
        for symbol, target_weight in target_weights.items():
            current_weight = self.get_position_weight(symbol)
            if abs(target_weight - current_weight) > self.REBALANCING_THRESHOLD:
                # Simulate execution with slippage
                slippage = self.simulate_slippage(symbol, current_prices[symbol])
                trade_price = current_prices[symbol] * (1 + slippage)
                
                # Calculate the deal size
                trade_volume = self.calculate_trade_volume(
                    symbol, current_weight, target_weight
                )
                
                # Consider commissions
                commission = abs(trade_volume * trade_price * self.commission)
                self.current_capital -= commission
                
                # Set a deal to history
                self.record_trade(symbol, trade_volume, trade_price, commission)
                
    def update_metrics(self, portfolio_return, current_var):
        self.balance_history.append(self.current_capital)
        self.var_history.append(current_var)
        
        # Updating performance metrics
        self.metrics['max_drawdown'] = self.calculate_drawdown()
        self.metrics['sharpe_ratio'] = self.calculate_sharpe()
        self.metrics['var_efficiency'] = self.calculate_var_efficiency()
        
    def calculate_final_metrics(self, portfolio_returns):
        returns_series = pd.Series(portfolio_returns)
        
        self.metrics['total_return'] = (self.current_capital / self.initial_capital - 1)
        self.metrics['volatility'] = returns_series.std() * np.sqrt(252)
        self.metrics['sortino_ratio'] = self.calculate_sortino(returns_series)
        self.metrics['calmar_ratio'] = self.calculate_calmar()
        self.metrics['var_breaches'] = self.calculate_var_breaches()
        
    def simulate_slippage(self, symbol, price):
        # Simulate realistic slippage
        base_slippage = 0.0001  # Basic slippage
        time_factor = self.get_time_factor()  # Time dependency
        volume_factor = self.get_volume_factor(symbol)  # Volume dependency
        
        return base_slippage * time_factor * volume_factor

テストの結果は非常に示唆的でした。ハイブリッドモデルは、従来の手法と比べて市場ショックに対する耐性が明らかに高いことが示されました。特に高ボラティリティ期において、VaRリミットが過剰なリスクからポートフォリオを効果的に保護した点は顕著でした。

最終デバッグ

数か月にわたる開発とテストを経て、ついにシステムの最終バージョンに到達しました。正直に言うと、当初の計画とは大きく異なるものになりました。実運用の過程で多くの修正を余儀なくされ、その中には予想外のものも少なくありませんでした。

最初の大きな変更はデータの扱い方でした。システムを過去データだけでテストするのでは不十分であり、様々な市場環境における挙動を確認する必要があると気づいたのです。そこで、合成データを生成する仕組みを開発しました。一見シンプルに思えますが、実際には数週間を要しました。

まず、すべての通貨ペアを流動性に基づいてグループに分けました。最初のグループは主要通貨ペア（EURUSD、GBPUSD）。次に資源国通貨ペア（AUDUSD、USDCAD）。その次がクロス（EURJPY、GBPJPYなど）。最後がエキゾチック（CADJPY、EURAUDなど）です。それぞれのグループに対して、できる限り実際に近いボラティリティと相関パラメータを設定しました。

しかし本当に面白くなったのは、市場モードを導入してからでした。たとえば、3分の1の期間は穏やかで低ボラティリティ、3分の1は通常の取引環境、残りは高ボラティリティで相場が大きく荒れる状況です。さらに、長期トレンドや循環的な変動も加えました。結果として、かなりリアルな市場環境に近いものが出来上がりました。

ポートフォリオ最適化も工夫が必要でした。当初は単純にポジション比率の制限で済ませようと思いましたが、それでは不十分だと気づきました。そこで動的なリスクプレミアムを導入しました。つまり、ボラティリティが高い通貨ペアほど期待リターンも高く設定するのです。さらに制約として、1ポジションの最低4%、最大25%という範囲を設けました。一見大きな数字に見えますが、レバレッジを考慮すれば妥当です。

レバレッジについても別の課題がありました。当初はほとんど使わずに安全策をとっていましたが、分析の結果、10倍程度の中程度のレバレッジを利用することでパフォーマンスが大きく改善することが分かりました。重要なのはコストを正しく織り込むことです。取引手数料（2bp）、レバレッジ維持金利（日次0.01%）、執行スリッページなど、多数のコストを最適化エンジンに組み込みました。

さらに頭を悩ませたのがマージンコール対策です。いくつかの失敗を経た末、シンプルな解決策に落ち着きました。ドローダウンが10%を超えたら全ポジションをクローズし、資本の一部を必ず保全するというルールです。保守的に聞こえるかもしれませんが、長期的には非常に有効でした。

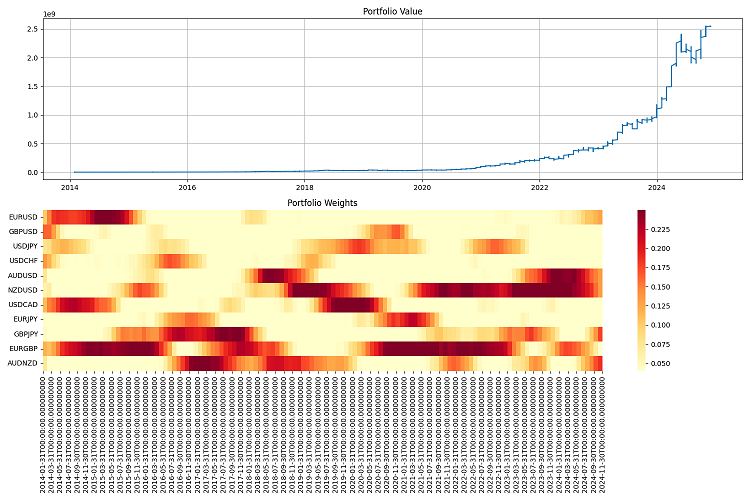
最も難しかったのはレポーティングでした。数十の通貨ペアを扱い、常に売買を繰り返すシステムでは、全体を把握するのは不可能です。そこで監視システムを開発し、膨大な指標を含む年次レポートや、ポートフォリオ価値の推移から重み分布のヒートマップまで、多彩なグラフを作成できるようにしました。

最終テストは2000年から2024年までの長期間で実施しました。初期資本を100万ドルとし、四半期ごとにリバランスしました。結果には満足しています。システムはさまざまな市場環境に適応し、リスクを管理下に置くことができました。深刻な危機の中でも資本の大部分を守り抜くことができたのです。

もちろん、まだ課題は残っています。ボラティリティ予測に機械学習を導入したいと考えています。現状では過去データに依存しているためです。また、レバレッジ管理をさらに柔軟にする方法も検討しています。リバランス頻度についても最適化の余地があります。四半期では長すぎる場合もあれば、半年間ポジションを維持できる場合もあるのです。

全体的に、当初の計画とはまったく異なる形になりました。しかし「最善は善の敵」という言葉があるように、このシステムは機能し、リスクを管理し、利益を生み出しています。それこそが最も重要なことです。

結論

本当に面白い道のりでした。最初にマーコウィッツ理論をいじり始めたときには、まさかこんな形になるとは想像もしていませんでした。ただ単に従来のアプローチをFXに適用したかっただけなのに、最終的には複数のリスク管理手法をつぎはぎした「フランケンシュタイン的な怪物」を作り上げることになったのです。

一番すごいのは、マーコウィッツとVaRを組み合わせることができた点です。そして、この仕組みは本当に機能します。面白いのは、どちらの手法も単独では平凡な結果しか出さなかったのに、組み合わせると素晴らしい成果を生むということです。特に市場が大きく揺れる局面での安定性には非常に満足しています。最適化の中でVaRがリミッターとして働くのは驚異的です。

もちろん、技術的な部分では多くの苦労がありました。しかし今では、スリッページ、手数料、執行特性まですべて考慮されています。

2000年から2024年までの過去データでシステムをテストしました。結果はかなり良好で、さまざまな市場環境に適応でき、危機の最中でも崩壊することはありませんでした。10倍レバレッジで運用すると、まるで時計仕掛けのように機能します。大切なのは、リスクを厳格にコントロールすることです。

とはいえ、まだやるべきことは山ほどあります。例えば：

• ボラティリティ予測に機械学習を導入する（これが次回の記事のテーマになります）
• リバランス頻度を整理する ― 最適化できる可能性がある
• レバレッジ管理をより賢くする（将来の記事では、動的レバレッジや動的な「スマート」入金の仕組みも実装予定）
• 異なる市場環境にさらに適応できるようにシステムを訓練する

全体としての主な結論はこうです。優れた取引システムとは、単なる教科書の方程式ではありません。市場を理解し、テクノロジーに精通し、特にリスクをコントロールする能力が重要です。これらの開発成果は、今やFXだけでなく他の市場にも応用できます。成長の余地はまだありますが、すでに基盤は整っており、機能しています。