ニューラルネットワークの実践：ニューロンのスケッチ

はじめに

皆さん、こんにちは。そしてニューラルネットワークに関する新たな記事へようこそ

前回の「ニューラルネットワークの実践：擬似逆行列(II)」では、専用計算システムの重要性と、その開発の背景について解説しました。今回の記事では、このテーマをさらに掘り下げていきます。この段階の内容を説明するのは決して簡単なことではありません。一見すると単純に思えるかもしれませんが、実は大きな混乱を招きやすい概念です。直感的に理解できそうでいて、実際には誤解を生みやすいものを説明するのは、なかなか難しい作業です。

では、今回の記事では何を扱うのでしょうか。本連載の目的は、ニューラルネットワークがどのように学習するのかを示すことです。これまで、ニューラルネットワークが異なるデータポイント間の相関関係をどのように確立するのかを探ってきました。ただし、これまでの方法は、前処理され、フィルタリングされたデータセットに対してのみ適用できるものでした。こうしたデータ環境では、ニューラルネットワークは既存の情報をもとに最適解を導き出せます。しかし、もしデータがフィルタリングされていない場合はどうなるのでしょうか。そのような状況で、ニューラルネットワークはどのようにして相関関係を見出すのでしょうか。ここで多くの人が誤解するのは、ニューラルネットワークが何らかのインテリジェンスを持っていると考えることです。人間のように自律的に物事を分類する方法を「学習する」と仮定しているのです。

この一般的な誤解が、ニューラルネットワークの説明を特に難しくしています。多くの場合、それを理解しようとする人々は、たとえデータ同士が何らかの関係を持っていたとしても、さまざまな種類の情報を選別する方法についての基本的な知識を欠いています。この点が、仕事をしたことがない人にとっては最も分かりにくい点です。その結果、説明を誤って解釈し、神経回路網がどのように機能するかについてさらなる混乱を招く可能性があります。

誤解のないように言っておきますが、私はニューラルネットワークが人間のように学習すると言っているのではありません。そこに何らかの「知性」が隠されているわけでもありません。もし隠されていると考えている方がいれば、それは間違いです。ニューラルネットワークはあくまで複雑な数式に過ぎません。しかし、この数式には、データを分析し、分類する驚異的な能力があります。データセットが一度分類されると、それに似た新しいデータポイントは、既存のカテゴリーに属する確率を割り当てられます。

この概念については、以前の記事でも取り上げましたが、今回は少し異なるアプローチを取ります。この方法は、シンプルでありながらも興味深いものです。基礎の基礎からスタートし、人工ニューロンを使ったニューラルネットワークの構築へと、少しずつ積み上げていきます。

基礎

私たちが情報を示すとき、ニューラルネットワークがどのように学習するのかを本当に理解するためには、人工知能やニューラルネットワークについて自分が知っていると思っていることをすべて忘れていただきたいと思います。あなたが知っている（と思っている）ことの多くは、特にニュースサイトや他の類似の情報源から得たものであれば、純粋なナンセンスや誤った情報である可能性が高いです。ニューラルネットワークというテーマが世間に広まったのは、主に一部の起業家がそれを金儲けの手段として考えたからですが、実際にはニューラルネットワークは何十年も前から開発されています。それは新しい技術でもなく、しばしば描かれているように機能しているわけでもありません。それは非常に有用ではありますが、主にプログラミングに強い関心を持つ人々に関連しています。

その本質的な部分では、すべてのニューラルネットワーク（人工知能と呼ばれることもあります）は、以前の記事で説明した単純な数学的原理に基づいています。ここでは、この概念についてさらに詳しく見ていきます。これが割線です。他の人たちがどう言おうと、ニューラルネットワークのすべては、この基本的な概念に集約されます。つまり、接線を近似する割線を見つけることです。実際、これは非常にシンプルなことです。

これまでの議論では、このステップを省略し、接線の特定に直接進みました。これが先に紹介した公式の説明となります。これらの公式は、プロセスをショートカットし、接線に直接到達するように特別に設計されています。このすべては、非常に特定の事実に関連しています。それは、私たちがデータベース内でフィルタリングし、選別された情報を持っている場合に当てはまります。このような場合、割線は必要なく、接線に直行し、このデータセットの内容を最もよく反映する数式を作成します。したがって、検索プログラムがこのデータセットに問い合わせると、与えられた情報に関してほぼ完璧な結果を返すことができます。多くの人はこの種のプログラムを人工知能と呼びます。しかし、データセットが不完全であったり、構造化されていない場合、別のアプローチが必要です。ニューラルネットワークは、一見無関係に見えるデータポイント間の相関関係を確立する必要があります。このプロセスは「訓練」として知られています。簡単に言うと、最初は相関関係がないように見える生データを、系統的にニューラルネットワークに入力していきます。ネットワークは徐々に接線を近似するように学び、このプロセスは最終的に、AIシステムが有用な予測を生成するための数式を生み出します。これは、ネットワークが未知のデータに対しても、たとえば人間がソートしたデータを使ってテストするときに確認されます。

この仕組みが理解できたかどうかはわかりませんが、プログラマーではないものの、すでに金融市場での経験がある方々に向けて、もう少しわかりやすく説明しましょう。マーケットでの仕事を始めるとき、最初に行うべきことは「バックテスト」と呼ばれる作業です。取引モデルを選択し、チャートにアクセスして、そのモデルが現れるすべてのシグナルを探します。これはニューラルネットワークの「訓練」段階に相当します。モデルが一定の期間完全にテストされたら、次に進むのは「テスト」段階です。ここでは、ランダムな時間枠を選び、そのモデルが有効かどうかを検証します。もしパターンがあまり明白でない場合でも、一貫してモデルを認識できれば、それは効果的に内面化され、数学的に表現できるようになったということです。最後のステップは「ブラインドテスト」です。ここではデモ口座を使って市場に参加し、数学的モデルが信頼できるかを評価します。もしこれを経験したことがあれば、100%の正確性はないことを知っているでしょう。システムには常に誤差の余地があります。それでも、誤差の少ないモデルは有効であると見なされます。

これこそがニューラルネットワークが目指すものです。すなわち、手書き文字、顔認識、分子構造、植物の種、動物、音、画像、あるいは他のあらゆる分類パターンを認識できる方程式を立てることです。

さて、次のトピックに進み、どのようにしてこれを実現するのかを見ていきましょう。

ニューロン

さて、前回までのトピックをカバーしたところで、作成できる最も単純なもの、つまり単一ニューロンから始めましょう。しかし、その重要性を過小評価してはいけません。まずは単一ニューロンから始めますが、複雑さはすぐにエスカレートします。そのため、各要素を理解しながら、計画的に進めることをお勧めします。この漸進的なアプローチは、ニューラルネットワークアーキテクチャ全体を構築し始めるときに非常に重要になります。

では、次のコードから始めましょう。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    Print("The first neuron...");
}
//+------------------------------------------------------------------+

この一見面白みのないコードは、単にターミナルにメッセージを表示するだけです。それだけです。しかし、これはスクリプトであり、サービスになる可能性があることに留意してください。とりあえず、シンプルなスクリプトとして残しておきましょう。では、神経細胞は何をするのでしょうか。千差万別のことを考えることができるが、それらを1つの共通の目標に落とし込んでみてほしい。これは最初の部分であり、神経細胞が実行しなければならない1つのタスクにすべてが集約されます。

ニューロンは、計算を実行する方法を知っている必要があります。これが重要なのは、何らかの情報を返さなければならないからです。しかし、これらの計算がどのようなものかはまだわかっておらず、ニューロンの訓練に必要なデータしかありません。そこで、上記のコードを修正し、以下のようなコードにしました。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };

    Print("The first neuron...");
}
//+------------------------------------------------------------------+

明らかに、訓練データを見ただけで、そこに何らかのパターンがあることはすぐにわかります。つまり、最初の数字を2倍します。しかし、私たちのニューロンはまだそれを知りません。私たちが求めているのは、数値が与えられたときに正しい答えを出せるように、方程式の立て方を学ばせることです。その後、ニューロンは学習した内容に基づいて、作成した方程式を使って出力を生成します。

でも、どうやって神経細胞にこの公式を発見させるのでしょうか。そして、ここにキャッチがあります。過去の記事の知識をそのまま使うことはできないのです。では、読者の皆さん、どうすればニューロンに訓練データを最もよく表す方程式を見つけさせることができるでしょうか。

ここで多くの人が混乱しがちです。私たちがやろうとしているのは、単にニューロンにランダムな値から始めるように指示し、それを正しい数式を見つけるための基礎として使うことです。これは重要な誤解です。掛け算に使われるべき正確な数を探すようにニューロンに言っているのではありません。結局のところ、足し算や割り算、あるいはランダムなデータを使う可能性もあります。私たちが実際に求めているのは、ニューロンに方程式を求めることであり、単なる1つの値を求めることではありません。私たちが使わせている初期値は、出発点に過ぎません。では、コードをもう少し洗練させてみましょう。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
}
//+------------------------------------------------------------------+

これからさらに前進していきますが、その前に重要な点を確認しておきましょう。通常、MathSrand関数を使用する際には、システムクロックの値で初期化します。これにより、乱数生成器が起動するたびに異なる値から始まることが保証されます。ただし、ここで注意が必要なのは、生成される数字は完全な乱数ではなく、あくまで「疑似乱数」であるという点です。つまり、完全に予測不能ではないものの、次の値を推測するのは非常に困難であるという特性を持っています。ここでは、開始点を制御するためにMathSrandに明示的な初期値を設定し、一貫性のあるテストを可能にしています。そして、ここで本当に注目すべきなのは、変数weightに格納されている値です。この値は、ニューロンが適切な方向に進んでいるかどうかを示します。初期値としてランダムな値が設定されるため、この段階ではまだ方向は決まっていません。

weightの値は0から1の範囲に収まるようになっています。これは、使用しているマクロ内でrand関数の結果をその戻り値の最大値で割っているためです。詳しくはドキュメントをご参照ください。この範囲に制限することで、後のステップを簡単にしていますが、もし必要であればrandの生の値をそのまま使用することも可能です。ただし、その場合、後続の計算で追加の調整が必要になることはご承知おきください。

では、いよいよ結果を見ていきましょう。私たちのニューロンは形を作り始めています。しかし、その前に、まず最初の数式を定義しなければなりません。何もないところからは何も生まれません。ニューラルネットワークには、どのように機能すべきかを教える必要があります。ゼロから自らを形成することはできません。数学の基本的な理解があれば、最も単純な方程式から複雑な多項式に至るまで、すべてが単一の基本概念に還元されることを知っているはずです。それが「微分」です。ただし、ここで必要なのは単なる微分ではなく、できるだけシンプルなものです。前回の記事で、直線の方程式が最も単純な数式であることを説明しました。あらゆる多項式や方程式は、微分を繰り返すことでこの一次方程式に還元されます。最終的に定数に収束する場合もありますが、それでは私たちにとって有益ではありません。私たちが求めているのは、最小限の計算ツールとして機能する「導関数」です。ここで、次の方程式に戻りましょう。

この段階では、微分の順序自体は重要ではありません。ここで大切なのは、単純化しすぎると定数になってしまい、その場合には役に立たなくなるという点です。ただし、定数b（切片）については、現時点ではゼロとみなします。一方で、定数a（傾き）は、重みとして格納された値に設定します。このアプローチを採用することで、以下のようにコードをさらに洗練させることができます。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, x;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    for (uint c = 0; c < Train.Size() / 2; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
    }
}
//+------------------------------------------------------------------+

このコードを実行すると、MetaTraderターミナルに下図のような画像が表示されます。

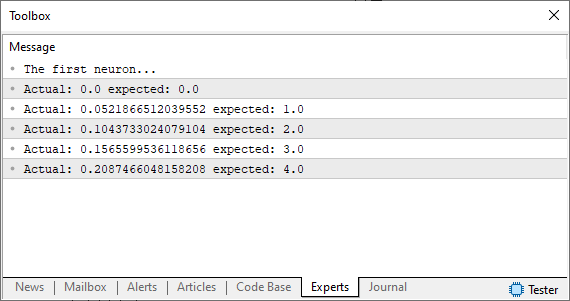
私たちは、ある仮定を用いています。それは、私たちが求めるものや期待するものに必ずしも近くない、同じ乱数を使用しているということです。この状況をどのように改善できるでしょうか。さて、基本的なニューロンは着実に形になりつつあります。ここで、これまでの記事で扱ったのと同じ原理を適用する必要があります。つまり、ニューロンが最適な方程式を見つけるために、どの方向へ進むべきかを判断できるように、誤差システムを定義するのです。以下のコードを見ればわかるように、これは非常にシンプルな処理です。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
void OnStart()
{
    double Train[][2] {
                        {0, 0},
                        {1, 2},
                        {2, 4},
                        {3, 6},
                        {4, 8},
                      };
    double weight, fx, dx, x, err;
    const uint nTrain = Train.Size() / 2;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;
    err = 0;
        
    for (uint c = 0; c < nTrain; c++)
    {
        x = Train[c][0];
        fx = x * weight;
        Print("Actual: ", fx , " expected: ", x);
        dx = fx - Train[c][1];
        err += MathPow(dx, 2);
    }
    Print("Err: ", err / nTrain);
}
//+------------------------------------------------------------------+

さて、このコードを実行すると、下の画像のようなものが表示されるはずです。

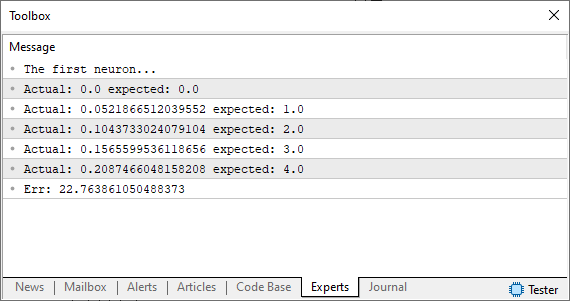
この時点で、私たちは重要な分岐点に差し掛かっています。以前であれば、この段階で誤差を最小限に抑えるために手動で値を調整しなければなりませんでした。もし、この意味がよく分からなければ、文脈を把握するために過去の記事を参照してください。しかし、今回は以前のように手作業で調整するのではなく、コンピューターにその役割を任せます。前回の方法で接線を求めるのではなく、今回は割線を用いたアプローチを取ります。そして、ここからが本当に面白いところです。マシンは、可能な限り最適な解を求めて「暴れ始める」のです。正しい解に収束することもあれば、完全に発散してしまうこともあるでしょう。

私たちの目標は、変数errの値を減らすことです。これこそが、マシンの予測不能な挙動を引き起こす原動力となります。この仕組みをより深く理解するために、次のトピックへと進みましょう。

割線の使用

「ニューラルネットワークの実践：割線」では、割線がニューラルネットワークにおいて基本的な役割を果たしていることを簡単に述べました。そこでは以下の図を示しました。

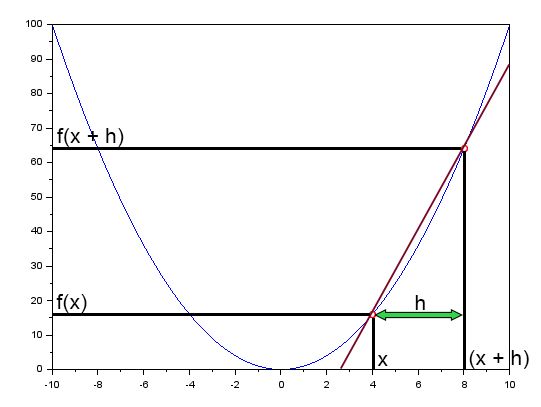
この図は、誤差曲線を直線で示したものです。これが割線です。図を簡略化し、割線だけを残せば、次のような図になります。

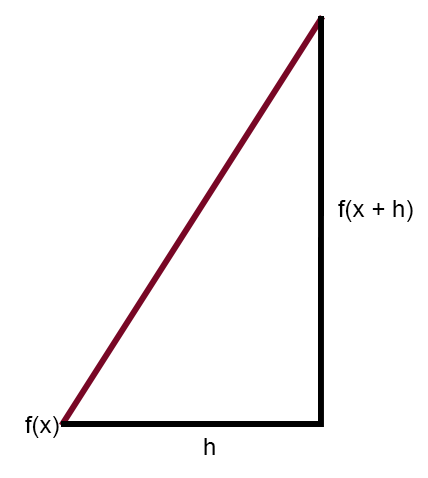
ここで、定数hがゼロになるようにこの図を修正すると、次の式が得られます。

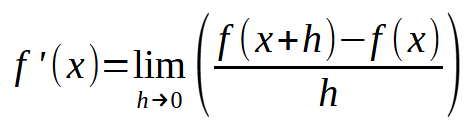
ここからが本当に面白くなるところです。上の式こそが、ニューラルネットワークがエラーから学習するための「魔法の公式」です。この方程式を適用することで、コンピューターに入力データを最も適切に表現する直線を見つけさせることができます。これにより、マシンは与えられた問題が何であれ、その解決方法を学習できるのです。どのようなデータをニューラルネットワークに入力しても、根本的な計算プロセスは変わりません。ただし、ここで重要なのはhの値を適切に設定することです。もしこの値がある一定の範囲を超えてしまうと、マシンは最適な直線を求めて「暴走」し始めます。逆に、値が小さすぎると、最適な方程式を見つけるまでに膨大な時間がかかってしまいます。そのため、この調整には適度なバランス感覚が求められます。慎重すぎてもいけませんし、無頓着でもいけません。ちょうど良いバランスを見つけることが重要です。

では、この仕組みをどのようにニューロンに組み込むのでしょうか。変更を加える前に、まずは簡単なテストをおこなってみましょう。以下が、更新後のコードになります。

//+------------------------------------------------------------------+
#property copyright "Daniel Jose"
//+------------------------------------------------------------------+
#define macroRandom (rand() / (double)SHORT_MAX)
//+------------------------------------------------------------------+
double Train[][2] {
                    {0, 0},
                    {1, 2},
                    {2, 4},
                    {3, 6},
                    {4, 8},
                  };
//+------------------------------------------------------------------+
const uint nTrain = Train.Size() / 2;
const double eps = 1e-3;
//+------------------------------------------------------------------+
double Cost(const double w)
{
    double err;

    err = 0;
    for (uint c = 0; c < nTrain; c++)
        err += MathPow((Train[c][0] * w) - Train[c][1], 2);

    return err / nTrain;
}
//+------------------------------------------------------------------+
void OnStart()
{
    double weight;

    Print("The first neuron...");
    MathSrand(512);
    weight = (double)macroRandom;

    Print("Err: ", Cost(weight));
    Print("Err: ", Cost(weight + eps));
}
//+------------------------------------------------------------------+

すごいです。これで本物のプログラムらしくなってきました。実行すると、以下の画像のような結果が得られるはずです。

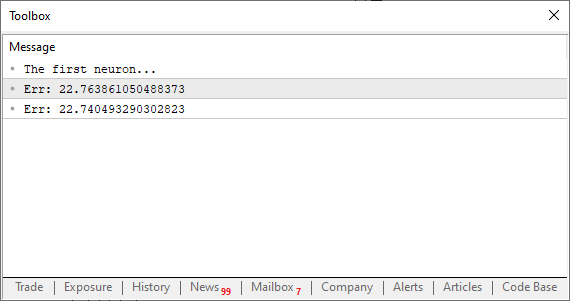
この段階で本当に重要なのは、誤差値が減少しているか、それとも増加しているかという点です。実際の数値そのものには、それほど意味はありません。ここで注意すべきなのは、変数epsが先ほどの数式に出てきたhに対応していることです。この値がゼロに近づくほど、反復ごとに接線へと収束しやすくなります。なぜなら、割線が極限点へと向かって収束し始めるからです。では、次のステップに進みましょう。やるべきことは非常にシンプルです。誤差（またはコスト）を毎回減少させるようなループを作成する必要があります。最終的に、誤差が減少しなくなり、逆に増加し始める地点に到達します。その瞬間、プログラムがこの変化を検知し、ループを終了するようにします。そうしないと、無限ループに陥るリスクがあるからです。また、無限ループを防ぐために、もう一つの安全策を導入することもできます。一般的な方法として、反復回数に上限を設け、収束しない場合や「暴走」し始めた場合には、強制的に停止させる手法があります。これは、ステップサイズが適切に設定されていないときに発生する可能性があります。この問題については後ほど詳しく解説しますが、今はあまり心配しなくても大丈夫です。とはいえ、どこまで誤差を減らすかは完全にあなたの自由です。プログラムを調整して、可能な限り低いコストを追求することもできます。ただし、ここではシンプルに進めるために、実際にどのように動作するのかを見てみましょう。以下のコードを確認して、その仕組みを理解してください。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err;
31. 
32.     Print("The first neuron...");
33.     MathSrand(512);
34.     weight = (double)macroRandom;
35. 
36.     for(ulong c = 0; c < 10; c++)
37.     {
38.         err = ((Cost(weight + eps) - Cost(weight)) / eps);
39.         weight -= (err * eps);
40.         Print(c, "  -->  ", weight, " :: ", err);
41.     }
42.     Print("Weight: ", weight);
43. }
44. //+------------------------------------------------------------------+

このコードを実行すると、ターミナルに下の画像のようなものが表示されます。

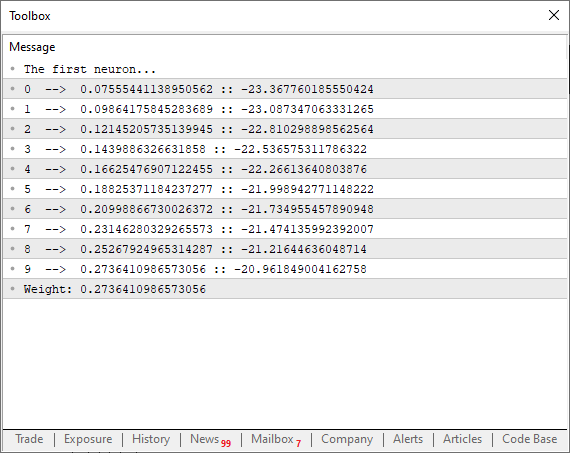
さて、ここで興味深いポイントに注目してみましょう。38行目では、先ほど説明した通り、セカント線を使って関数の収束を助けるために、できるだけ低い極限値を探索させています。しかし、39行目単純に生の誤差や総コスト値を使ってカーブのポイントを調整しているわけではないことに気づきましたか。これはなぜでしょうか。もし単純に誤差の値をそのまま使って調整してしまうと、プログラムは関数のカーブに沿ってカオス的に行ったり来たりしてしまいます。それは私たちが望んでいることではありません。スムーズでコントロールされた調整が必要です。では、epsを使って放物線の次のポイントを微調整するのはどうでしょう。実は、それをすると誤差が増えているのか減っているのかを常にチェックする必要が生じます。しかし、39行目の因数分解を適用すれば、その手間を完全に省くことができます。このアプローチにはもう一つ大きな利点があります。それは、学習の初期段階でニューロンの収束をより速く進められることです。そして、理想値に近づくにつれて減衰曲線が滑らかになり、逆対数減衰関数のように振る舞います。これは素晴らしいことです。なぜなら、最適な誤差値により素早く到達できるからです。

しかし、まだ改良の余地があります。何が起きているのかをよりよく理解するために、分析ツールを追加することもできます。同時に、最大反復回数に達する前であっても、ループが最小収束点に達すればすぐに終了するような追加テストを導入することもできます。それを念頭に置いて、改良版のコードを以下に示します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define macroRandom (rand() / (double)SHORT_MAX)
05. //+------------------------------------------------------------------+
06. double Train[][2] {
07.                     {0, 0},
08.                     {1, 2},
09.                     {2, 4},
10.                     {3, 6},
11.                     {4, 8},
12.                   };
13. //+------------------------------------------------------------------+
14. const uint nTrain = Train.Size() / 2;
15. const double eps = 1e-3;
16. //+------------------------------------------------------------------+
17. double Cost(const double w)
18. {
19.     double err;
20. 
21.     err = 0;
22.     for (uint c = 0; c < nTrain; c++)
23.         err += MathPow((Train[c][0] * w) - Train[c][1], 2);
24. 
25.     return err / nTrain;
26. }
27. //+------------------------------------------------------------------+
28. void OnStart()
29. {
30.     double weight, err, e1;
31.     int f = FileOpen("Cost.csv", FILE_COMMON | FILE_WRITE | FILE_CSV);
32. 
33.     Print("The first neuron...");
34.     MathSrand(512);
35.     weight = (double)macroRandom;
36. 
37.     for(ulong c = 0; (c < ULONG_MAX) && ((e1 = Cost(weight)) > eps); c++)
38.     {
39.         err = (Cost(weight + eps) - e1) / eps;
40.         weight -= (err * eps);
41.         if (f != INVALID_HANDLE)
42.             FileWriteString(f, StringFormat("%I64u;%f;%f\n", c, err, e1));
43.     }
44.     if (f != INVALID_HANDLE)
45.         FileClose(f);
46.     Print("Weight: ", weight);
47. }
48. //+------------------------------------------------------------------+

このコードの魅力は、試行錯誤するのが驚くほど楽しいという点です。勉強しながら調整したり、好きなようにカスタマイズしたり、自由に遊ぶことができます。今回は、MetaTrader 5のターミナルに値を出力するのではなく、ファイルに出力する方式 を採用しました。こうすることで、データをもとにグラフを作成し、より詳細に分析することができます。そして、現在の設定で得られたグラフがこちらです。

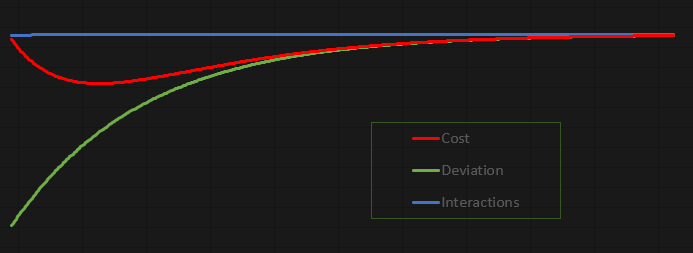
このグラフは、ニューロンが生成したファイルのデータを基にExcelで作成 しました。確かに、ファイルの作成方法は少し雑に感じるかもしれません。しかし、これは 学習目的の楽しい実験 なので、データの出力方法に多少の粗さがあっても問題ないでしょう。

最終的な考察

この記事では、基本的なニューロンを作りました。確かに シンプルなコード ですが、「単純すぎる」「意味がない」と感じる人もいるかもしれません。ぜひコードを自由に編集し、試行錯誤してください。コードを修正することを恐れず、完全に理解することが目標です。コードは添付しているので、以下の点を意識して試してみてください。この記事はゆっくり読んでください。コードをコピー＆ペーストするのではなく、一から入力してみてください。最終バージョンに達するまで、各ステップをテストします。私のやり方をただ真似るのではなく、自分にとって納得のいく方法で構築してください。重要なのは、同じ最終結果、つまり配列内の訓練データ間の相関を見つけることです。実際、これは非常にシンプルなことです。

コードは添付ファイルに含まれているので、ここでいくつかの興味深い改造を試すことができます。ひとつひとつの修正を冷静に検証することを忘れないでください。最初の要素は訓練配列で、アプリケーションコードの6行目にあります。そこに異なる値を入れて、ニューロンにその相関関係を見つけさせればいいです。

もう一つ非常に興味深い点は、15行目の定数の値の変化です。より高い値またはより低い値に変更し、その作業終了時にニューロンが報告する結果を観察します。値が低いほど処理に時間がかかるが、結果は理想的な値にかなり近くなることがわかるでしょう。

同じく興味深いのは35行目で、ここでは0と1の間で変動する重みを割り当てています。マクロが返す値を乗算することで変更できます。例えば、35行目に次のように書いてみましょう。

weight = (double)macroRandom * 50;

ニューロンの初期ウェイトを変えただけで、すべてがまったく違っていることに気づくでしょう。そして、何が起こっているのか完全に確認できたら、34行目のコードを以下のように変更することができます。

MathSrand(GetTickCount()); 

多くの人が考えているよりも、すべてがずっと面白いことに気づくでしょう。しかし、最も重要なことは、ニューラルネットワークの1つのニューロンがどのように何かを学ぶことができるかを理解することです。次回は、このニューロンをさらに興味深いものに変えてみましょう。次の記事に移る前に、このコードを勉強して実験してください。これは始まりに過ぎないからです。