MetaTrader 5 / 例
English Русский 中文 Español Deutsch Português
preview
適応型社会行動最適化(ASBO)：二段階の進化

適応型社会行動最適化(ASBO)：二段階の進化

MetaTrader 5 — 例 | 12 2月 2025, 07:52
74 0
Andrey Dik
Andrey Dik

内容
  1. はじめに
  2. アルゴリズムの実装
  3. テスト結果


1. はじめに

前の記事では、Schwefelの概念、ボックス=ミュラー法（正規分布）、自己適応型突然変異率の使用、適応度値に基づく最近傍決定について検討しました。現在、私たちは研究の新たな段階へと進んでいます。ここでは、二段階のプロセスを詳しく掘り下げ、アルゴリズムを数学モデルASBO（適応型社会的行動最適化）として完成させます。すでに使い慣れたテスト関数を用いてこの革新的なモデルの包括的な検証をおこない、その効率性について結論を導き出します。この記事では、最適化の分野における生物の社会的行動の新たな応用を探り、集団行動の原理をより深く理解し、それを複雑な問題の解決に活用するための新たな知見を紹介します。


2. アルゴリズムの実装

まず、ASBOアルゴリズムの疑似コードを作成しましょう（使用する方程式を以下に示します）。

入力：PZ（集団サイズ）、M（集団数）、P'（集団あたりのエポック数）、f(x)（目的関数）

初期化

1. PZの大きさを持つM個の集団を作成する
2. 各集団について

  • xiの解をランダムに初期化する
  • 各解のf(xi)目標関数の値を計算する
  • 大域的リーダーGbを、最も高いf (xi)を持つ解として定義する
  • 各xiの解について、最近傍Ncのグループを定義する
  • 個体ごとの最適解Sb = xiを初期化する
  • 適応パラメータCg、Cs、Cnを[-1.0; 1.0]の範囲内でランダムに初期化する

第1段階：独立した集団の処理
3. M個の集団のそれぞれについて

  •  各xiの解について
  • 式(3)と(4)に従い、自己適応突然変異を適用し、Cg、Cs、Cnの比率を更新する
  • 式(1)に従い、位置変化ΔX (i + 1) を計算する
  • 式(2)に従って位置xiを更新する
  • 新しい値f(xi)を計算する
  • f (xi) > f (Sb)の場合、個体の最良解Sbを更新する
  • f (xi) > f (Gb)の場合、大域的リーダーGbを更新する
  • P'エポックに達するまで繰り返す

4. 最終的な集団、f (xi)値、Cg、Cs、Cnパラメータを保存する

第2段階：結合された集団の処理
5. すべての最終集団から、f (xi)のPZ個の最適解を選択する
6. 選択されたPZ個の解に、保存されたCg、Cs、Cnパラメータを適用する
7. PZの大きさを持つ統合集団にASBOアルゴリズムを適用する
8. 停止基準に達するまで手順6～7を繰り返す

    結論：大域的最適解Gb

    重要な方程式

    • ΔX (i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi)  (1)
    • x (i + 1) = xi + ΔX (i + 1)                                                                           (2)
    • p'i (j) = pi (j) + σi (j) * N (0, 1)                                                                  (3)
    • σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1))                                        (4)

    ここで

    • Gb：大域的リーダー
    • Sb：個体の最良解
    • Nc：適応度による近隣グループの中心
    • R1、R2、R3：[0, 1]の範囲の乱数
    • Cg、Cs、Cn：適応パラメータ
    • N (0, 1)：正規分布からの乱数
    • Nj (0,1)：各j測定ごとに正規分布から得た乱数
    • τ、τ'：自己適応突然変異のスケーリング係数

    提示された疑似コードは、アルゴリズムが社会モデル開発の二段階の進化を実装していることを示しています。アルゴリズムのロジックは、次の段階で簡単に説明できます。

    1. 第1段階

    • 同じPZサイズのM個の集団を用意し、
    • それぞれの集団に対してASBOアルゴリズムを固定回数P'の反復回数で独立して適用します。
    • この段階の終了時には、すべての最終集団の個体について、適応度関数の値と適応突然変異パラメータが保存されます。

    2. 第2段階

    • 第1段階のすべての最終集団から、適応度関数の値が最も良いPZ個体を選択します。
    • 保存された適応突然変異パラメータをこれらのPZ個の最良個体に適用し、新たに
    • PZサイズの集団を作成します。その後、この新しい集団にASBOアルゴリズムを適用して最終解を得ます。

    二段階進化の意味

    1. 第1段階では、複数の集団が独立して進化することで、解の多様性が確保され、大域的最適領域の局地化がより適切におこなわれます。
    2. 第2段階では、第1段階の集団から最適な解を選び、その適応パラメータを利用して、大域的最適解への収束を加速させます。

    したがって、理論的には、二段階進化は第1段階での大域的探索と、第２段階での効率的な局地的最適化を組み合わせることができ、最終的にはアルゴリズム全体のパフォーマンス向上が期待できます。

    従来の複数集団二段階ASBOアルゴリズムでは、まず第1段階で複数の集団を並列かつ独立して進化させます。第2段階では、それらの集団から最適な解を取り出し、新しい集団を作成します。しかし、全ての集団アルゴリズムに単一のテンプレートを適用する場合、複数集団をどのように処理するかという問題が生じます。

    最初の解決策は、例えば50個体の通常の集団を5つの集団に分割する方法です。この場合、各集団には10個体が含まれ、複数の集団をあたかも1つの集団のように通常通りに扱えます。しかし、問題は第2段階で発生します。これら5つの集団から最適な解を選び、新しい集団に配置する必要がありますが、すべての個体を入れてしまうと、実質的に元の集団のコピーを作成することになり、必要な数を選べなくなります。

    次の解決策は、5つの集団をそれぞれ元の集団サイズと同じ50個体に設定する方法です。各集団には、例えば20エポックなどの固定回数が割り当てられます。これにより、第1段階では、5つの集団それぞれに固定回数のエポックを使って順番に処理を行い、合計で5 * 20 = 100エポックを費やします。第2段階では、残りの100エポック（合計200エポックのうち）を使って、これら5つの集団を1つの大きな集団（250個体）にまとめ、その中から最も優れた50個体を選び、新しい集団を作成します。その後、この新しい集団に対して、通常の方法で操作をおこない、最終的な解を得ます。このアプローチは、元のアルゴリズムと完全に一致し、私たちの集団アルゴリズムの使用というコンセプトに適合しています。私たちは、ネルダー-ミード法や化学CRO、進化的アルゴリズムなど、他のアルゴリズムに対しても革新的なアプローチを適用し、すべてのアルゴリズムが互換性を持ち、シームレスに交換できるようにしてきました。

    それでは、コードの記述に進みましょう。

    複数集団二段階ASBOアルゴリズムの検索エージェントを表すS_ASBO_Agent構造体を実装します。この構造体は、変数と、エージェントを初期化するInitメソッドを定義します。

    変数

    • c：座標の配列
    • cBest：最適座標の配列
    • f：適応度値
    • fBest：最高適応度値
    • Cg、Cs、Cn：適応パラメータ
    • u：C_AO_Utilitiesクラスオブジェクト

    Initメソッドはエージェントを初期化します。

    • coords座標の数、および各座標の最小値と最大値を表すrangeMin配列とrangeMax配列を受け入れます。
    • coords座標の数に基づいてcおよびcBest配列にメモリを割り当てます。
    • 初期値fBestを-DBL_MAXに設定します。
    • Cg、Cs、Cn適応パラメータにランダム値を生成します。
    • rangeMinとrangeMaxの範囲内でランダムな値をc配列に入力します。
    • cの値をcBest配列に割り当てます。
    //——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

    複数の集団を順番に処理するには、集団の配列を使用すると便利です。これを実現するには、1つのフィールドのみを含むS_ASBO_Population構造体を記述します。

    • agent：集団内のエージェントを表すS_ASBO_Agent型オブジェクトの配列
    //——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

    C_AOクラスの子孫であるC_AO_ASBOクラスを宣言します。このクラスには、最適化を処理するためのいくつかのメソッドと変数が含まれています。

    1. コンストラクタとデストラクタ

    • コンストラクタは、集団のサイズ、集団の数、各集団のエポック数、アルゴリズムの説明への参照などのアルゴリズムパラメータを初期化
    • デストラクタは空

    2. オプション

    • SetParams：params配列から設定されるアルゴリズムパラメータ
    • Init：アルゴリズムの初期化に使用される、検索範囲、検索ステップ、エポック数などの指定されたパラメータ
    • Moving：検索空間内でエージェントを移動する
    • Revision：検索空間内のエージェントを修正し、大域的最良解を更新しする

    3. 変数

    • numPop、epochsForPop：集団の数と各集団のエポック
    • epochs、epochNow、currPop、isPhase2、popEpochs、tau、tau_prime：アルゴリズムで使用される追加の変数
    • allAgentsForSortPhase2、allAgentsTemp、agentsPhase2、agentsTemp：アルゴリズムで使用されるエージェントの配列
    • pop：集団の配列

    4. 補助メソッド

    • AdaptiveMutation：エージェントの適応型変異を実行する
    • UpdatePosition：エージェントの位置を更新する
    • FindNeighborCenter：エージェントの近隣の中心を見つける
    • Sorting：エージェントを並び替える

    したがって、C_AO_ASBOクラスは、検索空間内でエージェントを移動および修正するためのさまざまなメソッドと操作を使用してASBOアルゴリズムを実装したものです。

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

    Initメソッドは、最適化を開始する前に、ASBOアルゴリズムに必要なパラメータとデータ構造を初期化するC_AO_ASBOクラスの重要な機能を実行します。以下は、Initメソッドの基本的な初期化手順です。

    1. 基本パラメータの確認と初期化

    • このメソッドは、最小および最大の検索範囲や検索ステップなどの基本パラメータを初期化するためにStandardInitを呼び出します。初期化に失敗した場合、メソッドはfalseを返します。

    2. 追加変数の初期化

    • epochs、epochNow、currPop、isPhase2、popEpochs変数の値が設定されます。
    • tau変数とtau_prime変数の値は、coords検索空間の次元に基づいて計算されます。

    3. 集団とエージェントの作成と初期化

    • 集団を格納するためのpop配列が作成され、各集団が初期化されます。集団内の各エージェントに対して、Initメソッドが呼び出され、指定された範囲内でその座標が初期化されます。
    • agentsPhase2配列は第2段階エージェント用に作成され、populationsと同様に初期化されます。
    • allAgentsForSortPhase2配列とallAgentsTemp配列は、並び替え中にエージェントを一時的に保存するために作成され、それぞれ初期化されます。

    4. 結果を返す

    •    初期化が成功した場合、メソッドはtrueを返します。
    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_ASBOクラスのMovingメソッドは、段階間の遷移や各段階における適切な操作の実行など、ASBOアルゴリズム内でエージェントが移動する基本的なプロセスを表します。以下は、Movingメソッドの主な手順です。

    1. epochNow値の増加

    • epochNow変数の値を1増やし、新たな最適化の世代の始まりを反映させます。

    2. 第1段階

    • アルゴリズムが2段階にない場合は、次の処理が実行されます。
      • 現在の集団のエポック数がepochsForPopの制限に達した場合、popEpochsカウンタがリセットされ、currPopカウンタが増加し、fB値もリセットされます。
      • numPop集団の最大数に達すると、アルゴリズムは第2段階に進みます。この場合、すべての集団からのエージェントが1つの配列に結合され、並び替えられます。最適なエージェントがagentsPhase2配列にコピーされます。
    • それ以外の場合、現在の集団内の各エージェントに対して、適応型突然変異、位置更新操作、および座標のコピーが実行されます。

    3. 第2段階

    • 第2段階では、agentsPhase2配列内の各エージェントに対して、適応型突然変異と位置更新操作、および座標のコピーも実行されます。
    //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Phase 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Phase 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    C_AO_ASBOクラスのRevisionメソッドは、fBの値の更新やASBOアルゴリズムの各段階の最適化結果の更新など、最適化結果を修正するプロセスを表します。以下は、コードの主なコンポーネントです。

    1. 変数とその初期化

    • int ind = -1; ：f関数の最適値を持つ要素のインデックスを格納する変数
    • fB：現在の段階で見つかった「f」関数の最適値を表す変数

    2. 最適なエージェントの検索

    • 最初のforループでは、popSizeサイズのa配列内のすべてのエージェント（決定を表すオブジェクト）を反復処理します。
    • 現在のエージェントのf関数が現在の最適なfB値より大きい場合、fBとindインデックスが更新されます。

    3. データのコピー

    • 関数の最適値を持つind != -1のエージェントが見つかった場合、cB配列（最適解のパラメータを表す）はa配列の値で更新されます。

    4. 第1段階

    • 現在の集団(currPop)が集団の合計数(numPop)より少ない場合、現在の集団のエージェントのf関数値が更新されます。
    • a配列内のfエージェント値がfBestの最適値を超えると、fBestが更新され、対応する特性がcBestにコピーされます。
    • 次に、現在の集団のエージェントはu.Sortingメソッドを使用して並び替えられます。

    5. 第2段階

    • 現在の集団が集団の総数以上である場合、agentsPhase2配列に対して同様のアクションが実行されます。
    • f関数の値が更新され、最適なfBest値がチェックおよび更新され、並び替えが実行されます。

    一般的なロジック

    • Revisionメソッドでは、最適なエージェントの検索と、現在の段階（1または2）に応じたエージェントのデータの更新という2つの主要なステップが実行されます。
    • 主な目標は、最適化中に見つかった最適な解を追跡および更新し、後で使用するためにエージェントの並び替えを維持することです。
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //phase 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //phase 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

      C_AO_ASBOクラスのAdaptiveMutationメソッドは、ガウス分布の使用やランダム変数に基づく新しい比率値の計算など、ASBOアルゴリズム内のagエージェント比率の適応型変異を表します。以下は、AdaptiveMutationメソッドの主な手順です。

      1. 比率の適応的突然変異

      • agエージェントのCg、Cs、Cnの比率はガウス分布を使用して変化します。
      • 各比率について、2つのガウス乱数変数の合計の指数関数を使用して新しい値が計算され、各ガウス乱数変数には対応するtau_primeとtau比率が乗算されます。
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

      C_AO_ASBOクラスのUpdatePositionメソッドは、さまざまな要因に基づいて位置の変更を計算し、指定された範囲内で位置を更新するなど、ASBOアルゴリズム内でエージェントの位置を更新することを表します。以下は、UpdatePositionメソッドの主な手順です。

      1. 位置の変化を計算する

      • cB、cBest、deltaX、rangeMin、rangeMax、rangeStepなどのさまざまな比率と値を使用して、すべての次元jにおけるag [ind]エージェントの位置の変化を計算します。

      2. エージェント位置の更新

      • j次元ごとに、deltaX [j]を追加し、指定された範囲内で値を修正することで、新しいエージェントの位置ag [ind].c [j]が計算されます。

      コードのコメント部分については、1)がオリジナルバージョン、3)がCg、Cs、Cnを考慮せず、代わりに正規分布を使用した私のバージョン、2)が私の選択肢です。3つの中で最も良い結果を示しました。

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————


      3. テスト結果

      ASBOアルゴリズムをリストすると、このアルゴリズムを本当にユニークなものにしている興味深い特徴がいくつも見えてきます。その中でも特に注目すべきは、優れたスケーラビリティです。これにより、アルゴリズムは高次元の問題を効率的に処理することができます。特に注目すべきは、1000個のパラメータを使用してForest関数とMegacity関数をテストした際に得られた結果です。この場合、ASBOは評価表の主要なアルゴリズムと同等の優れたパフォーマンスを示します。このような成果は、アルゴリズムの効率性を示すだけでなく、高品質な最適化を必要とするさまざまな分野への応用可能性を強調しています。

      ASBO|Adaptive Social Behavior Optimization|50.0|5.0|10.0|
      =============================
      5 Hilly's; Func runs:10000; result:0.7633114189858913
      25 Hilly's; Func runs:10000; result:0.4925279738997658
      500 Hilly's; Func runs:10000; result:0.3261850685263711
      =============================
      5 Forest's; Func runs:10000; result:0.7954558091769679
      25 Forest's; Func runs:10000; result:0.4003462752027551
      500 Forest's; Func runs:10000; result:0.26096981234192485
      =============================
      5 Megacity's; Func runs:10000; result:0.2646153846153846
      25 Megacity's; Func runs:10000; result:0.1716923076923077
      500 Megacity's; Func runs:10000; result:0.18200000000000044
      =============================
      All score:3.65710 (40.63%)

      ASBOアルゴリズムの結果を視覚化すると、注目すべき興味深い特徴がいくつか明らかになります。アルゴリズムの動作の最初から、非常に重要な解の領域を適切に識別する方法がわかり、パラメータ空間を効率的に探索する能力が示されています。

      収束グラフには、最初の段階で複数の集団が順次動作することによって生じる特徴的な中断が表示されています。これらのギャップは、各集団が空間の異なる部分を探索し、最適化に貢献していることを示しています。しかし、第2段階ではグラフが一貫した形に変化し、これは第1段階後に集められたすべての集団の最適解が結合されることを意味します。この統合によって、アルゴリズムは有望な領域をさらに洗練することに集中できるようになります。

      したがって、視覚化はアルゴリズムのダイナミクスを示すだけでなく、その適応的で協調的なメカニズムをも強調しています。

      Hilly

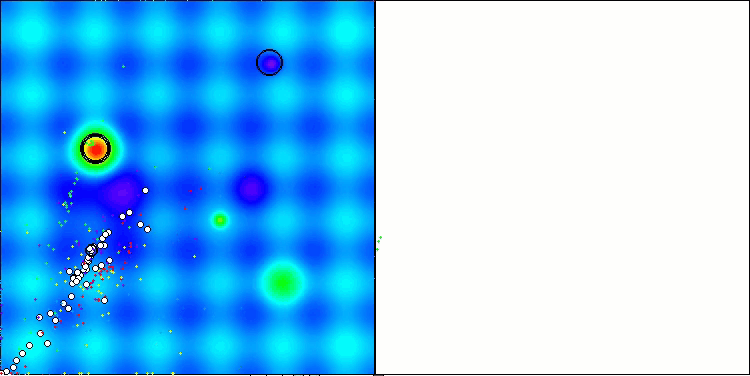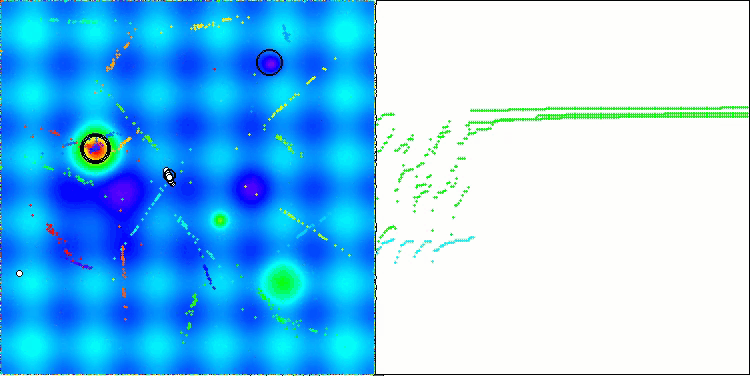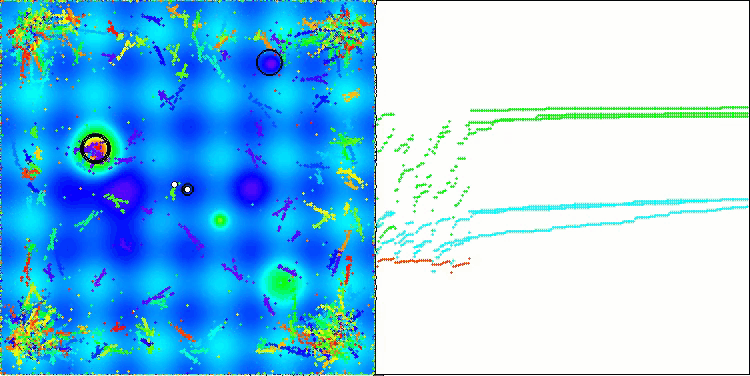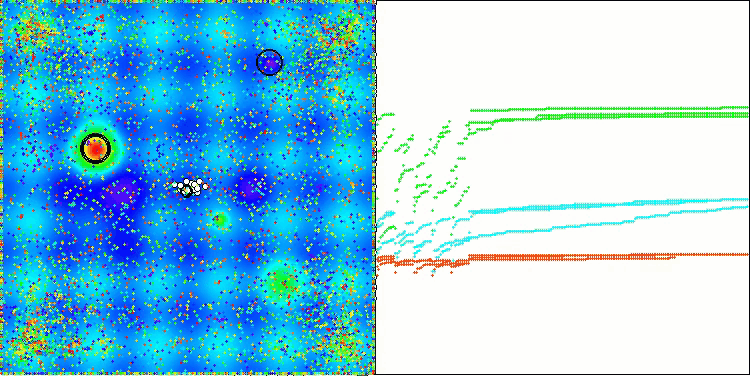
        Hillyテスト関数のASBO

      Forest

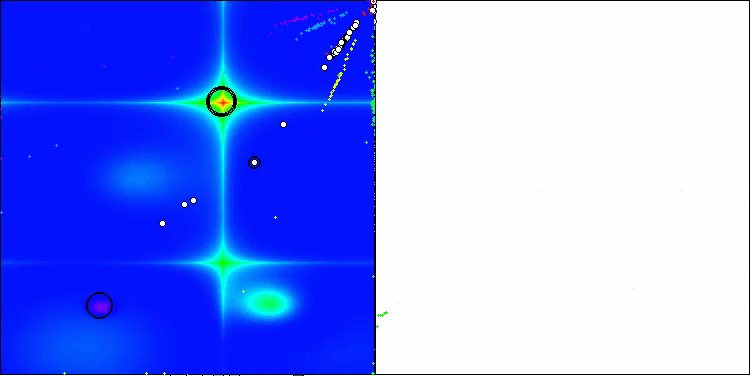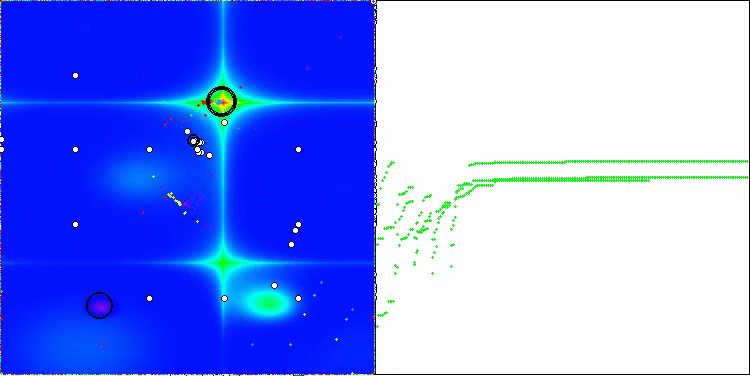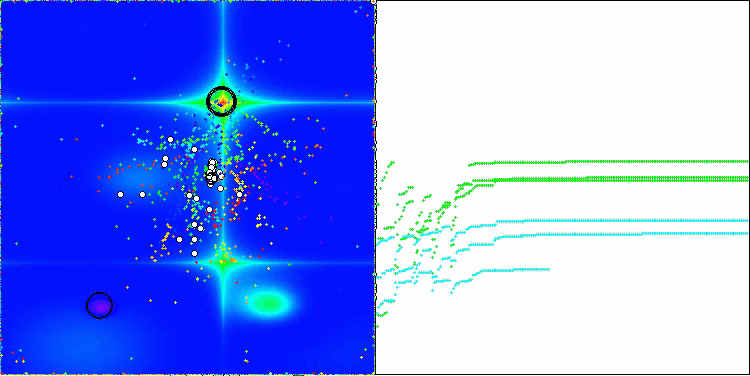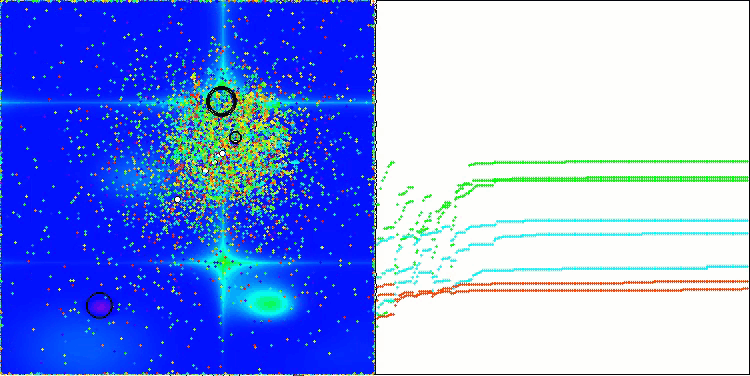
      Forestテスト関数のASBO

      Megacity

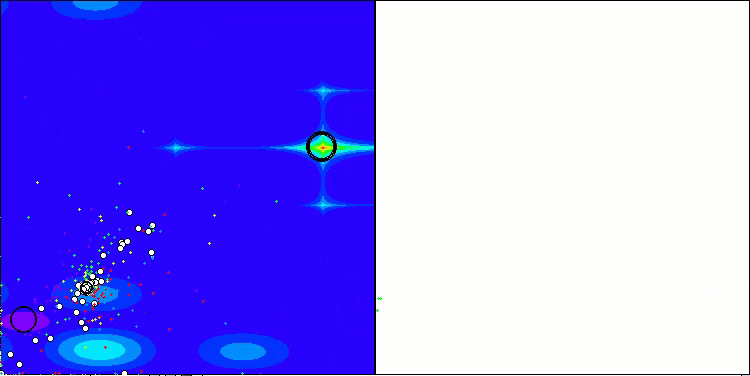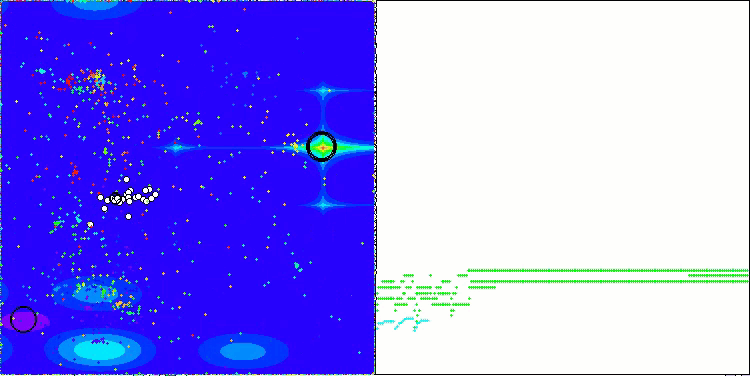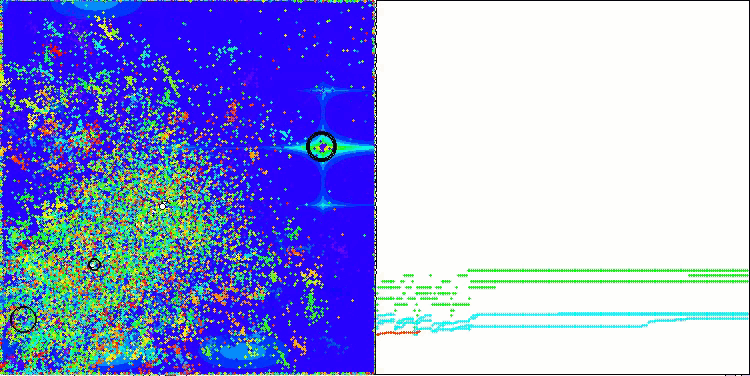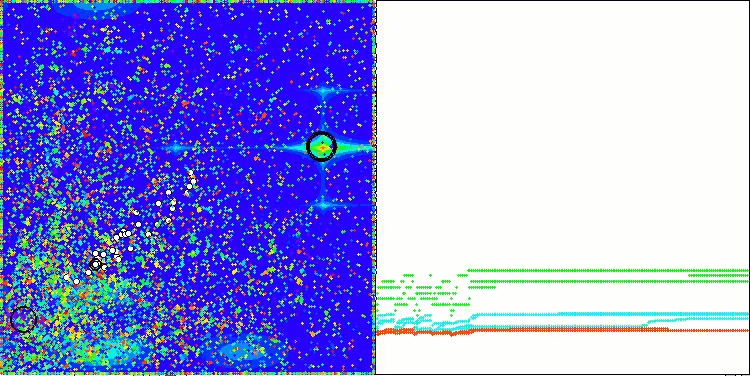
      Megacityテスト関数のASBO

      実施された調査の結果に基づくと、このアルゴリズムは自信を持って評価表の中間に位置します。

      # AO 詳細 Hilly Hilly最終 Forest Forest最終 Megacity（離散） Megacity最終 最終結果 MAXの%
      10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
      1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA コードロックアルゴリズム 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 (P+O)ES (P+O）進化戦略 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      4 CTA 彗尾アルゴリズム 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      5 SDSm 確率的拡散探索M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      6 ESG 社会母集団の進化 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      7 SIA 等方的焼きなまし 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      8 ACS 人工協調探索 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      9 TSEA 亀甲進化アルゴリズム 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      10 DE 差分進化 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      11 CRO 化学反応の最適化 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      12 BSA 鳥群アルゴリズム 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      13 HS ハーモニー検索 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      14 SSG 苗木の播種と育成 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      15 (PO)ES (PO）進化戦略 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      16 BSO ブレインストーム最適化 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      17 WOAm 鯨最適化アルゴリズムM 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      18 AEFA 人工電界アルゴリズム 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      19 ACOm 蟻コロニー最適化M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      20 BFO-GA 細菌採食の最適化：Ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      21 アズボ 適応型社会行動最適化(ASBO) 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      22 MEC Mind Evolutionary Computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      23 IWO 侵入雑草最適化 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      24 Micro-AIS 微小人工免疫系 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      25 COAm カッコウ最適化アルゴリズムM 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      26 SDOm 螺旋ダイナミクス最適化M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      27 NMm ネルダー=ミード法M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      28 FAm ホタルアルゴリズムM 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      29 GSA 重力探索法 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      30 BFO 細菌採餌最適化 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
      31 ABC 人工蜂コロニー 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
      32 BA コウモリアルゴリズム 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
      33 SA 焼きなまし 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
      34 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
      35 PSO 粒子群最適化 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
      36 ボイド ボイドアルゴリズム 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
      37 MA モンキーアルゴリズム 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
      38 SFL Shuffled Frog-Leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
      39 FSS 魚群検索 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
      40 RND ランダム 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
      41 GWO 灰色オオカミオプティマイザ 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
      42 CSS 荷電系探索 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
      43 EM 電磁気学的アルゴリズム 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


      まとめ

      このアルゴリズムは、その独創性と非標準的な動作が際立っており、視覚化はこれまでに知られている方法とは異なり、非常にユニークです。これにより注目を集め、アルゴリズム内部のメカニズムに対する興味を喚起します。

      小次元の問題に対する全体的な結果と収束は平均的ですが、アルゴリズムはより複雑な問題や広大な検索空間で作業する際にその真の可能性を発揮します。最初の段階では、複数の集団が順次実行されますが、限られた数のエポックを独立した集団の事前計算に分割することの賢明さに疑問が生じます。最初の段階で1つの集団だけを使用した実験では、結果が大きく悪化し、周囲の検索空間に関する情報を事前に収集することが有用であることが確認されました。これにより、アルゴリズムは第2段階の検索において最も成功した解である主要な個体をより効果的に活用できるようになります。

      さらに、このアルゴリズムにはさらなる研究の余地が多くあります。その機能はまだ完全には実現されていないと考えられ、アルゴリズムの利点を最大限に活用する方法を理解するためには、さらなる実験と分析が必要であると私は考えています。

      Tab

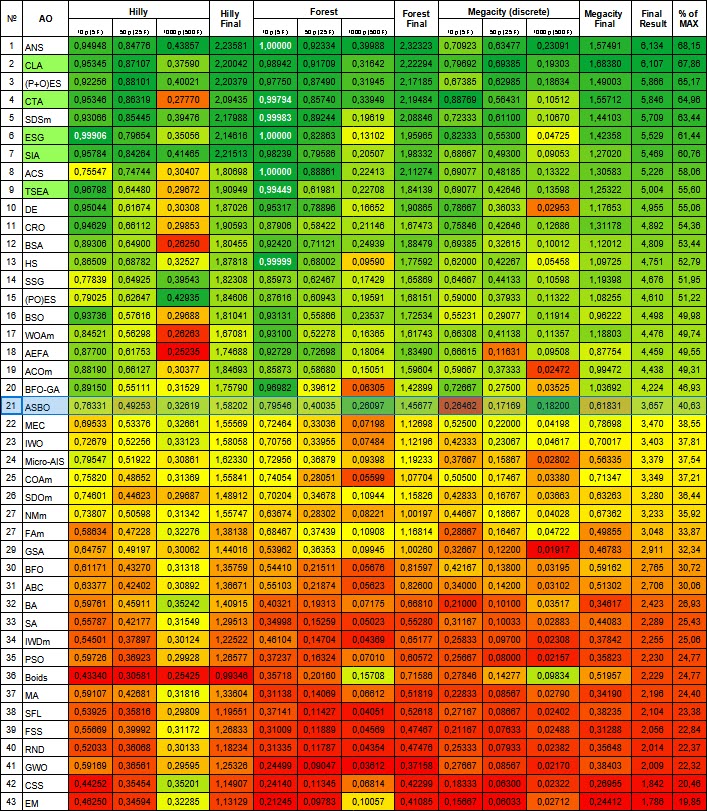
      図2：関連テストによるアルゴリズムのカラーグラデーション0.99以上の結果は白で強調表示されている。緑色でハイライトされている名前は私の独自のアルゴリズム

      チャート

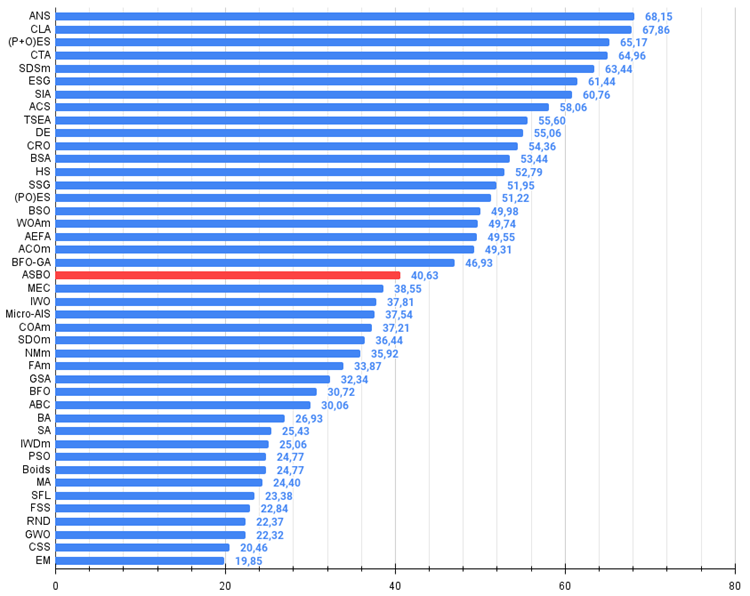
      図3：アルゴリズムのテスト結果のヒストグラム（0から100までのスケールで、多ければ多いほど良い、

      ここで、100は理論的に可能な最大の結果であり、アーカイブにはレーティング表を計算するスクリプトが含まれている）


      ASBOアルゴリズムの長所と短所

      長所

      1. 外部パラメータが少ない
      2. 複雑な高次元問題で良好な結果が得られる

      短所

      1. 低次元の問題では収束性が低い

      この記事には、最新版のアルゴリズムコードを含むアーカイブが添付されています。記事の著者は、正規アルゴリズムの説明の絶対的な正確さについて責任を負いません。検索機能を向上させるために、それらの多くに変更が加えられています。記事に示された結論と判断は、実験結果に基づいています。


      これまでの作業の中間結果のまとめ

      私たちの研究では、複雑な問題を解決するための独自のアプローチを提供する40を超える最適化アルゴリズムを検討しました。このプロセスは非常に楽しいものであり、また、最適化の分野における方法の豊かさと多様性を明らかにする、非常に教育的な経験でもありました。

      アルゴリズムの再作成と修正：検討したアルゴリズムの大部分には、広く利用できるソースコードが存在しませんでした。これを受けて、私は創造的なアプローチを採用しました。さまざまな出版物から引用した著者のテキスト説明のみを基に、コードを再作成しました。この方法により、各アルゴリズムの動作原理をより深く理解できたばかりでなく、それらを特定のニーズに合わせて適応させることができました。
      オープンソースで公開されていた一部のアルゴリズムは、一般的な最適化問題を解決するには適用できませんでした。そのため、汎用性を高め、幅広いタスクに簡単に適用できるように、大幅な修正が必要でした。

      革新と改善：ACO（グラフ上の問題を解決するための蟻コロニーアルゴリズム）などの一部のアルゴリズムは、元々連続空間の問題を扱うことを想定していなかったため、その適用範囲を広げるために変更が必要でした。他のアルゴリズムでは、探索戦略が改善され、効率が向上しました。これらの改良版には、その進化を反映して、名前に「m」の接尾辞が付けられました。さらに、集団の処理方法、新しい解の生成方法、選択方法に関しても、さまざまなアプローチを詳細に検討しました。

      最適化に対する新しいアイデアとアプローチのデモンストレーションとして、5つ以上の新しい独自のアルゴリズムが開発され、独占的に記事で発表されました。

      応用とさらなる研究：提示されたアルゴリズムはいずれも、追加の修正や変更を必要とせずに最適化問題を解決するためにそのまま適用できます。これにより、幅広い研究者や実務家が手軽にアクセスでき、便利に使用することができます。

      特定のタスクで最良の結果を目指す方のために、各アルゴリズムの特性を比較できる比較表やヒストグラムを提供しています。これにより、特定の要件を満たすための細かな調整や最適化の可能性が広がります。

      既存のアルゴリズムをそのまま使用する方法と、アルゴリズムを徹底的に研究して適応させる方法の両方が有効です。さまざまなアルゴリズムの探索戦略に関する細かな点やテクニックを理解することで、研究者は素晴らしい結果を達成するための新たな視点を得ることができます。

      すべての読者が最適な解決策を見つけ、目標を達成できることを心から願っています。最適化とアルゴリズム取引の世界での旅が、刺激的で実り多いものとなることを祈っています。


      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/15329

      添付されたファイル |
      ZIPをダウンロード
      ASBO.zip (27.6 KB)
      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この著者による他の記事

      ディスカッションに移動
      MQL5での暗号化の探索：ステップごとのアプローチ MQL5での暗号化の探索：ステップごとのアプローチ
      この記事では、MQL5内での暗号化の統合について探り、取引アルゴリズムのセキュリティと機能を強化する方法を紹介します。主要な暗号化手法と、それらを自動取引に実際に実装する方法について説明します。
      取引におけるカオス理論（第1回）：金融市場における導入と応用、リアプノフ指数 取引におけるカオス理論（第1回）：金融市場における導入と応用、リアプノフ指数
      カオス理論は金融市場に適用できるでしょうか。この記事では、従来のカオス理論とカオスシステムがビル・ウィリアムズが提案した市場のカオスの概念とどのように異なるかについて考察します。
      知っておくべきMQL5ウィザードのテクニック（第45回）：モンテカルロ法による強化学習 知っておくべきMQL5ウィザードのテクニック（第45回）：モンテカルロ法による強化学習
      モンテカルロは、ウィザードで組み立てられたエキスパートアドバイザー(EA)における実装を検討するために取り上げる、強化学習の4つ目の異なるアルゴリズムです。ランダムサンプリングに基づいていますが、多様なシミュレーション手法を活用できる点が特徴です。
      多通貨エキスパートアドバイザーの開発（第15回）：実際の取引のためのEAの準備 多通貨エキスパートアドバイザーの開発（第15回）：実際の取引のためのEAの準備
      既製のエキスパートアドバイザー(EA)の完成に徐々に近づくにつれ、取引戦略のテスト段階では二次的に思える問題にも注意を払う必要があります。これらの問題は、実際の取引に移行する際に重要となります。