取引におけるカオス理論（第1回）：金融市場における導入と応用、リアプノフ指数

カオス理論と金融市場との関係の紹介

カオス理論とは何か、そしてそれが金融市場にどのように適用できるのか、この問題についてこの記事で取り上げます。

カオス理論とは何か、そしてビル・ウィリアムズが提案する市場におけるカオスの概念が従来の科学的な理論とどう異なるのかを解明する一連の記事を執筆予定です。この理論は市場をどのように説明するのでしょうか。どのように、またどの取引分野に適用できるのでしょうか。 

理論的根拠を分析し、トレーダーが取引に役立つツールをいくつか提供します。

カオス理論の基本概念：アトラクター、フラクタル、バタフライ効果

カオス理論は、金融市場のような複雑なシステムをより深く理解するための数学と物理学の興味深い分野です。この理論の中でも特に重要な3つの概念を見てみましょう。

1. アトラクター：アトラクターはシステムの状態を引き寄せる「磁石」のようなもので、システムは時間が経つにつれてそれに引き寄せられます。金融市場では、これらは市場が繰り返し戻る特定の価格やパターンである場合があります。カオス的なシステムで見られる「奇妙なアトラクター」は特に注目されます。これらは複雑に見え、市場のランダムな動きの中に隠れた秩序を示すことがあります。

2. フラクタル：フラクタルは、どのレベルで拡大しても同じパターンが見られる幾何学的な形状です。金融市場では、価格チャートにフラクタルの特徴が見られ、短期と長期の時間枠で同じパターンが繰り返されます。これにより、異なる時間間隔で同じ分析方法を適用でき、価格変動の分析やリスク評価に役立ちます。

3. バタフライ効果：バタフライ効果は、最初は小さな変化でも、後に予想外の大きな結果を引き起こす可能性があることを示しています。金融の世界では、これはデータやモデルの小さな変更が予測を大きく変える可能性があることを意味します。これにより、長期的な予測が困難になり、市場の状況に合わせてモデルを常に更新し、適応させる重要性が強調されます。

これらの概念を理解することで、アナリストやトレーダーは市場を新たな視点で捉え、隠れたパターンや取引のエントリーポイント、エグジットポイントを発見することができます。カオス理論は、従来のモデルを超えた新たな分析と予測の道を開きます。

金融市場におけるカオスシステム

金融市場はカオスシステムの特徴を備えており、これが市場の分析と予測において重要な役割を果たします。

• 非線形性：小さな変化が大きな変動を引き起こすことがあります。
• 初期条件に対する感度：小さな出来事が予測以上の大きな動きに繋がることもあります。
• 自己組織化：外部からの制御なしで、自然に傾向やパターンが形成されます。
• フラクタル構造：価格チャートにはフラクタル特性が現れます。
• 予測可能性の限界：予測精度は時間が長くなるほど低下します。
• 奇妙なアトラクター：市場は特定のレベルや状態付近で変動します。
• 状態間の遷移：安定から不安定へ突然の変化が生じます。

これらを理解することは、精緻な分析手法、リスク管理、取引アルゴリズムの開発に貢献します。

取引のボラティリティ

ボラティリティは、カオス理論と関連する取引・金融における重要な概念です。これは、一定期間内で資産価格がどの程度変動するかを測定する指標です。取引において、ボラティリティはリスク評価、オプションの価格設定、取引戦略の策定に役立ちます。

金融市場は、しばしばカオスシステムのように振る舞います。バタフライ効果と同様に、市場は小さな変化に対して予測不可能な反応を示すことがあります。また、市場は自己組織化し、外部からの介入なしにトレンドやパターンを形成します。さらに、価格チャートには異なる時間枠にわたって類似性が見られ、これをフラクタル特性と呼びます。

カオス理論は、位相空間再構成やリアプノフ指数といったボラティリティ分析のための独自のツールを提供し、隠れたパターンを発見し、予測可能性を評価するのに役立ちます。これらのカオスモデルは、特に市場のレジームの特定やボラティリティの急激な変動の予測において、GARCHモデルなどの従来の手法を補完することができます。

ボラティリティのカオス的な特性を理解することで、市場動向のより正確な分析と予測が可能になり、効果的な取引戦略やリスク管理手法の開発につながります。

従来のカオス理論とビル・ウィリアムズのアプローチ

従来のカオス理論と、ビル・ウィリアムズが提唱する「カオス」の概念は大きく異なります。前者は厳密な数学的原理に基づき、洗練されたツールを用いてシステムを分析します。一方、後者はより直感的なアプローチを採用し、アリゲーターやフラクタルなど、カオス理論の数学的基盤とは直接関係のないテクニカル指標を活用します。

従来のカオス理論は、非線形力学の分野における厳密な数学従来のカオス理論は、非線形力学の分野における厳密な数学的原理と科学的研究に基づいています。この理論では、カオスを決定論的でありながら予測不可能な振る舞いを示すものと考え、数学的手法を用いて解析します。一方、ウィリアムズは「カオス」という言葉を、市場の一般的な予測不可能性を指す広義の意味で使用しています。彼の手法は、市場の混沌とした特性を深く分析することではなく、取引への実践的な応用に重点を置いています。

ウィリアムズはカオス理論から一部の用語を採用していますが、そのアプローチはテクニカル分析と市場の値動きに対する個人的な解釈に基づいています。この点は、カオス理論を専門とする研究者から批判を受けることもあり、彼らはウィリアムズの文脈で「カオス」という用語を使うことは誤解を招く可能性があると指摘しています。

市場分析におけるカオス理論

カオス理論は、金融市場の複雑さと予測不可能性を認識し、市場動向を分析する新たな視点を提供します。従来の分析手法とは異なり、市場プロセスの非線形性や複雑性を考慮に入れるのが特徴です。

このアプローチにより、なぜ小さな出来事が大きな市場変動を引き起こすのか、またなぜ長期予測が不正確になりやすいのかといった疑問に答えることができます。さらに、カオス理論を活用することで、市場の暴落やバブルといった現象をより深く分析でき、より正確かつ適応性の高い市場分析を実現するための新たなツールを提供します。

リアプノフ指数と金融時系列分析への応用

リアプノフ指数はカオス理論のツールであり、システムが初期条件に対してどの程度敏感であるかを理解するのに役立ちます。金融市場においては、市場環境のわずかな変化が価格にどの程度影響を与えるかを推定できるため、重要な指標となります。

リアプノフ指数が正である場合、システムはカオス的に振る舞い、小さな変化が将来的に大きな変動を引き起こす可能性が高まります。指数が負であれば、システムはより安定しており、価格変動は比較的小さく抑えられます。

この指数を活用することで、市場のボラティリティが高まるタイミングや、予測しやすい局面を特定することができます。指数の値が高い場合は、価格が急変する可能性を示唆しており、リスク評価や取引戦略の調整に役立ちます。

金融データにおけるリアプノフ指数の計算には、位相空間を構築し、近接する点がどの程度発散するかを分析する必要があります。このプロセスでは、次元や時間遅延などの適切なパラメータの選択が重要になります。

リアプノフ指数を活用する際の重要なポイントの一つは、予測の信頼性の期間を推定することです。指数の値が高いほど、信頼できる予測が可能な期間は短くなります。これは、短期取引やリスク管理に特に有効です。

これで、MQL5におけるリアプノフ指数の実装を開始できます。

MQL5を用いたリアプノフ指数の実装

このインジケーターは、金融時系列データの分析を目的としたリアプノフ指数の計算を実装します。これにより、市場のカオス性の度合いや価格変動の予測可能性を評価することができます。

入力：

input int    InpTimeLag = 1;       // Time lag
input int    InpEmbedDim = 2;      // Embedding dimension
input int    InpDataLength = 1000; // Data length for calculation

• InpTimeLag：位相空間再構築のための時間遅延
• InpEmbedDim：位相空間再構築のための埋め込み次元
• InpDataLength：インジケーターの計算に使用されるローソク足の数

グローバル変数（1つ）：

double LyapunovBuffer[];

初期化：

int OnInit()
{
   SetIndexBuffer(0, LyapunovBuffer, INDICATOR_DATA);
   IndicatorSetInteger(INDICATOR_DIGITS, 5);
   IndicatorSetString(INDICATOR_SHORTNAME, "Lyapunov Exponent");
   return(INIT_SUCCEEDED);
}

OnInit()関数では、インジケーターバッファを構成し、表示精度を小数点以下5桁に設定し、インジケーターの短い名前を設定します。

int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
{
   int start;
   if(prev_calculated == 0)
      start = InpDataLength;
   else
      start = prev_calculated - 1;
   
   for(int i = start; i < rates_total; i++)
   {
      LyapunovBuffer[i] = CalculateLyapunovExponent(close, i);
   }
   
   return(rates_total);
}

OnCalculate()関数はティックごとに呼び出され、InpDataLengthから始まる各ローソク足リアプノフ指数の計算を実行します。

リアプノフ指数の計算：

double CalculateLyapunovExponent(const double &price[], int index)
{
   if(index < InpDataLength)
      return 0;
   
   double sum = 0;
   int count = 0;
   
   for(int i = 0; i < InpDataLength - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      int nearestNeighbor = FindNearestNeighbor(price, index - InpDataLength + i, index);
      if(nearestNeighbor != -1)
      {
         double initialDistance = MathAbs(price[index - InpDataLength + i] - price[nearestNeighbor]);
         double finalDistance = MathAbs(price[index - InpDataLength + i + InpTimeLag] - price[nearestNeighbor + InpTimeLag]);
         
         if(initialDistance > 0 && finalDistance > 0)
         {
            sum += MathLog(finalDistance / initialDistance);
            count++;
         }
      }
   }
   
   if(count > 0)
      return sum / (count * InpTimeLag);
   else
      return 0;
}

CalculateLyapunovExponent()関数は、ローカルリアプノフ指数を計算するためのアルゴリズムを実装します。最近傍法を使用して、再構成された位相空間内の軌跡の発散を推定します。

最近傍の検索：

int FindNearestNeighbor(const double &price[], int startIndex, int endIndex)
{
   double minDistance = DBL_MAX;
   int nearestIndex = -1;
   
   for(int i = startIndex; i < endIndex - (InpEmbedDim - 1) * InpTimeLag; i++)
   {
      if(MathAbs(i - startIndex) > InpTimeLag)
      {
         double distance = 0;
         for(int j = 0; j < InpEmbedDim; j++)
         {
            distance += MathPow(price[startIndex + j * InpTimeLag] - price[i + j * InpTimeLag], 2);
         }
         distance = MathSqrt(distance);
         
         if(distance < minDistance)
         {
            minDistance = distance;
            nearestIndex = i;
         }
      }
   }
   
   return nearestIndex;
}

FindNearestNeighbor()関数は、ユークリッド距離を使用して再構成された位相空間内の最も近い点を検索します。

結果の解釈

• インジケーターの値が正の場合、市場がカオス的な挙動を示していることを意味します。
• インジケーターの値が負の場合、市場がより安定しており、価格動向が比較的予測しやすいことを示します。
• インジケーターの絶対値が高いほど、その特性（カオス的または安定的）がより顕著になります。

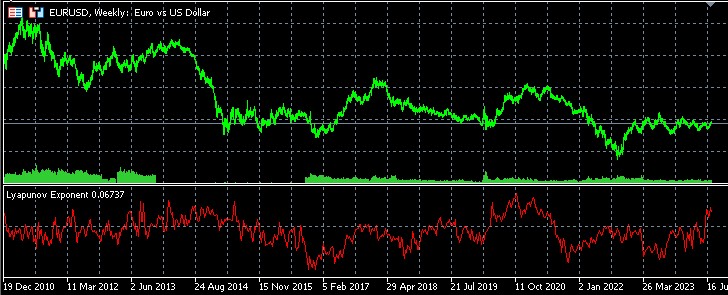
リアプノフ指数を用いたトレンド反転と継続の統計分析

私は、リアプノフ指数と金融市場のダイナミクスの関係を詳細に研究するために、MQL5言語を用いて専門的なスクリプトを開発しました。このツールにより、リアプノフ指数の値を基にトレンド反転と継続の統計分析を詳細に行うことができ、トレーダーやアナリストに市場の動向に関する貴重な洞察を提供します。

本スクリプトは、指定した金融商品の過去データを用いて、あらかじめ設定された一定期間（バー数）を分析します。各バーにおいて、位相空間再構成と最近傍探索法を用いて局所的なリアプノフ指数を算出し、その時点での市場のカオス性の度合いを評価します。

また、スクリプトは価格変動を分析し、トレンドの反転および継続を識別します。トレンドの反転は、現在の終値が前の終値より高く、次の終値が現在の終値より低い場合（またはその逆）と定義されます。それ以外のケースは、トレンド継続として分類されます。

このスクリプトの最大の特徴は、トレンドの反転と継続がリアプノフ指数の値とどのような関係にあるかを比較・分析できる点です。市場のカオス的な振る舞いと価格変動の統計的なパターンを特定することが可能になります。スクリプトは、リアプノフ指数が正の値または負の値のときに発生したトレンド反転および継続の回数を算出します。

分析結果として、スクリプトはリアプノフ指数の正負に対応するトレンド反転・継続の頻度（絶対値および割合）を詳細な統計データとして出力します。これにより、トレーダーは「トレンドの反転が市場のボラティリティ増加とどの程度相関するか」や「トレンド継続が安定した市場環境とどの程度一致するか」を評価できるようになります。

統計分析結果の解釈

リアプノフ指数を使用したトレンドの反転と継続の統計分析の結果は、EURUSD市場の動向に関する興味深いデータを提供します（時間足での分析）。

まず、正のリアプノフ指数と負のリアプノフ指数の間でのイベントの分布がほぼ均等であることに注目すべきです。正および負のリアプノフ指数を持つケースの約半数で、反転とトレンドの継続が観察されます。これにより、H1のEURUSD市場が相対的な安定期と混乱期が交互に現れるバランスの取れた状態であることが示唆されます。

通常、混沌とした予測不可能な動きに関連付けられる正のリアプノフ指数は、全ケースの半数以上（反転の場合50.61%、継続の場合51.09%）で観察されます。これは、市場におけるボラティリティや不確実性がわずかに支配的であることを示している可能性があります。

一方、負のリアプノフ指数は、より秩序だった予測可能な動きとして解釈され、49.39%（反転）および48.91%（トレンド継続）で観測されます。このような期間は、特定のパターンに従ったより安定した価格変動を示すことがあります。

興味深いことに、トレンドの反転と継続の割合は、正のリアプノフ値と負のリアプノフ値の両方でほぼ同じです。両者の差は0.5%未満であり、これにより、リアプノフ指数自体がトレンド反転や継続を予測する決定的な要因ではないことが示唆されます。

正と負のリアプノフ指数がほぼ均等に分布していることは、EURUSD市場が安定と混乱の期間を交互に経験している複雑な性質を示している可能性があります。 

結論

カオス理論は金融市場を分析するための革新的なアプローチを提供し、その複雑で非線形的な性質をより深く理解する手助けをします。この記事では、カオス理論の主要な概念（アトラクター、フラクタル、バタフライ効果）と、それらがどのように金融時系列に応用されるかについて解説しました。特に、市場動向の混乱の度合いを評価するツールとして、リアプノフ指数に注目しました。