MetaTrader 5 / Examples
Русский 中文 Español Deutsch 日本語 Português
preview
Adaptive Social Behavior Optimization (ASBO): Two-phase evolution

Adaptive Social Behavior Optimization (ASBO): Two-phase evolution

MetaTrader 5 — Examples | 20 January 2025, 13:18
1 099 0
Andrey Dik
Andrey Dik

Contents
  1. Introduction
  2. Implementation of the algorithm
  3. Test results


1. Introduction

In the previous article, we have considered an example of Schwefel's concept, which includes a normal distribution, the use of self-adaptive mutation rates, and a function for determining the nearest neighbors by their fitness value. Now our path leads us to a new stage of research, where we will dive into a two-phase process, completing the formation of the algorithm as a mathematical model - ASBO (Adaptive Social Behavior Optimization). We will undertake a comprehensive testing of this exciting model on the test functions that are already familiar to us and draw conclusions about its efficiency. In this article, we will uncover new applications of social behavior in living organisms in the field of optimization, and present unique results that will help us better understand and use the principles of collective behavior to solve complex problems.


2. Implementation of the algorithm

Let's start by forming a pseudocode of the ASBO algorithm (the equations used are presented below):

Inputs: PZ population size, M number of populations and P' number of epochs per population. f (x) - objective function.

Initialization:

1. Create M population each having the size of PZ
2. For each population:

  • initialize xi solutions randomly
  • Calculate the values of the f (xi) target function for each solution
  • Define the Gb global leader as a solution with the highest f (xi)
  • For each xi solution, definr a group of nearest neighbors Nc
  • Initialize personal best decisions Sb = xi
  • Initialize adaptive parameters Cg, Cs and Cn randomly within the range [-1.0; 1.0]

Phase 1: Independent handling of populations.
3. For each of M populations:

  •  For each xi solution:
  • Apply self-adaptive mutation to update Cg, Cs and Cn ratios according to the equations (3) and (4)
  • Calculate the change in the ΔX (i + 1) position according to the equation (1)
  • Update position xi according to the equation (2)
  • Calculate the new value f (xi)
  • Update personal best solution Sb if f (xi) > f (Sb)
  • Update the global leader Gb if f (xi) > f (Gb)
  • Repeat till reaching P' epochs

4. Save the final populations, f (xi) values, as well as Cg, Cs and Cn parameters

Phase 2: handling the combined population.
5. Out of all final populations, select PZ best solutions for f (xi)
6. Use the Cg, Cs and Cn saved parameters for these PZ solutions
7. Apply the ASBO algorithm to the combined population having the size of PZ
8. Repeat steps 6-7 until the stop criterion is reached

    Conclusion: Global optimum Gb

    Key equations:

    • ΔX (i + 1) = Cg * R1 * (Gb - xi) + Cs * R2 * (Sb - xi) + Cn * R3 * (Nc - xi)  (1)
    • x (i + 1) = xi + ΔX (i + 1)                                                                           (2)
    • p'i (j) = pi (j) + σi (j) * N (0, 1)                                                                  (3)
    • σ'i (j) = σi (j) * exp (τ' * N (0, 1) + τ * Nj (0, 1))                                        (4)

    Where;

    • Gb - global leader
    • Sb - personal best solution
    • Nc - center of the group of neighbors by fitness
    • R1, R2, R3 - random numbers in the range [0, 1]
    • Cg, Cs, Cn - adaptive parameters
    • N (0, 1) - random number from a normal distribution
    • Nj (0,1) - random number from a normal distribution for each j measurement
    • τ, τ' - scaling factors for self-adaptive mutation

    The presented pseudocode shows that the algorithm implements a two-phase evolution of the social model development. The logic of the algorithm can be described briefly in phases:

    1. First phase:

    • Take M populations of the same PZ size each.
    • ASBO algorithm is applied to each of these M populations independently within a fixed number of P' iterations.
    • At the end of this phase, the values of the fitness functions and adaptive mutation parameters are saved for each individual from all final populations.

    2. Second phase:

    • PZ of the best individuals in terms of fitness function value are selected out of all final populations of the first phase.
    • Their saved adaptive mutation parameters are applied to these PZ best individuals.
    • ASBO algorithm is applied to the new population of PZ size for obtaining the final solution.

    The meaning of two-phase evolution:

    1. The first phase provides a diversity of solutions and better localization of the global optimum region due to the independent evolution of several populations.
    2. The second phase uses the best solutions of the populations from the first phase and their adaptive parameters for accelerated convergence to the global optimum.

    Thus, two-phase evolution, in theory, allows combining global search in the first stage with more efficient local optimization in the second stage, which ultimately, presumably, improves the performance of the algorithm as a whole.

    The conventional version of the multi-population two-phase ASBO algorithm involves using several populations in parallel and independently in the first phase. During the second phase, the best solutions are taken from the populations and a new population is created. However, using our single template for all population algorithms raises the question of how to handle multiple populations.

    The first solution might be to split a normal population, say 50 individuals, into several populations, say 5. In this case, each of the 5 populations will contain 10 individuals. We can treat multiple populations in the usual way, as if they were one whole population. However, in the second phase, a problem arises: we need to take the best solutions from these 5 populations and place them into a new population. But we will not be able to get the required number because we would have to put them all in, which would efficiently mean creating a copy of the original population.

    The second solution to this problem is to create 5 populations with sizes equal to the size of our population, that is, 50 individuals. For each of these populations, a fixed number of epochs is allocated, for example 20. In this case, during the first phase, we will sequentially handle these 5 populations with a fixed number of epochs for each population, i.e. 5 * 20 = 100 epochs will be spent. The second phase will use the remaining 100 epochs (out of a total of 200 epochs). In this second phase, we will put these 5 populations into one big population of 250 individuals, sort them and take the best 50 individuals from them and create a new population. Next, we perform operations with this new population in the usual way according to the equations. This is completely consistent with the original algorithm, while we adhere to our concept of working with population algorithms. We have had to apply innovative approaches in other algorithms before, such as Nelder-Mead, chemical CRO, evolutionary algorithms and others, to ensure that all algorithms are compatible and can be seamlessly interchanged.

    Now let's move on to writing the code.

    Implement the S_ASBO_Agent structure, which will describe the search agent in the multi-population two-phase ASBO algorithm. The structure defines variables and the Init method, which initializes the agent.

    Variables:

    • c - array of coordinates
    • cBest - array of best coordinates
    • f - fitness value
    • fBest - best fitness value
    • Cg, Cs, Cn - adaptive parameters
    • u - C_AO_Utilities class object

    The Init method initializes the agent:

    • Accepts the number of coords coordinates, as well as rangeMin and rangeMax arrays, representing the minimum and maximum values for each coordinate.
    • Allocate memory for c and cBest arrays with the number of coords coordinates.
    • Set the initial value fBest as -DBL_MAX.
    • Generates random values for Cg, Cs and Cn adaptive parameters.
    • Fills in the c array with random values in the range between rangeMin and rangeMax.
    • Assigns values from c to the cBest array. 
    //——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Agent
{
    double c     [];   //coordinates
    double cBest [];   //best coordinates
    double f;          //fitness
    double fBest;      //best fitness

    double Cg, Cs, Cn; //adaptive parameters
    C_AO_Utilities u;

    void Init (int coords, double &rangeMin [], double &rangeMax [])
    {
      ArrayResize (c,     coords);
      ArrayResize (cBest, coords);
      fBest = -DBL_MAX;
      Cg = u.RNDprobab ();
      Cs = u.RNDprobab ();
      Cn = u.RNDprobab ();

      for (int i = 0; i < coords; i++)
      {
        c     [i] = u.RNDfromCI (rangeMin [i], rangeMax [i]);
        cBest [i] = c [i];
      }

    }
};
//——————————————————————————————————————————————————————————————————————————————

    To work with several populations in turn, it will be convenient to use an array of populations. To achieve this, we will write the S_ASBO_Population structure, which contains only one field:

    • agent - array of objects of S_ASBO_Agent type representing agents in the population.
    //——————————————————————————————————————————————————————————————————————————————
struct S_ASBO_Population
{
    S_ASBO_Agent agent [];
};
//——————————————————————————————————————————————————————————————————————————————

    Declare the C_AO_ASBO class - descendant of the C_AO class. The class contains a number of methods and variables for handling optimization:

    1. Constructor and destructor:

    • The constructor initializes the algorithm parameters such as population size, number of populations, number of epochs for each population, and references to the algorithm description.
    • The destructor is empty.

    2. The options available are:

    • SetParams - set algorithm parameters from the params array.
    • Init - initialize the algorithm with the given parameters: search range, search step and number of epochs.
    • Moving - move agents in the search space.
    • Revision - revise agents in the search space and update the best global solution.

    3. Variables:

    • numPop, epochsForPop - number of populations and epochs for each population.
    • epochs, epochNow, currPop, isPhase2, popEpochs, tau, tau_prime - additional variables used in the algorithm.
    • allAgentsForSortPhase2, allAgentsTemp, agentsPhase2, agentsTemp - arrays of agents used in the algorithm.
    • pop - population array.

    4. Auxiliary methods:

    • AdaptiveMutation - perform adaptive mutation for the agent.
    • UpdatePosition - update the agent position.
    • FindNeighborCenter - find the center of neighbors for the agent.
    • Sorting - sort agents.

    Thus, the C_AO_ASBO class is an implementation of the ASBO algorithm using various methods and operations to move and revise agents in the search space.

    //——————————————————————————————————————————————————————————————————————————————
class C_AO_ASBO : public C_AO
{
  public: //--------------------------------------------------------------------
  ~C_AO_ASBO () { }
  C_AO_ASBO ()
  {
    ao_name = "ASBO";
    ao_desc = "Adaptive Social Behavior Optimization";
    ao_link = "https://www.mql5.com/ru/articles/15283";

    popSize       = 50;   //population size
    numPop        = 5;    //number of populations
    epochsForPop  = 10;   //number of epochs for each population

    ArrayResize (params, 3);

    params [0].name = "popSize";      params [0].val = popSize;
    params [1].name = "numPop";       params [1].val = numPop;
    params [2].name = "epochsForPop"; params [2].val = epochsForPop;
  }

  void SetParams ()
  {
    popSize      = (int)params [0].val;
    numPop       = (int)params [1].val;
    epochsForPop = (int)params [2].val;
  }

  bool Init (const double &rangeMinP  [], //minimum search range
             const double &rangeMaxP  [], //maximum search range
             const double &rangeStepP [], //step search
             const int     epochsP = 0);  //number of epochs

  void Moving   ();
  void Revision ();

  //----------------------------------------------------------------------------
  int numPop;       //number of populations
  int epochsForPop; //number of epochs for each population

  private: //-------------------------------------------------------------------
  int  epochs;
  int  epochNow;
  int  currPop;
  bool isPhase2;
  int  popEpochs;

  double tau;
  double tau_prime;

  S_ASBO_Agent      allAgentsForSortPhase2 [];
  S_ASBO_Agent      allAgentsTemp          [];
  S_ASBO_Agent      agentsPhase2           [];
  S_ASBO_Agent      agentsTemp             [];
  S_ASBO_Population pop                    []; //M populations

  void   AdaptiveMutation   (S_ASBO_Agent &agent);
  void   UpdatePosition     (int ind, S_ASBO_Agent &ag []);
  void   FindNeighborCenter (int ind, S_ASBO_Agent &ag [], double &center []);
  void   Sorting (S_ASBO_Agent &p [], S_ASBO_Agent &pTemp [], int size);
};
//——————————————————————————————————————————————————————————————————————————————

    The Init method performs an important function of the C_AO_ASBO class initializing the parameters and data structures necessary for the ASBO algorithm before starting optimization. Basic initialization steps in the Init method:

    1. Checking and initializing basic parameters:

    • The method calls StandardInit for initializing basic parameters such as the minimum and maximum search ranges and the search step. If initialization fails, the method returns false.

    2. Initializing additional variables:

    • The values of the epochs, epochNow, currPop, isPhase2 and popEpochs variables are set.
    • The values of the tau and tau_prime variables are calculated based on the dimensionality of the coords search space.

    3. Creation and initialization of populations and agents:

    • The pop array is created for storing the populations and each population is initialized. For each agent in the population, the Init is called to initialize its coordinates in the specified range.
    • The agentsPhase2 array is created for phase 2 agents and initialized similarly to populations.
    • The allAgentsForSortPhase2 and allAgentsTemp arrays are created for temporary storage of agents during the sorting process, and each agent is initialized.

    4. Returning the result:

    •    The method returns true if initialization is successful.
    //——————————————————————————————————————————————————————————————————————————————
bool C_AO_ASBO::Init (const double &rangeMinP  [], //minimum search range
                      const double &rangeMaxP  [], //maximum search range
                      const double &rangeStepP [], //step search
                      const int     epochsP = 0)   //number of epochs
{
  if (!StandardInit (rangeMinP, rangeMaxP, rangeStepP)) return false;

  //----------------------------------------------------------------------------
  epochs    = epochsP;
  epochNow  = 0;
  currPop   = 0;
  isPhase2  = false;
  popEpochs = 0;

  tau       = 1.0 / MathSqrt (2.0 * coords);
  tau_prime = 1.0 / MathSqrt (2.0 * MathSqrt (coords));

  ArrayResize (pop, numPop);
  for (int i = 0; i < numPop; i++)
  {
    ArrayResize (pop [i].agent, popSize);

    for (int j = 0; j < popSize; j++) pop [i].agent [j].Init (coords, rangeMin, rangeMax);
  }

  ArrayResize (agentsPhase2, popSize);
  ArrayResize (agentsTemp,   popSize);
  for (int i = 0; i < popSize; i++) agentsPhase2 [i].Init (coords, rangeMin, rangeMax);

  ArrayResize (allAgentsForSortPhase2, popSize * numPop);
  ArrayResize (allAgentsTemp,          popSize * numPop);

  for (int i = 0; i < popSize * numPop; i++)
  {
    allAgentsForSortPhase2 [i].Init (coords, rangeMin, rangeMax);
    allAgentsTemp          [i].Init (coords, rangeMin, rangeMax);
  }

  return true;
}
//——————————————————————————————————————————————————————————————————————————————

    The Moving method of the C_AO_ASBO class represents the basic process of agent movement within the ASBO algorithm, including the transition between phases and the execution of appropriate operations for each phase. The main steps in the Moving method:

    1. Increase the epochNow value:

    • The value of the epochNow variable is increased by 1, which reflects the beginning of a new era of optimization.

    2. Phase 1:

    • If the algorithm is not in phase 2, then the following is done:
      • If the number of epochs for the current population has reached the limit of epochsForPop, the popEpochs counter is reset, the currPop counter is increased and the fB value is reset as well.
      • If the maximum number of numPop populations is reached, the algorithm moves to phase 2. In this case, agents from all populations are combined into a single array and sorted. The best agents are copied to the agentsPhase2 array.
    • Otherwise, adaptive mutation and position update operations, as well as copying coordinates, are performed for each agent in the current population.

    3. Phase 2:

    • In phase 2, adaptive mutation and position update operations, as well as copying of coordinates, are also performed for each agent in the agentsPhase2 array.
    //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Moving ()
{
  epochNow++;

  //Phase 1----------------------------------------------------------------------
  if (!isPhase2)
  {
    if (popEpochs >= epochsForPop)
    {
      popEpochs = 0;
      currPop++;

      fB = -DBL_MAX;
    }

    if (currPop >= numPop)
    {
      isPhase2 = true;

      int cnt = 0;
      for (int i = 0; i < numPop; i++)
      {
        for (int j = 0; j < popSize; j++)
        {
          allAgentsForSortPhase2 [cnt] = pop [i].agent [j];
          cnt++;
        }
      }

      u.Sorting (allAgentsForSortPhase2, allAgentsTemp, popSize * numPop);

      for (int j = 0; j < popSize; j++) agentsPhase2 [j] = allAgentsForSortPhase2 [j];
    }
    else
    {
      for (int i = 1; i < popSize; i++)
      {
        AdaptiveMutation (pop [currPop].agent [i]);
        UpdatePosition   (i, pop [currPop].agent);

        ArrayCopy (a [i].c, pop [currPop].agent [i].c);
      }

      popEpochs++;
      return;
    }
  }

  //Phase 2----------------------------------------------------------------------
  for (int i = 1; i < popSize; i++)
  {
    AdaptiveMutation (agentsPhase2 [i]);
    UpdatePosition   (i, agentsPhase2);

    ArrayCopy (a [i].c, agentsPhase2 [i].c);
  }
}
//——————————————————————————————————————————————————————————————————————————————

    The Revision method of the C_AO_ASBO class represents the process of revising the optimization results, including updating the value of fB and updating the optimization results for each phase of the ASBO algorithm. The main components of the code:

    1. Variables and their initialization:

    • int ind = -1; — variable for storing the index of the element with the best value of the f function.
    • fB — variable representing the best value of the "f" function found at the current stage.

    2. Searching for the best agent:

    • In the first for loop, iterate through all agents (objects representing decisions) in the a array of popSize size.
    • If the f function of the current agent is greater than the current best fB value, fB and ind index are updated.

    3. Copying data:

    • If an agent with the best function value has ind != -1, the cB array (representing the best solution parameters) is updated with values from the a array.

    4. Phase 1:

    • If the currPop current population is less than the total number of numPop populations, the f function values are updated for the agents of the current population.
    • If the f agent value in the a array exceeds its best value of fBest, fBest is updated and the corresponding characteristics are copied to cBest.
    • Then the agents of the current population are sorted using the u.Sorting method.

    5. Phase 2:

    • If the current population is equal to or greater than the total number of populations, then similar actions are performed for the agentsPhase2 array.
    • The values of the f function are updated, the best fBest values are checked and updated, and sorting is performed.

    General logic:

    • The Revision method performs two main steps: finding the best agent and updating data for agents depending on the current phase (phase 1 or phase 2).
    • The main goal is to track and update the best solutions found during the optimization, and to maintain sorting of agents for later use.
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::Revision ()
{
  //----------------------------------------------------------------------------
  int ind = -1;

  for (int i = 0; i < popSize; i++)
  {
    if (a [i].f > fB)
    {
      fB = a [i].f;
      ind = i;
    }
  }

  if (ind != -1) ArrayCopy (cB, a [ind].c, 0, 0, WHOLE_ARRAY);

  //----------------------------------------------------------------------------
  //phase 1
  if (currPop < numPop)
  {
    for (int i = 0; i < popSize; i++)
    {
      pop [currPop].agent [i].f = a [i].f;

      if (a [i].f > pop [currPop].agent [i].fBest)
      {
        pop [currPop].agent [i].fBest = a [i].f;
        ArrayCopy (pop [currPop].agent [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (pop [currPop].agent, agentsTemp, popSize);
  }
  //phase 2
  else
  {
    for (int i = 0; i < popSize; i++)
    {
      agentsPhase2 [i].f = a [i].f;

      if (a [i].f > agentsPhase2 [i].fBest)
      {
        agentsPhase2 [i].fBest = a [i].f;
        ArrayCopy (agentsPhase2 [i].cBest, a [i].c, 0, 0, WHOLE_ARRAY);
      }
    }

    u.Sorting (agentsPhase2, agentsTemp, popSize);
  }
}
//——————————————————————————————————————————————————————————————————————————————

      The AdaptiveMutation method of the C_AO_ASBO class represents adaptive mutation of the ag agent ratios within the ASBO algorithm, including the use of the Gaussian distribution and the calculation of new ratio values based on random variables. The main steps in the AdaptiveMutation method:

      1. Adaptive mutation of ratios:

      • The Cg, Cs and Cn ratios of the ag agent mutate using Gaussian distribution.
      • For each ratio, a new value is calculated using the exponential function of the sum of two Gaussian random variables, each of which is multiplied by the corresponding tau_prime and tau ratio.
      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::AdaptiveMutation (S_ASBO_Agent &ag)
{
  ag.Cg *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cs *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
  ag.Cn *= MathExp (tau_prime * u.GaussDistribution (0, -1, 1, 1) + tau * u.GaussDistribution (0, -1, 1, 8));
}
//——————————————————————————————————————————————————————————————————————————————

      The UpdatePosition method of the C_AO_ASBO class represents updating the agent position within the ASBO algorithm, including calculating the position change based on various factors and updating the position within specified ranges. The main steps in the UpdatePosition method:

      1. Calculating the change in position:

      • Calculate the change in the ag [ind] agent position in every dimension j using various ratios and values, such as cB, cBest, deltaX, rangeMin, rangeMax and rangeStep.

      2. Agent position update:

      • For each j dimension, a new agent position ag [ind].c [j] is calculated by adding deltaX [j] and subsequent correction of the value within the specified ranges.

      The commented part of the code 1) - original version, 3) - my version without considering Cg, Cs and Cn, the normal distribution was used instead. "2)" is my option. It showed the best results of all three.

      //——————————————————————————————————————————————————————————————————————————————
void C_AO_ASBO::UpdatePosition (int ind, S_ASBO_Agent &ag [])
{
  double deltaX [];
  ArrayResize (deltaX, coords);

  FindNeighborCenter (ind, ag, deltaX);

  for (int j = 0; j < coords; j++)
  {
    /*
    //1)
    deltaX [j] = ag [ind].Cg * u.RNDfromCI (-1, 1) * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * u.RNDfromCI (-1, 1) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * u.RNDfromCI (-1, 1) * (deltaX         [j] - ag [ind].c [j]);
    */
    
    //2)
    deltaX [j] = ag [ind].Cg * (cB             [j] - ag [ind].c [j]) +
                 ag [ind].Cs * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 ag [ind].Cn * (deltaX         [j] - ag [ind].c [j]);


    /*
    //3)
    deltaX [j] = u.GaussDistribution (0, -1, 1, 8) * (cB             [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (ag [ind].cBest [j] - ag [ind].c [j]) +
                 u.GaussDistribution (0, -1, 1, 8) * (deltaX         [j] - ag [ind].c [j]);
    */

    ag [ind].c [j] += deltaX [j];
    ag [ind].c [j] = u.SeInDiSp (ag [ind].c [j], rangeMin [j], rangeMax [j], rangeStep [j]);
  }
}
//——————————————————————————————————————————————————————————————————————————————


      3. Test results

      A printout of the ASBO algorithm reveals a number of interesting features that make it truly unique. One of its key characteristics is its outstanding scalability. This allows the algorithm to efficiently handle high-dimensional problems. Particularly noteworthy are the results obtained when testing the Forest and Megacity functions with 1000 parameters. In these cases, ASBO demonstrates impressive performance, comparable to the results of leading algorithms in the rating table. Such achievements highlight not only the efficiency of the algorithm, but also its potential for application in a variety of areas requiring high-quality optimization.

      ASBO|Adaptive Social Behavior Optimization|50.0|5.0|10.0|
      =============================
      5 Hilly's; Func runs: 10000; result: 0.7633114189858913
      25 Hilly's; Func runs: 10000; result: 0.4925279738997658
      500 Hilly's; Func runs: 10000; result: 0.3261850685263711
      =============================
      5 Forest's; Func runs: 10000; result: 0.7954558091769679
      25 Forest's; Func runs: 10000; result: 0.4003462752027551
      500 Forest's; Func runs: 10000; result: 0.26096981234192485
      =============================
      5 Megacity's; Func runs: 10000; result: 0.2646153846153846
      25 Megacity's; Func runs: 10000; result: 0.1716923076923077
      500 Megacity's; Func runs: 10000; result: 0.18200000000000044
      =============================
      All score: 3.65710 (40.63%)

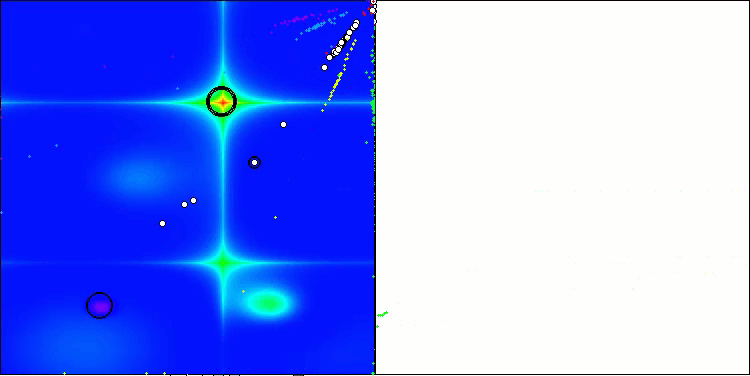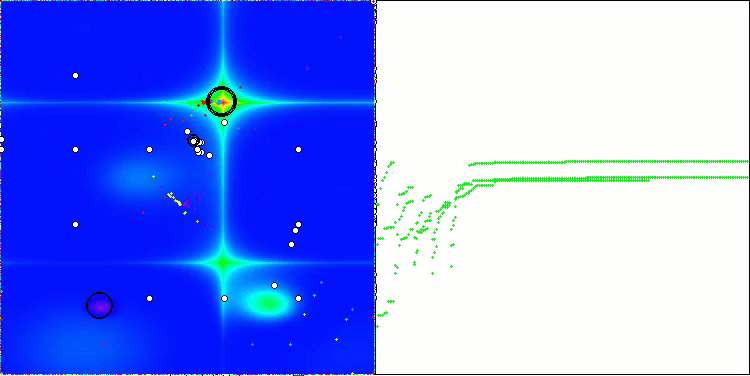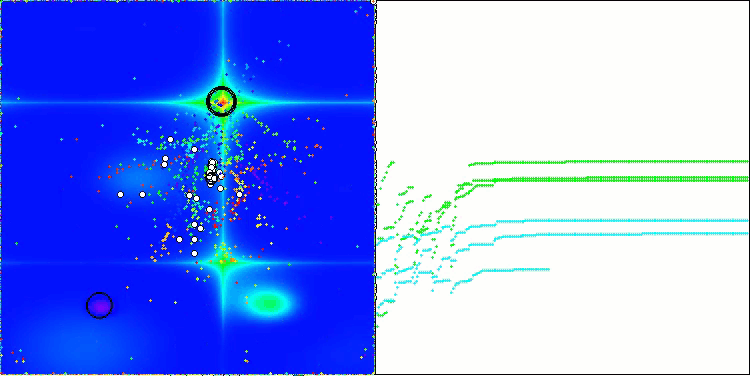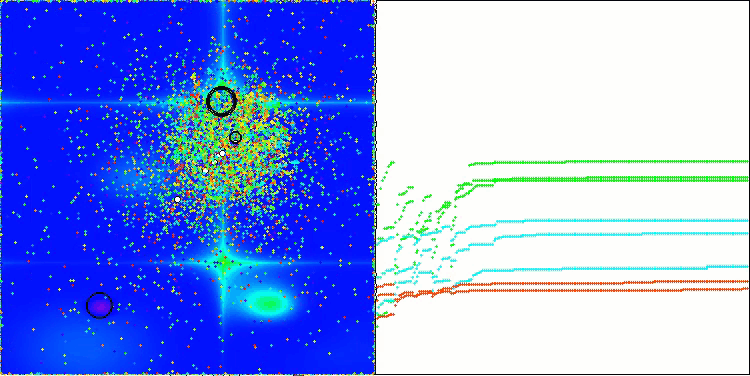
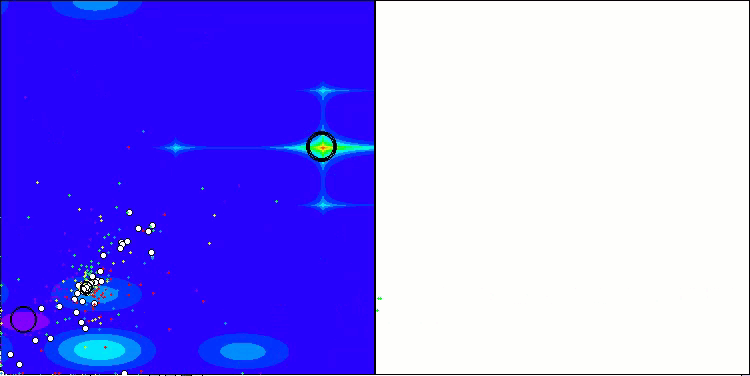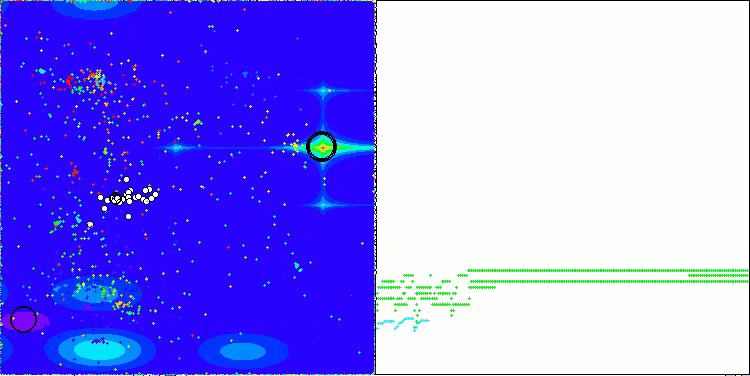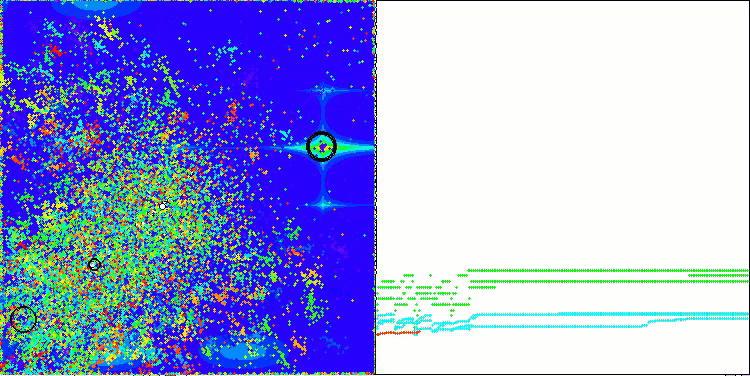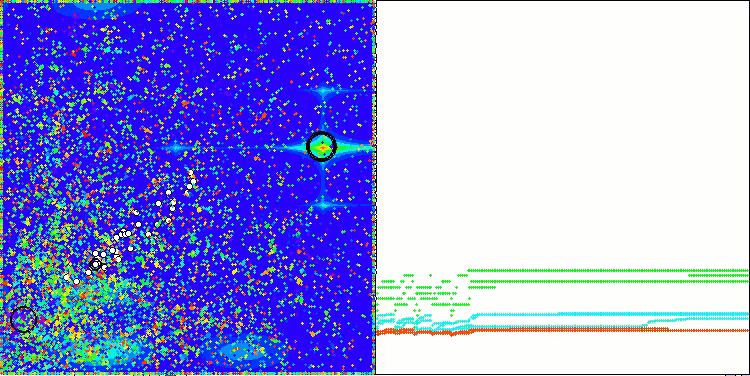
      Visualization of the ASBO algorithm results reveals a number of interesting features that deserve attention. From the very beginning of the algorithm's operation, one can see how it successfully identifies critically important solution regions, which demonstrates its ability to efficiently explore the parameter space.

      The convergence graph shows characteristic breaks in the line, which are caused by the sequential operation of several populations in the first phase. These gaps indicate that each population contributes to the optimization by exploring different parts of the space. However, in the second phase, the graph takes on a solid form, which means that the best solutions from all populations collected together after the first phase are combined. This unification allows the algorithm to focus on refining promising areas.

      Thus, the visualization not only illustrates the dynamics of the algorithm, but also highlights its adaptive and cooperative mechanisms.

      Hilly

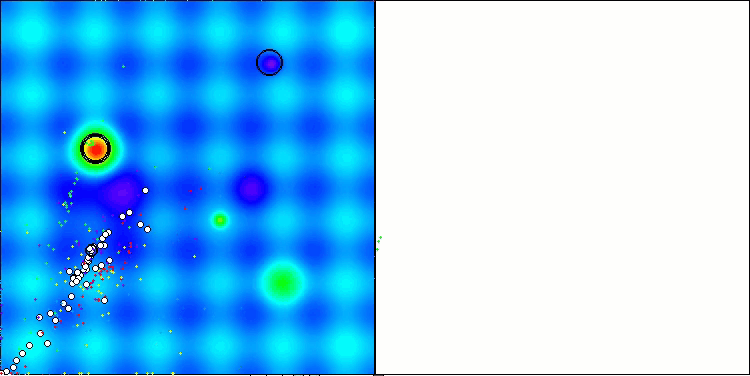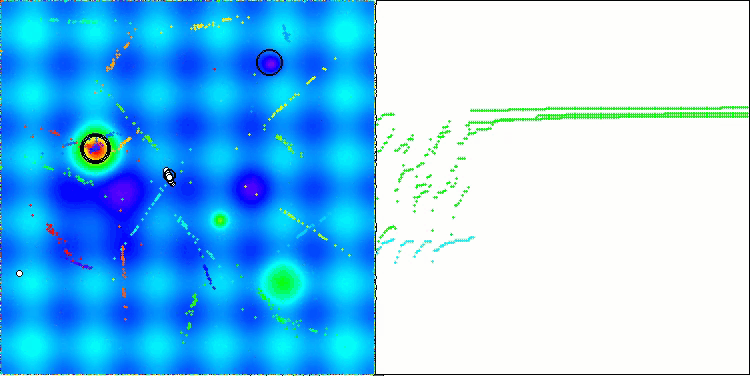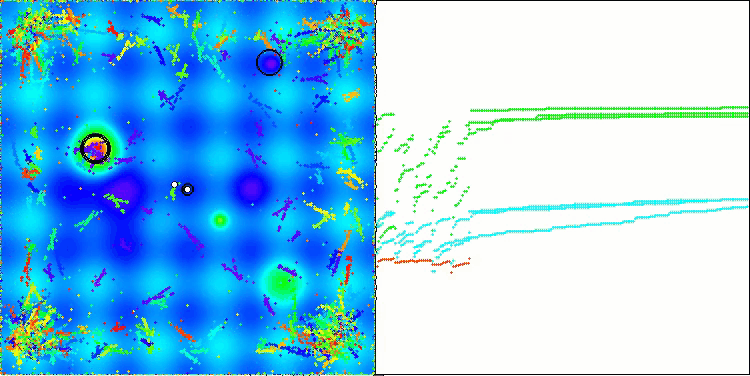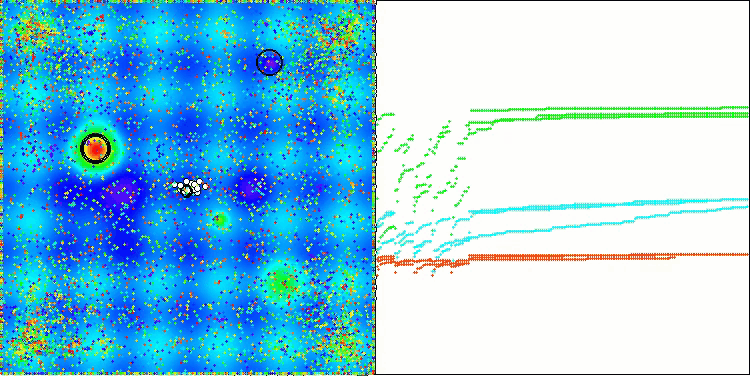
        ASBO on the Hilly test function

      Forest

      ASBO on the Forest test function

      Megacity

      ASBO on the Megacity test function

      Based on the results of the conducted research, the algorithm confidently takes a place in the middle of the rating table.

      # AO Description Hilly Hilly final Forest Forest final Megacity (discrete) Megacity final Final result % of MAX
      10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F) 10 p (5 F) 50 p (25 F) 1000 p (500 F)
      1 ANS across neighbourhood search 0.94948 0.84776 0.43857 2.23581 1.00000 0.92334 0.39988 2.32323 0.70923 0.63477 0.23091 1.57491 6.134 68.15
      2 CLA code lock algorithm 0.95345 0.87107 0.37590 2.20042 0.98942 0.91709 0.31642 2.22294 0.79692 0.69385 0.19303 1.68380 6.107 67.86
      3 (P+O)ES (P+O) evolution strategies 0.92256 0.88101 0.40021 2.20379 0.97750 0.87490 0.31945 2.17185 0.67385 0.62985 0.18634 1.49003 5.866 65.17
      4 CTA comet tail algorithm 0.95346 0.86319 0.27770 2.09435 0.99794 0.85740 0.33949 2.19484 0.88769 0.56431 0.10512 1.55712 5.846 64.96
      5 SDSm stochastic diffusion search M 0.93066 0.85445 0.39476 2.17988 0.99983 0.89244 0.19619 2.08846 0.72333 0.61100 0.10670 1.44103 5.709 63.44
      6 ESG evolution of social groups 0.99906 0.79654 0.35056 2.14616 1.00000 0.82863 0.13102 1.95965 0.82333 0.55300 0.04725 1.42358 5.529 61.44
      7 SIA simulated isotropic annealing 0.95784 0.84264 0.41465 2.21513 0.98239 0.79586 0.20507 1.98332 0.68667 0.49300 0.09053 1.27020 5.469 60.76
      8 ACS artificial cooperative search 0.75547 0.74744 0.30407 1.80698 1.00000 0.88861 0.22413 2.11274 0.69077 0.48185 0.13322 1.30583 5.226 58.06
      9 TSEA turtle shell evolution algorithm 0.96798 0.64480 0.29672 1.90949 0.99449 0.61981 0.22708 1.84139 0.69077 0.42646 0.13598 1.25322 5.004 55.60
      10 DE differential evolution 0.95044 0.61674 0.30308 1.87026 0.95317 0.78896 0.16652 1.90865 0.78667 0.36033 0.02953 1.17653 4.955 55.06
      11 CRO chemical reaction optimization 0.94629 0.66112 0.29853 1.90593 0.87906 0.58422 0.21146 1.67473 0.75846 0.42646 0.12686 1.31178 4.892 54.36
      12 BSA bird swarm algorithm 0.89306 0.64900 0.26250 1.80455 0.92420 0.71121 0.24939 1.88479 0.69385 0.32615 0.10012 1.12012 4.809 53.44
      13 HS harmony search 0.86509 0.68782 0.32527 1.87818 0.99999 0.68002 0.09590 1.77592 0.62000 0.42267 0.05458 1.09725 4.751 52.79
      14 SSG saplings sowing and growing 0.77839 0.64925 0.39543 1.82308 0.85973 0.62467 0.17429 1.65869 0.64667 0.44133 0.10598 1.19398 4.676 51.95
      15 (PO)ES (PO) evolution strategies 0.79025 0.62647 0.42935 1.84606 0.87616 0.60943 0.19591 1.68151 0.59000 0.37933 0.11322 1.08255 4.610 51.22
      16 BSO brain storm optimization 0.93736 0.57616 0.29688 1.81041 0.93131 0.55866 0.23537 1.72534 0.55231 0.29077 0.11914 0.96222 4.498 49.98
      17 WOAm wale optimization algorithm M 0.84521 0.56298 0.26263 1.67081 0.93100 0.52278 0.16365 1.61743 0.66308 0.41138 0.11357 1.18803 4.476 49.74
      18 AEFA artificial electric field algorithm 0.87700 0.61753 0.25235 1.74688 0.92729 0.72698 0.18064 1.83490 0.66615 0.11631 0.09508 0.87754 4.459 49.55
      19 ACOm ant colony optimization M 0.88190 0.66127 0.30377 1.84693 0.85873 0.58680 0.15051 1.59604 0.59667 0.37333 0.02472 0.99472 4.438 49.31
      20 BFO-GA bacterial foraging optimization - ga 0.89150 0.55111 0.31529 1.75790 0.96982 0.39612 0.06305 1.42899 0.72667 0.27500 0.03525 1.03692 4.224 46.93
      21 ASBO adaptive social behavior optimization 0.76331 0.49253 0.32619 1.58202 0.79546 0.40035 0.26097 1.45677 0.26462 0.17169 0.18200 0.61831 3.657 40.63
      22 MEC mind evolutionary computation 0.69533 0.53376 0.32661 1.55569 0.72464 0.33036 0.07198 1.12698 0.52500 0.22000 0.04198 0.78698 3.470 38.55
      23 IWO invasive weed optimization 0.72679 0.52256 0.33123 1.58058 0.70756 0.33955 0.07484 1.12196 0.42333 0.23067 0.04617 0.70017 3.403 37.81
      24 Micro-AIS micro artificial immune system 0.79547 0.51922 0.30861 1.62330 0.72956 0.36879 0.09398 1.19233 0.37667 0.15867 0.02802 0.56335 3.379 37.54
      25 COAm cuckoo optimization algorithm M 0.75820 0.48652 0.31369 1.55841 0.74054 0.28051 0.05599 1.07704 0.50500 0.17467 0.03380 0.71347 3.349 37.21
      26 SDOm spiral dynamics optimization M 0.74601 0.44623 0.29687 1.48912 0.70204 0.34678 0.10944 1.15826 0.42833 0.16767 0.03663 0.63263 3.280 36.44
      27 NMm Nelder-Mead method M 0.73807 0.50598 0.31342 1.55747 0.63674 0.28302 0.08221 1.00197 0.44667 0.18667 0.04028 0.67362 3.233 35.92
      28 FAm firefly algorithm M 0.58634 0.47228 0.32276 1.38138 0.68467 0.37439 0.10908 1.16814 0.28667 0.16467 0.04722 0.49855 3.048 33.87
      29 GSA gravitational search algorithm 0.64757 0.49197 0.30062 1.44016 0.53962 0.36353 0.09945 1.00260 0.32667 0.12200 0.01917 0.46783 2.911 32.34
      30 BFO bacterial foraging optimization 0.61171 0.43270 0.31318 1.35759 0.54410 0.21511 0.05676 0.81597 0.42167 0.13800 0.03195 0.59162 2.765 30.72
      31 ABC artificial bee colony 0.63377 0.42402 0.30892 1.36671 0.55103 0.21874 0.05623 0.82600 0.34000 0.14200 0.03102 0.51302 2.706 30.06
      32 BA bat algorithm 0.59761 0.45911 0.35242 1.40915 0.40321 0.19313 0.07175 0.66810 0.21000 0.10100 0.03517 0.34617 2.423 26.93
      33 SA simulated annealing 0.55787 0.42177 0.31549 1.29513 0.34998 0.15259 0.05023 0.55280 0.31167 0.10033 0.02883 0.44083 2.289 25.43
      34 IWDm intelligent water drops M 0.54501 0.37897 0.30124 1.22522 0.46104 0.14704 0.04369 0.65177 0.25833 0.09700 0.02308 0.37842 2.255 25.06
      35 PSO particle swarm optimisation 0.59726 0.36923 0.29928 1.26577 0.37237 0.16324 0.07010 0.60572 0.25667 0.08000 0.02157 0.35823 2.230 24.77
      36 Boids boids algorithm 0.43340 0.30581 0.25425 0.99346 0.35718 0.20160 0.15708 0.71586 0.27846 0.14277 0.09834 0.51957 2.229 24.77
      37 MA monkey algorithm 0.59107 0.42681 0.31816 1.33604 0.31138 0.14069 0.06612 0.51819 0.22833 0.08567 0.02790 0.34190 2.196 24.40
      38 SFL shuffled frog-leaping 0.53925 0.35816 0.29809 1.19551 0.37141 0.11427 0.04051 0.52618 0.27167 0.08667 0.02402 0.38235 2.104 23.38
      39 FSS fish school search 0.55669 0.39992 0.31172 1.26833 0.31009 0.11889 0.04569 0.47467 0.21167 0.07633 0.02488 0.31288 2.056 22.84
      40 RND random 0.52033 0.36068 0.30133 1.18234 0.31335 0.11787 0.04354 0.47476 0.25333 0.07933 0.02382 0.35648 2.014 22.37
      41 GWO grey wolf optimizer 0.59169 0.36561 0.29595 1.25326 0.24499 0.09047 0.03612 0.37158 0.27667 0.08567 0.02170 0.38403 2.009 22.32
      42 CSS charged system search 0.44252 0.35454 0.35201 1.14907 0.24140 0.11345 0.06814 0.42299 0.18333 0.06300 0.02322 0.26955 1.842 20.46
      43 EM electroMagnetism-like algorithm 0.46250 0.34594 0.32285 1.13129 0.21245 0.09783 0.10057 0.41085 0.15667 0.06033 0.02712 0.24412 1.786 19.85


      Summary

      The algorithm stands out for its originality and non-standard behavior, which makes its visualization unique and unlike any previously known methods. This attracts attention and arouses interest in its internal mechanisms.

      Despite the average overall results and convergence when solving small-dimensional problems, the algorithm demonstrates its true potential when working with more complex problems and within a large search space. It uses multiple populations that run sequentially in the first phase, which raises the question of the wisdom of splitting a limited number of epochs into pre-calculations of independent populations. Experiments conducted using only one population in the first phase show significantly worse results, which confirms the usefulness of pre-collecting information about the surrounding search space. This allows the algorithm to more effectively use leading individuals - the most successful solutions in the second phase of the search.

      Moreover, the algorithm has great potential for further research. I believe that its capabilities have not yet been fully realized and more experimentation and analysis are needed to understand how to best utilize its algorithmic benefits.

      Tab

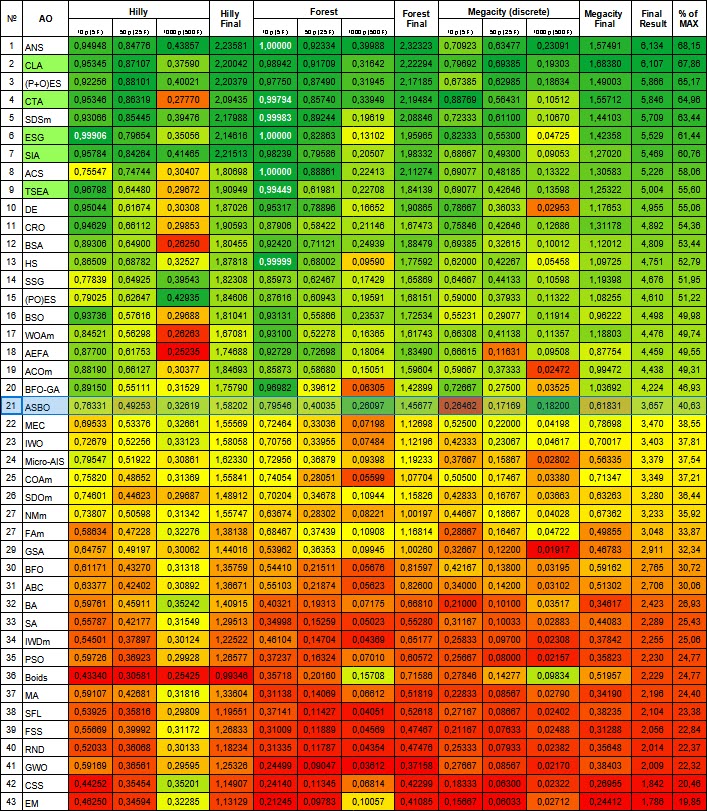
      Figure 2. Color gradation of algorithms according to relevant tests Results greater than or equal to 0.99 are highlighted in white. The names highlighted in green are my own algorithms

      chart

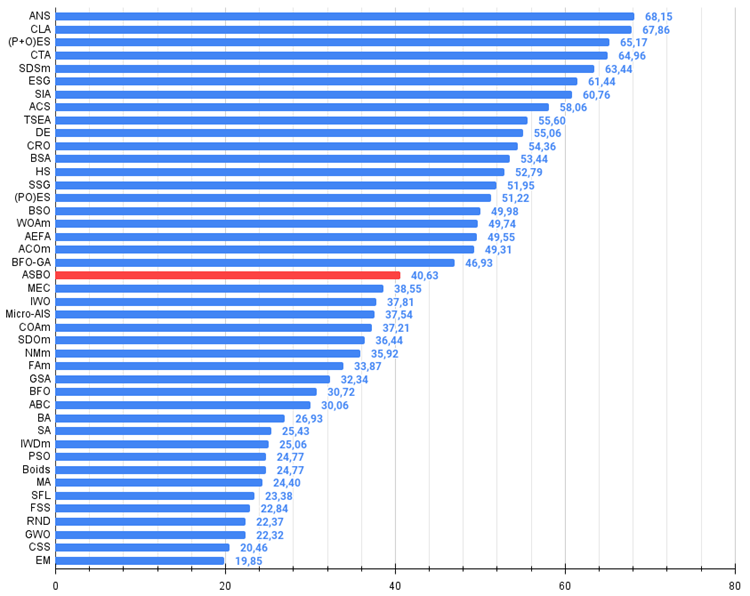
      Figure 3. The histogram of algorithm test results (on a scale from 0 to 100, the more the better,

      where 100 is the maximum possible theoretical result, the archive features a script for calculating the rating table)


      ASBO algorithm pros and cons:

      Advantages:

      1. A small number of external parameters.
      2. Good results on complex high-dimensional problems.

      Disadvantages:

      1. Low convergence on low-dimensional problems.

      The article is accompanied by an archive with the current versions of the algorithm codes. The author of the article is not responsible for the absolute accuracy in the description of canonical algorithms. Changes have been made to many of them to improve search capabilities. The conclusions and judgments presented in the articles are based on the results of the experiments.


      Summing up the interim results of the work done

      During our research, we considered more than forty optimization algorithms, each of which represents a unique approach to solving complex problems. This process was not only fun, but also extremely educational, revealing the richness and diversity of methods in the field of optimization.

      Recreation and modification of algorithms. For the vast majority of the algorithms considered, there was no widely available source code. This prompted me to take a creative approach: the code was recreated solely based on the text descriptions of the authors, taken from various publications. This approach not only allowed us to better understand the principles of operation of each algorithm, but also made it possible to adapt them to our specific needs.
      The few algorithms that were open source were not applicable to solving optimization problems in general. This required significant modification to make them general-purpose and easily applicable to a wide range of tasks.

      Innovations and improvements. Some algorithms, such as ACO (ant colony algorithms for solving problems on graphs), were not originally intended by their authors to work with problems in continuous space and required modification to expand their scope of application. Other algorithms have had improvements made to their search strategy, increasing their efficiency. These modified versions were given the "m" postfix in their names, reflecting their evolution. In addition, we looked in detail at many different methods for handling populations, generating new solutions, and selection methods.

      As a demonstration of new ideas and approaches to optimization, more than five of my new proprietary algorithms were developed and exclusively presented in articles.

      Application and further study. Any of the presented algorithms can be applied to solve optimization problems without the need for additional revision or modification. This makes them accessible and convenient for a wide range of researchers and practitioners.

      For those who seek to achieve the best results in specific individual tasks, comparative tables and histograms are provided to allow studying the individual properties of each algorithm. This opens up opportunities for finer tuning and optimization to meet specific requirements.

      Both approaches – the use of ready-made algorithms, as well as their deep study and adaptation – are viable. Understanding the subtleties and techniques in the search strategies of different algorithms opens up new horizons for researchers to achieve outstanding results.

      I sincerely wish all readers success in finding the best solutions and achieving their goals. May your journey in the world of optimization and algorithmic trading be exciting and successful!


      Translated from Russian by MetaQuotes Ltd.
      Original article: https://www.mql5.com/ru/articles/15329

      Attached files |
      Download ZIP
      ASBO.zip (27.6 KB)
      Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

      Other articles by this author

      Go to discussion
      Implementing the SHA-256 Cryptographic Algorithm from Scratch in MQL5 Implementing the SHA-256 Cryptographic Algorithm from Scratch in MQL5
      Building DLL-free cryptocurrency exchange integrations has long been a challenge, but this solution provides a complete framework for direct market connectivity.
      The Liquidity Grab Trading Strategy The Liquidity Grab Trading Strategy
      The liquidity grab trading strategy is a key component of Smart Money Concepts (SMC), which seeks to identify and exploit the actions of institutional players in the market. It involves targeting areas of high liquidity, such as support or resistance zones, where large orders can trigger price movements before the market resumes its trend. This article explains the concept of liquidity grab in detail and outlines the development process of the liquidity grab trading strategy Expert Advisor in MQL5.
      Introduction to MQL5 (Part 11): A Beginner's Guide to Working with Built-in Indicators in MQL5 (II) Introduction to MQL5 (Part 11): A Beginner's Guide to Working with Built-in Indicators in MQL5 (II)
      Discover how to develop an Expert Advisor (EA) in MQL5 using multiple indicators like RSI, MA, and Stochastic Oscillator to detect hidden bullish and bearish divergences. Learn to implement effective risk management and automate trades with detailed examples and fully commented source code for educational purposes!
      Neural Networks in Trading: Spatio-Temporal Neural Network (STNN) Neural Networks in Trading: Spatio-Temporal Neural Network (STNN)
      In this article we will talk about using space-time transformations to effectively predict upcoming price movement. To improve the numerical prediction accuracy in STNN, a continuous attention mechanism is proposed that allows the model to better consider important aspects of the data.