知っておくべきMQL5ウィザードのテクニック（第45回）：モンテカルロ法による強化学習

はじめに

本記事では、強化学習のさらなる考察として、モンテカルロ法を取り上げます。このアルゴリズムは、Q学習やSARSAと非常に類似しており、実際には オンポリシーおよびオフポリシーの両方で使用できるため、これらを包含する手法であるとも考えられます。しかし、モンテカルロの最大の特徴はエピソードを重視する点にあります。これは、以前の記事で紹介した強化学習サイクルの更新をバッチ処理する方法であり、QマップのQ値の更新頻度を抑える役割を果たします。

モンテカルロアルゴリズムでは、Q値の更新はエピソードが完了した後にのみ実行されます。エピソードとは、一連の学習サイクルをまとめたものです。本記事では、このエピソード内のサイクル数をm_episodes_sizeという入力パラメータとして定義しており、最適化や調整が可能になっています。モンテカルロ法は、市場の変動に対して非常に堅牢であるとされ、幅広い市場シナリオをシミュレートできる特性を持ちます。これにより、トレーダーは異なる市場環境における戦略のパフォーマンスを評価し、リスクとリターンのトレードオフをより深く理解することができます。

この優位性は、「長期的なパフォーマンス評価」に重点を置く点にあります。従来の手法は短期的な結果に着目することが多いですが、モンテカルロ法では、エピソードごとにしか更新がおこなわれないため、市場ノイズの影響を回避しやすくなります。 一方で、Q学習やSARSAはより頻繁に更新をおこなうため、市場ノイズの影響を受けやすい傾向があります。そのため、モンテカルロ法は 累積報酬を評価しながらトレード戦略の長期的なパフォーマンスを分析することを目的としています。複数のエピソードを分析することで、トレーダーは戦略の全体的な収益性や持続可能性について貴重な洞察を得ることができます。

モンテカルロアルゴリズムでは、単一のエピソード内の複数のサイクルを通じて、状態と行動のペアごとの平均リターンを算出し、行動価値（Q値）を推定します。これにより、トレーダーは過去のパフォーマンスを基に、どの行動（例：買い注文や売り注文）が最も好ましい結果をもたらす可能性が高いかを評価できるようになります。Q値の更新は、各Q値の報酬コンポーネントが次のように決定されることに基づいておこなわれます。

ここで

• R t+1 、R t+2 、…、RTは、時刻t以降の各ステップで受け取る報酬です。
• γ（ガンマ）は割引係数(0 ≤ γ ≤ 1)であり、将来の報酬をどれだけ「割引」する（つまり、即時の報酬よりも低い価値として評価する割合を決める）かを設定します。
• Tは、エピソードが終了する時間ステップ（エピソードサイズ、もしくは終了状態）を表します。

上記のQ値の更新によって考慮される包括的な報酬設計は、すでに述べたように、モンテカルロ法をより適応性の高いアルゴリズムにする傾向があります。この適応性の高さにより、トレーダーは市場の変化に応じて柔軟に戦略を調整できるのです。この特性は、金融市場において特に重要です。なぜなら、市場のトレンドは急速に変化するため、過去のパフォーマンスが必ずしも将来の結果を正確に予測するとは限らないからです。前回の記事ではSARSAを取り上げ、強化学習を単なる補助的な機械学習手法ではなく、価格変動を予測する独立したモデルとして機能させる方法について解説しました。通常、強化学習は教師あり学習・教師なし学習に加え、機械学習の「第3の訓練方法」として考えられますが、SARSAをEAに直接実装し、価格予測をおこなうモデルとして活用しました。本記事でも同様のアプローチを取ります。

したがって、モンテカルロ法において適応可能な戦略は、Qマップと状態の選択によって大きく左右されます。前回の記事では、強化学習アルゴリズム自体がEAの主要な予測モデルであったため、カスタムシグナルクラスを介して、短期的な時間軸と長期的な時間軸を横断する3つの環境状態を使用し、それらを組み合わせて9つのオプションを持つグリッド（行列）を作成しました。この3つの環境状態とは、単に強気・横ばい・弱気を捉えたものであり、比較的単純かつ粗い設計です。しかし、このモデルは、全体の次元を拡張するだけでなく、考慮すべき要素を増やすことで、市場に対してより敏感かつ精巧なものへと進化させる可能性を秘めています。これをモンテカルロ法と組み合わせることで、適応性の向上が期待できます。

取引における強化学習(RL)の概要

強化学習(RL)は、金融市場のような動的な環境で動作するように設計されており、エージェントがその「環境」と継続的に相互作用しながら学習を進める仕組みです。エージェントは、現在の状態（市場価格やテクニカル指標などによって定義）をもとに、「買い」「売り」「保有」といった行動をとります。これにより環境の状態が変化し、新たな観察と報酬がもたらされます。

トレーダーがQマップに組み込むことができる状態セットの例として、テクニカル指標ベースの状態が挙げられます。例えば、移動平均を活用する方法があります。短期MAが長期MAより大きい場合は強気状態、短期MAが長期MAより小さい場合は弱気状態、等しければ中立状態を意味します。

このように短期と長期の見通しを1つの軸に統合すると、別の軸を追加することで、移動平均以外の異なる指標を活用できるようになります。例えば、相対力指数(RSI)を考慮することも可能です。RSI > 70は買われすぎの状態であり、売りシグナルとなる可能性があります。一方、RSI < 30は売られすぎの状態を示し、買いシグナルとなる可能性があります。RSIが30以上70以下の範囲にある場合は、中立状態とみなされ、特にシグナルを発しない状態となります。

また、同じく指標ベースの状態として、ボリンジャーバンドを用いることも考えられます。価格が上限バンド付近またはそれを超えた場合は弱気状態と解釈され、反対に下限バンド付近またはそれを下回る場合は強気状態とされます。その他の価格位置については、中立状態が示唆されます。

テクニカル指標を用いた状態分類に加え、市場のボラティリティもまた環境状態の別の軸として取り入れることが可能です。ボラティリティの測定には、価格の標準偏差やATRなどが使用され、高ボラティリティ、低ボラティリティ、中程度のボラティリティといった異なる状態を設定できます。さらに細かく段階を設けることで、アルゴリズムが市場の変動により適応しやすくなります。これにより、エージェントは市場の状況に応じて、積極的な取引をおこなうか慎重な取引をおこなうかを決定するための指針を得ることができます。 さらに、株式市場においては取引量を考慮することもできます。

ボラティリティと同様に、取引量の変化も市場の動向を示唆するため、細かい段階を設定することで、戦略の精度を向上させることが可能となります。これまでの記事で扱ってきた価格行動における強気・弱気のトレンドに加えて、本記事でも状態として考慮していますが、さらに具体的な価格行動パターンとして、サポートやレジスタンスのブレイクアウトなどを取り入れることもできます。あるいは、強気と弱気の両方のシグナルに対して三尊天井（ヘッドアンドショルダー）パターンが使用され、その他のパターンはウィップソーとなる可能性があります。 最近の価格変動におけるこのようなパターンを認識することで、エージェントは継続または反転を予測できるようになります。

Qマップ状態の別の可能な軸は、時間ベースの状態です。この軸は、前述のプライスアクションやテクニカル指標などの別の軸と組み合わせることで、各時間帯においてどの価格アクションがより信頼できるかを推論できるようになります。考えられる時間ベースの状態としては、市場のオープン/クローズ、取引セッション、さらには曜日ごとのパターンなどが挙げられます。 また、センチメント（市場心理）に基づく状態も、環境状態の行列を形成する別の軸となり得ます。こうした市場センチメントの測定は、利用可能なさまざまな指標があることを踏まえると、経済ニュースカレンダーにおける特定の指標の数値に依存することになります。これらの状態の段階（グラデーション）は、ポジティブ・ニュートラル・ネガティブの範囲で設定し、より細かい分析をおこないたい場合には中間状態（サブカテゴリ）を追加することも可能です。 特にこれらの手法を活用してセンチメント状態を組み込むことで、市場に影響を与える外部要因に対してエージェントが適応的に対応する能力を向上させることができます。

これと類似し、代替となるものとして経済イベントベースの状態が挙げられます。しかし、これら2つとは異なるアプローチとして、ポートフォリオベースの状態も検討に値します。このカテゴリは外国為替市場以外の分野にも広く適用可能であり、いくつかの潜在的な軸を提供します。まず最初に考えられるのはエクスポージャーレベルです。これは、ポートフォリオが株式と債券の相対的なエクスポージャーに基づいて評価されるものです。グラデーションの範囲としては、一方の極が90-10、もう一方の極が10-90といった具合になります。このような軸は時間軸や他の関連する指標と組み合わせることが可能であり、ポートフォリオのパフォーマンス（エージェントの報酬に直結する要素）がQ値の更新プロセスを適切にガイドすることができます。

ポートフォリオベースの状態のもう一つの選択肢は、リスクレベルです。ここでは、各投資における資本配分率を考慮し、リスクのグラデーションを設定します。例えば、リスクの低い状態では0.5%未満の少額投資、リスクの高い状態では最大10%の資本配分といった範囲を設定できます。さらに、これを他のポートフォリオ固有の指標と組み合わせることで、データセットを最適化し、どのリスクレベルをいつ採用すべきかを示すQマップを構築することが可能になります。また、ドローダウンに基づく状態を考慮することもできます。総じて、これらのポートフォリオベースの状態を導入することで、エージェントは単なる市場シグナルに依存するのではなく、より広範な金融コンテキストを考慮した意思決定ができるようになります。

マクロトレンド状態についても言及できます。基本的な原則はこれまでのものと似ていますが、重要なのはここで挙げた例が決して網羅的ではないという点です。 環境状態の選択は、戦略を定義する上で極めて重要な役割を果たします。その独自性や、テストだけでなく交差検証にもどれだけ労力を注ぐかによって、トレーダーの優位性が決まると言っても過言ではありません。

環境状態に加えて、各行動後の報酬シグナルは、エージェントに対してその行動が成功したのか、失敗したのかを示すフィードバックを提供します。報酬は、利益/損失（これまで適用してきたように）、リスク調整後のリターン、またはその他の関連するパフォーマンス指標によって定量化されることが可能であり、エージェントがより有利な行動を取るための指針となります。忘れてはならないのは、報酬がQマップのQ値を更新する上で不可欠な要素であるということです。

強化学習は、予測をおこなう際に探索と活用のバランスを取ることでよく知られています。理論上、エージェントは、過去に成功した行動を活用する一方で、より高い報酬を得られる可能性のある新たな行動を探索するという戦略を交互に採用します。この探索と活用のバランスを調整するのが、入力パラメータepsilonであり、これがエージェントの意思決定に大きく影響を与えます。適切なバランスが取れないと、エージェントは局所最適に陥る可能性があり、長期的な学習の妨げとなるため、この調整は非常に重要です。

したがって、試行錯誤を通じて、エージェントは環境内での経験から学習し、行動選択方策を適応的に調整していきます。特にε-グリーディ法では、ある確率でランダムに行動を選択することで探索を促し、過去の成功体験に依存しすぎることを防ぎます。経験を積むごとに、どの行動がより高い報酬につながるかの理解が深まり、将来の類似した状況でより良い選択ができるようになります。

この改善は、エージェントのQマップ値や方策によるものです。Qマップは、状態と行動の対応関係を示す戦略を表し、観測された報酬に基づいて各状態における最適な行動を継続的に更新します。方策の改善は、累積報酬を最大化することを目的とした強化学習アルゴリズムによって導かれます。

ここまでの内容は、過去3回の記事で取り上げたRLの基本的な側面でした。しかし、RLにはまださらなる革新的な概念が存在します。その一例が価値関数推定です。エージェントは、多くの場合、特定の状態または状態・行動の組み合わせから得られる期待リターンを予測するために価値関数を推定します。価値関数を適切に近似することで、各行動の潜在的な長期的利益を評価できるようになり、より合理的な意思決定が可能になります。

時間的クレジット割り当ては、エージェントが過去に取った行動と、将来得られる報酬を結び付ける概念です。このアプローチにより、エージェントは過去の行動が将来の結果にどのように影響を及ぼすのかを理解できるようになり、より適切な計画を立てたり、デフォルトの行動・状態のペアリングを上書きするような特定の方策を事前に設定したりすることが可能になります。

もう一つの重要な概念が適応学習率です。これは以前、多層パーセプトロン(MLP)を扱った記事でも取り上げたテーマですが、Q値の更新時にalphaとして活用することができます。エージェントは、状態-行動値の不確実性に応じて学習率を調整し、不確実性が高い場合にはより積極的に更新し、確信が持てるようになった段階ではより保守的な更新を行うといった適応的な学習が可能になります。この適応性により、エージェントはさまざまな市場環境において効率的に学習することができます。

その他の強化学習に関連する注目すべき概念としては、学習効率を向上させるための状態間の一般化や、短期的な報酬にとらわれず長期的な視点で戦略を構築する長期戦略開発などが挙げられます。

モンテカルロアルゴリズム

モンテカルロ法で採用されている学習アプローチは、これまで検討してきた他のRLアルゴリズムとは異なり、経験の完全なエピソードから学習します。エピソードの終わりまで待ってから「学習」するのですが、その間に受け取った複数の報酬ポイントを通じて全体的なアプローチを取ります。したがって、エピソードが終了した時点で過去のすべての報酬値にアクセスできるよう、報酬値を複数回にわたってバッファリングする必要があります。これをMQL5では、カスタムシグナルクラスのgetOutput関数内で次のように実装します。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CSignalMC::GetOutput(Cql *QL, vector &Rewards)
{  vector _in, _in_row, _in_row_old, _in_col, _in_col_old;
   if
   (
      _in_row.Init(m_scale) &&
      _in_row.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_row.Size() == m_scale
      &&
      _in_row_old.Init(m_scale) &&
      _in_row_old.CopyRates(m_symbol.Name(), m_period, 8, 1, m_scale) &&
      _in_row_old.Size() == m_scale
      &&
      _in_col.Init(m_scale) &&
      _in_col.CopyRates(m_symbol.Name(), m_period, 8, 0, m_scale) &&
      _in_col.Size() == m_scale
      &&
      _in_col_old.Init(m_scale) &&
      _in_col_old.CopyRates(m_symbol.Name(), m_period, 8, m_scale, m_scale) &&
      _in_col_old.Size() == m_scale
   )
   {  _in_row -= _in_row_old;
      _in_col -= _in_col_old;
      vector _in_e;
      _in_e.Init(m_scale);
      QL.Environment(_in_row, _in_col, _in_e);
      int _row = 0, _col = 0;
      QL.SetMarkov(int(_in_e[m_scale - 1]), _row, _col);
      double _reward_float = _in_row[m_scale - 1];
      double _reward_max = _in_row.Max();
      double _reward_min = _in_row.Min();
      for(int i = m_episode_cycles - 1; i > 0; i--)
      {  Rewards[i] = Rewards[i - 1];
      }
      Rewards[0] = QL.GetReward(_reward_max, _reward_min, _reward_float);
      QL.transition_act = 1;
      if(Rewards[m_episode_cycles - 1] != -1.0)
      {  double _reward = Rewards[m_episode_cycles - 1];
         for(int i = m_episode_cycles - 2; i >= 0; i--)
         {  _reward += pow(QL.THIS.gamma, m_episode_cycles - 1 - i) * Rewards[i];
         }
         if(m_policy)
         {  QL.SetOnPolicy(_reward, _in_e);
         }
         else if(!m_policy)
         {  QL.SetOffPolicy(_reward, _in_e);
         }
      }
   }
}

対照的に、Q学習では、後続の状態行動値からブートストラップを使用して、各行動（または各サイクル）の後に値の推定値を更新する時間差分(TD学習方法を使用します。これはSARSAに似ていますが、ここでは値の更新が次の状態でおこなわれる行動を使っておこなわれ、方策に基づく学習アプローチを提供します。

モンテカルロの更新メカニズムは、エピソード内で複数のサイクルにわたって状態から行動を実行した後に観察される平均リターンに基づいています。各状態と行動のペアは、エピソードが完了した後にのみ更新され、真の長期的なリターンを反映します。したがって、この更新で使用される報酬値は、先ほど共有した式に加えて、上記のMQL5コードに示されている加重合計となります。

しかし、Q学習では、次の状態（オフポリシー）からの最大の将来報酬を使用して現在の状態の行動値を更新します。これにより、エピソード内の各サイクルステップで可能な限り最良の結果を考慮することができ、より積極的な学習が可能になります。同様に、SARSAは、次の状態（オンポリシー）で実行される実際の行動に基づいて値を更新し、エージェントの現在の方策を学習プロセスに統合します。これにより、Q学習よりもわずかに保守的な更新が可能になりますが、モンテカルロよりも積極的な更新になります。

モンテカルロは、原則としてエピソード内の複数のサイクルを通じて環境を完全に探索し、最適な行動を学習します。これにより、更新を行う前に状態と行動のペアを徹底的にサンプリングすることが可能になります。これは、Q学習の導入記事で紹介したεグリーディーアプローチに基づいており、更新はエージェントが実行しない行動に影響を受けます。

SARSAも探索と活用のバランスを取るアプローチにおいてはε貪欲ですが、次の状態で実際に実行される行動に基づいて値を更新するため、エージェントの現在の方策と探索の選択に対する応答性が向上します。モンテカルロとこれら二つとの違いは、エピソードで更新が1回のみおこなわれることに加えて、オンポリシーまたはオフポリシーのどちらでも実行できる点です。このため、モンテカルロ用のカスタムシグナルクラスにはブール値の入力パラメータm_on_policyがあり、その名前が示す通り、オンポリシー状態かオフポリシー状態で使用されるかを指示します。

このカスタムシグナルクラスのクラスインターフェイスを以下に示します。

//+------------------------------------------------------------------+
//| MCs CSignalMC.                                                   |
//| Purpose: MonteCarlo for Reinforcement-Learning.                  |
//|            Derives from class CExpertSignal.                     |
//+------------------------------------------------------------------+
class CSignalMC   : public CExpertSignal
{
protected:

   int                           m_actions;           // LetMarkov possible actions
   int                           m_environments;      // Environments, per matrix axis
   int                           m_scale;             // Environments, row-to-col scale
   bool                          m_use_markov;        // Use Markov
   double                        m_epsilon;           // Epsilon
   bool                          m_policy;            // On Policy
   int                           m_episode_cycles;    // Episode Size

public:
   void                          CSignalMC(void);
   void                          ~CSignalMC(void);

   //--- methods of setting adjustable parameters
   void                          QL_Scale(int value)
   {  m_scale = value;
   }
   void                          QL_Markov(bool value)
   {  m_use_markov = value;
   }
   void                          QL_Epsilon(bool value)
   {  m_epsilon = value;
   }
   void                          QL_Policy(bool value)
   {  m_policy = value;
   }
   void                          QL_EpisodeCycles(int value)
   {  m_episode_cycles = value;
   }

   //--- method of verification of arch
   virtual bool      ValidationSettings(void);
   //--- method of creating the indicator and timeseries
   virtual bool      InitIndicators(CIndicators *indicators);
   //--- methods of checking if the market models are formed
   virtual int       LongCondition(void);
   virtual int       ShortCondition(void);

protected:
   void              GetOutput(Cql *QL, vector &Rewards);
   Sql               RL;
   Cql               *QL_BUY, *QL_SELL;
   vector            REWARDS_BUY, REWARDS_SELL;
};

モンテカルロ法の収束は、更新に完全なエピソードを必要とするため遅くなる傾向があります。特にエピソードが長い環境や報酬がまばらな環境では、必ずしも効率的とは言えません。これは、ブートストラップ方式によってほとんどの場合速く収束するQ学習アルゴリズムとは対照的ですが、非定常報酬や高分散の環境では振動や発散を引き起こす可能性があり、不安定になることがあります。SARSAは、更新時にエージェントの実際の方策を考慮するため、よりスムーズな学習曲線をもたらす傾向があり、特定の状況ではQ学習よりも安定していると言われています。

サンプリング効率について言えば、モンテカルロ法は更新を得るために完全なエピソードを必要とするため、通常はサンプル効率が低くなります。状態行動空間が広い環境では、この点が大きな欠点となる可能性があります。一方、Q学習は各ステップで値を更新するためサンプル効率が高く、即時のフィードバックに基づいて迅速に変更を加えることができます。実際、SARSAは現在の方策と探索戦略に敏感であるため、Q学習よりも多くのサンプルを必要とする可能性があり、そのためQ学習の方が効率的と言えます。

モンテカルロ法は、エピソードを明確に定義でき、取引シミュレーションなど、長期的なリターンが短期的な急上昇よりも重要な環境に適しています。これは、バリューまたは長期的な「トレーダー」にとって重要な戦略として位置づけられます。Q学習は、明確な報酬構造と状態遷移が定義された環境で効果的で、デイトレードなどのタスクに最適です。一方、SARSAは、スイングトレードのように適応性が重要な動的または部分的に観測可能な環境において、エージェントの方策を厳密に反映する必要がある状況で有益です。

カスタムシグナルクラスでのモンテカルロの実装

ルートモデルおよび信号生成器としてモンテカルロRLを使用するカスタム信号を実装します。これを実現するための主な手順は、クラスインターフェイスと出力取得関数ですでに上で説明されています。以下は、売買条件関数です。

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalMC::LongCondition(void)
{  int result = 0;
   GetOutput(QL_BUY, REWARDS_BUY);
   if(QL_BUY.transition_act == 0)
   {  result = 100;
   }
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalMC::ShortCondition(void)
{  int result = 0;
   GetOutput(QL_SELL, REWARDS_SELL);
   if(QL_SELL.transition_act == 2)
   {  result = 100;//printf(__FUNCSIG__);
   }
   return(result);
}

この実装の完全なソースコードは下部に添付されています。ウィザードでEAを組み立てるためにこのソースコードを使用するためのガイドは、こちらとこちらにあります。マルコフ決定プロセスはQマップの使用に固有のものですが、Q値の更新時にマルコフ重み付けを使用するオプションを提供する入力パラメータがあります。さらに、方策を使用するかどうか、探索と活用のバランスを決定するεのサイズ、およびエピソード内でのサイクル数を最適化できます。これらの最適化を2022年のGBP/USDペアを対象に1時間足で実施した結果は以下の通りです。

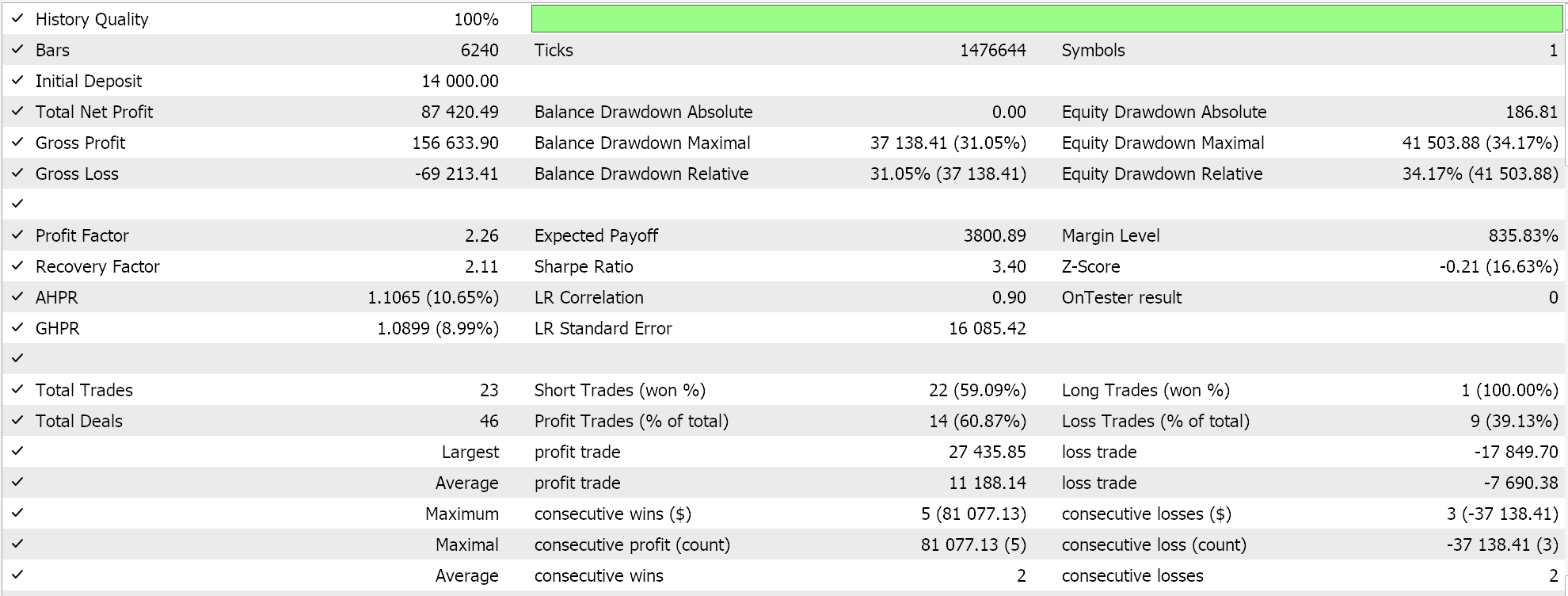
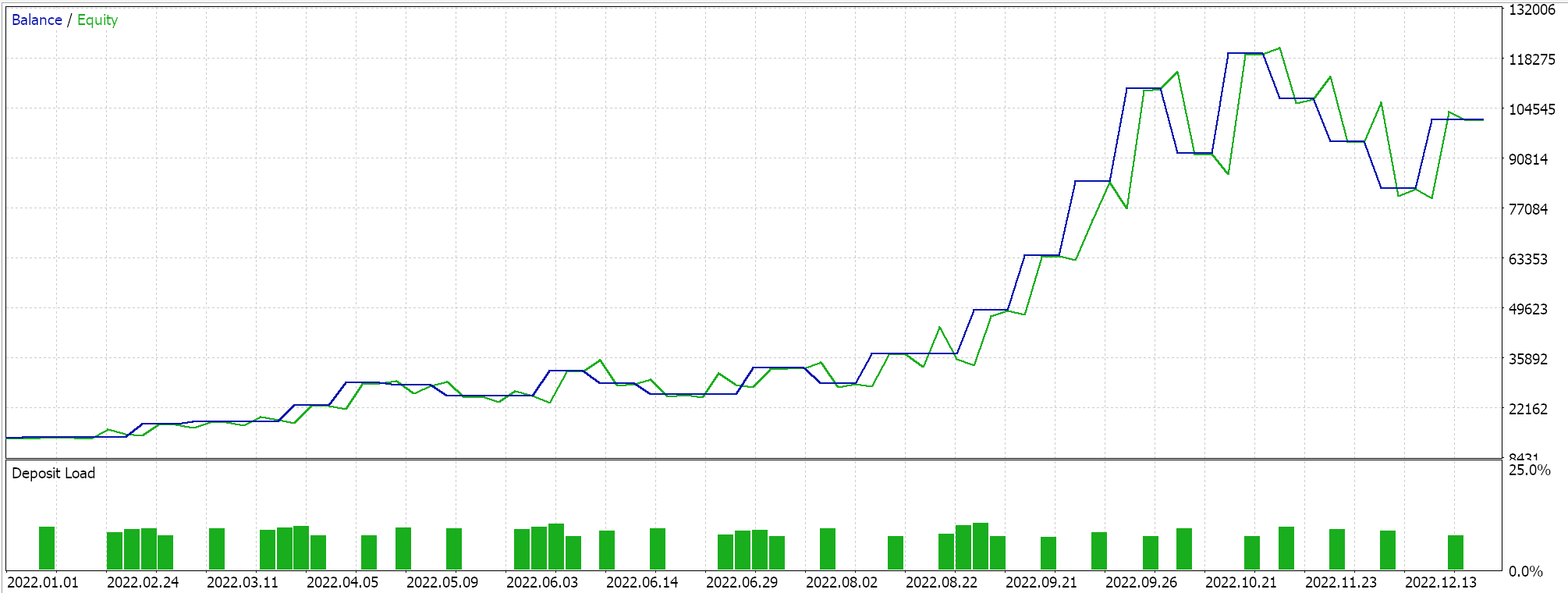
結論と追加の検討事項

要約すると、強化学習のモンテカルロアルゴリズムについて説明しました。このアルゴリズムは、以前の記事でそれぞれ取り上げたQ学習とSARSAという二つのアルゴリズム（こちらとこちらの記事を参照）から多くの特徴を取り入れており、環境の長期的な特性や属性に焦点を当てつつ、より動的で適応性の高い学習方法を提供します。この記事に記載された代替案で強調されているように、カスタマイズされた環境行列の使用に加えて、3つ以上の選択肢を持つ代替行動スケールを活用することもできます。

モンテカルロ(MC)を実装する際には、言及すべき追加の考慮事項がいくつかあります。MCは、更新報酬値の計算方法において、バイアスと分散のトレードオフをうまく調整します。エピソード内でサイクル数が少ない場合、バイアスが高く分散が低くなる傾向があり、サイクル数が多い長いエピソードではその逆が見られます。したがって、目的に応じて、Qマップを開発する際にはこれを考慮する必要があります。バイアスが高いとモデルが短期的な行動に適応しやすくなる一方、分散が高い場合は、アルゴリズムが長期的な特性や属性を捉えるという意図により合致するためです。

複数のnステップリターンを使用して異なる時点から複数の報酬を得ることで、状態行動空間のより詳細な探索が可能になります。可能なリターンの範囲を変化させることで（カスタムシグナルクラスの入力パラメータm_episode_cyclesで制御）、取引戦略のシグナル強度を微調整できます。この細かさが、エントリーポイントとエグジットポイントを決定する際により微妙な判断を可能にし、両方を最適化するとともに、信号のタイミングや強度の調整を可能にします。